Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3024 2013 Høst

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler

Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger:
Kilder for bilder, tegninger osv.

Alle grafer og figurer: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4D9R

Deriver funksjonene

a)

$f (x) = 5 x \cos x$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

$f (x)$ er produktet av de to funksjonene $5 x$ og $\cos x$ som vi vet hvordan vi skal derivere hver for seg. Derfor bør vi bruke produktregelen for derivasjon.

Produktregelen for derivasjon sier at hvis $u (x)$ og $v (x)$ er deriverbare funksjoner så må $(u v)' = u' v + u v'$ . Ved å sette $u (x) = 5 x$ og $v (x) = \cos x$ og bruke at $u' (x) = (5 x)' = 5$ og $v' (x) = (\cos x)' = - \sin x$ finner vi altså $\begin{matrix} f' (x) & = (5 x \cos x)' = (5 x)' (\cos x) + (5 x) (\cos x)' \\ = (5) (\cos x) + (5 x) (- \sin x) = 5 \cos x - 5 x \sin x . \end{matrix}$

Svar:

$\begin{matrix} f' (x) = 5 \cos x - 5 x \sin x . \end{matrix}$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

Visste du at

Produktregelen for derivasjon kan brukes til å lage en derivasjonsregel for å derivere funksjoner som er et produkt av $n$ funksjoner. Hvis $u_{1}$ , $u_{2}$ ,..., $u_{n}$ er deriverbare funksjoner og $\begin{matrix} f (x) = u_{1} u_{2} u_{3} . . . u_{n} \end{matrix}$ følger det at $\begin{matrix} f' (x) = u'_{1} u_{2} u_{3} . . . u_{n} + u_{1} u'_{2} u_{3} . . . u_{n} + u_{1} u_{2} u'_{3} . . . u_{n} + . . . + u_{1} u_{2} u_{3} . . . u'_{n} . \end{matrix}$ Dette kan vi for eksempel bruke til å vise at $(x^{n})' = n x^{n - 1}$ . Ved å sette $u_{1} = x$ , $u_{2} = x$ , $. . .$ , $u_{n} = x$ finner vi nemlig $\begin{matrix} f' (x) = \underset{n g a n g e r}{\underset{︸}{x^{n - 1} + x^{n - 1} + x^{n - 1} + . . . + x^{n - 1}}} = n x^{n - 1} . \end{matrix}$

b)

$g (x) = \frac{\sin (2 x)}{x}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Funksjonen $g (x)$ er et produkt av funksjonene $\sin 2 x$ og $\frac{1}{x}$ , som vi klarer å derivere. Derfor bruker vi produktregelen for derivasjon.

Produktregelen sier at hvis $u (x)$ og $v (x)$ er deriverbare funksjoner så må $(u v)' = u' v + u v'$ . Ved å sette $u (x) = \sin 2 x$ og $v (x) = \frac{1}{x}$ kan vi altså skrive $\begin{matrix} g' (x) = (\frac{\sin 2 x}{x})' = (\sin 2 x)' \frac{1}{x} + \sin 2 x (\frac{1}{x})' . \end{matrix}$ Fra regelen $(x^{n}) = n x^{n - 1}$ følger det at $\begin{matrix} (\frac{1}{x})' = (x^{- 1})' (- 1) x^{- 1 - 1} = - x^{- 2} = \frac{- 1}{x^{2}} . \end{matrix}$ Kjerneregelen for derivasjon sier at $(f (u (x)))' = u' (x) f' (u (x))$ . Det betyr at hvis vi setter $u (x) = 2 x$ så

må $(\sin 2 x) \begin{matrix} ' = (2 x)' \cdot \cos 2 x = = 2 \cos 2 x . \end{matrix}$

Altså har vi funnet at

$\begin{matrix} g' (x) & = (\sin 2 x)' \frac{1}{x} + \sin 2 x (\frac{1}{x})' \\ = 2 \cos 2 x \frac{1}{x} + \sin 2 x (\frac{- 1}{x^{2}}) \\ = \frac{2 x \cos 2 x}{x^{2}} - \frac{\sin 2 x}{x^{2}} \\ = \frac{2 x \cos 2 x - \sin 2 x}{x^{2}} . \end{matrix}$

Alternativ løsning

Brøkregelen for derivasjon sier at for to deriverbare funksjoner $v (x)$ og $u (x)$ er $\begin{matrix} (\frac{u}{v})' = \frac{u' v - u v'}{v^{2}} . \end{matrix}$ Ved å sette $u = \sin 2 x$ og $v = x$ følger det da, siden $u' (x) = 2 \cos 2 x$ og $v' = 1$ , at $\begin{matrix} g' (x) & = (\frac{\sin 2 x}{x})' = \frac{(\sin 2 x)' x - \sin 2 x (x)'}{x^{2}} \\ = \frac{(2 \cos 2 x) x - \sin 2 x (1)}{x^{2}} = \frac{2 x \cos 2 x - \sin 2 x}{x^{2}} . \end{matrix}$

Svar

$\begin{matrix} g' (x) = \frac{2 x \cos 2 x - \sin 2 x}{x^{2}} . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Deriverbarhet

Vi sier at en funksjon $f (x)$ er deriverbar i et punkt $a$ , hvis følgende grense finnes:

$f' (a) = \lim_{h \to 0} \frac{f (a + h) - f (a)}{h}$

Med "finnes" mener vi at den ikke er uendelig og blir det samme uavhengig av om h går mot null ovenfra eller nedenfra.

deriverbarhet

For flere forklaringer og eksempler på derivasjon, se artikkelen Å derivere sammensatte uttrykk.

Visste du at

Brøkregelen for derivasjon er faktisk bare en blanding av produktregelen og kjerneregelen. Vi kan nemlig skrive $\begin{matrix} \frac{u (x)}{v (x)} = u (x) \cdot \frac{1}{v (x)} = u (x) \cdot h (v (x)) \end{matrix}$ der $h (x) = \frac{1}{x}$ . Ifølge produktregelen er da $\begin{matrix} (\frac{u (x)}{v (x)})' = u' (x) \cdot h (v (x)) + u (x) \cdot (h (v (x)))' \end{matrix}$ og ifølge kjerneregelen kan dette skrives

$\begin{matrix} u' (x) \cdot h (v (x)) + u (x) \cdot (h (v (x)))' = u' (x) \cdot h (v (x)) + u (x) \cdot v' (x) h' (v (x)) . \end{matrix}$

Siden $h' (v (x)) = - \frac{1}{{(v (x))}^{2}}$ følger det at $\begin{matrix} (\frac{u}{v})' = u' \cdot \frac{1}{v} - u \cdot \frac{v'}{v^{2}} = \frac{u' v - u v'}{v^{2}}, \end{matrix}$ som er brøkregelen for derivasjon.

Oppgave 2 (3 poeng) Nettkode: E-4D9U

Bestem integralene

a)

$\int_{0}^{1} 2 e^{2 x} dx$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Dersom vi finner en funksjon $f (x)$ som tilfredsstiller $f' (x) = 2 e^{2 x}$ er løsningen gitt av $f (1) - f (0)$ .

Substitusjonsmetoden for integrasjon sier at $\begin{matrix} \int_{a}^{b} f (u (x)) u' (x) d x = \int_{u (a)}^{u (b)} f (u) d u . \end{matrix}$ Ved å sette $u (x) = 2 x$ og observere at $u' (x) = 2$ finner vi $\begin{matrix} \int_{0}^{1} 2 e^{2 x} d x = \int_{0}^{1} u' (x) e^{u (x)} d x = \int_{2 \cdot 0}^{2 \cdot 1} e^{u} d u = \int_{0}^{2} e^{u} d u \end{matrix}$ og siden $e^{x}$ er sin egen deriverte må $\begin{matrix} \int_{0}^{2} e^{u} d u = {[e^{u}]}_{0}^{2} = e^{2} - e^{0} = e^{2} - 1 . \end{matrix}$ Altså har vi funnet at $\begin{matrix} \int_{0}^{1} 2 e^{2 x} d x = e^{2} - 1 . \end{matrix}$

Alternativ løsning

Siden den deriverte av $e^{2 x}$ er $2 e^{2 x}$ må $\begin{matrix} \int_{0}^{1} 2 e^{2 x} d x = {[e^{2 x}]}_{0}^{1} = e^{2} - 1 . \end{matrix}$

Svar:

$\begin{matrix} \int_{0}^{1} 2 e^{2 x} d x = e^{2} - 1 . \end{matrix}$

Mer om

Denne oppgaven er om

Integralregning

Integralregning er forbundet med arealbegrepet. Et areal kan uttrykkes ved et bestemt integral, og det kan beregnes ved integrasjon. Integralet fra a til b av funksjonen f kan tolkes som arealet av det området som begrenses av funksjonens graf, x-aksen og de vertikale linjene x=a og x=b.

integralregning

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.

b)

$\int_{}^{} 2 x \cdot e^{x} dx$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne integralet av produktet av de to funksjonene $2 x$ og $e^{x}$ . Siden $e^{x}$ er sin egen integrerte og $2 x$ blir lettere når den deriveres bør vi bruke regelen for delvis integrasjon.

Regelen for delvis integrasjon sier at $\begin{matrix} \int u' v d x = u v - \int u v' d x . \end{matrix}$ Det betyr at hvis vi setter $u' (x) = e^{x}$ og $v (x) = 2 x$ og ser at $u (x) = e^{x}$ og $v' (x) = 2$ så må $\begin{matrix} \int 2 x e^{x} = u v + C_{1} - \int u v' d x = 2 x e^{x} + C_{1} - \int 2 e^{x} d x \end{matrix}$ der $C_{1}$ er en integrasjonskonstant. Siden $e^{x}$ er sin egen deriverte følger det videre at $\begin{matrix} \int 2 e^{x} d x = 2 e^{x} + C_{2} \end{matrix}$ der $C_{2}$ er integrasjonskonstanten. Det betyr at $\begin{matrix} \int 2 x e^{x} = 2 x e^{x} - 2 e^{x} + C = 2 e^{x} (x - 1) + C \end{matrix}$ der vi har valgt $C = C_{1} - C_{2}$ .

Svar:

$\begin{matrix} \int 2 x e^{x} = 2 e^{x} (x - 1) + C . \end{matrix}$

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Delvis integrasjon.

Visste du at

Regelen for delvis integrasjon en bare en annen måte å skrive produktregelen for derivasjon på. Produktregelen for derivasjon sier at $\begin{matrix} (u v)' = u' v + u v' . \end{matrix}$ Ved å integrere begge sider med hensyn på $x$ får vi $\begin{matrix} \int (u v)' d x = \int u' v d x + \int u v' d x \end{matrix}$ og siden integral og derivasjon utjevner hverandre er $\int (u v)' d x = u v$ . Ved å trekke fra $\int u v' d x$ på begge sider sitter vi da igjen med $\begin{matrix} \int u' v d x = u v - \int u v' d x \end{matrix}$ som er regelen for delvis integrasjon.

Oppgave 3 (5 poeng) Nettkode: E-4D9Y

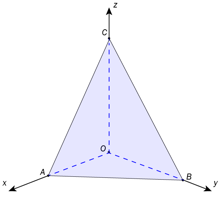
Gitt punktene $A (2, 0, 0)$ , $B (0, 3, 0)$ , $C (0, 0, 4)$ og $O (0, 0, 0)$ .

a)

Bestem $\vec{A B} \cdot \vec{A C}$ og $\vec{A B} \times \vec{A C}$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Ved å bruke koordinatene til punktene $A$ , $B$ og $C$ til å uttrykke vektorene $\vec{A B}$ og $\vec{A C}$ kan vi beregne skalarproduktet $\vec{A B} \cdot \vec{A C}$ og kryssproduktet $\vec{A B} \times \vec{A C}$ .

Vektorene $\vec{A B}$ og $\vec{A C}$ kan uttrykkes ved

$\begin{matrix} \vec{A B} & = \vec{O B} - \vec{O A} = [0, 3, 0] - [2, 0, 0] = [- 2, 3, 0] \\ \vec{A C} & = \vec{O C} - \vec{O A} = [0, 0, 4] - [2, 0, 0] = [- 2, 0, 4] . \end{matrix}$

Da følger det at

$\begin{matrix} \vec{A B} \cdot \vec{A C} = [- 2, 3, 0] \cdot [- 2, 0, 4] = (- 2) (- 2) + 3 \cdot 0 + 0 \cdot 4 = 4 \end{matrix}$

$\vec{A B} \times \vec{A C} = |\begin{matrix} \vec{e_{x}} & \vec{e_{y}} & \vec{e_{z}} \\ - 2 & 3 & 0 \\ - 2 & 0 & 4 \end{matrix}| = |\begin{matrix} 3 & 0 \\ 1 & 4 \end{matrix}| \vec{e_{x}} - |\begin{matrix} - 2 & 0 \\ - 2 & 4 \end{matrix}| \vec{e_{y}} + |\begin{matrix} - 2 & 3 \\ - 2 & 0 \end{matrix}| \vec{e_{z}}$

$= (3 \cdot 4) \vec{e_{x}} - (- 2 \cdot 4) \vec{e_{y}} + (- (- 2) \cdot 3) \vec{e_{z}} = 12 \vec{e_{x}} + 8 \vec{e_{y}} + 6 \vec{e_{z}} = [12, 8, 6] .$

Svar: $\vec{A B} \cdot \vec{A C} = 4 og \vec{A B} \times \vec{A C} = [12, 8, 6] .$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt av to vektorer.

b)

Bestem volumet av tetraederet $A B C O$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne volumet av tetraederet utspent av vektorene $\vec{A O}$ , $\vec{A B}$ og $\vec{A C}$ . Tetraederet utgjør nøyaktig $\frac{1}{6}$ av parallellpipedet utspent av de samme vektorene.

Tetraederet $A B C O$ er utspent av vektorene $\vec{A O}$ , $\vec{A B}$ og $\vec{A C}$ og må derfor ha volum

$V = \frac{1}{6} |\vec{A O} \cdot (\vec{A B} \times \vec{A C})| .$

Fra oppgave $a)$ har vi $\vec{A B} \times \vec{A C} = [12, 8, 6]$ og siden

$\begin{matrix} \vec{A O} = - \vec{O A} = [- 2, 0, 0] \end{matrix}$

må

$V = \frac{1}{6} |\vec{A O} \cdot (\vec{A B} \times \vec{A C})| = \frac{1}{6} |[- 2, 0, 0] \cdot [12, 8, 6]| =$

$= \frac{1}{6} |- 2 \cdot 12 + 0 \cdot 8 + 0 \cdot 6| = \frac{24}{6} = 4$

Alternativ løsning

Arealet av $Δ A O B$ er $\frac{1}{2} \cdot 2 \cdot 3 = 3$ siden $\vec{O A} ⊥ \vec{O B}$ . Videre står $\vec{O C}$ normalt på planet gjennom $Δ A O B$ . Vi kan bruke formelen for volum av pyramide. Volumet av $A B C O$ er

$\frac{1}{3} \cdot (areal av Δ A O B) \cdot |\vec{O C}| = \frac{1}{3} \cdot 3 \cdot 4 = 4 .$

Svar: $V = 4 .$

Mer om

Denne oppgaven er om

Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".

parallell

Tetraeder

Et legeme som begrenses av fire kongruente, likesidede trekanter.

Se Platonske legemer

tetraeder

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

For flere forklaringer og eksempler på geometri, se artikkelen Pyramider og kjegler.

c)

Punktene $A$ , $B$ og $C$ ligger i planet $α$ .

Vis at likningen til planet $α$ kan skrives

$\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

For å beskrive et plan holder det å ha et uttrykk for en vektor som står normalt på alle vektorer mellom punkter i planet, og kjennskap til et punkt som ligger i planet.

Siden $A$ , $B$ og $C$ ligger i $α$ må

$\begin{matrix} \vec{A B} \times \vec{A C} = [12, 8, 6] = 2 [6, 4, 3] \end{matrix}$

stå vinkelrett på alle vektorer mellom punkter i $α$ . Vi er bare interessert i retningen og kan derfor velge normalvektor $\vec{n} = [6, 4, 3]$ . Dersom $P_{0}$ er et punkt i $α$ må alle punkter $P (x, y, z)$ som ligger i $α$ tilfredsstille

$\begin{matrix} \vec{n} \cdot \vec{P_{0} P} = 0 . \end{matrix}$

Ved å velge $P_{0} = A$ kan vi skrive venstresiden av likningen

$\vec{n} \cdot \vec{A P} = \vec{n} \cdot \vec{O P} - \vec{n} \cdot \vec{O A}$

$= [6, 4, 3] \cdot [x, y, z] - [6, 4, 3] \cdot [2, 0, 0]$

$= 6 x + 4 y + 3 z - 6 (6 \cdot 2 + 4 \cdot 0 + 3 \cdot 0) = 6 x + 4 y + 3 z - 12,$

som betyr at likningen for planet $α$ er

$\begin{matrix} 6 x + 4 y + 3 z - 12 = 0 . \end{matrix}$

Ved å multiplisere begge sider av likhetstegnet med $\frac{1}{12}$ kan vi skrive planlikningen $\begin{matrix} \frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1, \end{matrix}$ som er det vi ønsket å vise.

Alternativ løsning

Likningen fremstiller et plan, så det er nok å se at $A$ , $B$ og $C$ ligger i planet. Når vi setter inn koordinatene til $A$ , $B$ og $C$ i venstre side, vil to brøker bli null og siste brøk vil få lik teller og nevner. Verdien blir da lik $1$ , så likheten holder.

Mer om

Denne oppgaven er om

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

planet

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normalvektor

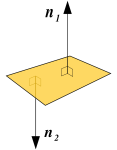
En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

Oppgave 4 (4 poeng) Nettkode: E-4DA2

a)

En rekke er gitt ved

$1 + e^{- 1} + e^{- 2} + e^{- 3} + . . .$

Forklar at dette er en konvergent, geometrisk rekke. Bestem summen av den uendelige rekken.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må vise at rekken $1 + e^{- 1} + e^{- 2} + . . .$ er en geometrisk rekke som konvergerer mot et endelig tall og deretter finne dette tallet.

En geometrisk rekke er en rekke der forholdet mellom hvert ledd og det foregående er konstant. I rekken $1 + e^{- 1} + e^{- 2} + . . .$ er alle ledd på formen $e^{- n}$ . Det betyr at forholdet mellom hvert ledd og det foregående kan skrives $\begin{matrix} \frac{e^{- n}}{e^{- (n - 1)}} = \frac{e^{- n}}{e^{- n} e^{1}} = \frac{1}{e} . \end{matrix}$ Siden dette er en konstant uavhengig av $n$ er rekken en geometrisk rekke. En uendelig geometrisk rekke $a + a k + a k^{2} + . . .$ er konvergent dersom $| k | < 1$ . Dette kan vi se ved først å studere en endelig geometrisk rekke $\begin{matrix} S_{n} = a + a k + a k^{2} + . . . + a k^{n}, \end{matrix}$ og se at $\begin{matrix} k S_{n} = a k + a k^{2} + . . . + a k^{n} + a k^{n + 1} \end{matrix}$ nesten er den samme rekken. Faktisk har vi at $\begin{matrix} S_{n} - k S_{n} = a - a k^{n + 1} = a (1 - k^{n + 1}) . \end{matrix}$ Ved å løse for $S_{n}$ finner vi at den endelige geometriske rekken tar verdien $\begin{matrix} S_{n} = a \frac{1 - k^{n + 1}}{1 - k} . \end{matrix}$ For uendelige geometriske rekker må vi ha $| k | < 1$ for å forsikre oss om at $k^{n + 1}$ går mot $0$ når $n$ går mot uendelig. En konvergent uendelig geometrisk rekke tar altså verdien $\begin{matrix} a + a k + a k^{2} + a k^{3} + . . . = \frac{a}{1 - k} . \end{matrix}$ Dette betyr at rekken $1 + e^{- 1} + e^{- 2} + . . .$ er konvergent siden $| e^{- 1} | \approx 0.35 < 1$ og derfor konvergerer mot $\begin{matrix} \frac{1}{1 - e^{- 1}} = \frac{e}{e - 1} . \end{matrix}$

Svar: Rekken er geometrisk siden forholdet mellom etterfølgende ledd er konstant og konvergerer siden denne konstanten er mindre enn én. Summen er $\begin{matrix} 1 + e^{- 1} + e^{- 2} + . . . = \frac{e}{e - 1} . \end{matrix}$

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Konvergens

Konvergens betyr i matematikk å nærme seg en grense.

Se Konvergent tallfølge

konvergens

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.

b)

En geometrisk rekke er gitt ved

$1 + e^{- x} + e^{- 2 x} + e^{- 3 x} + . . .$

Bestem konvergensområdet og summen av rekken.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne hvilke $x$ -verdier som gjør at rekken $1 + e^{- x} + e^{- 2 x} + . . .$ tar en veldefinert, endelig verdi og bestemme et uttrykk for summen av rekken.

Den uendelige geometriske rekken $1 + e^{- x} + e^{- 2 x} + . . .$ konvergerer for $| e^{- x} | < 1$ . Siden $e^{- x}$ alltid er positiv holder det å kreve $\begin{matrix} e^{- x} < 1 \Rightarrow - x < \ln 1 = 0 \Rightarrow x > 0 . \end{matrix}$ Altså konvergerer rekken for alle strengt positive verdier av $x$ . Den må da konvergere mot $\begin{matrix} \frac{1}{1 - e^{- x}} = \frac{e^{x}}{e^{x} - 1}, \end{matrix}$ siden den er en geometrisk rekke.

Svar: Rekken konvergerer mot $\begin{matrix} \frac{1}{1 - e^{- x}} = \frac{e^{x}}{e^{x} - 1} \end{matrix}$ for alle strengt positive verdier av $x$ .

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Konvergens

Konvergens betyr i matematikk å nærme seg en grense.

Se Konvergent tallfølge

konvergens

For flere forklaringer og eksempler på rekker, se artikkelen Uendelige rekker.

Oppgave 5 (2 poeng) Nettkode: E-4DAD

Antall individer i en populasjon etter $t$ timer kan beskrives av funksjonen $N (t)$ .

Vi antar at

$N' (t) = 4 t + 3$ og $N (0) = 800$

Bestem antall individer i populasjonen etter 10 h.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ønsker å finne en funksjon $N (t)$ som tilfredsstiller $N' (t) = 4 t + 3$ og $N (0) = 800$ . Siden $N (t)$ representerer antall individer i en populasjon etter $t$ timer vil det være nøyaktig $N (10)$ individer i populasjonen etter $10$ timer.

Siden $N (t)$ er en antiderivert til $N^{'} (t)$ , blir

$\begin{matrix} {N (10) - N (0) = \int}_{0}^{10} N' (t) d t \end{matrix}$

$\begin{matrix} \int_{0}^{10} (4 t + 3) d t & = {[2 t^{2} + 3 t]}_{0}^{10} = 230 \end{matrix}$

Dette gir

$\begin{matrix} N (10) = 230 + N (0) = 230 + 800 = 1030 . \end{matrix}$

Svar: Antall individer i populasjonen er $1030$ etter 10 timer.

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Integrasjon, første eksempel.

Oppgave 6 (4 poeng) Nettkode: E-4DAG

En funksjon $f$ er gitt ved

$f (x) = \frac{1}{2} x^{4} - 2 x^{3} + \frac{5}{2} x, D_{f} = ℝ$

a)

Bestem koordinatene til eventuelle vendepunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vendepunktene $(x, f (x))$ til en funksjon $f (x)$ er gitt ved alle de verdiene for $x$ som er slik at $f ″ (x) = 0 og f ″ (x)$ skifter fortegn.

Vi begynner med å beregne den annenderiverte av $f (x)$ . Siden den deriverte av funksjonen $a x^{n}$ er $a n x^{n - 1}$ for alle $n \neq 0$ må

$\begin{matrix} f' (x) & = (\frac{1}{2} x^{4} - 2 x^{3} + \frac{5}{2} x)' = \frac{1}{2} 4 x^{3} - 2 \cdot 3 x^{2} + \frac{5}{2} \\ = 2 x^{3} - 6 x^{2} + \frac{5}{2} . \end{matrix}$

Dette betyr at

$f^{''} (x) = {(f^{'} (x))}^{'} = {(2 x^{3} - 6 x^{2} + \frac{5}{2})}^{'} = 3 \cdot {2 x}^{2} - 2 \cdot 6 x + 0 = 6 x^{2} - 12 x .$

Vi finner nullpunktene til $f ″ (x) .$

$\begin{matrix} f ″ (x) = 6 x^{2} - 12 x = 0 \\ \Rightarrow & x^{2} - 2 x = 0 \\ \Rightarrow & x (x - 2) = 0 \\ \Rightarrow & x = 0 og x = 2 . \end{matrix}$

Siden $f ″ (- 1) = 18 > 0$ , $f ″ (1) = - 6 < 0$ og $f ″ (3) = 18 > 0$ bytter altså $f ″ (x)$ fortegn i både $x = 0$ og $x = 2$ . De to vendepunktene på grafen til $f$ har da koordinater

$(0, f (0)) = (0, 0)$

$(2, f (2)) = (2, \frac{1}{2} \cdot 2^{4} - 2 \cdot 2^{3} + \frac{5}{2} \cdot 2) = (2, 2^{3} - 2 \cdot 2^{3} + 5)$

$= (2, {- 2}^{3} + 5) = (2, - 8 + 5) = (2, - 3)$

Svar: Vendepunktene har koordinater $(0, 0) og (2, - 3)$ .

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vendepunkt, se artikkelen Vendepunkt og vendetangent.

b)

Bestem likningen for eventuelle vendetangenter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne rette linjer som tangerer grafen til $f$ i vendepunktene.

Vi lar $y = A x + B$ være en rett linje og ser at $A = f' (x_{0})$ hvis linjen tangerer grafen til $f$ i punktet $x_{0}$ . Siden den rette linjen og $f$ deler $y$ -verdi i punktet $x_{0}$ må vi videre ha $\begin{matrix} f (x_{0}) = f' (x_{0}) x_{0} + B \Rightarrow B = f (x_{0}) - f' (x_{0}) x_{0} . \end{matrix}$ Fra oppgave $a)$ har vi at $\begin{matrix} f' (x) = 2 x^{3} - 6 x^{2} + \frac{5}{2}, \end{matrix}$ som betyr at den deriverte i de to vendepunktene $(0, 0)$ og $(2, - 3)$ er henholdsvis

$\begin{matrix} f' (0) = \frac{5}{2} og f' (2) = 16 - 6 \cdot 4 + \frac{5}{2} = - \frac{11}{2} . \end{matrix}$

Siden tangentlinjen til $f$ i punktet $x_{0}$ kan skrives $\begin{matrix} y_{0} (x) = f' (x_{0}) (x - x_{0}) + f (x_{0}) \end{matrix}$ kan vi ved å sette inn for vendepunktkoordinatene finne $\begin{matrix} y_{1} (x) = f' (0) (x - 0) + f (0) = \frac{5}{2} x \end{matrix}$ for vendepunktet i $(0, 0)$ og $\begin{matrix} y_{2} (x) = f' (2) (x - 2) + f (2) = - \frac{11}{2} x + 2 \frac{11}{2} - 3 = - \frac{11}{2} x + 8 . \end{matrix}$ De to vendetangentene er altså beskrevet av de to rette linjene $y_{1} = \frac{5}{2} x og y_{2} = - \frac{11}{2} x + 8$

Svar: Vendetangent i $(0, 0)$ : $\begin{matrix} y_{1} = \frac{5}{2} x . \end{matrix}$ Vendetangent i $(2, - 3)$ : $\begin{matrix} y_{2} = - \frac{11}{2} x + 8 . \end{matrix}$

Mer om

Denne oppgaven er om

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangent

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på tangenter, se artikkelen Å finne tangenten - introduksjon.

Oppgave 7 (3 poeng) Nettkode: E-4DAJ

Bruk induksjon til å bevise påstanden

$P (n) : \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + . . . + \frac{1}{n \cdot (n + 1)} = \frac{n}{n + 1}, n \in ℕ$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi må vise at $P (1)$ stemmer og at hvis påstanden stemmer for $n = k$ , så må den nødvendigvis også stemme for $n = k + 1$ .

Vi kan lett sjekke at $P (1)$ er sann ved å sette inn $n = 1$ . Da sier påstanden at $\begin{matrix} P (1) : \frac{1}{1 \cdot 2} = \frac{1}{1 + 1}, \end{matrix}$ som alltid er sant. Vi antar nå at påstanden stemmer for $n = k$ . Det vil si $\begin{matrix} P (k) : \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + . . . + \frac{1}{k (k + 1)} = \frac{k}{k + 1} . \end{matrix}$ Vi lurer på om dette betyr at $\begin{matrix} P (k + 1) : \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + . . . + \frac{1}{(k + 1) (k + 2)} = \frac{k + 1}{k + 2} \end{matrix}$ også må være sann. Ved å trekke fra $\frac{1}{(k + 1) (k + 2)}$ på begge sider sitter vi igjen med $\begin{matrix} \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + . . . + \frac{1}{k (k + 1)} = \frac{k + 1}{k + 2} - \frac{1}{(k + 1) (k + 2)} \\ = \frac{(k + 1) (k + 1)}{(k + 1) (k + 2)} - \frac{1}{(k + 1) (k + 2)} = \frac{(k + 1) (k + 1) - 1}{(k + 1) (k + 2)} \\ = \frac{k^{2} + 2 k}{(k + 1) (k + 2)} = \frac{k (k + 2)}{(k + 1) (k + 2)} = \frac{k}{k + 1} \end{matrix}$ som er nøyaktig påstanden $P (k)$ . Ved å anta at $P (k)$ stemmer følger det altså umiddelbart at $P (k + 1)$ også er sann. Dermed er $P (n)$ sann for alle $n \in ℕ$ ved induksjon.

Mer om

Denne oppgaven er om

Matematisk induksjon

En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:

Bevis påstanden for n =1.
Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).

Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).

induksjon

For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.

Visste du at

Påstanden $P (n)$ kan også bevises direkte. Siden alle leddene i rekken er på formen $\begin{matrix} \frac{1}{n (n + 1)} \end{matrix}$ kan vi benytte omskrivingen $\begin{matrix} \frac{1}{n (n + 1)} = \frac{(n + 1) - n}{n (n + 1)} = \frac{1}{n} - \frac{1}{n + 1} \end{matrix}$ til å skrive $\begin{matrix} \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + . . . + \frac{1}{n (n + 1)} \\ = \frac{1}{1} - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + . . . + \frac{1}{n} - \frac{1}{n + 1} \\ = \frac{1}{1} - \frac{1}{n + 1} = \frac{n + 1}{n + 1} - \frac{1}{n + 1} = \frac{n}{n + 1}, \end{matrix}$ som er påstanden $P (n)$ .

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4DAM

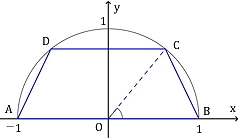
Figuren ovenfor viser et trapes $A B C D$ som er innskrevet i en halvsirkel med radius 1.

a)

Forklar at arealet $F$ av trapeset er gitt ved

$F (v) = (1 + \cos v) \sin v$

Hvilke verdier kan $v$ ha?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Siden trapeset er innskrevet i en enhetssirkel kan vi uttrykke koordinatene til $C$ . Arealet finner vi ved å multiplisere trapesets høyde med dets gjennomsnittlige bredde.

Siden punktet $C$ ligger på enhetssirkelen med vinkel $v$ fra $x$ -aksen må $C$ ha koordinater $\begin{matrix} (\cos v, \sin v) . \end{matrix}$ Siden $y$ -verdien til $C$ er høyden av trapeset og $x$ -verdien er halve bredden $D C$ holder det å konstatere at grunnlinjen $A B$ er diameter i sirkelen, og derfor lik $2$ , før vi uttrykker arealet $F (v)$ til trapeset ved $\begin{matrix} F (v) & = h ø y d e \cdot g j e n n o m s n i t t s b r e d d e = \sin v (\frac{2 + 2 \cos v}{2}) = (1 + \cos v) \sin v . \end{matrix}$ At trapeset er innskrevet i halvsirkelen med radius én betyr at $v$ ikke kan være mindre enn $0$ . Siden vi har brukt at $A B C D$ er et trapes kan vi få problemer når $v > \frac{π}{2}$ ettersom $C$ og $D$ da bytter plass. Hvis $v = 0 eller v = \frac{π}{2}$ , er ikke figuren et trapes. Altså må $v$ være i intervallet $(0, \frac{π}{2})$ .

Alternativ løsning

Siden $h = \sin v$ er høyden og $A B = 2$ og $D C = 2 \cos v$ er trapesets parallelle sider er arealet ifølge standardformelen gitt ved $\begin{matrix} \frac{A B + D C}{2} h = \frac{2 + 2 \cos v}{2} \sin v = (1 + \cos v) \sin v, \end{matrix}$ som er det vi ønsket å vise.

Svar: $\begin{matrix} v \in (0, \frac{π}{2}) . \end{matrix}$

Mer om

Denne oppgaven er om

Trapes

Firkant der to sider er parallelle.

Areal = $\frac{(a + b) h}{2}$

trapes

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

For flere forklaringer og eksempler på geometri, se artikkelen Et trapes.

b)

Bestem $∠ v$ ved regning slik at arealet av trapeset blir størst mulig.

Bestem arealet av det største trapeset.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Den vinkelen $v$ som gjør at arealet $F (v)$ er maksimalt må $F' (v) = 0$ .

Ved å derivere uttrykket for arealet $F (v)$ med hensyn på $v$ finner vi endringen i areal når vinkelen endrer seg. Ved å bruke produktregelen for derivasjon finner vi $\begin{matrix} F' (v) & = ((1 + \cos v) \sin v)' = (1 + \cos v)' \sin v + (1 + \cos v) (\sin v)' \\ = (- \sin v) \sin v + (1 + \cos v) (\cos v) = - \sin^{2} + \cos^{2} v + \cos v . \end{matrix}$ Siden $\sin^{2} v = 1 - \cos^{2} v$ følger det videre at $\begin{matrix} F' (v) & = - \sin^{2} + \cos^{2} v + \cos v = - (1 - \cos^{2} v) + \cos^{2} v + \cos v \\ = 2 \cos^{2} v + \cos v - 1 . \end{matrix}$ Vi må altså finne de verdiene for $v$ som tilfredsstiller $\begin{matrix} 2 \cos^{2} v + \cos v - 1 = 0 . \end{matrix}$ Annengradsformelen gir da $\begin{matrix} \cos v & = \frac{- 1 \pm \sqrt{1^{2} - 4 \cdot 2 \cdot (- 1)}}{2 \cdot 2} \\ = \frac{- 1 \pm 3}{4} = {\begin{matrix} \frac{1}{2} \\ - 1 \end{matrix} . \end{matrix}$ De vinklene som tilfredsstiller $F' (v) = 0$ er altså

$v = \{\begin{matrix} \pm \arccos \frac{1}{2} + 2 π n = \pm \frac{π}{3} + 2 π n, & n \in ℤ \\ \arccos (- 1) + 2 π n = μ + 2 π n, & n \in ℤ \end{matrix}$

Den eneste av disse verdiene som ligger innenfor intervallet $(0, \frac{π}{2})$ er $\begin{matrix} v = \frac{π}{3} . \end{matrix}$ For at $v$ skal være et toppunkt må vi imidlertid forsikre oss om at $F$ vokser før den har passert $v$ og avtar etter den har passert $v$ , altså at $v = \frac{π}{3}$ ikke er et. Siden $\frac{π}{3}$ er det eneste nullpunktet til $F' (v)$ kan vi sette inn endepunktene og dermed finne $\begin{matrix} F' (0) = 2 \cos^{2} 0 + \cos 0 - 1 = 2 > 0 \end{matrix}$ og $\begin{matrix} F' (\frac{π}{2}) = 2 \cos^{2} \frac{π}{2} + \cos \frac{π}{2} - 1 = - 1 < 0 . \end{matrix}$ Altså må $v = π / 3$ være et toppunkt. Arealet som hører til denne vinkelen er $\begin{matrix} F (\frac{π}{3}) & = (1 + \cos \frac{π}{3}) \sin \frac{π}{3} = (1 + \frac{1}{2}) \frac{\sqrt{3}}{2} \\ = \frac{3}{2} \frac{\sqrt{3}}{2} = \frac{3 \sqrt{3}}{4} \approx 1, 299 \end{matrix}$ og siden arealet til figuren er $0$ når $v = 0$ og $\begin{matrix} F (\frac{π}{2}) = (1 + \cos \frac{π}{2}) \sin \frac{π}{2} = 1 \end{matrix}$ har arealet sin største verdi når $v = \frac{π}{3}$ . Da er arealet $\begin{matrix} F (\frac{π}{3}) = \frac{3 \sqrt{3}}{4} \approx 1, 299 . \end{matrix}$

Alternativ løsning (numerisk)

Ved å løse denne oppgaven i CAS kan vi velge to fremgangsmåter. Vi kan enten be CAS gjøre nøyaktig det samme som vi ville gjort ved regning, eller vi kan be om et tallsvar for ekstremalpunktet til funksjonen $F (v)$ . Uansett må vi definere $F (v)$ . Det gjør vi ved å skrive kommandoen:
F(v):=(1+cos(v))sin(v)

Hvis vi bare er interessert i et tallsvar kan vi skrive kommandoen
Ekstremalpunkt[F, 0, \pi/2 ]
som gir punktet $(1.0472, 1.299)$ .

En alternativ løsning er å finne alle løsningene på likningen $F' (v) = 0$ . Det kan vi gjøre ved kommandoen
L:=Løsninger[Derivert[F(v)]=0,v]

Resultatet er da $\begin{matrix} {- π, - \frac{1}{3} π, \frac{1}{3} π, π} \end{matrix}$ og siden det tredje elementet, altså $\frac{1}{3} π$ , er det eneste som ligger i intervallet $(0, \frac{π}{2})$ må ekstremalverdien være gitt som $F (\frac{π}{3})$ . Verdien i dette punktet kan vi finne ved å skrive
F(Element[L, 3])

som gir $\frac{3 \sqrt{3}}{4}$ .

Svar: $\begin{matrix} F (\frac{π}{3}) = \frac{3 \sqrt{3}}{4} \approx 1, 299 . \end{matrix}$

Mer om

Denne oppgaven er om

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunkter

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Visste du at

Vi kunne også argumentert oss frem til dette resultatet uten å bruke noe uttrykk for trapesets areal. Trapetsets areal vil alltid være mindre enn sirkelens areal og differansen mellom disse vil alltid tilsvare de områdene som er igjen etter trapeset er skåret ut av sirkelen. Ved å fordele punktene $C$ og $D$ jevnt over sirkelen slik at $A D = D C = C B$ vil differansen mellom sirkelen og trapeset bli minst mulig. Siden halvsirkelen utspenner en vinkel lik $π$ radianer, og vi skal fordele denne likt på tre intevaller, må vinkelen $v$ være lik $\frac{π}{3}$ for å oppnå maksimalt areal.

Oppgave 2 (7 poeng) Nettkode: E-4DAP

Funksjonen $f$ er gitt ved

$f (x) = \sin (π x) + \sin (2 π x), x \in [0, 6]$

a)

Tegn grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Ved å benytte GeoGebras graftegner kan vi tegne grafen til $f$ på intervallet $[0, 6]$ .

Ved å skrive følgende kommando i geoGebras grafdel
f(x) := Dersom[0 \leq x \leq 6, sin(\pix) + sin(2\pix)]

eller eventuelt
f(x) := Funksjon[sin(\pix) + sin(2\pix),0,6]

sitter vi igjen med følgende figur:

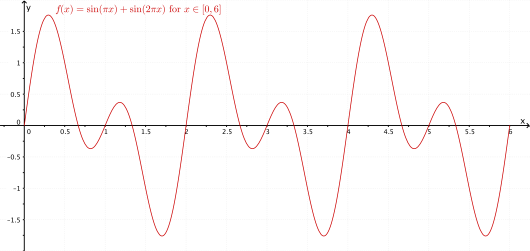
Svar:

Mer om

Denne oppgaven er om

Graf

graf

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

b)

Bruk grafen til å vise at $f$ er en periodisk funksjon, og bestem perioden til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må ved å studere grafen til $f$ gjenkjenne et repeterende mønster. Lengden av intervallet dette mønsteret strekker seg over på $x$ -aksen er da mønsterets periode.

En funksjon $g (x)$ er periodisk hvis det finnes et reelt tall $T > 0$ slik at

$g (x + T) = g (x)$

for alle $x$ i definisjonsmengden til $g$ . For funksjonen $f (x)$ i oppgaven kan det ikke finnes noen slik positiv $T$ som oppfyller dette kravet siden definisjonsmengden til $f$ er begrenset. Vi har at $6$ er i definisjonsmengden til $f$ , men $6 + T$ er ikke i definisjonsmengden hvis $T > 0$ . Dermed kan ikke

$f (6 + T) = f (6)$

Dersom vi endrer definisjonsmengden til $f$ slik at den er definert på hele mengden av reelle tall, så blir $f$ periodisk. Vi regner ut at

$\begin{matrix} f (x + 2) & = & \sin (π (x + 2)) + \sin (2 π (x + 2)) \\ = & \sin (π x + 2 π) + \sin (2 π x + 4 π) \\ = & \sin (π x) + \sin (2 π x) \\ = & f (x) \end{matrix}$

Dette viser at perioden er høyst $2$ .

Når vi erstatter $x$ i en funksjon med $x + T$ , translateres grafen $T$ enheter til venstre. At $f (x + T) = f (x)$ for alle $x$ i definisjonsmengden, betyr at grafen til $f$ dekker seg selv perfekt etter translasjon $T$ enheter til venstre.

Av grafen i oppgave a), ser vi at grafen må translateres minst $2$ enheter langs $x$ -aksen før den ser lik ut, så perioden er minst $2$ . Dermed må perioden være akkurat $2$ , siden vi så tidligere at den også er høyst $2$ .

Svar: Perioden er $2$ for funksjonen med utvidet definisjonsmengde.

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

graf

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

For flere forklaringer og eksempler på , se artikkelen Grafene til sin x, cos x og tan x.

Visste du at

At $f$ er en periodisk funksjon med periode $2$ kan også leses av fra funksjonsuttrykket til $f$ . Siden $f (x)$ er en sum av to periodiske funksjoner med periode $1$ og $2$ må $f$ være periodisk med periode lik minste felles multiplum av $1$ og $2$ . Med andre ord har $f$ periode lik $2$ siden $2$ både er delelig med $1$ og $2$ . Ved hjelp av samme argumentasjon kan vi se at funksjonen $\begin{matrix} g (x) = \sin \frac{2 π}{3} x + \sin \frac{2 π}{7} x + \sin \frac{2 π}{13} x, \end{matrix}$ som er en sum av funksjoner med periode henholdsvis lik $3$ , $7$ og $13$ , må ha periode lik $3 \cdot 7 \cdot 13 = 273$ .

c)

Vis at

$f (x) = \sin (π x) (1 + 2 \cos (π x))$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan uttrykke $\sin (2 π x)$ ved hjelp av $\cos (π x)$ og $\sin (π x)$ .

Siden $\sin (2 π x) = 2 \sin (π x) \cos (π x)$ følger det at $\begin{matrix} f (x) & = \sin (π x) + \sin (2 π x) = \sin (π x) + 2 \sin (π x) \cos (π x) \\ = \sin (π x) (1 + 2 \cos (π x)), \end{matrix}$ som er det vi ønsket å vise.

Mer om

Denne oppgaven er om

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Sinus

sinus

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Sinus, cosinus og tangens.

d)

Bruk uttrykket i oppgave c) til å bestemme nullpunktene til $f$ ved regning når $x \in [0, 2]$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Siden $f (x)$ kan skrives som et produkt av to ulike funksjoner må $f (x) = 0$ bety at én av dem, eller begge, er $0$ .

Nullpunktene til en funksjon $f (x)$ er nøyaktig de verdiene for $x$ som gjør at $f (x) = 0$ . Altså må nullpunktene tilfredsstille $\begin{matrix} f (x) = \sin (π x) (1 + 2 \cos (π x)) = 0, \end{matrix}$ som betyr at

$\begin{matrix} \sin (π x) = 0 eller 1 + 2 \cos (π x) = 0 . \end{matrix}$

For $x$ -verdiene betyr dette at

$\begin{matrix} x \in ℤ \end{matrix}$

eller

$\begin{matrix} π x = \pm \arccos (- \frac{1}{2}) + 2 π n, n \in ℤ \end{matrix}$

$x = \pm \frac{1}{π} \cdot \frac{2 π}{3} + 2 n, n \in ℤ$

$x = \pm \frac{2}{3} + 2 n, n \in ℤ$

Nullpunktene til $f (x)$ i intervallet $[0, 2]$ er altså $\begin{matrix} {0, 1, 2} \cup {\frac{2}{3}} \cup {\frac{4}{3}}, \end{matrix}$ som kan skrives $\begin{matrix} {0, \frac{2}{3}, 1, \frac{4}{3}, 2} . \end{matrix}$

Svar: $\begin{matrix} {0, \frac{2}{3}, 1, \frac{4}{3}, 2} . \end{matrix}$

Mer om

Denne oppgaven er om

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

arcus cosinus

Union

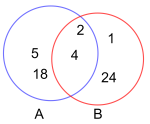
Unionen av to mengder A og B er en ny mengde $A \cup B$ som består av alle elementer som forekommer i minst en av A og B.

Eksempel: hvis $A = \{2, 4, 5, 18\} o g B = \{1, 2, 4, 24\}$ er to mengder, blir unionen $A \cup B = \{1, 2, 4, 5, 18, 24\}$ .

union

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

For flere forklaringer og eksempler på trigonometri, se artikkelen Mer kompliserte likninger.

Oppgave 3 (5 poeng) Nettkode: E-4DAU

Vi lar K være kapitalen i et fond t år etter første innskudd. Hvert år setter vi inn 20 000 kroner i fondet. Avkastningen i fondet er 8 % per år.

Kapitalen i fondet vokser slik differensiallikningen nedenfor viser

$K' (t) = 0, 08 \cdot K (t) + 20 000$

a)

Løs differensiallikningen. Finn et uttrykk for $K (t)$ når $K (0) = 20 000$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Differensiallikningen som beskriver kapitalen $K (t)$ i fondet etter $t$ år består av tre ledd. Siden disse leddene består av $K$ , $K'$ og et konstantledd er likningen en separabel første ordens differensiallikning.

Ved å benytte omskrivingen $\begin{matrix} K' (t) = 0, 08 K (t) + 20000 = 0, 08 (K (t) + 250000) \Rightarrow \frac{K' (t)}{K (t) + 250000} = 0, 08, \end{matrix}$ kan vi integrere med hensyn på $t$ på begge sider og få $\begin{matrix} \int \frac{K' (t) d t}{K (t) + 250000} = 0, 08 \int d t . \end{matrix}$ Mens høyresiden kan skrives $\begin{matrix} 0, 08 \int d t = 0, 08 t + C_{1} \end{matrix}$ for en konstant $C_{1}$ , kan venstresiden løses ved å bruke substitusjonsmetoden med substitusjonen $K = K (t)$ . Det gir $\begin{matrix} \int \frac{K' (t) d t}{K (t) + 250000} = \int \frac{d K}{K + 250000}, \end{matrix}$ og siden den deriverte av $\ln (K + 250000)$ er $\frac{1}{K + 250000}$ må $\begin{matrix} \int \frac{d K}{K + 250000} = \ln (K + 250000) + C_{2} \end{matrix}$ for en konstant $C_{2}$ . Dette kan også ses ved å gjenta substitusjonsmetoden med substitusjonen $u (K) = K + 250000$ . Vi har uansett funnet at $\begin{matrix} \ln (K (t) + 250000) + C_{2} = 0, 08 t + C_{1}, \end{matrix}$ som ved å kombinere de to konstantene $C_{1}$ og $C_{2}$ til én konstant $C = C_{1} - C_{2}$ kan skrives $\begin{matrix} \ln (K (t) + 250000) = 0, 08 t + C . \end{matrix}$ Siden $K (0) = 20000$ følger det videre at $\begin{matrix} \ln (K (0) + 250000) = 0, 08 \cdot 0 + C \Rightarrow C = \ln (20000 + 250000) = \ln (270000) . \end{matrix}$ Altså er den spesielle løsningen av likningen gitt av $\begin{matrix} \ln (K (t) + 250000) = 0, 08 t + \ln (270000) . \end{matrix}$ Fra omskrivingen $\begin{matrix} \ln (K (t) + 250000) = 0, 08 t + \ln (270000) \\ \Rightarrow & K (t) + 250000 = e^{0, 08 t + \ln (270000)} \\ \Rightarrow & K (t) = e^{\ln (270000)} e^{0, 08 t} - 250000 \\ \Rightarrow & K (t) = 270000 e^{0, 08 t} - 250000 \end{matrix}$ ser vi at løsningen også kan skrives $\begin{matrix} \Rightarrow & K (t) = 270000 e^{0, 08 t} - 250000, \end{matrix}$ som er den vanlige måten å oppgi funksjoner på.

Alternativ løsning

Vi kan først benytte omskrivingen $\begin{matrix} K' (t) = 0, 08 K (t) + 20000 = 0, 08 (K (t) + 250000) \Rightarrow \frac{K' (t)}{K (t) + 250000} = 0, 08 . \end{matrix}$ Deretter kan vi integrere begge sider av likningen med hensyn på $τ$ fra $τ = 0$ til $τ = t$ $\begin{matrix} \int_{0}^{t} \frac{K' (τ) d τ}{K (τ) + 250000} = 0, 08 \int_{0}^{t} d τ . \end{matrix}$ Vi kunne godt brukt $t$ i stedet for $τ$ her, men da kunne vi fort forvirret oss selv ettersom variabelnavnet $t$ allerede er brukt i integralets grenser. Mens høyresiden av likningen kan skrives $\begin{matrix} 0, 08 \int_{0}^{t} d τ = 0, 08 (t - 0) = 0, 08 t, \end{matrix}$ kan vi ved å bruke substitusjonsmetoden for integrasjon, først med substitusjonen $K = K (τ)$ og deretter med $u (K) = K + 250000$ , skrive venstresiden som $\begin{matrix} \int_{0}^{t} \frac{K' (τ) d τ}{K (τ) + 250000} & = \int_{K (0)}^{K (t)} \frac{d K}{K + 250000} \\ = \int_{K (0)}^{K (t)} \frac{u' (K) d K}{u (K)} \\ = \int_{K (0) + 250000}^{K (t) + 250000} \frac{d u}{u} \\ = [\ln (u)]_{K (0) + 250000}^{K (t) + 250000} \\ = \ln (K (t) + 250000) - \ln (K (0) + 250000) . \end{matrix}$

Siden $K (0) = 20000$ betyr dette at $\begin{matrix} \ln (K (t) + 250000) - \ln (K (0) + 250000) \\ = \ln (K (t) + 250000) - \ln (20000 + 250000) \\ = \ln (K (t) + 250000) - \ln (270000) . \end{matrix}$ Ved å sette høyresiden av likningen lik venstresiden finner vi da at løsningen av differensiallikningen er $\begin{matrix} \ln (K (t) + 250000) - \ln (270000) = 0, 08 t, \end{matrix}$ som kan skrives $\begin{matrix} K (t) = 270000 e^{0, 08 t} - 250000 . \end{matrix}$

Numerisk løsning:

Ved å skrive kommandoen

LøsODE[y’=0.08y+20000,(0,20000)]

i CAS finner vi løsningen $\begin{matrix} K (t) = 270000 e^{0, 08 t} - 250000 . \end{matrix}$

Svar: $\begin{matrix} K (t) = 270000 e^{0, 08 t} - 250000 . \end{matrix}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.

Visste du at

Differensiallikningen kan også løses med inetgrerende faktor. Siden $K' - 0.08 K = 20000$ og $\begin{matrix} (K (t) e^{- 0.08 t})' = K' (t) e^{- 0.08 t} - 0.08 K (t) e^{- 0.08 t} \end{matrix}$ kan vi skrive differensiallikningen som $\begin{matrix} (K (t) e^{- 0.08 t})' = 20000 e^{- 0.08 t} \end{matrix}$ som ved å integrere begge sider fra $0$ til $t$ gir $\begin{matrix} K (t) e^{- 0.08 t} - K (0) e^{- 0.08 \cdot 0} = - \frac{20000}{0.08} (e^{- 0.08 t} - e^{- 0.08 \cdot 0}) . \end{matrix}$ Siden $K (0) = 20000$ og $\frac{20000}{0.08} = 250000$ må vi ha $\begin{matrix} K (t) = 270000 e^{- 0.08 t} - 250000, \end{matrix}$ som er det vi fant i oppgaven ovenfor.

b)

Bestem størrelsen på kapitalen etter 20 år.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Ved å benytte løsningen fra oppgave $a)$ kan vi finne kapitalen i fondet etter $20$ år ved å sette inn for $t = 20$ .

Vi skal løse differensiallikningen

$K^{'} (t) = 0, 08 K (T) + 20 000$

Dette er en lineær 1. ordens differensiallikning. Først ordner vi den slik at den blir på formen

$K^{'} (t) + f (t) K (t) = g (t)$

slik at vi kan finne den integrerende faktor. Vår likning blir slik:

$K^{'} (t) - 0, 08 K (t) = 20 000$ .

Integrerende faktor er $e$ opphøyd i en antiderivert til $- 0, 08$ . Vi bruker $e^{- 0, 08}$ og multipliserer begge sider med integrerende faktor. Det gir

$K^{'} (t) e^{- 0, 08 t} - 0, 08 K (t) e^{- 0, 08 t} = 20 000 e^{- 0, 08 t}$

Metoden med integrerende faktor sikrer at venstresiden er den deriverte av produktet av $K$ og integrerende faktor. Dermed har vi

${(K (t) e^{- 0, 08 t})}^{'} = 20 000 e^{- 0, 08 t}$

Integrasjon av begge sider med hensyn på $t$ gir

$K (t) e^{- 0, 08 t} = \frac{20 000}{- 0, 08} e^{- 0, 08 t} + C = - 250 000 e^{- 0, 08 t} + C$

Vi multipliserer med $e^{0, 08 t}$ på begge sider og får

$K (t) = C e^{0, 08 t} - 250 000$

Siden $K (0) = C e^{0} - 250 000 = C - 250 000 = 20 000$ , må $C = 270 000$ . Løsningen på initialverdiproblemet er derfor

$K (t) = 270 000 e^{0, 08 t} - 250 000$

For $t = 20$ etter første innskudd får vi at

$\begin{matrix} K (20) & = 270000 e^{0, 08 \cdot 20} - 250000 \approx 1087319 \end{matrix}$

Altså størrelsen på kapitalen er rundt $1087319$ kroner $20$ år etter første innskudd.

Svar: Størrelsen på kapitalen er rundt $1087319$ kroner $20$ år etter første innskudd.

Mer om

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på funksjoner, se artikkelen Å bygge funksjoner.

c)

Hvor lang tid vil det gå før fondet øker med 35 000 kroner per år ifølge modellen ovenfor?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må finne et uttrykk for fondets økning per år og deretter kreve at denne økningen skal være lik $35000$ kroner. Den verdien for $t$ som gjør at dette kravet er oppfylt vil være tiden det tar før fondet øker med $35000$ kroner per år.

Fondets økning per år kan, som nesten alltid er tilfellet når det er snakk om endring, representeres som den deriverte av kapitalen med hensyn på tid. Altså representerer $\begin{matrix} K' (t) & = (270000 e^{0, 08 t} - 250000)' = 270000 (e^{0, 08 t})' \\ = 270000 (0, 08 t)' e^{0, 08 t} = 270000 \cdot 0, 08 \cdot e^{0, 08 t} \\ = 21600 e^{0, 08 t} \end{matrix}$ økningen av fondet per år. Tiden det vil ta før fondet øker med $35000$ kroner per år er altså den verdien for $t$ som tilfredsstiller $\begin{matrix} 21600 e^{0, 08 t} = 35000 . \end{matrix}$ Det betyr at $\begin{matrix} 21600 e^{0, 08 t} = 35000 \\ \Rightarrow & e^{0, 08 t} = \frac{35000}{21600} \\ \Rightarrow & 0, 08 t = \ln \frac{35000}{21600} \\ \Rightarrow & t = \frac{1}{0, 08} \ln \frac{35000}{21600} \approx 6, 0 . \end{matrix}$ Altså tar det omlag seks år før fondet øker med $35000$ per år ifølge modellen.

Svar: Ca. seks år.

Mer om

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på eksponentiallikninger, se artikkelen Eksponentiallikninger.

Oppgave 4 (6 poeng) Nettkode: E-4DAY

En uendelig, geometrisk rekke er gitt ved

$S (x) = 1 + x + x^{2} + . . .$

Når $x \in ⟨- 1, 1⟩$ , er $S (x) = \frac{1}{1 - x}$

Det kan vises at $\int_{}^{} 1 dx + \int_{}^{} x dx + \int_{}^{} x^{2} dx + . . . = \int_{}^{} \frac{1}{1 - x} dx$

a)

Forklar at

$x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + \frac{1}{4} x^{4} + . . . = - \ln (1 - x) + C$

Begrunn at

$C = 0$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å løse denne oppgaven, må først oppgavetekten presiseres litt. Vi ønsker å vise at hvis vi legger den naturlige logaritmen av $1 - x$ til summen av $\frac{1}{n} x^{n}$ for alle $n = 0, 1, 2, 3, . . .$ sitter vi igjen med en konstant uavhengig av $x$ når $x \in (- 1, 1)$ .

For å løse denne oppgaven, må først oppgaveteksten presiseres litt. Oppgaveteksten hevder at for $- 1 < x < 1$ , er

$\begin{matrix} \int 1 d x + \int x d x + \int x^{2} d x + \int x^{3} d x + . . . = \int_{}^{} \frac{1}{1 - x} d x . \end{matrix}$

Hvert ubestemt integral på venstresiden har imidlertid med seg en konstant, så venstresiden inneholder en uendelig sum av vilkårlige konstanter. Det er ingen kontroll på at denne rekken konvergerer, og det gjør utsagnet uklart.

Det som er sant, og som er akkurat det vi trenger for å løse oppgaven, er at for $- 1 < x < 1$ , er

$\int_{0}^{x} 1 d t + \int_{0}^{x} t d t + \int_{0}^{x} t^{2} d t + . . . = \int_{0}^{x} \frac{1}{1 - t} d t (1)$

For hver verdi av er nå rekken på venstre side en rekke der hvert ledd er et reelt tall. Utsagnet påstår at når vi velger en med tallverdi mindre enn 1 og regner ut begge sider av (1), så får vi samme resultat.

Generelt har vi at for $n \neq - 1$ er

$\int_{0}^{x} t^{n} d t = {[\frac{1}{n + 1} t^{n + 1}]}_{0}^{x} = \frac{1}{n + 1} x^{n + 1}$ .

Dermed blir venstresiden av likheten (1)

$x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + . . .$

Høyresiden av (1) blir

$\int_{0}^{x} \frac{1}{1 - t} d t = {[- \ln |1 - t|]}_{0}^{x} = - \ln (1 - x)$

Til sammen viser dette alt som skal vises i oppgaven. Likheten som skal vises stemmer for $C = 0$ .

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.

b)

Sett inn $x = \frac{1}{2}$ og vis at $\frac{1}{1} \cdot \frac{1}{2^{1}} + \frac{1}{2} \cdot \frac{1}{2^{2}} + \frac{1}{3} \cdot \frac{1}{2^{3}} + \frac{1}{4} \cdot \frac{1}{2^{4}} + . . . = \ln 2$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Etter å ha satt inn $x = \frac{1}{2}$ må vi skrive om uttrykket fra oppgave $a)$ slik at det sier at $\ln 2$ er lik summen av $\frac{1}{n} \frac{1}{2^{n}}$ for $n = 1, 2, 3, . . .$ .

Ved å sette inn $x = \frac{1}{2}$ i uttrykket fra oppgave $a)$ finner vi $\begin{matrix} \frac{1}{2} + \frac{1}{2} \frac{1}{2^{2}} + \frac{1}{3} \frac{1}{2^{3}} + \frac{1}{4} \frac{1}{2^{4}} + . . . = - \ln (1 - \frac{1}{2}) = - \ln (\frac{1}{2}) = \ln 2 . \end{matrix}$ Dette kan vi skrive som $\begin{matrix} \frac{1}{1} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2^{2}} + \frac{1}{3} \cdot \frac{1}{2^{3}} + \frac{1}{4} \cdot \frac{1}{2^{4}} + . . . = \ln 2, \end{matrix}$ som er det vi ønsket å vise.

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på logaritmer, se artikkelen Den naturlige logaritmen.

c)

Det generelle leddet i rekken ovenfor er $a_{n} = \frac{1}{n} \cdot \frac{1}{2^{n}}$ .

Det kan vises at de åtte første desimalene i $\ln 2$ er $0, 69314718$ .

Dersom vi summerer de $n$ første leddene $a_{1} + a_{2} + . . . + a_{n}$ i rekken i oppgave b), får vi en

tilnærmingsverdi for $\ln 2$ .

Hvor mange ledd må vi minst ta med for at vi skal få 6 korrekte desimaler?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Ved å bruke CAS i geoGebra kan vi prøve oss frem helt til vi finner antall ledd vi må ha med for å få $\ln 2$ med korrekt seks korrekte desimaler.

Vi begynner med å endre instillingene i geoGebra slik at tall rundes av med ti desimalers nøyaktighet. Dette gjør vi ved å gå inn på ”Innstillinger”, trykke på ”Avrunding” og deretter på ”10 desimaler”. Ved å systematisk prøve forskjellige verdier for $M$ med kommandoen

Sum[(1/n)*(1/2^n),n,1,M]

i CAS finner vi at

Sum[(1/n)*(1/2^n),n,1,18]

gir $\approx 0.69314699$ , mens

Sum[(1/n)*(1/2^n),n,1,19]

gir $\approx 0.69314701$ . Altså må minst $19$ ledd tas med for å få $6$ korrekte desimaler.

Svar: $19$ ledd må tas med.

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på følger, se artikkelen Konvergente tallfølger.

Oppgave 5 (7 poeng) Nettkode: E-4DB3

Funksjonene $f$ og $g$ er gitt ved

$f (x) = \cos x$

$g (x) = 1 - k^{2} \cdot x^{2}, k > 0$

Skisser av grafene til $f$ og $g$ er tegnet nedenfor.

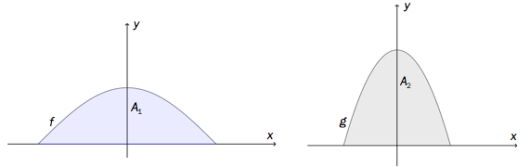
a)

Bestem nullpunktene til $g$ uttrykt ved $k$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må finne de verdiene for $x$ som gjør at $g (x) = 1 - k^{2} x^{2} = 0$ .

Siden nullpunktene til $g$ er nøyaktig de verdiene for $x$ som tilfredsstiller $\begin{matrix} 1 - k^{2} x^{2} = 0 \Leftrightarrow x^{2} = \frac{1}{k^{2}} \end{matrix}$ må de være gitt av $\begin{matrix} x = \pm \sqrt{\frac{1}{k^{2}}} = \pm \frac{1}{k} . \end{matrix}$

Alternativ løsning

Ifølge tredje kvadratsetning er $a^{2} - b^{2} = (a - b) (a + b)$ for alle tall $a$ og $b$ . Hvis $a = 1$ og $b = k x$ følger det da at $\begin{matrix} g (x) = 1 - k^{2} x^{2} = (1 - k x) (1 + k x) = k^{2} (\frac{1}{k} - x) (\frac{1}{k} + x) . \end{matrix}$ Nullpunktene til $g$ er de verdiene for $x$ som er slik at $\begin{matrix} g (x) = k^{2} (\frac{1}{k} - x) (\frac{1}{k} + x) = 0, \end{matrix}$ som betyr at $\begin{matrix} \frac{1}{k} - x = 0 eller \frac{1}{k} + x = 0 \end{matrix}$ siden $k^{2} \neq 0$ . Med andre ord er nullpunktene til $g$ gitt av $\begin{matrix} x = \pm \frac{1}{k} . \end{matrix}$

Svar: $\begin{matrix} x = \pm \frac{1}{k} \end{matrix}$ .

Mer om

Denne oppgaven er om

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetning

For flere forklaringer og eksempler på andregradsfunksjoner, se artikkelen Å bruke konjugatsetningen.

b)

Bestem $k$ slik at arealene $A_{1}$ og $A_{2}$ på figurene ovenfor er like store.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Siden arealet under grafen til en funksjon $f (x)$ mellom $x = a$ og $x = b$ er lik integralet av $f$ med hensyn på $x$ fra $a$ til $b$ er vi nødt til å velge $k$ slik at integralene av de to funksjonene er like.

Nullpunktene til $f (x)$ er nøyaktig de verdiene for $x$ som tilfredsstiller $\begin{matrix} f (x) = \cos x = 0 . \end{matrix}$ Med andre ord er de to nullpunktene som ligger nærmest $x = 0$ gitt av $\begin{matrix} x = \pm \frac{π}{2} . \end{matrix}$ Arealet $A_{1}$ under grafen til $f$ mellom disse nullpunktene dermed gitt som $\begin{matrix} A_{1} & = \int_{- \frac{π}{2}}^{\frac{π}{2}} f (x) d x = \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos (x) d x, \end{matrix}$ og siden den deriverte av $\sin x$ er $\cos x$ følger det at $\begin{matrix} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos (x) d x & = {[\sin x]}_{- \frac{π}{2}}^{\frac{π}{2}} = \sin (\frac{π}{2}) - \sin (- \frac{π}{2}) \\ = 2 \sin (\frac{π}{2}) = 2 \cdot 1 = 2 . \end{matrix}$ Arealet $A_{2}$ under grafen til $g$ mellom nullpunktene $\pm 1 / k$ er på tilsvarende måte gitt som $\begin{matrix} A_{2} & = \int_{- \frac{1}{k}}^{\frac{1}{k}} (1 - k^{2} x^{2}) d x = \int_{- \frac{1}{k}}^{\frac{1}{k}} 1 d x - k^{2} \int_{- \frac{1}{k}}^{\frac{1}{k}} x^{2} d x \\ = {[x]}_{- \frac{1}{k}}^{\frac{1}{k}} - k^{2} {[\frac{1}{3} x^{3}]}_{- \frac{1}{k}}^{\frac{1}{k}} = (\frac{1}{k} - (- \frac{1}{k})) - k^{2} (\frac{1}{3} {(\frac{1}{k})}^{3} - \frac{1}{3} {(- \frac{1}{k})}^{3}) \\ = (2 \frac{1}{k}) - \frac{2}{3} k^{2} {(\frac{1}{k})}^{3} = (2 - \frac{2}{3}) \frac{1}{k} = \frac{4}{3} \frac{1}{k} . \end{matrix}$ Den verdien for $k$ som gjør at arealene $A_{1}$ og $A_{2}$ er like må altså tilfredsstille $\begin{matrix} A_{1} = 2 = \frac{4}{3} \frac{1}{k} = A_{2} . \end{matrix}$ Det er bare én verdi for $k$ som tilfredsstiller denne likningen, og det er $\begin{matrix} k = \frac{1}{2} \frac{4}{3} = \frac{2}{3} . \end{matrix}$

Svar: $\begin{matrix} k = \frac{2}{3} . \end{matrix}$

Mer om

Denne oppgaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Graf

graf

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på integraler, se artikkelen Bestemte integraler.

Visste du at

Det kan vises at cosinus kan skrives $\begin{matrix} \cos x = 1 - \frac{x^{2}}{2} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + . . . \end{matrix}$ der $n! = 1 \cdot 2 \cdot . . . (n - 1) \cdot n$ . Dette, som er den såkalte ”Taylorutviklingen” til cosinus, er det kalkulatoren din benytter seg av når den beregner $\cos x$ .

c)

Bruk formelen $\cos (u + v) = \cos u \cos v - \sin u \sin v$ til å vise at

$\cos^{2} (x) = \frac{1}{2} + \frac{1}{2} \cdot \cos (2 x) (*)$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Siden formelen $\cos (u + v) = \cos (u) \cos (v) - \sin (u) \sin (v)$ holder for alle tall $u$ og $v$ må den også holde for $u = x$ og $v = x$ .

Ved å sette inn for $u = x$ og $v = x$ i formelen (*) finner vi at $\begin{matrix} \cos (x + x) = \cos (2 x) = \cos (x) \cos (x) - \sin (x) \sin (x) = \cos^{2} x - \sin^{2} x . \end{matrix}$ Siden Pytagoras læresetning krever at $\sin^{2} x = 1 - \cos^{2} x$ har vi videre at $\begin{matrix} \cos (2 x) = \cos^{2} x - \sin^{2} x = \cos^{2} x - (1 - \cos^{2} x) = 2 \cos^{2} x - 1 . \end{matrix}$ Med andre ord har vi funnet at $\begin{matrix} \cos 2 x = 2 \cos^{2} x - 1, \end{matrix}$ som kan skrives $\begin{matrix} \cos^{2} x = \frac{1}{2} \cos 2 x + \frac{1}{2} . \end{matrix}$

Mer om

Denne oppgaven er om

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

For flere forklaringer og eksempler på trigonometri, se artikkelen Trigonometriske formler.

Visste du at

Det kan vises at $\begin{matrix} \cos x = \frac{e^{i x} + e^{- i x}}{2} \end{matrix}$ der $i = \sqrt{- 1}$ . Ettersom kvadratet av et negativt tall er positivt og kvadratet av et positivt tall er positivt virker det absurd å snakke om tallet $\sqrt{- 1}$ . Av den grunn kaller man tall på formen $i x$ , der $x$ er et reelt tall, for ”imaginære tall”. Uansett, ved å bruke dette uttrykket for $\cos x$ følger det at $\begin{matrix} \cos^{2} x & = {(\frac{e^{i x} + e^{- i x}}{2})}^{2} = \frac{{(e^{i x})}^{2} + 2 e^{i x} e^{- i x} + {(e^{- i x})}^{2}}{4} \\ = \frac{1}{2} \frac{e^{2 i x} + 2 e^{i x - i x} + e^{- 2 i x}}{2} = \frac{1}{2} \frac{e^{2 i x} + 2 + e^{- 2 i x}}{2} \\ = \frac{1}{2} \frac{e^{2 i x} + e^{- 2 i x}}{2} + \frac{1}{2} = \frac{1}{2} \cos 2 x + \frac{1}{2}, \end{matrix}$ som er det vi viste i denne oppgaven.

d)

Når vi dreier flatestykket med arealet $A_{1}$ $360^{\circ}$ om x-aksen, får vi et omdreiningslegeme med volum $V_{1}$ .

Bruk formelen $(*)$ i oppgave c) til å bestemme et eksakt uttrykk for $V_{1}$ ved regning.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Ved å dele opp volumet av et omdreiningslegeme til en funksjon $f (x)$ i uendelig mange, uendelig tynne sylindere med volum $π {(f (x))}^{2} d x$ kan vi uttrykke det som et integral.

Arealet under grafen til $f$ finner vi ved å summere uendelig mange, uendelig tynne rektangler med høyde $f (x)$ og bredde $d x$ . På tilsvarende måte kan vi dele opp volumet av omdreiningslegemet i uendelig mange, uendelig tynne sylindere med radius $f (x)$ og høyde $d x$ . Volumet av en slik sylinder er da $π {(f (x))}^{2} d x$ . Volumet $V_{1}$ av omdreiningslegemet kan vi skrive som integralet av alle disse sylinderene. Altså må

$\begin{matrix} V_{1} & = \int_{- \frac{π}{2}}^{\frac{π}{2}} π {(f (x))}^{2} d x = π \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} x d x . \end{matrix}$

Ved å bruke formelen (*) finner vi da at $\begin{matrix} π \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} x d x = π \int_{- \frac{π}{2}}^{\frac{π}{2}} (\frac{1}{2} \cos 2 x + \frac{1}{2}) d x \\ = \frac{1}{2} π \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos 2 x d x + \frac{1}{2} π \int_{- \frac{π}{2}}^{\frac{π}{2}} 1 d x \\ = \frac{1}{2} π \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos 2 x d x + \frac{1}{2} π (\frac{π}{2} - (- \frac{π}{2})) \\ = \frac{1}{2} π \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos 2 x d x + \frac{π^{2}}{2} . \end{matrix}$ Ved enten å se at den deriverte av $\frac{1}{2} \sin 2 x$ er $\cos 2 x$ eller ved å bruke substitusjonsmetoden med substitusjonen $u (x) = 2 x$ , følger det at $\begin{matrix} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos 2 x d x = {[\frac{1}{2} \sin 2 x]}_{- \frac{π}{2}}^{\frac{π}{2}} \\ = \sin (2 \frac{π}{2}) - \sin (- 2 \frac{π}{2}) \\ = \sin (π) - \sin (- π) = 0 - 0 = 0 . \end{matrix}$ Altså er volumet $V_{1}$ av omdreiningslegemet $\begin{matrix} V_{1} & = \frac{1}{2} π \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos 2 x d x + \frac{π^{2}}{2} = \frac{1}{2} π \cdot 0 + \frac{π^{2}}{2} = \frac{π^{2}}{2} . \end{matrix}$

Svar: $\begin{matrix} V_{1} & = \frac{π^{2}}{2} \end{matrix}$

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Omdreiningslegeme

Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.

omdreiningslegeme

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

For flere forklaringer og eksempler på omdreiningslegemer, se artikkelen Volum av et omdreiningslegeme.

Oppgave 6 (7 poeng) Nettkode: E-4DBA

En rett linje i planet skjærer koordinataksene i $A (a, 0)$ og $B (0, b)$ . Se skissen nedenfor.

a)

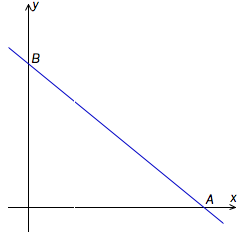
Vis at likningen til linjen kan skrives

$y = - \frac{b}{a} x + b$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi må finne funksjonsuttrykket for den rette linjen som går gjennom de to punktene $A (a, 0)$ og $B (0, b)$ .

Den rette linjen som går gjennom punktene $A (a, 0)$ og $B (0, b)$ må ha stigningstall lik $\begin{matrix} \frac{y_{A} - y_{B}}{x_{A} - x_{B}} = \frac{0 - b}{a - 0} = - \frac{b}{a} . \end{matrix}$ Siden linjen skjærer $y$ -aksen i punktet $B (0, b)$ følger det videre at konstantleddet er lik $y_{B} = b$ . Vi har altså funnet at likningen for den rette linjen som går gjennom $A$ og $B$ er gitt ved $\begin{matrix} y (x) = - \frac{b}{a} x + b . \end{matrix}$

Alternativ løsning:

Siden $A$ og $B$ har forskjellige $x$ -verdier kan den rette linjen skrives $y (x) = C_{1} x + C_{2}$ der $C_{1}$ og $C_{2}$ er konstanter. At linjen går gjennom punktet $A (a, 0)$ betyr at konstantene $C_{1}$ og $C_{2}$ må tilfredsstille $\begin{matrix} y (a) = C_{1} a + C_{2} = 0 . \end{matrix}$ Tilsvarende kan vi kreve at linjen skal gå gjennom punktet $B (0, b)$ ved å sette $\begin{matrix} y (0) = C_{1} \cdot 0 + C_{2} = C_{2} = b . \end{matrix}$ Dette gir likningssettet $\begin{matrix} (I) . & C_{1} a + C_{2} = 0 \\ (I I) . & C_{2} = b . \end{matrix}$ Siden vi allerede vet at $C_{2} = b$ følger det imidlertid at $$\begin{split} C_1a+b=0 \implies C_1 = -\frac{b}{a}. \end{split}$$ Altså kan likningen til den rette linjen som går gjennom punktene $A$ og $B$ skrives $\begin{matrix} y (x) = - \frac{b}{a} x + b . \end{matrix}$

Mer om:

Denne oppgaven er om

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineær funksjon

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

For flere forklaringer og eksempler på lineære funksjoner, se artikkelen Rette linjer (lineære funksjoner).

Visste du at:

Siden vi kan definere en rett linje som den korteste veien mellom to punkter kan det i enkelte sammenhenger være interessant å se hvordan rette linjer ser ut dersom vi studerer en geometri som ikke er flat. En rett linje på jordklodens overflate kan for eksempel ikke skrives på formen $y (x) = C_{1} x + C_{2}$ siden jordkloden er rund, og ikke flat. På jordkloden er de rette linjestykkene deler av sirkler som strekker seg rundt hele jorden. Dette er grunnen til at hvis du går langt nok langs en rett linje på jordkloden, vil du komme tilbake der du startet. At en geometri er flat betyr i praksis at enhver avstand $Δ s$ kan skrives som $\begin{matrix} Δ s^{2} = Δ x^{2} + Δ y^{2}, \end{matrix}$ der $Δ x$ og $Δ y$ er avstanden langs to vinkelrette akser. Dette er det du kanskje som pythagoras læresetning. Et litt mer interessant tilfelle er de geometriene som bare er flate i uendelig små områder. Her er pythagoras læresetning fortsatt sann, men bare for uendelig små avstander $d s$ , altså $\begin{matrix} d s^{2} = d x^{2} + d y^{2} . \end{matrix}$ Eksempler på slike geometrier kan være sfærer, slik som jordkloden, eller tid-rommet i Einsteins generelle relativitetsteori.

b)

Vis at dette også kan skrives

$\frac{x}{a} + \frac{y}{b} = 1$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi ønkser å omformulere likningen fra oppgave $a)$ slik at den sier $x / a + y / b = 1$ .

Fra oppgave $a)$ har vi at $\begin{matrix} y = - \frac{b}{a} x + b . \end{matrix}$ Ved å legge til $\frac{b}{a} x$ på begge sider av likhetstegnet kan vi skrive dette som $\begin{matrix} y + \frac{b}{a} x = b, \end{matrix}$ og ved å multiplisere begge sider av likningen med $\frac{1}{b}$ følger det at $\begin{matrix} \frac{y}{b} + \frac{x}{a} = 1, \end{matrix}$ som er det vi ønsket å vise.

Mer om:

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

For flere forklaringer og eksempler på lineære likninger, se artikkelen Førstegradslikninger.

c)

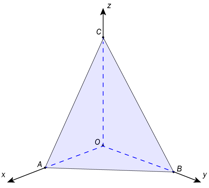
Et plan $α$ i rommet skjærer koordinataksene i $A (a, 0, 0)$ , $B (0, b, 0)$ og $C (0, 0, c)$ .

Vis at normalvektoren til planet $α$ er

$\vec{n} = [b c, a c, a b]$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi er nødt til å finne et uttrykk for en av vektorene som står vinkelrett på alle vektorer mellom to punkter i $α$ . Det kan vi gjøre ved å finne to vektorer mellom punkter i $α$ .

Siden $A (a, 0, 0)$ , $B (0, b, 0)$ og $C (0, 0, c)$ ligger i $α$ er vektorene $\begin{matrix} \vec{A B} & = \vec{O B} - \vec{O A} = [0, b, 0] - [a, 0, 0] = [- a, b, 0] \\ \vec{A C} & = \vec{O C} - \vec{O A} = [0, 0, c] - [a, 0, 0] = [- a, 0, c] \end{matrix}$ vektorer mellom punkter i $α$ . Altså må vektoren $\begin{matrix} \vec{A B} \times \vec{A C} & = | \begin{matrix} {\vec{e}}_{x} & {\vec{e}}_{y} & {\vec{e}}_{z} \\ - a & b & 0 \\ - a & 0 & c \end{matrix} | = | \begin{matrix} b & 0 \\ 0 & c \end{matrix} | {\vec{e}}_{x} - | \begin{matrix} - a & 0 \\ - a & c \end{matrix} | {\vec{e}}_{y} + | \begin{matrix} - a & b \\ - a & 0 \end{matrix} | {\vec{e}}_{z} \\ = b c {\vec{e}}_{x} - (- a c) {\vec{e}}_{y} + a b {\vec{e}}_{z} = [b c, a c, a b] \end{matrix}$ stå normalt på alle vektorer mellom punkter i $α$ . Med andre ord kan vi definere normalvektoren $\begin{matrix} \vec{n} = [b c, a c, a b], \end{matrix}$ som er det vi ønsket å vise. Legg merke til at det finnes uendelig mange normalvektorer. For alle $C \neq 0$ er nemlig $C \vec{n}$ også en normalvektor.

Alternativ løsning:

Hvis vi klarer å finne konstanter $C_{1}$ , $C_{2}$ og $C_{3}$ slik at $\begin{matrix} C_{1} x + C_{2} y + C_{3} z + 1 = 0 \end{matrix}$ er likningen for planet $α$ kan vi skrive velge normalvektoren som en konstant multiplisert med ${\vec{n}}_{0} = [C_{1}, C_{2}, C_{3}]$ . At punktene $A (a, 0, 0)$ , $B (0, b, 0)$ og $C (0, 0, c)$ ligger i $α$ gir følgende sett av likninger: $$\begin{split} (I) & \ \ \ \ \ C_1a+1=0 \implies C_1 = -\frac{1}{a}\\ (II) & \ \ \ \ \ C_2b+1=0 \implies C_2 = -\frac{1}{b} \\ (III) & \ \ \ \ \ C_3c+1=0 \implies C_3 = -\frac{1}{c}. \end{split}$$ Altså er likningen til planet gitt som $\begin{matrix} - \frac{1}{a} x - \frac{1}{b} y - \frac{1}{c} z + 1 = 0 . \end{matrix}$ Ved å multiplisere begge sider av likhetstegnet med $- a b c$ følger det at likningen for planet $α$ kan skrives $\begin{matrix} b c x + a c y + a b z - a b c = 0 . \end{matrix}$ Normalvektoren kan altså velges til å være $\begin{matrix} \vec{n} = [b c, a c, a b], \end{matrix}$ som er det vi ønsket å vise.

Mer om:

Denne oppgaven er om

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

d)

Vis at likningen til $α$ kan skrives

$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$

Løs oppgaven her

Løsningsforslag d)

Jeg tenker:

For å uttrykke likningen til planet $α$ kan vi enten finne en normalvektor $\vec{n}$ og et punkt i $α$ , eller tre konstanter $C_{1}$ , $C_{2}$ og $C_{3}$ slik at $C_{1} x + C_{2} y + C_{3} z + 1 = 0$ for alle punkter $P (x, y, z)$ i $α$ .

Siden punktet $A (a, 0, 0)$ ligger i $α$ og $\vec{n} = [b c, a c, a b]$ kan velges som normalvektor til planet må alle punkter $P (x, y, z)$ i $α$ tilfredsstille $\begin{matrix} \vec{n} \cdot \vec{A P} = [b c, a c, a b] \cdot [x - a, y, z] = 0 . \end{matrix}$ Altså er likningen for planet gitt av $\begin{matrix} b c x + a c y + a b z - a b c = 0 \end{matrix}$ og ved å multiplisere begge sider av likhetstegnet med $\frac{1}{a b c}$ finner vi at $\begin{matrix} \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1, \end{matrix}$ som er det vi ønsket å vise.

Alternativ løsning:

Vi må finne konstanter $C_{1}$ , $C_{2}$ og $C_{3}$ slik at $\begin{matrix} C_{1} x + C_{2} y + C_{3} z + 1 = 0 \end{matrix}$ er likningen til det planet $α$ som punktene $A (a, 0, 0)$ , $B (0, b, 0)$ og $C (0, 0, c)$ er en del av. At $A$ ligger i $α$ betyr at $C_{1} a + 1 = 0$ og derfor $C_{1} = - \frac{1}{a}$ . Siden $B$ ligger i $α$ må $C_{2} b + 1 = 0$ som betyr at $C_{2} = - \frac{1}{b}$ og at $C$ ligger i $α$ betyr at $C_{3} = - \frac{1}{c}$ . Vi har med andre ord funnet at likningen for planet $α$ kan skrives $\begin{matrix} - \frac{x}{a} - \frac{y}{b} - \frac{z}{c} + 1 = 0, \end{matrix}$ som ved å multiplisere begge sider med $- 1$ og deretter legge til én på begge sider kan skrives $\begin{matrix} \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 . \end{matrix}$

Mer om:

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Origo

I et koordinatsystem står to akser vinkelrett på hverandre. Punktet der aksene møtes kalles origo. Origo har koordinatene (0,0).

origo

For flere forklaringer og eksempler på vektorer, se artikkelen Enhetsvektor og normalisering.

Visste du at:

I den alternative løsningen brukte vi at ethvert plan kan skrives $\begin{matrix} C_{1} x + C_{2} y + C_{3} z + 1 = 0 \end{matrix}$ for tre konstanter $C_{1}$ , $C_{2}$ og $C_{3}$ . Dette er ikke sant! Det generelle uttrykket for et plan er nemlig $\begin{matrix} K_{1} x + K_{2} y + K_{3} z + K_{4} = 0, \end{matrix}$ for fire konstanter $K_{1}$ , $K_{2}$ , $K_{3}$ og $K_{4}$ . Hvis $K_{4} \neq 0$ , altså at Origo ikke ligger i planet, kan vi dele begge sider på $K_{4}$ og få $\begin{matrix} \frac{K_{1}}{K_{4}} x + \frac{K_{2}}{K_{4}} y + \frac{K_{3}}{K_{4}} z + 1 = 0 . \end{matrix}$ Hvis vi nå kaller konstanten $\frac{K_{1}}{K_{4}}$ for $C_{1}$ , konstanten $\frac{K_{2}}{K_{4}}$ for $C_{2}$ og konstanten $\frac{K_{3}}{K_{4}}$ for $C_{3}$ kan vi skrive likningen for et plan på formen $\begin{matrix} C_{1} x + C_{2} y + C_{3} z + 1 = 0 . \end{matrix}$ Dette er imidlertid bare mulig dersom planet ikke inneholder Origo. Hvis Origo ligger i planet $α$ stemmer altså ikke likningen for planet. Det kan vi se ved å sette en av konstantene $a$ , $b$ eller $c$ lik null. Da får vi nulldivisjon i likningen for planet – det er ikke bra! Måten vi kan løse dette på er imidlertid ganske enkel; hvis vi multipliserer begge sider av likhetstegnet med $a b c$ og skriver planlikningen på formen $\begin{matrix} b c x + a c y + a b z = a b c \end{matrix}$ holder den også for tilfellet der Origo ligger i planet.

e)

Planet $β$ skjærer $x$ -aksen i $D (5, 0, 0)$ og $y$ -aksen i $E (0, 4, 0)$ . Planet er parallelt med $z$ -aksen.

Forklar hvordan vi kan bruke resultatet i oppgave d) til å bestemme likningen for planet $β$ .

Løs oppgaven her

Løsningsforslag e)

Jeg tenker:

At planet $β$ er parallelt med $z$ -aksen kan vi enten tolke som at $β$ aldri skjærer $z$ -aksen, eller at $β$ skjærer $z$ -aksen i $z = \infty$ . Ved å benytte den siste tolkningen kan vi bruke resultatet i oppgave $d)$ til å uttrykke likningen for planet $β$ .

Fra oppgave $d)$ har vi at ethvert plan som skjærer $x$ -aksen i $x = a$ , $y$ -aksen i $y = b$ og $z$ -aksen i $z = c$ har likning $\begin{matrix} \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 . \end{matrix}$ Siden planet $β$ skjærer $x$ - og $y$ -aksen i henholdsvis $5$ og $4$ må $a = 5$ og $b = 4$ . Det betyr at likningen for $β$ er gitt av $\begin{matrix} \frac{x}{5} + \frac{y}{4} + \frac{z}{c} = 1 . \end{matrix}$ Siden planet $β$ er parallell med $z$ -aksen kan det ikke finnes noe punkt i $β$ som også er på $z$ -aksen. Et slikt skjæringspunkt mellom $z$ -aksen og planet $β$ må altså befinne seg uendelig langt borte – i $z = \infty$ . Det betyr at $c$ må være et uendelig stort tall, som videre betyr at $\frac{1}{c}$ må være et uendelig lite tall. Med andre ord er likningen for planet $β$ gitt av $\begin{matrix} \lim_{c \to \infty} (\frac{x}{5} + \frac{y}{4} + \frac{z}{c}) = \frac{x}{5} + \frac{y}{4} + 0 \cdot z = \frac{x}{5} + \frac{y}{4} = 1 . \end{matrix}$

Svar:

$\begin{matrix} \frac{x}{5} + \frac{y}{4} = 1 . \end{matrix}$

Mer om:

Denne oppgaven er om

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".

parallell

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Vektorfunksjon

En vektorfunksjon $\vec{r (t)}$ er en funksjon av en variabel t som gir en vektor fra origo for hver t:

$\vec{r (t)} = [x (t), y (t)]$

vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Avstand mellom et punkt og et plan.

REA3024 2013 Høst

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4D9R

a)

Løsningsforslag a)

Derivasjon

Cosinus

Funksjon

b)

Løsningsforslag b)

Alternativ løsning

Sinus

Funksjon

Derivasjon

Deriverbarhet

Oppgave 2 (3 poeng) Nettkode: E-4D9U

a)

Løsningsforslag a)

Alternativ løsning

Integralregning

Eksponentialfunksjon

b)

Løsningsforslag b)

Integrasjon

Eksponentialfunksjon

Oppgave 3 (5 poeng) Nettkode: E-4D9Y

a)

Løsningsforslag a)

Vektor

b)

Løsningsforslag b)

Alternativ løsning

Parallell

Tetraeder

Vektor

Volum

c)

Løsningsforslag c)

Alternativ løsning

Plan

Vektor

Normalvektor

Ligning

Oppgave 4 (4 poeng) Nettkode: E-4DA2

a)

Løsningsforslag a)

Sum

Konvergens

b)

Løsningsforslag b)

Sum

Konvergens

Oppgave 5 (2 poeng) Nettkode: E-4DAD

Løsningsforslag

Differensiallikning

Integrasjon

Oppgave 6 (4 poeng) Nettkode: E-4DAG

a)

Løsningsforslag a)

Derivasjon

Vendepunkt

Ligning

b)

Løsningsforslag b)

Vendepunkt

Tangent

Ligning

Graf

Funksjon

Oppgave 7 (3 poeng) Nettkode: E-4DAJ

Løsningsforslag

Matematisk induksjon

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4DAM

a)

Løsningsforslag a)

Alternativ løsning