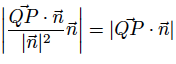Avstand mellom et punkt og et plan

La oss se på hvordan vi kan finne avstanden mellom et vilkårlig punkt i rommet og et gitt plan.

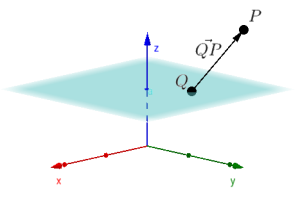
Likningen for planet $a x + b y + c z + d = 0$ har en normalvektor gitt ved $\vec{N} = [a, b, c]$ . Vi kan normalisere denne for å finne en normalvektor med lengde $1$ : $\vec{n} = \frac{\vec{N}}{| \vec{N} |} = \frac{[a, b, c]}{\sqrt{a^{2} + b^{2} + c^{2}}} .$ Vi fikserer et punkt $Q = (x_{0}, y_{0}, z_{0})$ i planet, det vil si $a x_{0} + b y_{0} + c z_{0} + d = 0 .$ La $P = (x_{1}, y_{1}, z_{1})$ være et vilkårlig punkt i rommet. Da kan vi betrakte vektoren $\vec{Q P} = (x_{1} - x_{0}, y_{1} - y_{0}, z_{1} - z_{0})$ som figuren viser.

Avstanden mellom punktet og planet er da gitt som:

siden $| \vec{n} | = 1$ . Vi får at avstanden er

$|[x_{1} - x_{0}, y_{1} - y_{0}, z_{1} - z_{0}] \cdot \frac{[a, b, c]}{\sqrt{a^{2} + b^{2} + c^{2}}}|$ $= |\frac{a (x_{1} - x_{0}) + b (y_{1} - y_{0}) + c (z_{1} - z_{0})}{\sqrt{a^{2} + b^{2} + c^{2}}}| .$

Vi kan forenkle denne formelen. Siden $Q = (x_{0}, y_{0}, z_{0})$ er et punkt på planet, vet vi at $a x_{0} + b y_{0} + c z_{0} = - d .$ Dette kan vi sette inn i formelen og vi får:

$|\frac{a x_{1} + b y_{1} + c z_{1} + d}{\sqrt{a^{2} + b^{2} + c^{2}}}| .$

Eksempel 1

Vi er gitt et plan med likning $3 x - 4 y + 2 z - 8 = 0$ og et punkt $P = (0, - 1, 2)$ . Vi ønsker å finne avstanden mellom punktet og planet. Det er to måter å gjøre dette på. Vi kan simpelthen merke at punktet $P$ faktisk ligger på planet, siden $3 \cdot 0 - 4 \cdot (- 1) + 2 \cdot 2 = 8 .$ Dermed må avstanden mellom punktet og planet være null. Vi kan bekrefte dette med formelen:

$|\frac{3 \cdot 0 - 4 \cdot (- 1) + 2 \cdot 2 - 8}{\sqrt{0^{2} + {(- 1)}^{2} + 2^{2}}}| = 0 .$

Eksempel 2

Vi er gitt et plan med likning $4 x + 2 y - 3 z - 4 = 0$ og et punkt $P = (1, 1, 1)$ . Denne gangen ligger ikke punktet på planet, da $4 \cdot 1 + 2 \cdot 1 - 3 \cdot 1 - 4 = - 1 \neq 0 .$ Vi bruker formelen for å finne avstand mellom punktet $P$ og planet:

$|\frac{4 \cdot 1 + 2 \cdot 1 - 3 \cdot 1 - 4}{\sqrt{4^{2} + 2^{2} + {(- 3)}^{2}}}| = |\frac{- 1}{\sqrt{29}}| = \frac{1}{\sqrt{29}} .$

Del på Facebook

Del på Facebook

Lynkurs 11.-13.trinn

Vektorer

Består av:

Skrevet av

Tommy Lundemo

Institusjon

Universitetet i Bergen