Stedvektor (posisjonsvektor)

Vi skal nå se på vektorer i et vanlig todimensjonalt koordinatsystem. Hva er en stedvektor? Når er vektorene like?

Hvis vi har et ordnet tallpar $(x, y)$ kan vi danne vektoren $\vec{v} = [x, y]$ . Vi tenker på $x$ -koordinaten til vektoren som antall enheter mellom start- og endepunkt i den positive $x$ -retningen, og tilsvarende for $y$ -koordinaten. Geometrisk kan vi dermed tegne mange representanter for samme vektor som vist på Figur 1.


Figur 1		Figur 2

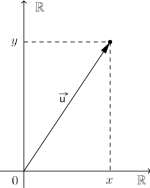
Vi kan altså tegne vektorer hvor som helst i planet. En vektor kan imidlertid parallellforskyves slik at origo er startpunktet, så vi tar ofte utgangspunkt i origo, og tegner vektoren $\vec{v} = [x, y]$ som pilen med startpunkt i origo og endepunkt i $(x, y)$ som vist på Figur 2.

Tallene $x$ og $y$ kalles koordinatene/komponentene til vektoren $\vec{v} = [x, y]$ , og $[x, y]$ kalles koordinatformen til $\vec{v}$ .

Eksempel

For å forflytte oss fra origo til punktet $(3, 2)$ kan vi tenkte at vi først beveger oss 3 sted i $x$ -retningen, så 2 steg i $y$ -retningen. Vektoren fra origo $(0, 0)$ til $P = (3, 2)$ kan beskrive denne forflytningen, og noteres på koordinatform med rette parenteser, slik: $[3, 2]$ .

Dette kaller vi stedvektoren eller posisjonsvektoren til punktet P.

definisjon av stedvektor (posisjonsvektor)

Stedvektoren eller posisjonsvektoren til punktet $P$ er vektoren fra origo $(0, 0)$ til punktet $P$ .

Stedvektoren til et punkt har alltid samme $(x, y)$ -koordinater som punktet selv.

Stedvektor (posisjonsvektor)

Eksempel

Lynkurs 11.-13.trinn

Vektorer

Består av: