Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3024 2016 HØST

Del 1
Del 2
Eksamensinformasjon

Eksamenstid
5 timer: 
Del 1 skal leveres inn etter 3 timer. 
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler på del 1
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler

Hjelpemidler på del 2
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte
Del 1 har 7 oppgaver. Del 2 har 4 oppgaver.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen
Poeng i del 1 og del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse  
gjennomfører logiske resonnementer  
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner  
kan bruke hensiktsmessige hjelpemidler  
vurderer om svar er rimelige  
forklarer framgangsmåter og begrunner svar  
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger
Kilder for bilder, tegninger osv.: 

Befolkning: www.dagbladet.no (06.05.2016)
Alle grafer og figurer: Utdanningsdirektoratet

DEL 1 uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4PBT

Deriver funksjonene

$f (x) = 3 \cos 2 x$

Løs oppgaven her

Løsningsforslag

Jeg tenker

$f (x)$ er en konstant multiplisert med en cosinusfunksjon med kjerne $2 x$ . Da kan vi bruke kjerneregelen for derivasjon.

Vi har $f (x) = 3 \cos (2 x)$ som er en sammensatt funksjon. Da kan vi bruke kjerneregelen for derivasjon som sier at den deriverte av en sammensatt funksjon $[f (u (x))]' = f' (u (x)) u' (x)]$ Vi kan sette $u (x) = 2 x$ .

$\begin{matrix} u' (x) & = & (2 x)' & = & 2 \\ f' (u) & = & (3 \cos u)' & = & - 3 \sin u \end{matrix}$

Når vi regner ut ved å bruke kjerneregelen får vi

$\begin{matrix} f' (u (x)) & = & f' (u (x)) u' (x) \\ = & - 3 \sin u \cdot 2 \\ = & - 6 \sin (2 x) \end{matrix}$

Svar: $f' (x) = - 6 \sin (2 x)$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

En trigonometrisk funksjon.
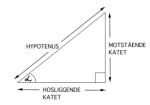
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av sammensatte uttrykk.

b)

$g (x) = e^{\sin x}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Dette er en sammensatt funksjon, og vi kan sette kjernen

u (x) = \sin x

og bruke kjerneregelen.

Vi kan bruke kjerneregelen da kan vi velge $u (x) = \sin x$ som kjerne. Kjerneregelen gir da

$\begin{matrix} g (u (x)' & = & g' (u) \cdot u' (x) \\ = & (e^{u})' \cdot (\sin x)' \\ = & e^{u} \cdot \cos x \\ = & e^{\sin x} \cdot \cos x \end{matrix}$

Svar: $g' (x) = e^{\sin x} \cdot \cos x$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen - tre eksempler.

c)

$h (x) = \frac{x}{\sin x}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi skal derivere en brøk med funksjoner i både teller og nevner. Da kan vi bruke brøkregelen.

Brøkregelen for derivasjon sier at for to deriverbare funksjoner $u (x)$ og $v (x)$ er

$(\frac{u}{v})' = \frac{u' v - u v'}{v^{2}}$

Vi kan sette $u (x) = x$ og $v (x) = \sin x$ . Vi har at $u' (x) = 1$ og $v' (x) = \cos x$ . Da følger det at

$\begin{matrix} h' (x) & = & \frac{x}{\sin x} \\ = & \frac{x' \sin x - x \cdot (\sin x)'}{\sin^{2} x} \\ = & \frac{\sin x - x \cos x}{\sin^{2} x} \end{matrix}$

Svar: $h' (x) = \frac{\sin x - x \cos x}{\sin^{2} x}$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av sammensatte uttrykk.

Oppgave 2 (5 poeng) Nettkode: E-4PBX

Bestem integralene

a)

$\int (x^{2} - 3 x + 2) dx$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Et intergral av en sum er det samme som summen av integralene til hvert av leddene, så vi kan integrere hvert ledd for seg.

Vi kan integrere leddene i polynomet hver for seg, så vi kan skrive

$\int (x^{2} - 3 x + 2) d x = \int x^{2} d x + \int (- 3 x) d x + \int 2 d x$

Når C er en konstant kan vi skrive $\int C f (x) d x = C \int f (x) d x$ , da får vi

$\int (x^{2} - 3 x + 2) d x = \int x^{2} d x - 3 \int x d x + 2 \int 1 d x$

Integralet av en funksjon $x^{n}$ er $\frac{1}{n + 1} x^{n + 1} + C$ .

Nå kan vi regne ut

$\begin{matrix} \int (x^{2} - 3 x + 2) d x & = & \int x^{2} d x - 3 \int x d x + 2 \int 1 d x \\ = & \frac{1}{3} x^{3} + C_{1} - \frac{3}{2} x^{2} + C_{2} + 2 x + C_{3} \\ = & \frac{1}{3} x^{3} - \frac{3}{2} x^{2} + 2 x + C \end{matrix}$

Her har vi satt $C = C_{1} + C_{2} + C_{3}$ .

Svar: $\int (x^{2} - 3 x + 2) d x = \frac{1}{3} x^{3} - \frac{3}{2} x^{2} + 2 x + C$

Mer om

Denne oppgaven er om

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynomer

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler, se artikkelen Delvis integrasjon.

b)

$\int x \cos x dx$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi skal finne integralet til produktet av $x$ og $\cos x$ . Vi kjenner den integrerte til $\cos x$ som er $\sin x$ , og $x$ blir lettere når vi deriverer den, så da kan det være lurt å bruke delvis integrasjon.

Delvis integrasjon sier at hvis vi har to deriverbare funksjoner $u (x)$ og $v (x)$ så er

$\int u (x) v' (x) d x = u (x) v (x) - \int u' (x) v (x) d x$

Ved å sette $u (x) = x$ og $v' (x) = \cos x$ får vi $u' (x) = 1$ og $v (x) = \sin x$ . Da har vi at

$\begin{matrix} \int x \cos x d x & = & \int u (x) v' (x) d x \\ = & u (x) v (x) - \int u' (x) v (x) d x \\ = & x \sin x + C_{1} - \int 1 \sin x d x \\ = & x \sin x + C_{1} + \cos x + C_{2} \\ = & x \sin x + \cos x + C \end{matrix}$

der $C = C_{1} + C_{2}$

Svar: $\int x \cos x d x = x \sin x + \cos x + C$

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler, se artikkelen Delvis integrasjon.

c)

$\int 2 x \sin x^{2} dx$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Her ser vi at sinusfunksjonen i integranden har en kjerne, $x^{2}$ . I tillegg er $(x^{2})' = 2 x$ en faktor i integranden. Det kan tyde på at vi bør prøve å integrere ved hjelp av substitusjon.

Vi kan prøve å løse integralet ved å bruke substitusjon. Regelen for intergrasjon sier at dersom vi har $F' = f$ og $u$ er deriverbar, så er

$\int f (u (x)) \cdot u' (x) d x = \int F (u (x)) + C$

Sinusfunksjonen har en kjerne $x^{2}$ , så vi kan prøve med $u (x) = x^{2}$ . Da blir $u' (x) = 2 x$ , og vi får følgende utregning:

$\int 2 x \sin x^{2} d x = \int \sin u \cdot u' (x) d x = \int \sin u d u = - \cos u + C$

Nå kan vi sette inn $u = u (x) = x^{2}$ . Resultatet av integrasjonen blir da

$\int 2 x \sin x^{2} d x = - \cos x^{2} + C$

Svar: $\int 2 x \sin x^{2} d x = - \cos x^{2} + C$

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på integrasjon, se artikkelen Integrasjon ved substitusjon.

Oppgave 3 (4 poeng) Nettkode: E-4PC1

En rett linje går gjennom $A (0, 0)$ og $B (h, r)$ der $h$ og $r$ er to positive tall.

a)

Bestem ligningen for linjen, uttrykt ved $h$ og $r$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi vil ha en ligning på formen $f (x) = a x + b$ , der $a$ er stigningstallet, og $b$ er konstantleddet som sier hvor linjen krysser $y$ -aksen.

Linjen går gjennom $A (0, 0)$ , så den krysser $y$ -aksen i $0$ , så $b = 0$ .

Stigningstallet kan vi finne ved å dividere hvor mye grafen vokser i $y$ -retning, $r$ , på hvor mye den vokser i $x$ -retning, $h$ , da finner vi får vi

$f (x) = \frac{r}{h} x$

Svar: $f (x) = \frac{r}{h} x$

Mer om

Denne oppgaven er om

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linjer

Stigningstall

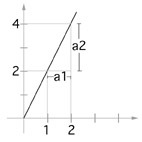
Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner).

b)

Linjestykket $A B$ roteres $360^{\circ}$ om $x$ -aksen. Vi får da et omdreiningslegeme.

Bestem et uttrykk for volumet til omdreiningslegemet.
Hva slags legeme har du regnet ut volumet til?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Formelen til volumet av et omdreiningslegeme, rotert $360^{\circ}$ om $x$ -aksen er $V = π \int_{a}^{b} (f (x))^{2} d x$ I deloppgave b) fant vi et uttrykk, $f (x)$ for linjestykket $A B$ .

I deloppgave b) fant vi at linjen gjennom punktene $A$ og

$B$ kan uttrykkes ved $f (x) = \frac{r}{h} x$ .

Nå skal vi bare se på linjestykket $A B$ . Det avgrenses av $x = 0$ og $x = h$ . For å finne volumet til omdreiningslegemet, bruker vi at $h > 0$ og får

$V = π \int_{0}^{h} (f (x))^{2} d x = π \int_{0}^{h} {(\frac{r}{h} x)}^{2} d x = π \int_{0}^{h} {(\frac{r}{h})}^{2} x^{2} d x$

Siden $\frac{r}{h}$ er en konstant, kan vi trekke den utenfor integralet. Vi kan bruke regelen for integralet til $x^{n}$ er $\frac{1}{n + 1} x^{n + 1}$ og da kan vi finne volumet $V$ ved å regne ut

$\begin{matrix} π \cdot \int_{0}^{h} {(\frac{r}{h})}^{2} x^{2} d x & = & π {(\frac{r}{h})}^{2} \int_{0}^{h} x^{2} d x \\ = & π \cdot {(\frac{r}{h})}^{2} {[\frac{1}{3} x^{3}]}_{0}^{h} \\ = & \frac{π \cdot r^{2}}{h^{2}} (\frac{1}{3} h^{3} - \frac{1}{3} 0^{3}) \\ = & π \cdot \frac{r^{2}}{h^{2}} \cdot \frac{1}{3} h^{3} \\ = & \frac{π \cdot h \cdot r^{2}}{3} \end{matrix}$

Volumet til omdreiningslegemet kan uttrykkes ved $V = \frac{π \cdot h \cdot r^{2}}{3}$ .

Dette er formelen for volumet til en kjegle. Den vil ha toppunkt i $(0, 0)$ , høyde $h$ og akse langs $x$ -aksen.

Svar: $V = \frac{π \cdot h \cdot r^{2}}{3}$ og er volumet til en kjegle.

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Kjegle

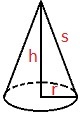
En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.

Kjeksen til en kroneis har form som en kjegle.

Volum : V = $\frac{π r^{2} h}{3}$
Overflate : A = $π r^{2} + π r s$

kjegle

For flere forklaringer og eksempler på volum, se artikkelen Halvar utleder formler for volum til kuler og kjegler.

Oppgave 4 (6 poeng) Nettkode: E-4P7A

En funksjon $f$ er gitt ved

$f (x) = 3 \sin (\frac{π}{2} x) + 5, D_{f} = ⟨ 0, 12 ⟩$

a)

Bestem perioden til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

En funksjon $g (x)$ har periode $p$ dersom $p$ er det minste positive tall slik at

$g (x) = g (x + p)$

for alle $x i D_{g}$ . En periodisk funksjon kan ikke ha begrenset definisjonsmengde, så funksjonen $f$ i oppgaven er ikke periodisk. Vi antar i oppgave a) at $D_{f} = ℝ$ for å kunne beregne en periode. Vi vet at

$h (x) = A \sin (c x + φ) + d$

har periode $\frac{2 π}{c}$ .

Funksjonen $f (x)$ er på formen

$A \sin (c x + φ) + d$

med $c = \frac{π}{2}$ . Perioden er derfor

$p = \frac{2 π}{\frac{π}{2}} = 4$ .

Svar: Perioden til $f$ er $4$ .

Mer om

Denne oppgaven er om

Trigonometriske funksjoner

Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.

trigonometriske funksjoner

Sinus

En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.

sinus

For flere forklaringer og eksempler på funksjoner, se artikkelen Periodiske funksjoner.

b)

Bestem ekstremalverdiene $y_{m i n}$ og $y_{m a k s}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Verdien til sinusfunksjon svinger mellom $- 1$ og $1$ . Funksjonen $f (x)$ vil ha ekstremverdier der $\sin (\frac{π}{2} x) = \pm 1$ dersom det kan oppnås innenfor $D_{f}$ .

Siden $D_{f} = ⟨0, 12⟩$ vil den harmoniske funksjonen gjennomløpe $3$ fulle perioder, og dermed oppnå ekstremalverdienen

$3 \cdot (\pm 1) + 5 = 5 \pm 3$ .

Dette gir $y_{m i n} = 2 og y_{maks} = 8$ .

Svar: $y_{m i n} = 2 og y_{maks} = 8$

Mer om

Denne oppgaven er om

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunkter

Sinus

sinus

For flere forklaringer og eksempler på sinus, se artikkelen Grafene til sin x, cos x og tan x.

c)

Forklar hvorfor grafen vil ha alle sine vendepunkter på likevektlinjen. Bestem koordinatene til vendepunktene.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Likevektslinjen til funksjonen er $y = 5$ . Vendepunktene til $f (x)$ er når den annenderiverte er $0$ og skifter fortegn.

Vendepunktene til $f (x)$ kan vi finne ved å finne ut når $f ″ (x) = 0$ .

Da kan vi begynne med $f' (x)$ . For å derivere $f (x)$ kan vi bruke kjerneregelen, med $u (x) = \frac{π}{2} x$ som kjerne. Utregning gir da

$f' (x) = (3 \sin (u) + 5)' = 3 \cos u \cdot (u)' \frac{π}{2} = \frac{3 π}{2} \cos (\frac{π}{2} x)$

$= 3 \cos (\frac{π}{2} x) \cdot \frac{π}{2} = \frac{3 π}{2} \cos (\frac{π}{2} x)$

Vi kan derivere dette uttrykket igjen for å finne $f ″ (x)$ . Da kan vi bruke samme kjerne.

$f ″ (x) = (\frac{3 π}{2} \cos u)' = \frac{3 π}{2} (- \sin u) \cdot u'$

$= \frac{3 π}{2} (- \sin (\frac{π}{2} x)) \cdot \frac{π}{2} = - \frac{{3 π}^{2}}{4} \sin (\frac{π}{2} x)$

$f ″ (x) = 0$ når $\sin \frac{π}{2} x = 0$ . For at dette skal være tilfelle må vi ha

$\frac{π}{2} x = k π \Rightarrow x = 2 k$

Da må $x$ -koordinaten til vendepunktet være $2 k$ . Siden $D_{f} = ⟨ 0, 12 ⟩$ må vi ha $k = 1, 2, 3, 4, 5$ .

For å finne $y$ -verdien til vendepunktene setter vi inn for $x = 2 k$ i $f (x)$

$f (2 k) = 3 \sin (\frac{2 π k}{2}) + 5 = 5$

Sinusuttrykket blir da lik $0$ , og $y$ -verdiene til koordinatene til vendepunktene er $5$ og dermed ser vi at alle vendepunktene ligger på likevektslinjen.

Svar: Vendepunktene har koordinater $(2 k, 5)$ , der $k = 1, 2, 3, 4, 5$

Mer om

Denne oppgaven er om

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Andrederiverte

Den andrederiverte til en funksjon $f (x)$ er funksjonen derivert to ganger og skrives $f'' (x)$ eller $f^{(2)} (x)$ . Kalles også annenderiverte eller dobbeltderiverte.

annenderivert

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler vendepunkt, se artikkelen Vendepunkt og vendetangent.

d)

Lag en skisse av grafen til $f$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi kan bruke den informasjonen vi har funnet i de tidligere deloppgavene. Da har vi funnet $y_{m a k s}$ og $y_{m i n}$ , likevektslinjen til $f$ og perioden.

Fra deloppgave c) vet vi at likevektslinjen til $f$ er $y = 5$ . Vi vet også at $y_{m a k s} = 8$ . Denne verdien fikk vi når $\sin \frac{π}{2} x = 1$ , for eksempel hvis $\frac{π}{2} x = \frac{π}{2}$ så $x = 1$ . Siden perioden $p = 4$ har vi $y_{m a k s}$ når $x = 1 + 4 n$ , altså for $x = 5$ og $x = 9$ . Minimumspunktene, når $f (x) = y_{m i n}$ vil ligge midt i mellom to maksimumspunkt, så vi $f (x) = y_{m i n}$ når $x = 3 + 4 n$ , altså $x = 3, x = 7$ og $x = 11$ . I tillegg vet vi at vi har vendepunkt i $(2 k, 5)$ , for $k = 1, 2, 3, 4, 5$ . Nå kan vi tegne inn de punktene vi har og skissere grafen som går gjennom disse punktene.

Svar: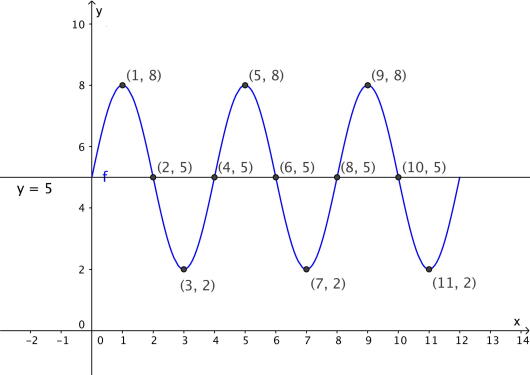

Mer om

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

For flere forklaringer og eksempler om grafer, se artikkelen Grafen til en funksjon.

Oppgave 5 (5 poeng) Nettkode: E-4PC4

Vi har gitt differensialligningen

$y ″ - 4 y' - 5 y = 0$

a)

Vis at $y = e^{r x}$ er en løsning til differensiallikningen når $r^{2} - 4 r - 5 = 0$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å finne ut om $y = e^{r x}$ er en løsning av differensiallikningen kan vi sette inn $e^{r x}$ for $y$ i ligningen.

Dersom $y = e^{r x}$ er en løsning av ligningen $y ″ - 4 y' - 5 y = 0$ , må vi ha at $(e^{r x}) ″ - 4 (e^{r x})' - 5 e^{r x} = 0$ .

Vi kan derivere $e^{r x}$ ved å bruke kjerneregelen med $u (x) = r x$ som kjerne. Det gir at

$(e^{r x})' = (e^{u (x)})' = (e^{u})' \cdot u' (x) = (e^{u})' \cdot (r x)' = e^{u} \cdot r = r \cdot e^{r x}$ .

Tilsvarende får vi

$(e^{r x}) ″ = (r \cdot e^{r x})' = r \cdot (e^{r x})' = r \cdot r \cdot e^{r x} = r^{2} e^{r x}$ .

Nå kan vi sette inn i ligningen

$(e^{r x}) ″ - 4 (e^{r x})' - 5 e^{r x} = r^{2} e^{r x} - 4 r e^{r x} - 5 e^{r x}$ .

Ved å faktorisere ut $e^{r x}$ får vi

$r^{2} e^{r x} - 4 r e^{r x} - 5 e^{r x} = (r^{2} - 4 r - 5) e^{r x}$ .

Siden $(r^{2} - 4 r - 5) = 0$ må også $(r^{2} - 4 r - 5) e^{r x} = 0$ som betyr at $e^{r x}$ er en løsning av ligningen.

Svar: $y = e^{r x}$ er en løsning.

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikninger

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler om differensiallikninger, se artikkelen Andre ordens differensiallikninger.

b)

Bestem den generelle løsningen til differensialligningen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Dette er en andre ordens differensiallikning med karakteristisk likning $r^{2} - 4 r - 5 = 0$ , så for å finne den generelle løsningen må vi finne løsningene til den karakteristiske likningen.

Siden $r^{2} - 4 r - 5 = 0$ er den karakteristiske likningen til differensiallikningen, vil vi finne for hvilken $r$ denne likningen stemmer. Da kan vi bruke andregradsformelen

$r = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

med $a = 1$ , $b = - 4$ og $c = - 5$ .

Det gir

$\begin{matrix} r & = & \frac{- (- 4) \pm \sqrt{(- 4)^{2} - 4 \cdot 1 \cdot (- 5)}}{2 \cdot 1} \\ = & \frac{4 \pm \sqrt{16 + 20}}{2} \\ = & \frac{4 \pm 6}{2} \end{matrix}$

$r_{1} = 5$ og $r_{2} = - 1$

Den karakteristiske ligningen har to reelle røtter, så da er den generelle løsningen på formen

$y = C e^{r_{1} x} + D e^{r_{2} x}$

Setter vi inn for $r_{1}$ og $r_{2}$ får vi $y = C e^{5 x} + D e^{- x}$

Svar: $y = C e^{5 x} + D e^{- x}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikninger

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Andre ordens differensiallikninger.

c)

Bestem den spesielle løsningen som tilfredsstiller betingelsene $y (0) = 6$ og $y' (0) = 0$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må finne konstantene $C$ og $D$ slik at betingelsene er tilfredstilt. Da kan vi regne ut $y (0) = 6$ og $y' (0) = 0$ og finne hva $C$ og $D$ må være.

Den første betingelsen gir at $y (0) = 6$ . I deloppgave b) fant vi den generelle løsningen. Nå kan vi sette inn $x = 0$

$y (0) = C e^{5 (0)} + D e^{- (0)} = C + D$

Dersom den første betingelsen skal være tilfredstilg må $C + D = 6$ .

Den andre betingelse gir at $y' (0) = 0$ . Da må vi begynne med å finne hva $y' (x)$ er. Vi bruker kjerneregelen med $5 x$ og $- x$ som kjerner, og da får vi

$\begin{matrix} y' (x) & = & (C e^{5 x} + D e^{- x})' \\ = & C (e^{5 x})' + D (e^{- x})' \\ = & C e^{5 x} \cdot 5 + D (e^{- x}) \cdot (- 1) \\ = & 5 C e^{5 x} - D e^{- x} \end{matrix}$

Videre kan vi sette inn for $x = 0$ som gir

$y' (0) = 5 C e^{5 (0)} - D e^{- (0)} = 5 C - D$

Skal den andre betingelsen være tilfredsstilt må vi ha at $5 C - D = 0$ .

De to betingelsene gir ligningsettet

$C + D = 6$
$5 C - D = 0$

Den andre ligningen gir $D = 5 C$ .

Setter vi dette inn i den første ligningen får vi

$C + 5 C = 6 \Rightarrow 6 C = 6 \Rightarrow C = 1$

Det gir

$D = 5 C = 5 \cdot 1 = 5$

Nå har vi funnet ut hva $C$ og $D$ må være for at betingelsene skal holde, og da blir løsningen av ligningen

$y = 1 e^{5 x} + 5 e^{- x}$

Svar: $y = e^{5 x} + 5 e^{- x}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikninger

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

Konstant

En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.

Eksempel: $A = π r^{2}$ , $π$ er en konstant og $r$ er en variabel.

Se Variabel

konstanter

For flere forklaringer og eksempler, se artikkelen Andre ordens differensiallikninger.

Oppgave 6 (5 poeng) Nettkode: E-4PC8

Brøken $B_{n}$ er definert ved at telleren er summen av de $n$ første oddetallene, mens nevneren er summen av de $n$ neste oddetallene.

a)

Regn ut $B_{2} = \frac{1 + 3}{5 + 7}$ , $B_{3} = \frac{1 + 3 + 5}{7 + 9 + 11}$ og $B_{4} = \frac{1 + 3 + 5 + 7}{9 + 11 + 13 + 15}$ .

Forkort svarene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her skal vi regne ut og forkorte brøkene.

Vi skal regne ut $B_{2}$ , $B_{3}$ og $B_{4}$ . Da får vi

$B_{2} = \frac{1 + 3}{5 + 7} = \frac{4}{12} = \frac{1}{3}$

$B_{3} = \frac{1 + 3 + 5}{7 + 9 + 11} = \frac{9}{27} = \frac{1}{3}$

$B_{4} = \frac{1 + 3 + 5 + 7}{9 + 11 + 13 + 15} = \frac{16}{48} = \frac{1}{3}$

Svar: $B_{2} = B_{3} = B_{4} = \frac{1}{3}$

Mer om

Denne oppgaven er om

Brøk

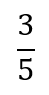
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

og forkorting av brøk.

For flere forklaringer og eksempler på brøk, se artikkelen Forkorte og utvide brøk.

b)

Vis at summen av de $n$ første oddetallene kan skrives $S_{n} = n^{2}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan vise at $S_{n} = n^{2}$ ved induksjon. Da må vi vise at det stemmer for $S_{1}$ og at hvis det stemmer for $S_{k}$ så må det også stemme for $S_{k + 1}$ .

Vi kan skrive det $n$ 'te oddetallet som $2 n - 1$ .

For å vise at $S_{n} = n^{2}$ kan vi bruke induksjon. Det første vi må vise er at formelen stemmer for $n = 1$ . Da sier påstanden at

$S_{1} = 1 = 1^{2}$

Formelen stemmer for $n = 1$ .

Nå antar vi at påstanden stemmer for $n = k$ . Vi kan skrive det $k$ -te oddetallet som $2 k - 1$ .

Da er altså

$S_{k} = 1 + 3 + . . . + (2 k - 1) = k^{2}$

Videre må vi vise at formelen stemmer for $n = k + 1$ , altså summen av de $(k + 1)$ minste oddetallene. Da må vi addere det neste oddetallet, $2 k + 1$ til summen $S_{k}$ .

$S_{k + 1} = S_{k} + (2 k + 1)$

Antagelsen vår sier at $S_{k} = k^{2}$ , dermed blir summen

$S_{k + 1} = k^{2} + (2 k + 1) = k^{2} + 2 k + 1 = (k + 1)^{2}$

Summen av de (k+1) minste oddetallene er altså lik $(k + 1)^{2}$ og formelen stemmer for $n = k + 1$ . Ved å anta at $S_{k}$ stemmer følger det at $S_{k + 1}$ også stemmer. Da stemmer $S_{n}$ for alle $n \in ℕ$ ved induksjon.

Alternativ

Vi kan også bruke formelen for sum av en aritmetisk rekke for å vise at dette stemmer.

Summen, $S_{n}$ av en aritmetisk rekke er gitt ved $S_{n} = \frac{n \cdot (a_{1} + a_{n})}{2}$ .

For oddetallene blir $a_{1} = 1$ og $a_{n}$ er det $n$ 'te oddetallet, og kan skrives som $2 n - 1$ .

Nå kan vi fylle inni formelen

$S_{n} = \frac{n (a_{1} + a_{n})}{2} = \frac{n (1 + 2 n - 1)}{2} = \frac{2 n^{2}}{2} = n^{2}$

og får det vi ville ha.

Svar: Vi har ved induksjon vist at $S_{n} = n^{2}$ stemmer for alle $n \in ℕ$

Mer om

Denne oppgaven er om

Oddetall

Tallene 1, 3, 5, 7, 9 og 11 er eksempler på oddetall.
Oddetall er heltall hvor svaret ikke blir et heltall når de deles med 2.

Alle oddetall kan skrives på formen 2n+1, der n er et helt tall.

Et heltall som ikke er oddetall er partall.

oddetall

Matematisk induksjon

En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:

Bevis påstanden for n =1.
Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).

Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).

matematisk induksjon

For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.

c)

Forklar at $B_{n} = \frac{S_{n}}{S_{2 n} - S_{n}}$ . Regn ut denne brøken.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

$S_{2 n}$ er summen av de $2 n$ første oddetallene. Vi kan bruke summen $S_{n} = n^{2}$ fra deloppgave b) til å regne ut brøken.

I $B_{n}$ er telleren summen av de $n$ første oddetallene, mens nevneren er summen av de $n$ neste oddetallene. I deloppgave b) skrev vi summen av de $n$ første oddetallene som $S_{n}$ , så telleren må være lik $S_{n}$ . I nevneren vil vi ha de $n$ neste oddetallene. Dersom vi tar summen $S_{2 n}$ vil vi få de $2 n$ første oddetallene og trekker vi fra $n$ første, $S_{n}$ sitter vi igjen med de neste $n$ oddetallene. Dermed kan $B_{n}$ skrives som $\frac{S_{n}}{S_{2 n} - S_{n}}$ .
Vi skal nå regne ut denne brøken. Da kan vi bruke resultatet fra deloppgave b), at $S_{n} = n^{2}$ . Setter vi inn for $S_{n}$ i $B_{n}$ får vi

$B_{n} = \frac{S_{n}}{S_{2 n} - S_{n}} = \frac{n^{2}}{(2 n)^{2} - n^{2}} = \frac{n^{2}}{4 n^{2} - n^{2}} = \frac{n^{2}}{3 n^{2}} = \frac{1}{3}$

Dette stemmer også med svarene vi fikk i deloppgave a)

Svar: $B_{n} = \frac{1}{3}$

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Oddetall

oddetall

Brøk

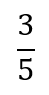
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler rekker , se artikkelen Aritmetiske rekker.

Oppgave 7 (7 poeng) Nettkode: E-4PCC

Ligningen til en kuleflate er gitt ved

$x^{2} - 2 x + y^{2} + 2 y + z^{2} - 6 z = 14$

a)

Vis at punktet $A (4, 3, 3)$ ligger på kuleflaten.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan sette inn for $x$ , $y$ og $z$ i ligningen til kuleflaten. Dersom ligningen stemmer ligger punktet på kuleflaten.

I punktet $A (4, 3, 3)$ har vi koordinatene $x = 4$ , $y = 3$ og $z = 3$ . For å finne ut om punktet ligger på kuleflaten kan vi sette inn for $x$ , $y$ og $z$ i ligningen for kuleflaten. Dersom likningen stemmer vil punktet ligge på kuleflaten.

$\begin{matrix} x^{2} - 2 x + y^{2} + 2 y + z^{2} - 6 z & = & 4^{2} - 2 \cdot 4 + 3^{2} + 2 \cdot 3 + 3^{2} - 6 \cdot 3 \\ = & 16 - 8 + 9 + 6 + 9 - 18 \\ = & 14 \end{matrix}$

Svar: Ligningen til kuleflaten stemmer for $A (4, 3, 3)$ , så punktet ligger på kuleflaten.

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.

b)

Vis at kulen har sentrum i $S (1, - 1, 3)$ . Bestem radien til kulen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

En kule med radius $r$ og sentrum i $S (x_{0}, y_{0}, z_{0})$ har likningen $(x - x_{0})^{2} + (y - y_{0})^{2} + (z - z_{0})^{2} = r^{2}$ , så vi må omforme likningen slik at den blir på denne formen. Dette kan vi gjøre ved hjelp av fullstendige kvadrater.

Vi vil få ligningen på formen $(x - x_{0}) + (y - y_{0}) + (z - z_{0}) = r^{2}$ , med $x_{0} = 1$ , $y_{0} = - 1$ og $z_{0} = 3$ , altså på formen $(x - 1)^{2} + (y + 1)^{2} + (z - 3)^{2} = r^{2}$ . Da må vi lage fullstendige kvadrater. Vi kan begynne med å samle alle leddene med $x$ til et fullstendig kvadrat

$\begin{matrix} x^{2} - 2 x + y^{2} + 2 y + z^{2} - 6 z & = & 14 \\ x^{2} - 2 x + 1 + y^{2} + 2 y + z^{2} - 6 z & = & 14 + 1 \\ (x - 1)^{2} + y^{2} + 2 y + z^{2} - 6 z & = & 15 \end{matrix}$

Tilsvarende kan vi gjøre for alle leddene med $y$

$\begin{matrix} (x - 1)^{2} + y^{2} + 2 y + z^{2} - 6 z & = & 15 \\ (x - 1)^{2} + y^{2} + 2 y + 1 + z^{2} - 6 z & = & 15 + 1 \\ (x - 1)^{2} + (y + 1)^{2} + z^{2} - 6 z & = & 16 \end{matrix}$

og til slutt også for alle leddene med $z$

$\begin{matrix} (x - 1)^{2} + (y + 1)^{2} + z^{2} - 6 z & = & 16 \\ (x - 1)^{2} + (y + 1)^{2} + z^{2} - 6 z + 9 & = & 16 + 9 \\ (x - 1)^{2} + (y + 1)^{2} + (z - 3)^{2} & = & 25 \end{matrix}$

Vi ser at ligningen nå er på den ønskede formen, med sentrum i $S (1, - 1, 3)$ og radius $r = \sqrt{25} = 5$

Svar: Sentrum er i $S (1, - 1, 3)$ og radius, $r$ , er $5$ .

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Radius

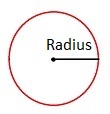
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.

radius

For flere forklaringer og eksempler, se artikkelen Likning for en kule.

c)

Bestem ligningen for tangentplanet $α$ til kuleflaten i punktet $A$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vektoren fra kulens sentrum $S$ til punktet $A$ , vil stå normalt på tangentplanet, så vi kan bruke $\vec{S A}$ til å finne ligningen til tangentplanet.

Kulens sentrum er $S (1, - 1, 3)$ og $A (4, 3, 3)$ ligger på kuleflaten. Vektoren

$\vec{S A} = \vec{O A} - \vec{O S} = [4, 3, 3] - [1, - 1, 3] = [3, 4, 0]$

går gjennom sentrum i kulen og står normalt på kuleflaten i punktet $A$ . Tangentplanet i punktet $A$ består av alle punkter innholdt i en linje som tangerer kulen i punktet $A$ , $\vec{S A}$ vil stå normalt på alle linjene i dette planet, og vil være en normalvektor. Det betyr at alle vektorer $\vec{v}$ mellom to punkter i planet må stå vinkelrett på $\vec{S A}$ og da må $\vec{v} \cdot \vec{S A} = 0$ . Siden $A$ ligger i tangentplanet må alle punkter $B (x, y, z)$ som også ligger i tangentplanet tilfredstille $\vec{S A} \cdot \vec{A B} = 0$ Vi kan uttrykke

$\vec{A B} = \vec{O B} - \vec{O A} = [x, y, z] - [4, 3, 3] = [x - 4, y - 3, z - 3]$ .

Da får vi

$\begin{matrix} \vec{S A} \cdot \vec{A B} & = & [3, 4, 0] \cdot [x - 4, y - 3, z - 3] \\ = & 3 (x - 4) + 4 (y - 3) + 0 (z - 3) \\ = & 3 x - 12 + 4 y - 12 \\ = & 3 x + 4 y - 24 \end{matrix}$

Siden $\vec{S A} \cdot \vec{A B} = 0$ , så tilfredstiller alle punktene i tangentplanet i $A$ likningen $3 x + 4 y - 24 = 0$ som da er likningen til planet.

Svar: $3 x + 4 y - 24 = 0$

Mer om

Denne oppgaven er om

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangent

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler på plan, se artikkelen Likning til et plan.

d)

Et annet plan $β$ går gjennom $S$ og $B (1, 0, 1)$ og står normalt på $α$ .
Bestem ligningen til $β$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Når planene $α$ og $β$ står normalt på hverandre, vil også normalvektorene, $\vec{n_{α}}$ og $\vec{n_{β}}$ , stå normalt på hverandre, og $\vec{n_{α}} \cdot \vec{n_{β}} = 0$ .

Siden normalvektorene $\vec{n_{α}}$ og $\vec{n_{β}}$ vil står normalt på hverandre og vi vil ha $\vec{n_{α}} \cdot \vec{n_{β}} = 0$ Fra deloppgave c) vet vi at $\vec{n_{α}} = \vec{S A} = [3, 4, 0]$ . Vi kan uttrykke $\vec{n_{β} = [a, b, c]}$ . Da kan vi regne

$\vec{n_{α}} \cdot \vec{n_{β}} = [3, 4, 0] \cdot [a, b, c] = 3 a + 4 b + 0 c = 0$ .

Denne ligningen sier ingenting om $c$ , så $c$ kan være et vilkårlig tall. Planet $β$ går gjennom $B (1, 0, 1)$ , så ligningen til $β$ kan uttrykkes

$a (x - 1) + b y + c (z - 1) = 0$

Siden punktet $S (1, - 1, 3)$ også ligger i planet må ligningen tilfredsstille

$a (1 - 1) + b (- 1) + c (3 - 1) = - b + 2 c = 0$

Nå har vi at

$3 a + 4 b = 0$

$- b + 2 c = 0$

Ingen av ligningene sier at $c = 0$ , og vi kan sette $c = - 3$ . Fra den nederste av de to ligningene får vi $b = - 6$ . Nå kan vi sette inn for $b$ i den øverste, dette gir

$3 a + 4 (- 6) = 0 \Rightarrow 3 a = 24 \Rightarrow a = 8$

Sette vi inn i ligningen for $β$ får vi

$\begin{matrix} 8 (x - 1) - 6 y - 3 (z - 1) & = & 8 x - 8 - 6 y - 3 z + 3 \\ = & 8 x - 6 y - 3 z - 5 \\ = & 0 \end{matrix}$

Alternativ

Planene $α$ og $β$ står normalt på hverandre, så normalvektorene, $\vec{n_{α}}$ og $\vec{n_{β}}$ , vil også stå normalt på hverandre. Normalvektoren til $β$ vil også stå normalt på vektoren $\vec{S B}$ , som ligger i $β$ . Vi kan finne en slik normalvektor ved å finne vektorproduktet $\vec{n_{α}} \times \vec{S B}$ . Før vi regner vektorproduktet finner vi at $\vec{S B} = [1, 0, 1] - [1, - 1, 3] = [1 - 1, 0 - (- 1), 1 - 3] = [0, 1, - 2]$ Fra deloppgave b) har vi at $\vec{S A} = [3, 4, 0]$ er en normalvektor til $α$ , så nå kan vi finne vektorproduktet mellom disse.

$\begin{matrix} \vec{S A} \times \vec{S B} & = & [3, 4, 0] \times [0, 1, - 2] \\ = & | \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 3 & 4 & 0 \\ 0 & 1 & - 2 \end{matrix} | \\ = & | \begin{matrix} 4 & 0 \\ 1 & - 2 \end{matrix} | \vec{i} - | \begin{matrix} 3 & 0 \\ 0 & - 2 \end{matrix} | \vec{j} + | \begin{matrix} 3 & 4 \\ 0 & 1 \end{matrix} | \vec{k} \\ = & - 8 \vec{i} + 6 \vec{j} + 3 \vec{k} \\ = & [- 8, 6, 3] \end{matrix}$

Nå har vi en normalvektor $\vec{n_{β}} = [- 8, 6, 3]$ og et punkt $B$ i planet $β$ , så da kan vi finne likningen til planet ved $- 8 (x - 1) + 6 (y - 0) + 3 (z - 1) = - 8 x + 6 y + 3 z + 5 = 0$ Mulitpliserer vi med $- 1$ på begge sider av likhetstegnet ser vi at vi får samme svar som i den andre løsningen.

Svar: $8 x - 6 y - 3 z - 5 = 0$

Mer om

Denne oppgaven er om

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektorer

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler på plan, se artikkelen Likning til et plan.

DEL 2 med hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4PCH

Ved inngangen til $2015$ var folketallet i Norge $5200000$ . I en modell for befolkningsveksten antar vi at

- netto innvandring per år vil være $44000$

- antall som blir født per år, vil være $1, 1 %$ av folketallet

- antall som dør per år, vil være $0, 8 %$ av folketallet

Vi lar folketallet være $y (t)$ , der $t$ er antall år etter $2015$ .

a)

Forklar at vi kan skrive

$y' = 0, 003 y + 44000, y (0) = 5200000$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Befolkningsveksten, $y'$ er endringen i folketall og endringen bestemmes av antall mennesker som blir født, dør og av netto innvandring.

Befolkningsveksten påvirkes av netto innvandring, og fødsler og død. Vi får oppgitt at antall som blir født hvert år er $1, 1 %$ av folketallet, og antall som dør er $0, 8 %$ . I tillegg må vi også ta hensyn til netto innvandring som vil være på $44000$ .

$\begin{matrix} Befolkningsvekst & = & antall som blir født - antall som dør + innvandring \\ y' & = & 0, 011 y - 0, 008 y + 44000 \\ y' & = & 0, 003 y + 44000 \end{matrix}$

Befolkningsveksten vil da kunne uttrykkes ved

$y' = 0, 003 y + 44000$

Siden vi ser på $y (t)$ , der $t$ er antall år etter 2015, vil $y (0)$ være folketallet i 2015, altså $5200000$ .

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikninger

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Matematisk modell

Matematiske modeller brukes ofte for å beskrive fenomener i naturen.

Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.

matematiske modeller

For flere forklaringer og eksempler på differensialfunksjoner, se artikkelen Første ordens lineære differensiallikninger.

b)

Løs differensialligningen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Dette er en lineær førsteordens differensiallikning. Denne kan vi enten løse ved regning, og da kan vi multiplisere med en integrerende faktor, eller vi kan løse den ved hjelp av CAS.

Vi kan enten løse likningen for hånd, eller ved hjelp av CAS. Løsningsforslag for å løse oppgaven for hånd ligger under Alternativ.

Vi kan bruke CAS til å løse differensialligningen ved å bruke kommandoen “LøsODE[<Likning>, <Punkt på f>]”.

Ligningen vi vil løse er $y' - 0.003 y = 44000$ , og punktet $(0, 5200000)$ er for å bestemme konstanten.

Vi vet at $y (0) = 5200000$ , så da er $(0, 5200000)$ et punkt på y.

Da skriver vi inn

LøsODE[y’-0.003y=44000, (0,5200000)].

Her er både eksakt og avrundet løsning.

Alternativ

For å løse likningen ved regning kan vi starte med å flytte begge leddene som avhenger av $y$ på samme side av likhetstegnet. Slik at vi får

$y' - 0, 003 y = 44000$

Videre nå kan vi introdusere en integrerende faktor $e^{- 0, 003 t}$ som vi multipliserer med på begge sider av ligningen. Da får vi

$\begin{matrix} (y' - 0, 003 y) e^{- 0, 003 t} & = & 44000 \cdot e^{- 0, 003 t} \\ y' \cdot e^{- 0, 003 t} - 0, 003 y \cdot e^{- 0, 003 t} & = & 44000 \cdot e^{- 0, 003 t} \end{matrix}$

Venstre side av ligningen er nå lik

$[y \cdot e^{- 0, 003 t}]'$ så nå har vi $[y \cdot e^{- 0, 003 t}]' = 44000 \cdot e^{- 0, 003 t}$

Nå kan vi integrere begge sider, og da bruker vi at $\int e^{k x} d x = \frac{1}{k} e^{k x} + C$ . Det gir

$\begin{matrix} \int [y \cdot e^{- 0, 003 t}]' d t & = & \int 44000 \cdot e^{- 0, 003 t} d t \\ y \cdot e^{- 0, 003 t} & = & \frac{44000}{- 0, 003} e^{- 0, 003 t} + C \end{matrix}$

Nå kan vi dividere på $e^{- 0, 003 t}$ på begge sider som gir

$y (t) = - \frac{44000}{0, 003} + \frac{C}{e^{- 0, 003 t}} = C e^{0, 003 t} - \frac{44000000}{3}$

For å finne konstanten $C$ , bruker vi at vi vet at $y (0) = 5200000$ . Om vi setter inn for $t = 0$ i ligningen over får vi

$y (0) = C e^{0, 003 (0)} - \frac{44000000}{3} = C - \frac{44000000}{3}$

Videre kan vi løse ligningen

$\begin{matrix} 5200000 & = & C - \frac{44000000}{3} \\ C & = & 5200000 + \frac{44000000}{3} \\ C & = & \frac{59600000}{3} \end{matrix}$

Løsningen på differensialligningen blir da $y (t) = \frac{1}{3} (59600000 e^{0, 003 t} - 44000000)$

Svar: $y (t) = \frac{1}{3} (59600000 e^{0, 003 t} - 44000000)$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikninger

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentialfunksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler, se artikkelen Separable differensiallikninger.

c)

Når vil folketallet passere $7$ millioner ifølge denne modellen?
Hvor stor er vekstfarten i folketallet da?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan løse ligningen $y (t) = 7000000$

Denne oppgaven kan vi løse grafisk ved hjelp av GeoGebra. Vi kan tegne inn grafen til funksjonen ved å skrive inn

$f (t) = 1 / 3 * (59600000 t^{\land} (0.003 t) - 44000000)$ ,

og for å finne når folketallet passerer $7$ millioner, kan vi finne ut når grafen til $f$ krysser linja $y = 7000000$ . Da må vi skrive inn $𝚢 = 7000000$ , og finne skjæringspunkt mellom de to grafene.

Da får vi punktet $A = (28, 91, 7000000)$ , som forteller oss at folketallet passerer $7$ millioner nesten $29$ år etter 2015, i slutten av år $2043$ .

Befolkningsveksten kan vi da finne ved å sette inn $y = 7000000$ i likningen fra deloppgave a).

Det gir $y' = 0, 003 \cdot 7000000 + 44000 = 65000$ som forteller at befolkningsveksten vil være en økning på $65000$ innbyggere i året.

Alternativ

Vi vil finne når folketallet, $y (t)$ passerer 7 millioner. Siden folketallet er gitt ved

$y (t) = \frac{1}{3} (59600000 e^{0, 003 t} - 44000000)$

kan vi løse $y (t) = 7000000$

$\frac{1}{3} (59600000 e^{0, 003 t} - 44000000) = 7000000$

$59600000 e^{0, 003 t} = 3 \cdot 7000000 + 44000000$

$e^{0, 003 t} = \frac{65000000}{59600000} = \frac{325}{298}$

$0, 003 t = ln (\frac{325}{298}) \Rightarrow t \approx \frac{0, 0867}{0, 003} \approx 28, 9$

I følge modellen vil folketallet passere $7$ millioner $28, 9$ år etter $2015$ , altså i på slutten av $2043$ .

Befolkningsveksten da kan vi finne ved å sette inn ligningen fra deloppgave a) med $y = 7000000$ . Da får vi

$y' = 0, 003 \cdot 7000000 + 44000 = 65000$

Befolkningsveksten vil være en økning på $65000$ innbyggere i året.

Svar: Mot slutten av 2043, og da vil befolkningsveksten være en økning på $65000$ innbyggere i året.

Mer om

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

, og

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere forklaringer og eksempler på funksjoner, se artikkelen Johannes viser eksponential- og logaritmefunksjoner.

Oppgave 2 (8 poeng) Nettkode: E-4PDI

Funksjonen $f$ er gitt ved

$f (x) = \sqrt{x^{2} - x^{4}}$

a)

Bruk graftegner til å tegne grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne funksjonen.

For å tegne grafen til funksjonen i GeoGebra skriver vi inn

$𝚏 (𝚡) = 𝚜 𝚚 𝚛 𝚝 (x^{\land} 2 - x^{\land} 4)$

Svar: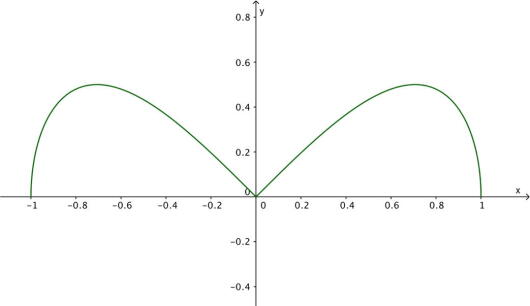

Mer om

Denne oppgaven er om

Graf

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

b)

Bruk CAS til å bestemme de eksakte koordinatene til toppunktene på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å finne ekstremalpunktene til grafen kan vi finne når $f' (x) = 0$ og for å sjekke om vi har toppunkt kan vi sjekke om $f ″ (x) < 0$ .

Vi begynner med å definere funksjonen i CAS. Da skriver vi inn

$𝚏 (𝚡) := 𝚜 𝚚 𝚛 𝚝 (x^{\land} 2 - x^{\land} 4)$

For å finne $f' (x) = 0$ kan vi skrive

$𝙻 ø 𝚜 [𝚏' (𝚡) = 0]$

Da får vi at

$f' (x) = 0$ når $𝚡 = - \frac{\sqrt{2}}{2} og 𝚡 = \frac{\sqrt{2}}{2}$

Vi kan sjekke at dette er toppunkt ved å sjekke om

$f ″ (\frac{\sqrt{2}}{2}) < 0$ og $f ″ (- \frac{\sqrt{2}}{2}) < 0$

Dersom det stemmer har vi et toppunkt. Da skriver vi inn $𝚏'' (𝚜 𝚚 𝚛 𝚝 (2) / 2)$ og $𝚏'' (- 𝚜 𝚚 𝚛 𝚝 (2) / 2)$ i CAS.

Da får vi

$f ″ (\frac{\sqrt{2}}{2}) = - 4$ og $f ″ (- \frac{\sqrt{2}}{2}) = - 4$

Dette forteller oss at vi har toppunkt når $x = \frac{\sqrt{2}}{2}$ og $x = - \frac{\sqrt{2}}{2}$ .

Videre må vi finne verdien til $f$ i toppunktene. Da skriver vi i CAS $𝚏 (𝚜 𝚚 𝚛 𝚝 (2) / 2)$ og $𝚏 (- 𝚜 𝚚 𝚛 𝚝 (2) / 2)$ , som gir $f (\frac{\sqrt{2}}{2}) = \frac{1}{2}$ og $f (- \frac{\sqrt{2}}{2}) = \frac{1}{2}$ .

Toppunktene til grafen er $(\frac{\sqrt{2}}{2}, \frac{1}{2})$ og $(- \frac{\sqrt{2}}{2}, \frac{1}{2})$ .

Svar: Toppunktene til grafen er $(\frac{\sqrt{2}}{2}, \frac{1}{2})$ og $(- \frac{\sqrt{2}}{2}, \frac{1}{2})$ .

Mer om

Denne oppgaven er om

Graf

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Toppunkt

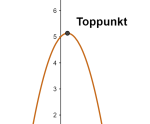
Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Andrederiverte

Den andrederiverte til en funksjon $f (x)$ er funksjonen derivert to ganger og skrives $f'' (x)$ eller $f^{(2)} (x)$ . Kalles også annenderiverte eller dobbeltderiverte.

annenderivert

For flere eksempler og forklaringer om ekstremalpunkt, se artikkelen Topp- og bunnpunkter.

c)

Bestem det samlede arealet av områdene som er avgrenset av grafen til $f$ og $x$ -aksen.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

For å finne arealet mellom grafen til $f$ og $x$ -aksen-aksen kan vi integrere $f (x)$ . Før vi regner dette ut må vi se om noe av området under grafen til $f$ vil ligge under $x$ -aksen.

Først kan vi se at $f (x) = \sqrt{x^{2} - x^{4}} \geq 0$ . På intervallet $[- 1, 1]$ vil vi alltid ha $x^{2} \geq x^{4}$ , så vi får kvadratroten av et ikke-negativt tall. Når $x$ er utenfor intervallet vil ikke funksjonen være definert.

Arealet under grafen til f er det samme som å finne integralet til $f$ fra $- 1$ til $1$ . Dersom vi bruker samme GeoGebravindu som i deloppgave a), er funksjonen $f$ allerede definert, hvis ikke kan vi definere $f$ ved å skrive $𝚏 (𝚡) := 𝚜 𝚚 𝚛 𝚝 (𝚡^{\land} 2 - 𝚡^{\land} 4)$ .

Nå kan vi finne arealet ved å bruke kommandoen Integral i CAS og skrive $𝙸 𝚗 𝚝 𝚎 𝚐 𝚛 𝚊 𝚕 [𝚏, - 1, 1]$ .

Da får vi $a = \frac{2}{3}$ .

Alternativ

Vi begynner med å se hvordan vi kan regne arealet mellom grafen til

$f$ og $x$ -aksen. I alternativ løsning vil vi se hvordan vi kan gjøre det uten hjelp av CAS.

Først kan vi se at $f (x) = \sqrt{x^{2} - x^{4}} \geq 0$ . På intervallet $[- 1, 1]$ vil vi alltid ha $x^{2} \geq x^{4}$ , så vi får kvadratroten av et positivt tall. Når $x$ er utenfor intervallet vil ikke integralet være definert. Skjæringspunktene mellom $f$ og $x$ -aksen finner vi ved å finne nullpunktene til $f (x)$ , med andre ord når $\sqrt{x^{2} - x^{4}} = 0$ .

$\begin{matrix} \sqrt{x^{2} - x^{4}} & = & 0 \\ x^{2} - x^{4} & = & 0 \\ x^{2} (1 - x^{2}) & = & 0 \\ x^{2} (1 - x) (1 + x) & = & 0 \end{matrix}$

Det betyr at $(0, 0), (1, 0)$ og $(- 1, 0)$ er nullpunkter, og siden $f (x)$ er positiv på hele intervallet, altså ligger hele området over $x$ -aksen. Da kan vi finne areal under grafen ved å regne $Areal = \int_{- 1}^{0} f (x) d x + \int_{0}^{1} f (x) d x$

Funksjonen $f (x)$ er symmetrisk om $x = 0$ , det vil si at

$f (- x) = \sqrt{(- x)^{2} - (- x)^{4}} = \sqrt{x^{2} - x^{4}} = f (x)$

på hele intervallet vårt, og dette medfører at $\int_{- 1}^{0} f (x) d x = \int_{0}^{1} f (x) d x$ og at $Areal = 2 \int_{0}^{1} f (x) d x = 2 \int_{0}^{1} \sqrt{x^{2} - x^{4}} d x$

Vi kan faktorisere $\sqrt{x^{2} - x^{4}} = \sqrt{x^{2} (1 - x^{2})} = x \sqrt{1 - x^{2}}$ og regne ut $Areal = 2 \int_{0}^{1} x \sqrt{1 - x^{2}} d x$

For å løse dette integralet kan vi bruke substitusjon ved å sette $u = 1 - x^{2}$ . Da får vi

$\frac{d u}{d x} = - 2 x \Rightarrow d x = \frac{d u}{- 2 x}$

De nye integrasjonsgrensene blir

$x = 0 \Rightarrow u = 1 - 0^{2} = 1$

$x = 1 \Rightarrow u = 1 - 1^{2} = 0$

Da kan vi regne ut

$\begin{matrix} 2 \int_{0}^{1} x \sqrt{1 - x^{2}} d x & = & 2 \int_{1}^{0} x \sqrt{u} \frac{d u}{- 2 x} \\ = & - \int_{1}^{0} \sqrt{u} d u \\ = & \int_{0}^{1} \sqrt{u} d u \\ = & \frac{2}{3} {[u^{\frac{3}{2}}]}_{0}^{1}_{}^{} \\ = & \frac{2}{3} [1 - 0] \\ = & \frac{2}{3} \end{matrix}$

Arealet under grafen til $f$ vil være $\frac{2}{3}$ .

Svar: Arealet er $\frac{2}{3}$ .

Mer om

Denne oppgaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Graf

graf

x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.

x-akse

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.

d)

Grafen til $f$ roteres $360^{\circ}$ om $x$ -aksen. Bestem volumet av omdreiningslegemet som da framkommer.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Volumet av omdreiningslegemeet til en funksjon $f (x)$ kan skrives som et integral av sylindere med høyde $d x$ og grunnflate $π f (x)^{2}$ , og vi kan finne volumet ved formelen $V = π \int_{- 1}^{1} {(f (x))}^{2} dx .$

For å finne volumet til omdreningslegemet kan vi bruke formelen

$V = π \int_{- 1}^{1} {(f (x))}^{2} dx$

og CAS. I CAS skriver vi inn

$𝙸 𝚗 𝚝 𝚎 𝚐 𝚛 𝚊 𝚕 [π \cdot f (x {)^{\land} 2}^{}, - 1, 1]$ , der $f (x)$ er definert som i deloppgave b).

Alternativ

Fra deloppgave c) har vi at

$π \int_{- 1}^{0} f (x)^{2} d x + π \int_{0}^{1} f (x)^{2} d x = 2 π \int_{0}^{1} f (x)^{2} d x$

på grunn av symmetrien til $f (x)$ .

Volumet til omdreiningslegemet kan vi finne ved å regne ut dette integralet.

$\begin{matrix} Volum & = & 2 π \int_{0}^{1} f (x)^{2} d x \\ = & 2 π \int_{0}^{1} {\sqrt{x^{2} - x^{4}}}^{2} d x \\ = & 2 π \int_{0}^{1} x^{2} - x^{4} d x \\ = & 2 π {[\frac{1}{3} x^{3} - \frac{1}{5} x^{5}]}_{0}^{1} \\ = & 2 π [\frac{1}{3} - \frac{1}{5}] \\ = & \frac{4 π}{15} \end{matrix}$

Svar: Volumet er $\frac{4 π}{15}$

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Omdreiningslegeme

Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.

omdreiningslegeme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Volum av et omdreiningslegeme.

Oppgave 3 (7 poeng) Nettkode: E-4PDW

To plan $α$ og $β$ er gitt ved

$α : x - y - 3 = 0$

$β : x + p z - 4 = 0, p \in ℝ$

a)

Vis at punktet $(4, 1, 0)$ ligger i begge planene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan sette inn for $x, y$ og $z$ i ligningene for planene, og dersom ligningene stemmer, er $A$ et punkt i planet.

Dersom punktet $A (4, 1, 0)$ ligger i planene vil det tilfredstille likningen til hvert av planene. Med andre ord kan vi sette inn for $x = 4$ , $y = 1$ og $z = 0$ i likningene og om likningen stemmer ligger punktet i planet.

$α : x - y - 3 = 4 - 1 - 3 = 0$

$β : x + p z - 4 = 4 - 0 p - 4 = 0$

Vi ser at likningen til begge planene stemmer når vi setter inn for koordinatene til $A$ , altså ligger $A$ i planene.

Svar: Punktet $A (4, 1, 0)$ ligger i begge planene

Mer om

Denne oppgaven er om

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinater

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler, se artikkelen Likning til et plan.

b)

Bestem $p$ slik at vinkelen mellom $α$ og $β$ blir $60^{\circ}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Et plan med ligning $a x + b y + c z + d = 0$ vil ha normalvektor $\vec{n} = [a, b, c]$ . Når vinkelen mellom normalvektorene til planene er $60^{\circ}$ vil også vinkelen mellom planene være $60^{\circ}$ .

Normalvektoren, $\vec{n_{α}}$ , til $α : x - y - 3 = 0$ vil være $\vec{n_{α}} = [1, - 1, 0]$ og normalvektoren, $\vec{n_{β}}$ til $β : x + p z - 40$ vil være $\vec{n_{β}} = [1, 0, p]$ . For å finne vinkelen mellom normalvektorene kan vi bruke skalarproduktet. Når vinkelen mellom vektorene er $60^{\circ}$ er skalarproduktet gitt ved

$\vec{n_{α}} \cdot \vec{n_{β}} = | \vec{n_{α}} | \cdot | \vec{n_{β}} | \cos 60^{\circ}$

Nå kan vi regne ut

$\vec{n_{α}} \cdot \vec{n_{β}} = 1 \cdot 1 + (- 1) \cdot 0 + 0 \cdot p = 1$

Vi vet at $\cos 60^{\circ} = \frac{1}{2}$ . og vi kan regne ut $| \vec{n_{α}} |$ og $| \vec{n_{β}} |$

$| \vec{n_{α}} | = \sqrt{1^{2} + (- 1)^{2} + 0^{2}} = \sqrt{2}$

$| \vec{n_{β}} | = \sqrt{1^{2} + 0^{2} + p^{2}} = \sqrt{1 + p^{2}}$

Vi kan nå sette inn i skalarproduktet og løse ligningen med hensyn på $p$

$\begin{matrix} \vec{n_{α}} \cdot \vec{n_{β}} & = & | \vec{n_{α}} | \cdot | \vec{n_{β}} | \cos 60^{\circ} \\ 1 & = & \sqrt{2} \cdot \sqrt{1 + p^{2}} \cdot \frac{1}{2} \\ 2 & = & \sqrt{2 (1 + p^{2})} \\ 4 & = & 2 (1 + p^{2}) \\ 1 & = & p^{2} \\ p & = & \pm 1 \end{matrix}$

Svar: Vi må ha $p = \pm 1$ for at vinkelen mellom planene skal være $60^{\circ}$ .

Mer om

Denne oppgaven er om

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektorer

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler om vektorer, se artikkelen Vinkelen mellom to vektorer.

c)

Hvilken verdi for $p$ vil gi den minste vinkelen mellom $α$ og $β$ ? Hvor stor er vinkelen?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke skalarproduktet til å finne en funksjon for $\cos v$ , der $v$ er vinkelen mellom $α$ og $β$ .

I deloppgave b) brukte vi skalarproduktet

$\vec{n_{α}} \cdot \vec{n_{β}} = | \vec{n_{α}} | \cdot | \vec{n_{β}} | \cos v$

mellom normalvektorene og vi fant at

$\vec{n_{α}} \cdot \vec{n_{β}} = 1$ og $| \vec{n_{α}} | \cdot | \vec{n_{β}} | = \sqrt{2 (1 + p^{2})}$

Når vi setter inn dette får vi

$1 = \sqrt{2 (1 + p^{2})} \cos v$

som gir

$\cos v = \frac{1}{\sqrt{2 (1 + p^{2})}}$

Vi kan finne maksimumsverdien for $\cos v$ ved hjelp av CAS. Da kan vi definere $\cos v = \frac{1}{\sqrt{2 (1 + p^{2})}}$ som en funksjon, $f (p)$ , slik at

$f (p) = \frac{1}{\sqrt{2 (1 + p^{2})}}$

Denne definerer vi i CAS ved å skrive inn

$𝚏 (𝚙) := 1 / 𝚜 𝚚 𝚛 𝚝 (2 (1 + 𝚙)^{\land} 2)$

For å finne ut når $f (p)$ har ekstremalpunkt må vi finne for hvilken $p$ vi har $f' (p) = 0$ . Dette kan vi finne ved å skrive Løs[f’(p)]=0 i CAS. Da får vi at $p = 0$ gir et ekstremalpunkt for $f$ .

Videre kan vi sjekke

$f ″ (0)$ for å se om $p = 0$ er maksimums- eller minimumspunkt. I CAS skriver vi f”(0), og får $f ″ (0) = - \frac{1}{\sqrt{2}}$ som forteller oss at vi har et maksimumspunkt.

Vi har altså funnet ut for hvilken $p$ som gir $f (p)$ , og dermed også $\cos v$ , størst verdi, og som gir at vinkelen $v$ vil være minst mulig. Setter vi inn for $p = 0$ får vi at $\cos v = \frac{1}{\sqrt{2}}$ , og vinkelen $v = 45^{\circ}$ .

Alternativ

Vi kan også se at for $\cos v$ er $\cos 0 = 1$ og $\cos 90^{\circ} = 0$ , så når $0 \leq v \leq 90^{\circ}$ har vi at jo større $\cos v$ er, dess mindre er vinkelen $v$ , med andre ord vil vi ha $\cos v$ størst mulig.

I uttrykket $\cos v = \frac{1}{\sqrt{1 + p^{2}}}$ har vi $p$ i nevneren, og vi vil velge $p$ slik at dette uttrykket blir størst mulig. Da vil vi ha minst mulig nevner, og det får vi når vi velger $p = 0$ . Dersom vi velger $p > 0$ vil brøken, og $\cos v$ bli mindre, og vinkelen større.

Så da må $p = 0$ og vi vil få at $\cos v = \frac{1}{\sqrt{2}}$ , som gir at vinkelen $v = 45^{\circ}$ .

Svar: $p = 0$ vil gi den minste vinkelen, og da er vinkelen $45^{\circ}$ .

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

For flere forklaringer og eksempler på ekstremalpunkt, se artikkelen Topp- og bunnpunkter.

d)

De to planene skjærer hverandre langs en linje $ℓ$ . Bestem en parameterframstilling for $ℓ$ uttrykt ved $p$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi har at $ℓ$ ligger i begge planene og da vil normalvektoren til både $α$ og $β$ stå normalt på linjen. Ved å finne kryssproduktet mellom normalvektorene, $n_{α}$ og $n_{β}$ , til planene, vil vi finne en vektor som står normalt på begge vektorene.

Retningsvektoren til $ℓ$ vil stå normalt på både $n_{α}$ og $n_{β}$ siden $ℓ$ ligger i begge planene. Vi kan finne en vektor som står normalt på både $n_{α}$ og $n_{β}$ ved å finne kryssproduktet mellom dem.
For å finne kryssproduktet kan vi bruke CAS.

Først definerer vi normalvektorene ved å skrive $𝚗_α := (1, - 1, 0)$ og $𝚗_β := (1, 0, p)$ . CAS bruker kommandoen Vektorprodukt for å finne kryssproduktet, så vi kan skrive $𝚅 𝚎 𝚔 𝚝 𝚘 𝚛 𝚙 𝚛 𝚘 𝚍 𝚞 𝚔 𝚝 [𝚗_α, 𝚗_β]$ .Da får vi vektoren $(- p, - p, 1)$ , som vil være retningsvektor til linjen $ℓ$ .

For å finne parameterfremstillingen til $ℓ$ trenger vi også et punkt på linjen. Fra a) vet vi at punktet $(4, 1, 0)$ ligger i begge planene, og må da også ligge på linjen. Nå har vi både retningsvektor og et punkt på linjen, og da kan vi finne parameterfremstillingen:

$ℓ : {\begin{matrix} x = 4 - p \cdot t \\ y = 1 - p \cdot t \\ z = t \end{matrix}$

Svar: En parameterfremstilling er gitt ved $ℓ : {\begin{matrix} x = 4 - p \cdot t \\ y = 1 - p \cdot t \\ z = t \end{matrix}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Retningsvektor

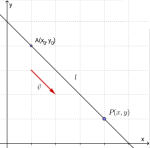
En linje $l$ går gjennom punktet $A (x_{0}, y_{0})$ og er parallell med vektoren $\vec{v} = [a, b]$ . Vektoren $\vec{v}$ kalles for retningsvektoren for linja.

retningsvektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler på vektorer, se artikkelen Parameterfremstilling av en rett linje.

Oppgave 4 (4 poeng) Nettkode: E-4PE0

Om en uendelig geometrisk rekke vet vi at

- summen er $8$

- summen av de tre første leddene er $7$

a)

Sett opp et ligningssystem som uttrykker opplysningene ovenfor. 

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

I en geometrisk rekke kan hvert ledd, $a_{n}$ uttrykkes ved $a_{1} \cdot k^{n - 1}$ der $k$ er en kvotienten. Siden summen av den uendelige rekker er 8, vet vi at den konvergerer, og at $| k | < 1$ , da er summen av en uendelig geometrisk rekke er gitt ved formelen $S = \frac{a_{1}}{1 - k}$ .

Vi får oppgitt at summen av den geometrisk rekken er 8, altså konvergerer den. Siden summen, $S$ , av en uendelig geometrisk rekke som konvergerer kan gis ved formelen

$S = \frac{a_{1}}{1 - k}$

har vi at

$8 = \frac{a_{1}}{1 - k}$

Det andre vi får oppgitt er at summen av de tre første leddene er 7, altså har vi at

$a_{1} + a_{2} + a_{3} = 7$

Siden vi har en geometrisk rekke kan hvert av leddene uttrykkes ved det første, $a_{n} = a_{1} \cdot k^{n - 1}$ . Da får vi at $a_{2} = a_{1} \cdot k$ og $a_{3} = a_{1} \cdot k^{2}$ . Altså kan vi skrive

$a_{1} + a_{2} + a_{3} = a_{1} + a_{1} \cdot k + a_{1} \cdot k^{2} = a_{1} (1 + k + k^{2}) = 7$

Nå har vi et ligningsett med to ligninger og to ukjente:
$\frac{a_{1}}{1 - k} = 8$
$a_{1} (1 + k + k^{2}) = 7$

Svar: $\frac{a_{1}}{1 - k} = 8$ , $a_{1} (1 + k + k^{2}) = 7$

Mer om

Denne oppgaven er om

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

Uendelige rekker

En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.

Eksempel : $\sum_{n = 1}^{\infty} x_{n}$

( ∞ er tegnet for uendelighet )

uendelige rekker

og konvergens.

For flere forklaringer og eksempler på rekker, se artikkelen Uendelig rekker.

b)

Bruk CAS til å bestemme kvotienten $k$ og det første leddet $a_{1}$ i rekken.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke “Løs”-kommandoen i CAS.

For å løse ligningssettet i CAS kan vi bruke kommandoen “Løs”. Da skriver vi

Løs[{a_1/(1-k)=8, a_1(1+k+k^2)=7}, {a_1,k}]

i CAS-vinduet. Da vil CAS løse ligningsettet fra deloppgave a) med hensyn på $a_{1}$ og $k$ .

Utregningen fra CAS viser at $a_{1} = 4$ og $k = \frac{1}{2}$

Svar: $a_{1} = 4$ og $k = \frac{1}{2}$

Mer om

Denne oppgaven er om

Trigonometrisk rekke

En rekke der hvert ledd er en potens av en trigonometrisk funksjon.

Eksempel: $S_{n} = \sum_{i = 0}^{n} \cos^{i} (x + i) = 1 + \cos (x + 1) + \cos^{2} (x + 2) +$

$\cos^{3} (x + 3) + . . .$

uendelige rekker

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

Kvotient

Resultatet av en divisjon kalles en kvotient.

Eksempel: $32 : 8 = 4$ , her er 4 en kvotient.

kvotient

Ledd

I en addisjon kalles tallene som legges sammen for ledd.

Eksempel: $8 + 3 + 5 = 16$ , her kalles tallene 8, 3 og 5 for ledd.

ledd

For flere forklaringer og eksempler på rekker, se artikkelen Geometrisk rekke.

REA3024 2016 HØST

Del 1

Del 2

Eksamensinformasjon

DEL 1 uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4PBT

Løsningsforslag

Derivasjon

Sinus

Cosinus

b)

Løsningsforslag b)

Derivasjon

Sinus

Cosinus

c)

Løsningsforslag c)

Derivasjon

Sinus

Cosinus

Oppgave 2 (5 poeng) Nettkode: E-4PBX

a)

Løsningsforslag a)

Polynom

Integrasjon

b)

Løsningsforslag b)

Integrasjon

Derivasjon

Sinus

Cosinus

c)

Løsningsforslag c)

Integrasjon

Derivasjon

Sinus

Cosinus

Oppgave 3 (4 poeng) Nettkode: E-4PC1

a)

Løsningsforslag a)

Linje

Stigningstall

b)

Løsningsforslag b)

Volum

Integrasjon

Kjegle

Oppgave 4 (6 poeng) Nettkode: E-4P7A

a)

Løsningsforslag a)

Trigonometriske funksjoner

Sinus

b)

Løsningsforslag b)

Ekstremalpunkter

Sinus

c)

Løsningsforslag c)

Vendepunkt

Andrederiverte

Derivasjon

d)

Løsningsforslag d)

Graf

Funksjon

Vendepunkt

Ekstremalpunkt

Oppgave 5 (5 poeng) Nettkode: E-4PC4

a)

Løsningsforslag a)

Differensiallikning

Derivasjon

b)

Løsningsforslag b)

Differensiallikning

abc-formelen

c)

Løsningsforslag c)

Differensiallikning

Derivasjon