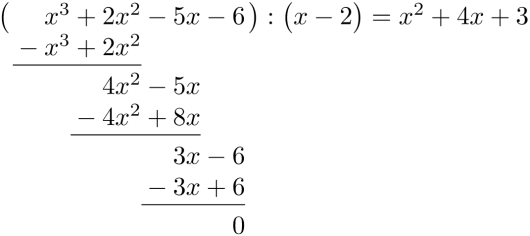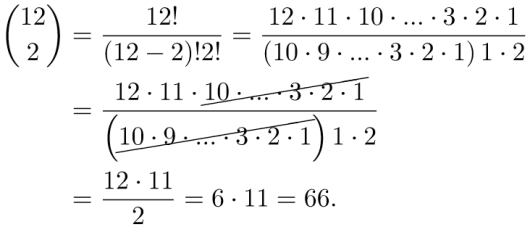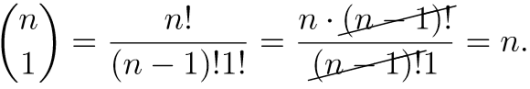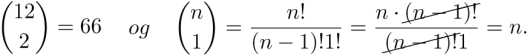Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3022 2015 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Del 1 har 9 oppgaver. Del 2 har 5 oppgaver.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
vurderer om svar er rimelige

Andre opplysninger:
Kilder for bilder, tegninger osv.:

Alle grafer og figurer: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4D6G

Deriver funksjonene

a)

$f (x) = x^{3} + 2 x^{2} - 3 x$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Funksjonen $f (x)$ er en sum av funksjoner på formen $a x^{n}$ der $a$ og $n$ er konstanter. Siden den deriverte av en sum er summen av de deriverte finner vi $\begin{matrix} f' (x) = (x^{3} + 2 x^{2} - 3 x)' = (x^{3})' + (2 x^{2})' + (- 3 x)' \end{matrix}$ og den deriverte av en funksjon på formen $a x^{n}$ er $n a x^{n - 1}$ .

$\begin{matrix} (x^{3})' + (2 x^{2})' + (- 3 x)' = 3 x^{2} + 2 \cdot 2 x^{1} + (- 3) = 3 x^{2} + 4 x - 3 . \end{matrix}$ $\begin{matrix} f' (x) = 3 x^{2} + 4 x - 3 . \end{matrix}$

Svar: $\begin{matrix} f' (x) = 3 x^{2} + 4 x - 3 . \end{matrix}$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

Visste du at

Hvis $x$ er sidelengden til et kvadrat har kvadratet areal lik $x^{2}$ . Ved å derivere $x^{2}$ finner vi hvor mye kvadratets areal endrer seg når vi endrer sidelengden. La oss si at sidelengden i kvadratet går fra å være $x$ til $x + Δ x$ . Da er arealet av kvadratet $\begin{matrix} {(x + Δ x)}^{2} = x^{2} + 2 x Δ x + Δ x^{2} . \end{matrix}$ Endringen i kvadratets areal er dermed $\begin{matrix} Δ (x^{2}) = x^{2} + 2 x Δ x + Δ x^{2} - x^{2} = 2 x Δ x + Δ x^{2} . \end{matrix}$ Siden det er mer hensiktsmessig å studere en generell endring i $x$ velger vi heller å studere endringen i kvadratets areal per endring i $x$ . Det vil si $\begin{matrix} \frac{Δ (x^{2})}{Δ x} = 2 x + Δ x . \end{matrix}$ Hvis endringen er uendelig liten sitter vi da igjen med uttrykket

$\frac{Δ (x^{2})}{Δ x} = 2 x når Δ x \to 0$

Dette er nøyaktig den deriverte til funksjonen $x^{2}$ .

b)

$g (x) = \ln (x - 2)$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Funksjonen $g (x)$ består en av naturlig logaritme, $\ln x$ , med en kjerne lik $x - 2$ . Kjerneregelen sier at $(f (h (x))) \begin{matrix} ' = f' (h (x)) h' (x) \end{matrix}$

Ved å velge kjernen $h (x) = x - 2$ , og huske at den deriverte til $\ln x$ er $\frac{1}{x}$ se at

$g' (x) = {(\ln (h (x)))}^{'} = \frac{1}{h (x)} \cdot h' (x) = \frac{1}{x - 2} \cdot 1 = \frac{1}{x - 2}$

Svar: $\begin{matrix} g' (x) & = \frac{1}{x - 2} . \end{matrix}$

Mer om

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler - eksempler.

Visste du at

Det finnes mange måter å skrive den deriverte av $g$ med hensyn på $x$ . Under ser du et par ulike skrivemåter: $\begin{matrix} \frac{d g}{d x} = g' (x) = \lim_{Δ x \to 0} \frac{g (x + Δ x) - g (x)}{Δ x} = \lim_{Δ \to 0} \frac{Δ g}{Δ x} = d_{x} g . \end{matrix}$ Dersom $x$ representerer tid er det også vanlig å skrive den deriverte av $g$ ved å sette en prikk over. Altså

$\frac{d g}{d x} = \dot{g}$

Dersom du bruker skrivemåten $\frac{d g}{d x}$ vil du kanskje oppdage at kjerneregelen ikke er annet en kjente brøkregler: $\begin{matrix} \frac{d g}{d x} = \frac{d g}{d h} \frac{d h}{d x} . \end{matrix}$

c)

$h (x) = {(2 x^{2} - 1)}^{3}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Funksjonen $h (x)$ består av en kjerne, lik $2 x^{2} - 1$ , som er opphøyd i tredje. Siden vi både klarer å derivere funksjonen av kjernen og kjernen selv bør vi benytte kjerneregelen for derivasjon.

Kjerneregelen sier at $\begin{matrix} (f (u (x)))' = f' (u (x)) u' (x) \end{matrix}$ . Husk at ${(u^{3})}^{'} = 3 \cdot u^{3 - 1} = 3 u^{2}$ følger det da at

$h' (x) = {({(2 x^{2} - 1)}^{3})}^{'} = 3 \cdot {(2 x^{2} - 1)}^{2} \cdot {(2 x^{2} - 1)}^{'} = 3 {(2 x^{2} - 1)}^{2} \cdot 2 \cdot 2 x = 12 x {(2 x^{2} - 1)}^{2}$

Svar: $\begin{matrix} h' (x) = 12 x {(2 x^{2} - 1)}^{2} . \end{matrix}$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen.

Oppgave 2 (5 poeng) Nettkode: E-4D6K

Polynomfunksjonen $P$ er gitt ved

$P (x) = x^{3} + {2 x}^{2} - 5 x - 6$

a)

Vis at $(x - 2)$ er en faktor i $P (x)$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Hvis $(x - 2)$ er en faktor i $P (x)$ kan polynomet skrives på formen $P (x) = (x - 2) \cdot f (x)$ for et andregradspolynom $f$ . Om vi setter inn $x = 2$ i $P$ får vi at $P (2) = 0 \cdot f (2)$ .

Siden $\begin{matrix} P (2) & = 2^{3} + 2 \cdot 2^{2} - 5 \cdot 2 - 6 \\ = 8 + 8 - 10 - 6 = 0 \end{matrix}$ har vi funnet at $P (2) = 0$ og dermed er $x - 2$ en faktor i polynomet.

Svar: $x - 2$ er en faktor.

Mer om:

Denne oppgaven er om

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Faktorisering av uttrykk

Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.

Eksempel: $x^{2} + 4 x + 3 = (x + 1) (x + 3)$

faktorisering av uttrykk i x

For flere forklaringer og eksempler på polynomer, se artikkelen Definisjon av et polynom.

b)

Bruk blant annet polynomdivisjon til å faktorisere $P (x)$ med lineære faktorer.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi fant en faktor til $P (x)$ i oppgave $2 a)$ . Vi begynner med å dividere denne ut. Når det er gjort har vi et andregradspolynom igjen å faktorisere. Det kan vi gjøre med annengradsformelen.

Vi utfører polynomdivisjonen $(x^{3} + 2 x^{2} - 5 x - 6) : (x - 2)$ .

Vi får at $P (x) = (x - 2) (x^{2} + 4 x + 3)$ , men vi leter etter lineære faktorer. Derfor forsøker vi å faktorisere $(x^{2} + 4 x + 3)$ . Vi gjør dette ved å finne nullpunktene til $(x^{2} + 4 x + 3)$ med annengradsformelen. Vi får da at $\begin{matrix} x = \frac{- 4 \pm \sqrt{4^{2} - 4 \cdot 3}}{2} = \frac{- 4 \pm \sqrt{4}}{2} = \frac{- 4 \pm 2}{2} \end{matrix}$ som gir de to røttene

$x_{1} = - 3 og x_{2} = - 1$

Det betyr at vi kan skrive $\begin{matrix} x^{2} + 4 x + 3 = (x + 3) (x + 1) . \end{matrix}$ Vi har altså funnet at $\begin{matrix} P (x) = (x - 2) (x + 1) (x + 3) . \end{matrix}$

$\begin{matrix} P (x) = (x - 2) (x + 1) (x + 3) \end{matrix}$

Svar: $\begin{matrix} P (x) = (x - 2) (x + 1) (x + 3) \end{matrix}$

Mer om:

Denne oppgaven er om

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

For flere forklaringer og eksempler på polynomdivisjon, se artikkelen Nullpunktsetningen - når går divisjonen opp?.

c)

Bestem $\lim_{x \to 2} \frac{x^{3} + 2 x^{2} - 5 x - 6}{x - 2}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Når $x$ nærmer seg $2$ , vil nevneren nærme seg null. Hvis grenseverdien skal bli et tall må vi altså kunne fortkorte bort faktoren $(x - 2)$ .

Fra oppgave $2 b)$ har vi at $\begin{matrix} x^{3} + 2 x - 5 x - 6 = (x - 2) (x + 1) (x + 3) \end{matrix}$ som betyr at vi kan skrive $\begin{matrix} \lim_{x \to 2} \frac{x^{3} + 2 x - 5 x - 6}{x - 2} \\ = \lim_{x \to 2} \frac{(x - 2) (x + 1) (x + 3)}{x - 2} \\ = \lim_{x \to 2} (x + 1) (x + 3) = (2 + 1) (2 + 3) \\ = 3 \cdot 5 = 15 . \end{matrix}$

$\begin{matrix} \lim_{x \to 2} \frac{x^{3} + 2 x - 5 x - 6}{x - 2} = 15 . \end{matrix}$

Svar: $\lim_{x \to 2} \frac{x^{3} + 2 x^{2} - 5 x - 6}{x - 2} = 15$

Mer om:

Denne oppgaven er om

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Faktorisering av uttrykk

Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.

Eksempel: $x^{2} + 4 x + 3 = (x + 1) (x + 3)$

faktorisering av uttrykk i x

For flere forklaringer og eksempler på grenseverdier, se artikkelen Grenseverdier.

Oppgave 3 (3 poeng) Nettkode: E-4D6O

Skriv så enkelt som mulig

$\frac{x - 2}{x^{2} + 2 x} + \frac{2}{x} + \frac{x + 2}{x^{2} - 2 x} - \frac{3 x}{x^{2} - 4}$

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Ved å finne minste fellesnevner kan vi sette uttrykket på felles brøkstrek. Da kan vi trolig forenkle uttrykket betraktelig.

Vi begynner med å observere at $\begin{matrix} \frac{x - 2}{x^{2} + 2 x} + \frac{2}{x} + \frac{x + 2}{x^{2} - 2 x} - \frac{3 x}{x^{2} - 4} \\ = \frac{x - 2}{x (x + 2)} + \frac{2}{x} + \frac{x + 2}{x (x - 2)} - \frac{3 x}{(x - 2) (x + 2)}, \end{matrix}$ som betyr at minste felles nevner er gitt ved $\begin{matrix} x (x - 2) (x + 2) . \end{matrix}$ Dermed har vi at $\begin{matrix} \frac{x - 2}{x^{2} + 2 x} + \frac{2}{x} + \frac{x + 2}{x^{2} - 2 x} - \frac{3 x}{x^{2} - 4} \\ = \frac{x - 2}{x (x + 2)} + \frac{2}{x} + \frac{x + 2}{x (x - 2)} - \frac{3 x}{(x - 2) (x + 2)} \\ = \frac{(x - 2)^{2}}{x (x + 2) (x - 2)} + \frac{2 (x + 2) (x - 2)}{x (x + 2) (x - 2)} + \frac{(x + 2)^{2}}{x (x - 2) (x + 2)} - \frac{3 x^{2}}{x (x - 2) (x + 2)} \\ = \frac{(x - 2)^{2} + 2 (x + 2) (x - 2) + (x + 2)^{2} - 3 x^{2}}{x (x + 2) (x - 2)} \\ = \frac{(x^{2} - 4 x + 4) + 2 (x^{2} - 4) + (x^{2} + 4 x + 4) - 3 x^{2}}{x (x + 2) (x - 2)} \\ = \frac{4 x^{2} - 3 x^{2}}{x (x + 2) (x - 2)} = \frac{x^{2}}{x (x + 2) (x - 2)} \\ = \frac{x}{(x + 2) (x - 2)} . \end{matrix}$

$\begin{matrix} = \frac{x}{x^{2} - 4} . \end{matrix}$

Svar: $\frac{x}{x^{2} - 4}$

Mer om:

Denne oppgaven er om

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

Faktorisering av uttrykk

Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.

Eksempel: $x^{2} + 4 x + 3 = (x + 1) (x + 3)$

faktorisering av uttrykk i x

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetningen

For flereforklaringer og eksempler på forenkling, se artikkelen Forkorte og utvide brøk.

Oppgave 4 (2 poeng) Nettkode: E-4D6Q

En sirkel er gitt ved likningen

$x^{2} - 2 x + y^{2} + 4 y - 20 = 0$

Bestem sentrum $S$ og radius $r$ i sirkelen.

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Vi skal finne sentrum og radius til en sirkel. Sirkelen kan skrives som $(x - a)^{2} + (y - b)^{2} = r^{2}$ , der sentrum er i $(a, b)$ og radiusen er $r$ . Vi skriver om uttrykket slik at vi får et fullstendig kvadrat med $x$ -ledd, og ett med $y$ -ledd.

Likningen for sirkelen kan skrives $\begin{matrix} x^{2} - 2 x + y^{2} + 4 y = 20, \end{matrix}$ og ved å fullføre kvadratet for $x$ kan vi skrive $\begin{matrix} (x - 1)^{2} - 1 + y^{2} + 4 y = 20 . \end{matrix}$ Ved å gjøre det tilsvarende for $y$ ser vi at uttrykket forenkles til $\begin{matrix} (x - 1)^{2} - 1 + (y + 2)^{2} - 4 = 20, \end{matrix}$ som kan skrives $\begin{matrix} (x - 1)^{2} + (y + 2)^{2} = 25 . \end{matrix}$ Dette betyr at sirkelen har radius $r = \sqrt{25} = 5$ og sentrum i punktet $\begin{matrix} S = (1, - 2) . \end{matrix}$

Svar: Sirkelen har radius $5$ , og sentrum i $(1, - 2)$ .

Mer om:

Denne oppgaven er om

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Radius

Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.

radius

For flere forklaringer og eksempler på å fullføre et kvadrat, se artikkelen Å fullføre kvadratet.

Oppgave 5 (5 poeng) Nettkode: E-4D6S

Vektoren $\vec{v} = [3, 4]$ er gitt.

a)

Bestem en vektor $\vec{u}$ som er parallell med $\vec{v}$ og motsatt rettet.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Hvis $\vec{v}$ er en vektor kan vi uttrykke enhver vektor $\vec{u}$ som er parallell med $\vec{v}$ ved $\vec{u} = C \vec{v}$ der $C$ er en konstant og $C \neq 0$ . Hvis $C$ er et negativt tall vil vektoren $\vec{u}$ være parallell med $\vec{v}$ samtidig som den er motsatt rettet.

Siden vektoren $\vec{u}$ skal være parallell med $\vec{v}$ må det finnes en konstant $C \neq 0$ slik at $\vec{u} = C \vec{v}$ . Siden $\vec{u}$ skal være motsatt rettet må $C$ være et negativt tall. Det betyr at vi kan velge $C = - 1$ , som gir $\begin{matrix} \vec{u} = - 1 \cdot \vec{v} = - 1 \cdot [3, 4] = [- 3, - 4] . \end{matrix}$

Alternativ løsning

Siden den vektoren $\vec{u}$ som har egenskapen $\vec{v} + \vec{u} = \vec{0}$ er parallell med $\vec{v}$ og motsatt rettet kan vi velge vektoren $\begin{matrix} \vec{u} = - \vec{v} = - [3, 4] = [- 3, - 4] . \end{matrix}$

Svar: $\begin{matrix} \vec{u} = [- 3, - 4] \end{matrix}$ (svaret er ikke unikt)

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".

parallell

For flere forklaringer og eksempler på vektorer, se artikkelen Parallelle vektorer.

b)

Bestem en vektor $\vec{w} \neq \vec{0}$ som står vinkelrett på $\vec{v}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

To vektorer $\vec{a}$ og $\vec{b}$ er vinkelrette hvis, og bare hvis, $\vec{a} \cdot \vec{b} = 0$ .

Hvis $\vec{w} = [x, y] \neq [0, 0]$ er en vektor som står vinkelrett på vektoren $\vec{v} = [3, 4]$ må vi ha $\begin{matrix} \vec{w} \cdot \vec{v} = 3 x + 4 y = 0 . \end{matrix}$ Ved å løse for $y$ ser vi at dette gir $\begin{matrix} y = - \frac{3}{4} x . \end{matrix}$ Vi kan altså velge vektoren $\begin{matrix} \vec{w} = [x, - \frac{3}{4} x] \end{matrix}$ uansett verdi av $x \neq 0$ . For å bli kvitt brøken kan vi for eksempel velge $x = 4$ . Det gir $\begin{matrix} \vec{w} = [4, - 3] . \end{matrix}$

Svar: $\begin{matrix} \vec{w} = [4, - 3] . \end{matrix}$

Mer om

Denne oppgaven er om

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

vinkelrett

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Ortogonale vektorer.

c)

Bestem konstantene $k$ og $t$ slik at

$\vec{v} = k \cdot \vec{u} + t \cdot \vec{w}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må finne to tall $k$ og $t$ slik at $\vec{v} = k \vec{u} + t \vec{w}$ .

I deloppgaven a) fant vi vektoren $\vec{u}$ slik at ved å sette $\vec{u} = - \vec{v}$ følger det at $\begin{matrix} \vec{v} = - \vec{u} \end{matrix}$ og dermed $\begin{matrix} \vec{v} = (- 1) \cdot \vec{u} + 0 \cdot \vec{w} . \end{matrix}$

Alternativ løsning

Vi må finne to tall $k$ og $t$ slik at $\begin{matrix} [3, 4] = k [- 3, - 4] + t [4, - 3] = [- 3 k + 4 t, - 4 k - 3 t] . \end{matrix}$ Siden likningen må være tilfredsstilt for de to koordinatene separat må vi løse likningssettet $\begin{matrix} (I) & 4 t - 3 k = 3 \\ (I I) & - 3 t - 4 k = 4 . \end{matrix}$ Ved å løse for $t$ i likning $(I)$ finner vi at $\begin{matrix} t = \frac{1}{4} (3 + 3 k) = \frac{3}{4} (1 + k) . \end{matrix}$ Det betyr at vi kan bytte ut $t$ med $\frac{3}{4} (1 + k)$ i likning $(I I)$ og få $\begin{matrix} - 3 \frac{3}{4} (1 + k) - 4 k = 4, \end{matrix}$ som kan skrives $\begin{matrix} - \frac{9}{4} - \frac{9}{4} k - 4 k = 4 . \end{matrix}$ Ved å bruke at $\frac{9}{4} + 4 = \frac{9 + 16}{4} = \frac{25}{4}$ kan vi dermed skrive $\begin{matrix} - \frac{9}{4} - \frac{25}{4} k = 4, \end{matrix}$ som kan omformuleres til $\begin{matrix} \frac{25}{4} k = - \frac{9}{4} - 4 = - \frac{25}{4} . \end{matrix}$ Det betyr at vi må ha $k = - 1$ . Ved å sette dette inn i likning $(I)$ får vi $\begin{matrix} 4 t - 3 (- 1) = 3, \end{matrix}$ som betyr at $t = 0$ . Vi har altså funnet at $\begin{matrix} \vec{v} = (- 1) \cdot \vec{u} + 0 \cdot \vec{w} . \end{matrix}$

Svar: $\vec{v} = (- 1) \cdot \vec{u} + 0 \cdot \vec{w}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på likninger, se artikkelen Lineære likninger med flere ukjente.

d)

Bestem en vektor $\vec{x}$ som har samme retning som $\vec{v}$ og som har lengde lik 7.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

At vektoren $\vec{x}$ har samme retning som $\vec{v}$ betyr at $\vec{x} = C \vec{v}$ der $C \neq 0$ er en positiv konstant. At $\vec{x} = [a, b]$ har lengde $7$ betyr at $a^{2} + b^{2} = 7^{2}$ .

Siden $\vec{x}$ har samme retning som $\vec{v}$ kan vi skrive $\begin{matrix} \vec{x} = C \vec{v} = C [3, 4] = [3 C, 4 C] \end{matrix}$ for en eller annen $C > 0$ . Lengden til $\vec{x}$ er videre gitt ved $\begin{matrix} | \vec{x} | = \sqrt{(3 C)^{2} + (4 C)^{2}} = \sqrt{C^{2} (9 + 16)} = C \sqrt{25} = 5 C . \end{matrix}$ Siden $\vec{x}$ skal ha lengde lik $7$ betyr dette at $\begin{matrix} 5 C = 7, \end{matrix}$ og dermed $C = \frac{7}{5}$ . Koordinatene til vektoren $\vec{x}$ er altså gitt ved $\begin{matrix} \vec{x} = [\frac{7}{5} \cdot 3, \frac{7}{5} \cdot 4] = [\frac{21}{5}, \frac{28}{5}] \end{matrix}$

Svar: $\begin{matrix} \vec{x} = [\frac{21}{5}, \frac{28}{5}] \end{matrix}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Like vektorer.

Oppgave 6 (4 poeng) Nettkode: E-4D6X

Binomialkoeffisientene er gitt ved $(\begin{matrix} n \\ r \end{matrix}) = \frac{n!}{(n - r)! \cdot r!}$

a)

Bestem $(\begin{matrix} 12 \\ 2 \end{matrix})$ . Vis at $(\begin{matrix} n \\ 1 \end{matrix}) = n$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Ved å bruke at $n! = n (n - 1) (n - 2) . . .3 \cdot 2 \cdot 1$ kan vi finne et uttrykk for binomialkoeffisientene $(\begin{matrix} 12 \\ 2 \end{matrix})$ og $(\begin{matrix} n \\ 1 \end{matrix})$ .

Fra definisjonen av binominalkoeffisientene har vi at

Siden vi alltid kan skrive at $n! = n \cdot (n - 1)!$ kan vi videre skrive

Svar:

Mer om:

Denne oppgaven er om

Binomialkoeffisienter

De koeffisientene man får når en opphøyer (x+y) i et naturlig tall.

binomialkoeffisienter

For flere forklaringer og eksempler på sannsynlighet, se artikkelen Repetisjon av begreper.

b)

Bruk det du fant i oppgave a) til å løse likningen $\frac{(\begin{matrix} x \\ 1 \end{matrix}) \cdot (\begin{matrix} 12 - x \\ 1 \end{matrix})}{(\begin{matrix} 12 \\ 2 \end{matrix})} = \frac{6}{11}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Ved å bruke definisjonen av binomialkoeffisientene og resultatene fra oppgave $6 a)$ kan vi skrive likningen på en mer kjent form.

Fra oppgave $6 a)$ har vi at

$\frac{(\begin{matrix} x \\ 1 \end{matrix}) \cdot (\begin{matrix} 12 - x \\ 1 \end{matrix})}{(\begin{matrix} 12 \\ 2 \end{matrix})} = \frac{x (12 - x)}{66}$ .

Det betyr at likningen kan skrives $\begin{matrix} \frac{x (12 - x)}{66} = \frac{6}{11} . \end{matrix}$ Ved å multiplisere begge sider av likningen med $66$ får vi $\begin{matrix} x (12 - x) = 66 \cdot \frac{6}{11} = 6^{2} = 36 . \end{matrix}$ Når vi multipliserer ut parentesen kan vi altså skrive $\begin{matrix} 12 x - x^{2} = 36 \end{matrix}$ eller, ved å trekke fra $12 x - x^{2}$ på begge sider, $\begin{matrix} x^{2} - 12 x + 36 = 0 . \end{matrix}$ Denne likningen kan enten løses ved å bruke annengradslikningen eller ved å gjenkjenne den andre kvadratsetningen. Vi finner uansett at uttrykket kan skrives $\begin{matrix} (x - 6)^{2} = 0, \end{matrix}$ som betyr at likningen bare har én løsning, nemlig $x = 6$ .

Svar: $\begin{matrix} x = 6 . \end{matrix}$

Mer om:

Denne oppgaven er om

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikning

For flere forklaringer og eksempler på andregradslikninger, se artikkelen Kvadratsetningene.

Oppgave 7 (5 poeng) Nettkode: E-4D70

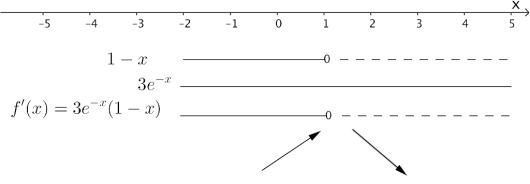
Funksjonen $f$ er gitt ved

$f (x) = 3 x \cdot e^{- x}, x \in ⟨- 1, 4⟩$

a)

Bruk $f' (x)$ til å avgjøre hvor $f (x)$ vokser og hvor $f (x)$ avtar. Bestem $x$ -verdien til eventuelle topp- eller bunnpunkter.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

En funksjon $f (x)$ er voksende hvis $f' (x) > 0$ og avtagende hvis $f' (x) < 0$ . Videre har $f (x)$ et toppunkt i punktene der $f' (x)$ går fra å være positiv til å være negativ og et bunnpunkt der $f' (x)$ går fra å være negativ til å være positiv.

Ifølge produktregelen for derivasjon, som sier at $(u v)' = u' v + u v'$ , har vi at $\begin{matrix} f' (x) & = (3 x e^{- x})' = (3 x)' e^{- x} + 3 x (e^{- x})' \\ = 3 e^{- x} + 3 x (e^{- x})' . \end{matrix}$ Videre gir kjerneregelen, som sier at $(g (u (x)))' = u' (x) g' (u)$ , med kjerne lik $u = - x$ at $\begin{matrix} 3 e^{- x} + 3 x (e^{- x})' = 3 e^{- x} + 3 x (- x)' e^{- x} = 3 e^{- x} - 3 x e^{- x} . \end{matrix}$ Den deriverte av $f (x)$ er altså gitt ved $\begin{matrix} f' (x) = 3 e^{- x} - 3 x e^{- x} = 3 e^{- x} (1 - x) . \end{matrix}$ Siden $3 e^{- x}$ alltid er et positivt tall er fortegnet til $f' (x)$ lik fortegnet til faktoren $(1 - x)$ . Siden faktoren $(1 - x)$ er negativ for $x > 1$ og positiv $x < 1$ har vi at $f (x)$ er voksende for $x < 1$ og avtagende for $x > 1$ . Ettersom $f' (x)$ går fra å være positiv til å bli negativ i punktet $x = 1$ må $f (x)$ ha et toppunkt i $x = 1$ . Se fortegnskjema:

Svar: $f (x)$ er voksende for $x < 1$ , avtagende for $x > 1$ og har et toppunkt i $x = 1$ .

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.

fortegnsskjema

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

b)

Bruk $f'' (x)$ til å bestemme x-verdien til eventuelle vendepunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Funksjonen $f (x)$ har et vendepunkt i $x = x_{0}$ hvis $f ″ (x_{0}) = 0$ .

Ifølge produktregelen har vi at $\begin{matrix} f ″ (x) & = (3 e^{- x} (1 - x))' = (3 e^{- x})' (1 - x) + 3 e^{- x} (1 - x)' \\ = 3 (- 1) e^{- x} (1 - x) + 3 e^{- x} (0 - 1) = - 3 e^{- x} (1 - x) - 3 e^{- x} \\ = 3 e^{- x} (- (1 - x) - 1) = 3 e^{- x} (x - 2) . \end{matrix}$ Det betyr at vendepunktene til $f (x)$ er nøyaktig de punktene som tilfredsstiller likningen $\begin{matrix} f ″ (x) = 3 e^{- x} (x - 2) = 0 . \end{matrix}$ Siden $3 e^{- x}$ ikke kan være skyld i at $f ″ (x) = 0$ må vi da ha $\begin{matrix} x - 2 = 0, \end{matrix}$ som betyr at $f (x)$ har et vendepunkt i $x = 2$ .

Svar: $f (x)$ har et vendepunkt i $x = 2$ .

Mer om:

Denne oppgaven er om

Andrederiverte

Den andrederiverte til en funksjon $f (x)$ er funksjonen derivert to ganger og skrives $f'' (x)$ eller $f^{(2)} (x)$ . Kalles også annenderiverte eller dobbeltderiverte.

andrederivert

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

For flere forklaringer og eksempler på vendepunkter, se artikkelen vendepunkt og vendetangent.

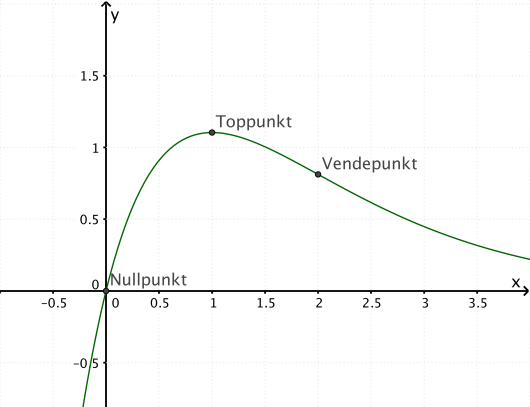
c)

Lag en skisse av grafen til $f$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Ved å merke av hvor funksjonen har topp- og bunnpunkter, vendepunkter og nullpunkter sammen med hvor den er voksende og avtagende kan vi lage en skisse av hvordan grafen til $f (x)$ ser ut.

Vi begynner med å se at nullpunktene til $f (x)$ er gitt ved $\begin{matrix} f (x) = 3 x e^{- x} = 0 \end{matrix}$ som, siden $3 e^{- x}$ aldri blir null, må være gitt av $x = 0$ . Vi har altså at grafen til $f$ er voksende og negativ frem til $x = 0$ , der den er null. Deretter fortsetter den å vokse frem til den når det eneste toppunktet på grafen, som ligger ved $x = 1$ . Grafen fortsetter så å avta med krumning nedover helt til den passerer punktet $x = 2$ . Da fortsetter grafen å avta, men nå med krumning oppover.

Svar:

Mer om:

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

Oppgave 8 (6 poeng) Nettkode: E-4D75

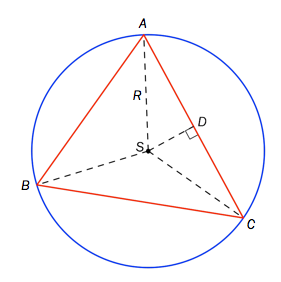
En vilkårlig $Δ A B C$ er gitt. En sirkel har radius $R$ og sentrum i $S$ og omskriver $Δ A B C$ . En normal fra $S$ til siden $A C$ har fotpunkt $D$ . Se skissen nedenfor.

a)

Forklar at $∠ B = ∠ D S A$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi kan bruke at en periferivinkel er halvparten så stor som gradtallet av den sirkelbuen som ligger mellom vinkelens bein til å uttrykke $∠ B$ ved hjelp av $∠ C S A$ .

Oppgaveteksten sier at $Δ A B C$ er vilkårlig, men vi må anta at $Δ A B C$ er spissvinklet. Hvis ikke er ikke resultatet i oppgave a) riktig. Siden vinklene $∠ B$ og $∠ C S A$ spenner ut samme sirkelbue, der $∠ B$ er en periferivinkel og $∠ C S A$ er en sentralvinkel, kan vi skrive $\begin{matrix} 2 ∠ B = ∠ C S A . \end{matrix}$ Siden linjestykket $S D$ står vinkelrett på linjestykket $A C$ må $D$ dele linjestykket $A C$ i to like store deler. Ettersom $△ D S A$ og $△ D S C$ er kongruente må også vinkelen $∠ C S A$ deles i to like store deler av punktet $D$ . Vi har altså at $\begin{matrix} ∠ D S A = \frac{1}{2} ∠ C S A . \end{matrix}$ Siden vi allerede vet at $2 ∠ B = ∠ C S A$ følger det dermed at $\begin{matrix} ∠ B = \frac{1}{2} ∠ C S A = ∠ D S A, \end{matrix}$ som er det vi ønsket å vise.

Alternativ løsning

Ved å dele opp vinkelen $∠ B$ i $∠ C B S$ og $∠ S B A$ kan vi skrive $\begin{matrix} ∠ B = ∠ C B S + ∠ S B A \end{matrix}$ og siden $△ B S A$ og $△ B C S$ begge er likebenede trekanter må $\begin{matrix} ∠ S B A = ∠ B A S og ∠ C B S = ∠ S C B . \end{matrix}$ Vi kan altså skrive vinkelsummen i $△ A B C$ ved $\begin{matrix} 180^{\circ} = 2 ∠ C B S + 2 ∠ S B A + 2 ∠ S A C . \end{matrix}$ Ved å trekke $2 ∠ S A C$ fra begge sider av likningen og dividere med to finner vi videre at $\begin{matrix} 90^{\circ} - ∠ S A C = ∠ C B S + ∠ S B A, \end{matrix}$ og siden $∠ B = ∠ C B S + ∠ S B A$ må $\begin{matrix} ∠ B = 90^{\circ} - ∠ S A C . \end{matrix}$ Dermed gjenstår det bare å se at siden $∠ S A C = ∠ S A D$ og $90^{\circ} - ∠ S A C = ∠ D S A$ . Da får vi $\begin{matrix} ∠ B = ∠ D S A, \end{matrix}$ som er det vi ønsket å vise.

Mer om:

Denne oppgaven er om

Sirkel

Sirkel brukes i to betydninger:

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

For flere forklaringer og eksempler på vinkler, se artikkelen Forskjellige typer vinkler.

b)

Vi setter $A C = b$ .

Vis at $\frac{b}{\sin B} = 2 R$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Ved å bruke resultatet fra $8 a)$ og at sinus til en vinkel er lik lengden av den motstående kateten dividert på lengden av hypotenusen kan vi finne et uttrykk som relaterer $b$ , $R$ og $∠ B$ .

Siden $△ D S A$ er rettvinklet må vi ha at $\begin{matrix} \sin (∠ D S A) = \frac{D A}{S A} = \frac{\frac{1}{2} A C}{R} = \frac{b}{2 R} . \end{matrix}$ Fra oppgave $8 a)$ har vi at $\begin{matrix} ∠ B = ∠ D S A, \end{matrix}$ som betyr at vi kan skrive $\begin{matrix} \sin B = \frac{b}{2 R} . \end{matrix}$ Ved å multiplisere begge sider av likningen med $2 R / \sin B$ ser vi at $\begin{matrix} \frac{b}{\sin B} = 2 R . \end{matrix}$

Mer om:

Denne oppgaven er om

Trigonometri

Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.

trigonometri

Hypotenus

Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.

hypotenus

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

For flere forklaringer og eksempler på trigonometri, se artikkelen Sinus, cosinus og tangens.

c)

Vi setter $B C = a$ og $A B = c$ .

Bruk tilsvarende resonnement som i oppgave b) til å vise at

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Ved å repetere argumentasjonen fra oppgave $8 a$ og $8 b$ kan vi finne liknende uttrykk for $a, c, A$ og $C$ .

Vi tegner inn et fotpunkt $E$ på linjen $B C$ og et fotpunkt $F$ på linjen $A B$ . Situasjonen er da som vist i figuren under

Ved å gjenta argumentasjonen fra oppgave $8 a)$ får vi da at

$∠ C = ∠ F S B og ∠ A = ∠ E S C$

Ved deretter å gjenta argumentasjonen i oppgave $8 b)$ for hver av de to vinklene $∠ A$ og $∠ C$ får vi at

$\frac{a}{\sin (A)} = 2 R og \frac{c}{\sin (C)} = 2 R$

Siden radius $R$ i sirkelen er den samme for alle de tre punktene får vi dermed at $\begin{matrix} \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R, \end{matrix}$ som er det vi ønsket å vise.

Alternativ løsning

Siden trekanten $△ A B C$ er en vilkårlig trekant, og argumentasjonen i oppgave $8 a$ og $8 b$ er gyldig for alle punkter $B$ , må resulatet også stemme for de andre to punktene. Altså

$\frac{a}{\sin (A)} = 2 R og \frac{c}{\sin (C)} = 2 R$

Siden radius er den samme uavhengig av hvilket punkt vi ser på må dette bety at $\begin{matrix} \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R, \end{matrix}$ som er det vi ønsket å vise.

Mer om:

Denne oppgaven er om

Sinus

sinus

For flere forklaringer og eksempler på trigonometri, se artikkelen Sinussetningen.

Oppgave 9 (2 poeng) Nettkode: E-4D79

Løs likningen

$9^{x} - 3^{x} - 12 = 0$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Ved å uttrykke likningen ved hjelp av $u = 3^{x}$ trenger vi ikke gjøre annet enn å løse en annengradslikning for å få verdien av $u$ som tilfredsstiller likningen. Da vet vi også verdien av løsningene $x$ .

Siden $\begin{matrix} 9^{x} = {(3^{2})}^{x} = {(3^{x})}^{2}, \end{matrix}$ kan vi skrive likningen på formen $\begin{matrix} {(3^{x})}^{2} - 3^{x} - 12 = 0, \end{matrix}$ som ved å sette $u = 3^{x}$ kan skrives $\begin{matrix} u^{2} - u - 12 = 0 . \end{matrix}$ Annengradsformelen gir deretter de to løsningene $\begin{matrix} u = \frac{1 \pm \sqrt{(- 1)^{2} - 4 \cdot (- 12)}}{2} = \frac{1 \pm \sqrt{49}}{2} = \frac{1 \pm 7}{2} . \end{matrix}$ Dette tilsvarer

$u_{1} = - 3 og u_{2} = 4$

Siden $u = 3^{x}$ må vi altså løse likningene

$3^{x} = - 3 og 3^{x} = 4$

Den første likningen må imidlertid elimineres ettersom det ikke finnes et løsning. Uansett hva $x$ er må nemlig $3^{x}$ være et positivt tall – da kan ikke $3^{x} = - 3$ . Den andre likningen løser vi ved å ta logaritmen av begge sider av likningen. Da får vi $\begin{matrix} \ln (3^{x}) = x \ln (3) = \ln (4) . \end{matrix}$ Vi har altså funnet at løsningen av likningen er gitt som $\begin{matrix} x = \frac{\ln (4)}{\ln (3)} = \frac{\ln (2^{2})}{\ln (3)} = \frac{2 \ln (2)}{\ln (3)} . \end{matrix}$

Svar: $\begin{matrix} x = \frac{2 \ln (2)}{\ln (3)} . \end{matrix}$

Mer om

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

For flere forklaringer og eksempler på logaritmer, se artikkelen Logaritmelikninger.

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4D7D

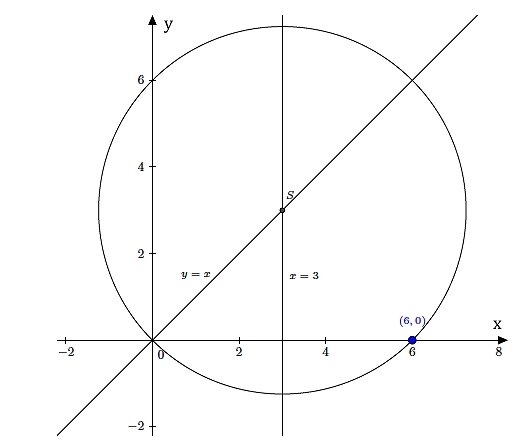
En sirkel har følgende egenskaper:

- Sentrum i sirkelen ligger på linjen $y = x$

- Sentrum i sirkelen ligger like langt fra origo som fra punktet $A (6, 0)$

- Origo og punktet $A$ ligger begge på sirkelperiferien

a)

Tegn sirkelen i et koordinatsystem.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi får oppgitt tre biter med informasjon om sirkelen. Vi forsøker å følge hvert punkt og se om det holder til å tegne figuren.

Vi tegner linjen $y = x$ i Geogebra. Vi vet at sentrum skal ligge på denne linjen, og like langt fra $(6, 0)$ som fra $(0, 0)$ . Alle punkt som er like langt fra $(6, 0)$ som fra $(0, 0)$ er på linjen $x = 3$ . Sentrum av sirkelen er ved skjæringspunktet mellom linjen $x = 3$ og $y = x$ . Geogebra har et sirkeltegneverktøy som tegner en sirkel gjennom et definert sentrum, hvor man stiller inn radiusen selv.

Svar:

Mer om

Denne oppgaven er om

Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).

koordinatsystem

Sirkel

Sirkel brukes i to betydninger:

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere forklaringer og eksempler på sirkler, se artikkelen Alt om sirkel.

b)

Bestem en likning for sirkelen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Formelen til sirkelen vi tegnet i a) står i algebrafeltet i Geogebra og kan skrives over direkte. For bruksskyld har vi skissert en alternativ løsning.

Vi har et bilde av sirkelen og vi skal finne et uttrykk for den. Vi vet at alle sirkler kan skrives på formen $(x - a)^{2} + (y - b)^{2} = r^{2}$ der $(a, b)$ er sentrum av sirkelen, og $r$ er radiusen.

Sentrum er der $x = 3$ og $x = y$ , så $(3, 3)$ .

Vi kan regne ut radiusen med Pytagoras læresetning, på trekanten med hjørner $(0, 0), (3, 0), (3, 3)$ .
Avstanden fra origo til sentrum av sirkelen er da

$\sqrt{3^{2} + 3^{2}} = \sqrt{18} = 3 \sqrt{2}$ .

Likningen for sirkelen er $(x - 3)^{2} + (y - 3)^{2} = 18$ .

Svar: $(x - 3)^{2} + (y - 3)^{2} = 18$

Mer om:

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Radius

Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.

radius

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Sirkel

Sirkel brukes i to betydninger:

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Origo

I et koordinatsystem står to akser vinkelrett på hverandre. Punktet der aksene møtes kalles origo. Origo har koordinatene (0,0).

origo

For flere forklaringer og eksempler på koordinatsystemet, se artikkelen Koordinatsystem.

Visste du at

Her kan man sette svaret på prøve ved å skrive inn $(x - 3)^{2} + (y - 3)^{2} = 18$ i Geogebra, og skjule den orginale figuren. Om figurene overlapper fullstendig stemmer hvertfall svaret i b) med svaret fra a). Dette vil typisk gi god uttelling på oppgave b) selv om sirkelen vi tegnet i a) skulle vært feil.

Oppgave 2 (6 poeng) Nettkode: E-4D7K

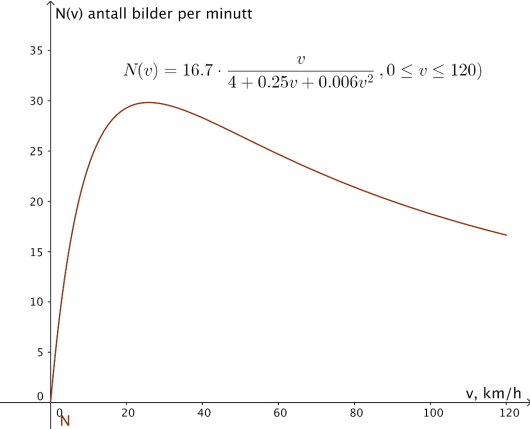
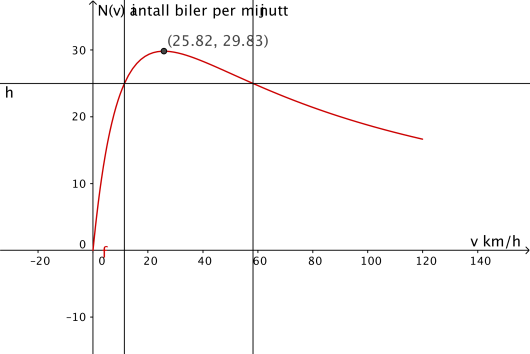
Bilene i en bilkø holder en fart på $v$ km/h. Ifølge køteori vil antall biler $N$ som passerer et bestemt sted per minutt være gitt ved modellen

$N (v) = \frac{16, 7 v}{4 + 0, 25 v + 0, 006 v^{2}}$

a)

Bruk graftegner til å tegne grafen til $N$ for $v \in [0, 120]$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Her skal vi bare plotte funksjonen i et digitalt verktøy. Det er viktig å huske å stille inn forholdet mellom aksene, og begrense intervallet.

Bruk Funksjon[ <Funksjon>, <Start>, <Slutt> ] i GeoGebra slik at vi begrenser oss til intervallet $v \in [0, 120]$ . Vi tilpasser aksene så hele grafen synes, med minimalt med tomrom.

Svar:

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

graf

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

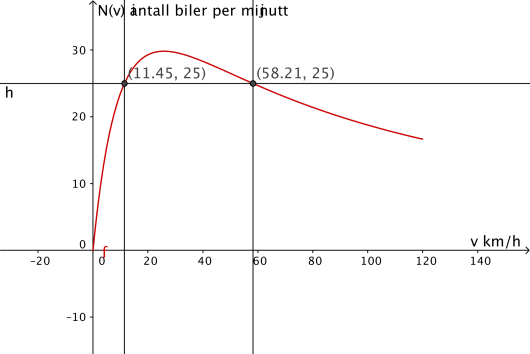
b)

Bestem grafisk hva farten bør være for at minst 25 biler skal kunne passere stedet per minutt.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi skal løse oppgaven grafisk, så her holder det ikke å løse ligningen ulikheten $N (v) \geq 25$ .

Vi tegner $N = 25$ i Geogebra, og bruker knappen i verktøylinjen 'Skjæring mellom to objekter' og leser av skjæringspunktene. Vi ser at en fart $v$ mellom $11, 45$ og $58, 21$ km/h gir en flyt på mer enn $25$ biler i minuttet.

Svar: Det passerer minst $25$ biler i minutter når farten er mellom $11, 45$ km/h og $58, 21$ km/h.

Mer om

Denne oppgaven er om ulikhet,

Graf

graf

Skjæringspunkt

skjæringspunkt

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på matematiske modeller, se artikkelen Hva er matematisk modellering?.

c)

Bestem grafisk hva farten må være for at flest mulig biler skal kunne passere stedet per minutt. Hvor mange biler passerer stedet per minutt da?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Her og skal vi løse oppgaven grafisk. Algebraiske løsninger er gode til å sjekke svar, men det er ikke det oppgaven spør etter.

Vi kan bruke kommandoen Ekstremalpunkt i Geogebra og lese av at toppunktet er på $v = 25, 82$ , som gir $N = 29, 83$ . ALtså passerer det nesten $30$ biler per minutt.

Svar: Det passerer flest biler om farten er $25, 82$ km/h. Da passerer det nesten $30$ biler i minuttet.

Mer om

Denne oppgaven er om

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Graf

graf

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Visste du at

Både oppgave b) og c) skal løses grafisk. Geogebra har verktøy for å finne svarene nøyaktig, men her kan det være slingringsrom. Om man plotter linjen $N = 25$ i oppgave b) og leser av omtrentlige $v$ -verdier på øyemål er det kanskje det oppgaven spør etter. Det finnes mange måter å tolke oppgaveteksten, og like mange forskjellige riktige løsninger.

Oppgave 3 (6 poeng) Nettkode: E-4D7P

Posisjonen til to båter $A$ og $B$ er gitt ved

${\vec{r}}_{A} (t) = [18 t - 8, 10 - 3 t]$

${\vec{r}}_{B} (t) = [10 t, 20 - 6 t]$

Alle lengdemål er gitt i kilometer, og tiden $t$ er gitt i timer.

a)

Bestem farten (banefarten) til hver av båtene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi skal regne ut farten til hver av båtene. For en av vektorene finner vi farten ved å derivere hvert ledd. Dette gir oss en fartsvektor. Størrelsen på farten er da lengden (absoluttverdien) av fartsvektoren.

$\vec{r_{A}} (t) = [18 t - 8, 10 - 3 t]$

$\vec{r_{A}}' (t) = \vec{v_{A}} (t) = [18, - 3]$

$| \vec{v_{A}} (t) | = \sqrt{18^{2} + (- 3)^{2}} = 3 \sqrt{37}$

$\vec{r_{B}} (t) = [10 t, 20 - 6 t]$

$\vec{r_{B}}' (t) = \vec{v_{B}} (t) = [10, - 6]$

$| \vec{v_{B}} (t) | = \sqrt{10^{2} + (- 6)^{2}} = 2 \sqrt{34}$

Svar: Båt A har fart $3 \sqrt{37} \approx 18, 2$ km/h. Båt B har fart $2 \sqrt{34} \approx 11, 7$ km/h.

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Lengden til en vektor.

b)

Forklar at avstanden $d$ mellom båtene er gitt ved

$d (t) = \sqrt{{(8 t - 8)}^{2} + {(3 t - 10)}^{2}}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi kan beskrive en vektor som alltid angir avstanden mellom båtene. Denne vektoren er posisjonsvektoren til en båt, minus posisjonsvektoren til den andre. I denne oppgaven spørres det etter størrelsen på denne avstandsvektoren.

Avstandsvektoren mellom båt A og båt B er gitt ved $\vec{d} (t) = \vec{r_{A}} (t) - \vec{r_{B}} (t) = [18 t - 8 - 10 t, 10 - 3 t - (20 - 6 t)]$
$\vec{d} (t) = [8 t - 8, - 10 + 3 t]$

Avstanden mellom båtene er lengden av avstandsvektoren.
$| \vec{d} (t) | = \sqrt{(8 t - 8)^{2} + (3 t - 10)^{2}} = d (t)$

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Stedvektor (posisjonsvektor).

c)

Når er denne avstanden minst? Hvor langt fra hverandre er båtene da?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi skal finne bunnpunktet til funksjonen $d (t)$ .

Vi finner når $d' (t) = 0$ i CAS. Vi kan eventuellt plotte $d (t)$ i Geogebra, og bruke minimumsverktøyet. Vi finner et bunnpunkt når $t = \frac{94}{73} \approx 1, 29$ . Vi finner $d (\frac{94}{73}) = \frac{56}{\sqrt{73}} \approx 6, 55$

Svar: Etter ca $1, 29$ timer ( $1$ time, $17$ minutter og $24$ sekunder) er avstanden minst. Båt $A$ og båt $B$ er da $6, 55$ km fra hverandre.

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av vektorfunksjoner 1 - Parameterframstilling.

Oppgave 4 (4 poeng) Nettkode: E-4D7X

En funksjon $f$ er gitt ved

$f (x) = x^{4} + a x^{3} + b x^{2} + c x + 1, D_{f} = ℝ$

Om denne funksjonen vet vi at

- $f$ har nullpunkt i $x = 1$

- $x = 2$ er $x$ -koordinaten til vendepunktet på grafen til $f$

- Grafen til $f$ går gjennom punktet $(3, 4)$

a)

Sett opp tre likninger som svarer til opplysningene ovenfor.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Hver bit med informasjon gir oss en ligning. Vi skal ikke bare finne svaret “ $f (1) = 0$ ”, men skrive ut $f (1)$ og sette opp fulle ligninger.

$f$ har nullpunkt i $x = 1$ . Dette vil si at $f (1) = 0$ . Dette gir oss ligningen $1 + a + b + c + 1 = 0$ , eller $a + b + c + 2 = 0$ .

$f$ har vendepunkt i $x = 2$ . Det vil si at $f ″ (2) = 0$ . Dette gir oss ligningen $48 + 12 a + 2 b = 0$ som forenkles til $24 + 6 a + b = 0$ .

Den siste ligningen får vi av at $f$ går gjennom $(3, 4)$ . Altså er $f (3) = 4$ . Dette gir oss ligningen $81 + 27 a + 9 b + 3 c + 1 = 4$ , eller $78 + 27 a + 9 b + 3 c = 0$ . Deler vi på $3$ får vi $26 + 9 a + 3 b + c = 0$

Svar: $a + b + c + 2 = 0$ , $24 + 6 a + b = 0$ , $26 + 9 a + 3 b + c = 0$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

b)

Bruk CAS til å bestemme konstantene $a$ , $b$ og $c$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi må sette inn de tre likningene fra a) inn i CAS og løse.

Vi skriver inn ${a + b + c + 2 = 0, 24 + 6 a + b = 0, 26 + 9 a + 3 b + c = 0}$ i CAS og bruker solve-verktøyet. Vi får svaret $a = - 6, b = 12, c = - 8$ . Dette svaret kan sjekkes ved innsetting.

Svar:

$a = - 6, b = 12, c = - 8$ .

Mer om:

Denne oppgaven er om

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

For flere forklaringer og eksempler på likninger, se artikkelen Likningssett med flere enn to ukjente.

Oppgave 5 (4 poeng) Nettkode: E-4D82

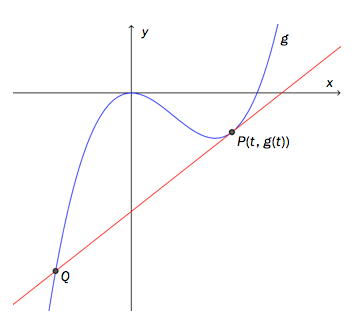
Funksjonen $g$ er gitt ved

$g (x) = a x^{3} - x^{2}, D_{g} = ℝ$

Grafen til $g$ har en tangent i punktet $P (t, g (t))$ . Tangenten skjærer grafen til $g$ i et annet punkt $Q$ . Se skissen nedenfor.

a)

Vis at tangenten har likningen

$y = (3 a t^{2} - 2 t) x + t^{2} - 2 a t^{3}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kjenner likningen for en rett linje. Vi kan uttrykke stigningen til $g (x)$ i punktet $P$ . Deretter trenger vi bare et uttrykk for konstantleddet av tangenten.

Tangenten har likning $y = α \cdot x + b$ der $α$ er stigningstallet til $g (x)$ i punktet $P$ , og $b$ er konstantleddet til linjen. $g' (t) = 3 a \cdot t^{2} - 2 t$ , så tangenten har ligningen $y = (3 a t^{2} - 2 t) x + b$ .

Vi kan finne $b$ siden vi vet at tangenten går gjennom punktet $P = (t, g (t)) = (t, a t^{3} - t^{2})$ .

Vi setter inn $t$ for $x$ og $a t^{3} - t^{2}$ for $y$ i likningen for tangenten.

$y = (3 a t^{2} - 2 t) x + b$
$a t^{3} - t^{2} = 3 a t^{3} - 2 t^{2} + b$
$- 2 a t^{3} + t^{2} = b$

Setter vi dette sammen har tangenten ligning $y = (3 a t^{2} - 2 t) x + t^{2} - 2 a t^{3}$ .

Dette er uttrykket vi skulle komme frem til.

Med CAS:

Mer om

Denne oppgaven er om

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangent

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på tangenter, se artikkelen Ettpunktsformelen og likning for tangentlinjen.

b)

Bruk CAS til å bestemme koordinatene til $Q$ , uttrykt ved $a$ og $t$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

$Q$ er det andre skjæringspunktet mellom tangenten og $g (x)$ .

Vi løser $g (x) = (3 a t^{2} - 2 t) x + t^{2} - 2 a t^{3}$ i GeoGebra.

Den ene løsningen er $x = t$ , altså tangeringspunktet $P$ .

Den andre er når $x = \frac{- 2 a t + 1}{a}$ . Vi regner ut $g (\frac{- 2 a t + 1}{a})$ i CAS:

Svar: $Q = (\frac{- 2 a t + 1}{a}, \frac{- 8 a^{2} t^{3} + 8 a t^{2} - 2 t}{a})$

Mer om

Denne oppgaven er om

Skjæringspunkt

skjæringspunkt

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på polynomer, se artikkelen Definisjon av et polynom.

REA3022 2015 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4D6G

a)

Løsningsforslag a)

Derivasjon

Polynom

b)

Løsningsforslag b)

Logaritme

Derivasjon

c)

Løsningsforslag c)

Derivasjon

Polynom

Oppgave 2 (5 poeng) Nettkode: E-4D6K

a)

Løsningsforslag a)

Polynom

Faktorisering av uttrykk

b)

Løsningsforslag b)

Polynom

Nullpunkt

abc-formelen

c)

Løsningsforslag c)

Grenseverdi

Polynom

Faktorisering av uttrykk

Oppgave 3 (3 poeng) Nettkode: E-4D6O

Løsningsforslag

Fellesnevner

Faktorisering av uttrykk

Konjugatsetningen

Oppgave 4 (2 poeng) Nettkode: E-4D6Q

Løsningsforslag

Sirkel

Radius

Oppgave 5 (5 poeng) Nettkode: E-4D6S

a)

Løsningsforslag a)

Alternativ løsning

Vektor

Parallell

b)

Løsningsforslag b)

Rett vinkel

Vektor

Ligning

c)

Løsningsforslag c)

Alternativ løsning

Vektor

Ligning

d)

Løsningsforslag d)

Vektor

Ligning

Oppgave 6 (4 poeng) Nettkode: E-4D6X

a)

Løsningsforslag a)

Binomialkoeffisienter

b)

Løsningsforslag b)

Andregradslikning

Oppgave 7 (5 poeng) Nettkode: E-4D70

a)

Løsningsforslag a)

Eksponentialfunksjon

Fortegnsskjema

Toppunkt

Derivasjon

b)

Løsningsforslag b)

Andrederiverte

Vendepunkt