Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3024 2013 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler

Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger:
Kilder for bilder, tegninger osv.

Alle grafer og figurer (Utdanningsdirektoratet)

DEL 1 Uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4DBN

Deriver funksjonene

a)

$f (x) = 3 \cos x$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Funksjonen $f (x)$ er en konstant multiplisert med funksjonen $\cos x$ . Det holder altså å derivere $\cos x$ og deretter multiplisere den deriverte med den samme konstanten.

Siden den deriverte av $\cos x$ er $- \sin x$ følger det at $\begin{matrix} f' (x) = (3 \cos x)' = 3 (\cos x)' = 3 (- \sin x) = - 3 \sin x . \end{matrix}$

Svar:

$\begin{matrix} f' (x) = - 3 \sin x . \end{matrix}$

Mer om

Denne oppgaven er om

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

Visste du at

Vi kan definere den deriverte til en funksjon $f (x)$ som grenseverdien $\begin{matrix} f' (x) = \lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x} . \end{matrix}$ Den deriverte av en konstant $C$ multiplisert med en funksjon $f (x)$ er da $\begin{matrix} (C f (x))' = \lim_{Δ x \to 0} \frac{C f (x + Δ x) - C f (x)}{Δ x} = C \lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x} = C f' (x) . \end{matrix}$ Fra dette kan vi konkludere med at den deriverte til en funksjon multiplisert med en konstant, er lik konstanten multiplisert med den deriverte til funksjonen.

b)

$g (x) = 6 \sin (π x) + 7$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Funksjonen $g (x)$ består av et konstantledd og en sinusfunksjon med en kjerne $π x$ . Derfor kan det være lurt å bruke kjerneregelen for derivasjon.

Vi observerer først at $\begin{matrix} g' (x) = 6 {(\sin (π x))}^{'} \end{matrix}$ siden den deriverte av et konstantledd alltid er null og konstante koeffisienter alltid kan tas utenfor derivasjonen. Kjerneregelen for derivasjon sier at $\begin{matrix} (f (h (x)))' = h' (x) f' (h (x)) . \end{matrix}$ Ved å sette $f (x) = \sin x$ og $h (x) = π x$ finner vi da at

$g^{'} (x) = 6 {(\sin (π x))}^{'} = 6 {(f (h (x)))}^{'} = 6 f^{'} (h (x)) \cdot h^{'} (x)$

$= 6 \cos (h (x)) \cdot π = 6 π \cos (π x)$

Svar: $\begin{matrix} g' (x) = 6 π \cos (π x) . \end{matrix}$

Mer om

Denne oppgaven er om

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Sinus

sinus

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen.

Visste du at

En mer vanlig, og kanskje også mer meningsfull, måte å skrive den deriverte med hensyn på $x$ av en funksjon $f (x)$ er ved å skrive $\frac{d f}{d x}$ . Dette kan vi forstå som ”en uendelig liten endring $d f$ i $f$ per en uendelig liten endring $d x$ i $x$ ”. Spesielt fint er det at vi med denne skrivemåten kan kjenne igjen den mystiske faktoren $d x$ som alltid dukker opp når vi holder på med integrasjon. Kjerneregelen for derivasjon kan da skrives $\begin{matrix} \frac{d f}{d x} = \frac{d f}{d x} \frac{d h}{d h} = \frac{d f}{d h} \frac{d h}{d x}, \end{matrix}$ som ikke ser ut til å si noe annet enn at brøkregelene fremdeles holder.

c)

$h (x) = 3 e^{2 x} \cdot \sin (3 x)$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Funksjonen $h (x)$ er et produkt av to funksjoner, $3 e^{2 x}$ og $\sin (3 x)$ , som er mye lettere å derivere hver for seg. Derfor kan det være lurt å prøve produktregelen for derivasjon.

Produktregelen for derivasjon sier at hvis $u (x)$ og $v (x)$ er deriverbare funksjoner, så må $\begin{matrix} (u v)' = u' v + u v' . \end{matrix}$ Hvis vi setter $u (x) = 3 e^{2 x}$ og $v (x) = \sin (3 x)$ følger det da at $\begin{matrix} h' (x) & = (3 e^{2 x} \sin (3 x))' = (u v)' = u' v + u v' \\ = (3 e^{2 x})' \sin (3 x) + 3 e^{2 x} (\sin (3 x))' \\ = 3 (e^{2 x})' \sin (3 x) + 3 e^{2 x} (\sin (3 x))' . \end{matrix}$ Videre gir kjerneregelen, som sier at $(f (g (x)))' = g' (x) f' (g (x))$ , med kjernen $g (x) = 2 x$ at $\begin{matrix} (e^{2 x})' = (2 x)' e^{2 x} = 2 e^{2 x}, \end{matrix}$ siden $e^{x}$ er sin egen deriverte. Hvis vi igjen bruker kjerneregelen, men nå på $\sin (3 x)$ med kjernen $g = 3 x$ finner vi at

${(\sin (3 x))}^{'} = \cos (3 x) \cdot {(3 x)}^{'} = 3 \cos (3 x)$

siden den deriverte av $\sin x$ er $\cos x$ . Altså er $\begin{matrix} h' (x) & = 3 (e^{2 x})' \sin (3 x) + 3 e^{2 x} (\sin (3 x))' \\ = 3 (2 e^{2 x}) \sin (3 x) + 3 e^{2 x} (3 \cos (3 x)) \\ = 6 e^{2 x} \sin (3 x) + 9 e^{2 x} \cos (3 x) \\ = 3 e^{2 x} (2 \sin (3 x) + 3 \cos (3 x)) . \end{matrix}$

Svar: $\begin{matrix} h' (x) = 3 e^{2 x} (2 \sin (3 x) + 3 \cos (3 x)) . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

sinus

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Å derivere sammensatte uttrykk.

Visste du at

Siden vi kan definere den deriverte av en funksjon $f (x)$ som grenseverdien $\begin{matrix} f' (x) = \lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x} \end{matrix}$ må den deriverte av produktet $u (x) v (x)$ av to funksjoner $u (x)$ og $v (x)$ tilfredsstille $\begin{matrix} (u v)' & = \lim_{Δ x \to 0} \frac{u (x + Δ x) v (x + Δ x) - u (x) v (x)}{Δ x} \\ = \lim_{Δ x \to 0} \frac{u (x + Δ x) v (x + Δ x) + [0] - u (x) v (x)}{Δ x} \\ = \lim_{Δ x \to 0} \frac{u (x + Δ x) v (x + Δ x) + [u (x + Δ x) v (x) - u (x + Δ x) v (x)] - u (x) v (x)}{Δ x} \\ = \lim_{Δ x \to 0} \frac{u (x + Δ x) v (x + Δ x) + u (x + Δ x) v (x) - u (x + Δ x) v (x) - u (x) v (x)}{Δ x} \\ = \lim_{Δ x \to 0} \frac{u (x + Δ x) (v (x + Δ x) - v (x)) + (u (x + Δ x) - u (x)) v (x)}{Δ x} \\ = \lim_{Δ x \to 0} u (x + Δ x) \frac{v (x + Δ x) - v (x)}{Δ x} + \frac{u (x + Δ x) - u (x)}{Δ x} v (x) \\ = u (x) \lim_{Δ x \to 0} \frac{v (x + Δ x) - v (x)}{Δ x} + \lim_{Δ x \to 0} \frac{u (x + Δ x) - u (x)}{Δ x} v (x) \\ = u (x) v' (x) + u' (x) v (x), \end{matrix}$ som er det vi kjenner som produktregelen for derivasjon.

Oppgave 2 (4 poeng) Nettkode: E-4DBR

Bestem integralet $\int_{}^{} \frac{2 x}{x^{2} - 4} dx$ ved å bruke

a)

variabelskifte

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Siden den deriverte av $x^{2} - 4$ er $2 x$ kan det være lurt å bruke variabelskiftet $u = x^{2} - 4$ .

Metoden for integrasjon ved substitusjon sier at $\begin{matrix} \int f (u (x)) u' (x) d x = \int f (u) d u . \end{matrix}$ Ved å introdusere variabelskiftet $u (x) = x^{2} - 4$ finner vi da, siden $u' (x) = (x^{2} - 4)' = 2 x$ , at $\begin{matrix} \int \frac{2 x}{x^{2} - 4} d x = \int \frac{u' (x)}{u (x)} d x = \int \frac{d u}{u} . \end{matrix}$ Siden den deriverte av $\ln x$ er $\frac{1}{x}$ må $\begin{matrix} \int \frac{d u}{u} = \ln | u | + C, \end{matrix}$ der $C$ er integrasjonskonstanten. Legg merke til at vi har lagt til et absoluttverditegn inne i logaritmen. Dette er fordi $\ln x$ bare gir mening å snakke om hvis $x$ er et positivt tall. Ved å legge til en absoluttverdi kan vi også ta høyde for verdier som er negative. Ved nå å sette inn for $u = x^{2} - 4$ følger det at $\begin{matrix} \int \frac{2 x}{x^{2} - 4} d x = \ln | x^{2} - 4 | + C . \end{matrix}$

Svar:

$\begin{matrix} \int \frac{2 x}{x^{2} - 4} d x = \ln | x^{2} - 4 | + C . \end{matrix}$

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på integrasjon, se artikkelen Integrasjon ved substitusjon.

Visste du at

Integrasjon ved substitusjon følger så direkte fra kjerneregelen for derivasjon at de egentlig bør hete det samme. Kjerneregelen for derivasjon sier at $\begin{matrix} (f (u (x)))' = u' (x) f' (g (x)) \end{matrix}$ og ved å integrere begge sider av likningen med hensyn på $x$ finner vi at $\begin{matrix} \int (f (u (x)))' d x = \int u' (x) f' (u (x)) d x . \end{matrix}$ Siden den integrasjon og derivasjon utjevner hverandre sitter vi igjen med $\begin{matrix} \int f' (u (x)) u' (x) d x = f (u (x)) + C \end{matrix}$ der $C$ er integrasjonskonstanten. Dette kan vi skrive $\begin{matrix} \int f' (u (x)) u' (x) d x = \int f' (u) d u, \end{matrix}$ og hvis vi omdøper $h (x) = f' (x)$ ser vi at $\begin{matrix} \int h (u (x)) u' (x) d x = \int h (u) d u, \end{matrix}$ som er det vi kjenner som integrasjon ved substitusjon.

b)

delbrøkoppspalting

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Ved å faktorisere $x^{2} - 4$ kan vi skrive brøken $\frac{2 x}{x^{2} - 4}$ som en sum av to enklere brøker. Forhåpentligvis vil dette forenkle integrasjonen.

Funksjonen $x^{2} - 4$ kan ifølge tredje kvadratsetning faktoriseres $\begin{matrix} x^{2} - 4 = (x - 2) (x + 2) . \end{matrix}$ Vi ønsker å finne to konstanter $A$ og $B$ slik at $\begin{matrix} \frac{2 x}{x^{2} - 4} = \frac{2 x}{(x - 2) (x + 2)} = \frac{A}{x - 2} + \frac{B}{x + 2} . \end{matrix}$ Ved å multiplisere begge sider av likningen med $(x - 2) (x + 2)$ følger det at $\begin{matrix} 2 x = (x + 2) A + (x - 2) B = (A + B) x + 2 (A - B) . \end{matrix}$ Siden denne likningen må være sann for alle $x$ må den stemme for alle konstantledd og $x$ -ledd separat. Det vil si at $$\begin{split} \mbox{ konstantledd: } & \ \ \ A-B=0 \\ \mbox{ $x$-ledd: } & \ \ \ A+B=2. \end{split}$$ Den første likningen gir at $B = A$ , som ved innsetting i den andre likningen gir $$\begin{split} A+A=2 \implies A = 1 \implies B=A=1. \end{split}$$ Altså kan vi skrive $\begin{matrix} \frac{2 x}{x^{2} - 4} = \frac{1}{x - 2} + \frac{1}{x + 2} . \end{matrix}$ Det betyr at $\begin{matrix} \int \frac{2 x}{x^{2} - 4} d x = \int \frac{1}{x - 2} d x + \int \frac{1}{x + 2} d x \end{matrix}$ og siden den deriverte av $\ln (x - 2)$ er $\frac{1}{x - 2}$ og den deriverte av $\ln (x + 2)$ er $\frac{1}{x + 2}$ får vi $\begin{matrix} \int \frac{1}{x - 2} d x + \int \frac{1}{x + 2} d x = \ln | x - 2 | + \ln | x + 2 | + C, \end{matrix}$ der $C$ er integrasjonskonstanten. Vi har altså funnet at $\begin{matrix} \int \frac{2 x}{x^{2} - 4} d x = \ln | x - 2 | + \ln | x + 2 | + C . \end{matrix}$ Merk at dette er det samme svaret som i oppgave $a)$ siden vi kan skrive $\begin{matrix} \ln | x - 2 | + \ln | x + 2 | + C = \ln | (x - 2) (x + 2) | + C = \ln | x^{2} - 4 | + C . \end{matrix}$

Svar:

$\begin{matrix} \int \frac{2 x}{x^{2} - 4} d x = \ln | x - 2 | + \ln | x + 2 | + C . \end{matrix}$

Mer om

Denne oppgaven er om

Faktorisering av uttrykk

Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.

Eksempel: $x^{2} + 4 x + 3 = (x + 1) (x + 3)$

faktorisering av uttrykk i x

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Integrasjon av rasjonale uttrykk.

Visste du at

En delbrøkoppspalting kan ofte gjøres på en mye raskere og mer intuitiv måte enn metoden brukt ovenfor. Uttrykket $\begin{matrix} \frac{2 x}{(x - 2) (x + 2)} \end{matrix}$ kan delbrøkoppspaltes ved å finne en måte å kombinere faktorene $x + 2$ og $x - 2$ på en slik måte at kombinasjonen blir lik $2 x$ . I dette tilfellet kan vi skrive $\begin{matrix} 2 x = (x + 2) + (x - 2) . \end{matrix}$ Det betyr at delbrøkoppspaltingen er gitt som $\begin{matrix} \frac{2 x}{(x - 2) (x + 2)} = \frac{(x + 2) + (x - 2)}{(x - 2) (x + 2)} \\ = \frac{x + 2}{(x - 2) (x + 2)} + \frac{x - 2}{(x - 2) (x + 2)} = \frac{1}{x - 2} + \frac{1}{x + 2} . \end{matrix}$ Et annet tilfelle er $\begin{matrix} \frac{1}{(x + 1) (x + 2)} . \end{matrix}$ Siden $\begin{matrix} 1 = (x + 2) - (x + 1) \end{matrix}$ er delbrøkoppspaltingen gitt av $\begin{matrix} \frac{1}{(x + 1) (x + 2)} = \frac{(x + 2) - (x + 1)}{(x + 1) (x + 2)} = \frac{1}{x + 1} - \frac{1}{x + 2} . \end{matrix}$

Oppgave 3 (4 poeng) Nettkode: E-4DBU

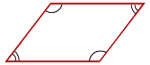
Punktene $A (1, - 1, 0)$ , $B (3, 1, 1)$ og $C (0, 0, 0)$ er gitt.

a)

Bestem $\vec{A B} \times \vec{A C}$ . Bruk resultatet til å bestemme arealet av $Δ A B C$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å beregne $\vec{A B} \times \vec{A C}$ må vi først bestemme $\vec{A B}$ og $\vec{A C}$ . Deretter kan vi bruke at lengden $| \vec{A B} \times \vec{A C} |$ er lik arealet av parallellogrammet utspent av $\vec{A B}$ og $\vec{A C}$ til å bestemme arealet av $△ A B C$ .

Gitt de tre punktene $A (1, - 1, 0)$ , $B (3, 1, 1)$ og $C (0, 0, 0)$ kan vi konstruere vektorene $\begin{matrix} \vec{A B} & = \vec{O B} - \vec{O A} = [3, 1, 1] - [1, - 1, 0] = [2, 2, 1] \\ \vec{A C} & = \vec{O C} - \vec{O A} = [0, 0, 0] - [1, - 1, 0] = [- 1, 1, 0] . \end{matrix}$

Det gir at

$\vec{A B} \times \vec{A C} = |\begin{matrix} \vec{e_{x}} & \vec{e_{y}} & \vec{e_{z}} \\ 2 & 2 & 1 \\ - 1 & 1 & 0 \end{matrix}| = |\begin{matrix} 2 & 1 \\ 1 & 0 \end{matrix}| \vec{e_{x}} - |\begin{matrix} 2 & 1 \\ - 1 & 0 \end{matrix}| \vec{e_{y}} + |\begin{matrix} 2 & 2 \\ - 1 & 1 \end{matrix}| \vec{e_{z}}$

$= (- 1) \vec{e_{x}} - (1) \vec{e_{y}} + (2 - (- 2)) \vec{e_{z}} = [- 1, - 1, 4]$

som har lengde

$\begin{matrix} | \vec{A B} \times \vec{A C} | & = | [- 1, - 1, 4] | = \sqrt{(- 1)^{2} + (- 1)^{2} + 4^{2}} \\ = \sqrt{18} = 3 \sqrt{2} . \end{matrix}$

Siden lengden av vektoren $\vec{A B} \times \vec{A C}$ er lik arealet av parallellogrammet utspent av $\vec{A B}$ og $\vec{A C}$ , og $△ A B C$ utgjør nøyaktig halvparten av parallellogrammet, følger det at arealet av $△ A B C$ er $\begin{matrix} \frac{1}{2} | \vec{A B} \times \vec{A C} | = \frac{3}{2} \sqrt{2} . \end{matrix}$

Svar: $\vec{A B} \times \vec{A C} = [- 1, - 1, 4] og arealet av Δ A B C = \frac{3}{2} \sqrt{2}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Parallellogram

Et parallellogram er en firkant med parvis parallelle sider. Vinklene er parvis like store.

parallellogram

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt av to vektorer.

b)

Bestem $\vec{A B} \cdot \vec{A C}$ . Bruk blant annet dette resultatet til å bestemme arealet av $Δ A B C$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi ønsker å beregne skalarproduktet $\vec{A B} \cdot \vec{A C}$ og bruke resultatet til å bestemme arealet av $△ A B C$ .

Siden $\begin{matrix} \vec{A B} & = [2, 2, 1] og \vec{A C} = [- 1, 1, 0] \end{matrix}$ må

$\vec{A B} \cdot \vec{A C} = [2, 2, 1] \cdot [- 1, 1, 0] = 2 \cdot (- 1) + 2 \cdot 1 + 1 \cdot 0 = 0 .$

Altså står $\vec{A B}$ og $\vec{A C}$ vinkelrett på hverandre, noe som betyr at $△ A B C$ er rettvinklet og $∠ A = 90^{\circ}$ . Arealet av $△ A B C$ er dermed

$\begin{matrix} Arealet av △ A B C & = \frac{| \vec{A B} | \cdot | \vec{A C} |}{2} = \frac{\sqrt{2^{2} + 2^{2} + 1^{2}} \cdot \sqrt{(- 1)^{2} + 1^{2}}}{2} \\ = \frac{\sqrt{9} \cdot \sqrt{2}}{2} = \frac{3}{2} \sqrt{2}, \end{matrix}$

som passer med det vi fant i forrige oppgave.

Svar: $\vec{A B} \cdot \vec{A C} = 0 og arealet av Δ A B C = \frac{3}{2} \sqrt{2}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

For flere forklaringer og eksempler på vektorer, se artikkelen Prikkprodukt og norm.

Oppgave 4 (3 poeng) Nettkode: E-4DBX

Løs differensiallikningen

$y' = 6 x y$ når $y (0) = 2$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Differensiallikningen er første ordens og lineær. Den kan løses med metoden med integrerende faktor. Akkurat denne likningen er også separabel. Hvis jeg separerer variabler, må jeg integrerer funksjonen $\frac{1}{y}$ . Det vil gi meg et uttrykk med absoluttverdien til som $y$ må håndteres korrekt.

Først observerer vi at $y = 0$ er en løsning av differensiallikningen siden begge sider da er konstant lik $0$ . For å finne andre løsninger, kan vi dele på $y$ på begge sider for å separere variabler. Da får vi

$\frac{y^{'}}{y} = 6 x$

Integrasjon med hensyn på $x$ på begge sider gir

$\begin{matrix} \int_{}^{} \frac{y^{'}}{y} d x & = & \int_{}^{} 6 x d x \\ \ln (|y|) & = & 3 x^{2} + C \\ |y| & = & e^{3 x^{2} + C} \\ y & = & \pm e^{c} \cdot e^{3 x^{2}} \end{matrix}$

der $C$ er et vilkårlig reelt tall.

Når C gjennomløper alle reelle tall, vil $e^{C}$ gjennomløpe alle positive tall. Dermed er alle løsningene til likningen, inkludert den trivielle løsningen $y = 0$ , gitt ved

$y = D e^{3 x^{2},}$

der $D$ er et vilkårlig reelt tall.

Løsningen som tilfredsstiller initialbetingelsen må ha

$y (0) = D e^{3 \cdot 0^{2}} = D e^{0} = D = 2 .$

Svar: $\begin{matrix} y (x) = 2 e^{3 x^{2}} . \end{matrix}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.

Visste du at

Vi kunne også løst differensiallikningen ved å gjette på ulike funksjoner. Siden den deriverte til $y$ må være $6 x y$ kan det virke rimelig å begynne å gjette på en funksjon av typen $e^{K x}$ der $K$ er et tall. Siden $\begin{matrix} (e^{K x})' = K (e^{K x}) \end{matrix}$ må imidlertid $K = 6 x$ , som betyr at $K$ ikke er konstant. Vi kan likevel se hva som skjer om vi prøver med $K = 6 x$ . Da får vi $\begin{matrix} (e^{K x})' = (e^{6 x^{2}})' = 6 \cdot 2 x (e^{6 x^{2}}), \end{matrix}$ som er nesten riktig – vi har bare en $2$ -er for mye. Det kan vi ta høyde for ved heller å sette $K = 3 x$ . Da finner vi $\begin{matrix} y' = (e^{3 x^{2}})' = 3 \cdot 2 x (e^{3 x^{2}}) = 6 x y, \end{matrix}$ som betyr at vi har løst differensiallikningen. Hvis $y (x) = e^{3 x^{2}}$ er en løsning er imidlertid også $y (x) = C e^{3 x^{2}}$ en løsning så lenge $C$ er en konstant ulik null. At $y (0) = 2$ kan vi da kreve ved å sette $\begin{matrix} y (0) = C e^{3 \cdot 0^{2}} = C = 2, \end{matrix}$ som betyr at den spesielle løsningen på differensiallikningen er $\begin{matrix} y (x) = 2 e^{3 x^{2}} . \end{matrix}$

Oppgave 5 (5 poeng) Nettkode: E-4DBZ

En rekke er gitt ved

$S_{n} = 1 + 3 + 5 + 7 + . . . + a_{n}$

a)

Bestem $a_{16}$ og $S_{16}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må finne et uttrykk for det $16$ -ende leddet $a_{16}$ i rekken, og summen $S_{16}$ av de $16$ første leddene. Det kan vi gjøre ved å legge merke til at følgen $a_{n}$ er en oppramsing av de positive oddetallene.

For å løse denne oppgaven må vi egentlig også løse oppgave $b)$ . Med dette i tankene begynner vi med å observere at leddene $a_{n}$ i rekken $\begin{matrix} S_{n} = 1 + 3 + 5 + 7 + . . . + a_{n} \end{matrix}$ representerer det $n$ -te oddetallet. Siden annenhvert tall er et oddetall må differansen mellom to tall i rekken være $2$ . Siden den rekken begynner på $1$ kan vi skrive $\begin{matrix} a_{n} = 2 n - 1 . \end{matrix}$ Det betyr at $\begin{matrix} a_{16} = 2 \cdot 16 - 1 = 31 . \end{matrix}$ For å finne summen $S_{16}$ kan man enten huske at summen av de første $n$ oddetallene er det $n$ te kvadrattallet og at derfor $S_{16} = 16^{2}$ , eller dele opp summen. Siden $S_{n}$ er summen av oddetallene fra og med $1$ til og med $2 n - 1$ kan vi ved å bytte rekkefølge på addisjonen finne at $\begin{matrix} S_{n} & = 1 + 3 + 5 + . . . [2 (n - 2) - 1] + [2 (n - 1) - 1] + [2 n - 1] \\ = \underset{2 n}{\underset{︸}{1 + [2 n - 1]}} + \underset{2 n}{\underset{︸}{3 + [2 (n - 1) - 1]}} + . . . + \underset{2 n}{\underset{︸}{[2 (\frac{n}{2}) - 1] + [2 (\frac{n}{2} + 1) - 1]}} \\ = \underset{\frac{n}{2} g a n g e r}{\underset{︸}{2 n + 2 n + 2 n + . . . + 2 n}} \\ = \frac{n}{2} \cdot 2 n = n^{2} . \end{matrix}$ Uansett finner vi at $\begin{matrix} S_{16} = 16^{2} = 256 . \end{matrix}$

Svar: $a_{16} = 31 og S_{16} = 16^{2} = 256$

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Kvadrattall

Et kvadrattall er det positive heltallet som vi får når et heltall multipliserers med seg selv.

Eksempel: 25 er et kvadrattall, fordi $5 \cdot 5 = 25$

kvadrattall

Oddetall

Tallene 1, 3, 5, 7, 9 og 11 er eksempler på oddetall.
Oddetall er heltall hvor svaret ikke blir et heltall når de deles med 2.

Alle oddetall kan skrives på formen 2n+1, der n er et helt tall.

Et heltall som ikke er oddetall er partall.

oddetall

For flere forklaringer og eksempler på rekker, se artikkelen Aritmetiske rekker.

Visste du at

En annen måte å se at summen av de $n$ første oddetallene er det $n$ -te kvadrattallet er ved å gjennomføre et geometrisk argument. Figuren under viser hvordan hvordan summen av de første oddetallene er et kvadrat. For hvert nye oddetall som legges til vil kvadratet øke sin sidelengde med én.

b)

Forklar at rekken er aritmetisk, og bruk dette til å finne et uttrykk for $a_{n}$ og $S_{n}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

En rekke er aritmetisk dersom differansen $d$ mellom nærstående ledd i rekken alltid er den samme.

Leddene i rekken $\begin{matrix} S_{n} = 1 + 3 + 5 + 7 + 9 + . . . + a_{n} \end{matrix}$ er oddetall og kan derfor skrives $\begin{matrix} a_{n} = 2 n - 1 f o r n \in ℕ . \end{matrix}$ Siden differansen mellom nærstående ledd, $\begin{matrix} d = a_{n + 1} - a_{n} = 2 (n + 1) - 1 - (2 n - 1) = 2 (n + 1) - 2 n = 2 \end{matrix}$ for alle $n$ er rekken aritmetisk. Siden leddene øker med like mye vil summen av dem, altså verdien til rekken, alltid være $n$ ganger så stor som gjennomsnittsverdien $\frac{1}{2} (a_{1} + a_{n})$ av leddene i den. Det betyr at $\begin{matrix} S_{n} = n \frac{a_{1} + a_{n}}{2} = n \frac{1 + 2 n - 1}{2} = n \frac{2 n}{2} = n^{2} . \end{matrix}$

Svar: Aritmetisk rekke: $a_{n} = 2 n - 1 og S_{n} = n^{2}$

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Oddetall

oddetall

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data

Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1) $2 + 2 + 4 + 3 = 11$
2) antall data er 4. $11 : 4 = 2, 75$

gjennomsnitt

For flere forklaringer og eksempler på rekker, se artikkelen Aritmetiske tallfølger.

c)

Bestem hvor mange ledd rekken minst må ha for at $S_{n} > 400$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

For å bestemme hvor mange ledd, $n$ , rekken minst må ha for at $S_{n} > 400$ kan vi bruke uttrykket fra oppgave $b)$ og deretter løse ulikheten for $n$ .

Fra oppgave $b)$ har vi at $\begin{matrix} S_{n} = n^{2} . \end{matrix}$ De mulige antallene ledd $n$ som gjør at $S_{n} > 400$ må dermed tilfredsstille $$\begin{split} S_n=n^2>400 \implies n > \sqrt{400}=20. \end{split}$$ Altså må rekken minst ha $21$ ledd for at $S_{n} > 400$ .

Svar: $21$ .

Mer om

Denne oppgaven er om ulikhet og

Kvadratrot

Kvadratrot har symbolet $\sqrt{}$ .

Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.

Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi $4 \cdot 4 = 16$ . Det skrives $\sqrt{16} = 4$ .

kvadratrot

For flere forklaringer og eksempler på ulikheter, se artikkelen Lineære ulikheter.

Oppgave 6 (2 poeng) Nettkode: E-4DC3

Følgende informasjon er gitt om en kontinuerlig funksjon $f$ :

- $f (x) > 0$ for alle $x \in ℝ$

- $f' (x) < 0$ for alle $x \in ⟨\leftarrow, - 2⟩ \cup ⟨2, \to⟩$

- $f' (x) = 0$ for $x = - 2$ og for $x = 2$

- $f'' (x) = 0$ for $x = 1$ og for $x = 3$

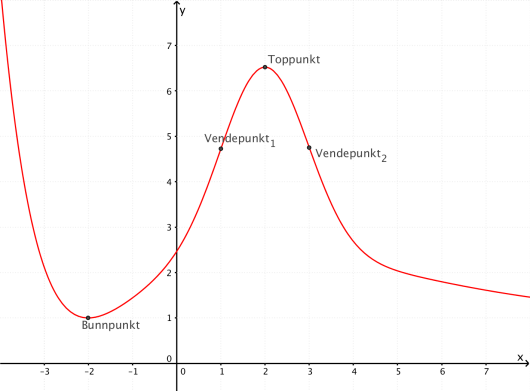
Lag en skisse som viser hvordan grafen til $f$ kan se ut.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Ved å notere hvor $f (x)$ er positiv, voksende og avtagende, hvor det er ekstremalpunkter og hvor det ikke er noen krumning kan vi skissere en mulig graf for $f$ .

Siden $f (x) > 0$ må grafen til $f$ alltid være over $x$ -aksen. Siden

$f^{'} (x) < 0 for x \in (- \infty, - 2) \cup (2, \infty)$

må grafen være avtagende på $(- \infty, - 2) og på (2, \infty)$ og kan derfor være voksende på $(- 2, 2)$ . Dette passer godt overens med kravet

$\begin{matrix} f' (x) = 0 for x = - 2 og x = 2 . \end{matrix}$

Siden $f ″ (x) = 0$ for $x = 1$ og $x = 3$ må grafen ha vendepunkter i $x = 1$ og $x = 3$ . Én mulig løsning er skissert i figuren under.

Mer om

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunkter

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

interval

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på funksjoner, se artikkelen Kritiske punkter.

Oppgave 7 (2 poeng) Nettkode: E-4DC5

Bruk induksjon til å bevise påstanden

$P (n) : a + a k + a k^{2} + a k^{3} + . . . + a k^{n - 1} = a \cdot \frac{k^{n} - 1}{k - 1}, n \in ℕ$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Det holder å vise at påstanden er sann for $n = 1$ og at hvis den er sann for $n = m$ så må den nødvendigvis også være sann for $n = m + 1$ .

For $n = 1$ er påstanden $\begin{matrix} P (1) : a = a \cdot \frac{k^{1} - 1}{k - 1} = a \cdot \frac{1}{1} = a, \end{matrix}$ som er sant! Vi antar nå at påstanden stemmer for $n = m$ . Det betyr at $\begin{matrix} P (m) : a + a k + a k^{2} + a k^{3} + . . . + a k^{m - 1} = a \frac{k^{m} - 1}{k - 1} . \end{matrix}$ Vi ønsker å se om dette betyr at også $\begin{matrix} P (m + 1) : a + a k + a k^{2} + a k^{3} + . . . + a k^{m - 1} + a k^{m} = a \frac{k^{m + 1} - 1}{k - 1} \end{matrix}$ er sann. Siden vi har antatt at $P (m)$ er sann kan vi skrive $\begin{matrix} P (m + 1) : a \frac{k^{m} - 1}{k - 1} + a k^{m} = a \frac{k^{m + 1} - 1}{k - 1} . \end{matrix}$ Dette kan vi omformulere ved

$a \frac{k^{m} - 1}{k - 1} + a k^{m} = a \frac{k^{m + 1} - 1}{k - 1}$

$\Rightarrow a k^{m} = a \frac{k^{m + 1} - 1}{k - 1} - a \frac{k^{m} - 1}{k - 1}$

$= a \frac{k^{m + 1} - 1 - k^{m} + 1}{k - 1} = a \frac{k^{m} (k - 1)}{k - 1} = a k^{m},$

som betyr at $P (m + 1)$ stemmer hvis $P (m)$ stemmer. Vi har altså bevist at påstanden $P (n)$ er sann for alle $n \in ℕ$ , ved induksjon.

Mer om

Denne oppgaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Matematisk induksjon

En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:

Bevis påstanden for n =1.
Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).

Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).

matematisk induksjon

For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.

Visste du at

Påstanden $P (n)$ kan bevises direkte ved først å legge merke til at hvis $\begin{matrix} S_{n} = a + a k + a k^{2} + a k^{3} + . . . + a k^{m - 1}, \end{matrix}$ så må $\begin{matrix} k S_{n} = a k + a k^{2} + a k^{3} + a k^{4} + . . . + a k^{m - 1} + a k^{m} = S_{n} - a + a k^{m} . \end{matrix}$ Vi har altså funnet $\begin{matrix} k S_{n} = S_{n} - a + a k^{m} \end{matrix}$ som kan skrives $\begin{matrix} S_{n} (k - 1) = a (k^{m} - 1) . \end{matrix}$ Det betyr at $\begin{matrix} S_{n} = a + a k + a k^{2} + a k^{3} + . . . + a k^{m - 1} = a \frac{k^{m} - 1}{k - 1}, \end{matrix}$ som er det vi har bevist i denne oppgaven.

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4DC7

En pasient får 8 mL av en medisin hver time. Den totale mengden medisin i kroppen $t$ timer etter at medisineringen startet, er $y (t)$ mL. I løpet av en time skiller kroppen ut 5% av den totale medisinmengden.

a)

Forklar at

$y' = 8 - 0, 05 \cdot y$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må bruke det vi vet om mengden medisin i kroppen $y (t)$ til å lage en relasjon mellom endringen av mengden medisin i kroppen over tid og hvor mye medisin det er i kroppen på et visst tidspunkt.

Vi lar $y (t)$ være mengden medisin, målt i milliliter, i kroppen $t$ timer etter at medisineringen startet. Siden pasienten får $8$ mL av medisinen hver time må $\begin{matrix} y' (t) = 8 . \end{matrix}$ At pasienten skiller ut $5$ % av den totale medisinmengden hver time betyr imidlertid at vi må trekke $5$ % av $y (t)$ fra endringen $y' (t)$ . Med andre ord må vi ha $\begin{matrix} y' = 8 - 0, 05 y . \end{matrix}$

Mer om

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på funksjoner, se artikkelen Johannes bygger nye funksjoner.

b)

Vis at $y (t) = 160 - 160 e^{- 0, 05 t}$ når $y (0) = 0$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi ønsker å vise at funksjonen $y (t) = 160 - 160 e^{- 0, 05 t}$ løser differensiallikningen og tilfredsstiller $y (0) = 0$ .

Siden oppgaven ber oss om å vise at $y (t) = 160 - 160 e^{- 0, 05 t}$ er en løsning av differensiallikningen når $y (0) = 0$ holder det å vise at $y (t)$ tilfredstiller differensiallikningen og at $y (0) = 0$ . Sistnevnte kan vi observere ved $\begin{matrix} y (0) = 160 - 160 e^{- 0, 05 \cdot 0} = 160 - 160 e^{0} = 160 - 160 = 0 . \end{matrix}$ Fra kjerneregelen følger det at $\begin{matrix} y' (t) = (160 - 160 e^{- 0, 05 t})' = (- 0, 05 t)' (- 160 e^{- 0, 05 t}) = 8 e^{- 0, 05 t} . \end{matrix}$ For å undersøke om $y$ tilfredsstiller likningen $\begin{matrix} y' = 8 - 0, 05 y \end{matrix}$ holder det å sette inn uttrykkene for $y'$ og $y$ og se om likningen er oppfylt. Ved å gjøre dette får vi $\begin{matrix} 8 e^{- 0, 05 t} = 8 - 0, 05 (160 - 160 e^{- 0, 05 t}) = 8 - 8 + 8 e^{- 0, 05 t}, \end{matrix}$ som betyr at $y$ løser differensiallikningen.

Alternative løsninger

Siden differensiallikningen kan skrives på formen $\begin{matrix} y' + 0.05 y = 8 \end{matrix}$ og $\begin{matrix} (y e^{0.05 t})' = y' e^{0.05} + 0.05 y e^{0.05} \end{matrix}$ kan vi multiplisere begge sider av likningen med den intgrerende faktoren $e^{0.05 t}$ og deretter skrive $\begin{matrix} (y e^{0.05 t})' = 8 e^{0.05 t} . \end{matrix}$ Integralet av hver side er henholdsvis $\begin{matrix} \int (y e^{0.05 t})' d t = y e^{0.05 t} + C_{1} \end{matrix}$ og $\begin{matrix} \int 8 e^{0.05 t} d t = \frac{8}{0.05} e^{0.05 t} + C_{2} = 160 e^{0.05 t} + C_{2} . \end{matrix}$ Ved å sette $C = C_{2} - C_{1}$ finner vi videre at løsningen kan skrives $\begin{matrix} y e^{0.05 t} = 160 e^{0.05 t} + C . \end{matrix}$ En videre omformulering kan oppnås ved å multiplisere begge sider med $e^{- 0.05 t}$ . Det gir $\begin{matrix} y = e^{- 0.05 t} (160 e^{0.05 t} + C) = 160 + C e^{- 0.05 t} \end{matrix}$ og siden $y (0) = 0$ må vi ha $$\begin{split} 0=y(0)=160+Ce^{0}=160+C \implies C=-160. \end{split}$$ Den spesielle løsningen av differensiallikningen er altså $\begin{matrix} y = 160 - 160 e^{- 0.05 t} . \end{matrix}$

ii)

Ved å skrive kommandoen
LøsODE[ y’ = 8-0.05y,(0,0) ]
i CAS får vi følgende løsning $\begin{matrix} y = 160 - 160 e^{- t / 20} \end{matrix}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.

Visste du at

I utregningen over fant vi at integrasjonskonstanten $C$ måtte være $\ln (- 160)$ for at $y (0) = 0$ . Selv om utregningen gikk fint er dette et litt problematisk tall. Vi kan forstå den naturlig logaritmen $\ln x$ som ”det tallet $e$ må opphøyes i for å bli $x$ ”. Problemet er at uansett hva $x$ er vil $e^{x}$ være et positivt tall. Hvordan kan vi da si at tallet $\ln (- 160)$ eksisterer? Løsningen er å finne i et annet og enda mer absurd tall, nemlig $i = \sqrt{- 1}$ . Det kan vises at $e^{i π} = - 1$ , som betyr at $\begin{matrix} \ln (- 160) = \ln (160 e^{i π}) = \ln 160 + i π . \end{matrix}$ Det er med andre ord ikke helt sant at $e^{x}$ er positiv for alle $x$ .

En annen måte å unngå problemet er å samle integrasjonskonstantene i variable $y_{0}$ og $t_{0}$ slik at $\begin{matrix} \ln (\frac{y - 160}{y_{0} - 160}) = - 0, 05 (t - t_{0}) . \end{matrix}$ Ved å sette inn $y_{0} = 0$ og $t_{0} = 0$ finner vi da at $\begin{matrix} \ln (\frac{160 - y}{160}) = - 0, 05 t, \end{matrix}$ som er helt uproblematisk så lenge $y < 160$ .

c)

Bestem $\lim_{t \to \infty} y (t)$ . Kommenter svaret.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må finne hvor mye av medisinen pasienten har i kroppen, $y (t)$ , når tiden $t$ går mot $\infty$ .

Vi må beregne grenseverdien $\begin{matrix} \lim_{t \to \infty} y (t) = \lim_{t \to \infty} [160 - 160 e^{- 0, 05 t}] . \end{matrix}$ Når $t$ går mot uendelig må $0, 05 t$ gå mot uendelig. Det betyr at $e^{0, 05 t}$ må gå mot uendelig og derfor må $e^{- 0, 05 t} = 1 / e^{0, 05 t}$ gå mot én over uendelig – altså null. Med andre ord må $\begin{matrix} \lim_{t \to \infty} y (t) & = \lim_{t \to \infty} [160 - 160 e^{- 0, 05 t}] = 160 - 160 \lim_{t \to \infty} e^{- 0, 05 t} \\ = 160 - 160 \cdot 0 = 160 . \end{matrix}$ Dette er egentlig det eneste rimelige svaret. Hvis vi hadde funnet at $\lim_{t \to \infty} y (t) = \infty$ hadde dette betydd at pasienten, og hele universet, etterhvert vil bli fylt opp av medisin – det høres ikke fornuftig ut! Hvis vi på den annen side hadde funnet at $\lim_{t \to \infty} y (t) = 0$ hadde det ikke vært noen vits for pasienten å innta $8$ mL av medisinen hver time. Dessuten hadde ikke dette gitt mening ettersom pasienten da måtte ha skilt ut $100$ % av den totale medisinmengden hver time. Den eneste fornuftige verdien $\lim_{t \to \infty} y (t)$ kan ta er altså slik at fem prosent av medisinmengden er nøyaktig lik $8$ mL. Dette kan vi skrive som $0.05 \cdot y (\infty) = 8$ . Svaret er da det samme som vi fant ovenfor – pasienten vil etter en veldig lang behandling ende opp med å ha omlag $160$ mL medisin i kroppen.

Svar: $\begin{matrix} \lim_{t \to \infty} y (t) = 160 . \end{matrix}$

Mer om

Denne oppgaven er om

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler på grenseverdier, se artikkelen Når x går mot uendelig.

Oppgave 2 (6 poeng) Nettkode: E-4DCB

Funksjonen $f$ er gitt ved

$f (x) = 12 e^{- 0, 5 x} \cdot \sin (0, 5 x), x \in [0, 4 π]$

a)

Tegn grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan plotte grafen til $f$ i GeoGebra.

Ved å bruke kommandoen
f(x):=Funksjon[12exp(-0.5x)sin(0.5x),0,4\pi]
i geoGebras grafdel sitter vi igjen med følgende graf:

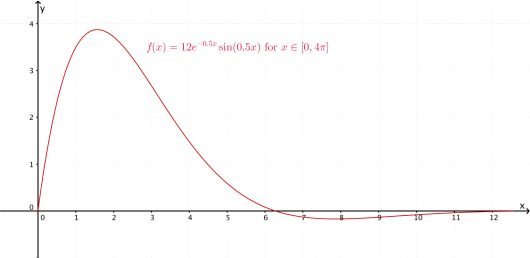
Svar:

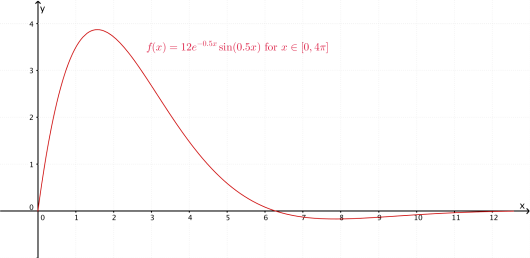
Mer om

Denne oppgaven er om

Graf

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

Visste du at

Hvis du har en mac, eller linux med fungerende python, kan du åpne programmet som heter ”terminal”. Ved å skrive
python etterfulgt av ENTER kan du bruke kommandoene

from pylab import *
x = linspace(0,4*pi,1000)
plot(x, 12*exp(-0.5*x)*sin(0.5*x) )
show()

Da dukker grafen til $f$ opp på skjermen.

b)

Bestem eventuelle topp- og bunnpunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Topp- og bunnpunktene på grafen til $f$ er nøyaktig de verdiene for $x$ som tilfredsstiller $f' (x) = 0$ .

Ved å benytte produktregelen og kjerneregelen for derivasjon finner vi at $\begin{matrix} f' (x) & = (12 e^{- \frac{1}{2} x} \sin (\frac{x}{2}))' \\ = (12 e^{- \frac{1}{2} x})' \sin (\frac{x}{2}) + 12 e^{- \frac{1}{2} x} (\sin (\frac{x}{2}))' \\ = (- \frac{1}{2}) 12 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) + 12 e^{- \frac{1}{2} x} (\frac{1}{2}) \cos (\frac{x}{2}) \\ = 6 e^{- \frac{1}{2} x} (\cos (\frac{x}{2}) - \sin (\frac{x}{2})) . \end{matrix}$ Topp- og bunnpunktene, $x$ , på grafen til $f$ må altså tilfredsstille $\begin{matrix} f' (x) = 6 e^{- \frac{1}{2} x} (\cos (\frac{x}{2}) - \sin (\frac{x}{2})) = 0 \end{matrix}$ og siden $6 e^{- \frac{1}{2} x}$ aldri er null må $\begin{matrix} \cos (\frac{x}{2}) - \sin (\frac{x}{2}) = 0 . \end{matrix}$ Ved å dividere begge sider av likningen på $\cos (\frac{x}{2})$ følger det at

$1 - \tan (\frac{x}{2}) = 0 \Rightarrow \tan (\frac{x}{2}) = 1$

Det betyr at

$\frac{x}{2} = \frac{π}{4} + π n for n \in ℤ$

og dermed

$x = \frac{π}{2} + 2 π n for n \in ℤ$

De punktene som ligger i intervallet $[0, 4 π]$ er da

$x = \frac{π}{2} og x = \frac{5 π}{2}$

Ved enten å se på tegningen av grafen til $f$ fra oppgave $a)$ eller å legge merke til at

$f' (0) = 6 > 0, f' (2 π) = - 6 e^{- π} < 0 og f' (4 π) = 6 e^{- 2 π} > 0,$

som betyr at $f' (x)$ går fra å være positiv til å være negativ i $x = \frac{π}{2}$ og fra å være negativ til å være positiv i $x = \frac{5 π}{2}$ , følger det at $\begin{matrix} T o p p u n k t : & (\frac{π}{2}, f (\frac{π}{2})) = (\frac{π}{2}, 12 e^{- \frac{π}{4}} \sin (\frac{π}{4})) = (\frac{π}{2}, 6 \sqrt{2} e^{- \frac{π}{4}}) \\ B u n n p u n k t : & (\frac{5 π}{2}, f (\frac{5 π}{2})) = (\frac{5 π}{2}, 12 e^{- \frac{5 π}{4}} \sin (\frac{5 π}{4})) = (\frac{5 π}{2}, - 6 \sqrt{2} e^{- \frac{5 π}{4}}) . \end{matrix}$

Alternativ løsning (numerisk)

Ved å bruke kommandoen
Ekstremalpunkt[f, 0, 4\pi]
i geoGebras grafdel finner vi de to punktene

$(1.57, 3.87) og (7.85, - 0.17)$

På grafen til $f$ fra oppgave $a)$ ser vi at de første punktet er et toppunkt og at det andre er et bunnpunkt. Altså har vi funnet at $\begin{matrix} T o p p u n k t : & (1.57, 3.87) \\ B u n n p u n k t : & (7.85, - 0.17) . \end{matrix}$

Svar: Toppunktet er $(\frac{π}{2}, 6 \sqrt{2} e^{- \frac{π}{4}})$ og bunnpunktet er $(\frac{5 π}{2}, - 6 \sqrt{2} e^{- \frac{5 π}{4}})$ .

Mer om

Denne oppgaven er om

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

c)

Bestem arealet som er begrenset av grafen til $f$ og $x$ -aksen.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Siden integralet av en funksjon $f (x)$ er arealet under funksjonens graf kan vi uttrykke arealet som er avgrenset av grafen til $f$ og $x$ -aksen ved et integral. Vi må imidlertid passe på at $f (x)$ ikke blir negativ. Da blir arealet negativt og det vil vi ikke. Vi kan løse dette ved heller å integrere $| f (x) |$ .

Vi begynner med å observere at nullpunktene til $f$ på intervallet $[0, 4 π]$ er punktene $\begin{matrix} x \in {0, 2 π, 4 π} \end{matrix}$ siden

$f (x) = 12 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) = 0$

$\Rightarrow \sin (\frac{x}{2}) = 0$

$\Rightarrow \frac{x}{2} = π n for n \in ℤ$

$\Rightarrow x = 2 π n for n \in ℤ .$

Siden $f (x)$ er positiv på intervallet $[0, 2 π]$ og negativ på intervallet $[2 π, 4 π]$ kan vi uttrykke arealet $A$ avgrenset av grafen til $f$ og $x$ -aksen ved $\begin{matrix} A & = \int_{0}^{4 π} | f (x) | d x = \int_{0}^{2 π} f (x) d x + \int_{2 π}^{4 π} - f (x) d x \\ = 12 \int_{0}^{2 π} e^{- \frac{1}{2} x} \sin (\frac{x}{2}) d x - 12 \int_{2 π}^{4 π} e^{- \frac{1}{2} x} \sin (\frac{x}{2}) d x . \end{matrix}$ Ved å benytte metoden for delvis integrasjon ved å integrere $e^{- \frac{1}{2} x}$ og derivere $\sin \frac{x}{2}$ , finner vi at $\begin{matrix} I & = \int e^{- \frac{1}{2} x} \sin (\frac{x}{2}) d x \\ = - 2 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) + 2 \int e^{- \frac{1}{2} x} \frac{1}{2} \cos (\frac{x}{2}) d x \\ = - 2 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) + \int e^{- \frac{1}{2} x} \cos (\frac{x}{2}) d x \end{matrix}$ Vi kan nå gjenta delvis integrasjon på det gjenværende integralet ved å integrere $e^{- \frac{1}{2} x}$ og derivere $\cos (\frac{x}{2})$ . Da får vi $\begin{matrix} \int e^{- \frac{1}{2} x} \cos (\frac{x}{2}) d x & = - 2 e^{- \frac{1}{2} x} \cos (\frac{x}{2}) - \int 2 e^{- \frac{1}{2} x} \frac{1}{2} \sin (\frac{x}{2}) d x \\ = - 2 e^{- \frac{1}{2} x} \cos (\frac{x}{2}) - I . \end{matrix}$ Det betyr at vi har integralet $I$ må tilfredsstille $\begin{matrix} I & = - 2 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) + \int e^{- \frac{1}{2} x} \cos (\frac{x}{2}) d x \\ = - 2 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) - 2 e^{- \frac{1}{2} x} \cos (\frac{x}{2}) - I, \end{matrix}$ som ved å legge til $I$ på begge sider av likhetstegnet kan skrives $\begin{matrix} 2 I = - 2 e^{- \frac{1}{2} x} \sin (\frac{x}{2}) - 2 e^{- \frac{1}{2} x} \cos (\frac{x}{2}) . \end{matrix}$ Altså må $\begin{matrix} I & = \int e^{- \frac{1}{2} x} \sin (\frac{x}{2}) d x = - e^{- \frac{1}{2} x} (\sin (\frac{x}{2}) + \cos (\frac{x}{2})) . \end{matrix}$ Merk at vi med vilje har latt være å ta med en integrasjonskonstant ettersom den uansett bortfaller når resultatet brukes i et bestemt integral. Dette betyr at arealet $A$ kan skrives $\begin{matrix} A & = 12 \int_{0}^{2 π} e^{- \frac{1}{2} x} \sin (\frac{x}{2}) d x - 12 \int_{2 π}^{4 π} e^{- \frac{1}{2} x} \sin (\frac{x}{2}) d x \\ = 12 {[- e^{- \frac{1}{2} x} (\sin (\frac{x}{2}) + \cos (\frac{x}{2}))]}_{0}^{2 π} - 12 {[- e^{- \frac{1}{2} x} (\sin (\frac{x}{2}) + \cos (\frac{x}{2}))]}_{2 π}^{4 π} \\ = 12 [- e^{- π} (- 1) + 1] - 12 [- e^{- 2 π} (\sin 2 π + \cos 2 π) + e^{- π} (- 1)] \\ = 12 + 12 e^{- π} - 12 [- e^{- 2 π} - e^{- π}] = 12 + 12 e^{- π} + 12 e^{- π} + 12 e^{- 2 π} \\ = 12 (1 + 2 e^{- π} + e^{- 2 π}) \approx 13, 0595 . \end{matrix}$

Alternativ løsning (numerisk)

Numerisk løsning:

Vi trenger bare å benytte to kommandoer i geoGebras grafdel for å beregne arealet avgrensen at grafen til $f$ og $x$ -aksen. Vi definerer først funksjonen $f (x)$ ved å bruke kommandoen
f(x):=Funksjon[12exp(-0.5x)sin(0.5x),0,4\pi]

Deretter beregner vi integralet av $| f (x) |$ mellom de to endepunktene $x = 0$ og $x = 4 π$ ved å bruke kommandoen
Integral[abs(f(x)), 0, 4\pi]

Resultatet er da arealet $\begin{matrix} A = 13, 06 . \end{matrix}$

Svar: $\begin{matrix} 12 (1 + 2 e^{- π} + e^{- 2 π}) \approx 13, 0595 . \end{matrix}$

Mer om

Denne oppgaven er om

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Sinus

sinus

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

Graf

graf

x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.

x-akse

y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.

y-akse

For flere forklaringer og eksempler på integrasjon, se artikkelen Delvis integrasjon.

Oppgave 3 (8 poeng) Nettkode: E-4DDB

Skissen nedenfor viser en pyramide $O A B C D$ som er plassert i et romkoordinatsystem.

Hjørnene i pyramiden er $O (0, 0, 0)$ , $A (3, 0, 0)$ , $B (3, 3, 0)$ , $C (0, 3, 0)$ og $D (0, 0, 4)$ .

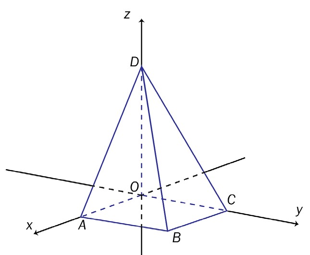
a)

Bestem ved regning arealet av sideflaten $A B D$ i pyramiden.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Arealet av sideflaten $A B D$ utgjør halvparten av parallellogrammet utspent av vektorene $\vec{A B}$ og $\vec{A D}$ .

Vi begynner med å observere at

$\begin{matrix} \vec{A B} & = \vec{O B} - \vec{O A} = [3, 3, 0] - [3, 0, 0] = [0, 3, 0] \\ \vec{A D} & = \vec{O D} - \vec{O A} = [0, 0, 4] - [3, 0, 0] = [- 3, 0, 4] . \end{matrix}$

Det betyr at

$\vec{A B} \times \vec{A D} = |\begin{matrix} \vec{e_{x}} & \vec{e_{y}} & \vec{e_{z}} \\ 0 & 3 & 0 \\ - 3 & 0 & 4 \end{matrix}| = |\begin{matrix} 3 & 0 \\ 0 & 4 \end{matrix}| \vec{e_{x}} - |\begin{matrix} 0 & 0 \\ - 3 & 4 \end{matrix}| \vec{e_{y}} + |\begin{matrix} 0 & 3 \\ - 3 & 0 \end{matrix}| \vec{e_{z}}$

$= 3 \cdot 4 \vec{e_{x}} - 0 \vec{e_{y}} + (- 3 \cdot (- 3)) \vec{e_{z}} = [12, 0, 9] .$

Siden lengden av vektoren $\vec{A B} \times \vec{A D}$ er lik arealet av parallellogrammet utspent av $\vec{A B}$ og $\vec{A D}$ , og paralleogrammet har nøyaktig dobbelt så stort areal som sideflaten $A B D$ , følger det at arealet $A$ av sideflaten $A B D$ er

$\begin{matrix} A & = \frac{1}{2} | \vec{A B} \times \vec{A D} | = \frac{1}{2} \sqrt{12^{2} + 9^{2}} = \frac{3}{2} \sqrt{4^{2} + 3^{2}} \\ = \frac{3}{2} \sqrt{25} = \frac{3}{2} \cdot 5 = \frac{15}{2} = 7, 5 . \end{matrix}$

Alternativ løsning

Siden punktene $A$ og $D$ begge ligger i planet $y = 0$ og $B$ ligger i planet $z = 0$ må trekanten $A B D$ være rettvinklet med hypotenus $B D$ . Arealet av sideflaten $A B D$ er dermed

$Areal av Δ A B D = \frac{1}{2} A B \cdot A D = \frac{1}{2} \sqrt{3^{2}} \cdot \sqrt{{(- 3)}^{2} + 4^{2}} = \frac{1}{2} \cdot 3 \cdot 5 = \frac{15}{2} = 7, 5 .$

Svar: $Areal av Δ A B D = \frac{15}{2} = 7, 5 .$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Hypotenus

Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.

hypotenus

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

rett vinkel

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt - areal og volum.

b)

Sideflaten $A B D$ ligger i et plan $α$ .

Vis ved regning at planet $α$ har likningen

$4 x + 3 z - 12 = 0$

Løs oppgaven her

Løsningsforslag b)

Tanker

Vi kan uttrykke planet $α$ hvis vi finner en vektor $\vec{n}$ som står normalt på alle vektorer mellom punkter i planet, og minst ett punkt som ligger i planet.

Vektoren $\vec{A B} \times \vec{A D}$ , som vi i oppgave $a)$ fant at er lik $[12, 0, 9]$ , står vinkelrett på planet $α$ . Det betyr at vi må velge normalvektoren $\vec{n}$ som en konstant $λ$ multiplisert med retningen $[12, 0, 9]$ . Ett mulig valg er da å sette

$\begin{matrix} \vec{n} = \frac{1}{3} [12, 0, 9] = [4, 0, 3] . \end{matrix}$

Hvis $\vec{v}$ er en vektor mellom to punkter i $α$ er da likningen til $α$ gitt som

$\vec{n} \cdot \vec{v} = 0$ .

Siden $A (3, 0, 0)$ ligger i alpha må altså alle punkter $P (x, y, z)$ som ligger i $α$ tilfredsstille

$\begin{matrix} \vec{n} \cdot \vec{A P} = [4, 0, 3] \cdot ([x, y, z] - [3, 0, 0]) = [4, 0, 3] \cdot [x - 3, y, z] = 4 (x - 3) + 3 z = 0 . \end{matrix}$

Det kan skrives $\begin{matrix} 4 x + 3 z - 12 = 0, \end{matrix}$ som er det vi ønsket å vise.

Alternativ løsning:

Ved å huske at hvis $\vec{n} = [a, b, c]$ er normalvektoren til et plan som inneholder punktet $(x_{0}, y_{0}, z_{0})$ , så må likningen til planet være gitt som

$\begin{matrix} a (x - x_{0}) + b (y - y_{0}) + c (z - z_{0}) = 0, \end{matrix}$

holder det å se at vi kan velge

$\begin{matrix} \vec{n} = [a, b, c] = \frac{1}{3} \vec{A B} \times \vec{A D} = [4, 0, 3], \end{matrix}$

og $\begin{matrix} (x_{0}, y_{0}, z_{0}) = A = (3, 0, 0) . \end{matrix}$

Då får vi

$\begin{matrix} 4 (x - 3) + 0 (y - 0) + 3 (z - 0) = 0, \end{matrix}$

som kan skrives $\begin{matrix} 4 x + 3 z - 12 = 0 . \end{matrix}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

rett vinkel

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

Visste du at

Vi kunne også argumentert oss frem til likningen for planet uten å regne. Siden $A$ og $B$ deler $x$ - og $z$ -koordinat må de ligge på en linje som er parallell med $y$ -aksen. Derfor kan ikke normalvektoren til planet ha noen komponent i $y$ -retning. Med andre ord kan normalvektoren skrives $\vec{n} = [a, 0, b]$ for to konstanter $a$ og $b$ . Siden $\vec{n}$ skal stå normalt på linjen $A D$ må $\vec{n}$ peke like mye mer i $x$ -retning enn $z$ -retning som vektoren $\vec{O D}$ peker i $z$ -retning og $\vec{O A}$ peker i $x$ -retning. Altså kan vi velge $\vec{n} = [4, 0, 3]$ . Siden $A$ ligger i planet må $\vec{n} \cdot \vec{O A} = 12$ være det konstantleddet som må trekkes fra i likningen for planet. Altså er likningen for planet

$\begin{matrix} \vec{n} \cdot [x, y, z] - 12 = 4 x + 3 z - 12 = 0 . \end{matrix}$

c)

Bestem avstanden fra punktet $O$ til planet $α$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan finne avstanden fra punktet $O$ til planet $α$ ved å finne et punkt $P$ i $α$ som er slik at $\vec{O P}$ er parallell, eller antiparallell, med normalvektoren $\vec{n}$ .

Vi husker først at hvis to vektorer $\vec{a}$ og $\vec{b}$ er parallelle, eller antiparallelle, tilfredsstiller de likningen

$|\vec{a} \cdot \vec{b}| = |\vec{a}| \cdot |\vec{b}|$

der $|\vec{a}|$ og $|\vec{b}|$ er lengden til henholdsvis $\vec{a}$ og $\vec{b}$ . Siden likningen til planet, $\begin{matrix} 4 x + 3 z - 12 = 0, \end{matrix}$ kan skrives

$\begin{matrix} \vec{n} \cdot \vec{O P} = 12, \end{matrix}$

der $P (x, y, z)$ er et punkt i planet og $\vec{n} = [4, 0, 3]$ er normalvektoren til planet, følger det at

$\begin{matrix} |\vec{n} \cdot \vec{O P}| = |\vec{n}| \cdot |\vec{O P}| = 12 \end{matrix}$

hvis $\vec{n}$ og $\vec{O P}$ er parallelle, eller antiparallelle. Da er $P$ det punktet i $α$ som er nærmest $O$ , som betyr at lengden $|\vec{O P}|$ må være avstanden $d$ fra punktet $O$ til planet $α$ . Vi har altså at

$\begin{matrix} d = |\vec{O P}| = \frac{12}{|\vec{n}|} = \frac{12}{\sqrt{4^{2} + 3^{2}}} = \frac{12}{5} = 2, 4 . \end{matrix}$

Svar: $\begin{matrix} 2, 4 . \end{matrix}$

Mer om

Denne oppgaven er om

Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".

parallell

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

For flere forklaringer og eksempler på vektorer, se artikkelen Parallelle vektorer.

d)

Bestem ved regning vinkelen mellom de to planene som sideflatene $A B D$ og $B C D$ ligger i.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vinkelen mellom de to planene som sideflatene $A B D$ og $B C D$ ligger i er lik vinkelen mellom normalvektorene til de to planene, eller supplementvinkelen til disse.

Først observerer vi at

$\begin{matrix} \vec{C B} & = \vec{O B} - \vec{O C} = [3, 3, 0] - [0, 3, 0] = [3, 0, 0] \\ \vec{C D} & = \vec{O D} - \vec{O C} = [0, 0, 4] - [0, 3, 0] = [0, - 3, 4] . \end{matrix}$

Deretter ser beregner vi vektoren

$\vec{C B} \times \vec{C D} = |\begin{matrix} \vec{e_{x}} & \vec{e_{y}} & \vec{e_{z}} \\ 3 & 0 & 0 \\ 0 & - 3 & 4 \end{matrix}| = |\begin{matrix} 0 & 0 \\ - 3 & 4 \end{matrix}| \vec{e_{x}} - |\begin{matrix} 3 & 0 \\ 0 & 4 \end{matrix}| \vec{e_{y}} + |\begin{matrix} 3 & 0 \\ 0 & - 3 \end{matrix}| \vec{e_{z}}$

$= 0 \vec{e_{x}} - 3 \cdot 4 \vec{e_{y}} + 3 \cdot (- 3) \vec{e_{z}} = [0, - 12, - 9] .$

Siden normalvektoren til planet $α$ er $\vec{n} = [4, 0, 3]$ og vektoren $\vec{C B} \times \vec{C D}$ er normal på planet $B C D$ ligger i må vinkelen $θ$ mellom de to planene tilfredsstille

$\vec{n} \cdot \vec{C B} \times \vec{C D} = |\vec{n}| \cdot |\vec{C B} \times \vec{C D}| \cos (θ)$

Med andre ord er vinkelen mellom de to planene gitt ved

$\begin{matrix} θ & = \arccos (\frac{\vec{n} \cdot \vec{C B} \times \vec{C D}}{| \vec{n} | \cdot | \vec{C B} \times \vec{C D} |}) = \arccos (\frac{[4, 0, 3] \cdot [0, - 12, - 9]}{\sqrt{4^{2} + 3^{2}} \cdot \sqrt{(- 12)^{2} + (- 9)^{2}}}) \\ = \arccos (\frac{- 3 \cdot 9}{5 \cdot 15}) = \arccos (\frac{- 9}{25}) \approx 111, 1^{\circ} . \end{matrix}$ Siden vi tenker på vinkelen mellom to plan som en vinkel i første kvadrant bør vi heller velge $\begin{matrix} θ \approx 180^{\circ} - {111, 1}^{\circ} = 68, 9^{\circ} . \end{matrix}$

Svar: $\begin{matrix} Ca . 68, 9^{\circ} . \end{matrix}$

Mer om

Denne oppgaven er om

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler på vektorer, se artikkelen Vinkelen mellom to vektorer.

Oppgave 4 (6 poeng) Nettkode: E-4DDH

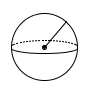
Figuren nedenfor viser en sirkelsektor $O B C$ der $C$ ligger i første kvadrant. Buen $B C$ er en del av sirkelen med likning $x^{2} + y^{2} = 9$ . Punktet $A$ har koordinatene $(2, 0)$ og $∠ O A C = 90^{\circ}$

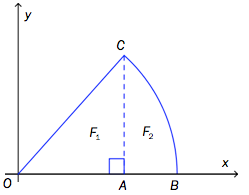
a)

Vis at koordinatene til $C$ er $(2, \sqrt{5})$ .

Bestem likningen for den rette linjen gjennom $O$ og $C$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Punktet $C$ ligger både rett over punktet $A$ og på sirkelen $x^{2} + y^{2} = 9$ . Det kan vi bruke til å bestemme koordinatene til $C$ .

Siden $C$ ligger rett over $A$ må $A$ og $C$ dele $x$ -koordinat. Det betyr at $C$ har $x$ -koordinat lik $2$ . Siden $C$ også må tilfredsstille likningen for sirkelen finner vi da at $y$ -koordinaten til $C$ , $y_{C}$ , må tilfredsstille

$2^{2} + y_{C}^{2} = 9 \Rightarrow y_{C} = \pm \sqrt{9 - 2^{2}} = \pm \sqrt{5}$

Ettersom $C$ ligger over $x$ -aksen må den positive løsningen være den rikitige. Altså har vi funnet at $\begin{matrix} C = (2, \sqrt{5}) . \end{matrix}$ Likningen for punktene som ligger på den rette linjen gjennom $O$ og $C$ kan skrives $\begin{matrix} y = a x + b \end{matrix}$ for to konstanter $a$ og $b$ . Siden linjen skjærer $y$ -aksen i Origo må konstantleddet, $b$ , være null, og siden $C$ har koordinater $(2, \sqrt{5})$ må stigningstallet til linjen være gitt som $\begin{matrix} a = \frac{y_{C}}{x_{C}} = \frac{\sqrt{5}}{2} . \end{matrix}$ Likningen for linjen som går gjennom $O$ og $C$ kan altså skrives $\begin{matrix} y = \frac{\sqrt{5}}{2} x . \end{matrix}$

Dersom vi ikke husker hvordan vi kan finne konstantleddet og stigningstallet til en rett linje kunne vi også sagt at linjen gjennom $O$ og $C$ kan uttrykkes $\begin{matrix} C_{x} x + C_{y} y + C = 0, \end{matrix}$ for tre konstanter $C_{x}$ , $C_{y}$ og $C$ . At $O (0, 0)$ ligger på linjen impliserer

$C_{x} \cdot 0 + C_{y} \cdot 0 + C = 0 \Rightarrow C = 0 .$

Siden $C (2, \sqrt{5})$ også ligger på denne linjen må

$C_{x} \cdot 2 + C_{y} \cdot \sqrt{5} \Rightarrow C_{x} = - \frac{\sqrt{5}}{2} C_{y}$

Altså kan likningen for den rette linjen skrives

$- \frac{\sqrt{5}}{2} C_{y} x + C_{y} y = 0 \Rightarrow C_{y} y = \frac{\sqrt{5}}{2} C_{y} x .$

Ved å dele på $C_{y}$ på begge sider av likningen finner vi uttrykket

$\begin{matrix} y = \frac{\sqrt{5}}{2} x, \end{matrix}$

som er likningen for den rette linjen mellom $O$ og $C$ .

Alternativ løsning

Siden sirkelen $x^{2} + y^{2} = 9 = 3^{2}$ har radius $3$ og $C$ ligger på sirkelen må $O C = 3$ . Siden $O A = 2$ og $△ O A C$ er rettvinklet følger det da at $\begin{matrix} A C = \sqrt{3^{2} - O A^{2}} = \sqrt{9 - 4} = \sqrt{5} . \end{matrix}$ Ettersom $A C$ er $y$ -koordinaten til $C$ og $O A$ er $x$ -koordinaten til $C$ må koordinatene til $C$ være gitt som $\begin{matrix} C (2, \sqrt{5}) . \end{matrix}$ Funksjonen for den rette linjen mellom $O$ og $C$ kan skrives $y = a x + b$ , der $a$ er stigningstallet og $b$ er der linjen skjærer $y$ -aksen. Ettersom stigningstallet er gitt av $\begin{matrix} a = \frac{A C}{O A} = \frac{\sqrt{5}}{2}, \end{matrix}$ holder det å konstatere at $b = 0$ siden linjen skjærer $y$ -aksen i $y = 0$ før vi uttrykker den rette linjen ved $\begin{matrix} y = \frac{\sqrt{5}}{2} x . \end{matrix}$

Svar: $\begin{matrix} y = \frac{\sqrt{5}}{2} x . \end{matrix}$

Mer om

Denne oppgaven er om

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

rett vinkel

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.

x-akse

y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.

y-akse

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

lineær likning

For flere forklaringer og eksempler på rette linjer, se artikkelen Rette linjer (lineære funksjoner).

b)

Når flatestykket $F_{1}$ $(Δ O A C)$ dreies $360^{\circ}$ om $x$ -aksen, får vi en kjegle.

Bestem volumet av denne kjeglen ved hjelp av integralregning.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Hvis $f (x)$ er funksjonen til linjen $O C$ kan vi ved å dele opp kjeglen i uendelig mange, uendelig tynne sylindere med radius $f (x)$ og høyde $d x$ , og derfor volum $π f (x)^{2} d x$ , finne kjeglens volum ved å beregne integralet $\int_{x_{O}}^{x_{A}} π f (x)^{2} d x$ .

I oppgave $a)$ fant vi at den rette linjen gjennom $O$ og $C$ tilsvarer grafen til funksjonen $y (x) = \frac{\sqrt{5}}{2}$ . Kjeglen som oppstår når denne linjen roteres om $x$ -aksen kan deles opp i uendelig mange, uendelig tynne sylindere med radius $f (x)$ og høyde $d x$ . Volumet av hver sylinder er dermed $π f (x)^{2} d x$ og integralet av disse volumene er volumet $V$ av kjeglen. Altså har vi at

$\begin{matrix} V & = \int_{x_{O}}^{x_{A}} π {(y (x))}^{2} dx = \int_{0}^{2} π {(\frac{\sqrt{5}}{2} x)}^{2} d x = \frac{5 π}{4} \int_{0}^{2} x^{2} d x \end{matrix}$

og siden den deriverte av $\frac{1}{3} x^{3}$ er $x^{2}$ må

$\frac{5 π}{4} \int_{0}^{2} x^{2} dx = \frac{5 π}{4} {[\frac{1}{3} x^{3}]}_{0}^{2} = \frac{5 π}{4} (\frac{1}{2} \cdot 2^{3} - \frac{1}{3} \cdot 0^{3}) = \frac{5 π}{4} \cdot \frac{1}{3} \cdot 2^{3} = \frac{10 π}{3} \approx 10, 47 .$

Altså er arealet av kjeglen gitt av

$\begin{matrix} V = \frac{10 π}{3} \approx 10, 47 . \end{matrix}$

Svar: $\begin{matrix} \frac{10 π}{3} \approx 10, 47 . \end{matrix}$

Mer om

Denne oppgaven er om

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Integralregning

Integralregning er forbundet med arealbegrepet. Et areal kan uttrykkes ved et bestemt integral, og det kan beregnes ved integrasjon. Integralet fra a til b av funksjonen f kan tolkes som arealet av det området som begrenses av funksjonens graf, x-aksen og de vertikale linjene x=a og x=b.

integralregning

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Kjegle

En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.

Kjeksen til en kroneis har form som en kjegle.

Volum : V = $\frac{π r^{2} h}{3}$
Overflate : A = $π r^{2} + π r s$

kjegle

For flere forklaringer og eksempler på integrasjon, se artikkelen Volum av et omdreiningslegeme.

Visste du at

Integrasjon er muligens en av de viktigste oppdagelsene innen matematikk. Ideen går ut på å løse et problem ved å dele det opp i uendelig mange, uendelig små biter og deretter beregne summen av disse bitene. Hvis du kjenner hastigheten til et objekt kan du for eksempel dele opp reisetiden i uendelig mange, uendelig små biter og bruke at en bitteliten strekning $d s$ er så langt du forflytter deg med hastighet $v (t)$ i løpet av det bittelille tidsrommet $d t$ . Med andre ord kan man bruke formelen $\begin{matrix} Strekning = s = \int_{s_{0}}^{s_{1}} d s = \int_{t_{0}}^{t_{1}} v (t) d t \end{matrix}$ for å beregne strekning i fysikk. Hvis du lurer på hvor lang strek du må tegne når du skal tegne grafen til en funksjon $f (x)$ på intervallet $[a, b]$ kan du bruke nøyaktig samme argumentasjon. Først deler vi den totale strekningen $S$ inn i uendelig mange, uendelig små avstander $d S$ slik at vi får $\begin{matrix} S = \int_{S_{0}}^{S_{1}} d S . \end{matrix}$ Deretter kan vi bruke pythagoras læresetning til å si at denne uendelig korte strekningen $d S$ må tilfredsstille $d S^{2} = d x^{2} + d y^{2}$ og derfor $\begin{matrix} S = \int_{(a, f (a))}^{(b, f (b))} \sqrt{d x^{2} + d y^{2}} = \int_{x = a}^{x = b} \sqrt{1 + {(\frac{d y}{d x})}^{2}} d x . \end{matrix}$ Hvis vi til slutt legger merke til at $\frac{d y}{d x}$ er den deriverte av $f (x)$ siden $y = f (x)$ og $\frac{d y}{d x}$ derfor er stigningstallet til $f (x)$ kan vi skrive $\begin{matrix} S = \int_{x = a}^{x = b} \sqrt{1 + {(f' (x))}^{2}} d x . \end{matrix}$

c)

Når flatestykket $F_{2}$ dreies $360^{\circ}$ om $x$ -aksen, får vi et kulesegment.

Bestem volumet av dette kulesegmentet ved hjelp av integralregning.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Siden vi har et uttrykk for sektoren $B C$ kan vi gjenta fremgangsmåten fra oppgave $b)$ , men nå med en annen funksjon og med andre grenser i integralet.

Ettersom likningen for sirkelen er $\begin{matrix} x^{2} + y^{2} = 9 \end{matrix}$ kan vi skrive funksjonsuttrykket for sektoren $B C$ som $\begin{matrix} y = \sqrt{9 - x^{2}} . \end{matrix}$ Ved å gjenta prosedyren med å dele opp omdreiningslegemet i uendelige mange, uendelig tynne sylindere med volum $π {(y (x))}^{2} d x$ kan vi uttrykke volumet $V$ av omdreiningslegemet ved $\begin{matrix} V = \int_{x_{C}}^{x_{B}} π {(y (x))}^{2} d x . \end{matrix}$ Siden $C$ har $x$ -koordinat lik $2$ og $B$ må ha $x$ -koordinat lik radius i sirkelen, nemlig $3$ , følger det at $\begin{matrix} \int_{x_{C}}^{x_{B}} π y (x)^{2} d x = \int_{2}^{3} π {\sqrt{9 - x^{2}}}^{2} d x = π \int_{2}^{3} (9 - x^{2}) d x \\ = π (\int_{2}^{3} 9 d x - \int_{2}^{3} x^{2} d x) = 9 π \int_{2}^{3} 1 d x - π \int_{2}^{3} x^{2} d x . \end{matrix}$ At den deriverte av $x$ og $\frac{1}{3} x^{3}$ er henholdsvis $1$ og $x^{2}$ gir dermed at $\begin{matrix} 9 π \int_{2}^{3} 1 d x - π \int_{2}^{3} x^{2} d x = 9 π [x]_{2}^{3} - π {[\frac{1}{3} x^{3}]}_{2}^{3} \\ = 9 π (3 - 2) - π (\frac{1}{3} 3^{3} - \frac{1}{3} 2^{3}) \\ = 9 π - π (9 - \frac{8}{3}) = \frac{8 π}{3} \approx 8, 38 . \end{matrix}$

Svar: $\begin{matrix} \frac{8 π}{3} \approx 8, 38 . \end{matrix}$

Mer om

Denne oppgaven er om

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.

Oppgave 5 (6 poeng) Nettkode: E-4DDM

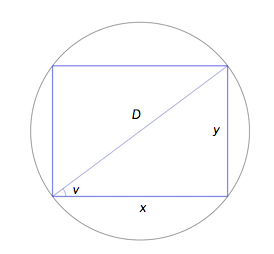
På figuren er et rektangel med sider $x$ og $y$ innskrevet i en sirkel. Sirkelen har diameteren $D$ .

$∠ v$ er vinkelen mellom $x$ og $D$ .

a)

Forklar at omkretsen $O$ til rektangelet kan skrives som

$O (v) = 2 D \cos v + 2 D \sin v$

Bestem også et funksjonsuttrykk for arealet $A (v)$ av rektangelet.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Siden vi kan uttrykke sidene $x$ og $y$ ved hjelp av diameteren $D$ til sirkelen og sinus og cosinus til vinkelen $v$ .

Siden

$\sin (v) = \frac{Motstående katet}{Hypotenus} og \cos (v) = \frac{Hosliggende katet}{Hypotenus}$

kan vi skrive

$\sin (v) = \frac{y}{D} og \cos (v) = \frac{x}{D}$

og dermed få

$x = D \cos (v) og y = D \sin (v)$

Omkretsen $O$ av rektangelet kan da skrives

$\begin{matrix} O = 2 x + 2 y = 2 D \cos v + 2 D \sin v, \end{matrix}$

som er det første vi ønsket å vise. Arealet $A (v)$ av rektangelet blir da

$\begin{matrix} A (v) = x y = D^{2} \sin (v) \cos (v) = \frac{D^{2}}{2} \sin (2 v) . \end{matrix}$

Svar: $\begin{matrix} A (v) = D^{2} \sin (v) \cos (v) = \frac{D^{2}}{2} \sin (2 v) . \end{matrix}$

Mer om

Denne oppgaven er om

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Sinus

sinus

Hypotenus

Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.

hypotenus

Katet

Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter.

katet

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Klara definerer sinus, cosinus og tangens.

b)

Bruk $O' (v)$ og vis at det rektangelet som har størst omkrets, er et kvadrat.

Bestem den største omkretsen av rektangelet uttrykt ved diameteren $D$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Det rektangelet med størst omkrets er gitt av den vinkelen $v$ som tilfredsstiller $O' (v) = 0$ .

Ettersom

$\begin{matrix} O (v) = 2 D \cos (v) + 2 D \sin (v) \end{matrix}$

følger det at

$\begin{matrix} O' (v) = 2 D (\cos (v))' + (2 D \sin (v))' = - 2 D \sin (v) + 2 D \cos (v) . \end{matrix}$

De ekstreme verdiene til omkretsen $O (v)$ er dermed gitt av de vinklene $v$ som tilfredsstiller

$O^{'} (v) = - 2 D \sin (v) + 2 D \cos (v) = 0$

$\Rightarrow 2 D \sin (v) = 2 D \cos (v)$

$\Rightarrow \sin (v) = \cos (v)$

$\Rightarrow \tan (v) = 1$

Siden denne verdien for $v$ er slik at $\sin (v) = \cos (v)$ følger det at

$\begin{matrix} x = D \cos (v) = D \sin (v) = y, \end{matrix}$

som betyr at rektangelet da er et kvadrat. Ettersom vinkelen $v$ må være i intervallet $[0, \frac{π}{2}]$ er den eneste løsningen av denne likningen gitt ved $v = \frac{π}{4}$ . Siden $O (v) \to 0 når v \to 0^{+} eller v \to {\frac{π}{2}}^{-}$ , må $\frac{π}{4}$ være et makspunkt. Dette gir en maksimal omkrets lik

$\begin{matrix} O_{m a k s} & = O (\frac{π}{4}) = 2 D \cos (\frac{π}{4}) + 2 D \sin (\frac{π}{4}) \\ = 2 D \frac{\sqrt{2}}{2} + 2 D \frac{\sqrt{2}}{2} = 2 \sqrt{2} D . \end{matrix}$

Svar: $\begin{matrix} O_{m a k s} & = 2 \sqrt{2} D . \end{matrix}$

Mer om

Denne oppgaven er om

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Sinus

sinus

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Derivasjon av trigonometriske funksjoner.

c)

Bruk $A' (v)$ og vis at det rektangelet som har størst areal, også er et kvadrat.

Bestem det største arealet av rektangelet uttrykt ved diameteren $D$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Det største arealet $A (v)$ er gitt av den vinkelen $v$ som tilfredsstiller $A' (v) = 0$ .

Ettersom

$\begin{matrix} A (v) = \frac{1}{2} D^{2} \sin (2 v) \end{matrix}$

følger det at

$\begin{matrix} A' (v) & = \frac{1}{2} D^{2} (\sin (2 v))' = \frac{1}{2} D^{2} (2 v)' \cos (2 v) = \frac{1}{2} D^{2} 2 \cos (2 v) = D^{2} \cos (2 v) . \end{matrix}$

Siden det største arealet $A (v)$ er gitt av den vinkelen $v$ som tilfredsstiller $A' (v) = 0$ og

$A^{'} (v) = D^{2} \cos (2 v) = 0$

$\Rightarrow \cos (2 v) = 0 \Rightarrow 2 v = \frac{π}{2} + π n$

må vinkelen som maksimerer arealet $A (v)$ være $\begin{matrix} v = \frac{π}{4} . \end{matrix}$ Siden $O (v) \to 0 når v \to 0^{+} eller v \to {\frac{π}{2}}^{-}$ , må $\frac{π}{4}$ være et makspunkt. Merk imidlertid at også $v = \frac{π}{2}$ er en løsning likningen $A' (v) = 0$ . Denne forkaster vi ettersom den fører til et areal lik $0$ . Det maksimale arealet $A_{m a k s}$ er altså gitt av

$\begin{matrix} A_{m a k s} = A (\frac{π}{4}) = \frac{1}{2} D^{2} \sin (\frac{2 π}{4}) = \frac{1}{2} D^{2} \sin (\frac{π}{2}) = \frac{1}{2} D^{2} . \end{matrix}$

Siden vinkelen er den samme som i oppgave $b)$ følger det at rektangelet med maksimalt areal er et kvadrat. Alternativt kan vi observere dette ved

$\begin{matrix} x = D \cos (v) = D \cos (\frac{π}{4}) = D \frac{\sqrt{2}}{2} = D \sin (\frac{π}{4}) = y . \end{matrix}$

Svar: $\begin{matrix} A_{m a k s} = \frac{1}{2} D^{2} . \end{matrix}$

Mer om

Denne oppgaven er om

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på funksjonsdrøfting, se artikkelen Tom forteller om areal.

Oppgave 6 (6 poeng) Nettkode: E-4DDU

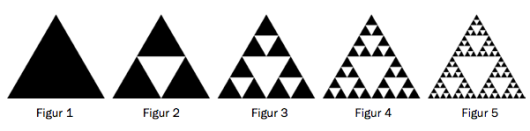
Sierpiński-trekanten, som har sitt navn etter den polske matematikeren Wacław Franciszek Sierpiński (1882–1969), lages slik:

1. Vi starter med en likesidet, svart trekant som har areal A. Se figur 1.

2. Midtpunktet på hver av sidene i trekanten er hjørnene i en ny hvit, likesidet trekant. Denne hvite trekanten fjerner vi. Vi står da igjen med tre likesidede, svarte trekanter. Se figur 2.

3. Vi gjentar denne prosessen med hver av de svarte trekantene. Se figurene 3–5. Vi tenker oss at prosessen blir utført uendelig mange ganger. Den «gjennomhullede» figuren vi da står igjen med, kalles Sierpiński-trekanten.

Summen av arealene som fjernes (de hvite trekantene), er gitt ved rekken

$A \cdot (\frac{1}{4} + \frac{3}{16} + \frac{9}{64} + \frac{27}{256} + . . .)$

a)

Bestem summen av rekken ovenfor.

Hva forteller svaret ditt om arealet av Sierpiński-trekanten?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Leddene i rekken er på formen $A \frac{3^{n}}{4^{n + 1}}$ for $n = 0, 1, 2, 3, . . .$ . Det kan vi skrive som en geometrisk rekke.

Rekken kan skrives $\begin{matrix} A \cdot (\frac{1}{4} + \frac{3}{16} + \frac{9}{64} + \frac{27}{256} + . . .) \\ = A \cdot (\frac{3^{0}}{4^{1}} + \frac{3^{1}}{4^{2}} + \frac{3^{2}}{4^{3}} + \frac{3^{3}}{4^{4}} + . . .) \\ = \frac{A}{4} \cdot ({(\frac{3}{4})}^{0} + {(\frac{3}{4})}^{1} + {(\frac{3}{4})}^{2} + {(\frac{3}{4})}^{3} + . . .) . \end{matrix}$ Det holder altså å finne verdien av $\begin{matrix} S_{n} = {(\frac{3}{4})}^{0} + {(\frac{3}{4})}^{1} + {(\frac{3}{4})}^{2} + . . . + {(\frac{3}{4})}^{n} \end{matrix}$ og deretter beregne $\frac{1}{4} A S_{n}$ når $n$ går mot uendelig. Siden vi kan skrive $\begin{matrix} (\frac{3}{4}) S_{n} & = {(\frac{3}{4})}^{1} + {(\frac{3}{4})}^{2} + {(\frac{3}{4})}^{3} + . . . + {(\frac{3}{4})}^{n} + {(\frac{3}{4})}^{n + 1} \\ = [{(\frac{3}{4})}^{0} + {(\frac{3}{4})}^{1} + {(\frac{3}{4})}^{2} + {(\frac{3}{4})}^{3} + . . . + {(\frac{3}{4})}^{n}] - 1 + {(\frac{3}{4})}^{n + 1} \\ = S_{n} + {(\frac{3}{4})}^{n + 1} - 1 \end{matrix}$ følger det imidlertid at $\begin{matrix} S_{n} (1 - (\frac{3}{4})) = 1 - {(\frac{3}{4})}^{n + 1} \end{matrix}$ som betyr at $\begin{matrix} S_{n} = \frac{1 - {(\frac{3}{4})}^{n + 1}}{1 - (\frac{3}{4})} . \end{matrix}$ Ettersom $\frac{3}{4} < 1$ blir ${(\frac{3}{4})}^{n}$ mindre og mindre etterhvert som $n$ blir større. Med andre ord må $\begin{matrix} S = \lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \frac{1 - {(\frac{3}{4})}^{n + 1}}{1 - (\frac{3}{4})} = \frac{1}{1 - \frac{3}{4}} = \frac{4}{4 - 3} = 4 . \end{matrix}$ Summen av rekken kan altså skrives $\begin{matrix} A \cdot (\frac{1}{4} + \frac{3}{16} + \frac{9}{64} + \frac{27}{256} + . . .) = \frac{A}{4} \cdot 4 = A . \end{matrix}$ Det betyr at Sierpinski-trekanten har areal lik null ettersom alt det opprinnelige arealet $A$ fjernes etter uendelig mange steg.

Svar:

$\begin{matrix} A \cdot (\frac{1}{4} + \frac{3}{16} + \frac{9}{64} + \frac{27}{256} + . . .) = A . \end{matrix}$ Sierpinski-trekanten har areal lik null.

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.

Visste du at

Pascals trekant, som du kanskje har sett i forbindelse med kombinatorikk, tar følgende form

Hvert tall er altså summen av de to tallene over. Hvis du setter ring rundt alle oddetallene i Pascals trekant vil du se at Sierpinskis trekant dukker opp. Hvorfor tror du dette skjer?

b)

Sidene i trekanten i figur 1 er lik $a$ .

Forklar at omkretsene av de svarte trekantene i figurene 2 − 5 ovenfor er henholdsvis

$3 \cdot \frac{3}{2} \cdot a, 3 \cdot \frac{9}{4} \cdot a, 3 \cdot \frac{27}{8} \cdot a og 3 \cdot \frac{81}{16} \cdot a$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Ved først å uttrykke omkretsen av trekanten i figur 1 kan vi bruke at trekanten som er fjernet i figur 2 må dele sidelengden i den opprinnelige trekanten i to like store biter til å uttrykke omkretsen til trekanten i figur 2. Denne tankegangen kan vi fortsette for å finne omkretsen av Sierpinskis trekant etter vilkårlig mange delinger.

Hvis den opprinnelige trekanten har sidelengde $a$ , vil den ha en omkrets lik $\begin{matrix} O_{0} = 3 a . \end{matrix}$ Ettersom trekanten som er fjernet i figur 2 utgjør nøyaktig $\frac{1}{4}$ av den opprinnelige trekanten må den ha sidelengde lik $\frac{1}{2} a$ . Det betyr at omkretsen av figuren i figur 2 er $\begin{matrix} O_{1} = 3 a + \frac{3}{2} a = \frac{9}{2} a = 3 \cdot \frac{3}{2} a . \end{matrix}$ Siden figur 3 består av tre kopier av figur 2 som er halvert i størrelse må omkretsen av figur 3 være gitt som $\begin{matrix} O_{2} = \frac{3}{2} O_{1} = \frac{3}{2} \cdot 3 \cdot \frac{3}{2} a = 3 \cdot \frac{9}{4} a . \end{matrix}$ Nøyaktig det samme er tilfellet i figur 4 – den består av tre kopier av figur 3 i halvert størrelse. Altså må $\begin{matrix} O_{3} = \frac{3}{2} O_{2} = \frac{3}{2} \cdot 3 \cdot \frac{9}{4} a = 3 \cdot \frac{27}{8} a . \end{matrix}$ Helt tilsvarende må omkretsen av figur $5$ være gitt som $\begin{matrix} O_{4} = \frac{3}{2} O_{3} = \frac{3}{2} \cdot 3 \cdot \frac{27}{8} a = 3 \cdot \frac{81}{16} a . \end{matrix}$

Mer om

Denne oppgaven er om

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske tallfølger.

Visste du at

Sierpinskis trekant er et eksempel på det som man innen matematikken kaller fraktaler. Disse formene er ikke bare ekstremt nyttige innen teknologi, der de brukes til alt fra å generere realistiske fjellkjeder eller til å konstruere gode mobilantenner, de er også viktige innen matematikken. Mens ”Hilbertkurven” kan brukes til å vise at det er mulig å dekke hele planet med en kurve, brukte Georg Cantor en fraktal, som går under navnet ”Cantormengden”, til å studere egenskapen til en spesielt matematisk rom.

Eksempler på andre kjente fraktaler er: Mandelbrotmengden, Julia mengden, Sierpinskiteppet og Kochs snøkrystall.

c)

Vi gjør prosessen som forklart i trinn 2 ovenfor $n$ ganger. Forklar at omkretsen av de svarte trekantene da er lik $3 \cdot {(\frac{3}{2})}^{n} \cdot a$

Forklar at $3 \cdot {(\frac{3}{2})}^{n} \cdot a \to \infty$ når $n \to \infty$

Hva forteller dette om omkretsen til Sierpiński-trekanten?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Ved å legge merke til mønsteret funnet i oppgave $b)$ kan vi uttrykke omkretsen av de sorte trekantene etter $n$ steg.

I oppgave $b)$ fant vi at omkretsen av den første trekanten (figur 1), er lik $O_{0} = 3 a$ . Videre fant vi at

$O_{n} = \frac{3}{2} O_{n - 1} for n = 1, 2, 3, . . . .$

Det betyr at $\begin{matrix} O_{0} & = 3 a \\ O_{1} & = 3 \cdot \frac{3}{2} a \\ O_{2} & = 3 \cdot \frac{9}{4} a = 3 \cdot {(\frac{3}{2})}^{2} a \\ O_{3} & = 3 \cdot \frac{27}{8} a = 3 \cdot {(\frac{3}{2})}^{3} a \\ O_{4} & = 3 \cdot \frac{81}{16} a = 3 \cdot {(\frac{3}{2})}^{4} a \end{matrix}$ og dermed er omkretsen til de sorte trekantene lik $\begin{matrix} O_{n} = 3 \cdot {(\frac{3}{2})}^{n} a \end{matrix}$ etter $n$ steg. Siden $\frac{3}{2} > 1$ følger det at ${(\frac{3}{2})}^{n}$ vokser når $n$ vokser. Altså må $\begin{matrix} \lim_{n \to \infty} O_{n} = 3 a \lim_{n \to \infty} {(\frac{3}{2})}^{n} = \infty . \end{matrix}$ Dette betyr at Sierpinski-trekanten har uendelig stor omkrets.

Svar: Sierpinski-trekanten har uendelig stor omkrets.

Mer om

Denne oppgaven er om

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

For flere forklaringer og eksempler på rekker, se artikkelen Uendelige rekker.

REA3024 2013 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4DBN

a)

Løsningsforslag a)

Cosinus

Sinus

Derivasjon

b)

Løsningsforslag b)

Cosinus

Sinus

Pi (π)

Derivasjon

c)

Løsningsforslag c)

Sinus

Eksponentialfunksjon

Derivasjon

Oppgave 2 (4 poeng) Nettkode: E-4DBR

a)

Løsningsforslag a)

Integrasjon

Brøk

Polynom

b)

Løsningsforslag b)

Faktorisering av uttrykk

Brøk

Logaritme

Integrasjon

Oppgave 3 (4 poeng) Nettkode: E-4DBU

a)

Løsningsforslag a)

Vektor

Parallellogram

b)

Løsningsforslag b)

Vektor

Trekant

Oppgave 4 (3 poeng) Nettkode: E-4DBX

Løsningsforslag

Differensiallikning

Logaritme

Derivasjon

Integrasjon

Eksponentialfunksjon

Oppgave 5 (5 poeng) Nettkode: E-4DBZ

a)

Løsningsforslag a)

Sum

Kvadrattall

Oddetall

b)

Løsningsforslag b)

Sum

Oddetall

Gjennomsnitt

c)

Løsningsforslag c)

Kvadratrot

Oppgave 6 (2 poeng) Nettkode: E-4DC3

Løsningsforslag

Graf

Ekstremalpunkter

Intervall

Vendepunkt

Derivasjon

Oppgave 7 (2 poeng) Nettkode: E-4DC5

Løsningsforslag

Brøk

Matematisk induksjon

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4DC7

a)

Løsningsforslag a)

Prosent