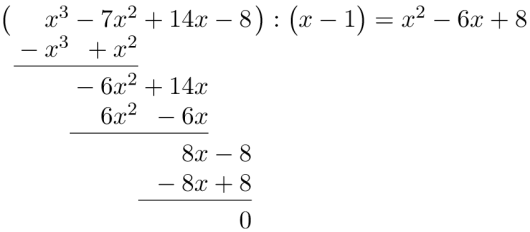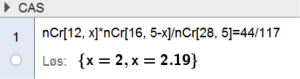Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3022 2014 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger:
Kilder for bilder, tegninger osv.

Alle grafer og figurer: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4CZW

Deriver funksjonene

a)

$f (x) = \ln (x^{2} + x)$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Her skal vi bruke kjerneregelen for derivasjon. Vi ser dette siden det er en annen funksjon inne i ln-funksjonen.

$(\ln (x^{2} + x))' = (x^{2} + x)' \cdot \frac{1}{x^{2} + x}$

Svar: $\frac{2 x + 1}{x^{2} + x}$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på logaritmer, se artikkelen Den naturlige logaritmen.

b)

$g (x) = x \cdot e^{x}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Her bruker vi produktregelen for derivasjon siden uttrykket er to funksjoner multiplisert sammen.

$(u v)' = u' v + u v'$

$(x \cdot e^{x})' = 1 \cdot e^{x} + x \cdot e^{x} = e^{x} (1 + x)$

Svar: $e^{x} (1 + x)$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjonen

For flere forklaringer og eksempler på derivasjon, se artikkelen Å derivere sammensatte uttrykk.

c)

$h (x) = {(x^{2} + 3)}^{4}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Som i oppgave a) bruker vi kjerneregelen igjen. Vi har en funksjon inne i parentesen, og en funksjon utenpå som opphøyer i $4$ .

$((x^{2} + 3)^{4})' = (x^{2} + 3)' \cdot 4 (x^{2} + 3)^{3}$

$(2 x) \cdot 4 (x^{2} + 3)^{3}$

Svar: $8 x (x^{2} + 3)^{3}$ .

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på kjerneregelen, se artikkelen Kjerneregelen - tre eksempler.

Oppgave 2 (5 poeng) Nettkode: E-4D00

Polynomfunksjonen $P$ er gitt ved

$P (x) = x^{3} - 7 x^{2} + 14 x - 8, D_{P} = ℝ$

a)

Det kan vises at alle heltallige løsninger av $P (x) = 0$ går opp i konstantleddet $(- 8)$ .

Bruk dette til å finne et nullpunkt.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Tallene som går opp i $- 8$ er $\pm 1, \pm 2, \pm 4, \pm 8$ . Vi prøver oss frem, og det er naturlig å begynne med de minste absoluttverdiene siden disse er lettere å regne med.

Vi setter inn $1$ først.
$P (1) = 1 - 7 + 14 - 8 = 0$

$x = 1$ gir et nullpunkt. Vi trenger bare ett nullpunkt, så vi er ferdige. Hadde ikke $x = 1$ passet hadde vi prøvd $x = - 1, x = 2, x = - 2$ osv.

Svar: $x = 1$ gir et nullpunkt av $P (x)$ .

Mer om:

Denne oppgaven er om

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på nullpunkt, se artikkelen Nullpunktsetningen - når går divisjonen opp?.

b)

Faktoriser $P (x)$ i førstegradsfaktorer.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi kjenner til en av faktorene, nemlig $x - 1$ . Vi kan sette inn de gjenværende tallene som går opp i $- 8$ , til vi finner to til faktorer. En litt mer elegant løsning er å bruke polynomdivisjon og deretter abc-formelen.

Vi utfører polynomdivisjonen $x^{3} - 7 x^{2} + 14 x - 8 : x - 1$

Vi vet da at $P (x) = (x - 1) (x^{2} - 6 x + 8)$
Vi faktoriserer $(x^{2} - 6 x + 8)$ ved å løse $x^{2} - 6 x + 8 = 0$ med abc-formelen.
$x = \frac{6 \pm \sqrt{36 - 4 \cdot 8}}{2} = \frac{6 \pm 2}{2} = 3 \pm 1$

Altså er $x = 2$ og $x = 4$ nullpunkter av $x^{2} - 6 x + 8$ og dermed også av $P (x)$ .
Dette gir oss faktorene $(x - 2)$ og $(x - 4)$

Svar: $P (x) = (x - 1) (x - 2) (x - 4)$

Mer om:

Denne oppgaven er om

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på polynomdivisjon, se artikkelen Polynomdivisjon - skritt for skritt.

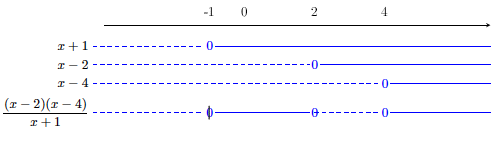
c)

Løs ulikheten $\frac{x^{3} - 7 x^{2} + 14 x - 8}{x^{2} - 1} \geq 0$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi kan tegne fortegnsskjema siden vi har faktorisert store deler av uttrykket i oppgave b). Siden uttrykket har en nevner med mulige nullpunkt må vi se spesielt nøye etter disse når vi løser ulikheten.

Vi deler opp ulikheten i lineære faktorer.

$\frac{x^{3} - 7 x^{2} + 14 x + 8}{x^{2} - 1} \geq 0$

$\frac{(x - 1) (x - 2) (x - 4)}{(x - 1) (x + 1)} \geq 0$

$\frac{(x - 2) (x - 4)}{x + 1} \geq 0$

Vær obs på at når $x = - 1$ OG $x = 1$ er ikke funksjonen definert.

Vi tegner fortegnslinjen for uttrykket.

Husk, $x = - 1$ og $x = 1$ er ikke en løsning, da funksjonen ikke er definert der.

Svar: $\frac{(x - 2) (x - 4)}{x + 1} \geq 0$ når $x \in ⟨ - 1, 1 ⟩ \cup ⟨ 1, 2] \cup [4, \to ⟩$

Mer om:

Denne oppgaven er om

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.

fortegnslinje

, ulikhet og

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på fortegnslinje, se artikkelen Fortegnsskjema.

Oppgave 3 (4 poeng) Nettkode: E-4D04

Vektorene $\vec{a} = [- 2, 1]$ , $\vec{b} = [3, 6]$ og $\vec{c} = [k - 1, 4]$ er gitt, der $k \in ℝ$ .

a)

Bestem $- 2 \vec{a} + \vec{b}$ og $\vec{a} \cdot \vec{b}$ ved regning.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi regner ut verdiene med vanlige regler for vektorregning, altså for

$\vec{u} = [x_{1}, y_{1}], \vec{v} = [x_{2}, y_{2}]$

og $s, t \in ℝ$ , har vi

$s \cdot u + t \cdot v = [{s \cdot x}_{1} + t \cdot x_{2}, s \cdot y_{1} + t \cdot y_{2}]$

$- 2 \vec{a} + \vec{b} = - 2 [- 2, 1] + [3, 6] = [7, 4]$

$\vec{a} \cdot \vec{b} = - 2 \cdot 3 + 1 \cdot 6 = 0$

Svar: $- 2 \vec{a} + \vec{b} = [7, 4]$ og $\vec{a} \cdot \vec{b} = 0$

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler på vektorer, se artikkelen Addisjon av vektorer.

b)

Bestem $k$ slik at $\vec{b} ∥ \vec{c}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

$\vec{b} ∥ \vec{c}$ betyr at også $\vec{a} \cdot \vec{c} = 0$ , siden $\vec{b} ⊥ \vec{a}$ som vi viste i a).

$\vec{a} \cdot \vec{c} = 0$

$[- 2, 1] \cdot [k - 1, 4] = - 2 (k - 1) + 4 = 0$

$- 2 k = - 6$

$k = 3$

Svar: $k = 3$ .

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler på vektorer, se artikkelen Parallelle vektorer.

c)

Bestem $k$ slik at $|\vec{c}| = |2 \vec{a}|$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi kan regne ut $| \vec{c} |$ og $| 2 \vec{a} |$ . Deretter løser vi ligningen $| \vec{c} | = | 2 \vec{a} |$ . Lengden av en vektor er gitt ved

$u = [x, y] \Rightarrow | u | = \sqrt{x^{2} + y^{2}}$

$| \vec{c} | = \sqrt{(k - 1)^{2} + 4^{2}} = \sqrt{16 + (k - 1)^{2}}$

$| 2 \vec{a} | = \sqrt{(- 4)^{2} + 2^{2}} = \sqrt{16 + 2^{2}}$

$| \vec{c} | = | 2 \vec{a} |$ når $(k - 1)^{2} = 2^{2}$

$k^{2} - 2 k + 1 = 4$

$k^{2} - 2 k - 3 = 0$

$k = \frac{2 \pm \sqrt{2^{2} - 4 \cdot (- 3)}}{2} = \frac{2 \pm \sqrt{16}}{2} = \frac{2 \pm 4}{2} = 1 \pm 2$

Svar: $k = - 1$ og $k = 3$ .

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler på vektorer, se artikkelen Lengden til en vektor.

Oppgave 4 (4 poeng) Nettkode: E-4D08

Funksjonen $f$ er gitt ved

$f (x) = 3 x^{4} - 6 x^{2}, D_{f} = ℝ$

a)

Bestem nullpunktene til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi skal finne nullpunktene til et fjerdegradspolynom. Det finnes en formel som gjør dette direkte, men den er ikke et læremål i R1 og vi må finne et alternativ. Et alternativ er å forsøke å redusere problemet foran oss til noe vi kan løse. Vi forsøker å faktorisere ut felles ledd.

Vi faktoriserer $f (x)$ .

$f (x) = 3 x^{2} (x^{2} - 2)$

Vi deler $x^{2} - 2$ opp i lineære faktorer, enten ved abc-formelen eller ved direkte bruk av konjugatsetningen.

$f (x) = 3 x^{2} (x - \sqrt{2}) (x + \sqrt{2})$

Vi får nullpunktene $x = \sqrt{2}$ , $x = - \sqrt{2}$ og $x = 0$ . Merk at fjerdegradspolynomet bare har tre forskjellige røtter, fordi $x = 0$ er en rot av multiplisitet $2$ .

Svar: $f$ har nullpunkter i $x = \sqrt{2}$ , $x = - \sqrt{2}$ og $x = 0$

Mer om:

Denne oppgaven er om

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på polynomer, se artikkelen Definisjon av et polynom.

b)

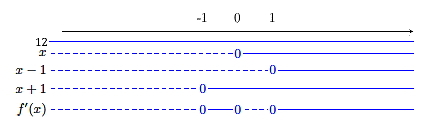
Bestem $f' (x)$ . Bestem eventuelle topp- og bunnpunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi skal bestemme topp- og bunnpunktene til $f$ . Vi finner disse ved å løse $f' (x) = 0$ . For å se hva slags ekstremalpunkt vi finner er det nyttig å tegne en fortegnslinje.

$f' (x) = 4 \cdot 3 x^{3} - 2 \cdot 6 x$

$f' (x) = 12 x^{3} - 12 x = 12 x (x^{2} - 1)$

Vi faktoriserer $x^{2} - 1$ på samme måte som vi faktoriserte $x^{2} - 2$ i deloppgave a).

$f' (x) = 12 x (x - 1) (x + 1)$

Vi tegner fortegnslinjen til $f' (x)$ .

Fra fortegnslinjen ser vi at $x = - 1$ og $x = 1$ gir bunnpunkt, og $x = 0$ gir et toppunkt. Vi regner ut funksjonsverdien i punktene. $f (1) = - 3, f (- 1) = - 3, f (0) = 0$

Svar: $f' (x) = 12 x^{3} - 12 x$ . $f$ har toppunkt i $(0, 0)$ og bunnpunkt i $(- 1, - 3)$ og $(1, - 3)$ .

Mer om:

Denne oppgaven er om

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkter

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.

fortegnslinje

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

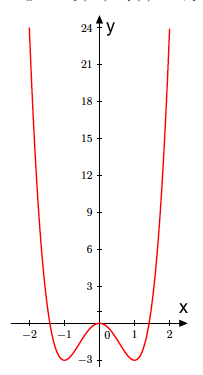
c)

Tegn en skisse av grafen til $f$ for $x \in ⟨- 2, 2⟩$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

For å skissere grafen kan vi bruke ekstremalpunktene og nullpunkt fra forrige oppgave. Vi skal bare skissere i intervallet $x \in < - 2, 2 >$ så vi kan gjerne regne ut verdien i endepunktene også.

Vi regner ut $f (- 2) = f (2) = 24$ , $f (- 1) = f (1) = - 3$ , og $f (0) = 0$ .

Mer om:

Denne oppgaven er om

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunkter

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

Oppgave 5 (2 poeng) Nettkode: E-4D0D

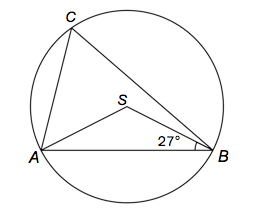
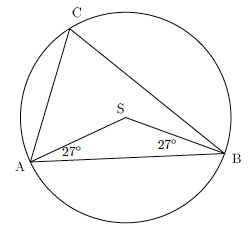
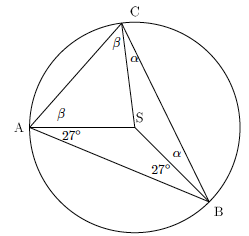
En $Δ A B C$ er innskrevet i en sirkel med sentrum $S$ der $∠ A B S = 27^{\circ}$ . Bestem $∠ A C B$ ved et geometrisk resonnement.

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Det oppgis bare en vinkel, så vi må bruke våre geometrikunnskaper om vinkelsummer og likebeinte trekanter og lignende til å bestemme de andre vinklene. Både $A S$ og $B S$ er like lange som radiusen i sirkelen. Dermed er $△ A B S$ likebeint, og $∠ S A B = ∠ A B S = 27^{\circ}$ . For å finne en sammenheng mellom $△ A B S$ og $△ A B C$ skisserer vi to løsninger. Det første alternativet bruker sentralvinkelteoremet, og det andre bruker bare vinkelsummen i en trekant.

Alternativ 1, løsning og svar:

$∠ B S A = 180^{\circ} - 27^{\circ} - 27^{\circ} = 126^{\circ}$

Sentralvinkelteoremet gir oss at $∠ A C B = \frac{1}{2} ∠ B S A = 63^{\circ}$

Alternativ 2, løsning og svar:

Vi trekker linjen $C S$ og gir de ukjente vinklene navn, som vist under.

Vinkelsummen av $△ A B C = 180^{\circ} = 27^{\circ} + 27^{\circ} + 2 α + 2 β$

$90^{\circ} - 27^{\circ} = α + β$

$∠ A C B = α + β = 63^{\circ}$

Mer om:

Denne oppgaven er om

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Vinkelsum

Summen av alle vinklene i en mangekant.

Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader.

vinkelsummen i en trekant

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

For flere forklaringer og eksempler på sirkeler, se artikkelen Alt om sirkel.

Oppgave 6 (3 poeng) Nettkode: E-4D0F

La $p$ være et oddetall større enn $1$ .

a)

Forklar at $\frac{p + 1}{2}$ og $\frac{p - 1}{2}$ begge er hele tall.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Oppgaven sier forklar. Det holder ikke å komme med eksempler eller lignende her. Siden $p$ er et oddetall er $p + 1$ og $p - 1$ partall.

Svar: Vi får oppgitt at $p > 1$ og at $p$ er et oddetall. Siden $p$ er et oddetall er både $p + 1$ og $p - 1$ partall. Altså er begge tallene dividerbar med 2, så $\frac{p + 1}{2}$ og $\frac{p - 1}{2}$ er heltall.

Mer om:

Denne oppgaven er om

Partall

Tallene 2, 4, 6, 8 og 10 er eksempler på partall.
Partall er heltall som delt med 2 gir et heltall som svar.

Alle partall kan skrives på formen 2n, der n er et helt tall.

Et heltall som ikke er partall er et oddetall.

partall

Oddetall

Tallene 1, 3, 5, 7, 9 og 11 er eksempler på oddetall.
Oddetall er heltall hvor svaret ikke blir et heltall når de deles med 2.

Alle oddetall kan skrives på formen 2n+1, der n er et helt tall.

Et heltall som ikke er oddetall er partall.

oddetall

For flere forklaringer og eksempler på bevis, se artikkelen Direkte bevis.

b)

Regn ut ${(\frac{p + 1}{2})}^{2} - {(\frac{p - 1}{2})}^{2}$ .

Bruk resultatet til å skrive $151$ som differansen mellom to kvadrattall.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Her kan vi starte med å multiplisere ut parentesene og sette på felles brøkstrek. Deretter kan vi forkorte uttrykket etter beste evne og håpe det ser pent ut.

$(\frac{p + 1}{2})^{2} - (\frac{p - 1}{2})^{2} = \frac{(p + 1)^{2} - (p - 1)^{2}}{4} = \frac{p^{2} + 2 p + 1 - (p^{2} - 2 p + 1)}{4}$
Vi stryker felles ledd og står bare igjen med $\frac{4 p}{4} = p$
$(\frac{p + 1}{2})^{2} - (\frac{p - 1}{2})^{2} = p$

Vi skal skrive $151$ som differansen mellom to kvadrattall. Vi merker oss at $151$ er et oddetall som er rikelig større enn $1$ . Vi kan da sette inn $151$ for $p$ i formelen. Formelen holder uansett, men siden vi har et oddetall større enn 1 blir begge leddene heltall.

$151 = (\frac{151 + 1}{2})^{2} - (\frac{151 - 1}{2})^{2}$

$151 = 76^{2} - 75^{2}$

Svar: $(\frac{p + 1}{2})^{2} - (\frac{p - 1}{2})^{2} = p$ , og $151 = 76^{2} - 75^{2}$ .

Mer om:

Denne oppgaven er om

Kvadrattall

Et kvadrattall er det positive heltallet som vi får når et heltall multipliserers med seg selv.

Eksempel: 25 er et kvadrattall, fordi $5 \cdot 5 = 25$

kvadrattall

Oddetall

oddetall

Partall

partall

Første kvadratsetning

Første kvadratsetning sier at

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .

første kvadratsetning

Andre kvadratsetning

Andre kvadratsetning sier at

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ .

andre kvadratsetning

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på kvadratsetningene, se artikkelen Kvadratsetningene.

Visste du at:

Denne formelen er morsom i seg selv, men skriver vi den om litt har den en annen bruk. $p + (\frac{p - 1}{2})^{2} = (\frac{p + 1}{2})^{2}$ ligner nesten på Pytagoras læresetning. For alle oddetall $p$ som er et kvadrattall vil dette gi oss Pytagoreiske tripler. Disse triplene vil alle ha to ledd med avstand $1$ . Det laveste eksempelet er $p = 9 = 3^{2}$ . Vi får $9 + (\frac{9 - 1}{2})^{2} = (\frac{9 + 1}{2})^{2}$ , eller $3^{2} + 4^{2} = 5^{2}$ . Kvadrerer vi $5$ i stedet får vi $5^{2} + 12^{2} = 13^{2}$ . På denne måten kan vi finne Pytagoreiske tripler på formen $p^{2} + a^{2} = (a + 1)^{2}$ for alle oddetall $p > 1$ .

Oppgave 7 (2 poeng) Nettkode: E-4D0I

Funksjonen $h$ er gitt ved

$h (x) = x^{x}, x > 0$

a)

Forklar at vi kan skrive

$h (x) = e^{x \cdot \ln x}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Her er det viktig å huske at $f = e^{ln f}$ . Uten dette kommer vi ingen vei. Heldigvis har vi et svar å gå etter, så selv om vi ikke husker alt går det an å få hint ved å se i oppgaven.

I denne oppgaven betyr det at $x = e^{ln x}$ .

Svar: For alle funksjoner $f$ er $e^{ln (f)} = f$ . Vi bruker også potensregelen ln ${(a^{p})}^{q} = a^{p \cdot q}$ . Vi har dermed også for $h (x)$ at

$x^{x} = {(e^{\ln x})}^{x} = e^{x \ln x}$

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på logaritmer, se artikkelen Logaritmelikninger.

b)

Bestem $h' (x)$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

$x^{x}$ er ikke spesielt kjekt å derivere. Det er et stort hint at vi omskrev $h (x)$ i oppgave a). Det er derfor fristende å forsøke å derivere $h (x)$ slik vi har omskrevet den.

$h' (x) = (e^{x \cdot ln (x)})'$

Når vi deriverer $e^{f}$ for en funksjon $f$ får vi $f' \cdot e^{f}$ . I vårt tilfelle er $f = x$ ln $x$ .

$h' (x) = (x \cdot ln (x))' \cdot e^{x \cdot ln (x)}$

$(x \cdot ln (x))' = 1 \cdot \ln x + x \cdot \frac{1}{x} = \ln x + 1$

Vi setter inn dette i uttrykket for $h' (x)$ .

$h' (x) = (ln x + 1) \cdot e^{x \cdot ln (x)} = (ln x + 1) \cdot x^{x}$

Svar: $h' (x) = (ln x + 1) \cdot x^{x}$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

DEL 2 Med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4D0L

Tre punkter $A (1, 3)$ , $B (5, - 1)$ og $C (4, 4)$ er gitt.

a)

Bestem et punkt $D$ på $y$ -aksen slik at $\vec{C D} ∥ \vec{B A}$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Alle punkt på $y$ -aksen har koordinat på formen $(0, b)$ . Vi vil finne et slikt punkt slik at vektorene blir parallelle.

La $D (0, b)$ være et generelt punkt på $y$ -aksen.

$\vec{C D} = [- 4, b - 4]$

$\vec{B A} = [1 - 5, 3 - (- 1)] = [- 4, 4]$

Siden $x$ -koordinatene er like i vektorene (og ikke null) må også $y$ -koordinatene være like. Dermed er $b - 4 = 4$

$b = 8$ .

Svar: $D (0, 8)$

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler på vektorer, se artikkelen Parallelle vektorer.

b)

La $M$ være midtpunktet på $B C$ . Bestem koordinatene til $M$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi kjenner til koordinatene til $B$ og $C$ , så vi kan regne ut $\vec{B C}$ . Dermed kan vi og gå halve $\vec{B C}$ , som tar oss til $M$ om vi starter i $B$ .

Vektoren fra origo til $M$ er lik vektorsummen vi får ved å først gå fra origo til $B$ , og gå halve veien til $C$ .

$\vec{B C} = [4 - 5, 4 - (- 1)] = [- 1, 5]$
$\vec{O B} = [5, - 1]$
$\vec{O M} = O \vec{B} + \frac{1}{2} \vec{B C} = [5, - 1] + [- \frac{1}{2}, \frac{5}{2}]$
$\vec{O M} = [5 - \frac{1}{2}, - 1 + \frac{5}{2}]$
$\vec{O M} = [\frac{9}{2}, \frac{3}{2}]$

Svar: $M (\frac{9}{2}, \frac{3}{2})$

Mer om:

Denne oppgaven er om

Origo

I et koordinatsystem står to akser vinkelrett på hverandre. Punktet der aksene møtes kalles origo. Origo har koordinatene (0,0).

origo

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler vektorer, se artikkelen Addisjon av vektorer.

c)

Punktet $P$ er gitt slik at $\vec{A M} = \frac{1}{3} \vec{M P}$ .

Bestem ved regning koordinatene til $P$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi setter inn punkt $M$ som vi regnet ut i oppgave b) og bruker dette til å løse ligningen for det ukjente punktet $P$ .

$\vec{A M} = [\frac{9}{2} - 1, \frac{3}{2} - 3] = [\frac{7}{2}, - \frac{3}{2}]$

$3 \cdot \vec{A M} = \vec{M P}$

$\vec{M P} = [\frac{21}{2}, - \frac{9}{2}]$
La $P (α, β)$ være et generelt punkt i planet. Da er $\vec{M P} = [α - \frac{9}{2}, β - \frac{3}{2}]$

$\vec{M P} = [\frac{21}{2}, - \frac{9}{2}] = [α - \frac{9}{2}, β - \frac{3}{2}]$

$α - \frac{9}{2} = \frac{21}{2}$ og $β - \frac{3}{2} = - \frac{9}{2}$

$α = \frac{30}{2}$ og $β = - \frac{6}{2}$

$(α, β) = (\frac{30}{2}, - \frac{6}{2}) = (15, - 3)$

Svar: $P$ har koordinater $(15, - 3)$ .

Mer om:

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Like vektorer.

Oppgave 2 (6 poeng) Nettkode: E-4D0P

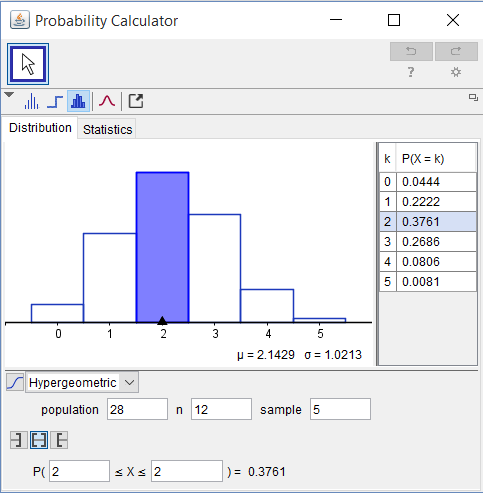
I en klasse er det 12 gutter og 16 jenter. Det skal trekkes ut en gruppe på 5 elever på en tilfeldig måte.

a

Bestem sannsynligheten for at det blir med akkurat én gutt i gruppen.

Løs oppgaven her

Løsningsforslag a

Jeg tenker:

Vi trekker elevene uten tilbakelegging. Vi trekker $5$ elever fra et utvalg på totalt $28$ . Sannsynligheten for å trekke akkurat $1$ gutt er antall måter å trekke $1$ gutt blant $12$ , multiplisert med antall måter å trekke $4$ jenter blant $16$ , delt på totalt antall kombinasjoner.

$\frac{(\begin{matrix} 12 \\ 1 \end{matrix}) \cdot (\begin{matrix} 16 \\ 4 \end{matrix})}{(\begin{matrix} 28 \\ 5 \end{matrix})} = \frac{2}{9} \approx 0, 22$

Svar: Sannsynligheten for akkurat $1$ gutt er $\frac{2}{9}$

Mer om:

Denne oppgaven er om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

For flere forklaringer og eksempler på sannsynlighet, se artikkelen Repetisjon av begreper.

b)

Sannsynligheten er $\frac{44}{117}$ for at et bestemt antall gutter blir med i gruppen.

Hvor mange gutter blir det da med i gruppen?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi kan enten prøve oss frem her. Da regner vi på samme måte som i oppgave a). Vi må maks gjennom $4$ like utregninger for å finne svaret, så dette er mulig. Et annet alternativ er å bruke Geogebra sin sannsynlighetskalkulator. Vi stiller den inn på hypergeometisk fordeling, med populasjon $= 28$ , $n = 12$ (antall gutter), sample $= 5$ . Dette gir oss et stolpediagram med sannsynligheten for hvert antall gutter. (se skjermbildet under)

CAS:

Bare den heltallige løsningen er relevant.

Svar: 2 gutter.

Alternativ løsning

Et tredje alternativ er å bruke CAS til å løse likningen:

$\frac{(\begin{matrix} 12 \\ x \end{matrix}) \cdot (\begin{matrix} 16 \\ 5 - x \end{matrix})}{(\begin{matrix} 28 \\ 5 \end{matrix})} = \frac{44}{117}$

Dette gir svaret $x = 2$ .

Mer om:

Denne oppgaven er om

Sannsynlighet

sannsynlighet

For flere forklaringer og eksempler på sannsynlighet, se artikkelen Hvordan finner vi sannsynligheten?.

c)

Arne og Betsy går i klassen. Vi definerer følgende hendelser:

A: Arne blir med i gruppen.

B: Betsy blir med i gruppen.

Forklar at $P (A | B) = \frac{(\begin{matrix} 1 \\ 1 \end{matrix}) \cdot (\begin{matrix} 26 \\ 3 \end{matrix})}{(\begin{matrix} 27 \\ 4 \end{matrix})}$ og bestem sannsynligheten.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Her ser vi ikke lengre på mengdene {gutt} og {ikke gutt}, men på {Arne} og {ikke Arne}. Når Betsy allerede er valgt er det $4$ elever som skal velges blant $27$ . Det er altså $(\begin{matrix} 27 \\ 4 \end{matrix})$ totale kombinasjoner igjen.

Det finnes akkurat $(\begin{matrix} 1 \\ 1 \end{matrix}) = 1$ måte å velge Arne. Det finnes $(\begin{matrix} 26 \\ 3 \end{matrix})$ måter å velge tre andre elever fra de resterende $26$ elevene som ikke er Arne eller Betsy.

$P (A | B) = \frac{(\begin{matrix} 1 \\ 1 \end{matrix}) \cdot (\begin{matrix} 26 \\ 3 \end{matrix})}{(\begin{matrix} 27 \\ 4 \end{matrix})} = \frac{4}{27}$

Svar: $P (A | B) = \frac{4}{27}$

Mer om:

Denne oppgaven er om

Betinget sannsynlighet

Den betingede sannsynligheten $P (A | B)$ er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.

$P (A | B) = \frac{P (A \cap B)}{P (B)}$ .

betinget sannsynlighet

For flere forklaringer og eksempler på sannsynlighet, se artikkelen Betinget sannsynlighet.

Oppgave 3 (6 poeng) Nettkode: E-4D0T

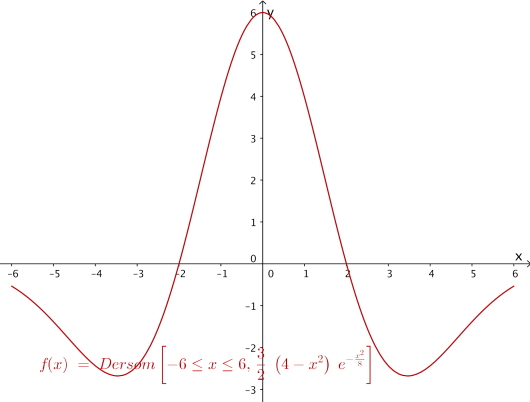
Funksjonen $f$ er gitt ved

$f (x) = 6 x \cdot e^{- \frac{x^{2}}{8}}, D_{f} = ℝ$

a)

Bruk produktregelen og kjerneregelen til å vise at

$f' (x) = \frac{3}{2} (4 - x^{2}) \cdot e^{- \frac{x^{2}}{8}}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Dette er en rett frem regneoppgave der det er viktig å ta ting et steg av gangen, og holde tungen rett i munnen.

$f (x) = 6 x \cdot e^{- \frac{x^{2}}{8}}$

Når vi deriverer $e^{- \frac{x^{2}}{8}}$ bruker vi kjerneregelen. $(e^{u})' = u' \cdot e^{u}$ .
Vi har $u = - \frac{x^{2}}{8}$ som kjerne, med $u' = - \frac{x}{4}$

$f' (x) = (6 x)' \cdot e^{- \frac{x^{2}}{8}} + 6 x \cdot (e^{- \frac{x^{2}}{8}})'$

$f' (x) = 6 \cdot e^{- \frac{x^{2}}{8}} + 6 x \cdot (- \frac{x}{4}) \cdot e^{- \frac{x^{2}}{8}}$

$f' (x) = 6 \cdot e^{- \frac{x^{2}}{8}} - \frac{6 x^{2}}{4} \cdot e^{- \frac{x^{2}}{8}}$

$f' (x) = (6 - \frac{3 x^{2}}{2}) \cdot e^{- \frac{x^{2}}{8}}$

$f' (x) = \frac{3}{2} (4 - x^{2}) \cdot e^{- \frac{x^{2}}{8}}$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen.

b)

Tegn grafen til $f'$ for $x \in ⟨- 6, 6⟩$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Siden dette er på del 2 tegner vi i et digitalt verktøy, for eksempel Geogebra. Vi må huske å begrense området til $x \in < - 6, 6 >$ .

Vi skrive inn kommandoen Funksjon[<Funksjon>, <Start>, <Slutt>] inn i kommandofeltet.

Dessuten bytter vi ut <Funksjon> med $(3 / 2) (4 - x^2) e^(- ((x^2) / 8))$ , og <Start> med $- 6$ og <Slutt> med $6$ .

Svar:

Mer om:

Denne oppgaven er om

Graf

grafer

For flere forklaringer og eksempler på grafer, se artikkelen Fra en funksjon til en graf.

c)

Bruk grafen til $f'$ til å bestemme eventuelle topp-, bunn- og vendepunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi tegnet $f' (x)$ i forrige deloppgave. Der $f' (x) = 0$ har $f (x)$ ekstremalpunkt. Der $f' (x)$ har ekstremalpunkt er $f ″ (x) = 0$ , som betyr at $f (x)$ har vendepunkt.

Vi ser at $f' = 0$ i $x = - 2$ og $x = 2$ . Siden $f' < 0$ før $x = - 2$ og $f' > 0$ etter $x = - 2$ gir dette et bunnpunkt. Motsatt gir $x = 2$ et toppunkt. Der grafen til $f' (x)$ har ekstramalpunkt er $f ″ (x) = 0$ . Det skjer i $x = 0$ og $x = \pm 3, 46$ .

Svar: $f$ har toppunkt i $(2, f (2)) = (2, 7.28)$ , og bunnpunkt i $(- 2, f (- 2)) = (- 2, - 7.28)$ . $f$ har tre vendepunkt i intervallet
1) $(0, f (0)) = (0, 0)$
2) $(- 3.46, f (- 3.46)) = (- 3.46, - 4.65)$
3) $(3.46, f (3.46)) = (3.46, 4.65)$

Mer om:

Denne oppgaven er om

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

topppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

For flere forklaringer og eksempler på vendepunkter, se artikkelen Vendepunkt og vendetangent.

Oppgave 4 (6 poeng) Nettkode: E-4D0Y

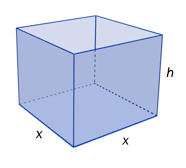
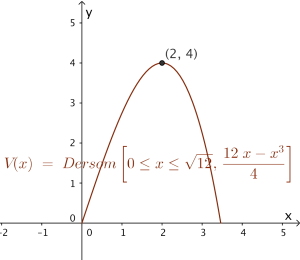
Vi skal lage et kar med form som et rett prisme uten lokk. Grunnflaten skal være et kvadrat med side $x$ dm, og karet skal ha høyde $h$ dm. Vi vil lage karet slik at det samlede overflatearealet blir 12 dm² .

a)

Forklar at $x^{2} + 4 x h = 12$ . Bestem et uttrykk for $h$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi får oppgitt at overflatearealet til karet skal være $12$ dm. Tallet $12$ dukker også opp i ligningen vi skal forklare. Derfor er det naturlig å tenke at vi kan uttrykke overflaten av karet med $x$ og $h$ for å løse oppgaven.

Overflatearealet til figuren er $12$ dm $^{2}$ . Overflaten består av en bunn, fire sider, og ikke noe tak. Altså er overflatearealet $A_{bunn} + 4 A_{side}$
Bunnen har areal $x^{2}$ . En side har areal $x \cdot h$ .
$12 = x^{2} + 4 x h$

Vi isolerer $h$ .

$h = \frac{12 - x^{2}}{4 x}$

Svar: $h = \frac{12 - x^{2}}{4 x}$ .

Mer om:

Denne oppgaven er om

Overflate

Med overflate av en tredimensjonal figur, for eksempel et prisme eller en sylinder, menes summen av arealene til alle flatene som den tredimensjonale figuren er satt sammen av.

overflate

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

For flere forklaringer og eksempler på overflateareal, se artikkelen Overflatearealet til en terning.

b)

Bestem hvilke verdier $x$ kan ha.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Her er det snakk om hvilke mulige verdier av $x$ som fortsatt gir den figuren oppgaven beskriver. Negative verdier gir ingen sidelengde, for eksempel. Det blir heller ikke mye til kar om høyden er $0$ .

Vi skal løse $12 - x^{2} > 0$ . $x$ kan ikke være null eller mindre. Om $x$ er null blir det ingen boks. Det samme gjelder om $h = 0$ . Om $x \geq \sqrt{12}$ blir $h \leq 0$ . Dermed er $x \in < 0, \sqrt{12} >$

Svar: $x \in < 0, \sqrt{12} >$ .

Mer om:

Denne oppgaven er om

Definisjonsmengde

En funksjon tar verdier fra en bestemt mengde, og denne mengden kalles definisjonsmengden til funksjonen.

Eksempel:

$f (x) = \frac{1}{x} f o r x \in (0, \infty)$

har definisjonsmengde $(0, \infty)$ . Merk at funksjonen ikke kan være definert i $x = 0$ fordi vi ikke kan dele på $0$ .

definisjonsmengde

For flere forklaringer og eksempler på definisjonsmengde, se artikkelen Definisjons- og verdimengde.

c)

Bestem et uttrykk for volumet $V (x)$ av karet.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Volumet av en boks er grunnflate $\cdot$ høyde.

$V (x) = x^{2} \cdot h$

Vi setter inn uttrykket for $h$ som vi fant i oppgave a).

$V (x) = x^{2} \cdot (\frac{12 - x^{2}}{4 x})$

$V (x) = \frac{12 x - x^{3}}{4}$

Svar: $V (x) = \frac{12 x - x^{3}}{4}$ .

Mer om:

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

For flere forklaringer og eksempler på volum, se artikkelen Tom forteller om volum.

d)

Vi ønsker å fylle vann i karet. Bestem ved regning $x$ slik at karet rommer mest mulig vann.

Hvor mange liter blir det da plass til?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker:

Vi kjenner til en formel for volumet av karet. Vi leter etter toppunktet til $V (x)$ .

Vi finner toppunktet til $V (x)$ , enten i Geogebra, eller ved å løse $V' (x) = 0$ .
$V' (x) = 3 - \frac{3}{4} x^{2} = \frac{3}{4} (4 - x^{2}) = \frac{3}{4} (2 - x) (2 + x)$
$x = \pm 2$ , men vi ser bare etter positive $x$ -verdier. $V (x)$ har et ekstremalpunkt i $(2, V (2)) = (2, 4)$ .

Husk at $4$ dm $^{3} = 4$ L, ettersom det spørres etter liter i oppgaven. For å se at det er et toppunkt kan vi tegne grafen i Geogebra, eller lage et fortegnsskjema. Vi tegner grafen i GeoGebra. Først skriver vi inn funksjonen og deretter velger

Ekstremalpunkt[ <Funksjon>, <Start>, <Slutt> ]

Vi får:

$V (x)$ har et toppunkt i $(2, V (2)) = (2, 4)$ .

Svar: Volumet er størst når $x = 2$ . Da er det plass til $4$ L vann i karet.

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

topppunkt

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.

fortegnsskjema

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Oppgave 5 (7 poeng) Nettkode: E-4D14

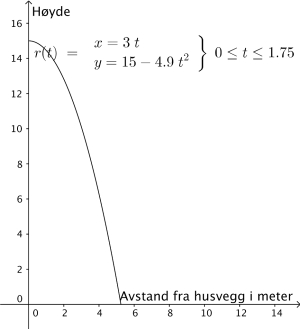
En liten ball triller horisontalt utfor et flatt tak, 15,0 m over bakken.

Posisjonsvektoren til ballen $t$ sekunder etter at den har forlatt taket, er

$\vec{r} (t) = [3 t, 15 - 4, 9 t^{2}]$

a)

Hvor lang tid tar det før ballen treffer bakken?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Ballen begynner å falle ved $t = 0$ , $15$ meter over bakken. Andrekoordinaten beskriver høyden til ballen. Ballen treffer bakken når $y$ -koordinaten er null.

Vi løser ligningen $15 - 4, 9 t^{2} = 0$
$t = \pm 1, 75$

Vi ser bare etter positive løsninger, altså treffer ballen bakken etter $1, 75$ sekunder.

Svar: Ballen treffer bakken etter $1, 75$ sekunder.

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsfunksjon

For flere forklaringer og eksempler på posisjonsvektor, se artikkelen Stedvektor (posisjonsvektor).

b)

Tegn grafen til $\vec{r}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Digitale verktøy som GeoGebra har ofte en måte å tegne parametriske kurver.

Vi tegner den parametriske kurven i GeoGebra med kommandoen

Kurve[ <Uttrykk>, <Uttrykk>, <Parametervariabel>, <Start>, <Slutt> ]

$Kurve [3 t, 15 - 4.9 t^{2}, t, 0, 1.75]$

Husk å stille inn antall desimaler.

Svar:

Mer om:

Denne oppgaven er om

Graf

grafer

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

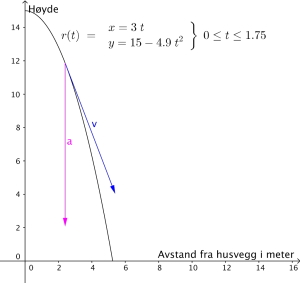
c)

Bestem farten til ballen etter $0, 8$ s. Tegn inn fartsvektoren $\vec{v} (0, 8)$ i det aktuelle punktet på grafen til $\vec{r}$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi kan finne en fartsvektor ved å derivere hvert ledd i posisjonsvektoren $\vec{r} (t)$ . Deretter kan vi finne størrelsen på fartsvektoren etter $0, 8$ sekund.

Vi finner $\vec{r}' (t) = \vec{v} (t) = [3, - 2 \cdot 4, 9 t] = [3, - 9, 8 t]$

$\vec{v} (0, 8) = [3, - 7.84]$

Farten til ballen etter $0, 8$ sekund er $| \vec{v} (0, 8) | \approx 8, 39$ m/s For å tegne fartsvektoren i GeoGebra trenger vi et start, og sluttpunkt. Vi starter i $\vec{r} (0, 8)$ , og slutter i $\vec{r} (0, 8) + \vec{v} (0, 8)$ . På denne måten får vektoren riktig størrelse, i tillegg til retning.

Vektor $[r (0.8), r (0.8) + (3, - 7.84)]$

$| \vec{v} (0, 8) | = \sqrt{3^{2} + (- 7, 84)^{2}} \approx 8, 39$

Svar: Farten etter $0, 8$ sekund er $| \vec{v} (0, 8) | \approx 8, 39$ m/s.

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av vektorfunksjoner 1 - Parameterframstilling.

d)

Bestem akselerasjonen $\vec{a} (t)$ . Tegn inn akselerasjonsvektoren $\vec{a} (0, 8)$ i det aktuelle punktet på grafen til $\vec{r}$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker:

Vi finner akselerasjonsvektoren ved å derivere hvert ledd i fartsvektoren.

$\vec{a} (t) = \vec{v}' (t) = [0, - 9, 8]$ .

For å tegne inn akselerasjonsvektoren bruker vi samme fremgangsmåte som for fartsvektoren.

Vi trenger et startpunkt og et sluttpunkt. Vi starter i $\vec{r} (0, 8)$ og ender i $\vec{r} = (0, 8) + \vec{a} (0, 8)$ .

I GeoGebra velger vi kommandoen

Vektor[ <Startpunkt>, <Sluttpunkt> ]

Vi skriver inn Vektor $[r (0.8), r (0.8) + (0, - 9.8)]$ for å plotte vektoren.

Svar: $\vec{a} (t) = [0, - 9, 8]$ .

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av vektorfunksjoner 2.

Oppgave 6 (5 poeng) Nettkode: E-4D19

Vi skal løse likningen nedenfor med hensyn på $x$

$n^{n} \cdot {(\frac{x}{n})}^{\lg x} = x^{n}, x > 0, n > 0$

a)

Vis at denne likningen kan omformes til

$\lg {(\frac{x}{n})}^{\lg x} = \lg {(\frac{x}{n})}^{n}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi får oppgitt hva svaret skal bli, og vi ser at vi må ta logaritmen av begge sider en gang.

Svar: $n^{n} (\frac{x}{n})^{lg x} = x^{n}$
Vi deler på $n^{n}$ på begge sider. $(\frac{x}{n})^{lg x} = (\frac{x}{n})^{n}$
Tar vi logaritmen av hver side har vi uttrykket vi leter etter. lg $\lg (\frac{x}{n})^{lg x} = \lg {(\frac{x}{n})}^{n}$

Mer om:

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på logaritmer, se artikkelen Logaritmelikninger.

b)

Vis at likningen videre kan skrives

$(\lg x - n) \cdot (\lg x - \lg n) = 0$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Igjen får vi oppgitt hva det endelige uttrykket skal bli. Vi har logaritmeuttrykk med divisjon, og vi skal ende opp med logaritmeuttrykk trukket fra hverandre. Heldigvis har vi en regneregel som hjelper oss med dette.

Svar: Vi bruker først at $\lg a^{b} = b \cdot \lg a$ . Likningen vår omformes slik:

$\lg (\frac{x}{h})^{lg x} = \lg {(\frac{x}{n})}^{n}$ $\lg x \cdot \lg \frac{x}{n} = n \cdot \lg \frac{x}{n}$

$\lg x \cdot \lg \frac{x}{n} - n \cdot \lg \frac{x}{n} = 0$

$(\lg x - n) \cdot \lg \frac{x}{n} = 0$

Vi bruker nå logaritmeregelen at $\lg \frac{a}{b} = \lg a - \lg b$ til å skrive om
$\lg \frac{x}{n}$ .

$(\lg x - n) \cdot (\lg x - \lg n) = 0$

Mer om:

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på logaritmer, se artikkelen Mer om logaritmer.

c)

Bruk likningen i oppgave b) til å bestemme $x$ uttrykt ved $n$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Her spørres det egentlig om å løse ligningen med hensyn på $x$ .

Vi løser $(\lg x - n) \cdot (\lg x - \lg n) = 0$ .

Uttrykket er bare null om en av parentesene er null. Altså enten når

1) $\lg x - n = 0$ eller
2) $\lg x - \lg n = 0$

1):

$\lg x - n = 0$

$\lg x = n$

$x = 10^{n}$

2):

$\lg x = \lg n$

$x = n$

Svar: Likningen har to løsninger, $x = 10^{n}$ og $x = n$ .

Mer om:

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på logaritmer, se artikkelen Logaritmelikninger.

REA3022 2014 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4CZW

a)

Løsningsforslag a)

Derivasjon

Logaritme

b)

Løsningsforslag b)

Derivasjon

Eksponentialfunksjon

c)

Løsningsforslag c)

Derivasjon

Funksjon

Polynom

Oppgave 2 (5 poeng) Nettkode: E-4D00

a)

Løsningsforslag a)

Nullpunkt

Polynom

b)

Løsningsforslag b)

abc-formelen

Polynom

c)

Løsningsforslag c)

Fortegnsskjema

Brøk

Oppgave 3 (4 poeng) Nettkode: E-4D04

a)

Løsningsforslag a)

Vektor

b)

Løsningsforslag b)

Vektor

c)

Løsningsforslag c)

Vektor

Oppgave 4 (4 poeng) Nettkode: E-4D08

a)

Løsningsforslag a)

Nullpunkt

Polynom

Funksjon

b)

Løsningsforslag b)

Ekstremalpunkt

Fortegnsskjema

c)

Løsningsforslag c)

Ekstremalpunkter

Nullpunkt

Graf

Funksjon

Oppgave 5 (2 poeng) Nettkode: E-4D0D

Løsningsforslag

Trekant

Sirkel

Vinkel

Vinkelsum

Linje

Oppgave 6 (3 poeng) Nettkode: E-4D0F

a)

Løsningsforslag a)

Partall

Oddetall

b)

Løsningsforslag b)

Kvadrattall

Oddetall

Partall

Første kvadratsetning

Andre kvadratsetning

Brøk

Oppgave 7 (2 poeng) Nettkode: E-4D0I

a)