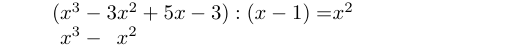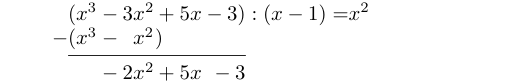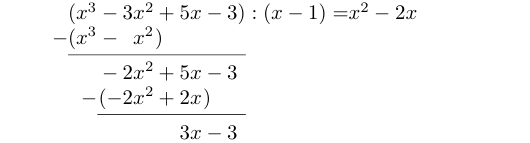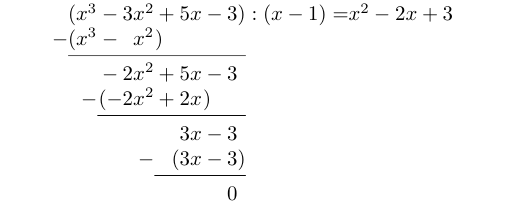Polynomdivisjon - skritt for skritt

Vårt valgte eksempel er brøken

$\frac{x^3-3x^2+5x-3}{x-1}$.

For å regne ut hva dette blir, benytter vi det samme oppsettet som i talldivisjon. Vi bruker altså divisjonstegnet «:» i stedet for brøkstrek:

$\left(x^3-3x^2+5x-3\right):\left(x-1\right)=?$

Det første vi gjør, er å identifisere de høyeste potensene i hvert polynom. Disse er her henholdsvis $x^3$ og $x$. Så spør vi: Hva må vi gange $x$ med for å få $x^3$? Svaret er $x^2$, og dette skriver vi rett etter likhetstegnet. Deretter ganger vi $x^2$ med $x-1$, og skriver resultatet (som blir $x^2\cdot (x-1)=x^3-x^2$) under det første polynomet:

De to polynomene som står under hverandre, skal så subtraheres fra hverandre. Her er det lett å surre med fortegnene, så pass på! Resultatet blir:

Legg merke til at $x^3$-leddet forsvant etter subtraksjonen. Dette er hele poenget med at vi valgte $x^2$ som vårt første ledd i svaret. Vi gjentar prosedyren med $-{2x}^2+5x-3$. Hva må vi gange $x$ med for å få $-{2x}^2$? Det må bli $-2x$, som dermed er neste ledd i svaret. Videre regner vi ut at $-2x\cdot (x-1)={-2x}^2+2x$, og dette skriver vi opp under $-{2x}^2+5x-3$. Etter subtraksjonen står vi da igjen med følgende:

Nå står vi igjen med divisjonen $(3x-3):(x-1)$. Her kan man enten se direkte at dette blir 3, eller man kan tenke som før: Hva må vi gange $x$ med for å få $3x$? Jo, tallet 3. Den fullstendige regningen blir uansett seende slik ut:

Siden vi står igjen med 0 nederst, gikk divisjonen opp. Svaret er det som står etter likhetstegnet. Skifter vi tilbake til brøkstrek igjen, har vi altså fått resultatet

$\frac{x^3-3x^2+5x-3}{x-1}=x^2-2x+3$.

Ganger vi med $x-1$ på begge sider, får vi en faktorisering av telleren:

 $(x^3-{3x}^2+5x-3)=(x-1)(x^2-2x+3)\mathrm{.}$

Å oppnå en slik faktorisering er ofte hensikten med å utføre en polynomdivisjon.