Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT0010 2013 VÅR
Eksamenstid:
5 timer totalt:
Del 1 og Del 2 skal deles ut samtidig.
Del 1 skal du levere innen 2 timer.
Del 2 skal du levere innen 5 timer.
Hjelpemidler på Del 1:
Ingen hjelpemidler er tillatt, bortsett fra vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Framgangsmåte og forklaring:
Del 1 har 17 oppgaver. Du skal svare på alle oppgavene.
Skriv med penn når du krysser av eller fører inn svar i Del 1.
I regneruter skal du vise hvordan du kommer fram til svaret.
Ved konstruksjon skal du bruke passer, linjal og blyant.
Du skal ikke kladde på oppgavearkene. Bruk egne kladdeark.
På flervalgsoppgavene setter du bare ett kryss per spørsmål.
Del 2 har 10 oppgaver. Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Vis hvordan du har kommet fram til svarene. Før inn nødvendige mellomregninger. Skriv med penn.
I regnearkoppgaver skal du ta utskrift av det ferdige regnearket. Husk å vise hvilke formler du har brukt i regnearket.
Du skal levere utskriften sammen med resten av besvarelsen.
Dersom du bruker en digital graftegner, skal skala og navn på aksene være med på utskriften.
Eksempel:
Uttrykket har verdien
35 50 62 75
○ ○ ○ ⊗
Veiledning om vurderingen:
Den høyeste poengsummen i Del 1 er 24 og poengsum i Del 2 er høyst 36, men den er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering på grunnlag av Del 1 og Del 2. Sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer ser sammenhenger i faget, er kreativ og kan anvende fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4G6A
Regn ut
a)
b)
c)
d)
Oppgave 2 (2 poeng) Nettkode: E-4AS8
Gjør om
a)
____ h ____ min
b)
____ kg
c)
____ m
d)
____
Oppgave 3 (1 poeng) Nettkode: E-4ASD
Regn ut
a)
b)
Oppgave 4 (2 poeng) Nettkode: E-4ASG
Regn ut, og forkort brøken hvis mulig
a)
b)
c)
d)
Oppgave 5 (1,5 poeng) Nettkode: E-4ASL
Løs likningene
a)
b)
Oppgave 6 (1 poeng) Nettkode: E-4ASQ
14,90 kroner per flaske 48,20 kroner per kilogram
Omtrent hvor mye må du betale for 6 flasker vann og 2 kg druer?
Oppgave 7 (0,5 poeng) Nettkode: E-4AX4
Prisen for et lesebrett er satt ned med og koster nå
Før prisen ble satt ned, kostet lesebrettet
- kroner
- kroner
- kroner
- kroner
Oppgave 8 (1 poeng) Nettkode: E-4AXC
På en matematikkprøve fikk 10 elever disse karakterene:
| Karakter | 1 | 2 | 3 | 4 | 5 | 6 |
| Frekvens (antall) | 1 | 0 | 1 | 3 | 3 | 2 |
a)
Summen av alle karakterene for de elevene ble ____
b)
Gjennomsnittskarakteren for de elevene ble ____
Oppgave 9 (1,5 poeng) Nettkode: E-4AYR
Skriv så enkelt som mulig
a)
b)
Oppgave 10 (0,5 poeng) Nettkode: E-4AZ0
Hva er mest sannsynlig å få?
- A er mest sannsynlig
- B er mest sannsynlig
- Det er umulig å sammenligne A og B
- A og B er like sannsynlige
Oppgave 11 (1,5 poeng) Nettkode: E-4AZ3
Sondre kjøper dobbelt så mange epler som bananer. Han betaler tilsammen 80 kroner.
Regn ut hvor mange epler og bananer Sondre kjøper.
Oppgave 12 (0,5 poeng) Nettkode: E-4AZ5
Avstanden i luftlinje mellom to steder er . På et kart er målestokken
Avstanden på kartet mellom de to stedene er
- 0,25 cm
- 2,5 cm
- 25 cm
- 250 cm
Oppgave 13 (0,5 poeng) Nettkode: E-4AZG
En bil kjører med farten .
På h kjører bilen
- km
- km
- km
- km
Oppgave 14 (2,5 poeng) Nettkode: E-4AZS
a)
Fyll ut det som mangler i verditabellen for funksjonene og
b)
Tegn grafene til f og g i koordinatsystemet nedenfor.
c)
Skjæringspunktene mellom grafene til f og g er (____ , ____) og (____ , ____)
Oppgave 15 (3 poeng) Nettkode: E-4AZZ
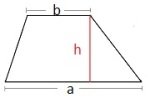
Konstruer der
er en del av trapeset der
Konstruer trapeset .
Ta med hjelpefigur og konstruksjonsforklaring.
Oppgave 16 (2 poeng) Nettkode: E-4B07
Et område har form som et rektangel og en rettvinklet trekant. Se skissen.
Vi skal legge et tykt lag med grus jevnt utover hele området.
a)
Regn ut hvor mange kubikkmeter grus vi trenger til dette området.
b)
Vi skal sette opp et gjerde rundt området. Vis ved regning at vi trenger 180 m gjerde.
Oppgave 17 (1 poeng) Nettkode: E-4B0H
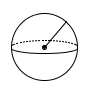
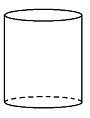
Tre like store kuler har alle radius . En sylinder har samme radius som kulene og høyde .
Sylinderen skal ha like stort volum som de tre kulene tilsammen.
Formelen for volumet av en kule er
Bruk formler og bestem høyden i sylinderen uttrykt ved .
DEL 2 Med hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4B88
Live trenger denne behandlingen hos tannlegen:
Nedenfor ser du prisene (i kroner) for de ulike behandlingene hos tannlegen. Live får 75 % rabatt fordi hun er mellom 18 og 20 år.
Regn ut hvor mye Live må betale totalt for behandlingen hos tannlegen.
Oppgave 2 (4 poeng) Nettkode: E-4B8D
I butikken kan Live velge mellom 11 typer tannbørste, 10 typer tannkrem og 8 typer tanntråd.
a)
På hvor mange ulike måter kan Live velge én type tannbørste, én type tannkrem og én type tanntråd?
b)
Tannlegen anbefalte Live å kjøpe en bestemt type tannbørste og en bestemt type tanntråd som de har i butikken. Men Live har glemt hva tannlegen anbefalte, og velger tilfeldig én type tannbørste og én type tanntråd.
Live velger tannbørsten og tanntråden som vist nedenfor.
Bestem sannsynligheten for at dette er de typene som tannlegen anbefalte.
Oppgave 3 (2 poeng) Nettkode: E-4B8I
En flaske munnskyllevann inneholder . Live vil blande det ut med vann i forholdet (1 del munnskyllevann og 3 deler vann).
Hun bruker ferdig utblandet munnskyllevann to ganger per dag.
Regn ut hvor mange dager en flaske med munnskyllevann vil vare for Live.
Oppgave 4 (2 poeng) Nettkode: E-4B8Q
Live bruker et plastbeger til munnskylling. Plastbegeret med innvendige mål ser du nedenfor.
Formelen for volumet av et slikt plastbeger er
Bruk formelen og vis at volumet av plastbegeret er ca. .
Oppgave 5 (7 poeng) Nettkode: E-4B9R
Oppgave 5 skal løses ved hjelp av regneark. Vis hvilke formler du har brukt.
Live skal få satt inn en ny tann. Behandlingen koster 10 000 kroner. Hun får tilbud om et lån som skal nedbetales i løpet av 10 måneder med avdrag på 1 000 kroner per måned. Renten er 2 % per måned. Alle beløp er i kroner.
a)
Bruk formler og lag ferdig nedbetalingsplanen for Live. Ta med formelutskrift.
b)
Framstill terminbeløpene for lånet i et stolpediagram.
c)
En annen bank tilbyr Live et lån med en rente på 1,5 % per måned. Lånene er ellers like.
Hvor mye sparer Live totalt på å velge dette lånet? Du trenger ikke ta ny formelutskrift.
Oppgave 6 (6 poeng) Nettkode: E-4B9Y
I X-Fighters hopper motorsykkelen fra rampe 1 til rampe 2. En forenklet modell som beskriver et slikt hopp, er funksjonen gitt ved
Her viser hvor mange meter motorsykkelen er over bakken når den er meter fra
rampe , målt langs bakken. Se skissen av hoppet nedenfor.
a)
Motorsykkelen er høyest over bakken fra rampe 1, altså når .
Bruk funksjonsuttrykket, og vis ved regning at motorsykkelen da er over bakken.
b)
Tegn grafen til når .
c)
Bestem grafisk hvor langt motorsykkelen har flyttet seg fra rampe , målt langs bakken,
når motorsykkelen er over bakken.
Oppgave 7 (4 poeng) Nettkode: E-4BAD
Ta utgangspunkt i skissen nedenfor.
- ACB er halvsirkelen med sentrum i O og med diameter AB.
- AEC er halvsirkelen med sentrum i D og med diameter AC.
a)
Forklar at . Vis ved regning at .
b)
Vis at arealet til halvsirkelen er (Bruk at ).
Oppgave 8 (3 poeng) Nettkode: E-4BAJ
Figuren nedenfor er den samme som i oppgave 7, men den er utvidet slik at to kvadrater,
og , kommer fram.
Regn ut omkretsen av figuren, det vil si (markert med blå farge).
Oppgave 9 (3 poeng) Nettkode: E-4BAO
Se figuren i oppgave 8.
Hippokrates fant at . Med figurer vil dette se slik ut:
a)
Vis at arealet av halvsirkelen er (Bruk at ).
b)
Bruk blant annet opplysningene i oppgave 7 og oppgave 9 a), og vis ved regning at
Oppgave 10 (2 poeng) Nettkode: E-4BAW
Vis ved regning at Hippokrates-månen har samme areal som , det vil si .
Tips: Vis først at AC =