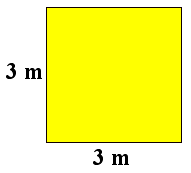
Et kvadrat
Ønsker vi å finne arealet til et kvadrat med vilkårlig lange sidekanter, må vi finne ut hvor mange kvadratmeter vi kan plassere i kvadratet.
Eksempel 1
Et kvadrat har sidelengde . Hva stort er arealet til kvadratet?
Spørsmålet blir: Hvor mange kvadratmeter kan plasseres inn i kvadratet?
Vi kan dele opp i kvadratiske ruter med størrelsen ved å dele alle sidene i tre like store deler.
Vi kan altså plassere kvadratmeter inn kvadratet med sidelengde . Arealet til dette
kvadratet er altså .
Vi oppdager at vi kan regne ut antall ruter vi kan plassere inn i kvadratet ved å multiplisere sidelengden med seg selv. Vi kan dermed regne ut arealet av et kvadrat ved hjelp av formelen:
Bokstaven står for sidelengde.
Del på Facebook
Lynkurs, 8.-10.trinn
Geometri - areal og volum
Består av:
- Tom forteller om areal
- Et kvadrat
- Et rektangel
- En trekant
- Et parallellogram
- Et trapes
- Tom forteller om overflatearealer
- Overflatearealet til en terning
- Tom forteller om volum
- Et rett prisme
- En sylinder
- Pyramider og kjegler
- En kule
- Pytagoras læresetning
- Tom forteller om formlikhet og Pytagoras læresetning
- Test deg selv i geometri (areal og volum)!
- Test deg selv i tallet π (PI)
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Arealenheter
Mål for areal:
km², m², dm², cm², mm²Andre mål:
1 ar = 100 m2
1 dekar = 10 ar = 1000 m2 = 1 mål
(deka betyr 10)Omgjøring mellom enheter:
1 m² = 1 m · 1 m = 10 dm · 10 dm = 100 dm²
1 dm² = 1 dm · 1 dm = 10 cm · 10 cm = 100 cm²
1 cm² = 1 cm · 1 cm = 10 mm · 10 mm = 100 mm² -
Kvadrat
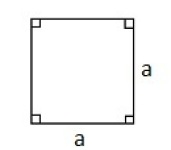
En firkant der alle sider er like lange og alle vinkler 90°.