Et rett prisme
Vi skal finne overflateareal og volum til et rett prisme.
Et rett prisme med rektangulær grunnflate (en kuboide) består av seks sideflater, som alle er rektangler og parvis like store. Prismet kan dermed beskrives ved tre størrelser: lengden , bredden og høyden .
Overflatearealet er summen av arealene til de seks rektanglene:
Volumet av prismet får vi ved å multiplisere lengde, bredde og høyde:
Siden vi kjenner til at grunnflaten har et areal , kan vi også ta med denne formelen for volumet av et rett prisme:
Vi bare noterer som en kjensgjerning, uten å gå inn på et resonnement for dette, at også for prismer med andre grunnflater enn rektangler og for skjeve prismer kan vi regne ut volumet på samme måte: grunnflate ganger høyde.
Eksempel
Hvor mye vann vil et akvarium på meter i lengde, meter i bredde og meter i høyde holde på?
Vi må først regne ut grunnflaten, , og deretter multiplisere den med høyden .
i volum utgjør liter. Det er mye vann!
Del på Facebook
Lynkurs, 8.-10.trinn
Geometri - areal og volum
Består av:
- Tom forteller om areal
- Et kvadrat
- Et rektangel
- En trekant
- Et parallellogram
- Et trapes
- Tom forteller om overflatearealer
- Overflatearealet til en terning
- Tom forteller om volum
- Et rett prisme
- En sylinder
- Pyramider og kjegler
- En kule
- Pytagoras læresetning
- Tom forteller om formlikhet og Pytagoras læresetning
- Test deg selv i geometri (areal og volum)!
- Test deg selv i tallet π (PI)
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Meter
Meter er måleenheten for lengde og forkortes m. Mange andre lengdemål er avledet av meter:
kilometer: 1 km = 1000 m
desimeter: 10 dm = 1 m
centimeter: 100 cm = 1 m
millimeter: 1000 mm = 1 m -
Prisme
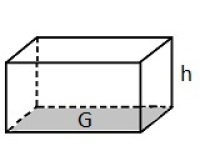
Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.
Har et prisme grunnflate G og høyde h, er volumet lik G · h. -
Volum
Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).