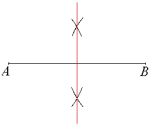
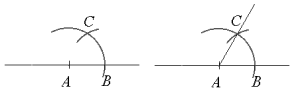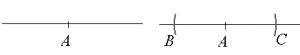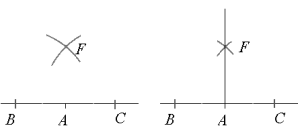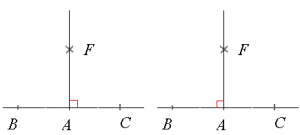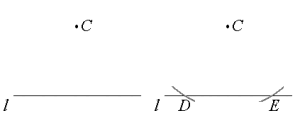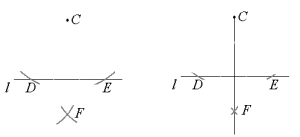Konstruksjon av figurer
Ved hjelp av passer og linjal kan vi konstruere mange figurer. Nå til dags gjør datamaskinen jobben for oss, men blant annet håndverkere bruker metodene vi nå skal se på til daglig.
Vi vil nå vise hver konstruksjon steg for steg. For å unngå misforståelser, vil vi sette navn på (hjelpe)punkter. Navnene er store bokstaver som , , og så videre. Når man først er litt dreven i å konstruere, trenger man ikke å markere disse hjelpepunktene slik vi gjør det her.
Konstruksjon av en - vinkel
- Tegn en linje ved å bruke en linjal. Merk av et punkt midt på denne linjen og kall det for .
- Sett passerspissen i punktet og slå en bue som krysser linjen til høyre for punktet . Punktet der buen krysser linjen til høyre for , kaller du for .
- Behold avstanden i passeren og sett den i punktet . Slå en ny bue som skjærer den gamle. Punktet der disse to buene krysser hverandre, kaller du for .
- Tegn en linje som går fra punktet og gjennom punktet .
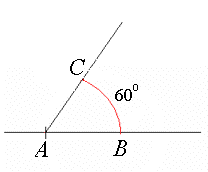
- Gratulerer! Nå har du konstruert en -vinkel .
Oppsummering: Vi utfører dette i prinsippet ved å sette av tre punkter som kan være hjørner i en likesidet trekant. Med passeren kan vi plassere tre punkter i like avstander fra hverandre. Disse tre punktene vil da danne hjørnene i en likesidet trekant, og da vet vi at vinklene er på .
Halvering av vinkler
Alle vinkler kan halveres ved hjelp av passer og linjal.
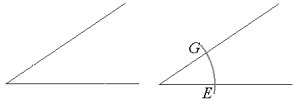
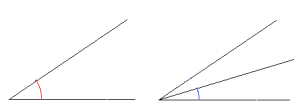
- Tegn eller konstruer en vilkårlig vinkel.
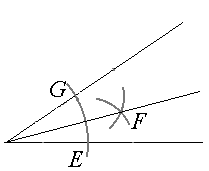
- Sett passerspissen i toppunktet og slå en bue. Buen vil krysse hvert av vinkelbeina i et punkt. Det ene punktet kaller vi G og det andre E.
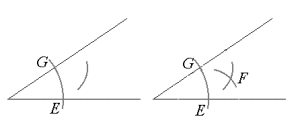
- Sett passerspissen i punktet G og slå en ny bue.
- Behold avstanden i passeren, sett passerspissen i E og slå en ny bue. Buene krysser hverandre i et punkt. Kall dette punktet for F.
- Tegn en linje som går fra toppunktet og gjennom F.
- Gratulerer! Nå har du halvert vinkelen du begynte med.
Oppsummering: Vi lager en sirkelbue med sentrum i vinkelens toppunkt, og så bruker vi passeren til å lage et kryss som markerer et punkt som er like langt fra begge de to punktene hvor sirkelbuen skjærer vinkelbeina. Gjennom dette punktet går da halveringslinja for vinkelen.
Konstruksjon av -vinkel
Den enkleste måten å konstruere en vinkel på er å halvere en vinkel på . Legg også merke til at vi tegner et lite kvadrat i stedet for en bue når vi ønsker å vise på en tegning at en vinkel er .
- Tegn en rett linje. Merk av et punkt på linjen.
- Sett passerspissen i punktet og slå en bue. Buen krysser linjen både til venstre og til høyre for . Kall disse punktene for og .
- Sett passerspissen i punktet og slå en bue. Behold avstanden i passeren, sett passerspissen i punktet og slå en bue til. Buene krysser hverandre i et punkt. Kall dette punktet for .
- Tegn en linje som går fra og gjennom .
- Gratulerer! Nå har du konstruert en -vinkel. Legg merke til at denne konstruksjonen tar utgangspunkt i halveringen av . Vi har derfor konstruert to -vinkler, og .
Nedfelle normal fra et punkt ned på ei linje
Vi har en rett linje og et punkt utenfor linjen. Så vil vi konstruere den linjen som går gjennom og står vinkelrett på . Denne linjen kalles for normalen til linjen .
- Sett passerspissen i punkt og slå en bue som krysser linjen i to punkter. Kall disse punktene for og .
- Sett passerspissen i og slå en bue på den siden av linjen der punktet ikke ligger (i dette tilfellet under linjen siden punktet ligger over linjen). Behold avstanden i passeren, sett passerspissen i punktet og slå en bue til (tilsvarende som du gjorde i punktet ). Buene krysser hverandre i et punkt. Kall dette punktet for . (Dersom buene ikke krysser hverandre, må du ta større avstand i passeren når du slår den første buen.)
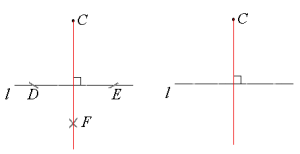
- Tegn en linje som går gjennom og .
- Gratulerer! Nå har du felt ned normalen fra punktet ned på linjen .
Midtnormal
Hvis vi skal dele et linjestykke i to nøyaktig like deler, kan vi konstruere en midtnormal til linjestykket.
Vi plasserer først passerspissen i ett av endepunktene for linjestykket, for eksempel A. Passeråpningen må være større enn halvparten av linjestykkets lengde (ellers vil ikke buene krysse hverandre). Marker to passende buer omtrent over midten på AB. Slå en ny bue fra B med den samme passeråpningen. Buene krysser hverandre slik at vi får to punkter. Da tegner vi en linje som går gjennom disse to punktene. Denne linjen er midtnormalen til linjestykket AB.
Del på Facebook
Begrep
-
Kvadrat
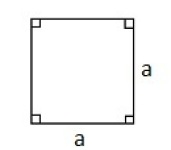
En firkant der alle sider er like lange og alle vinkler 90°.
-
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
-
Linjestykke
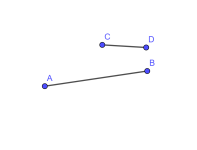
Et linjestykke er en sammenhengende bit av en linje, avgrenset av to endepunkter. Navnet på et linjestykke er vanligvis gitt ved de to endepunktene: AB, CD, ...
-
Midtnormal
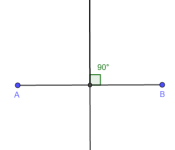
Midtnormalen til et rett linjestykke er den rette linja som går gjennom linjestykkets midtpunkt, og som står vinkelrett på linjestykket.
-
Normal
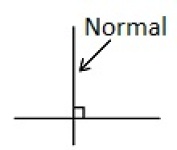
En linje som står 90 grader på en annen linje.
-
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.Areal:
Omkrets: -
Sirkelbue
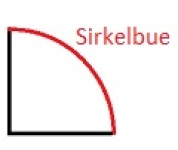
Er en sammenhengende del av sirkellinjen.
-
Vinkel
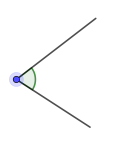
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.