
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1011 2015 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 8 oppgaver. Del 2 har 7 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- orklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Olje og dollarkurs: (http://www.bbc.com/, 5.07.2016)
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4AQC
g salt inneholder g natrium. Helsemyndighetene anbefaler et inntak av natrium på maksimalt g per dag.
a)
Hvor mange gram salt kan du maksimalt innta i løpet av en dag dersom du skal følge anbefalingen?
Løsningsforslag a)
Jeg tenker:
Vi må finne ut hvor mye salt man må spise for å få i seg natrium.
La betegne den maksimale mengden salt man skal innta i følge anbefalingen. Vi vet at hvert gram salt inneholder gram natrium, og da må gram salt inneholde natrium. Hvis vi skal spise såpass mye salt at vi er helt på yttergrensen til det som er anbefalt å ha i seg av natrium, så må mengden natrium i saltet være . Dette kan vi sette opp som en likning. Vi vil finne ut hva er, og vil derfor ha alene på venstre side av likhetstegnet. Vi dividerer med og forkorter. For å regne ut brøken , kan det være lurt å multiplisere med 10 over og under brøkstreken. Dette er for å få bort kommategnet; heltall er ofte lettere å regne med. Vi har at Vi kan regne ut for hånd, men vi vet at , så . Dermed er og vi kan konkludere med at man ikke burde spise mer enn 6 gram salt hver dag.
Svar: 6 gram.
Mer om:
Denne oppgaven er om
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
For flere eksempler og forklaringer se artiklene Målingsforhold, Løs en førstegradslikning! i lynkurset Likninger eller Lineære likninger i lynkurset Likning med én ukjent.
For å øve mer, se oppgavesetet om førstegradslikninger i Treningsleieren.
b)
100 g pizza inneholder 0,8 g salt. En porsjon pizza er beregnet til 300 g.
Hvor mange gram salt inneholder en porsjon pizza?
Løsningsforslag b)
Jeg tenker:
Vi må multiplisere opp mengden salt slik at det tilsvarer en hel porsjon pizza, altså 300 gram, og ikke bare 100 gram.
Hvis 100 gram pizza inneholder salt, så må tre ganger så mye pizza, altså 300 gram, inneholde tre ganger så mye salt. Dermed blir mengden salt i en porsjon pizza lik .
Svar: gram.
Mer om:
Denne oppgaven er om
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
For flere eksempler og forklaringer se artikkelen Målingsforhold.
c)
Hvor mange prosent av anbefalt daglig inntak av natrium svarer dette til?
Løsningsforslag c)
Jeg tenker:
Legg merke til at vi har gram salt, ikke natrium! Derfor blir ikke svaret . Vi kan regne ut hvor mange
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Én måte å løse problemet på er å regne ut hvor mye natrium det er i gram salt. Det er natrium i salt, så i salt er det natrium. Anbefalt daglig mengde er , og er av . Brøken kan være litt kjedelig å regne ut for hånd, men det lønner seg å multiplisere med 100 over og under brøkstreken. Det finnes dog en annen måte å løse oppgaven på – i stedet for å finne ut hvor mye natrium det er i 300 gram pizza, kan vi finne prosentandelen direkte ved å finne ut hvor mange prosent salt det er i 300 gram pizza i forhold til den anbefalte mengden. Det er salt, og anbefalt daglig inntak er , så prosentandelen blir Vi vil regne ut . Først multipliserer vi med 10 over og under brøkstreken, for å få bort kommategnet. Da får vi Før vi begynner å dividere for hånd er det lurt å faktorisere ut telleren og nevneren og forkorte. Vi starter med 24, som vi umiddelbart kan se er delelig med 2 siden det er et partall. Vi har . Vi ser at 12 også er delelig med 2, så . Til sist er , så vi har . Deretter til 60, som også er et partall. Vi ser at Dermed kan vi skrive brøken som Her kan vi forkorte to totall og ett tretall over og under brøkstreken, og vi står igjen med Vi vet at , så svaret er , noe vi fikk til helt uten å dividere for hånd.
Svar: Mengden natrium i én porsjon pizza er av anbefalt daglig inntak.
Mer om:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere eksempler og forklaringer se artiklene Prosent av hva da? og Regneregler i lynkurset Prosent.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 2 (3 poeng) Nettkode: E-4AQG
Funksjonene og er gitt ved
a)
Tegn grafene til og i samme koordinatsystem, og bestem skjæringspunktet grafisk.
Løsningsforslag a)
Jeg tenker:
Begge
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi skal tegne grafene til funksjonene og . Først tegner vi et koordinatsystem. Ofte er det slik at funksjonene man får oppgitt oppfører seg mest spennende rundt origo, så vi lar og variere mellom og 5.

Vanligvis, når vi skal tegne grafen til en funksjon , så velger vi en del punkter på -aksen, finner funksjonsverdiene i disse punktene, og tegner en kurve gjennom punktene vi får. I dette tilfellet trenger vi faktisk bare å bruke to punkter på -aksen per graf for å tegne dem helt riktige. Det er fordi begge funksjonene er lineære, altså rette linjer. Dette kan vi se ved at det ikke er noen ledd i funksjonene hvor det står noe med opphøyd i noen annen potens; funksjonene er på formen der og er konstante tall.
Vi starter først med , og setter inn . Da får vi at , så den rette linjen som er grafen til går gjennom origo. Videre kan vi sette inn . Vi velger akkurat 2 for å få bort brøken. Vi har at . Nå har vi funnet at grafen til er en rett linje som går gjennom punktene og . Vi tegner inn disse punktene i koordinatsystemet, og bruker linjalen for å tegne en rett linje mellom dem.
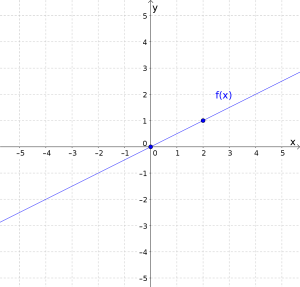
Vi gjør det samme for . I får vi at funksjonsverdien til er , og i er funksjonsverdien . Grafen går altså gjennom punktene og . Vi tegner de to punktene og linjen mellom dem inn i koordinatsystemet.
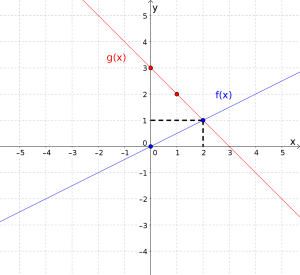
På grafen ser vi at de to grafene krysser hverandre når og , så skjæringspunktet er .
Svar: Skjæringspunktet er . Se graf over.
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer se artiklene Rette linjer (lineære funksjoner) og Grafisk løsning av likninger.
For å øve mer, se oppgavesettene om grafisk fremstilling og skjæringspunkt i Treningsleieren.
b)
Bestem skjæringspunktet ved regning.
Løsningsforslag b)
Jeg tenker:
Et
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Vi vil finne en som er slik at . En annen måte å skrive dette på er hvor vi bare har fylt inn definisjonene av henholdsvis og . Vi vil finne en som passer inn i ligningen over; dette tilsvarer å løse ligningen. En god strategi er å få alt som har med å gjøre på én side av likhetstegnet, og alt annet på en annen side. For å få flyttet -en fra høyre side til venstre, adderer vi med på hver side. Vi faktoriserer ut på venstre side. Her kan vi trekke sammen de to tallene på venstre side. For å få alene igjen på venstre side, multipliserer vi med på hver side. Her kan vi forkorte både på venstre og høyre side, og vi står igjen med Dette betyr at . Vi vil finne -koordinaten til skjæringspunktet også; dette gjør vi rett og slett ved å sette inn 2 i enten eller . Vi ser at så skjæringspunktet er .
Svar: Skjæringspunktet er .
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger. Hvis du vil vite mer om lineære likninger, se artikkelen Lineære likninger.
For å øve mer, se oppgavesettene om grafisk fremstilling og skjæringspunkt i Treningsleieren.
Visste du at:
Vi har funnet skjæringspunktet til to linjer ved regning, akkurat som vi gjorde grafisk i forrige oppgave.
Oppgave 3 (2 poeng) Nettkode: E-4AQL
Et år hadde Siri en reallønn på 360 000 kroner. Den nominelle lønnen til Siri dette året var 450 000 kroner.
Bestem konsumprisindeksen dette året.
Løsningsforslag
Jeg tenker:
Dette er en oppgave om
Konsumprisindeks
Konsumprisindeks (KPI) er en indeks som viser endringer i prisene på varer og tjenester som kjøpes av husholdninger, sammenlignet med et basisår. De varer og tjenester som utgjør det meste av husholdningsbudsjettet, tillegges størst vekt.
(hentet fra http://snl.no/konsumprisindeks)
Nominell lønn
Nominell lønn er det vi vanligvis bare kaller lønn.
Om du slår opp i en ordbok finner du følgende om ordene nominell;
- nominell
det er to måter å bruke ordet på
1 - som gjelder (bare) i navnet det er han som er lederen, iallfall nominelt
2 - pålydende obligasjonene har en nominell verdi på 1000 kr / nominell inntekt inntekt uttrykt i pengeverdien til enhver tid / nominell rente, til forskjell fra effektiv rente
Vi har følgende sammenheng mellom konsumprisindeks, reallønn og nominell lønn: Vi vil finne konsumprisindeksen, og da kan uttrykket over tolkes som en likning der konsumprisindeksen er ukjent. Derfor lar vi betegne konsumprisindeksen videre; altså skal vi finne en verdi for som passer inn i likningen Vanligvis er det lurt å først løse likningen, og deretter sette inn verdiene vi vet hva er – men i dette tilfellet er det like greit å sette inn tallene med én gang. Vi vet at reallønnen til Siri er på kroner og den nominelle lønnen på kroner. Vi setter dette inn i uttrykket over og får På venstre side dividerer vi på 100, og det tilsvarer å fjerne to nuller fra . Dermed må vi løse følgende likning: Vi vil gjerne få opp fra nevneren på høyre side; derfor multipliserer vi med på hver side av likhetstegnet og forkorter. For å få alene på venstre side, dividerer vi med på hver side. Vi forkorter på venstre side og får Nå må vi regne ut brøken som står på høyre side. Et godt første steg er å krysse bort like mange nuller i tallene over og under brøkstreken. I vårt tilfelle er det to. Dette kan vi gjøre fordi det betyr at teller og nevner har 100 som felles faktor: La oss regne ut for hånd. Vi starter med å skrive delestykket på en linje.
| 4 | 5 | 0 | 0 | : | 3 | 6 | = |
I utgangspunktet skal vi finne ut hvor mange ganger tallet til høyre (36) går opp i det første sifferet på venstre side (4). At et tall går opp ganger i et annet, betyr at multiplisert med det første tallet er mindre enn det siste. Hvis vi skal multiplisere 36 med et heltall som er større eller lik 0 for å få det til å bli mindre enn 4, må vi multiplisere med 0, siden 36 allerede er større enn 4. Derfor går 36 kun 0 ganger opp i 4, så vi må ta med enda et siffer.
| 4 | 5 | 0 | 0 | : | 3 | 6 | = |
Altså skal vi finne ut hvor mange ganger 36 går opp i 45. Svaret her er 1, fordi , og det er større enn 45. Det vi har regnet ut nå er at første siffer i svaret er 1.
| 4 | 5 | 0 | 0 | : | 3 | 6 | = | 1 |
Nå skal vi multiplisere sifferet vi fikk med nevneren (36). Da får vi . Dette tallet setter vi under de to sifrene i telleren som vi brukte i sted (45). Neste steg er å trekke fra tallet vi skrev under telleren (36) fra de to sifrene som står på tilsvarende plass i telleren (45). Dette blir .
| 4 | 5 | 0 | 0 | : | 3 | 6 | = | 1 | |||
| - | 3 | 6 | |||||||||
| 9 |
Vi fortsetter prosessen, og etter vi har utført utregningen står vi igjen med følgende.
| 4 | 5 | 0 | 0 | : | 3 | 6 | = | 1 | 2 | 5 | |
| - | 3 | 6 | |||||||||
| 9 | 0 | ||||||||||
| - | 7 | 2 | |||||||||
| 1 | 8 | 0 | |||||||||
| - | 1 | 8 | 0 | ||||||||
| 0 |
Dermed blir svaret 125. Setter vi dette inn i ([o3]), får vi altså var konsumprisindeksen 125.
Svar: Konsumprisindeksen var 125.
Mer om:
Denne oppgaven er om
Konsumprisindeks
Konsumprisindeks (KPI) er en indeks som viser endringer i prisene på varer og tjenester som kjøpes av husholdninger, sammenlignet med et basisår. De varer og tjenester som utgjør det meste av husholdningsbudsjettet, tillegges størst vekt.
(hentet fra http://snl.no/konsumprisindeks)
I Ofte stilte spørsmål har Orakelen forklart hva konsumprisindeks er. For flere eksempler og forklaringer om divisjon se artikkelen Divisjon.
For å øve mer, se oppgavesettet om divisjon i Treningsleieren.
Oppgave 4 (2 poeng) Nettkode: E-4AQO
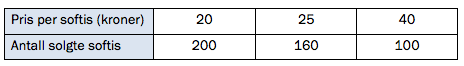
Tabellen ovenfor viser pris per softis og antall solgte softis i tre ulike kiosker en dag.
Gjør beregninger og avgjør om pris per softis og antall solgte softis er omvendt proporsjonale størrelser.
Løsningsforslag
Jeg tenker:
At to størrelser er
Omvendt proporsjonal
og er omvendt proporsjonale dersom (dvs. ), der er konstant.
For at størrelsene skal være omvendt proposjonale, må produktet av tallene i hver kolonne i tabellen være konstant. Altså må være det samme som og . Hvis alle er like er størrelsene omvendt proposjonale; vi må derfor regne ut og se. Vi ser først at Dette kan vi regne ut i hodet; hvis vi har tall med mange nuller på slutten, kan vi legge sammen antall nuller og multiplisere det som står igjen. Ovenfor har vi tre nuller til sammen, og det som står igjen er , så svaret blir .
Nå må vi regne ut et av de andre produktene og sammenligne. Vi kunne regnet ut , men regnestykket er lettere å finne ut av hva er, så vi tar det først. Når vi multipliserer med 100 er det eneste vi trenger å gjøre å legge til to nuller. Det ble det samme som forrige gang. Hvis tallet hadde vært forskjellig fra , hadde vi ikke trengt å regne ut det siste produktet, siden vi allerede hadde visst at størrelsene ikke var omvendt proposjonale. Det var derfor vi valgte å ta det letteste produktet først; det kunne ha spart oss tid på eksamen. Så må vi sjekke det siste produktet – størrelsene er nemlig omvendt proposjonale hvis (og bare hvis) er lik . Vi regner ut for hånd.
| 3 | ||||||||||||||
| 2 | 5 | 1 | 6 | 0 | = | 4 | 0 | 0 | 0 | |||||
| 0 | 0 | |||||||||||||
| 1 | 2 | 0 | ||||||||||||
| + | 2 | 5 | ||||||||||||
| = | 4 | 0 | 0 | 0 |
Dermed har vi regnet ut at Dette er det samme som tidligere, og det betyr at størrelsene er omvendt proposjonale.
Svar: Størrelsene er omvendt proposjonale.
Mer om:
Denne oppgaven er om
Omvendt proporsjonal
og er omvendt proporsjonale dersom (dvs. ), der er konstant.
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.
Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
For flere eksempler og forklaringer se artikkelen Proporsjonalitet. Hvis du vil vite mer om multiplikasjon se artikkelen Multiplikasjon.
For å øve mer, se oppgavesettet om multiplikasjon og omvendt proporsjonale funksjoner i Treningsleieren.
Oppgave 5 (3 poeng) Nettkode: E-4AQQ
Formlene nedenfor kan brukes for å anslå hvor høyt et barn vil bli i voksen alder.
Gutt: (fars høyde + mors høyde) cm
Jente: (fars høyde + mors høyde) cm
Mors og fars høyde oppgis i centimeter.
En familie består av mor, far og barna Ola og Kari. Mor er 160 cm høy, og far er 180 cm høy.
a)
Hvor høye vil Ola og Kari bli i voksen alder ifølge formlene ovenfor?
Løsningsforslag a)
Jeg tenker:
Vi må sette inn mors og fars høyde inn i
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Vi vet at mor er høy, og at far er høy. Ola er en gutt, så da setter vi inn dette i den første oppgitte formelen. Dermed blir Ola i følge formelen. Vi merker oss at vi regnet ut at , og at vi skal regne ut akkurat det samme når vi finner Karis høyde. Det sparer oss tid å bruke dette tallet direkte, i stedet for å regne det ut igjen. Kari er en jente, og vi bruker jenteformelen for å finne hennes anslåtte høyde: altså er det anslått at Kari blir .
Svar: for Ola, og for Kari.
Mer om:
Denne oppgaven er om
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Hvis du vil vite mer om de fire regneartene se lynkurset Tallregning - de fire regneartene.
For å øve mer, se oppgavesettet de fire regneartene i Treningsleieren.
Visste du at:
Tallet er
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
b)
En annen familie består av mor, far og sønnen Per, som nå er voksen. Far er 186 cm høy. Per er 189 cm høy.
Hvor høy er mor i denne familien ifølge den første formelen ovenfor?
Løsningsforslag b)
Jeg tenker:
Vi må bruke
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Formelen i oppgaven sier at Vi vet at Per er 189 høy og at faren er 186 høy, og vi setter dette inn i uttrykket ovenfor. Dette tolker vi som en ligning med mors høyde som ukjent. Derfor lar vi betegne høyden til mor. Vi dropper foreløpig alle enhetsbetegnelser (altså der hvor det står cm) for enkelhets skyld. Ligningen blir da Vi vil ha alene på en side, og det første vi gjør er å flytte alle ledd uten i seg på venstre side. Derfor subtraherer vi med på hver side av likhetstegnet. Vi ser at -en vår er inne i en parentes. Vi kunne multiplisert ut parentesen, men i stedet multipliserer vi med 2 på begge sider. Det siste vi må gjøre for å få alene er å subtrahere 186 fra hver side. Dermed har vi funnet ut at moren er høy.
Svar: Moren er høy.
Mer om:
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
For flere eksempler og forklaringer se artikkelen Lineære likninger og lynkurset Likninger.
For å øve mer, se oppgavesettet om lineære likninger i Treningsleieren.
Oppgave 6 (4 poeng) Nettkode: E-4AQU

På bildet ovenfor ser du rundballer som inneholder fôr til husdyr. En rundball har tilnærmet form som en sylinder med diameter og høyde lik 1,2 m.
a)
Gjør overslag og bestem volumet av en rundball. Gi svaret i liter.
Løsningsforslag a)
Jeg tenker:
Vi skal gjøre
Overslag
Brukes for å vite omtrent hvor mye noe vil koste eller hvor stort noe er. Overslag utføres ofte i hodet og tallene som inngår i regnestykket rundes av. Det finnes regler for avrunding, slik at forskjellen mellom nøyaktig svar og overslaget ikke blir for stort.
Fordi svaret ikke er nøyaktig, erstattes likhetstegnet med tegnet for tilnærmet lik .
Eksempel:
Rundballene har cirka form som en
Sylinder
En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.
Én måte å gjøre overslag på her er å runde høyden ned til 1 m og radius ned til m. Da har vi rundet ganske mye ned, så vi har råd til å runde opp til 4. Det anslåtte volumet blir da Her er det lurt å vite at er det samme som en fjerdedel. Derfor blir volumet cirka Vi skal gi svaret i liter, og vi husker at én kubikkmeter gir 1 000 liter (som tilsvarer ett tonn i vekt). Volumet blir derfor cirka 1 000 L.
Svar: Cirka 1000 L.
Mer om:
Denne oppgaven er om
Overslag
Brukes for å vite omtrent hvor mye noe vil koste eller hvor stort noe er. Overslag utføres ofte i hodet og tallene som inngår i regnestykket rundes av. Det finnes regler for avrunding, slik at forskjellen mellom nøyaktig svar og overslaget ikke blir for stort.
Fordi svaret ikke er nøyaktig, erstattes likhetstegnet med tegnet for tilnærmet lik .
Eksempel:
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.
Areal:
Omkrets:
For flere eksempler og forklaringer se En sylinder i lynkurset Geometri - areal og volum.
En artikkel om overslag er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om overslagsregning i Treningsleieren.
Visste du at:
Det egentlige volumet er rundt 1 357 L, så vi kunne ha rundet flere ting oppover.
b)
Gjør overslag og bestem overflaten av en rundball.
Løsningsforslag b)
Jeg tenker:
Vi kan bruke de samme avrundingene som før.
Arealet til en sylinder er lik arealet av lokket, bunnen og sideflaten summert. Lokket og bunnen har samme areal, nemlig ; siden har areal lik omkretsen til sirkelbunnflaten multiplisert med høyden, . Vi anslår at høyden er 1 meter, radius i bunnen og toppen er meter og at er 4. Da blir overslaget av overflaten lik
Svar: Overflaten er på cirka .
Mer om:
Denne oppgaven er om
Overslag
Brukes for å vite omtrent hvor mye noe vil koste eller hvor stort noe er. Overslag utføres ofte i hodet og tallene som inngår i regnestykket rundes av. Det finnes regler for avrunding, slik at forskjellen mellom nøyaktig svar og overslaget ikke blir for stort.
Fordi svaret ikke er nøyaktig, erstattes likhetstegnet med tegnet for tilnærmet lik .
Eksempel:
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.
Areal:
Omkrets:
For flere eksempler og forklaringer se En sylinder i lynkurset Geometri - areal og volum.
En artikkel om overslag er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettene om overslagsregning og overflateareal i Treningsleieren.
Visste du at:
Det eksakte arealet er rundt kvadratmeter, så vi var ikke så langt unna.
Oppgave 7 (4 poeng) Nettkode: E-4AQY
Forskere skal prøve ut en ny test for å avgjøre om en person er smittet av en bestemt sykdom.
Testen skal prøves ut på 360 personer. På forhånd vet forskerne at 60 av disse personene er smittet av sykdommen, mens resten ikke er smittet.
Det viser seg at 68 av personene tester positivt (det vil si at testen viser at de er smittet av sykdommen). Av disse 68 er det 10 personer som forskerne vet ikke er smittet.
a)
Tegn av og fyll ut krysstabellen nedenfor.
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
Løsningsforslag a)
Jeg tenker:
Vi skal sette opp en
Krysstabell
En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
Først lager vi tabellen slik den er satt opp i oppgaven.
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
Vi vet at det var totalt 68 personer som testet positivt. Det betyr at vi skal skrive 68 i raden “Tester positivt” under kolonnen “Sum”. Vi vet også at det var 360 personer med i forsøket, og siden 68 personer testet positivt, må de resterende ikke ha testet positivt. Dette fører vi inn under “Sum” i rekken ``Tester ikke positivt. Vi vet også at det er totalt 360 personer med i forsøket totalt, så vi skriver 360 nederst i høyre hjørne.
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
Vi kan gjøre det tilsvarende i “Sum”-raden, med de som er smittet og ikke smittet. Av 360 er 60 personer smittet, så er ikke smittet.
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
I ruten øverst til venstre skal vi altså skrive hvor mange av de smittede som testet positivt for sykdommen. Helst skulle alle som var smittet teste positivt, men av de 68 personene som testet positivt var det 10 som ikke var smittet. Da var det av de smittede som testet positivt. Siden det var 10 personer uten sykdommen som testet positivt, skriver vi dette inn i ruten ved siden av.
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
Siden bare 58 av de 60 smittede testet positivt, må 2 av de smittede ikke ha testet positivt. Dette fyller vi inn der “Smittet”-kolonnen krysser “Tester ikke positivt”-kolonnen. I den siste ruten skal vi skrive hvor mange som ikke hadde sykdommen, og som heller ikke testet positivt. Vi slår opp i tabellen vår og ser at det var 292 personer som ikke testet positivt, men vi vet fra tidligere at 2 av disse faktisk hadde sykdommen. Derfor skal vi skrive i den siste ruten.
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
Vi kan sjekke om vi har skrevet den riktige tabellen ved å se at det som står i “Sum”-kolonnen faktisk er summen av det som står i sin rad. I den første raden er , og , så det stemmer. Det samme må gjøres med “Sum”-raden også, hvis vi vil vite at alt er korrekt.
Svar:
| Smittet | Ikke smittet | Sum | |
| Tester positivt | |||
| Tester ikke positivt | |||
| Sum |
Mer om:
Denne oppgaven er om
Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
For flere forklaringer og eksempler se artikkelen Gruppering av data.
b)
Bestem sannsynligheten for at en person som er smittet, tester positivt.
Løsningsforslag b)
Jeg tenker:
Vi må gå til
Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Vi ser på krysstabellen vår. Sannsynligheten for at en person som er smittet tester positivt, er Dette kan vi finne ut av ved hjelp av krysstabellen vår. Under “Smittet”-kolonnen i “Tester positivt”-raden står det 58, så 58 av personene som var smittet testet positivt. Totalt var det 60 personer som var smittet, så brøken over er lik eller ved å dele på to over og under brøkstreken. Hvis vi vil ha sannsynligheten i prosent, multipliserer vi med , og sannsynligheten blir Denne brøken kan vi regne ut på vanlig måte for hånd, men vi kan forenkle den litt først. Vi kan flytte 100 inn i brøken og krysse ut to nuller. Veldig ofte er det en god idé å faktorisere brøker før man regner dem ut for hånd. Vi ser at både telleren og nevneren ender med sifre som er partall, og det betyr at begge tallene kan divideres på 2. Vi vet at . For å finne er det lurt å først prøve seg på . Dette kan vi skrive som og vi vet at og at . Derfor er , og følgelig er . Dermed kan vi skrive brøken ([7b]) som der vi har forkortet den felles faktoren 2. Vårt nye regnestykke er altså . Dette kan virke som en lang omvei for å gjøre utregningen bare litt lettere, men meningen er at vi skal gjøre utregningene ovenfor i hodet. Det er dessuten god trening, og hvis man mestrer hoderegningen er denne måten å gjøre det på veldig grei.
Vi lurer kanskje på om vi kan faktorisere 290 enda mer slik at vi kan stryke 3-tallet i nevneren også. Her kan vi bruke et triks. Det viser seg at det er slik at et tall er delelig med 3 hvis og bare hvis tallets tverrsum er delelig med 3. Tverrsummen er alle sifrene til tallet lagt sammen; i dette tilfellet er tverrsummen . Vi vet at 11 ikke er delelig med 3, og derfor er heller ikke 290 delelig med 3. Derfor må vi regne ut på vanlig måte.
| 2 | 9 | 0, | 0 | : | 3 | = | 9 | 6, | 6 | |
| 2 | 7 | |||||||||
| 2 | 0 | |||||||||
| - | 1 | 8 | ||||||||
| 2 | 0 |
Vi kan fortsette videre, men vi vil få samme svar igjen. Vi får dermed at svaret blir cirka .
Svar: Cirka , eller .
Mer om:
Denne oppgaven er om
Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
For flere eksempler og forklaringer om sannsynlighet se artikkelen Hvordan finner vi uniform sannsynlighet? Hvis du vil vite mer om prosent og prosentregning, se lynkurset Prosent. Hvis du vil vite mer om divisjon og de fire regneartene, se artikkelen Divisjon.
For å øve mer, se oppgavesettene om sannsynlighet, prosentregning og divisjon i Treningsleieren.
Visste du at:
Sannsynligheten for at hendelsen inntreffer er den samme som prosentandelen av de som ble smittet og testet positivt, av antall som ble smittet totalt.
c)
Bestem sannsynligheten for at en person som tester positivt, ikke er smittet.
Løsningsforslag c)
Jeg tenker:
Denne oppgaven er nesten helt lik som den forrige. Vi må igjen gå til krysstabellen vår og se på forholdet mellom det som står i de riktige rutene.
Sannsynligheten for at en person som tester positivt ikke er smittet, er Som i forrige oppgave ser vi på krysstabellen vår. Der står det at 10 av de som testet positivt ikke var smittet, og at det var 68 personer som testet positivt totalt. Brøken over blir da Altså er det rundt sannsynlighet for at en person som ikke er smittet tester positivt for sykdommen. Dette kalles en “falsk positiv”.
Svar: Cirka , eller .
Mer om:
Denne oppgaven er om
Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
For flere eksempler og forklaringer om sannsynlighet se artikkelen Hvordan finner vi uniform sannsynlighet? Hvis du vil vite mer om prosent og prosentregning, se lynkurset Prosent. Hvis du vil vite mer om divisjon og de fire regneartene, se artikkelen Divisjon.
For å øve mer, se oppgavesettene om sannsynlighet, prosentregning og divisjon i Treningsleieren.
Visste du at:
Igjen er det en sammenheng mellom sannsynlighet og prosentandel.
Oppgave 8 (3 poeng) Nettkode: E-4AR8
Funksjonene , og er gitt ved
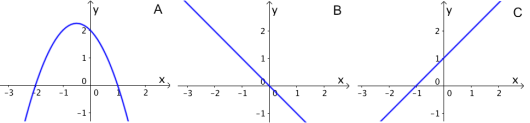
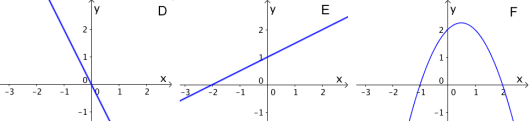
Nedenfor ser du grafene til seks ulike funksjoner. Hvilken graf er grafen til , hvilken graf er grafen til , og hvilken graf er grafen til ? Begrunn svarene dine.
Løsningsforslag
Jeg tenker:
Først kan vi bruke det vi vet om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Vi kunne valgt å sette inn forskjellige verdier for i funksjonene , og og se hvilke grafer som passer inn, men dette tar gjerne en del tid. For å gjøre arbeidet mindre kan vi først luke ut hvilke grafer som ikke kan tilhøre de forskjellige funksjonene.
Det første vi ser er at fire av grafene er rette linjer, altså at de er grafer til lineære funksjoner. Lineære funksjoner er funksjoner på formen , der og er konstanter. Vi kan dermed se at både og er lineære: For er og , og for er og . Derfor kan ikke grafene og tilhøre eller . Derimot må en av dem tilhøre , siden ikke er lineær og og er de eneste ikke-lineære grafene.
Videre kan vi se på funksjonenes konstantledd. Funksjonen har 0 som konstantledd, så grafen til må gå gjennom origo (midten av koordinatsystemet). Derfor må grafen til enten være eller . Konstantleddet til er 1, så grafen til må krysse punktet i koordinatsystemet. De eneste grafene som gjør det er og , så det må være en av disse.
Vi kan også se på stigningstallet til de lineære (rette) funksjonene, altså det tallet som multipliseres med . For har vi , så stigningstallet er -1. Kandidatene til grafen til er og , og vi ser at er den eneste av de to med stigningstall -1. Vi ser dette fordi stigningstallet betyr hvor mange enheter på -aksen man går per enhet på -aksen; går én nedover, mens går to. Vi gjør det samme for . Stigningstallet til er , så grafen til skal være ganske slak. Kandidatene er og , og er den eneste av de to som passer. Dermed har vi funnet ut at grafen til er , og at grafen til er .
Til slutt må vi finne ut av hvilken av grafene og som passer til . Dette kan vi gjøre ved å sammenligne nullpunkter. Vi ser at har et nullpunkt i og at har et nullpunkt i . Vi setter disse verdiene inn i funksjonsuttrykket til . Om så er riktig graf, og hvis så er riktig graf. Vi får at dermed har et nullpunkt i , så er den riktige grafen.
Svar: Grafen til er , grafen til er og grafen til er .
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
For flere eksempler og forklaringer se artiklene Rette linjer (lineære funksjoner) og Hvofor ser grafen ut som den gjør? i lynkurset Funksjoner (del I). Hvis du vil vite enda mer om funksjoner og deres grafer se lynkurset Funksjoner (del II).
For å øve mer, se oppgavesettet om funksjoner i Treningsleieren.
Visste du at:
Vi kunne også ha skilt de to ikke-lineære grafene ved å sammenligne deres toppunkter. For å finne toppunktet til en funksjon kan vi bruke . Alt dette er en del av en gren av matematikken som heter funksjonsdrøfting. Hvis du vil vite mer om funksjonsdrøfting, se lynkurset Funksjonsdrøfting.
DEL 2 Med hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4ARH
En bedrift produserer og selger en vare. Kostnadene kroner og inntektene kroner ved produksjon og salg av enheter av varen er gitt ved
a)
Bruk graftegner til å tegne grafene til funksjonene og i samme koordinatsystem.
Løsningsforslag a)
Jeg tenker
Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Vi skal tegne grafene for -verdier mellom 10 og 100, så vi drar -aksen slik at vi ser disse verdiene. Vi ser også at konstantleddet til er veldig høyt, så vi må ha ganske høye verdier på -aksen for å kunne se hele grafen. Vi velger å la -aksen gå til . Vi kan eventuelt høyreklikke på en av koordinataksene og stille inn verdiene der, eller så kan vi tegne grafen først og tilpasse aksene etterpå. I “Skriv inn”-boksen skriver vi
K(x) = Funksjon[8.5x^2 + 25x + 11900, 10, 100]og deretter trykker vi “Enter”. Vi skriver “Funksjon[...]” fordi vi bare vil tegne grafen mellom og . Etter det skriver vi det tilsvarende for .
I(x) = Funksjon[790x, 10, 100]Resultatet blir noe tilsvarende bildet under.
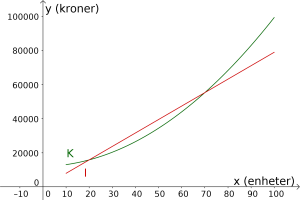
Svar: 
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer se artiklene Koordinatsystem, Rette linjer (lineære funksjoner) og Hvor ser grafen ut som den gjør? i lynkurset Funksjoner (del I). For enda mer om funksjoner se Funksjoner (del II).
For å øve, se oppgavesettet om grafisk framstilling i Treningsleieren.
b)
For hvilke verdier av x er inntektene og kostnadene like store?
Løsningsforslag b)
Jeg tenker:
Inntektene og kostnadene er like store der
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi bruker den samme
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Skjæring[ <Funksjon>, <Funksjon>,
<Startverdi for x>, <Sluttverdifor x> ]i “Skriv inn”-boksen. Vi kan også trykke direkte på skjæringspunktene. Vi fyller inn funksjonene våre, og lar gå mellom 10 og 100:
Skjæring[ I, K, 10, 100 ]Resultatet blir slik.
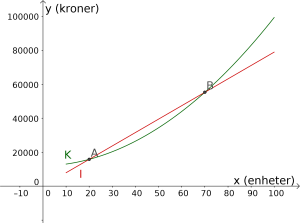
I algebrafeltet kan vi se at koordinatene til og er henholdsvis og . Det betyr at for og for så er inntektene og kostnadene like store.
Svar: For og for .
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
For flere eksempler og forklaringer se Grafisk løsning av likninger. For mer om funskjoner se lynkurs Funksjonsdrøfing.
Lynkurs om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om skjæringspunkt i Treningsleieren.
Visste du at:
I denne oppgaven har vi løst likningen ved hjelp av graftegneren. Vi kunne også ha løst det ved å bruke annengradsformelen. Det finnes en stor teori bak å løse slike og mye mer kompliserte likninger ved hjelp av datamaskin, og man kan løse likninger på datamaskin som er praktisk umulig å løse for hånd. Denne teorien kalles numerisk matematikk.
c)
Hvor mange enheter av varen må bedriften produsere og selge for at overskuddet skal bli størst mulig? Hvor stort blir overskuddet da?
Løsningsforslag c)
Jeg tenker:
Vi må lage et uttrykk for overskuddet og finne ut når dette er størst.
Vi bruker samme Geogebra-fil som i forrige oppgave. Vi vet at overskudd er inntekt minus kostnad. Med andre ord er et uttrykk for bedriftens overskudd. Vi kan regne ut og se at
og deretter plotte dette inn i koordinatsystemet, men vi kan i stedet skrive
O(x) = I(x) - K(x)direkte inn i “Skriv inn”-boksen. Resultatet er vist under.
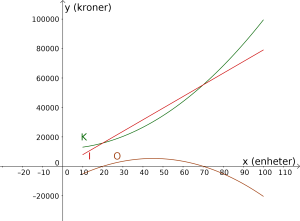
Vi vil finne når overskuddet er størst. Vi bruker kommandoen
Ekstremalpunkt[ <Funksjon>, <Start>, <Slutt> ]Vi fyller inn funksjonen vår, og vi lar gå fra 10 til 100, som vanlig.
Ekstremalpunkt[ O, 10, 100 ]Resultatet er vist under.
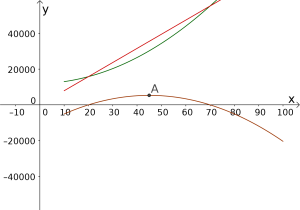
I algebrafeltet ser vi at toppunktet til grafen er . Det betyr at overskuddet har sin høyeste verdi, , når .
Svar: Overskuddet har størst verdi, , når .
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Ekstremalpunkt

Vi sier at et punkt er et ekstremalpunkt for en funksjon hvis det enten er et toppunkt eller bunnpunkt for funksjonen.
For flere eksempler og forklaringer se artiklene Grafisk løsning av likninger og Topp- og bunnpunkt i lynkurs Funksjonsdrøfting.
Lynkurs om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleieren.
Oppgave 2 (3 poeng) Nettkode: E-4ARL
For 3 år siden kjøpte Silje en ny scooter. Verdien av scooteren har falt med 15 % per år. I dag har scooteren en verdi på ca. 8 600 kroner.
a)
Bestem scooterens verdi om 2 år.
Løsningsforslag a)
Jeg tenker:
Hvis vi
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.
Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
Scooterens verdi er kroner, og den vil falle i verdi hvert år. Vi kan finne hva scooterens verdi er etter ett år ved å multiplisere med vekstfaktoren Hvis vi er usikre på hvordan vi kommer fram til vekstfaktoren, kan vi regne oppgaven fra bunnen av. Vi vil da finne ut hva av er. Det regner vi ut slik: Prisen etter ett år vil da være kroner. Vi kan gjøre det samme igjen med kroner i stedet for for å finne scooterens verdi etter to år, men la oss først se på en snarvei som kan gjøre hele oppgaven lettere. I ligningen over finner vi av beløpet og trekker dette fra totalbeløpet. Vi kunne i stedet ha funnet av totalbeløpet, og vi ville ha fått svaret med én gang: I ligningen over skriver vi . Dette er det samme som Dette er vekstfaktoren. Altså kunne vi ha kommet fram til scooterens verdi direkte ved å multiplisere med . Det samme kan vi gjøre for år nummer to:
Vi må da regne ut dette,
Altså er scooterens verdi etter to år lik kroner. Vi kunne kommet fram til samme svar ved å multiplisere med to ganger:
Svar: Scooterens verdi etter to år er kroner.
Mer om:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere eksempler og forklaringer se artikkelen Regneregler lynkurset Prosent.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Visste du at:
Vi kan gjøre trikset vårt med å multiplisere med mer generelt. Hvis vi har en verdi, , som minker i verdi hvert år, så er verdien etter år lik I denne oppgaven er , og .
En annen nyttig ting vi kan ta fra denne oppgaven er at av alltid er lik . For eksempel er av lik .
b)
Hvor mye kostet scooteren da den var ny?
Løsningsforslag b)
Jeg tenker:
Her må vi tenke litt baklengs: Vi har en verdi som faller med hvert år. Hva må den opprinnelige verdien være dersom verdien etter tre år er ? Vi må komme fram til en ligning.
La oss først prøve å finne verdien til scooteren året før, og deretter prøve å generalisere metoden vår. La være den ukjente verdien til scooteren året før. Vi vet at den falt med i verdi til kroner. Det betyr at kroner er av verdien . Med andre ord, Dette kan skrives på en annen måte som Vi vil finne , så vi dividerer med på hver side av likhetstegnet, forkorter venstre side og regner ut høyre side. Dette betyr at verdien året før var cirka kroner. Dette kan vi gjøre igjen, med i stedet for , og deretter enda en gang – men vi kan løse hele problemet med én ligning hvis vi tenker litt lurt. La være den ukjente opprinnelige verdien til Siljes scooter. Etter tre år med synking i verdi har den gått ned til kroner. Det betyr at Dette er nesten det samme som vi gjorde i forrige oppgave, bare andre veien. Denne ligningen kan vi løse ved å dividere med på begge sider av likhetstegnet og forkorte: Dette betyr at scooteren opprinnelig kostet cirka kroner, eller cirka 14 000 kroner.
Svar: Scooteren kostet opprinnelig cirka kroner, eller cirka 14 000 kroner.
Mer om:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere eksempler og forklaringer se artikkelen Regneregler lynkurset XXXX.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 3 (5 poeng) Nettkode: E-4ARR
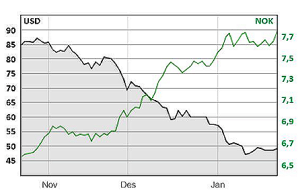
Den svarte grafen i diagrammet ovenfor viser hvordan prisen for et fat olje, gitt i dollar (USD), utviklet seg fra slutten av oktober 2014 til slutten av januar 2015. Den grønne grafen viser hvordan dollarkursen utviklet seg i den samme perioden.
Dollarkurs er prisen for 1 dollar (USD) i norske kroner (NOK).
Prisen for et fat olje (i USD) er gitt til venstre i diagrammet og dollarkursen (i NOK) til høyre i diagrammet.
a)
Hvor mange USD har prisen for et fat olje gått ned i løpet av perioden som er vist i diagrammet? Hvor mange prosent tilsvarer dette?
Løsningsforslag a)
Jeg tenker:
Vi må se på differansen mellom der oljeprisen startet og der den sluttet. Disse tallene finner vi henholdsvis til venstre og til høyre der den svarte grafen krysser kantene.
Den svarte grafen og tallene på venstre side viser oljeprisen. Den starter på rundt 85 USD per fat, og avtar til cirka 50 USD per fat. Det betyr at den har falt USD på tre måneder. Vi skal regne ut hvor mange prosent dette er av utgangspunktet, altså av 85 USD. Det blir
Svar: Oljeprisen har gått ned cirka 35 USD, som tilsvarer om lag .
b)
Bestem prisen for et fat olje i NOK i starten av perioden som er vist i diagrammet.
Løsningsforslag b)
Jeg tenker:
Vi må først finne
Valutakurs
Valutakursen forteller hvilken verdi pengene i to land har i forhold til hverandre.
Denne kursen bestemmes fra dag til dag i de enkelte land.
Vi er interesserte i den grønne grafen, og vi undersøker den helt til venstre av diagrammet. Den starter på et tall cirka midt mellom 45 og 50 av tallene til venstre. Vi er derimot interesserte i de grønne tallene som står til høyre, siden det er de som sier noe om dollarkursen. Hvis vi følger linjene til høyre side, ser vi at et tall midt mellom 45 og 50 på venstre side svarer til et tall mellom og på høyre side, med andre ord cirka . Dermed kostet 1 USD rundt NOK i starten av perioden. Prisen for et fat olje var 85 USD, og i NOK var dette Altså kostet et fat olje 561 NOK i begynnelsen av perioden.
Svar: Et fat olje kostet 561 NOK i begynnelsen av perioden.
Mer om:
Denne oppgaven er om
Valutakurs
Valutakursen forteller hvilken verdi pengene i to land har i forhold til hverandre.
Denne kursen bestemmes fra dag til dag i de enkelte land.
Lynkurset om valuta er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om norske penger og andre valuta i Treningsleiren.
c)
Hvor mange NOK har oljeprisen gått ned i løpet av perioden som er vist i diagrammet? Hvor mange prosent tilsvarer dette?
Løsningsforslag c)
Jeg tenker:
Først må vi finne ut hva som var prisen i NOK for et fat olje i slutten av perioden, og så kan vi regne ut prisforskjellen.
Oljeprisen gikk ned fra 85 USD til 50 USD. Vi må regne ut dollarkursen i slutten av perioden for å omregne 50 USD til NOK. Vi ser at den grønne grafen er på cirka i slutten av perioden, så 50 USD blir til norske kroner. Det betyr at oljeprisen sank med NOK. Vi vil vite hvor mange prosent dette er av startbeløpet, altså av 561. Det blir
Svar: Prisen i NOK for et fat olje falt med 176 NOK, eller cirka .
Mer om:
Denne oppgaven er om
Valutakurs
Valutakursen forteller hvilken verdi pengene i to land har i forhold til hverandre.
Denne kursen bestemmes fra dag til dag i de enkelte land.
For flere eksempler og forklaringer se artikkelen Regneregler i lynkurset
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Lynkurset om valuta er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om norske penger og andre valuta i Treningsleiren.
d)
Sammenlikn svarene i oppgave a) og oppgave c), og kommenter.
Løsningsforslag d)
Jeg tenker
Her ser vi på svarene i a) og c) og vi bruker prosentpoeng.
Ifølge svaret i deloppgave a):
oljeprisen har gått ned cirka 35 USD, som tilsvarer om lag .
Ifølge svaret i deloppgave c):
prisen i NOK for et fat olje falt med 176 NOK, eller cirka .
Når vi sammenligner to prosenttall, kan vi bruke prosentpoeng. Vi ser at prisen i USD falt omlag prosentpoeng mer enn prisen i NOK. Hvis vi ser på dollarkursen i samme tidsrom, ser vi at denne steg mye.
Svar: Prisen i USD falt om lag ti prosentpoeng mer ned enn prisen i NOK. Dette kan vi knytte til at dollarkursen steg mye i tidsrommet.
Oppgave 4 (8 poeng) Nettkode: E-4ARX
Under ser du Sofies timeliste for februar. Ordinær arbeidstid er 37,5 timer per uke. Arbeid utover dette regnes som overtid.
| Timeliste februar |
|
| Uke 6 | 40 timer |
| Uke 7 | 41 timer |
| Uke 8 | 37,5 timer |
| Uke 9 | 39 timer |
a)
Lag et regneark som vist i figur 1 nedenfor, og bruk dette til å bestemme nettolønnen til Sofie i februar. Legg inn opplysningene fra timelisten i de gule cellene, og lag formler i de mørkegrå cellene.
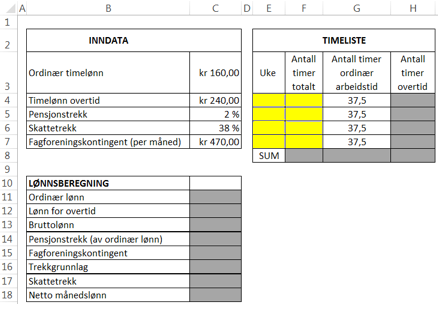
Løsningsforslag a)
Jeg tenker:
Vi lager regneark i programmet Excel. Det første vi må gjøre er å fyllle inn antall timer Sofie har jobbet i de forskjellige ukene i februar, og deretter regne ut overtid og lønn.
Først setter vi opp regnearket som i oppgaven.
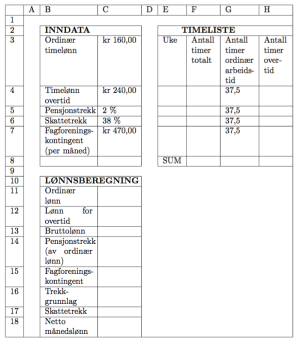
I første rekke er vi ute etter timelisten. Først skriver vi på de forskjellige uketallene. I den utfylte timelisten står det at vi er i ukene 6, 7, 8 og 9. Ved siden av uketallene skriver vi hvor mye Sofie arbeidet den uken. Det står på høyre side av der uketallene står i timelisten.
| E | F | G | H | |
| 1 | ||||
| 2 | TIMELISTE | |||
| 3 |
Uke |
Antall timer totalt
|
Antall timer ordinær arbeidstid |
Antall timer overtid |
| 4 | 6 | 40 | 37,5 | |
| 5 | 7 | 41 | 37,5 | |
| 6 | 8 | 37,5 | 37,5 | |
| 7 | 9 | 39 | 37,5 | |
| 8 | SUM | |||
Nå må vi regne ut hvor mye Sofie jobbet i overtid hver uke. I timelisten vi fylte ut står det at antall timer med ordinær arbeidstid er – og det betyr at alt over timer regnes som overtid. I uke 6 jobbet Sofie dermed timer overtid. Dette er vi bedt om å skrive en generell formel for, så i ruten til høyre, altså i H4, skriver vi
=F4-G4Dette betyr at vi tar antall ordinære arbeidstimer, som står i G4, blir trukket fra det faktiske antallet timer Sofie jobbet, som står i F4. Vi skal ikke skrive
=40-37.5direkte inn i ruten, for poenget med slike regneark er at tallene endrer seg etter vært som vi endrer informasjonen.
Vi skal skrive det tilsvarende videre nedover til H7, altså til uke 9. Vi gjør dette ved å markere H4 og “dra” ruten nedover. Dermed ser regnearket slik ut.
| E | F | G | H | |
| 1 | ||||
| 2 | TIMELISTE | |||
| 3 |
Uke |
Antall timer totalt
|
Antall timer ordinær arbeidstid |
Antall timer overtid |
| 4 | 6 | 40 | 37,5 | 2,5 |
| 5 | 7 | 41 | 37,5 | 3,5 |
| 6 | 8 | 37,5 | 37,5 | 0 |
| 7 | 9 | 39 | 37,5 | 1,5 |
| 8 | SUM | |||
I SUM-rekken skal vi summere kolonnene vi er i; i F8 skal vi altså summere alle F-rutene over. Dette gjør vi ved å skrive
=F4+F5+F6+F7i ruten F8. Vi “drar” ruten bortover til H8, og regnearket ser slik ut:
| E | F | G | H | |
| 1 | ||||
| 2 | TIMELISTE | |||
| 3 |
Uke |
Antall timer totalt
|
Antall timer ordinær arbeidstid |
Antall timer overtid |
| 4 | 6 | 40 | 37,5 | 2,5 |
| 5 | 7 | 41 | 37,5 | 3,5 |
| 6 | 8 | 37,5 | 37,5 | 0 |
| 7 | 9 | 39 | 37,5 | 1,5 |
| 8 | SUM | 157,5 | 150 | 7,5 |
Så går vi over til lønnsberegningen. I C11 skal vi skrive inn ordinær lønn, det vil si lønnen Sofie får av den ordinære arbeidstiden. Antall timer ordinær arbeidstid står i rute G8, som vi nettopp regnet ut, og den ordinære timelønnen står i rute C3. Dermed skriver vi i C11 det følgende:
=G8*C3I C12, altså lønn for overtid, gjør vi det samme med overtidsarbeidet og -timelønnenlønnen. Bruttolønnen er ordinær lønn addert med overtidslønnen, og vi skriver
=C11+C12i ruten C13. Deretter skal vi regne ut pensjonstrekket, som er av ordinær lønn. Prosenttallet står i C5, og for å regne ut trekket multipliserer vi tallet i C5 med bruttolønnen i C11.
=C11*C5Fagforeningskontingenten er det samme tallet hver måned, uavhengig av lønnen, og denne avgiften står i C7. Derfor skriver vi bare “=C7” i denne ruten. Trekkgrunnlaget er da summen av C14 og C15, trukket fra bruttolønnen i C13. Skattetrekket regner vi ut på samme vis som med pensjonstrekket:
=C16*C6Netto månedslønn får vi ved å trekke skatten fra trekkgrunnlaget.
=C16-C17Til slutt står vi igjen med følgende regneark.
| A | B | C | |
| 10 | LØNNSBEREGNING | ||
| 11 | Ordinær lønn | 24000 | |
| 12 | Lønn for overtid | 1800 | |
| 13 | Bruttolønn | 25800 | |
| 14 | Pensjonstrekk (av ordinær lønn) | 480 | |
| 15 | Fagforeningskontigent | 470 | |
| 16 | Trekkgrunnlag | 24850 | |
| 17 | Skattetrekk | 9443 | |
| 18 | Netto månedslønn | 15407 | |
Dermed er netto månedslønn lik kroner.
Svar: Netto månedslønn er lik kroner.
Mer om:
Denne oppgaven er om regneark,
Netto månedslønn
Lønnen du får utbetalt. Da er skatt, fagforeningskontigent og lignende trukket fra bruttolønna.
Lynkurs om regneark og lønnsberegning er under utarbeidelse og kommer snart.
b)
Utvid regnearket fra oppgave a) som vist i figuren under. Lag formler i de mørkegrå cellene. Bruk regnearket til å bestemme hvor stort beløp Sofie overførte til sparekontoen i februar.
| 20 | SPARING | |
| 21 |
Overføring til sparekonto, 20% av netto månedslønn |
|
| 22 |
Ekstra overføring til sparekont, 60% av netto månedslønn som overstiger 15 000 kr |
|
| 23 | Sum overføring sparekonto |
Sofie overfører noe av månedslønnen til en sparekonto. Se figuren over. Beløpet som overføres til sparekontoen, rundes av nedover til nærmeste hele krone.
Løsningsforslag b)
Jeg tenker:
Vi utvider regnearket og regner videre som i forrige oppgave.
Først skal vi regne ut C21, altså overføring til sparekontoen som består av av nettolønnen til Sofie. Nettolønnen står i C18, så i C21 skriver vi
=C18*20%I neste rute skal vi regne ut den ekstra sparingen. Sofie vil nemlig spare av de pengene hun tjener utover 15 000. Da må vi først trekke 15 000 fra nettolønnen, og regne ut av dette. Vi må dessuten sørge for at vi ikke får negative tall hvis nettolønnen er under 15 000. Det gjør vi slik:
=IF(C18>15000; (C18-15000)*60%; 0)Her har vi lagt til en kommando som sier at hvis netto månedslønn ikke er over 15 000, så skal vi heller ikke spare ekstra feriepenger.
I den siste ruten summerer vi de to foregående. Vi står igjen med følgende regneark.
| 20 | SPARING | |
| 21 |
Overføring til sparekonto, 20% av netto månedslønn |
3081,4 |
| 22 |
Ekstra overføring til sparekont, 60% av netto månedslønn som overstiger 15 000 kr |
244,2 |
| 23 | Sum overføring sparekonto | 3325,6 |
Vi husker at svaret skal rundes nedover, så Sofie overførte kroner til sparekontoen i februar.
Svar: Sofie overførte kroner til sparekontoen i februar.
Mer om:
Denne oppgaven er om Regneark,
Netto månedslønn
Lønnen du får utbetalt. Da er skatt, fagforeningskontigent og lignende trukket fra bruttolønna.
Lynkurs om regneark og lønnsberegning er under utarbeidelse og kommer snart.
c)
Anta at Sofie jobbet nøyaktig 37,5 timer hver av de fire ukene i februar.
Bruk regnearket du laget i oppgave a) og b), til å bestemme hvor stort beløp hun da ville ha overført til sparekontoen.
Løsningsforslag c)
Jeg tenker:
Alt vi trenger å gjøre er å fylle inn de nye arbeidstimene i regnearket, og lese av der feriepengene står.
Vi fyller inn i hver av rutene vi skal fylle timetall inn i. Regnearket gjør jobben for oss, og vi leser av 2 858,20 kroner. Det skal rundes ned til 2 858 kroner.
Svar: Sofie ville ha overført kroner til sparekontoen i februar.
Mer om:
Denne oppgaven er om Regneark,
Netto månedslønn
Lønnen du får utbetalt. Da er skatt, fagforeningskontigent og lignende trukket fra bruttolønna.
Lynkurs om regneark og lønnsberegning er under utarbeidelse og kommer snart.
Visste du at:
Dette viser styrken i å skrive formler i stedet for å legge inn verdiene direkte. Vi trenger bare skrive inn formlene én gang, og neste gang vi vil regne ut noe trenger vi bare å endre på noen få ruter.
Oppgave 5 (5 poeng) Nettkode: E-4AX0
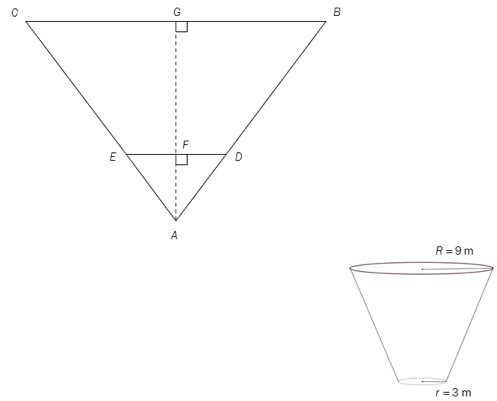
I figuren ovenfor er , , og .
a)
Bestem og .
Løsningsforslag a)
Jeg tenker:
Først tegner vi opp alt vi vet, og deretter ser vi hvordan vi kan finne
Lengde
Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
Pytagoras læresetning

Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Først tegner vi av tegningen og setter på lengdene vi fikk oppgitt.
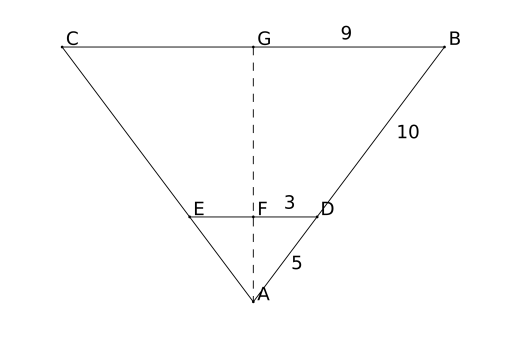
Vi er ute etter lengdene AF og FG. La oss først se på . Vi vet at er , så dette er en rettvinklet trekant med hypotenus med lengde 5 og en katet med lengde 3. Trekanter med nøyaktig disse lengdene møter man ofte på når man jobber med Pytagoras’ setning, siden det viser seg at den andre kateten har lengde 4 – så sidelengdene er alle heltall. Vi sjekker dette ved å bruke Pytagoras’ setning, som sier at hvis vi har en rettvinklet trekant med hypotenus av lengde og kateter av lengdene og , så vet vi at I vårt tilfelle er og . Vi setter inn og får følgende likning. Vi vet at og at , så likningen blir til Vi trekker fra 9 på begge sider for å få alene på høyre side, og vi får Med andre ord skal vi finne et tall slik at . Da vet vi at , så .
Så skal vi finne FG. Hvis vi kan finne AG, så kan vi finne FG ved å trekke fra AF, som vi nettopp har funnet. Vi ser at AG er en katet i . Vi vet de to andre sidelengdene til denne trekanten, så vi kan bruke Pytagoras setning igjen. Vi merker oss at . Pytagoras setning gir oss og hvis vi setter inn det vi vet får vi Vi løser med hensyn på og får Til slutt får vi at .
Svar: og .
Mer om:
Denne oppgaven er om
Lengde
Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
Pytagoras læresetning

Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
For flere eksempler og forklaringer se artikkelen Pytagoras setning.
For å øve mer, se oppgavesettet om Pytagoras læresetning i Treningsleieren.
Visste du at:
I denne oppgaven har vi brukt rettvinklede trekanter der sidene har heltallige lengder. Den ene trekanten hadde lengdene 3, 4 og 5, og den andre trekanten hadde lengdene 9, 12 og 15. Disse to triplettene med tall kalles (dette begrepet finnes ikke på nettsidene!). Et pytagoreisk trippel er tre heltall , og som er slik at Det finnes uendelig slike mange pytagoreiske tripler, og de kan finnes ved blant annet å bruke Euklids formel.
b)
Figuren til høyre viser en tank formet som en rettavkortet kjegle. Radius i bunnen er m, og radius i toppen er m.
Hvor mange liter rommer vanntanken?
Løsningsforslag b)
Jeg tenker:
Vi ser at tverrsnittet til tanken tilsvarer
Parallellogram
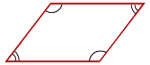
Et parallellogram er en firkant med parvis parallelle sider. Vinklene er parvis like store.
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Kjegle
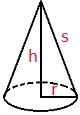
En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.
Kjeksen til en kroneis har form som en kjegle.
Volum : V =
Overflate : A =
Tverrsnittet til en kjegle må være en likebeint trekant (hvis tverrsnittet er tatt loddrett og gjennom midten av kjeglen). Dimensjonene til tanken viser at den eneste trekanten som kan være tverrsnittet til tanken, er trekanten i oppgaven over. En annen måte å se dette på er å se for seg at parallellogrammet dreier seg i rommet, og at den resulterende figuren må være tanken. I alle fall betyr dette at vi har funnet høyden av tanken – den er nemlig , som vi fant i forrige oppgave. Vi vil finne volumet av tanken, og vi har ingen direkte formel for volumet av en rettavkortet kjegle – men vi har en formel for volumet av en kjegle. Dermed kan vi finne volumet til tanken ved å finne volumet av kjeglen som tanken er en del av, og ta bort volumet av den nederste delen av kjeglen. Volumet av hele kjeglen er det volumet vi får dersom vi roterer trekanten rundt . Volumet for vi ved å rotere rundt . Volumet til tanken blir da Volumet til en kjegle med radius og høyde er Vi avventer med å sette på enheter på lengdene til slutten, for å spare skrivetid. Vi vet at høyden til hele kjeglen er , og at høyden til den lille kjeglen som vi vil ta bort er . Radiusene vet vi også er henholdsvis 9 og 3. Med dette kan vi regne ut volumene og : Til slutt setter vi inn i , og får Dermed er volumet til tanken cirka m.
Svar: Volumet til tanken er cirka m.
Mer om:
Denne oppgaven er om
Parallellogram

Et parallellogram er en firkant med parvis parallelle sider. Vinklene er parvis like store.
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Kjegle

En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.
Kjeksen til en kroneis har form som en kjegle.
Volum : V =
Overflate : A =
For flere eksempler og forklaringer se artikkelen Pyramider og kjegler i lynkurset Geometri - areal og volum.
For å øve mer, se oppgavesettet om volum i Treningsleieren.
c)
Tanken fylles med vann. Vannet renner inn i tanken med konstant fart.
Hvilken av de tre grafene nedenfor illustrerer best hvordan vannhøyden i tanken endres med tiden? Begrunn svaret ditt.
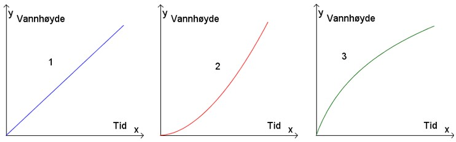
Løsningsforslag c)
Jeg tenker:
Vannstanden vokser raskere i begynnelsen, fordi volumet i bunnen er mindre enn i toppen.
Svar:
Vanent renner inn i tanken med konstant fart. Med andre ord er volumet vanns om kommer inn i tanken per sekund, konstand. Siden tanken blir videre mot toppen, vil det kreve mer vann for å øke vannstanden med 1 cm mot toppen av tanken enn det gjør i bunnen. Siden vannet renner inn i tanken med konstant fart, tar det også lengre tid å øke vannstanden med 1 cm i toppen enn det gjør i bunnen. Grafen til vannstanden skal derfor øke fortere i begynnelsen enn på slutten, og dermed er graf 3 den eneste som passer.
Mer om:
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer se artiklene Hvorfor ser grafen ut som den gjør? og Rette linjer (lineære funksjoner). Hvis du vil vite mer om grafer og funksjoner, se lynkurset Funksjoner (del II).
For å øve mer, se oppgavesettet om grafisk fremstilling i Treningsleieren.
Oppgave 6 (2 poeng) Nettkode: E-4AX9

Petter er en ivrig løper og trener hver dag. Han har tre ulike skopar som han veksler på å bruke. Når han skal ut og løpe, tar han tilfeldig et skopar.
a)
Bestem sannsynligheten for at han kommer til å bruke samme skopar de neste tre dagene.
Løsningsforslag a)
Jeg tenker:
Dette er utvalg
Sannsynlighet med tilbakelegging
Fra et utvalg trekker vi en tilfeldig gjenstand. Hvis vi legger tilbake gjenstanden før vi trekker neste, sier vi at forsøket er gjort med tilbakelegging.
Eksempel: Du skal trekke to kuler fra ei eske. Det er 5 røde og 5 blå kuler i eska. Du trekker en kule og noterer resultatet. Før du trekker neste kule, må den første legges tilbake i eska. Du har fortsatt 5 røde og 5 blå kuler i eska.
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
Petter skal trekke tre par sko av tre mulige, med tilbakelegging. Vi vil regne ut sannsynligheten for at disse tre er de samme. Sannsynligheten for at Petter velger et visst par sko den første dagen, er . Sannsynligheten for at han velger det samme paret igjen neste dag, er fremdeles . Dermed er sannsynligheten for at han velger akkurat dette skoparet to dager på rad, lik For å finne sannsynligheten for at han trekker det samme paret igjen den tredje dagen, må vi multiplisere enda en gang med , og vi får . Vi er ikke ferdige ennå! Vi har regnet ut sannsynligheten for at Petter trekker et spesifikt par alle tre dagene – for eksempel det blå paret som vist på bildet i oppgaven. Men hva om han velger det røde eller blå paret tre dager på rad? Det er like stor sannsynlighet for at han valgte det blå paret. Til sammen blir sannsynligheten for at han velger et hvilket som helst par tre dager på rad, lik Vi kunne også regnet dette ut ved å si at sannsynligheten for at han trekker et par sko første dag er 1, og sannsynligheten for at han trekker nøyaktig dette paret de to neste dagene er . Totalt blir da sannsynligheten .
Svar: Sannsynligheten er .
Mer om:
Denne oppgaven er om utvalg
Sannsynlighet med tilbakelegging
Fra et utvalg trekker vi en tilfeldig gjenstand. Hvis vi legger tilbake gjenstanden før vi trekker neste, sier vi at forsøket er gjort med tilbakelegging.
Eksempel: Du skal trekke to kuler fra ei eske. Det er 5 røde og 5 blå kuler i eska. Du trekker en kule og noterer resultatet. Før du trekker neste kule, må den første legges tilbake i eska. Du har fortsatt 5 røde og 5 blå kuler i eska.
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
For flere eksempler og forklaringer se artiklene Med eller uten tilbakelegging i lynkurset Sannsynlighet (del I) og Produktsetningen i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om produktsetningen i Treningsleieren.
b)
Bestem sannsynligheten for at han kommer til å bruke tre ulike skopar de neste tre dagene.
Løsningsforslag b)
Jeg tenker:
Vi kan igjen bruke
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Sannsynligheten for at Petter i det hele tatt velger et par sko første dag, er 1, som i forrige oppgave. Dette er fordi han uansett velger ut et par. La oss si at han valgte ut det blå paret. Sannsynligheten for at han velger ut et nytt par neste dag, altså enten det røde eller grønne paret, er . Det er like stor sannsynlighet for å velge det røde eller grønne tre dager på rad, som for å velge det blå tre dager på rad. Den tredje dagen er det bare ett par igjen han kan velge for å velge tre forskjellige, og sannsynligheten for at han velger dette paret er . Dermed blir sannsynligheten for at han velger tre forskjellige par lik Vi merker oss at vi ikke trenger å multiplisere svaret med 3 som forrige gang, fordi vi ikke gjorde noen antagelser på hvilket par Petter valgte første gang. Vi måtte i så fall ha endret at sannsynligheten for å trekke det visse paret første dag var , gjøre dette tre ganger, og summere opp svarene. Dette ville gitt nøyaktig det samme.
Alternativ løsning
En annen måte å løse oppgaven på, er å se på forholdet mellom antall gunstige og antall mulige sko Petter kan velge mellom. Den første dagen er alle gunstige, så forholdet blir . Den neste dagen er bare to av skoparene gunstige, og den siste dagen er det bare ett par sko – så forholdene blir henholdsvis og . Sannsynligheten for å velge et gunstig par sko hver dag, blir dermed akkurat som før.
Svar: Sannsynligheten er .
Mer om:
Denne oppgaven er om
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
For flere eksempler og forklaringer se artiklene Med eller uten tilbakelegging i lynkurset Sannsynlighet (del I) og Betinget sannsynlighet og produktsetningen i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om produktsetningen i Treningsleieren.
Oppgave 7 (8 poeng) Nettkode: E-4AYV
En formel for utregning av bremselengde er gitt ved
der bremselengde (m), fart (m/s), friksjonsfaktor
På tørt sommerføre er friksjonsfaktor mellom 0,8 og 1,0. På glatt vinterføre kan være nede i .
a)
Vis at en fart på km/h tilsvarer en fart på ca. m/s.
Løsningsforslag a)
Jeg tenker:
Vi regner om km/t til m/s, og multipliserer med . Dette kalles konvertering. Vi må bruke at kilometer er meter, og vi må finne ut hvor mange sekunder det er i en time.
Vi vil finne ut hvor mange meter per sekund én kilometer per time er. Vi kan sette dette opp som en likning. Vi vet at 1 kilometer er 1 000 meter. For å regne om timer til sekunder, regner vi først om til minutter. Det er 60 minutter i 1 time, og det er 60 sekunder i 1 minutt – dermed blir det sekunder i 1 time. Vi kan skrive dette som og . Vi setter dette inn i og får Tallet foran skal være likt på begge sider av likhetstegnet, og dermed ser vi at det vil si at én kilometer per time er det samme som meter per sekund. Vi ville vite at , så vi multipliserer med 40 og får at
Svar:
Herved har vi vist at km/h tilsvarer en fart på ca. m/s.
Mer om:
Denne oppgaven er om
Fart
Fart er tilbakelagt distanse per tidsenhet.
Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.
Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
Tidsenhet
Det grunnleggende tidsmålet er sekund. Andre tidsenheter er minutt, time og døgn.
Sammenhengen mellom tidsenhetene er ikke basert på 10-tallsystemet, slik vi er vant til fra lengde og vekt.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
For flere eksempler og forklaringer se artiklene Målingsforhold og Enheter.
For å øve mer, se oppgavesettene om timer, minutter og sekunder og fart i Treningsleieren.
b)
Bestem bremselengden på sommerføre med når farten er km/h, og når farten er km/h.
Bestem bremselengden på vinterføre med når farten er km/h, og når farten er km/h.
Løsningsforslag b)
Jeg tenker:
Alt vi trenger å gjøre er å sette inn verdiene for og i den oppgitte
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Først skal vi regne ut bremselengden når og farten er . Vi vet fra forrige oppgave at . Vi setter dette inn i formelen: så bremselengden er cirka meter. Videre skal vi finne bremselengden når friksjonsfaktoren fremdeles er , men når farten dobles til , eller cirka . Vi setter dette inn i formelen: Vi ser at selv om farten bare dobles, så firedobles bremselengden.
Nå skal vi se på bremselengden med de samme hastighetene som før, men på glatt vinterføre, altså med . Vi regner ut som før, med farten henholdsvis og . Dette betyr at bremselengden med vinterføre og i fart er lik bremselengden på sommerføre med dobbelt så høy fart. Bremselengden på vinterføre i er farlig lang.
Svar: Bremselengdene er henholdsvis cirka , , og .
Mer om:
Denne oppgaven er om
Fart
Fart er tilbakelagt distanse per tidsenhet.
Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.
Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
Tidsenhet
Det grunnleggende tidsmålet er sekund. Andre tidsenheter er minutt, time og døgn.
Sammenhengen mellom tidsenhetene er ikke basert på 10-tallsystemet, slik vi er vant til fra lengde og vekt.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
For flere eksempler og forklaringer se artiklene Målingsforhold og Enheter.
For å øve mer, se oppgavesettene om timer, minutter og sekunder og fart i Treningsleieren.
c)
Hvordan endrer bremselengdene i oppgave b) seg når farten dobles? Er bremselengde og fart på glatt vinterføre proporsjonale størrelser?
Løsningsforslag c)
Jeg tenker:
Vi kan regne ut
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Vi bruker tallene fra forrige oppgave og ser at
og
Vi ser at hvis vi dobler farten vår, så firedobler vi bremselengden, både på sommerføre og vinterføre. Med dette kan vi også si at størrelsene ikke er proposjonale, for i så fall ville en dobling i farten gitt en dobling i bremselengden. For ordens skyld regner vi det også ut på vanlig måte.
Vi finner ut om bremselengde og fart på vinterføre er proposjonale størrelser. Det betyr at det finnes et eller annet tall slik at for alle verdier av fart og bremselengde. Vi setter inn verdiene vi vet om, altså bremselengdene når farten er og . Disse forholdene var ikke like, så størrelsene er ikke proposjonale.
Vi kan også se dette direkte ut i fra formelen . Når farten dobles, så firedobles telleren, fordi , mens nevneren forblir uendret.
Svar: Bremselengden firedobles når vi dobler farten, og størrelsene er ikke proposjonale.
Mer om:
Denne oppgaven er om
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
For flere eksempler og forklaringer artikkelen Proporsjonalitet.
For å øve mer, se oppgavesettet om proporsjonale funksjoner i Treningsleieren.
d)
Gjør beregninger og finn en regel for hvor fort du kan kjøre på glatt vinterføre med for å få samme bremselengde som du har på sommerføre med .
Løsningsforslag d)
Jeg tenker:
Vi må sette inn de forskjellige friksjonsfaktorene i
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
På sommerføre er bremselengden med fart lik og på vinterføre med fart er bremselengden Vi vil finne ut hvor fart vi kan ha på vinterføre for å få lik bremselengde med fart på sommerføre. Derfor setter vi de to uttrykkene over lik hverandre. Vi vil ha vinterfarten uttrykt ved sommerfarten , så vi vil ha alene på en side av likhetstegnet. Derfor multipliserer vi med nevneren som står under , og forkorter. For å få bort potensen på venstre side, tar vi kvadratroten av begge sider av likhetstegnet. Dette betyr at vi må halvere farten om vinteren for å få samme bremselengde som på sommeren. Dette stemmer med at bremselengden vi fant i b) for om vinteren var den samme som for om sommeren.
Svar: Farten om vinteren må halveres for å få samme bremselengde.
Mer om:
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Andregradslikning
En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:
Likningen kan løses ved hjelp av abc-formelen.
For flere eksempler og forklaringer se artikkelen Fra problem til likning og lynkurset Andregradslikninger.
For å øve mer, se oppgavesettet om andregradslikninger i Treningsleieren.




