Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1013 2014 Høst

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:

Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Del 2:

Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Du skal svare på alle oppgavene.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger:

Kilder for bilder, tegninger osv.

Tegninger, grafer og figurer: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4BBT

Regn ut og skriv svaret på standardform

$25 000 000 000 \cdot 0, 0005$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan begynne med å skrive begge

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

tallene på standardform

, og når vi skal finne produktet av dem er det samme hvilken rekkefølge vi mulitpliserer faktorene i.

Vi begynner med å skrive hver av faktorene på standardform:

Vi kan skrive

$0, 0005 = 5 \cdot 10^{- 4}$

$25 000 000 000 = 2, 5 \cdot 10^{10}$ .

Da har vi at

$25 000 000 000 \cdot 0, 0005 = 2, 5 \cdot 10^{10} \cdot 5 \cdot 10^{- 4}$

Vi skriver faktorene i rekkefølgen der tiereksponentene står etter hverandre og bruker potensregelen:

$p^{a} \cdot p^{b} = p^{a + b}$

Da får vi:

$2, 5 \cdot 5 \cdot 10^{10} \cdot 10^{- 4} = 2, 5 \cdot 5 \cdot 10^{10 - 4} = 12, 5 \cdot 10^{6}$

Et tall på standardform er på formen $a \cdot 10^{n}$ , der $a$ er et tall mellom $1$ og $10$ . Det medfører at tallet vårt er ikke på standardform, fordi $12, 5$ ikke er i intervallet $[1, 10)$ .

Dette kan vi ordne ved å skrive $12, 5 = 1, 25 \cdot 10$ . Det gir:

$12, 5 \cdot 10^{6} = 1, 25 \cdot 10 \cdot 10^{6} = 1, 25 \cdot 10^{7}$

Svar: $1, 25 \cdot 10^{7}$

Mer om

Denne oppgaven er om

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

tall på standardform

Flere forklaringer og eksempler på hvordan man skriver tall på standardform finner du i artikkelen Tall på standardform og om potensregler i artikkelen Potenser med samme grunntall.

For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.

Oppgave 2 (1 poeng) Nettkode: E-4BBV

Løs likningen

$2^{2 + \frac{x}{2}} = 16$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi har en likning der den ukjente $x$ er i

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger
eksponenten

til grunntallet

2

. Vi ser at vi også kan skrive høyresiden som en toerpotens.

Vi har at $16 = 2^{4}$ og dermed kan vi skrive

$\begin{matrix} 2^{2 + \frac{x}{2}} & = 16 \\ 2^{2 + \frac{x}{2}} & = 2^{4} \end{matrix}$

Begge sidene av likningen er nå potenser med samme grunntall. For at likningen skal stemme, må eksponentene være like, så da kan vi løse:

$\begin{matrix} 2 + \frac{x}{2} & = & 4 \\ \frac{x}{2} & = & 4 - 2 \\ x & = & 2 \cdot 2 \\ x & = & 4 & . \end{matrix}$

Svar: $x = 4$

Mer om

Denne oppgaven er om

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$

potens

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Ukjent

I algebra brukes bokstaver for å betegne en ukjent størrelse. En ukjent størrelse kan være et tall som skal tilfredsstille en bestemt ligning.

Eksempel: x + 7 = 16. Her er x en ukjent.

ukjente

For flere eksempler og forklaringer om potenser se Rask gjennomgang av regneregler for potens og røtter i lynkurset Potenser og røtter. Flere forklaringer og eksempler på hvordan man løser lineære likninger finner du i artikkelen Lineære likninger i lynkurset Likninger med én ukjent.

For å øve mer, se oppgavesettet om potenser og førstegradslikninger i Treningsleiren.

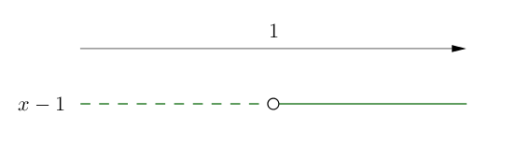
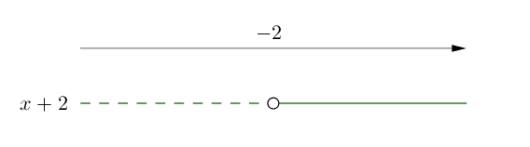
Oppgave 3 (1 poeng) Nettkode: E-4BBX

Løs likningen

$\lg (2 x - 3) = 0$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Dette er en

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmelikning

, da kan det være lurt å opphøye

10

i hver side av likningen. Logaritmen til

x

\lg x

er kun definert for

x > 0

. Det betyr i dette tilfellet at

2 x - 3 > 0

Vi ser på likningen

$\lg (2 x - 3) = 0$

Vi kan bruke den egenskapen til logaritmer at $10^{\lg a} = a$ . For å utnytte dette opphøyer vi 10 i hver side av likningen. Da får vi

$10^{\lg (2 x - 3)} = 10^{0}$

som gir

$2 x - 3 = 1$

Da får vi:

$\begin{matrix} 2 x & = & 1 + 3 \\ x & = & \frac{4}{2} \\ x & = & 2 \end{matrix}$

Da har vi at $2 x - 3 = 2 \cdot 2 - 3 = 1$ som er større enn $0$ , så vi har en gyldig $x$ -verdi.

Svar: $x = 2$

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer.

Flere forklaringer på hvordan man løser logaritmelikninger finner du i artikkelen Logaritmelikninger i lynkurset Likninger med én ukjent.

For å øve mer, se oppgavesettet om likninger med logartimefunksjoner i Treningsleiren.

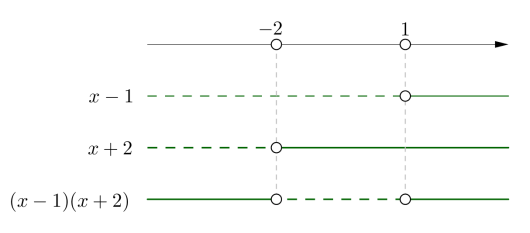
Oppgave 4 (2 poeng) Nettkode: E-4BBZ

Løs ulikheten

$x^{2} + x > 2$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Ulikheten kan løses som en andregradslikning. Vi bruker

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .
abc-formelen

til å faktorisere uttrykket og lager deretter et

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.
fortegnsskjema
.

Vi kan skrive ulikheten vår $x^{2} + x > 2$ om til $x^{2} + x - 2 > 0$ .

På venstresiden har vi et andregradsuttrykk vi kan finne nullpunktene til, og faktorisere. Da bruker vi abc-formelen til først å finne nullpunktene til $x^{2} + x - 2$ , altså ved å løse likningen $x^{2} + x - 2 = 0$ :

For et generelt andregradsuttrykk, $a x^{2} + b x + c$ , har vi at nullpunktene er gitt ved formelen
$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

I vår likning er $a = 1, b = 1 og c = - 2$ , og vi kan sette inn i formelen. Da får vi:

$x = \frac{- 1 \pm \sqrt{1 - 4 \cdot 1 \cdot (- 2)}}{2 \cdot 1}$

$x = \frac{- 1 \pm \sqrt{9}}{2}$

Dette gir de to løsningene:

$x_{1} = \frac{- 1 + 3}{2} = 1 \lor x_{2} = \frac{- 1 - 3}{2} = - 2$

Nå kan vi faktorisere venstresiden vår i ulikheten, og skriver $x^{2} + x - 2 = (x - (- 2)) (x - 1) = (x + 2) (x - 1)$ .

Videre kan vi tegne fortegnslinjer for faktorene:

$x - 1$ er negativ for $x < 1$ .

$x + 2$ er negativ for $x < - 2$

Vi setter fortegnslinjene for $x - 1$ og $x + 2$ sammen, og finner fortegnsskjema for produktet.

Fortegsnsskjemaet viser at $x^{2} + x - 2 = (x + 2) (x - 1)$ er positiv når $- 2 > x og x > 1$ og da må vi også ha at $x^{2} + x > 2$ for samme verdier.

Svar: $x^{2} + x > 2$ for $x \in ⟨ \leftarrow, - 2 ⟩ \cup ⟨ 1, \to ⟩$ .

Mer om

Denne oppgaven er om å løse ulikheter.

Flere forklaringer og eksempler på hvordan man finner løsningen av en ulikhet finner du i lynkurset Ulikheter.

For å øve mer, se oppgavesettet om ulikheter i Treningsleiren.

Oppgave 5 (2 poeng) Nettkode: E-4BC1

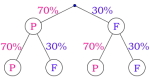
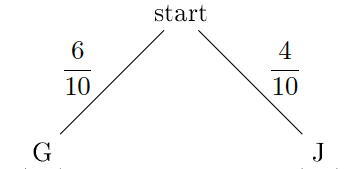
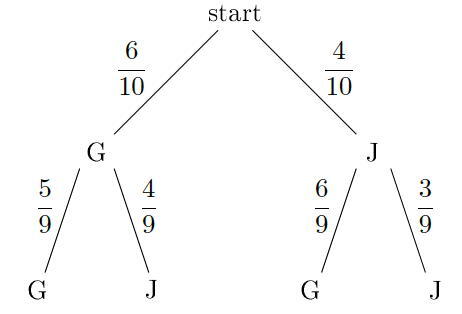
I en klasse er det seks gutter og fire jenter. To elever velges tilfeldig til å være med i en spørreundersøkelse.

Tegn et valgtre, og bruk dette til å bestemme sannsynligheten for at én jente og én gutt velges ut.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Valgtre

Gir oss oversikt over alle mulige kombinasjoner av utfall for en gitt hendelse.

Valgtre er det samme som utfallstre.

valgtre

hjelper oss å systematisere de opplysingene vi har. Det gir oss god oversikt over alle de mulige kombinasjonene vi kan kan få.

Hver gang det blir valgt en elev så er det to mulige

Hendelse

En hendelse eller begivenhet er en delmengde av utfallsrommet. En hendelse består av ett eller flere utfall.

Se Gunstig utfall

hendelser

, gutt(G) eller jente(J). Vi har en uniform sannsynlighetsmodell, og da er sannsynligheten for en hendelse:

$\frac{antall gunstige utfall}{antall mulige utfall}$

Det er $6$ gutter og $4$ jenter i klassen, så totalt $10$ elever, som er antall mulige utfall. Antall gunstige utfall er avhengig av om vi vil trekke en gutt eller jente. Sannsynlightene for at det først blir valgt en gutt er:

$P (G) = \frac{6}{10}$

Sannsynligheten for at det først blir valgt en jente er:

$P (J) = \frac{4}{10}$

Vi kan sette opp øverste del av valgtreet:

Etter at det første valget er tatt, er antallet mulige utfall blitt én mindre, altså lik $9$ .

Nå kan vi se på andre valget, og da starter vi med å se på sannsynlighetene hvis det første valget var en gutt. Da er antallet gunstige utfall for å trekke en gutt redusert med én. Sannsynligheten for å velge en gutt til er da:

$P (G G | G) = \frac{5}{9}$

Og sannsynligheten for en jente:

$P (G J | G) = \frac{4}{9}$

Hvis det første valget var ei jente, er antallet gunstige utfall for å trekke en jente redusert med én. Sannsynligheten for å velge en jente til er da:

$P (J J | J) = \frac{3}{9}$

Og sannsynligheten for en gutt:

$P (J G | J) = \frac{6}{9}$

Det gir oss dette valgtreet:

Vi skal finne sannsynligheten for å få én gutt og ei jente. Vi ser på valgtreet at det er to mulige kombinasjoner for å velge en elev av hvert kjønn. $G J$ og $J G$ tilfredstiller dette kravet. Ved

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

finner vi at sannsynligheten for hver av de to hendelsene er

$P (G J) = P (G) \cdot P (G J | G) = \frac{6}{10} \cdot \frac{4}{9} = \frac{24}{90}$ og $P (J G) = P (J) \cdot P (J G | J) = \frac{4}{10} \cdot \frac{6}{9} = \frac{24}{90}$

Vi kan nå finne sannsynligheten for at én gutt og ei jente ved å addere sannsynligheten for hver av hendelsene. Den blir da:

$P (G J) + P (J G) = \frac{24}{90} + \frac{24}{90} = \frac{48}{90} = \frac{8}{15}$

Svar: Sannsynligheten for at det velges ut én gutt og ei jente er $\frac{8}{15}$ .

Mer om

Denne oppgaven er om

Valgtre

Gir oss oversikt over alle mulige kombinasjoner av utfall for en gitt hendelse.

Valgtre er det samme som utfallstre.

valgtre

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

Du kan lese mer om hvordan man lager et valgtre i artikkelen Utfallstre og om addisjonssetningen i artikkelen Addisjonssetningen i lynkurset Sannsynlighet (del II).

For å øve mer, se oppgavesettet om addisjonssetningen i Treningsleiren.

Oppgave 6 (3 poeng) Nettkode: E-4BC4

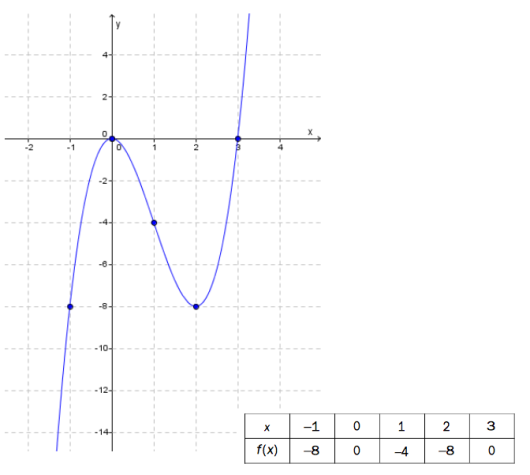
Ovenfor ser du grafen til en tredjegradsfunksjon $f$ .

a)

For hvilke verdier av $x$ er $f (x) \geq 0$ ?

For hvilke verdier av $x$ er $f' (x) < 0$ ?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal avgjøre når $f (x) \geq 0$ , det betyr at $y$ -verdiene skal være større enn, eller lik $0$ . Vi må huske å ta med

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunktene

. Der den

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

deriverte

er mindre enn null er det samme som området der grafen er avtagende. Når

Først skal vi finne for hvilke verdier av $x$ som gir at $f (x) \geq 0$ . Her må vi merke oss at vi har "større enn, eller lik"-tegn, vi vil altså ha med de punktene der $f (x) = 0$ .

For å finne når $f (x)$ er større enn $0$ , må vi finne for hvilke $x$ -verdier grafen har positive $y$ -verdier, altså ligger over $x$ -aksen.

I tabellen ser vi at nullpunktene til $f$ er $0$ og $3$ . Grafen viser oss at for $x = 0$ har $f$ et lokalt toppunkt og for $x > 3$ er $f$ alltid positiv.

Så vi har $f (x) \geq 0 når x = 0 og når x \geq 3$ .

Det andre vi skal se på er når $f' (x) < 0$ . Den deriverte sier noe om vekstfarten til grafen. Når funksjonen er voksende, er den deriverte positiv, og når funksjonen avtar, er den deriverte negativ. Siden vi skal finne når $f' (x) < 0$ , må vi se på når funksjonen avtar.

Vi ser på grafen at dette skjer mellom $x = 0$ og $x = 2$ . I ekstremalpunktene er den deriverte lik null, altså når $x = 0$ og $x = 2$ . Siden vi har "strengt mindre enn"-tegn skal ikke disse punktene tas med.

Svar: $f (x) \geq 0$ for $x \geq 3$ og $x = 0$ , $f' (x) < 0$ for $x \in ⟨0, 2⟩$ .

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

deriverte

Flere eksempler og forklaringer på funksjoner finner du i lynkurset Funksjonsdrøfting. Forklaringer på hva den deriverte er og hvordan man deriverer finner du i lynkurset Derivasjon.

For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.

b)

Bestem den gjennomsnittlige vekstfarten til $f$ fra $x = 0$ til $x = 2 .$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å finne

Gjennomsnittlig vekstfart

En funksjon $f (x)$ har gjennomsnittlig vekstfart

$\frac{Δ y}{Δ x} = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$

mellom $x_{2}$ og $x_{1}$ . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.

gjennomsnittlig vekstfart

finner vi forholdet mellom endringen i funksjonsverdien og endringen i

x

, altså stigningstallet for den rette linjen gjennom punktene med de oppgitte

Førstekoordinat

Førstekoordinat er et punkts verdi langs første-aksen, eller x-aksen i koordinatsystemet. Når et punkt beskrives med et tallpar (7,3), er førstekoordinaten det første tallet i tallparet, 7 i dette eksempelet.

x-koordinatene

Gjennomsnittlig vekstfart er lik

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstallet

for den rette linja gjennom punktene med

x

-koordinatene

x_{1} = 0

x_{2} = 2

, altså gjennom punktene

$(0, f (0)) = (0, 0) og (2, f (2)) = (2, - 8)$ .

Stigningstallet til en rett linje gjennom to punkt $(x_{1}, f (x_{1})) og (x_{2}, f (x_{2}))$ er gitt ved

$\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$ .

Vi finner verdiene fra tabellen og setter inn i uttrykket over:

$\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} = \frac{f (2) - f (0)}{2 - 0} = \frac{- 8 - 0}{2} = - 4$ .

Svar: Gjennomsnittlig vekstfart til $f$ fra $x = 0$ til $x = 2$ er $- 4$ .

Mer om

Denne oppgaven er om

Gjennomsnittlig vekstfart

En funksjon $f (x)$ har gjennomsnittlig vekstfart

$\frac{Δ y}{Δ x} = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$

mellom $x_{2}$ og $x_{1}$ . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.

gjennomsnittlig vekstfart

Du finner flere forklaringer og eksempler i lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettet om veksthastighet i Treningsleiren.

Oppgave 7 (2 poeng) Nettkode: E-4BCB

Trekk sammen og skriv så enkelt som mulig

$\frac{3 x}{x + 3} - \frac{3}{x - 3} - \frac{x^{2} - 12 x + 9}{x^{2} - 9}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

For å kunne legge sammen eller trekke fra brøker, må vi først finne en

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

, slik at vi kan sette alle leddene på felles brøkstrek.

Når vi skal lete etter fellesnevneren, er det alltid lurt å se på alle nevnere i brøkene. De to første nevnere er førstegradsuttrykk vi ikke kan gjøre noe med, men den siste brøken har et

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

som nevner. Denne kan vi se om vi kan faktorisere og vi ser først at

$x^{2} - 9 = x^{2} - 3^{2}$

Nå kan vi bruke

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetningen

til å faktorisere uttrykket og får at

$x^{2} - 9 = (x - 3) (x + 3)$

Faktorene i denne nevneren er akkurat de samme som nevnerene i de to andre brøkene, altså har vi funnet en fellesnevner. Vi utvider den første brøken med $\frac{x - 3}{x - 3}$ og den andre med $\frac{x + 3}{x + 3}$ slik at begge får fellesnevneren $(x + 3) (x - 3)$ :

$\frac{x - 3}{x - 3} \cdot \frac{3 x}{x + 3} - \frac{x + 3}{x + 3} \cdot \frac{3}{x - 3} - \frac{x^{2} - 12 x + 9}{(x + 3) (x - 3)}$

Vi multipliserer hvert ledd og setter på felles brøkstrek:

$\begin{matrix} \frac{(x - 3) (3 x) - (x + 3) \cdot 3 - (x^{2} - 12 x + 9)}{(x + 3) (x - 3)} & = & \frac{(3 x^{2} - 9 x) - (3 x + 9) - x^{2} + 12 x - 9}{(x + 3) (x - 3)} \\ = & \frac{3 x^{2} - 9 x - 3 x - 9 - x^{2} + 12 x - 9}{(x + 3) (x - 3)} \\ = & \frac{2 x^{2} - 18}{(x + 3) (x - 3)} \end{matrix}$

Nå kan vi faktorisere telleren; ${2 x}^{2} - 18 = 2 (x^{2} - 9) = 2 (x + 3) (x - 3)$ , og kan igjen forkorte brøken og får at

$\frac{2 x^{2} - 18}{(x + 3) (x - 3)} = \frac{2 (x + 3) (x - 3)}{(x + 3) (x - 3)} = 2$

Svar: $2$

Mer om

Denne oppgaven er om

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

Utvide brøk

Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.

Eksempel: $\frac{3}{7}$ er utvidet til $\frac{6}{14}$ , fordi $\frac{3 \cdot 2}{7 \cdot 2} = \frac{6}{14}$

utvide brøk

og å forkorte brøk.

For flere forklaringer og eksempler se Parenteser og faktorisering. For flere eksempler og forklaringer om konjugatsetningen se artikkelen Konjugatsetningen. For mer om å utvide og forkorte brøk se artikkelen Forkorte og utvide brøk.

For å øve mer, se oppgavesettet om forenkling av sammensatte rasjonale uttrykk i Treningsleiren.

Oppgave 8 (3 poeng) Nettkode: E-4BCD

Forklar hvorfor hver av påstandene nedenfor er riktige.

a)

${(\frac{2}{5})}^{- 1} > 2$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal vise at uttrykket på venstresiden er større enn tallet $2$ . Vi skriver om

Potens

potensen

og regner ut verdien av den.

I denne oppgaven kan vi bruke følgende potensregel:

$a^{- m} = \frac{1}{a^{m}}, for alle a \in ℝ, a \neq 0$ .

Den gir oss at:

$(\frac{2}{5})^{- 1} = \frac{1}{\frac{2}{5}} = 1 \cdot \frac{5}{2} = 2, 5$ .

Da har vi at ${(\frac{2}{5})}^{- 1} = 2, 5 > 2$ .

Svar: Venstresiden er lik $2, 5$ og høyresiden er lik $2$ som betyr at påstanden stemmer.

Mer om

Denne oppgaven handler om

Potens

potenser

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger

eksponenter

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Flere forklaringer og eksempler på regneregler for potenser finner du i artikkelen Rask gjennomgang av regneregler for potens og røtter i lynkurset Potenser og røtter.

For å øve mer, se oppgavesettet om potenser i Treningsleiren.

b)

$\tan 45^{\circ} = 1$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Tangens

En trigonometrisk funksjon.

Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.

Tangens

til en vinkel i en

Rettvinklet trekant

En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.

rettvinklet trekant

er forholdet mellom motstående

Katet

Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter.

katet

og hosliggende katet.

Siden vi blir bedt om å finne $\tan (45^{\circ})$ , kan vi se på en trekant med vinkler $90^{\circ}, 45^{\circ} og 45^{\circ}$ .

Denne trekanten er en

Likebeint trekant

I en likebeint trekant er to sider like lange og to vinkler like store.

likebeint trekant

, og i en rettvinklet, likebeint trekant er katetene like lange.

Siden tangens er forholdet mellom motstående katet og hosliggende, og disse er like lange, er $\tan (45^{\circ}) = 1$ . Dermed er påstanden riktig.

Mer om

Denne oppgaven handler om

Trigonometri

Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.

trigonometri

Likebeint trekant

I en likebeint trekant er to sider like lange og to vinkler like store.

likebeint trekant

Tangens

En trigonometrisk funksjon.

Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.

tangens

Flere forklaringer og eksempler på tangens i en trekant finner du i lynkurset Trigonometri.

For å øve mer, se oppgavesettet om vinkelberegninger ved hjelp av sinus, cosinus og tangens i Treningsleiren.

c)

$\log 200 > 2$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

Logaritmen

til et tall er

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger

eksponenten

vi opphøyer

10

i for å få tallet.

Vi vet at $10^{2} = 100$ , så $2 = \log (100)$ . Det tallet vi må opphøye $10$ i for å få $200$ må være større enn det vi må opphøye $10$ for å få $100$ , altså må vi ha at

$\log (200) > \log (100)$

og siden $\log (100) = 2$ har vi at

$\log (200) > \log (100) = 2$ og $\log (200) > 2$ .

Alternativ løsning

Ut fra definisjonen til $\lg x$ er $\lg 100 = {\lg 10}^{2} = 2$ og $\lg 1000 = \lg 10^{3} = 3$ , altså må $\lg 200$ ligge mellom $2$ og $3$ .

Mer om

Denne oppgaven handler om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Potens

potens

Flere forklaringer og eksempler på hvordan vi regner med logaritmer finner du i lynkurset Logaritmer.

For å øve mer, se oppgavesettet om logaritmer i Treningsleieren.

Visste du at?

Når vi snakker om logaritmer er det sjelden vi mener tier-logaritmen, men heller den naturlige logaritmen. Den naturlige logaritmen er eksponentene til det irrasjonelle tallet e

$e = 2.718 281 . . .$ .

Oppgave 9 (4 poeng) Nettkode: E-4BCI

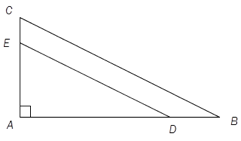
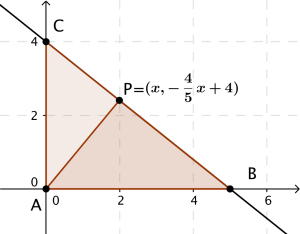
Gitt $Δ A B C$ . Punktet $D$ ligger på $A B$ og punktet $E$ ligger på $A C$ slik at $D E ∥ B C$ . Se skissen ovenfor.

$A B = 8$ , $A E = 3$ og arealet av $Δ A B C$ er $16$ .

a)

Bestem $A C$ og $A D$ ved regning.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi ser $Δ A B C$ er

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlik

med

Δ A D E

siden

D E | | B C

. Vi får bruk for formelen for arealet av en trekant.

Formelen for arealet til en trekant er $A_{△} = \frac{g \cdot h}{2}$ .

I oppgaven får vi vite at $A_{△ A B C} = 16$ . Dette kan brukes til å finne $A C$ .

I $△ A B C$ har vi $g = A B$ og $h = A C$ . Nå kan vi sette inn i formelen for areal, og får da:

$\begin{matrix} A_{△ A B C} & = & \frac{A B \cdot A C}{2} \\ 16 & = & \frac{8 \cdot A C}{2} \\ A C & = & \frac{16 \cdot 2}{8} \\ A C & = & 4 \end{matrix}$

For å finne $A D$ bruker vi at $△ A B C$ er formlik med $△ A D E$ , dette fordi $D E | | B C$ . Da er forholdet mellom samsvarende sider like, og vi må ha at:

$\begin{matrix} \frac{A B}{A C} = & \frac{A D}{A E} \\ \frac{8}{4} = & \frac{A D}{3} \\ A D = & 6 \end{matrix}$

Svar: $A C = 4$ og $A D = 6$ .

Mer om

Denne oppgaven er om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlikhet

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Flere forklaringer og eksempler på formlike figurer finner du i artikkelen Formlikhet og kongruens. For mer om areal an en trekant se artikkelen En trekant.

For å øve mer, se oppgavesettet om formlikhet i Treningsleiren.

b)

Vis ved regning at $B C - D E = \sqrt{5}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi bruker

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

for å regne ut sidelengdene.

Vi har to rettvinklete trekanter, $Δ A B C og Δ A D E$ , og vil finne differansen mellom hypotenusene, $B C og D E$ , i hver av dem. Da begynner vi med å finne lengdene til $B C$ og $D E$ med Pytagoras læresetning:

Da har vi at

${B C}^{2} = {A B}^{2} + {A C}^{2}$ og får at

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{8^{2} + 4^{2}} = \sqrt{64 + 16} = \sqrt{80}$

Tilsvarende har vi at

${D E}^{2} = {A D}^{2} + {A E}^{2}$ og

$D E = \sqrt{{A D}^{2} + {A E}^{2}} = \sqrt{6^{2} + 3^{2}} = \sqrt{36 + 9} = \sqrt{45}$

Vi forenkler $\sqrt{80}$ og $\sqrt{45}$ :

$\sqrt{80} = \sqrt{16 \cdot 5} = \sqrt{16} \cdot \sqrt{5} = 4 \sqrt{5}$

$\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3 \sqrt{5}$

Da får vi at:

$B C - D E = 4 \sqrt{5} - 3 \sqrt{5} = \sqrt{5}$

som var det vi skulle frem til.

Mer om

Denne oppgaven er om Pytagoras læresetning og kvadratrøtter.

Du kan lese om kvadratrøtter i lynkurset Potenser og røtter.

Oppgave 10 (5 poeng) Nettkode: E-4BCL

Karin har lært at det er mulig å bruke derivasjonsregelen $(x^{n})' = n x^{n - 1}$ til å derivere funksjonen $f$ ved

$f (x) = \frac{1}{\sqrt{x}}$

Hun starter med å skrive

$f (x) = \frac{1}{\sqrt{x}} = \frac{1}{x^{\frac{1}{2}}} = x^{- \frac{1}{2}}$

Så deriverer hun

$f' (x) = - \frac{1}{2} x^{- \frac{1}{2} - 1}$

a)

Skriv om uttrykket for $f' (x)$ ovenfor, og vis at

$f' (x) = - \frac{1}{2 \sqrt{x^{3}}}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her må vi bruke

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$
potensreglene

, innledningen til oppgaven gir oss hjelp til å huske noen av disse reglene.

Vi har fått oppgitt at $f' (x) = - \frac{1}{2} x^{- \frac{1}{2} - 1}$

Det første vi gjør er å trekke sammen

$- \frac{1}{2} x^{- \frac{1}{2} - 1} = - \frac{1}{2} x^{- \frac{3}{2}}$

Videre bruker vi at $x^{- a} = \frac{1}{x^{a}}$ , da får vi:

$- \frac{1}{2} x^{- \frac{3}{2}} = - \frac{1}{2} \cdot \frac{1}{x^{\frac{3}{2}}}$

Vi har også at $x^{\frac{3}{2}} = \sqrt{x^{3}}$ . Dermed får vi:

$- \frac{1}{2} \cdot \frac{1}{x^{\frac{3}{2}}} = - \frac{1}{2} \cdot \frac{1}{\sqrt{x^{3}}} = - \frac{1}{2 \sqrt{x^{3}}}$

som var det vi skulle vise.

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

deriverte

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

For flere forklaringer og eksempler om potensregning se lynkurset Potenser og røtter. Flere forklaringer og eksempler på hva den deriverte er og hvordan man deriverer finner du i lynkurset Derivasjon.

For å øve mer, se oppgavesettet om derivasjon i Treningsleiren.

b)

Funksjonene $g$ og $h$ gitt ved $g (x) = \frac{1}{x^{2}}$ og $h (x) = \sqrt{x}$ kan også deriveres ved å bruke derivasjonsregelen ovenfor.

Bestem $g' (x)$ og $h' (x)$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi vil finne de

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

deriverte

, og bruker derivasjonsreglene som er oppgitt.

Vi tar først for oss $g (x)$ , og skriver funksjonsuttrykket slik at det er på formen

$x^{n}$ . Da får vi

$g (x) = \frac{1}{x^{2}} = x^{- 2}$

Nå kan vi bruke derivasjonsregelen $(x^{n})' = {n x}^{n - 1}$ . Da får vi

$g' (x) = (x^{- 2})' = - 2 \cdot x^{- 2 - 1} = - 2 x^{- 3} = - \frac{2}{x^{3}}$

Vi vil også ha funksjonsuttrykket til $h$ på formen $x^{n}$ og kan skrive

$h (x) = \sqrt{x} = x^{\frac{1}{2}}$

Da gir derivasjonsregelen over at

$h' (x) = (x^{\frac{1}{2}})' = \frac{1}{2} \cdot x^{\frac{1}{2} - 1} = \frac{1}{2} \cdot x^{- \frac{1}{2}} = \frac{1}{2 \cdot x^{\frac{1}{2}}} = \frac{1}{2 \sqrt{x}}$

Svar: $g' (x) = - \frac{2}{x^{3}}$ og $h' (x) \frac{1}{2 \sqrt{x}}$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Flere derivasjonsregler og eksempler på hvordan de brukes finner du i lynkurset Derivasjon.

For å øve mer, se oppgavesettet om derivasjon i Treningsleiren.

DEL 2 Med hjelpemidler

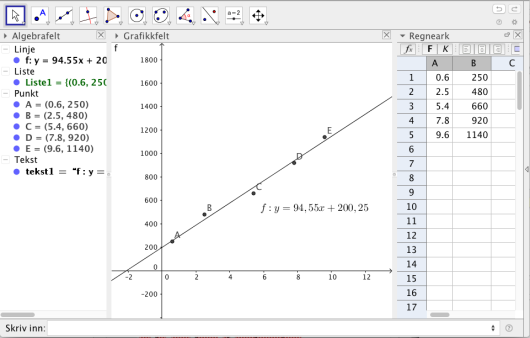
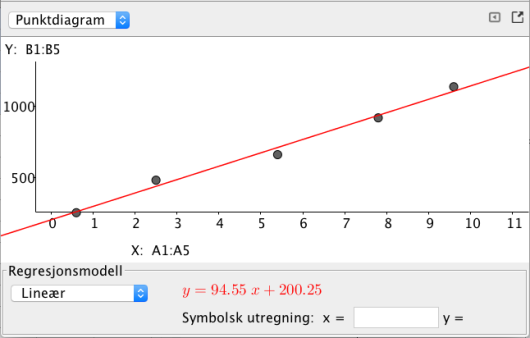
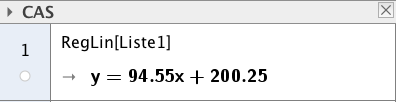
Oppgave 1 (2 poeng) Nettkode: E-4BCP

Det er en tilnærmet lineær sammenheng mellom størrelsene $x$ og $y$ . Se tabellen ovenfor. Bruk regresjon til å bestemme denne sammenhengen.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Hver kolonne kan skrives som et punkt $(x, y)$ . Vi bruker GeoGebra for å finne den

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjonen

Vi skriver punktene som er gitt i oppgaven i et regneark i GeoGebra. Regneark finner du ved å velge "Regneark" i "Vis"-menyen.

Vi skriver $x$ -verdiene i kolonne $A$ og $y$ -verdiene i kolonne $B$ . Så markerer vi begge kolonnene, høyreklikker, velger "Lag" og deretter "Liste med punkt". Da får vi opp en liste med punktene som kalles "Liste1".

Det skal være en tilnærmet lineær sammenheng mellom størrelsene, og vi vil derfor bruke lineær regresjon. I GeoGebra kan vi da bruke følgende kommando som passer med verdiene i tabellen:

    RegLin[<Liste med punkt>]

Siden punktene våre ble lagret som "Liste1" skriver vi:

    RegLin[Liste1]

Da får vi denne grafen og funksjonsutrykket:

Her har vi tilpasset skalaen på aksene så den passer med den lineære funksjonen.

Svar: $y = 94, 55 x + 200, 25$

Alternativ løsning

Når vi har skrevet inn punktene i regnearket kan vi markere rutene og velge "Regresjonssanalyse" i dropmenyen fra knappen med histogram på. Vi velger "Analyser" i det første vinduet som kommer opp.

Siden det skal være en tilnærmet lineær sammenheng, velger vi "Lineær" under "Regresjonsmodell". Da får vi opp

Alternativ løsning

Etter vi har skrevet inn informasjonen og laget listen med punkt kan vi bruke CAS i GeoGebra. Da skriver vi inn samme kommando: "RegLin[Liste1]".

Mer om

Denne oppgaven er om lineær

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

Flere forklaringer og eksempler finner du i artikkelen Regresjon 1 i lynkurset Kultur og modellering.

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.

Oppgave 2 (6 poeng) Nettkode: E-4BCR

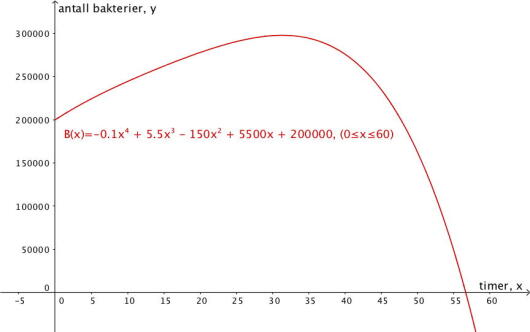
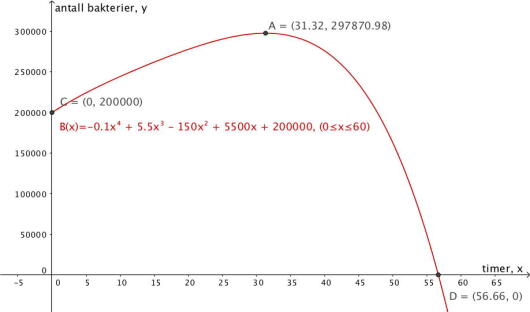
Grete observerer en bakteriekultur. Funksjonen $B$ gitt ved

$B (x) = - 0, 1 x^{4} + 5, 5 x^{3} - 150 x^{2} + 5500 x + 200 000$

viser antall bakterier $B (x)$ i bakteriekulturen $x$ timer etter at hun startet observasjonene.

a)

Tegn grafen til $B$ for $x \in [0, 60]$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan tegne funksjonsgrafen med GeoGebra.

I GeoGebra kan vi bruke følgende kommando for å tegne grafen av en funksjon definert over et gitt intervall:

    Funksjon[ <Funksjon>, <Start>, <Slutt> ]

Som i vår tilfelle blir:

    B(x)=Funksjon[ -0.1x^4+5.5x^3-150x^2+5500x+200000, 0, 60]

Vi skriver navn på, og endrer aksene slik at de passer til grafen.

Resultatet blir da denne grafen:

Svar:

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Hvordan man tegner grafen til en funksjon kan du lese om i lynkurset Funksjonsdrøfting. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.

b)

Bestem toppunktet på grafen og skjæringspunktene mellom grafen og aksene.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

er et

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.
ekstremalpunkt
. Vi skal også finne der grafen krysser x-aksen og y-aksen.

Et toppunkt er et ekstremalpunkt, og GeoGebra finnes det en kommando som finner ekstremalpunktene til en funksjon;

    Ekstremalpunkt[ <Funksjon>, <Start>, <Slutt> ]

I vårt tilfelle er funksjonen $B$ , så vi skriver:

    Ekstremalpunkt[ B, 0, 60]

Da får vi opp et punkt $A = (31, 32, 297870, 98)$ , på grafen, som vi ser er toppunktet.

For å finne skjæringspunktene mellom grafen og aksene bruker vi verktøyet:

    Skjæring mellom to objekt

Bruker musepekeren til å trykke på de to objektene vi ønsker å finne skjæringspunktet til. I vårt tilfelle blir det $x$ -aksen og grafen $B (x)$ som gir oss punktet $C = (0, 200000)$ , og $y$ -aksen og grafen $B (x)$ som gir punktet $D = (56, 66, 0)$ ).

Svar: Toppunktet er $(31.32, 297870.98)$ og grafen skjærer $y$ -aksen i $(0, 200000)$ og $x$ -aksen i $(56.66, 0)$ .

Alternativ løsning

Vi kan finne skjæringspunktet med $x$ -aksen ved å skrive inn følgende kommando i inntastingsfeltet:

    Nullpunkt[B]

Konstantleddet til funksjonen $B$ forteller oss hva skjæringspunktet med $y$ -aksen er.

Mer om

Denne oppgaven er om

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkter og Grafisk løsning av likninger. Mer om funksjoner finner du i lynkurset Funksjonsdrøfting.

Flere forklaringer og regler for hvordan man regner ut den deriverte finner du i lynkurset Derivasjon.

For å øve mer, se oppgavesettet om ekstremalpunkter og skjæringspunkt i Treningsleiren.

c)

Hva forteller svarene i oppgave b) om bakteriekulturen?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi skal forklare hva punktene vi fant i b) har av praktisk betydning. Fra innledningen til oppgaven vet vi at funksjonen $B (x)$ forteller oss antall bakterier i bakteriekulturen $x$ timer etter Grete startet observasjonene.

Svarene i oppgave b) forteller oss at antallet bakterier ved start er $200 000$ . Det får vi vite fra skjæringspunktet med $y$ -aksen, $(0, 200 000)$ . Da finner vi verdien til $B (0)$ , altså ved start.

Toppunktet forteller oss antallet bakterier i bakteriekulturen var størst etter ca $31, 3$ timer, og da var antallet på omtrent $297 900$ bakterier.

Det siste punktet forteller oss at etter ca $56, 7$ timer er bakterietallet blitt 0.

Mer om

Denne oppgaven handler om

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Skjæringspunkt

skjæringspunkt

Flere forklaringer og eksempler på hvordan vi tolker en graf finner du i lynkurset Funksjonsdrøfting.

For å øve mer, se på oppgavesettet om skjæringspunkter og ekstremalpunkter i Treningsleiren.

d)

Bestem den momentane vekstfarten til bakteriekulturen etter 40 timer.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Den momentane vekstfarten i et punkt er det samme som den deriverte i det punktet.

Vi skal finne den momentane vekstfarten etter $40$ timer, det vil si når $x = 40$ .

Vi bruker CAS i GeoGebra for å finne den deriverte til $B (x)$ .

$B (x)$ ligger inne fra før, så den trenger vi ikke å definere på nytt.

For å finne den deriverte skriver vi inn "B'(x)", og videre skriver vi "B'(40)".

Vi ser at den momentane vekstfarten når $x = 40$ er $- 5700$ . Dette betyr at $40$ timer etter at observasjonen startet minker bakteriekulturen med $5700$ bakterier i timen.

Det trenger ikke å bety at $B (41) = B (40) - 5700$ - vi har kun funnet vekstfarten etter nøyaktig $40$ timer.

Svar: Etter $40$ timer var den momentane vekstfarten $- 5700$ bakterier i timen.

Mer om

Denne oppgaven er om

Momentan vekstfart

Den momentane vekstfarten til funksjonen $f (x)$ i et punkt $x = a$ , er stigningstallet til tangenten til kurven i punktet.

momentan vekstfart

Momentan vekstfart kan man finne ved derivasjon, og reglene for å derivere kan du lese om i lynkurset Derivasjon.

For å øve mer, se oppgavesettet om veksthastighet i Treningsleiren.

Oppgave 3 (4 poeng) Nettkode: E-4BCW

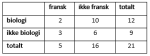
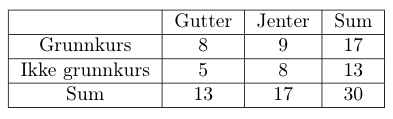
I en klasse er det 13 gutter og 17 jenter. 8 av guttene og 9 av jentene har tatt trafikalt grunnkurs.

a)

Vi velger tilfeldig en elev fra klassen. Eleven har ikke tatt trafikalt grunnkurs.

Bestem sannsynligheten for at eleven er en jente.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Dette handler om

Betinget sannsynlighet

Den betingede sannsynligheten $P (A | B)$ er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.

$P (A | B) = \frac{P (A \cap B)}{P (B)}$ .
betinget sannsynlighet

. Vi skal finne sannsynligheten for en

Hendelse

En hendelse eller begivenhet er en delmengde av utfallsrommet. En hendelse består av ett eller flere utfall.

Se Gunstig utfall
hendelse
. Det er lurt å systematisere opplysningene.

Vi kan begynne med å lage en

Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
krysstabell

for å få en god oversikt over opplysningene.

Av $13$ gutter har $8$ av dem tatt trafikalt grunnkurs, det betyr at $13 - 8 = 5$ gutter har ikke trafikalt grunnkurs.

$9$ av de $17$ jentene har trafikalt grunnkurs, som betyr at $17 - 9 = 8$ av jentene har ikke trafikalt grunnkurs.

Totalt har $8 + 9 = 17$ tatt trafikalt grunnkurs, og $5 + 8 = 13$ har ikke tatt trafikalt grunnkurs.

Krysstabellen vil da se slik ut:

Sannsynligheten er gitt ved

$\frac{antall gunstige}{antall mulige}$ .

Gunstig utfall er å trekke en jente som ikke har trafikalt grunnkurs, som vi kan lese av i krysstabellen, er $8$ . Mulige utfall er alle de elevene som ikke har grunnkurs, som altså er $13$ .

Sannsynligheten blir da:

$P (Jente| ikke grunnkurs) = \frac{jente og ikke grunnkurs}{ikke grunnkurs} = \frac{8}{13}$ .

Svar: Sannsyligheten er $\frac{8}{13}$ for at eleven er en jente.

Mer om

Denne oppgaven er om

Sannsynlighet

sannsynlighet

For flere forklaringer og eksempler se artikkelen Betinget sannsynlighet og produktsetningen i lynkurset Sannsynlighet (del II).

For å øve mer, se oppgavesettet om betinget sannsynlighet i Treningsleiren.

b)

Vi velger tilfeldig to elever fra klassen.

Bestem sannsynligheten for at minst én av dem har tatt trafikalt grunnkurs.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Enten trekker vi minst én elev som trafikalt grunnkurs, eller så trekker vi ingen som har trafikalt grunnkurs. Disse to hendelsene er

Komplement

Komplementet til A, betegnet med $A^{c}$ , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, $A^{c} = U ∖ A$ .

komplementære

, og summen av komplementære hendelser er lik

1

Hendelsene "ingen har trafikalt grunnkurs" og "minst én har trafikalt grunnkurs" er komplementære, og vi har at

$P (ingen har trafikalt grunnkurs) + P (minst én har trafikalt grunnkurs) = 1$ ,

så vi kan finne sannsynligheten for at minst én elev har tatt trafikalt grunnkurs ved

$1 - P (ingen har trafikalt grunnkurs)$

Det er lettere å regne ut sannsyligheten for at ingen av elevene har tatt grunnkurs.

Vi ser på hendelsene

$A$ : "elev 1 har ikke trafikalt grunnkurs" og

$B$ : "elev 2 har ikke trafikalt grunnkurs"

Sannsynligheten for at første elev ikke har trafikalt grunnkurs er

$P (A) = \frac{elever uten trafikalt grunnkurs}{totalt antall elever} = \frac{13}{30}$

Vi antar at første elev ikke hadde trafikalt grunnkurs. Nå er antall gunstige og antall mulige redusert med én. Sannynligheten for at elev 2 ikke har trafikalt grunnkurs, når elev 1 ikke har det er da:

$P (B | A) = \frac{12}{29}$

Nå kan vi bruke

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

til å finne sannsynligheten for at verken elev 1 eller elev 2 har trafikalt grunnkurs.

Da får vi at:

$P (A \cap B) = P (A) \cdot P (B | A) = \frac{13}{30} \cdot \frac{12}{29} = \frac{156}{870} = \frac{26}{145}$ .

Sannsynligheten for at minst en av elevene har tatt trafikalt grunnkurs blir da:

$1 - P (A \cap B) = 1 - \frac{26}{145} = \frac{119}{145} \approx 0, 821 = 82, 1 %$ .

Svar: Sannsynligheten for at minst én av elevene har tatt trafikalt grunnkurs er omtrent $82, 1 %$ .

Mer om

Denne oppgaven er om

Sannsynlighet

sannsynlighet

For flere forklaringer og eksempler se artikklen Sannsynlighet ved komplementære hendelser i lynkurset Sannsynlighet (del II).

For å øve mer, se oppgavesettet om sannsynlighetsregning i Treningsleiren.

Oppgave 4 (4 poeng) Nettkode: E-4BD0

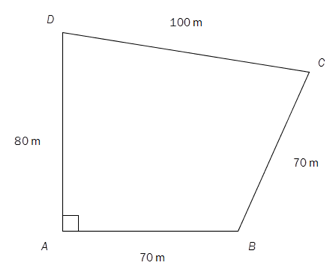
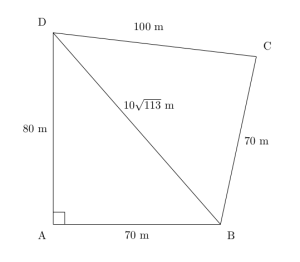
En tomt har form som vist på figuren ovenfor.

Bestem arealet av tomta ved regning.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan dele opp figuren i to trekanter, og deretter kan vi bruke

Pytagoras læresetning

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$

cosinussetningen

Arealsetningen

For en trekant $△ A B C$ er arealet gitt ved $A = \frac{sin (∠ A) \cdot A B \cdot A C}{2}$ .

arealsetningen

til å bestemme arealet.

Vi deler figuren inn i to trekanter ved å tegne en rett linje mellom $B$ og $D$ . Nå har vi delt inn tomten inn i de to trekantene $△ A B D$ og $△ B C D$ .

Siden $△ A B D$ er en rettvinklet trekant kan vi regne ut $B D$ med Pytagoras læresetning:

Ved den har vi at

$B D^{2} = A B^{2} + A D^{2}$

$B D = \sqrt{A B^{2} + A D^{2}} = \sqrt{80^{2} + 70^{2}} = \sqrt{11300} = 10 \sqrt{113} \approx 106, 3$ .

Vi kan også regne ut arealet til $△ A B D$ :

$A_{△ A B D} = \frac{g \cdot h}{2} = \frac{A B \cdot A D}{2} = \frac{70 m \cdot 80 m}{2} = 2800 m^{2}$

For å finne arealet til $△ B C D$ ønsker vi å bruke vi arealsetningen, men da må vi først finne en vinkel. Da kan vi bruke cosinussetningen. Den gir oss at

$B D^{2} = B C^{2} + C D^{2} - 2 \cdot B C \cdot C D \cdot \cos (∠ C)$

Vi kan sette inn verdier for sidelengdene og får

$(10 \sqrt{113})^{2} = 70^{2} + 100^{2} - 2 \cdot 70 \cdot 100 \cdot \cos (C °)$ .

Dette kan vi løse i CAS. Da skriver vi inn likningen og løser ved å trykke på " $x \approx$ ".

Da får vi at $∠ C \approx 75, 1^{\circ}$ .

Vi har nå funnet en vinkel i $△ B C D$ , og har nok informasjon til å kunne bruke arealsetningen:

$A_{△ B C D} = \frac{\sin (∠ C) \cdot B C \cdot C D}{2} = \frac{\sin (75, 1^{\circ}) \cdot 70 m \cdot 100 m}{2} \approx 3382, 3 m^{2}$

Arealet av hele figuren blir da:

$A_{△ A B D} + A_{△ B C D} = 2800 m^{2} + 3382, 3 m^{2} = 6182, 3 m^{2}$

Svar: Arealet er $6182, 3 m^{2}$ .

Alternativ løsning

Vi kan også finne $∠ C$ ved regning.

Vi har fra cosinussetningen at at

$B D^{2} = B C^{2} + C D^{2} - 2 \cdot B C \cdot C D \cdot \cos (∠ C)$

Ettersom det er vinkelen vi ønsker å finne, gjør vi om på uttrykket og får at:

$\cos (∠ C) = \frac{B D^{2} - B C^{2} - C D^{2}}{- 2 \cdot B C \cdot C D}$

Vi setter inn den informasjonen vi har:

$\cos (∠ C) = \frac{(10 \sqrt{113})^{2} - 70^{2} - 100^{2}}{- 2 \cdot 70 \cdot 100} = \frac{- 3600}{- 14000} = \frac{9}{35} \approx 0, 257$

Nå har vi at $\cos (∠ C) \approx 0, 257$ og vi finner

$∠ C = \cos^{- 1} (0, 257)$

Da får vi at:

$∠ C \approx 75, 1^{\circ}$

Vi har nå funnet en vinkel i $△ B C D$ , og har nok informasjon til å kunne bruke arealsetningen:

$A_{△ B C D} = \frac{\sin (∠ C) \cdot B C \cdot C D}{2} = \frac{\sin (75, 1^{\circ}) \cdot 70 m \cdot 100 m}{2} \approx 3382, 3 m^{2}$

Arealet av hele figuren blir da:

$A_{△ A B D} + A_{△ B C D} = 2800 m^{2} + 3382, 3 m^{2} = 6182, 3 m^{2}$

Mer om

Denne oppgaven er om

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Arealsetningen

For en trekant $△ A B C$ er arealet gitt ved $A = \frac{sin (∠ A) \cdot A B \cdot A C}{2}$ .

arealsetningen

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$

cosinussetningen

For flere forklaringer og eksempler se artiklene Arealsetningen og Cosinussetningen i lynkurset Trigonometri.

For å øve mer, se oppgavesettet om trigonometri i Treningsleiren.

Oppgave 5 (4 poeng) Nettkode: E-4BD2

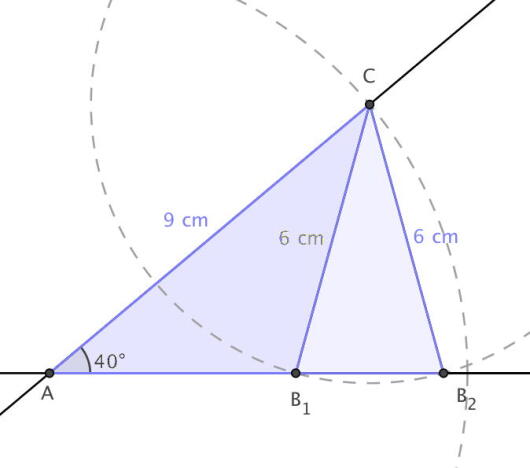
Gitt to ulike trekanter $A B C$ som er slik at $∠ A = 40^{\circ}$ , $B C = 6, 0$ cm og $A C = 9, 0$ cm.

a)

Lag en skisse som viser hvordan de to trekantene kan se ut.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi tegner skissen i GeoGebra.

Vi tegner en rett linje og markerer punktet $A$ , og i det punktet lager vi $∠ A = 40^{\circ}$ .

Vi kan lage en sirkel med sentrum i $A$ og radius lik $9, 0$ cm. Avstanden fra $A$ til skjæringspunktet mellom venstre vinkelbein og sirkelen er nå $9, 0$ cm, og vi kan markere punktet $C$ .

$B C$ skal være $6, 0$ cm, så nå lager vi en sirkel med sentrum i $C$ og radius $6, 0$ cm. Sirkelen vil skjære den rette linja med punktet $A$ , som vi startet med, på to steder. Disse to skjæringspunktene $B_{1}$ og $B_{2}$ tilfredsstiller begge oppgaveteksten.

Svar:

Mer om

Denne oppgaven handler om

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Flere forklaringer og eksempler på hvordan man konstruerer en trekant finner du i artikkelen Konstruksjon av figurer.

For å øve mer, se oppgavesettet om konstruksjon i Treningsleiren.

b)

Sett opp uttrykk som du kan bruke til å bestemme lengden av siden $A B$ i hver av trekantene. Bruk uttrykkene til å bestemme de to lengdene.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kjenner to sidelengder og en vinkel, så her kan vi bruke

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$
cosinussetningen

Vi kan bruke cosinussetningen til å finne et uttrykk for den siste siden, $A B$ i trekanten.

Ved setningen har vi at:

${B C}^{2} = {A C}^{2} + {A B}^{2} - 2 \cdot A C \cdot A B \cdot \cos (∠ A)$

Nå kan vi sette inn den informasjonen vi har:

$6^{2} = 9^{2} + {A B}^{2} - 2 \cdot 9 \cdot A B \cdot \cos (40^{\circ})$

${A B}^{2} - 18 \cdot \cos (40^{\circ}) \cdot A B + 45 = 0$

Denne andregradslikningen kan vi løse ved hjelp av CAS.

Da skriver vi inn likningen og trykker " $x \approx$ " for å få omtrentlige lengder av $A B$ .

Svar: ${A B}_{1}$ har lengde $5, 3 cm$ og ${A B}_{2}$ har lengde $8, 5 cm$ .

Mer om

Denne oppgaven er om

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$

cosinussetningen

For flere eksempler og forklaringer se artikkelen Cosinussetningen .

For å øve mer, se oppgavesettet om cosinussetningen i Treningsleiren.

Oppgave 6 (4 poeng) Nettkode: E-4BD5

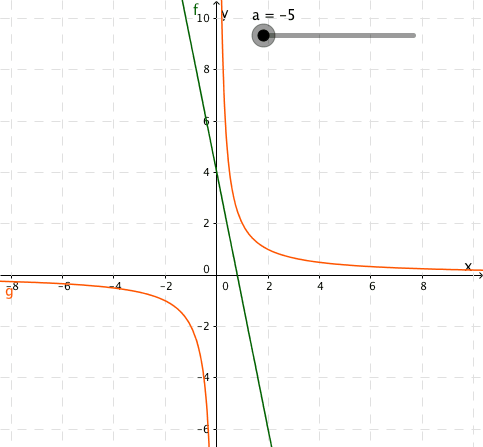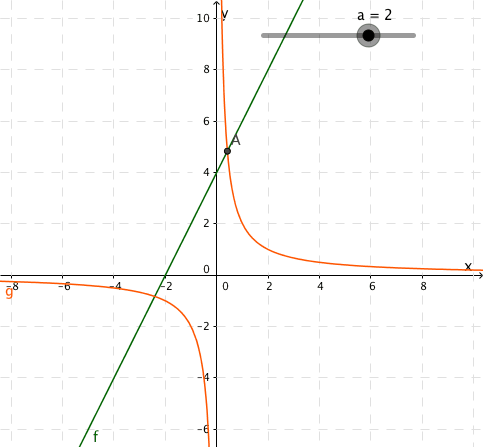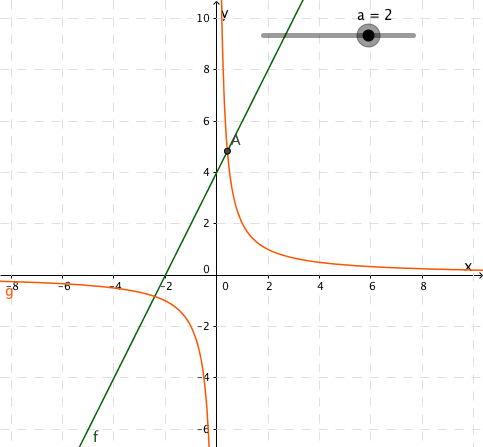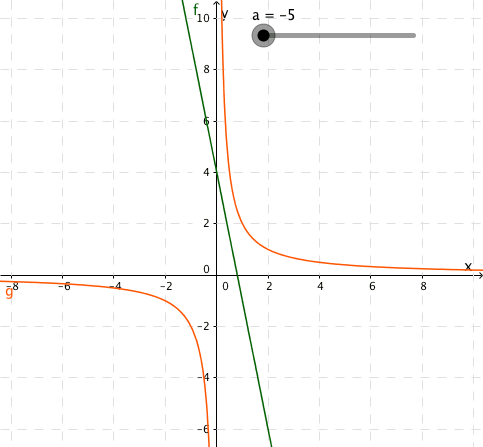
Funksjonene $f$ og $g$ er gitt ved

$f (x) = a x + 4$

$g (x) = \frac{2}{x}, x \neq 0$

a)

Illustrer grafisk at likningen $f (x) = g (x)$ kan ha ingen løsning, én løsning eller to løsninger, avhengig av verdien av $a$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi ville vise når grafene til $f$ og $g$ har null, ett eller to skjæringspunkt. Vi bruker GeoGebra til å tegne de to grafene. For å få ulike verdier av $a$ kan vi bruke verktøyet glider.

Vi skal se på likningen $f (x) = g (x)$ og om denne likningen har null, én eller to løsninger. Antall løsninger vil være det samme som antall skjæringspunkt mellom de to grafene, og vi kan bruke GeoGebra til å tegne grafene til de to funksjonene.

GeoGebra har verktøyet glider som gjør at vi enkelt kan eksprimentere med ulike verdier av $a$ . Glideren finner du her:

For å opprette glideren trykker du der du ønsker å plassere den i grafikkfeltet. Da kan vi velge navn, som vi vil skal være $a$ , og minimums- og maksimumsverdier. Her kan vi begynne med det som ligger inne, og heller eventuelt endre på innstillingene etterhvert. Vi kan velge animasjonstrinn $1$ . Den sier hvor stor avstand det skal være mellom de ulike verdiene for $a$ .

Nå kan vi tegne inn funksjonene:

    f(x)=a*x+4

    g(x)=2/x

Vi varierer verdiene til $a$ ved å dra glideren til høyre eller venstre.

Nå kan finne ut for hvilke verdier for $a$ grafene har null, ett eller to skjæringspunkt. Da vil likningen $f (x) = g (x)$ ha henholdsvis null, én eller to løsninger.

Vi ser at når $a = - 3$ , altså at $f (x) = - 3 x + 4$ , så skjærer ikke grafene hverandre. Dette er derfor et eksempel på ingen løsning.

For $a = - 2$ har vi at grafen til $f (x) = - 2 x + 4$ og $g (x)$ møtes i ett punkt, og er et eksempel på at likningen har én løsning.

Grafen til $f (x) = 2 x + 4$ , altså når $a = 2$ , skjærer $g (x)$ i to punkter og er derfor et eksempel på to løsninger.

Mer om

Denne oppgaven er om

Skjæringspunkt

skjæringspunkt

For flere eksempler og forklaringer se Grafisk løsning av likninger. lere forklaringer og eksempler på skjæringspunkter og hva de forteller oss finner du i lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.

b)

Bestem ved regning verdiene av $a$ slik at likningen $f (x) = g (x)$ har

- ingen løsning

- én løsning

- to løsninger

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi setter funksjonene lik hverandre, og ser hvilke verdier av $a$ som gir to, en eller ingen løsninger.

Vi vil løse likningen $f (x) = g (x)$ ,

$a x + 4 = \frac{2}{x}$

Vi multipliserer med $x$ på begge sider, og flytter over.

$a x^{2} + 4 x - 2 = 0$ , $x \neq 0$

Vi ser først på tilfellet om $a = 0$ . Da får vi

$4 x - 2 = 0 \Rightarrow x = \frac{1}{2}$

Når $a \neq 0$ kan vi løse andregradsligningen med

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

. Da vil vi ikke risikere å få

0

i nevner.

$x = \frac{- 4 \pm \sqrt{16 - 4 \cdot a \cdot (- 2)}}{2 a} = \frac{- 4 \pm \sqrt{8 (2 + a)}}{2 a}$

For å finne antall løsninger ser vi på uttrykket under kvadratroten, $8 (2 + a)$ .

Dersom dette uttrykket er negativt vil likningen ikke ha noen løsninger, og det får vi når $2 + a < 0 \Rightarrow a < - 2$ .

Når $a = - 2$ blir dette uttrykket lik $0$ , og likningen vil bare ha én løsning.

For alle $a \in ⟨ - 2, 0 ⟩ \cup ⟨ 0, \to ⟩$ får vi to løsninger.

Svar: Ingen løsninger for $a < - 2$ , én løsning for $a = - 2$ og $a = 0$ og to løsninger for $a \in ⟨ - 2, 0 ⟩ \cup ⟨ 0, \to ⟩$ .

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkter

For flere forklaringer og eksempler se artikkelen abc-formelen i lynkurset Andregradslikninger og lynkurset Likninger med én ukjent.

For å øve mer, se oppgavesettet om andregradslikninger i Treningsleiren.

Oppgave 7 (4 poeng) Nettkode: E-4BD8

Gitt punktene $A (0, 0)$ , $B (5, 0)$ og $C (0, 4)$ .

Et punkt $P$ ligger på den rette linjen $l$ som går gjennom punktene $B$ og $C$ .

a)

Forklar at koordinatene til $P$ kan skrives på formen $(x, - \frac{4}{5} x + 4)$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan finne funksjonsuttrykket til den rette linjen som punktet $P$ ligger på.

En rett linje er en

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineær funksjon

som alltid kan skrives på formen

y = a x + b

der

a

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstallet

b

Konstant

En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.

Eksempel: $A = π r^{2}$ , $π$ er en konstant og $r$ er en variabel.

Se Variabel

konstantleddet

Vi kaller linjen gjennom $B$ og $C$ for $l$ . For å finne stigningtallet trenger vi to punkter som ligger på linjen. Vi vet at linjen $l$ går gjennom $(x_{1}, y_{1}) = (0, 4)$ og $(x_{2}, y_{2}) = (5, 0)$ .

Stigningstallet finner vi ved å se på forholdet mellom hvor mye grafen vokser i $y$ -verdi og i $x$ -verdi, og det finner vi ved å se på

$\frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{0 - 4}{5 - 0} = \frac{- 4}{5} = - \frac{4}{5}$

Stigningstallet til $l$ er $- \frac{4}{5}$ , og linjen kan skrives på formen $y = - \frac{4}{5} x + b$

Konstantleddet, $b$ , kan vi finne ved å sette inn verdien i et punkt, for eksempel punkt $C = (0, 4)$ . Da er $x = 0, y = 4$ , og vi setter inn verdiene i uttrykket for linjen $y = - \frac{4}{5} x + b$ .

Vi får at $4 = - \frac{4}{5} \cdot 0 + b$ , som gir oss $b = 4$ , og linjen $l$ kan skrives på formen $y = - \frac{4}{5} x + 4$ .

Alle punkt på linjen $l$ må være på formen $(x, y) = (x, - \frac{4}{5} x + 4)$ , og det vil si at også $P$ er på denne formen.

Mer om

Denne oppgaven er om

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinater

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

For mer om lineære funksjoner se artikkelen Rette linjer (lineære funksjoner) og Koordinatsystem i lynkurset Funksjoner (del I). For flere eksempler og forklaringer se lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.

b)

Bestem ved regning koordinatene til $P$ slik at arealet av $Δ A B P$ blir halvparten så stort som arealet av $Δ A B C$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan tegne en hjelpefigur. Ettersom punkt $A$ og punkt $B$ ligger på $x$ -aksen kan vi bruke $y$ -verdien til punktene $C$ og $P$ som høyden på de to trekantene.

Arealet til en trekant er gitt ved

$A = \frac{grunnlinje \cdot høyde}{2}$ .

Både $△ A B C$ og $△ A P B$ har grunnlinje $A B$ som er lik $5$ . Høydene i trekanten er gitt ved $y$ -verdiene til henholdsvis punkt $C$ og punkt $P$ .

For at arealet til $△ A B P$ skal være halvparten av arealet til $△ A B C$ må vi ha at høyden halveres.

Høyden i $△ A B C$ er $4$ , som betyr at høyden i $△ A B P$ må være $2$ , altså må vi ha at $y$ -verdien til $P$ , som er gitt ved $- \frac{4}{5} x + 4$ , er $2$

Vi skal finne koordinatene til $P$ , så for å finne $x$ -verdien i dette punktet kan vi løse likningen:

$\begin{matrix} - \frac{4}{5} x + 4 & = & 2 \\ - \frac{4}{5} x & = & - 2 \\ - 4 x & = & - 10 \\ x & = & \frac{- 10}{- 4} \\ x & = & \frac{5}{2} \end{matrix}$

Det betyr at $A_{△ A B P}$ er halvparten av $A_{△ A B C}$ når $P = (\frac{5}{2}, 2)$ .

Svar: $P = (\frac{5}{2}, 2)$

Mer om

Denne oppgaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Flere forklaringer og eksempler på hvordan man løser førstegradslikninger finner du i lynkurset Likninger med én ukjent.

For å øve mer, se oppgavesettet om areal i Treningsleiren.

Oppgave 8 (2 poeng) Nettkode: E-4BDB

Per og Kari er på vei opp trappene i et tårn. Per er hele tiden 52 trappetrinn foran Kari. Når Per er kommet halvveis opp, roper han til Kari: «Når jeg er helt oppe, er du kommet tre ganger så langt som du er nå.»

Hvor mange trappetrinn er det i tårnet?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan bruke informasjonen i teksten til å lage et likningsett som vi kan løse i CAS.

Vi vil lage et likningsett, og lar $x$ være hvor mange trinn Per har gått når han er halvveis og $y$ være hvor mange trinn Kari da har gått.

Siden Per alltid er $52$ trinn foran Kari, må vi ha at

$y = x - 52$

Når Per er på toppen er Kari kommet tre ganger så langt som hun var da Per var halvveis. Hun ligger fortsatt $52$ trinn bak Per. Det betyr at vi må ha

$3 y = 2 x - 52$

Dette likningsystemet kan vi løse i CAS.

Vi hadde at $x$ var antall trinn Per hadde gått når han var halvveis. Antall trappetrinn i tårnet blir da $2 x = 2 \cdot 104 = 208$ .

Svar: Tårnet har $208$ trinn.

Alternativ løsning

Vi kan også lage likninger med kun én ukjent, og lar $T$ være antall trinn i hele tårnet.

Når Per er på toppen, er Kari kommet til trinn $T - 52$ .

Da Per var halvveis, var Kari på trinn $\frac{T}{2} - 52$ .

Når Per er på toppen, er Kari kommet tre ganger så langt som da Per ropte. Det betyr at vi kan uttrykke antall trinn Kari har gått når Per er på toppen på to måter, $T - 52$ og $3 (\frac{T}{2} - 52)$ . Disse to må være like, og det gir oss denne likningen

$T - 52 = 3 \cdot (\frac{T}{2} - 52)$

som vi løser i CAS:

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

For flere eksempler og forklaringer se artikkelen Fra problem til liknin. Flere forklaringer og eksempler på hvordan man løser førstegradsliknigner finner du i lynkurset Likninger med én ukjent.

For å øve mer, se oppgavesettet om lineære likninger i Treningsleiren.

Oppgave 9 (6 poeng) Nettkode: E-4BDE

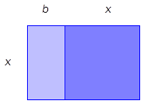
Figuren ovenfor er sammensatt av et rektangel med lengde $x$ og bredde $b$ , og et kvadrat med sider $x$ . Figuren har areal lik $c$ .

a)

Forklar hvorfor $x$ må være en løsning av likningen

$x^{2} + b x = c$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan finne arealet for det sammensatte rektangelet uttrykt ved $x og b$ .

Figuren er et

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

med

Lengde

Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.

lengde

b + x

og bredde

x

. Rektangelet har derfor

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

$(b + x) \cdot x = x^{2} + b x$ .

Vi får oppgitt at arealet er lik $c$ så derfor er $x^{2} + b x = c$ , og $x$ må være en positiv løsning av denne likningen.

Mer om

Denne oppgaven er om

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikninger

Flere eksempler på andregradsliknigner finner du i lynkurset Andregradslikninger.

b)

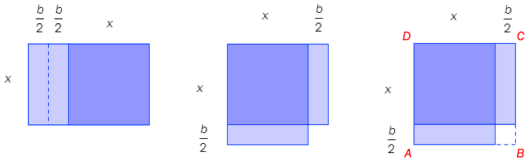
Allerede for 4000 år siden var babylonerne i stand til å løse andregradslikninger av samme type som likningen i oppgave a).

Babylonerne brukte et geometrisk resonnement. De startet med figuren i oppgave a) og tegnet så rektangler og kvadrater som vist nedenfor.

Vis at arealet av kvadratet ABCD er gitt ved $c + \frac{b^{2}}{4}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må legge sammen arealene av de fire figurene som utgjør kvadratet $A B C D$ .

Arealet av det tre blå figurene har vi fått opplyst i innledningen at er lik $c$ . Vi mangler derfor bare arealet til det lille hvite kvadratet for å få arealet av kvadratet $A B C D$ .

Det hvite kvadratet har sidekanter med lengde $\frac{b}{2}$ . Arealet til kvadratet er da ${(\frac{b}{2})}^{2}$ .

Arealet til kvadratet $A B C D$ blir derfor

$c + {(\frac{b}{2})}^{2} = c + \frac{b^{2}}{4}$ .

Mer om

Denne oppgaven handler om

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikninger

For flere forklaringer og eksempler se artikklen Et kvadrat i lynkurset Geometri - areal og volum.

For å øve mer, se oppgavesettet om areal i Treningsleiren.

c)

Forklar hvorfor $x$ må være den positive løsningen av likningen

${(x + \frac{b}{2})}^{2} = c + \frac{b^{2}}{4}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Dette er en andregradslikning. Likningen kan ha to løsninger. Vi ser på hva det betyr at $x$ er positiv og negativ.

Kvadratet $A B C D$ har sidelengde $x + \frac{b}{2}$ og arealet til kvadratet er lik $(x + \frac{b}{2})^{2}$ .

I deloppgave b) fant vi at arealet også kan skrives som $c + \frac{b^{2}}{4}$ , så vi må ha at

$(x + \frac{b}{2})^{2} = c + \frac{b^{2}}{4}$

Vi kan ta kvadratroten på begge sider av likningen og får da

$x + \frac{b}{2} = \sqrt{c + \frac{b^{2}}{4}}$

$x = \frac{- b}{2} + \sqrt{c + \frac{b^{2}}{4}}$

$x = \frac{- b}{2} + \sqrt{\frac{4 c}{4} + \frac{b^{2}}{4}}$

$x = \frac{- b + \sqrt{4 c + b^{2}}}{2}$

Uttrykket under rottegnet er altså ${4 c + b}^{2}$ , og vil alltid være positivt siden $c > 0$ . Derfor har denne likningen to løsninger. Siden $x$ er et linjestykke, må $x$ være den positive løsningen av likningen.

Svar: $x$ må være positiv fordi den er en lengde.

Mer om

Denne oppgaven er om

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikninger

Flere forklaringer og eksempler på hvordan man løser andregradsliknignene og hva løsningene betyr finner du i lynkurset Andregradslikninger.

For å øve mer, se oppgavesettet om andregradslikninger i Treningsleiren.

d)

Bruk oppgave c) til å vise at

$x = \frac{- b + \sqrt{b^{2} + 4 c}}{2}$

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi må løse likningen i oppgave c).

Vi vil løse likningen i c) med hensyn på x:

$(x + \frac{b}{2})^{2} = c + \frac{b^{2}}{4}$

$x + \frac{b}{2} = \sqrt{c + \frac{b^{2}}{4}}$

$x = - \frac{b}{2} + \sqrt{c + \frac{b^{2}}{4}}$

$x = - \frac{b}{2} + \sqrt{\frac{4 c + b^{2}}{4}}$

$x = - \frac{b}{2} + \frac{\sqrt{4 c + b^{2}}}{2}$

$x = \frac{- b + \sqrt{b^{2} + 4 c}}{2}$

som var det vi ville frem til.

Alternativ løsning

Vi kan også løse likningen ved å bruke CAS:

Da ser vi at den andre løsningen var det vi ville frem til.

Mer om

Denne oppgaven er om

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikninger

Flere eksempler på hvordan man løser andregradslikninger finner du i lynkurset Andregradslikninger.

For å øve mer, se oppgavesettet om andregradslikninger i Treningsleiren.

MAT1013 2014 Høst

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4BBT

Løsningsforslag

Standardform

Standardform

Oppgave 2 (1 poeng) Nettkode: E-4BBV

Løsningsforslag

Eksponent

Potens

Ligning

Ukjent

Oppgave 3 (1 poeng) Nettkode: E-4BBX

Løsningsforslag

Logaritme

Ligning

Logaritme

Oppgave 4 (2 poeng) Nettkode: E-4BBZ

Løsningsforslag

abc-formelen

Fortegnsskjema

Oppgave 5 (2 poeng) Nettkode: E-4BC1

Løsningsforslag

Valgtre

Hendelse

Produktsetningen

Valgtre

Sannsynlighet

Oppgave 6 (3 poeng) Nettkode: E-4BC4

a)

Løsningsforslag a)

Nullpunkt

Derivasjon

Funksjon

Derivasjon

b)

Løsningsforslag b)

Gjennomsnittlig vekstfart

Førstekoordinat

Stigningstall

Gjennomsnittlig vekstfart

Oppgave 7 (2 poeng) Nettkode: E-4BCB

Løsningsforslag

Fellesnevner

Andregradsuttrykk

Konjugatsetningen

Algebra

Fellesnevner

Faktorisering

Utvide brøk

Oppgave 8 (3 poeng) Nettkode: E-4BCD

a)

Løsningsforslag a)

Potens

Potens

Eksponent

Brøk

b)

Løsningsforslag b)

Tangens

Rettvinklet trekant

Katet

Likebeint trekant

Trigonometri

Likebeint trekant

Tangens

c)

Løsningsforslag c)

Logaritme

Eksponent

Alternativ løsning

Logaritme

Potens

Oppgave 9 (4 poeng) Nettkode: E-4BCI

a)

Løsningsforslag a)

Formlike trekanter