Sannsynlighet ved komplementære hendelser
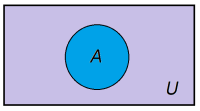
I enkelte tilfeller kan det være fornuftig å gå via komplementære hendelser for å beregne sannsynligheter. Hvis en vi har en begivenhet A i et utfallsrom, vil den komplementære hendelsen til A (Ac) være alle hendelser som ikke er A. Dersom A er den blå sirkelen i Venn-diagrammet under, vil Ac være alt utenom det blå området.
Husk at ifølge definisjonen er A og Ac alltid disjunkte og deres union er alltid lik hele utfallrommet U, A∪Ac=U. Det er 100% sannsynlig å treffe et av utfallene i utfallsrommet og derfor er P(U)=1.
Dette gir oss at
P(A∪Ac)=P(A)+P(Ac)=1.
Merk at den første likheten får vi ved addisjonssetningen. Vi kan utlede en ny regel.
REGEL
P(Ac)=1−P(A)
Regelen kan også omskrives til P(A)=1−P(Ac).
Karakter på en norskprøve
På en norskprøve i en skoleklasse fikk 20% av elevene seks og 35% fem. Vi velger en tilfeldig elev i klassen. Hvor stor er sannsynligheten for at eleven fikk mindre enn fem på prøven?
Vi lar begivenheten A være at eleven får seks, P(A)=20%.
Vi lar begivenheten B være at eleven får fem, P(B)=35%.
La D være at eleven får enten seks eller fem. Da kan vi regne ut at
P(D)=P(A∪B)=P(A)+P(B)=20%+35%=55%.
Sannsynligheten for at eleven fikk dårligere karakter enn fem er sannsynligheten for den komplementære hendelsen til D, og er lik
P(Dc)=1−P(D)=1−55%=45%.
Del på Facebook
Lynkurs 11.-13.trinn
Sannsynlighet (del II)
Består av:
- Repetisjon av begreper
- Hvordan finner vi uniform sannsynlighet?
- Venn-diagram og mengdelære
- Addisjonssetningen
- Sannsynlighet ved komplementære hendelser
- Betinget sannsynlighet og produktsetningen
- Bayes-setningen
- Uavhengige hendelser og produktsetningen
- Ikke-uniforme sannsynlighetsmodeller
- Ordnede utvalg
- Uordnede utvalg uten tilbakelegging
- Binomiske forsøk
- Hypergeometriske forsøk
Begrep
-
Addisjonssetningen
Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.
P(A∪B)=P(A)+P(B)−P(A∩B)
-
Begivenhet
En begivenhet er en delmengde av utfallsrommet og består av ett eller flere utfall.
· Å få 6 på en terning er et eksempel på en begivenhet, der utfallsrommet består av 1, 2, 3, 4, 5 og 6. Å få høyere enn 3, altså 4, 5 eller 6, er et annet eksempel på en begivenhet.
-
Disjunkte hendelser
A og B kalles disjunkte dersom de ikke har noen felles elementer. Dette betyr at A∩B=∅, altså at det ikke er noen elementer som er både i A og i B.
-
Komplement
Komplementet til A, betegnet med Ac, består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, Ac=U∖A.
-
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1. -
Utfall
Mulig resultat av en hendelse.
Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.
-
Utfallsrom
Alle mulige utfall en hendelse kan ha. Utfallsrom betegnes med U.
Eksempel: Karakterer på en matematikkprøve har utfallsrommet U={1,2,3,4,5,6}.
