Potenser og røtter
Dette kurset er lagt opp slik at du finner en rask gjennomgang av alle regneregler i "Rask gjennomgang av regneregler for potenser og røtter", og så finner du mer utdypende artikkeler under.
Potenser
En potens er et tall ganget med seg selv et bestemt antall ganger. er for eksempel ganget med seg selv ganger, altså . Vi bruker for eksempel potenser når vi snakker om veldig store eller veldig små tall. Jorda veier omkring , men dette er skrekkelig upraktisk å skrive, så vi skriver istedet .
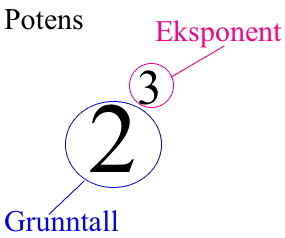
En potens består av et grunntall opphøyet i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal ganges med seg selv. Potensen under har grunntall og eksponent . Eksponenten forteller hvor mange ganger grunntallet skal multipliseres med seg selv.
Det er enklest å forstå hva en potens er når både grunntallet og eksponenten er positive. Vi kan immidlertid ha både grunntall og eksponenter og grunntall som er både negative og brøker.
Røtter
kvadratroten
La være større enn 0. Da er kvadratroten av , , det tallet som opphøyet i andre gir , altså . Vi skriver .
Eksempel: fordi . Men legg merke til at også , derfor skriver vi gjerne . Dette gjelder generelt for kvadratrøtter, vi får alltid en positiv og en negativ løsning.
Kubikkroten
La være et tall. Da er kubikkroten av , , det tallet som opphøyet i tredje gir , altså . Vi skriver .
Eksempel: fordi . I motsetning til med kvadratrøtter, kan vi ta kubikkroten av et negativt tall. For eksempel er fordi .
Siden , er og siden er . Slik kan vi fortsette: siden , er og siden er . Vi kaller dette for henholdsvis fjerderoten og femteroten. Vi kan definere en generell n-te rot:
n-te roten
For et positivt tall og et tall , er n-te roten av , tallet slik at . Vi skriver . Hvis er et partall, må være et postivt tall.
Hvis er et partall, må vi forutsette , og da har vi . Dersom er et oddetall, er definert for alle tall og er positiv eller negativ avhengig av om eller .
Lynkurs 11.-13.trinn
Består av:
- Rask gjennomgang av regneregler for potens og røtter
- Potenser med samme grunntall
- Et produkt eller en potens som grunntall
- Potenser med brøk som grunntall
- Null og negative tall som eksponenter
- Inger Christin forteller om potensregler
- Potenser med rasjonale og reelle eksponenter
- Kubikkrøtter
- Kvadratrøtter
- Regneregler for kvadratrøtter
- n-te røtter
- Sammenhengen mellom røtter og potenser
- Tall på standardform
Begrep
-
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger -
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.