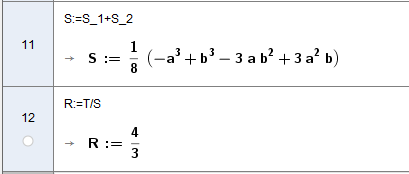Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3024 2016 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Del 1 har 8 oppgaver. Del 2 har 4 oppgaver.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
vurderer om svar er rimelige

Andre opplysninger:
Kilder for bilder, tegninger osv.:

Bergen, rykte (www.freeimages.com, 5.07.2016)
Alle grafer og figurer: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4DVS

Deriver funksjonene

a)

$f (x) = 2 \cos 5 x$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Funksjonen $f (x)$ er en sammensatt funksjon. Vi ser at $u (x) = 5 x$ befinner seg inne i $f (u) = 2 cos u$ . Vi kaller $f (u)$ den ytre funksjonen og $u (x)$ kjernen eller den indre funksjonen. Det er kjerneregelen som gjelder!

La $u (x) = 5 x$ . Da er $f (x) = 2 cos (5 x) = 2 cos (u (x))$ . Kjerneregelen gir $f^{'} (x) = {(2 \cos (u (x)))}^{'} = - 2 \sin (u (x)) \cdot u^{'} (x) = - 2 \sin (5 x) \cdot 5 = - 10 \sin (5 x)$

Svar: $f^{'} (x) = - 10 \sin (5 x)$

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen.

b)

$g (x) = e^{- 2 x} \sin x$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi ser at $g$ er produktet av to funksjoner, $e^{- 2 x}$ og $cos x$ , så produktregelen kan vi få bruk for $(u \cdot v)^{'} = u^{'} \cdot v + u \cdot v^{'}$ $sin x$ vet hvordan vi deriverer, men vi må også derivere $e^{- 2 x}$ . Her ser vi at uttrykket er på formen $e^{k x}$ , der $k$ er en konstant, og vi har derivasjonsregelen $(e^{k x})^{'} = k \cdot e^{k x}$

Vi setter bruker produktregelen $(u \cdot v)^{'} = u^{'} \cdot v + u \cdot v^{'}$ der $u = e^{- 2 x}$ og $v = sin x$ , da blir

$\begin{matrix} g^{'} (x) & = & (e^{- 2 x} \cdot sin x)^{'} \\ = & (e^{- 2 x})^{'} \cdot sin x + e^{- 2 x} \cdot (sin x)^{'} \\ = & - 2 e^{- 2 x} \cdot sin x + e^{- 2 x} \cdot cos x \\ = & e^{- 2 x} (- 2 sin x + cos x) \\ = & - \frac{2 sin x - cos x}{e^{2 x}} \\ = & (- 2 sin x + cos x) \cdot e^{- 2 x} \end{matrix}$

Svar: $g^{'} (x) = - \frac{2 sin x - cos x}{e^{2 x}}$

Mer om

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Å derivere sammensatte uttrykk.

Oppgave 2 (4 poeng) Nettkode: E-4DVV

Bestem integralene

a)

$\int_{1}^{e} \frac{3}{x} dx$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi ser at funksjonen vi skal integrere er $\frac{3}{x} = 3 \cdot \frac{1}{x}$ , altså en konstant ganger en funksjon vi kan integrere.

$\begin{matrix} \int_{1}^{e} \frac{3}{x} dx & = & 3 \cdot \int_{1}^{e} \frac{1}{x} dx \\ = & 3 [ln | x |]_{1}^{e} \\ = & 3 (ln | e | - ln | 1 |) \\ = & 3 (1 - 0) \\ = & 3 \end{matrix}$

Svar: $\int_{1}^{e} \frac{3}{x} d x = 3$

Mer om

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.

b)

$\int_{}^{} \frac{2}{x^{2} - 1} dx$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Inne i integralet er det en brøk med polynom i nevner og teller. Dette ville vært mye lettere å løse dersom vi klarte å dele opp integralet ved hjelp av delbrøkoppspalting.

Før vi kan bruke delbrøkoppspalting må vi faktorisere polynomet i nevneren $x^{2} - 1 = (x + 1) (x - 1)$ . Nå kan vi enten se at $2 = (x + 1) - (x - 1)$ , eller sette opp kravet $\frac{2}{(x + 1) (x - 1)} = \frac{A}{(x + 1)} + \frac{B}{(x - 1)}$ Dette kan vi skrive som $2 = A (x - 1) + B (x + 1)$ . Siden denne likningen må være oppfylt for alle verdier av $x$ må $0 = A x + B x og 2 = - A + B$ . Delbrøkoppspaltingen løses altså av $A = - 1$ og $B = 1$ . Integralet kan altså skrives på formen $\int \frac{2}{x^{2} - 1} d x = - \int \frac{1}{(x + 1)} d x + \int \frac{1}{(x - 1)} d x$ Disse integralene kan vi løse ved enten å bruke substitusjonen $u = x + 1$ og $v = x - 1$ slik at $\int \frac{2}{x^{2} - 1} d x = - \int \frac{d u}{u} + \int \frac{d v}{v} = - ln | u | + ln | v | + C = - ln | x + 1 | + ln | x - 1 | + C$ eller ved å komme på at den deriverte til $ln |x + a|$ er $\frac{1}{x + a}$ .

Svar: $\int \frac{2}{x^{2} - 1} d x = - ln | x + 1 | + ln | x - 1 | + C$

Mer om

Denne oppgaven er om

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på integrasjon, se artikkelen Integrasjon av rasjonale uttrykk.

Oppgave 3 (6 poeng) Nettkode: E-4DVY

Funksjonen $f$ er gitt ved

$f (x) = \sin x, x \in [0, π]$

Et flatestykke er avgrenset av $x$ -aksen og grafen til $f$ .

a)

Regn ut arealet av flatestykket.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må forsikre oss om at hele arealet ligger over $x$ -aksen. Siden $\sin x$ er positiv på intervallet $(0, π)$ , ligger hele arealet over $x$ - aksen.

Vi ser at arealet vi skal regne ut er arealet under grafen med grensene $x = 0$ og $x = π$ .

Vi må regne ut det bestemte integralet

$\begin{matrix} \int_{0}^{π} sin x dx & = & [- cos x]_{0}^{π} \\ = & - cos π - (- cos 0) \\ = & - (- 1) - (- 1) \\ = & 2 \end{matrix}$

Svar: Arealet av flatestykket er 2.

Mer om

Denne oppgaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.

x-akse

For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.

b)

Vis ved derivasjon at $\int_{}^{} \sin^{2} x dx = \frac{1}{2} x - \frac{1}{2} \sin x \cdot \cos x + C$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Fordi den integrerte er den antideriverte, kan vi sjekke om svaret til den integrerte av en funksjon stemmer, ved å derivere svaret.

Vi skal derivere $\frac{1}{2} x - \frac{1}{2} sin x \cdot cos x + C$ . Vi ser at den vanskelige delen er å derivere $sin x \cdot cos x$ . Dette kan vi gjøre med produktregelen $(u \cdot v)^{'} = u^{'} \cdot v + u \cdot v^{'}$ vi setter $u = sin x$ og $v = cos x$ . Da får vi

$\begin{matrix} (sin x \cdot cos x)^{'} & = & u^{'} \cdot v + u \cdot v^{'} \\ = & cos x \cdot cos x + sin x \cdot (- sin x) \\ = & {cos}^{2} x - {sin}^{2} x \\ = & 1 - {sin}^{2} x - {sin}^{2} x \\ = & 1 - 2 {sin}^{2} x \end{matrix}$

Til slutt brukte vi at ${sin}^{2} x + {cos}^{2} x = 1$ .

Vi kan nå derivere hele uttrykket

$\begin{matrix} (\frac{1}{2} x - \frac{1}{2} sin x \cdot cos x + C)^{'} \\ = & \frac{1}{2} - \frac{1}{2} (1 - 2 {sin}^{2} x) + 0 \\ = & {sin}^{2} x \end{matrix}$

som var akkurat det vi ville vise.

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Derivasjon av trigonometriske funksjoner.

c)

Vi roterer flatestykket $360^{\circ}$ om $x$ -aksen.

Regn ut volumet av omdreiningslegemet vi da får.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi vet at formelen til volumet av et omdreiningslegeme, rotert $360^{\circ}$ om $x$ -aksen er gitt ved $V = π \int_{a}^{b} (f (x))^{2} dx$

Bruker vi denne formelen, og resultatet fra deloppgave b) får vi

$\begin{matrix} V & = & π \int_{a}^{b} (f (x))^{2} dx \\ = & π \int_{0}^{π} {sin}^{2} dx \\ = & π [\frac{1}{2} x - \frac{1}{2} sin x \cdot cos x]_{0}^{π} \\ = & π ((\frac{1}{2} \cdot π - \frac{1}{2} sin π \cdot cos π) - (\frac{1}{2} \cdot 0 - \frac{1}{2} sin 0 \cdot cos 0)) \\ = & π \cdot (\frac{π}{2} - 0) \\ = & \frac{π^{2}}{2} \end{matrix}$

Svar: $V = \frac{π^{2}}{2}$

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Omdreiningslegeme

Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.

omdreiningslegeme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

For flere forklaringer og eksempler på integrasjon, se artikkelen Volum av et omdreiningslegeme.

Oppgave 4 (5 poeng) Nettkode: E-4DW2

Rekken $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + . . . + \frac{1}{2^{n}}$ er gitt.

a)

Forklar at dette er en geometrisk rekke. Bestem et uttrykk for summen $S_{n}$ av de $n$ første leddene i rekken.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi vet at en geometrisk rekke er summen av elementene i en geometrisk progresjon. At elementer i en tallfølge $(a_{n})$ der $n \in ℕ$ er i geometrisk progresjon betyr at hvert tall er et konstant multippel av det forrige, dvs $\frac{a_{n + 1}}{a_{n}} = k$ for en konstant $k$ . Slike tall kan skrives på formen $a_{n} = a_{1} \cdot k^{n - 1}$ .

La $a_{1} = \frac{1}{2}$ , $a_{2} = \frac{1}{4}$ , og så videre. Vi ser da at vi kan skrive $a_{n} = a_{1} \cdot (\frac{1}{2})^{n - 1}$ . Altså er dette en geometrisk rekke.

Summen av leddene i en geometrisk rekke er gitt ved $S_{n} = a_{1} \cdot \frac{k^{n} - 1}{k - 1}$ så for oss blir det $S_{n} = \frac{1}{2} \cdot \frac{(\frac{1}{2})^{n} - 1}{\frac{1}{2} - 1} = 1 - (\frac{1}{2})^{n}$

Svar: $S_{n} = 1 - (\frac{1}{2})^{n}$

Mer om:

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.

b)

Vi har gitt produktet $P_{n} (x) = \sqrt{x} \cdot \sqrt[4]{x} \cdot \sqrt[8]{x} \cdot \sqrt[16]{x} \cdot . . . \cdot \sqrt[2^{n}]{x}, x > 0$

Vis at $P_{n} (x) = x^{(1 - \frac{1}{2^{n}})}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi ser et produkt av røtter. Men røtter kan man skrive som potenser, og når potenser har samme grunntall kan man gange de sammen slik at eksponentene adderes.

Vi begynner med å skrive om
$\sqrt[2^{r}]{x} = x^{\frac{1}{2^{r}}}$
Når vi bruker at $a^{m} \cdot a^{n} = a^{m + n}$ blir produktet $\begin{matrix} P_{n} (x) & = \sqrt{x} \cdot \sqrt[4]{x} \cdot \sqrt[8]{x} \cdot \sqrt[16]{x} \cdot . . . \cdot \sqrt[2^{n}]{x} \\ = x^{\frac{1}{2}} \cdot x^{\frac{1}{4}} \cdot x^{\frac{1}{8}} \cdot x^{\frac{1}{16}} \cdot . . . \cdot x^{\frac{1}{2^{n}}} \\ = x^{\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots + \frac{1}{2^{n}}} \\ = x^{S_{n}} \\ = x^{1 - (\frac{1}{2})^{n}} \end{matrix}$

Mer om:

Denne oppgaven er om

Grunntall

En potens består av et grunntall og en eksponent.

Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.

grunntall

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$

potens

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger

eksponent

Kvadratrot

Kvadratrot har symbolet $\sqrt{}$ .

Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.

Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi $4 \cdot 4 = 16$ . Det skrives $\sqrt{16} = 4$ .

kvadratrot

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på polynomer, se artikkelen Definisjon av et polynom.

c)

Bestem $\lim_{n \to \infty} P_{n} (x)$

Løs oppgaven her

Løsningsforslag c)

Tanker:

Når vi lar $n \to \infty$ , ser vi at $\frac{1}{2^{n}} \to 0$ .

$\begin{matrix} \lim_{n \to \infty} P_{n} (x) & = \lim_{n \to \infty} x^{1 - (\frac{1}{2})^{n}} \\ = x^{1 - 0} \\ = x \end{matrix}$

Svar: $\lim_{n \to \infty} P_{n} (x) = x$

Mer om:

Denne oppgaven er om

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger

eksponent

Grunntall

En potens består av et grunntall og en eksponent.

Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.

grunntall

For flere forklaringer og eksempler på grenseverdier, se artikkelen Grenseverdier.

Oppgave 5 (6 poeng) Nettkode: E-4DW6

Funksjonen $f$ er gitt ved

$f (x) = 3 \cos 2 x, x \in ⟨0, 2 π⟩$

a)

Bestem eventuelle nullpunkter til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi vet at funksjonen $cos x$ har nullpunkter i $x = \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, . . .$ , altså har vi at $cos x = 0$ betyr at $x = \frac{π}{2} + k π$ for en $k \in ℤ$ . Vår oppgave nå er å finne hvilken påvirkning det har at vi har $2 x$ som argument isteden for $x$ , og at $x \in ⟨ 0, 2 π ⟩$ .

At $3 cos 2 x = 0$ må bety at $cos 2 x = 0$ . Som nevnt over må vi ha at argumentet til cos-funksjonen, må være på formen $\frac{π}{2} + k π$ for en $k \in ℤ$ . Altså $2 x = \frac{π}{2} + k π \Leftrightarrow x = \frac{π}{4} + \frac{k π}{2}$ Siden $x \in ⟨ 0, 2 π ⟩$ vet vi at $x > 0$ og $x < 2 π$ . Dette gir

$x > 0$ som gir $\frac{π}{4} + \frac{k π}{2} > 0$ som igjen gir $k > - \frac{1}{2}$ , og siden $k \in ℤ$ betyr det at $k \geq 0$ .

$x < 2 π$ som gir $\frac{π}{4} + \frac{k π}{2} < 2 π$ som igjen gir $k < \frac{7}{2}$ og siden $k \in ℤ$ betyr det at $k \leq 3$ .

De eneste mulige verdiene for $k$ er derfor $k = 0$ , $k = 1$ , $k = 2$ og $k = 3$ . Dette gir oss nullpunkter i $x = \frac{π}{4}$ , $x = \frac{3 π}{4}$ , $x = \frac{5 π}{4}$ og $x = \frac{7 π}{4}$ .

Svar: $f$ har nullpunkter i $x = \frac{π}{4}$ , $x = \frac{3 π}{4}$ , $x = \frac{5 π}{4}$ og $x = \frac{7 π}{4}$ .

Mer om

Denne oppgaven er om ulikhet,

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

For flere forklaringer og eksempler på likninger, se artikkelen Trigonometriske likninger.

b)

Bestem eventuelle topp- eller bunnpunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi vet at i ekstremalpunktene til $f$ har vi at $f^{'} (x) = 0$ , tangenten har stigningstall lik null. Derfor begynner vi med å derivere $3 cos 2 x$ . Her går vi fram akkurat slik vi gjorde i deloppgave 1). Eller se at $f$ når maksimum når $cos 2 x = 1$ og minimum når $cos 2 x = - 1$ .

Vi starter med å derivere $f$ $\begin{matrix} f^{'} (x) = (3 cos 2 x)^{'} & = (2 x)^{'} \cdot 3 (- sin 2 x) = - 6 sin 2 x \end{matrix}$ Her brukte vi kjerneregelen på tilsvarende måte som i deloppgave 1a). Det neste vi gjør er å løse likningen

$\begin{matrix} f^{'} (x) & = & 0 \\ - 6 sin 2 x & = & 0 \\ sin 2 x & = & 0 \\ 2 x & = & k \cdot π, & k \in ℤ \\ x & = & \frac{k π}{2}, & k \in ℤ \end{matrix}$

Altså har vi ekstremalpunkter når $x$ er på formen $\frac{k π}{2}$ for $k \in ℤ$ , og i intervallet $⟨ 0, 2 π ⟩$ er dette $x = \frac{π}{2}$ , $x = π$ og $x = \frac{3 π}{2}$ . Den letteste måten å sjekke hvilke av disse som toppunkter og hvilke som er bunnpunkter, er ved å regne ut funksjonsverdien i hvert punkt.

$f (\frac{π}{2}) = 3 cos (2 \cdot \frac{π}{2}) = 3 cos π = 3 \cdot (- 1) = - 3$

$f (π) = 3 cos (2 \cdot π) = 3 cos 2 π = 3 \cdot 1 = 3$

$f (\frac{3 π}{2}) = 3 cos (2 \cdot \frac{3 π}{2}) = 3 cos 3 π = 3 \cdot (- 1) = - 3$

Derfor ser vi at grafen til $f$ har de to bunnpunktene $(\frac{π}{2}, - 3)$ og $(\frac{3 π}{2}, - 3)$ , og toppunktet $(π, 3)$ .

Svar: Grafen til $f$ har de to bunnpunktene $(\frac{π}{2}, - 3)$ og $(\frac{3 π}{2}, - 3)$ , og toppunktet $(π, 3)$ .

Mer om

Denne oppgaven er om

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Graf

graf

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

c)

Lag en skisse av grafen til $f$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi vet at $f$ er en konstant, $3$ , multiplisert med cosinus til $2 x$ . Derfor vet vi at grafen til $f$ ser ut som grafen til $\cos (x)$ , med amplitude lik $3$ , og periode $\frac{2 π}{2} = π$ .

Vi tegner skissen og legger inn både nullpunktene og topp-og bunnpunktene

Mer om

Denne oppgaven er om

Graf

graf

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

Oppgave 6 (3 poeng) Nettkode: E-4DWA

Løs differensiallikningen

$y' - x y = x, y (0) = 1$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Dette er en lineær, første ordens differensiallikning som ser ut til å være separabel. Vi kan enten bruke metoden med integrerende faktor, eller så kan vi separere variablene på hver sin side av likhetstegnet, for så å integrere opp begge sider.

Vi skal løse den linære differensiallikningen $y^{'} - x y = x$ , og da kan vi enten bruke metoden med integrerende faktor, som vi ser på under. I den alternative løsningen løser vi den ved å separere variablene.

Integrerende faktor for differensiallikningen er $e^{- \frac{1}{2} x^{2}}$ , så ${(y e^{- \frac{1}{2} x^{2}})}^{'} = x e^{- \frac{1}{2} x^{2}}$

Vi integrerer begge sider med hensyn på $x$ :

$y e^{- \frac{1}{2} x^{2}} = \int_{}^{} x e^{- \frac{1}{2} x^{2}} dx$

For å løse integralet på høyre side bruker vi substitusjonen $u = - \frac{1}{2} x^{2}$ og $du = - x dx$ . Det gir

$\int_{}^{} x e^{- \frac{1}{2} x^{2}} dx = - \int_{}^{} e^{u} du = - e^{u} + C = - e^{- \frac{1}{2} x^{2}} + C$

Likningen blir dermed

$y e^{- \frac{1}{2} x^{2}} = - e^{- \frac{1}{2} x^{2}} + C$

$y = - 1 + C e^{\frac{1}{2} x^{2}}$

Med $y (0) = 1$ , får vi $y (0) = - 1 + C e^{0} = - 1 + C = 1$ , så $C = 2$ .

Løsningen på initialverdiproblemet er

$y = 2 e^{\frac{1}{2} x^{2}} - 1$ .

Svar: $y = 2 e^{\frac{1}{2} x^{2}} - 1$

Alternativ løsning

Likningen $y^{'} - x y = x$ kan skrives $y^{'} = x + x y = x (y + 1)$ . Gjør vi litt om på likningen ser vi at vi kan skrive $\frac{y^{'}}{y + 1} = x$ . Da gjenstår det bare å integrere begge sider av likhetstegnet $\int \frac{y^{'} d x}{y + 1} = \int x d x = \frac{1}{2} x^{2} + C_{1}$ For en eller annen konstant $C_{1}$ . I integralet til venstre kan vi bruke substitusjonsregelen for integrasjon for å få $\int \frac{y^{'} d x}{y + 1} = \int \frac{d y}{y + 1} = ln (y + 1) + C_{2}$ For en eller annen konstant $C_{2}$ . Vi får altså $ln (y + 1) = \frac{1}{2} x^{2} + C$ Der $C = C_{1} - C_{2}$ . Vi kan finne verdien til $C$ ved å bruke initialbetingelsen $y (0) = 1$ . Vi får da at $\begin{matrix} ln (y (0) + 1) & = \frac{1}{2} \cdot 0^{2} + C C = ln 2 \end{matrix}$ Nå har vi egentlig løst differensiallikningen, men det kan være fint å skrive den på en mer gjenkjenbar form $ln (y + 1) = \frac{1}{2} x^{2} + ln 2 \Rightarrow y + 1 = e^{\frac{1}{2} x^{2} + ln 2} = 2 e^{\frac{1}{2} x^{2}} \Rightarrow y = 2 e^{\frac{1}{2} x^{2}} - 1$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.

Oppgave 7 (7 poeng) Nettkode: E-4DWC

Punktene $A (1, - 4, 1)$ og $B (3, 0, 5)$ ligger i planet $α$ .

Vektoren $\vec{n_{α}} = [k, 1, - k]$ står normalt på $α$ for en bestemt verdi av konstanten $k$ .

a)

Vis at planet $α$ er gitt ved $2 x + y - 2 z + 4 = 0$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Siden $\vec{n_{α}}$ står normalt på $α$ , må den også stå normalt på $\vec{A B}$ . Men da må vi jo ha at skalarproduktet er null. Altså $\vec{A B} \cdot \vec{n_{α}} = 0$ . Videre vet vi at et plan med normalvektor $\vec{n} = [a, b, c]$ har likning $a x + b y + c z + d = 0$ for et passende tall $d$ .

Vi starter med å regne ut vektoren $\vec{A B} = [3 - 1, 0 - (- 4), 5 - 1] = [2, 4, 4]$ . Deretter vet vi at $\vec{A B} \cdot \vec{n_{α}} = 0$ så vi har

$\begin{matrix} \vec{A B} \cdot \vec{n_{α}} & = 0 \\ [2, 4, 4] \cdot [k, 1, - k] & = 0 \\ 2 k + 4 - 4 k & = 0 \\ 2 k & = 4 \\ k & = 2 \end{matrix}$

Så koordinatene til normalvektoren blir $\vec{n_{α}} = [k, 1, - k] = [2, 1, - 2]$ . Derfor blir likningen til planet $2 x + y - 2 z + d = 0$

For et reellt tall $d$ . Siden vi vet at $A (1, - 4, 1)$ ligger i planet, kan vi bruke dette til å finne $d$ $\begin{matrix} 2 \cdot 1 + (- 4) - 2 \cdot 1 + d & = 0 \\ d & = 4 \end{matrix}$

Derfor blir likningen til planet

$2 x + y - 2 z + 4 = 0$

som var det vi ville vise.

Mer om

Denne oppgaven er om

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

b)

Planet $α$ skjærer $z$ -aksen i punktet $C$ .

Bestem koordinatene til $C$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Punktet $C$ ligger på linjen som er $z$ -aksen, og følgelig må $C$ ha koordinater $(0, 0, c)$ .

Siden har koordinater $(0, 0, c)$ og ligger i planet $α$ , oppfyller $(0, 0, c)$ likningen til $α$ , altså

$\begin{matrix} 2 \cdot 0 + 0 - 2 \cdot c + 4 & = & 0 \\ - 2 c & = & - 4 \\ c & = & 2 \end{matrix}$

Svar: $C$ har koordinater $(0, 0, 2)$ .

Mer om

Denne oppgaven er om

z-akse

Vanlig betegnelse på den tredje aksen i et koordinatsystem.

z-akse

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

c)

Bestem volumet av pyramiden $A B C O$ , der $O$ er origo.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

For en pyramide med trekantet grunnflate, utspent av vektorene $\vec{a}, \vec{b} og \vec{c}$ . har vi formelen for volumet $V = \frac{1}{6} | (\vec{a} \times \vec{b}) \cdot \vec{c} |$

I vår oppgave er det vektorene $\vec{O A}$ , $\vec{O B}$ og $\vec{O C}$ som utspenner pyramiden. $\vec{O A}$ , $\vec{O B}$ og $\vec{O C}$ er koordinatvektorer, så vi har

1. $\vec{O A} = [1, - 4, 1]$

2. $\vec{O B} = [3, 0, 5]$

3. $\vec{O C} = [0, 0, 2]$

$V = \frac{1}{6} | (\vec{O A} \times \vec{O B}) \cdot \vec{O C} |$

Vi starter med å regne ut

$\begin{matrix} \vec{O A} \times \vec{O B} & = & [1, - 4, 1] \times [3, 0, 5] \\ = & |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & - 4 & 1 \\ 3 & 0 & 5 \end{matrix}| \\ = & |\begin{matrix} - 4 & 1 \\ 0 & 5 \end{matrix}| \vec{i} - |\begin{matrix} 1 & 1 \\ 3 & 5 \end{matrix}| \vec{j} + |\begin{matrix} 1 & - 4 \\ 3 & 0 \end{matrix}| \vec{k} \\ = & - 20 \vec{i} - 2 \vec{j} + 12 \vec{k} \\ = & [- 20, - 2, 12] \end{matrix}$

Deretter regner vi ut skalarproduktet $\begin{matrix} [- 20, - 2, 12] \cdot [0, 0, 2] = - 20 \cdot 0 + (- 2) \cdot 0 + 12 \cdot 2 = 24 \end{matrix}$ Vi er nå klare til å regne ut volumet av pyramiden

$V = \frac{1}{6} | (\vec{O A} \times \vec{O B}) \cdot \vec{O C} | = \frac{1}{6} |24| = \frac{24}{6} = 4$

Svar: Volumet av pyramiden $A B C O$ er $4$ .

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt - areal og volum.

d)

En kule har sentrum i origo og tangerer planet $α$ i et punkt $P$ .

Bestem koordinatene til punktet $P$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

At kulen tangerer $α$ , betyr at radien i kula er lik avstanden fra origo til planet. Altså vet vi at $\vec{O P}$ står normalt på planet $α$ .

Siden $\vec{O P}$ står normalt på planet $α$ i likhet med $\vec{n_{α}} = [2, 1, - 2]$ må vi nødvendig vis ha at $\vec{O P} | | \vec{n_{α}}$ . Ut ifra dette vet vi nå at det finnes et reellt tall $s$ slik at

$\vec{O P} = s \cdot \vec{n_{α}} = s \cdot [2, 1, - 2] = [2 s, s, - 2 s]$

Siden $\vec{O P} = [2 s, s, - 2 s]$ er koordinatvektoren til punktet $P$ , vet vi at $P$ har koordinater $(2 s, s, - 2 s)$ . Når vi vet at $P$ ligger på planet $α$ får vi $\begin{matrix} 2 x + y - 2 z + 4 & = 0 \\ 2 \cdot 2 s + s - 2 \cdot (- 2 s) + 4 & = 0 \\ 9 s & = - 4 \\ s = - \frac{4}{9} \end{matrix}$ Og derfor blir koordinatene til $P$ $(2 s, s, - 2 s) = (2 \cdot (- \frac{4}{9}), - \frac{4}{9}, - 2 \cdot (- \frac{4}{9})) = (- \frac{8}{9}, - \frac{4}{9}, \frac{8}{9})$

Svar: $P (- \frac{8}{9}, - \frac{4}{9}, \frac{8}{9})$

Mer om

Denne oppgaven er om

Normal

En linje som står 90 grader på en annen linje.

normal

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangent

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.

Oppgave 8 (2 poeng) Nettkode: E-4DWH

Bruk induksjon til å bevise påstanden $P$ gitt ved

$P (n) : \frac{k^{n} - 1}{k - 1} = 1 + k + k^{2} + k^{3} + . . . + k^{n - 1}, n \in ℕ$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Et induksjonsbevis fungerer som dominobrikker. Du får den første brikken til å falle, og du viser at hver brikke faller på den neste.

Vi starter med å vise nullhypotesen, at $P (1)$ er sann.

$P (1) : \frac{k^{1} - 1}{k - 1} = \frac{k - 1}{k - 1} = 1$

Altså stemmer $P (1)$ . Det neste vi må vise er induksjonssteget, altså at $P (n)$ sann, impliserer $P (n + 1)$ sann. Så vi antar at påstanden $P (n)$ stemmer. $\begin{matrix} P (n + 1) : & \frac{k^{n + 1} - 1}{k - 1} = \frac{(k^{n + 1} - k^{n}) + (k^{n} - 1)}{k - 1} \\ = \frac{k^{n} (k - 1) + (k^{n} - 1)}{k - 1} \\ = \frac{k^{n} (k - 1)}{k - 1} + \frac{(k^{n} - 1)}{k - 1} \\ = k^{n} + 1 + k + k^{2} + k^{3} + \dots + k^{n - 1} \\ = 1 + k + k^{2} + k^{3} + \dots + k^{n - 1} + k^{n} \end{matrix}$

som var det vi ville vise.

Mer om

Denne oppgaven er om

Matematisk induksjon

En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:

Bevis påstanden for n =1.
Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).

Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).

matematisk induksjon

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.

DEL 2 Med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4DWK

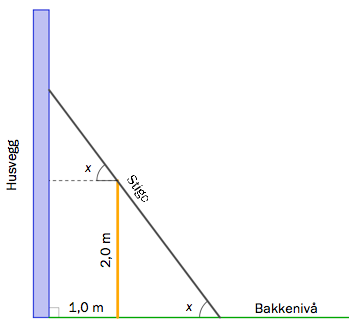
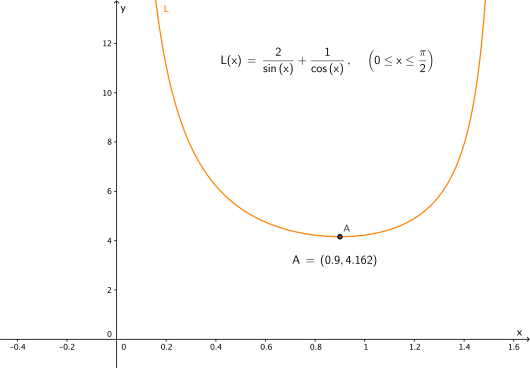
En stige, som kan justeres, skal stå på skrå mot en husvegg og berøre et 2,0 m høyt gjerde. Gjerdet står 1,0 m fra husveggen. La $x$ være vinkelen mellom stigen og bakken. Se skissen nedenfor.

a)

Vis at lengden av stigen, målt i meter, er

$L (x) = \frac{1}{\cos x} + \frac{2}{\sin x}$ , der $0^{\circ} < x < 90^{\circ}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi ser at lengden på stigen er summer av de to hypotenusene i de to mindre trekantene på bildet. I begge er $x$ en vinkel, og i den nederste er den motstående kateten lik $2, 0$ m og i den øverste er hosliggende katet lik $1, 0$ m. Vi kaller hypotenusen i den nederste trekanten $H_{1} (x)$ og i den øverste for $H_{2} (x)$ . Da har vi $L (x) = H_{1} (x) + H_{2} (x)$

Vi bruker definisjonene av cosinus og sinus. I den nederste trekanten har vi

$\begin{matrix} sin x & = & \frac{motstående katet}{hypotenus} \\ \sin x & = & \frac{2}{H_{1} (x)} \\ H_{1} (x) & = & \frac{2}{sin x} \end{matrix}$

I den øverste trekanten har vi

$\begin{matrix} cos x & = & \frac{hosliggende katet}{hypotenus} \\ \cos x & = & \frac{1}{H_{2} (x)} \\ H_{2} (x) & = & \frac{1}{cos x} \end{matrix}$

Derfor på vi

$L (x) = H_{1} (x) + H_{2} (x) = \frac{2}{sin x} + \frac{1}{cos x}$

Mer om

Denne oppgaven er om

Hypotenus

Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.

hypotenus

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

Katet

Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter.

katet

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Klara definere sinus, cosinus og tangens.

b)

Bestem $x$ slik at lengden av stigen blir kortest mulig.

Hvor høyt opp på veggen rekker stigen da?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi ser etter bunnpunktet til grafen til $L$ . Vi kan bruke graftegner til å tegne opp funksjonen, og finne bunnpunktet.

Framgangsmåte:

Vi tegner grafen til $L$ med kommandoen: funksjon[<funksjon>, <start>, <slutt>], der vi bytter ut funksjonen med $\frac{2}{sin x} + \frac{1}{cos x}$ og legger inn riktige grenser. Merk at vi må gjøre om til radianer ( $0 < x < \frac{π}{2}$ ).
Gir nytt navn til funksjonen: $L$
Vi finner ekstremalpunktene med kommandoen: ekstremalpunkt[<funksjon>, <start>, <slutt>], der vi bytter ut funksjon med $L$ .
Leser av koordinatene ekstremalpunktene.

Den korteste lengden stigen kan ha er $4, 16$ m. Da er $x = 0, 9$ i radianer. Dette kan vi gjøre om med formelen $v = \frac{180^{\circ} r}{π}$ som gir en vinkel på $51, 6^{\circ}$ .

Høyden på veggen, $h$ får vi ved å legge sammen høyden i det lille rektangelet ( $2$ m) og motstående katet i den øvre trekanten. Der har vi at

$\begin{matrix} tan 51, 6^{\circ} & = & \frac{motstående katet}{hosliggende katet} \\ \tan {51, 6}^{\circ} & = & \frac{h - 2}{1} \\ 1, 26 & = & h - 2 \\ h & = & 3, 26 \end{matrix}$

Høyden på veggen er da $3, 26$ m.

Svar: Den korteste lengden stigen kan ha er $4, 16$ m. Da er $x = 51, 6^{\circ}$ . Og høyden på veggen er da $3, 26$ m.

Mer om

Denne oppgaven er om

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Graf

graf

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkel

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Oppgave 2 (8 poeng) Nettkode: E-4DWN

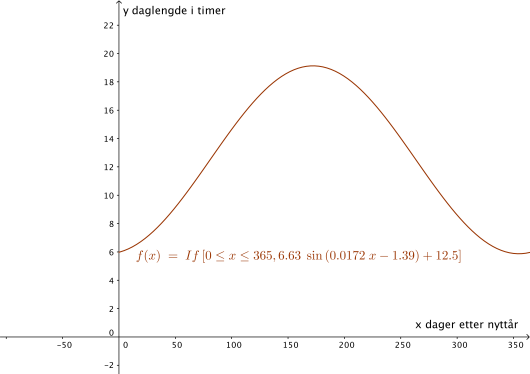
Daglengden $D$ i Bergen er tilnærmet gitt ved funksjonen

$D (t) = 6, 63 \sin (0, 0172 t - 1, 39) + 12, 5$

Her er $D (t)$ daglengden målt i timer, og $t$ er antall dager fra nyttår.

a)

Bruk uttrykket $D (t)$ til å bestemme den korteste og den lengste daglengden i Bergen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi ser at $D (t)$ er en kostant multiplisert med sinus av et lineært uttrykk i $x$ , i tillegg adderer vi med $12, 5$ . Det eneste som kan variere er sinus. Men det har vi kontroll på!

Siden $- 1 \leq sin v \leq 1$ , vet vi at den minste verdien til $D (t)$ er når $sin (0, 0172 t - 139) = - 1$ og den største verdien når $sin (0, 0172 t - 139) = 1$ . Altså

Den korteste daglengden: $6, 63 \cdot (- 1) + 12, 5 = 5, 87$ timer.

Den lengste daglengden: $6, 63 \cdot 1 + 12, 5 = 19, 13$ timer.

Svar: Den korteste daglengden er 5 timer og 52 minutter, mens den lengste daglengden er 19 timer og 8 minutter.

Mer om

Denne oppgaven er om

Sinus

sinus

og ulikhet.

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Sinus, cosinus og tangens.

b)

Bruk graftegner til å tegne grafen til $D$ for $t \in [0, 365]$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her gjelder det å gi riktig kommando når vi legger inn grafen.

Framgangsmåte:

Vi tegner grafen til $D$ med kommandoen: funksjon[<funksjon>, <start>, <slutt>], der vi bytter ut funksjonen med $6, 63 sin (0, 0172 t - 1, 39) + 12, 5$ og legger inn riktige grenser. Merk at vi må gjøre om til radianer ( $0 \leq x \leq 365$ ).
Gir nytt navn til funksjonen: $D$

Mer om

Denne oppgaven er om

Graf

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

c)

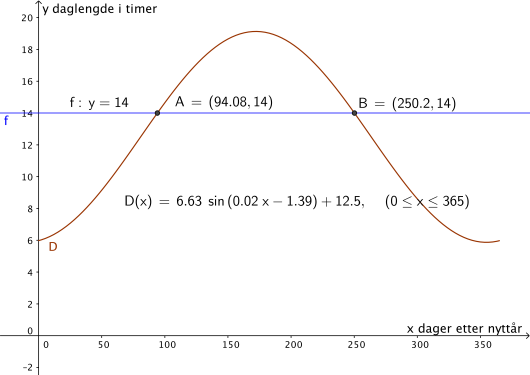
Når er daglengden i Bergen 14 timer?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

At daglengden er $14$ timer, betyr at $D (t) = 14$ . Dette er en likning vi kan løse grafisk.

Vi tegner den horisontale linja $y = 14$ , og markerer hvor den skjærer med grafen til $D$ .

Svar: Daglengden er $14$ timer $94$ og $250$ dager etter nyttår.

Mer om

Denne oppgaven er om

Graf

graf

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på grafer, se artikkelen Grafisk løsning av likninger.

d)

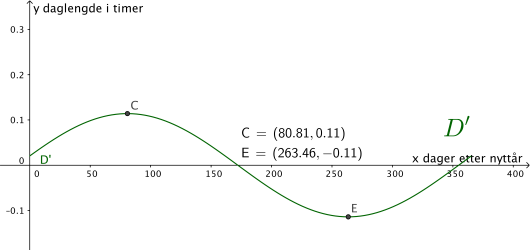
Undersøk på hvilken dato daglengden vokser raskest.

Hvor mye øker daglengden per døgn da?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Når vi skal finne hvor fort daglengden voker eller avtar, er det naturlig å se på grafen til den deriverte til $D$ . Der den deriverte har sin største positive verdi, vokser grafen til $D$ raskest. Den deriverte forteller oss stigningstallet til tangenten til $D$ . Det er akkurat så mye daglengden øker per døgn da. Alternativt ser vi at dette er en harmonisk svingning og da vil vendepunktene ligge i skjæringspunktene ved likevektslinja $y = 12, 5$ . Vi kan da finne dette skjæringspunktet.

Vi bruker kommandoen $D'$ , for å tegne grafen til den deriverte. Deretter bruker vi kommandoen ekstremalpunkt[<funksjon>, <start>, <slutt>], der vi bytter ut funksjon med $D'$ .

Vi ser at det er i toppunktet til $D^{'}$ hvor $D$ vokser raskest. Det er i punktet $(80.8, 0.11)$ . Altså inntreffer det etter nesten $81$ dager etter nyttår, og da øker daglengden med $0, 11$ timer per døgn.

Svar: Daglengden vokser raskest nesten $81$ dager etter nyttår, og da øker daglengden med $0, 11$ timer per døgn.

Mer om

Denne oppgaven er om

Skjæringspunkt

skjæringspunkt

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Graf

graf

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Oppgave 3 (6 poeng) Nettkode: E-4DWS

Funksjonen $f$ er gitt ved

$f (x) = x^{2}$

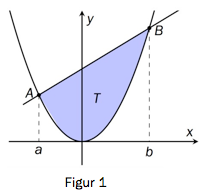
Punktene $A (a, a^{2})$ og $B (b, b^{2})$ der $a < b$ , ligger på grafen til $f$ . Se figur 1 nedenfor.

a)

Grafen til $f$ og linjestykket $A B$ avgrenser et flatestykke med areal $T$ .

Bruk CAS til å bestemme $T$ uttrykt ved $a$ og $b$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her gjelder det å gi CAS der riktige kommandoene. Vi vil både definere $f$ , $A$ , $B$ og linjen gjennom de to punktene. Deretter vil vi finne arealet under linja og over grafen til $f$ . Dette kan vi gjøre ved å integrere området vi får ved å trekke $f$ fra uttrykket for linja.

Framgangsmåte:

Vi starter med å definere $f$ med kommandoen f(x):=x**2
Deretter definerer vi $A$ og $B$ med kommandoene A:=(a,f(a)) og B:=(b,f(b)).
Så definerer vi linja gjennom $A$ og $B$ med kommandoen Linje[<start>, <slutt>] og bytter ut start og slutt med $A$ og $B$ .
Til slutt integrerer vi området vi får ved å trekke $f$ fra utrykket for linja med kommandoen Integral[<funksjon>,<start>, <slutt>] og legger inn riktig funksjon og start- og sluttverdier.

Svar: $𝐓 := \frac{- 𝐚^{3} + 3 𝐚^{2} 𝐛 - 3 𝐚 𝐛^{2} + 𝐛^{3}}{6} = \frac{(𝐛 - 𝐚)^{3}}{6}$

Mer om

Denne oppaven er om

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Graf

graf

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

b)

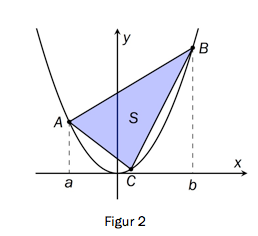
Punktet $C$ på grafen har koordinatene $(c, c^{2})$ , der $c = \frac{a + b}{2}$ . Se figur 2 nedenfor.

Bruk CAS til å vise at arealet $S$ av $Δ A C B$ er $S = \frac{1}{8} {(b - a)}^{3}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å finne et uttrykk for arealet $S$ , deler vi opp arealet i to deler. Den ene delen består av punkter over linjestykket $A C$ , det andre området er det resterende. Nå vil vi beskrive linjestykkene som deler av grafene til lineære funksjoner og beregne integralet av differenser av de funksjonene. Alt gjøres i CAS. på følgende måteHer er det fullt mulig at det finnes en mer elegant løsning med å bruke CAS.

Framgangsmåte:

I celle 1 defineres funksjonen $f (x)$ . Celle 2 og 3 definerer punktene $A og B$ . I celle 4 og 5 defineres verdien $c$ og punktet $C$ .
Cellene 6 - 8 beskriver linjene gjennom de angitte punktene som grafen til funksjonene $g, h og k$ .
I celle 9 beregnes $\int_{a}^{c} (k (x) - g (x)) dx$ som er arealet av den delen av området som ligger over $A C$ .
I celle 10 beregnes $\int_{a}^{c} (k (x) - h (x)) dx$ som er arealet av den delen av området som ligger over $C B$ .
Celle 11 definerer $S$ til å være summen av de to arealene, akkurat slik oppgaven krever.
Celle 12 sjekker at verdien av $S$ .

Svar: $𝐒 := \frac{1}{8} (- 𝐚^{3} + 𝐛^{3} - 3 𝐚 𝐛^{2} + 3 𝐚^{2} 𝐛) = \frac{(b - a)^{3}}{8}$

Mer om

Denne oppaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Graf

graf

For flere forklaringer og eksempler på areal, se artikkelen Tom forteller om areal.

c)

Bestem forholdet $\frac{T}{S}$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Ettersom at vi nå har regnet ut både $T$ og $S$ , er dette relativt enkelt, og noe vi kan gjøre enten for hånd eller med CAS. Vi gjør det med CAS her, bare for å illustrere hvor enkelt det kan gjøres.

Taster inn kommandoen R:=T/S (vi definerer $R$ som forholdet)

Svar: $\frac{T}{S} = \frac{4}{3}$

Mer om

Denne oppaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

For flere forklaringer og eksempler på algebra, se artikkelen Forkorte og utvide brøk.

Oppgave 4 (4 poeng) Nettkode: E-4DX0

I en bygd med 1200 innbyggere spres et rykte. La $y$ være antall innbyggere som kjenner til ryktet ved tiden $t$ , der $t$ er tiden målt i dager etter at ryktet oppsto.

Vi antar at ryktet spres med en fart som til enhver tid er proporsjonal med produktet av antall innbyggere som kjenner ryktet, og antall innbyggere som ikke kjenner det. Proporsjonalitetskonstanten har verdien $0, 0006$ .

Ved tiden $t = 0$ var det kun én person som kjente til ryktet.

a)

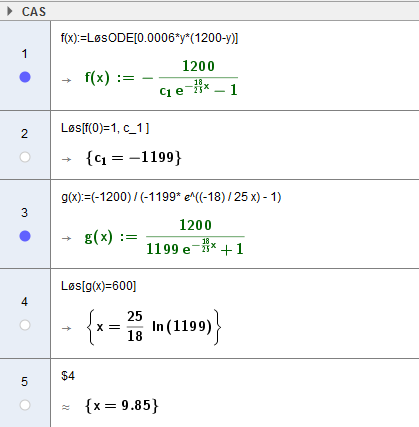
Sett opp en differensiallikning som beskriver situasjonen ovenfor.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her trenger vi bare å sette opp differensiallikningen som beskriver situasjonen. Vi trenger ikke løse den. $y$ er antall innbyggere som kjenner til ryktet ved tiden $t$ , og farten ryktet spres med er $y^{'}$ . Videre får vi vite at ryktet spres med en fart som til enhver tid er proporjonal med produktet av antall innbyggere som kjente ryktet, og antall innbyggere som ikke kjenner det. Proporsjonalitetskonstanten har verdien $0, 0006$ . Det er denne informasjonen vi bruker til å sette opp likningen.

At ryktet spres med en fart som til enhver tid er proporsjonal med produktet av antall innbyggere som kjente ryktet ( $y$ ), og antall innbyggere som ikke kjenner det( $1200 - y$ ), kan vi sette opp som differensiallikningen (vi bruker også at proporsjonalitetskonstanten har verdien $0, 0006$ ) $y^{'} = 0, 0006 \cdot y (1200 - y)$ Fordi ved tiden $t = 0$ var det kun én person som kjente til ryktet, får vi initialverdien $y (0) = 1$

Svar: Vi får differensiallikningen $y^{'} = 0, 0006 \cdot y (1200 - y) y (0) = 1$

Mer om

Denne oppaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på funksjoner, se artikkelen Johannes bygger nye funksjoner.

b)

Hvor lang tid tar det før halve bygda kjenner til ryktet?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her kan vi begi oss ut på å prøve å løse differensiallikningen som vi fant over, og hvis vi er flinke får vi det kanskje til også. Heldigvis kan vi gjøre dette på CAS! CAS kan løse differensiallikningen med kommandoen LøsODE[<likning>], der du oppgir høyre side av likningen, i $x$ og $y$ , dersom $y^{'}$ står på venstre side. I vårt tilfelle er det $0, 0006 \cdot y (1200 - y)$ .

Framgangsmåte

Vi løser differensiallikningen med kommandoen LøsODE[0.0006* y*(1200-y)], og definerer løsningen til å være $f (x)$
Vi bruker initialverdien $y (0) = 1$ , som nå lyder $f (0) = 1$ til å finne verdien konstanten $c_{1}$ . Altså løser vi med hensyn på $c_{1}$ , med kommandoen Løs[f(0)=1, c_1 ]
Nå vil vi definere funksjonen med riktig verdi av $c_{1}$ , så vi definerer funksjonen $g (x)$ som dette med kommandoen g(x):=(-1200) / (-1199* e**((-18) / 25 x) - 1). Alternativt sett inn initialbetingelsen direkte i LøsODE: LøsODE[0.0006* y*(1200-y), (0,1)] og da blir svaret lik $g (x) = \frac{1200}{1199 e^{- 18 \cdot \frac{x}{25}} - 1}$
Til slutt vil vi finne når ryktet har nådd halve bygda, altså når $g (x) = 600$ . Vi løser likningen med kommandoen Løs[g(x)=600]

Svar: Vi ser at ryktet har nådd halve befolkningen etter nesten $10$ dager ( $9, 85$ dager).

Mer om

Denne oppaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på logaritme- og eksponentialfunksjoner, se artikkelen Johannes viser eksponential- og logaritmefunksjoner.

REA3024 2016 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4DVS

a)

Løsningsforslag a)

Derivasjon

Sinus

Cosinus

b)

Løsningsforslag b)

Eksponentialfunksjon

Sinus

Cosinus

Derivasjon

Oppgave 2 (4 poeng) Nettkode: E-4DVV

a)

Løsningsforslag a)

Logaritme

Brøk

Integrasjon

b)

Løsningsforslag b)

Polynom

Integrasjon

Logaritme

Brøk

Oppgave 3 (6 poeng) Nettkode: E-4DVY

a)

Løsningsforslag a)

Areal

Graf

Integrasjon

x-akse

b)

Løsningsforslag b)

Derivasjon

Sinus

Cosinus

Integrasjon

c)

Løsningsforslag c)

Volum

Omdreiningslegeme

Integrasjon

Sinus

Cosinus

Pi (π)

Oppgave 4 (5 poeng) Nettkode: E-4DW2

a)

Løsningsforslag a)

Sum

Brøk

b)

Løsningsforslag b)

Grunntall

Potens

Eksponent

Kvadratrot

Polynom

c)

Løsningsforslag c)

Grenseverdi

Eksponent

Grunntall

Oppgave 5 (6 poeng) Nettkode: E-4DW6

a)

Løsningsforslag a)

Sinus

Cosinus

Nullpunkt

Pi (π)

b)

Løsningsforslag b)

Toppunkt

Bunnpunkt

Sinus

Cosinus