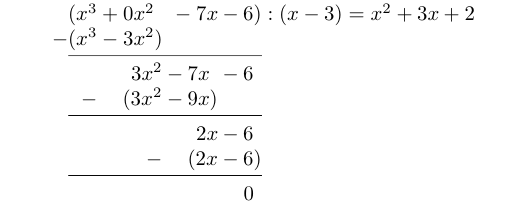Delbrøksoppspalting - et eksempel til

Eksempel 

Oppgave. La $f\left(x\right)=\frac{x^2+1}{x^3-7x-6}$. Vis at $x^3-7x-6 = 0, når x=3$, og bruk dette til å finne en delbrøkoppspalting av uttrykket.

Løsning. Første mål er å få faktorisert nevneren $g\left(x\right)=x^3-7x-6$. Fordi $g\left(3\right)=27-7\cdot 3-6=0$, sier nullpunktsetningen at $x-3$ er en av faktorene i $g\left(x\right)$. Da kan vi bruke polynomdivisjon til å finne en foreløpig faktorisering:

Dermed er $x^3-7x-6=\left(x-3\right)\left(x^2+3x+2\right)$.

Annengradsuttrykket $x^2+3x+2$ faktoriserer vi videre ved hjelp av de vanlige formlene: Likningen $x^2+3x+2=0$ har løsningene $x=-1$ og $x=-2$, slik at $x^2+3x+2=\left(x+1\right)\left(x+2\right)$. Den endelige faktoriseringen blir dermed

$x^3-7x-6=\left(x-3\right)\left(x+1\right)\left(x+2\right)$.

Nå kan vi begynne selve delbrøkoppspaltingen. Vi må finne konstanter $A$, $B$ og $C$ slik at

$\frac{x^2+1}{\left(x-3\right)\left(x+1\right)\left(x+2\right)}=\frac{A}{x-3}+\frac{B}{x+1}+\frac{C}{x+2}$.

Som i forrige eksempel ganger vi overalt med fellesnevneren, $\left(x-3\right)\left(x+1\right)\left(x+2\right)$:

$x^2+1=A\left(x+1\right)\left(x+2\right)+B\left(x-3\right)\left(x+2\right)+C\left(x-3\right)\left(x+1\right)$.

Vi velger å bruke metoden vi kalte "innsetting av lure verdier" for å finne $A$, $B$ og $C$. Her, som i forrige eksempel, bruker vi røttene i den opprinnelige nevneren, altså $x=3,x=-1$ og $x=-2$. Vi tar dem etter hverandre.

$x=3$:

$3^2+1=A\cdot 4\cdot 5+B\cdot 0+C\cdot 0 \iff A=\frac{1}{2}$.

$x=-1$:

${\left(-1\right)}^2+1=A\cdot 0+B\cdot \left(-4\right)\cdot 1+C\cdot 0 \iff B=-\frac{1}{2}$.

$x=-2$:

${\left(-2\right)}^2+1=A\cdot 0+B\cdot 0+C\cdot \left(-5\right)\cdot \left(-1\right) \iff C=1$.

Dermed har vi funnet alle de tre ukjente verdiene. Konklusjonen blir at

$\frac{x^2+1}{x^3-7x-6}=\frac{\frac{1}{2}}{x-3}-\frac{\frac{1}{2}}{x+1}+\frac{1}{x+2}$.