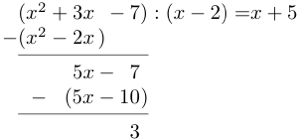Restpolynom

En polynomdivisjon går ikke alltid opp. Da får vi det som kalles et restpolynom.

En vanlig divisjon går ikke alltid opp. Prøv for eksempel å regne ut $163 : 7$ for hånd med metoden vi minnet om i begynnelsen av kurset – dette er barneskolelærdom, men du ender opp med å få en rest. Dette kan også skje i polynomdivisjon, og som med resten av det vi ser på her takler vi det mye på samme måte som for "vanlig" divisjon.

Eksempel

Regn ut $\frac{x^{2} + 3 x - 7}{x - 2}$ ved å bruke polynomdivisjon.

Løsning. Regningen blir slik:

Dersom vi skulle ha fortsatt divisjonen nå, ville neste ledd i svaret blitt $\frac{3}{x}$ (fordi det er det $x$ må ganges med for å få 3). Men da ville ikke svaret vært et polynom lenger, så dette vil vi ikke ha. I stedet sier vi at 3 er restpolynomet i divisjonen, og skriver

$\frac{x^{2} + 3 x - 7}{x - 2} = x + 5 + \frac{3}{x - 2}$ .

Polynomdivisjonsteoremet

Vi tar med et teorem som sier formelt når en polynomdivisjon går opp. Man kan langt på vei se hva som må gjelde ut fra å tenke på når vi fikk problemer i divisjonen over, men dette er et viktig teorem.

Teorem. Polynomdivisjon

Anta at vi holder på med en polynomdivisjon $P (x) : Q (x)$ , og at $R (x)$ er polynomet som står igjen under streken.

Hvis graden til $R (x)$ er større eller lik graden til $Q (x)$ , kan polynomdivisjonen fortsette.
Hvis graden til $R (x)$ er mindre enn graden til $Q (x)$ , stopper divisjonen opp. $R (x)$ kalles restpolynomet eller bare resten i divisjonen.
Hvis resten er lik 0 går divisjonen opp.

Vi kaller det som står etter likhetstegnet for $S (x)$ , og skriver

$\frac{P (x)}{Q (x)} = S (x) + \frac{R (x)}{Q (x)}$ ,

som blir til $P (x) = Q (x) S (x)$ hvis divisjonen gikk opp; dette kalles en faktorisering av $P (x)$ .

Restpolynom

Eksempel

Polynomdivisjonsteoremet

Lynkurs 11.-13.trinn

Polynomdivisjon

Består av: