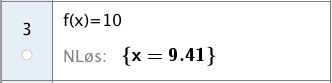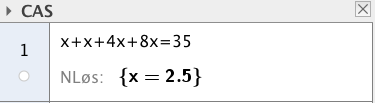Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2014 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Båt: (http://lokalhistoriewiki.no/, 7.07.2016)
- Andre tegninger, grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4BDP
Regn ut og skriv svaret på standardform
Oppgave 2 (2 poeng) Nettkode: E-4BDR
Regn ut og skriv svaret så enkelt som mulig
Oppgave 3 (1 poeng) Nettkode: E-4BDT
Løs likningen
Oppgave 4 (1 poeng) Nettkode: E-4BDV
Bestem slik at uttrykket
blir et fullstendig kvadrat.
Oppgave 5 (2 poeng) Nettkode: E-4BDX
Løs likningssystemet
Oppgave 6 (3 poeng) Nettkode: E-4BDZ
Trekk sammen og skriv så enkelt som mulig
Oppgave 7 (4 poeng) Nettkode: E-4BE1
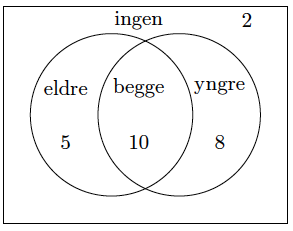
I en klasse er det 25 elever. 15 av elevene har eldre søsken. 18 av elevene har yngre søsken. 2 av elevene har ikke søsken.
a)
Systematiser opplysningene ovenfor i et venndiagram.
b)
Vi velger tilfeldig én elev fra klassen.
Bestem sannsynligheten for at eleven har eldre, men ikke yngre, søsken.
c)
Vi velger tilfeldig én av elevene som har eldre søsken.
Bestem sannsynligheten for at eleven også har yngre søsken.
Oppgave 8 (3 poeng) Nettkode: E-4BEC
I er , og .
Lag en skisse, gjør beregninger, og avgjør om følgende påstander er riktige:
1) Arealet av trekanten er større enn
2)
Oppgave 9 (5 poeng) Nettkode: E-4BEE
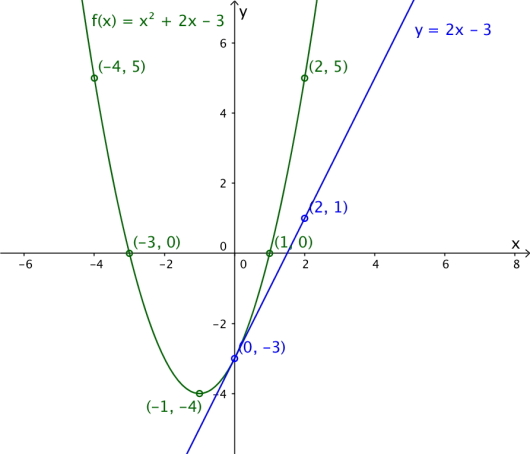
Funksjonen er gitt ved
a)
Bestem nullpunktene til ved regning.
b)
Grafen til har en tangent med stigningstall .
Bestem likningen til denne tangenten.
c)
Tegn grafen til sammen med tangenten fra oppgave b).
Oppgave 10 (2 poeng) Nettkode: E-4BEI
Funksjonen er gitt ved
Grafen til skjærer - aksen i punktet og har ett nullpunkt.
Bestem og .
DEL 2 Med hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4BEM
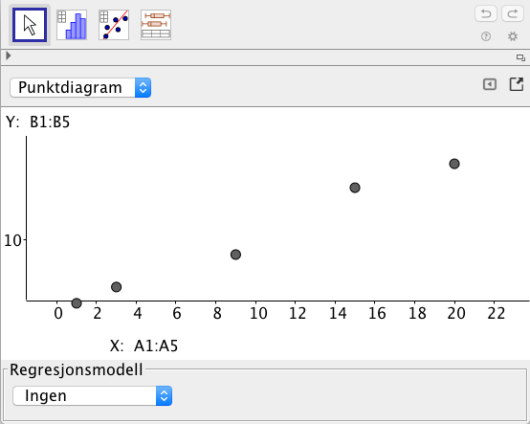
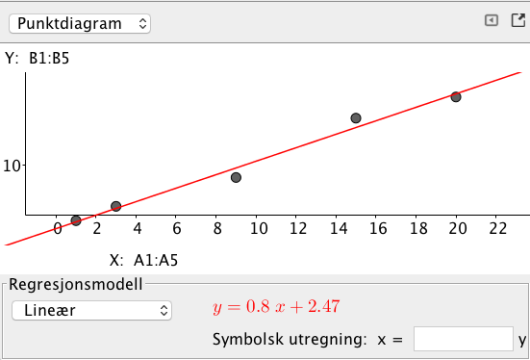
| Uke (x) | 1 | 3 | 9 | 15 | 20 |
| Lengde (y) | 3,4 km | 5, 1 km | 8, 5km | 15, 5km | 18,0 km |
Tabellen ovenfor viser hvor langt Janne jogget noen uker etter at hun begynte å trene. Den første uka jogget hun 3,4 km, den tredje uka jogget hun 5,1 km, og så videre.
a)
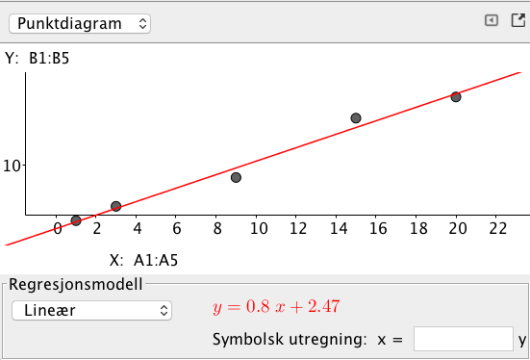
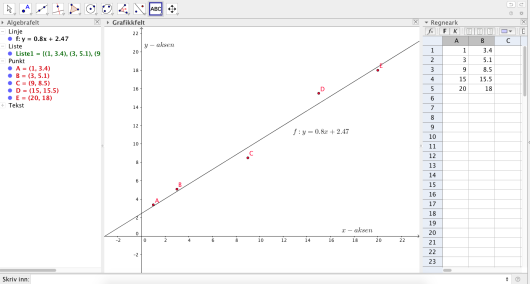
Bestem den lineære funksjonen som passer best med tallene i tabellen ovenfor.
b)
Hvor langt vil Janne jogge i uke 25 ifølge funksjonen i oppgave a) ?
c)
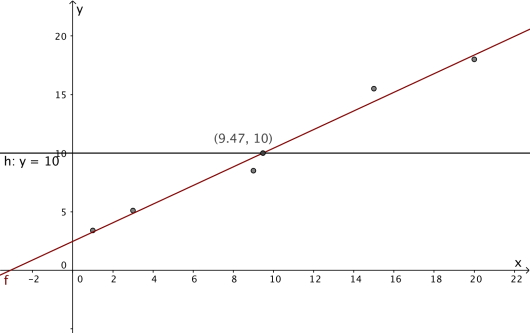
I hvilken uke jogget Janne for første gang mer enn 10 km ifølge funksjonen i oppgave a) ?
Oppgave 2 (9 poeng) Nettkode: E-4BEQ
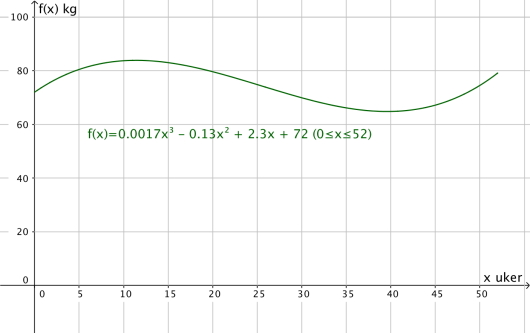
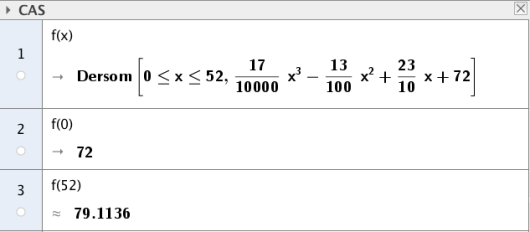
Funksjonen gitt ved
viser hvor mange kilogram en idrettsutøver veide uker etter 1. januar 2013.
a)
Tegn grafen til .
b)
Hvor mye veide idrettsutøveren 1. januar 2013, og hvor mye veide han ett år (52 uker) senere?
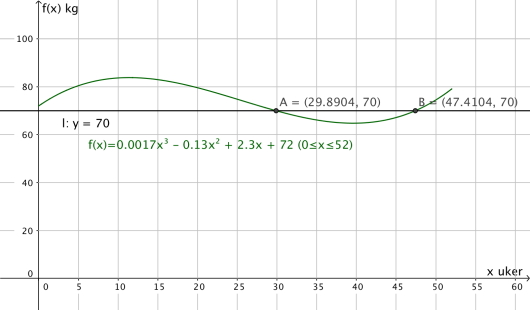
c)
Omtrent hvor mange uker i løpet av 2013 veide han mer enn 70 kg?
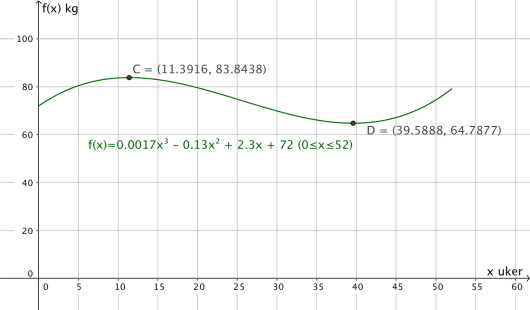
d)
Når veide idrettsutøveren mest, og når veide han minst?
Hvor mye gikk han i gjennomsnitt ned i vekt per uke i den perioden han gikk ned i vekt?
e)
Bestem og
Hva forteller disse to svarene om vekten til idrettsutøveren?
Oppgave 3 (4 poeng) Nettkode: E-4BEW
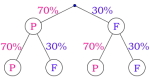
En bedrift produserer to ulike typer soveposer. Undersøkelser viser at 10 % av soveposene av type 1 og 15 % av soveposene av type 2 har en feil med glidelåsen.
På lageret ligger 1000 soveposer av type 1 og 4000 soveposer av type 2.
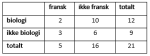
a)
Systematiser opplysningene ovenfor i en krysstabell.
b)
Bjarne har tilfeldig tatt to soveposer fra lageret. Det viser seg at begge soveposene har feil med glidelåsen.
Bestem sannsynligheten for at én av soveposene er av type 1 og at én er av type 2.
Oppgave 4 (4 poeng) Nettkode: E-4SJL
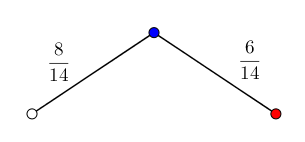
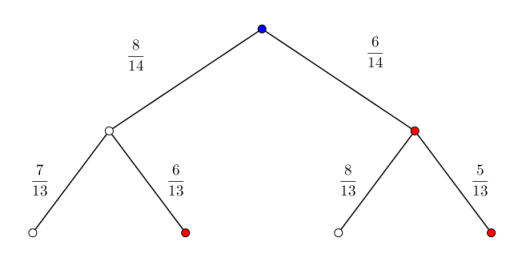
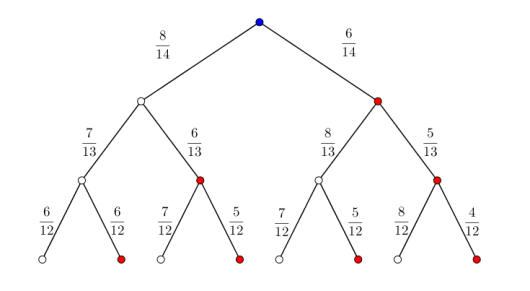
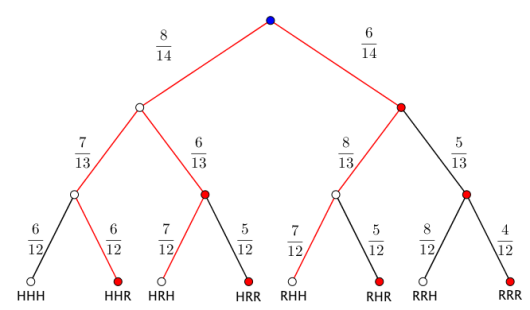
I en skål er det åtte hvite og seks røde kuler. Du skal trekke tre kuler tilfeldig.
a)
Systematiser de ulike utfallene i et valgtre.
b)
Bestem sannsynligheten for at du trekker to hvite og én rød kule. Marker hvordan du finner løsningen i valgtreet i oppgave a).
Oppgave 5 (2 poeng) Nettkode: E-4BF2
Et trestykke er 35 cm langt. Trestykket skal deles i fire deler.
To deler skal være like lange. Den tredje delen skal være dobbelt så lang som de to like delene til sammen, og halvparten så lang som den fjerde delen.
Bestem lengden av hver av de fire delene.
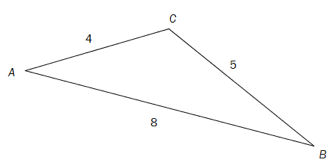
Oppgave 6 (3 poeng) Nettkode: E-4BF8
Regn ut arealet av .
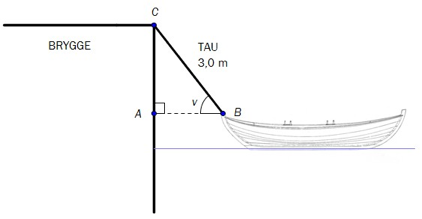
Oppgave 7 (4 poeng) Nettkode: E-4BFC
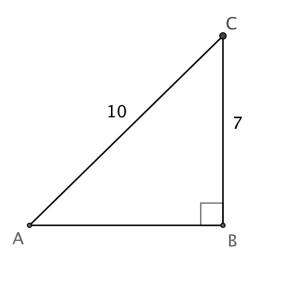
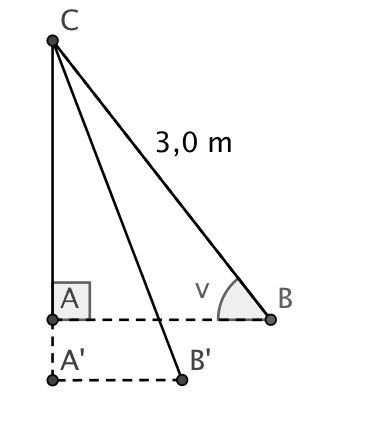
En båt ligger fortøyd ved en brygge med et stramt tau som går fra C til B. Tauet er 3,0 m langt. Se skissen ovenfor.
a)
Bestem avstanden fra båten til bryggen når .
b)
Vannstanden synker med 30 cm.
Bestem avstanden fra båten til bryggen nå.
Oppgave 8 (4 poeng) Nettkode: E-4BFG
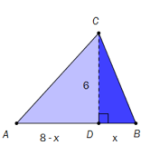
har grunnlinje .
Punktet ligger på . og . Se skissen til høyre.
Vi setter
a)
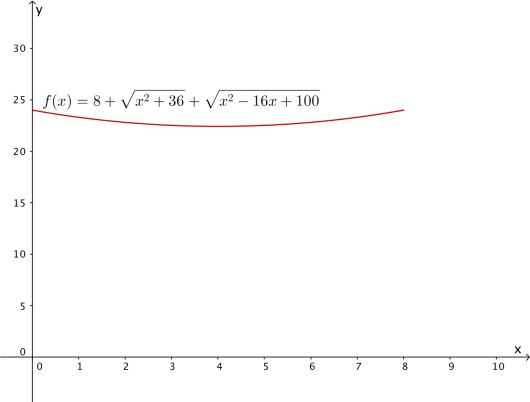
Vis at sammenhengen mellom lengden og omkretsen av er gitt ved
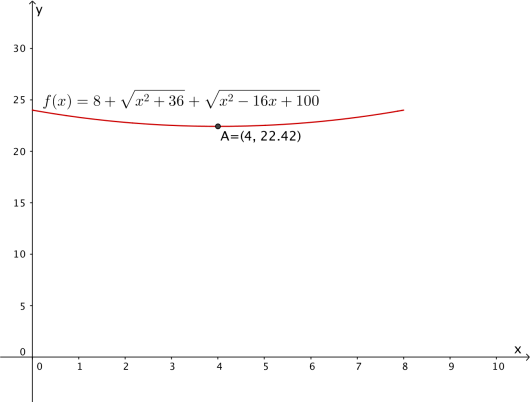
b)
Bestem slik at omkretsen av blir minst mulig.
Forklar at trekanten da vil være likebeint.
Oppgave 9 (2 poeng) Nettkode: E-4BFO
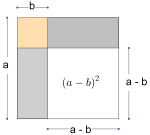
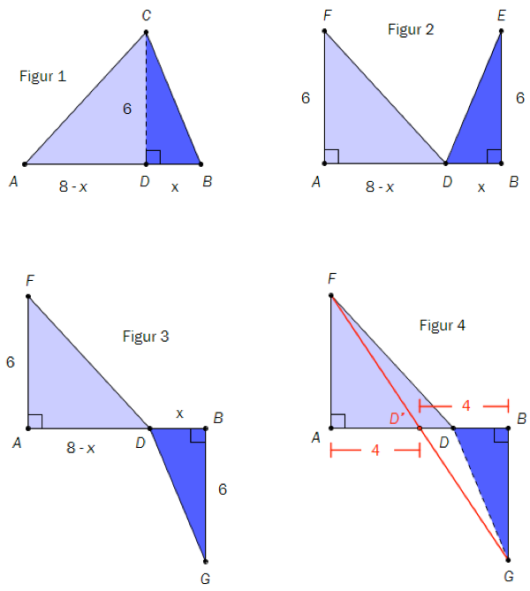
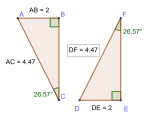
Petter får i oppgave å vise at når omkretsen av trekanten i oppgave 8 er minst mulig, er trekanten likebeint. Han løser oppgaven med figurer. Se nedenfor.
Ved hjelp av figurene viser han hvor punktet må plasseres på linjestykket for at lengden i figur 1 skal bli kortest mulig.
Forklar hva Petter har gjort, og at han har løst oppgaven riktig.