
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3024 2014 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.:
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4DEQ
Deriver funksjonene
a)
Løsningsforslag a)
Jeg tenker
Funksjonen er en konstant multiplisert med en cosinus funksjon med en kjerne . Det kan derfor være lurt å benytte kjerneregelen for derivasjon.
Siden den deriverte av en konstant er lik kan vi skrive Videre kan vi bruke kjerneregelen for derivasjon, som sier at den deriverte av en sammensatt funksjon er . Ved å sette får vi altså siden og siden får vi
Svar:
Mer om
Denne oppgaven er om Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Derivasjon
For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen.
Visste du at
En annen måte å skrive den deriverte av med hensyn på er ved å skrive . Denne måten å skrive kan virke krunglete, men gir faktisk mye mer mening. Hvis hadde vært en rett linje ville stigningstallet vært – endring i per endring i . Vi kan tenke på som en uendelig liten endring i per uendelig liten endring i . I stedet for å skrive kjerneregelen kan vi med denne notasjonen skrive kjerneregelen . Dette likner mer på en velkjent brøkregel, , enn en mystisk derivasjonsregel.
b)
Løsningsforslag b)
Jeg tenker
Funksjonen er et produkt av to forskjellige funksjoner, og , som ser greie ut å derivere hver for seg. Av den grunn bør vi benytte produktregelen for derivasjon.
Produktregelen konstanterer at hvis og er to funksjoner, må . Hvis vi setter og ser vi at Videre finner vi ved å derivere . Siden konstanter alltid kan tas utenfor derivasjonen og er sin egen deriverte må Videre finner vi ved å derivere . Kjerneregelen for derivasjon sier at hvis vi setter er Altså Den deriverte av blir altså
Svar:
Mer om
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En trigonometrisk funksjon. Cosinus er en trigonometrisk funksjon. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Eksponentialfunksjon

Sinus
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Derivasjon
For flere forklaringer og eksempler på derivasjon, se artikkelen Å derivere sammensatte uttrykk.
Visste du at
Ved å studere uttrykket for kan vi gjenkjenne . Vi kan nemlig skrive og siden er . Dette er en første ordens inhomogen differensiallikning. I stedet for å løse en differensiallikning har vi altså brukt en funksjon og dens deriverte til å lage en differensiallikning som løses av funksjonen.
Oppgave 2 (3 poeng) Nettkode: E-4DET
Bestem integralene
a)
Løsningsforslag a)
Jeg tenker
Inne i integraltegnet er det et polynom. Siden et integral av en sum er en sum av integraler kan vi integrere hvert ledd i polynomet enkeltvis.
Siden et integral av en sum er en sum av integraler kan vi skrive og siden for alle konstanter og integrerbare funksjoner kan vi skrive Videre vet vi at integralet av en funksjon er siden den deriverte av er . Altså har vi at
Svar:
Mer om
Denne oppgaven er om Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og . En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Integrasjon
Polynom
Derivasjon
For flere forklaringer og eksempler på integrasjon, se artikkelen Ubestemte integraler.
Visste du at
At den generelle konstanten, ofte kalt integrasjonskonstanten, må legges til kan forstås ved å se på et eksempel fra fysikken. Siden farten til et objekt er objektets endring i posisjon per tid må fart være den deriverte av objektets posisjon. Dette betyr at integralet av objektets fart må være posisjonen til objektet. Men det holder selvfølgelig ikke å vite hvor fort noe beveger seg hvis du ønsker å finne ut hvor objektet befinner seg. Du må også vite hvor objektet var, eller kommer til å være, på ett bestemt tidspunkt. Det er integrasjonskonstanten som tar høyde for dette problemet.
b)
Løsningsforslag b)
Jeg tenker:
For å finne integralet av fra til bør vi velge en integrasjonsmetode der vi unngår å integrere . Siden er mye lettere å derivere enn den er å integrere kan det være lurt å prøve delvis integrasjon.
Delvis integrasjon sier at hvis og er to funksjoner, så er .
Ved å sette og får vi og . Altså har vi at
Alt som gjenstår nå er å evaluere grensene Vi har altså funnet at
Svar:
Mer om:
Denne oppgaven er om Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10. Eksempel: log10(1000) = 3 ettersom 103 = 1000. Integrasjon
Logaritme
For flere forklaringer og eksempler på derivasjon, se artikkelen Delvis integrasjon.
Visste du at:
Selv om det ikke er en veldig annerkjent metode kan det ofte være vel så lett å løse et integral ved bare å gjette på ulike løsninger. For å finne integralet av kunne for eksempel den første gjetningen vært . Siden ser vi at ved å halvere begge sider får vi . Dette er nesten riktig, vi har bare fått for mye! Siden den deriverte av er kan vi imidlertid bare trekke fra funksjonen vår. Da sitter vi igjen med , som er riktig ettersom . Ved å legge til en integrasjonskonstant har vi altså vist at
bare ved å gjette.
Oppgave 3 (4 poeng) Nettkode: E-4DEW
a)
Løs differensiallikningen
når
Løsningsforslag a)
Jeg tenker
Utenom konstantledd inngår bare og dens førstederiverte, i likningen
.
Vi må altså løse en lineær differensiallikning av første orden.
Vi kan løse differensiallikningen ved å benytte et lurt triks kjent som ”integrerende faktor”. Idéen er å multiplisere begge sider av likningen med en funksjon slik at vi kan kjenne igjen produktregelen for derivasjon. Hvis
er en deriverbar funksjon kan vi skrive og ved å kreve at dette skal være lik venstresiden i differensiallikningen multiplisert med får vi
som betyr at vi må ha . En funksjon som tilfredsstiller dette er . Ved å multiplisere begge sider av differensiallikningen med kan vi altså skrive Hvis vi nå integrerer begge sider av likningen med hensyn på finner vi at for en konstant og for en konstant . Ved å kombinere de to konstantene til en felles konstant kan vi altså skrive løsningen av differensiallikningen som Ved å multiplisere begge sider av likningen med følger det at og siden må
Den spesielle løsningen av differensiallikningen er altså
Svar:.
Mer om
Denne oppgaven er om Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10. Eksempel: log10(1000) = 3 ettersom 103 = 1000. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår. Et eksempel er y'' - y = 0 eller Integrasjon
Logaritme
Eksponentialfunksjon

Differensiallikning
For flere forklaringer og eksempler på integrasjon, se artikkelen Integrerende faktor.
Visste du at
At løsningen til differensiallikningen betyr ikke noe annet enn at er den funksjonen som når den deriveres blir og som i tillegg går gjennom punktet . Det siste kravet er bare en annen måte å formulere kravet på.
b)
Bestem likningen til tangenten i punktet på grafen til .
Løsningsforslag b)
Jeg tenker
For å skrive likningen til tangenten i et punkt må vi både ha et stigningstall og et konstantledd for linjen. Stigningstallet får vi fra den deriverte, mens konstantleddet får vi fra hvor linjen skjærer -aksen.
Siden tangenten på grafen til funksjonen fra oppgave i punktet er en rett linje kan den skrives som en lineær funksjon , der er stigningstallet og er konstantleddet til linjen. Siden per definisjon deler stigningstall med i punktet må . Selv om det er helt uproblematisk å derivere for deretter å sette inn punktet , er det enda lettere å huske at tilfredsstiller likningen i 3a. Altså er Konstantleddet, , finner vi ved å se hvor skjærer -aksen. Vi vet imidlertid at går gjennom punktet , som ligger på -aksen. Altså må konstantleddet være gitt som -koordinaten . Dette betyr at tangenten er gitt av funksjonsuttrykket
Svar:
Mer om
Denne oppgaven er om Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2. Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Lineære funksjoner er funksjoner som er skrevet på formen . En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Stigningstall

Tangent

Graf
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Funksjon
For flere forklaringer og eksempler på tangenter, se artikkelen Ettpunktsformelen og likning for tangentlinjen.
Oppgave 4 (4 poeng) Nettkode: E-4DEZ
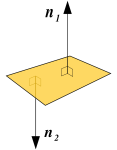
Punktene , og ligger i planet .
a)
Bestem likningen til .
Løsningsforslag a)
Jeg tenker
For å beskrive planet holder det å finne en vektor som står normalt på planet og et punkt i planet. For å finne normalvektoren kan vi beregne kryssproduktet mellom to vektorer i planet.
Vi begynner med å finne to vektorer mellom punkter i planet. Et naturlig valg er da vektorene og gitt ved
Deretter beregner vi kryssproduktet
Det eneste viktige med denne vektoren er retningen. Det betyr at vi kan dividere vektorens lengde med og heller velge som normalvektor for planet. Alle vektorer mellom punkter i planet må altså tilfredsstille
Likningen for planet er imidlertid en likning for alle punkter – ikke alle vektorer! Dette kan vi ta høyde for ved å kreve at
der er et eller annet punkt i planet . Ved å velge får vi at er likningen for planet .
Alternativ løsning
Ved å huske at formelen til et plan som inneholder punktet og har normalvektor kan skrives holder det å bemerke at står normalt på planet siden og at punktet ligger i . Da får vi som er likningen til planet .
Svar:
Mer om
Denne oppgaven er om Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. En normalvektor for et plan står vinkelrett på alle linjer i planet. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Plan
Normalvektor
Ligning
For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.
b)
Et punkt ligger på linjen gjennom punktene og .
Bestem mulige koordinater til slik at volumet av tetraederet blir .
Løsningsforslag b)
Jeg tenker
Dersom vi først klarer å bestemme volumet av tetraederet som funksjon av koordinatene til vil vi kunne bruke kravet om at volumet er til å bestemme .
At punktet ligger mellom og betyr at vi kan uttrykke det ved der . Volumet av et tetraeder utspent av tre vektorer er nøyaktig en sjettedel av volumet til parallellepipedet utspent av de samme vektorene. Siden volumet av parallellpipedet utspent av er er altså volumet av tetraederet utspent av og gitt av
Vektorene og kan vi uttrykke
I a) fant vi at kryssproduktet . Volumet av tetraederet er altså
For at volumet skal være lik må vi altså enten ha eller . Det er med andre ord to mulige koordinater for , nemlig
Svar:
Mer om
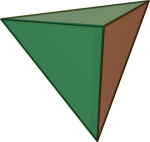
Denne oppgaven er om Et legeme som begrenses av fire kongruente, likesidede trekanter. Se Platonske legemer Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3). En vektor er en størrelse med en retning. I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren. Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = . En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se Koordinatsystem I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.Tetraeder
Volum

Vektor

Linje
Koordinat
Punkt

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt - areal og volum.
Oppgave 5 (4 poeng) Nettkode: E-4DF4
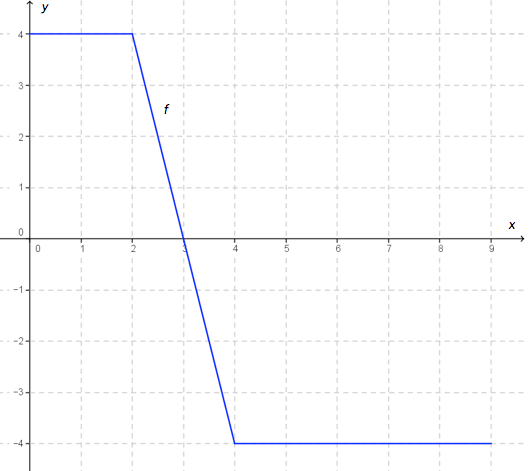
Figuren viser grafen til en funksjon , der .
La , der
a)
Bestem . Forklar at den største verdien til er .
Løsningsforslag a)
Jeg tenker
For å bestemme må vi integrere funksjonen fra til . Siden dette integralet er lik arealet under grafen til holder det å beregne dette arealet.
Siden er arealet under grafen til fra til , og er konstant lik på intervallet må Siden de eneste positive bidragene til kommer fra punkter der , og for , kan aldri ta større verdier enn . Vi kan dele opp arealet under mellom og i den rektangulære biten og den triangulære biten . Vi får da at Altså kan ikke ta større verdier enn .

Svar:
Mer om
Denne oppgaven er om Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.Integrasjon
Graf
Intervall
Areal
Noen måleenheter for areal er m2, dm2 og cm2.
For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.
Visste du at
Det at det bestemte integralet av en funksjon fra til representerer arealet av området under grafen til mellom og er en veldig fin måte å tolke det bestemte integralet på. Når vi multipliserer to tall og kan vi ofte tenke på resultatet som arealet av rektangelet med lengde og bredde . På samme måte kan vi tenke på som arealet av et uendelig tynt rektangel bredde og med høyde . Det mystiske integraltegnet, , er faktisk bare en litt rar ”S” og er en forkortelse for ”sum”. Med andre ord kan vi lese som ”summen av alle uendelig tynne rektangler med høyde mellom og ”.
b)
Bestem nullpunktet til . Avgjør hvilke verdier av som gjør negativ.
Løsningsforslag b)
Jeg tenker
Nullpunktet til er nøyaktig den verdien for der grafen til har like stort areal over -aksen, som under -aksen.
Arealet over -aksen avgrenset av grafen til og intervallet er like stort som arealet under -aksen avgrenset av og intervallet .
Siden er positiv for alle og negativ for alle betyr det at . Dette betyr at er et nullpunkt for og at er negativ for alle siden da er negativ. Merk imidlertid at også forsvinner når ettersom arealet under mellom og nødvendigvis må være .
Altså er nullpunktene for nøyaktig de to punktene . Hvis er altså arealet under -aksen større enn arealet over -aksen. Det betyr at .
Svar:
Mer om
Denne oppgaven er om Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. Den horisontale aksen i et koordinatsystem. Den loddrette aksen i et koordinatsystem. Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.Nullpunkt

Intervall
x-akse

Kalles også førsteakse.y-akse

Kalles også andreaksen.Areal
Noen måleenheter for areal er m2, dm2 og cm2.
For flere forklaringer og eksempler på integrasjon, se artikkelen Halvar forteller om fundamentalteoremet.
Visste du at
Det å vite at en funksjon er antisymmetrisk (like stor på begge sider, men med motsatt fortegn) rundt et punkt kan være veldig nyttig når man beregner integraler. For eksempel kan vi med en gang si at siden funksjonen er antisymmetrisk rundt Origo. Dette er fordi en funksjon som er er antisymmetrisk rundt Origo bidrar med like mye positivt areal fra den ene siden som den bidrar med negativt areal fra den andre siden.
Eksempler på funksjoner som er antisymmetriske rundt er der , og .
Oppgave 6 (4 poeng) Nettkode: E-4DF8
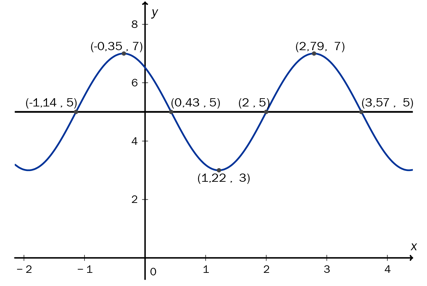
Ovenfor ser du grafen til en funksjon .
a)
Bestem , , og ved hjelp av grafen og de punktene som er markert på grafen.
Skriv opp funksjonsuttrykket til f (x).
Løsningsforslag a)
Jeg tenker
Ved å se på grafen kan vi lese av verdier som funksjonens største -verdi, avstanden mellom toppene og gjennomsnittshøyden til . Vi kan bruke disse verdiene til å bestemme og .
Vi begynner med å finne likevektslinjen . Fra grafen ser vi at maksimalt tar verdien og minimalt . Disse toppene må komme fra sinusfunksjonen i og siden sinus avviker like mye fra null i både positiv og negativ retning må likevektslinjen være verdien midt mellom maksimal- og minimalverdien til . Altså må . Det følger at forskjellen mellom likevektslinjen og maksimalverdien til må være nøyaktig verdien av . Altså har vi at .
For nå å finne finner vi først avstanden mellom to nærstående topper – altså perioden til funksjonen. Fra grafen finner vi at den er som er omtrent lik . Avstanden mellom to topper på grafen til funksjonen er . Da må vi ha , noe som betyr at . Vi har altså funnet at Ved å benytte omskrivingen ser vi at størrelsen må være grafens faseforskyvning, som vi ved å lese av ser at er omlag . Det betyr at Altså har vi tilnærmet funksjonsuttrykket til å være
Svar:
Merk at vi alltid kan legge til, eller trekke fra, fra vinkelen uten å endre verdien til uttrykket.
Mer om
Denne oppgaven er om Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten. er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Trigonometriske funksjoner
Pi (π)
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Toppunkt

Graf
For flere forklaringer og eksempler på trigonometri, se artikkelen Periodiske funksjoner.
b)
Grafen ovenfor kan også være grafen til .
Skriv opp funksjonsuttrykket til .
Løsningsforslag b)
Jeg tenker
Formen til en cosinusfunksjon er identisk med en sinusfunksjon, den eneste forskjellen er en faseforskyvning.
En cosinusfunksjon ligger alltid et kvart omløp foran en sinusfunksjon. Med andre ord er det ikke behov for å gjøre annet enn å forskyve vinkelen inne i sinusfunksjonen fra oppgave slik at vinkelen alltid ligger bak. Med andre ord kan vi bruke at til å finne følgende tilnærmede uttrykk for :
Alternativ løsning
Amplituden , likevektslinjen og vinkelfrekvensen vil alle være like som i oppgave . Faseforskyvningen , vil imidlertid være annerledes ettersom en cosinusfunksjon alltid begynner på sin maksimale verdi. Fra grafen finner vi da at faseforskyvningen er og derfor at Da finner vi Alternativt kunne vi valgt faseforskyvningen , som gir .
Svar:Merk at vi alltid kan legge til, eller trekke fra, fra vinkelen uten å endre uttrykket.
Mer om
Denne oppgaven er om Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader. er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Vinkel
Pi (π)
Toppunkt

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Sinus, cosinus og tangens.
Oppgave 7 (2 poeng) Nettkode: E-4DFB
Bruk induksjon til å bevise påstanden
Løsningsforslag
Jeg tenker
For å bevise en påstand ved hjelp av induksjon må vi vise at den første påstanden gjelder, nemlig at . Deretter må vi vise at hvis stemmer for , så stemmer den nødvendigvis også for .
Vi skal vise at utsagnet
er sant for alle naturlige tall .
Med blir produktet på venstre side bestående av bare én faktor, nemlig . Høyre side blir . Dette viser at er sann.
Anta at er sann, altså at
Da må vi ha
Dette er presis utsagnet , så vi har vist at . Dermed er sant.
Mer om
Denne oppgaven er om
Matematisk induksjon
En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:
- Bevis påstanden for n =1.
- Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).
Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.
Visste du at
Vi kunne også bevist dette ved omskriving av produktet på venstresiden av likningen i oppgaveteksten. Det holder nemlig å observere at
DEL 2 Med hjelpemidler
Oppgave 1 (8 poeng) Nettkode: E-4DFE
a)
Vi har en uendelig geometrisk rekke som er konvergent.
Vis at summen av rekken kan skrives
Løsningsforslag a)
Jeg tenker
En rekke er en geometrisk rekke hvis er uavhengig av .
Siden rekken er geometrisk, er er kvotienten til rekka. Summen er
Mer om
Denne oppgaven er om En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer. Eksempel : ( ∞ er tegnet for uendelighet ) Resultatet av en addisjon. Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Uendelige rekker
Sum
Brøk

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.
Visste du at
Uendelige rekker kan faktisk gi mening selv om de ikke konvergerer. Ta for eksempel rekken som er lik det uendelig store tallet . Dersom vi later som om rekken er konvergent må den ifølge påstanden over konvergere mot tallet , som ved første øyekast ikke gir veldig mye mening. Vi kan imidlertid hevde at dersom skulle vært et endelig tall, burde det vært . Dette kan vi se ved for eksempel å undersøke hva verdien av må være, Siden er tallet som består av uendelig mange nitall forskyver vi ettallet uendelig langt bort. Altså ser det ut til at , som betyr at . Helt tilsvarende kan vi vise at . Selv om det ikke gir noen mening virker det altså ikke helt utenkelig å si at .
b)
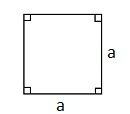
Figuren nedenfor viser en rettvinklet og likebeint der katetene har lengde 12. Inne i trekanten har vi en rekke kvadrater (markert med blått på figuren). Det største kvadratet har side 6, det nest største har side 3, slik at sidene til kvadratene blir halvert i det uendelige.
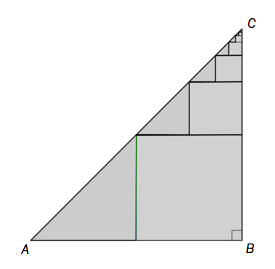
Forklar at summen av arealene til kvadratene kan skrives som en uendelig geometrisk rekke. Bruk formelen i oppgave a) til å bestemme .
Løsningsforslag b)
Jeg tenker
For å uttrykke arealene til kvadratene som en uendelig geometrisk rekke er vi først nødt til å finne arealet av det første, og hvor mye mindre hvert kvadrat er enn det foregående.
Siden er likebeint og rettvinklet må det største kvadratet ha sidelengde . Det neste kvadratets nedre, venstre hjørne må på tilsvarende måte dele i to like store segmenter. Det betyr at det neste kvadratets sidelengde er . Ettersom dette mønsteret fortsetter på samme måte må , og så videre. Summen av arealene til kvadratene kan da uttrykkes ved og ved å ta i bruk formelen i oppgave finner vi
Svar:
Mer om
Denne oppgaven er om En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre. I en likebeint trekant er to sider like lange og to vinkler like store. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Rett vinkel
Likebeint trekant
Brøk

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske tallfølger.
c)
inneholder også uendelig mange rettvinklete og likebeinte trekanter (markert med grønt på figuren) der sidene også halveres fra gang til gang. Skriv summen av arealene til disse trekantene som en uendelig geometrisk rekke. Bestem denne summen.
Løsningsforslag c)
Jeg tenker
Arealet av hver trekant er nøyaktig halvparten av arealet av kvadratet på dets høyre side.
Siden arealet av hver trekant er halvparten av kvadratet på dets høyre side og summen av arealene til kvadratene kan skrives følger det at summen av trekantene er gitt av den uendelige geometriske rekken Verdien av denne summen finner vi lettest ved å se at , slik at
Alternativt kunne vi brukt formelen fra .
Svar:
Mer om
Denne oppgaven er om En firkant der alle sider er like lange og alle vinkler 90°. Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Resultatet av en addisjon. Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum. En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer. Eksempel : ( ∞ er tegnet for uendelighet )Kvadrat
Areal
Noen måleenheter for areal er m2, dm2 og cm2.Trekant

Sum
Uendelige rekker
For flere forklaringer og eksempler på rekker, se artikkelen Uendelige rekker.
d)
Forklar hvordan du kunne ha funnet de to summene i oppgave b) og oppgave c) ved hjelp av et geometrisk resonnement.
Løsningsforslag d)
Jeg tenker
Siden vi kjenner lengden av katetene i kan vi finne arealet. Vi kan også finne et forhold mellom summen av arealene til trekantene og summen av arealene til kvadratene i .
Siden er en rettvinklet, likebeint trekant der lengden av katetene er , har areal . Videre vet vi at hvis er summen av arealene til kvadratene og er summen av arealene til trekantene, så må fordi hver trekant utgjør nøyaktig halvparten av det tilsvarende kvadratet. Siden alle de små og trekantene og kvadratene fyller må vi også ha at er arealet av , altså Det betyr at vi har likningsettet
som løses av og .
Alternativ løsning
Ettersom arealet er og summen av trekantene og kvadratene til sammen utgjør hele holder det å observere at summen av trekantene utgjør nøyaktig halvparten av summen kvadratene. Det betyr at hvis vi deler i tre like store deler med areal , må summen av trekantene være , mens summen av kvadratene være .
Mer om
Denne oppgaven er om Resultatet av en addisjon. Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum. Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En firkant der alle sider er like lange og alle vinkler 90°.Sum
Katet
Trekant

Areal
Noen måleenheter for areal er m2, dm2 og cm2.Kvadrat

For flere forklaringer og eksempler på areal, se artikkelen Tom forteller om areal.
Oppgave 2 (8 poeng) Nettkode: E-4DFJ
En differensiallikning er gitt ved
a)
Sett opp den karakteristiske likningen, løs denne og bruk løsningen til å bestemme et generelt uttrykk for .
Løsningsforslag a)
Jeg tenker
Siden høyresiden er null er likningen homogen, og siden den andrederiverte av , og ingen høyere deriverte, inngår i likningen er den en andre ordens differensiallikning. Den karakteristiske likningen finner vi ved å anta at løsningene er på formen .
En andre ordens homogen differensiallikning har alltid to uavhengige løsninger. Dersom vi klarer å gjette oss frem til to forskjellige løsninger har vi altså løst likningen. Mennesker før oss har heldigvis funnet ut at det er lurt å gjette på løsninger på formen . Da er og . Ved å sette dette inn i likningen over får vi og siden aldri blir null må dette være sant fordi Dette er den karakteristiske likningen! Denne kan vi løse ved å bruke annengradsformelen
der . De to løsningene er altså
Ettersom og løser likning i oppgaveteksten, må nødvendigvis også løse likningen for to konstanter og . Vi kan altså skrive den generelle løsningen på formen Dersom du kjenner til formelen kan du bruke til å komme frem til, etter mye jobb, uttrykket for noen andre konstanter og . Her er det imidlertid mye enklere å bruke kommandoenSolveODE[4y”+4y’+5y=0]
som gir
Numerisk løsning:
Skriv følgende kommando i CAS:LøsODE[4y”+4y’+5y=0]
Det gir
Svar: Karakteristisk likning: Generell løsning:
Mer om
Denne oppgaven er om abc-formelen sier at en likning på formen har løsningene . Komplekse tall er en utvidelse av de reelle tall. De er satt sammen av en realdel og en imaginærdel. Tallene kan fremstilles i et tallplan hvor førsteaksen er de reelle tallene og andreaksen de imaginære tallene. Den imaginære enheten er . Et komplekst tall angis ofte på formen a + ib, hvor a og b er reelle tall. Funksjoner definert for komplekse tall med komplekse funskjonsverdier. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår. Et eksempel er y'' - y = 0 eller abc-formelen
Komplekse tall
Komplekse funksjoner
Eksponentialfunksjon

Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Differensiallikning
For flere forklaringer og eksempler på differensiallikninger, se artikkelen Andre ordens differensiallikninger.
Visste du at
Likningen kalles av mange for verdens vakreste likning. Spesielt kjent er uttrykket , som inneholder fem av de kanskje viktigste konstantene i matematikk: og . Du kan også bruke likningen, som kalles for ”Eulers formel”, til å uttrykke sinus og cosinus ved som kan brukes til å produsere alle de trigonometriske likningene man ofte blir bedt om bare å memorere.
b)
Finn integrasjonskonstantene når du får vite at og .
Løsningsforslag b)
Jeg tenker
Ved å vite to punkter grafen til løsningen går gjennom kan vi bestemme de to konstantene og .
Ved først å kreve at får vi Ved deretter å kreve at får vi Den spesielle løsningen er altså
Numerisk løsning:
Skriv følgende kommando i CAS:LøsODE[4y”+4y’+5y=0,{(0,3),(3 \pi /4,0)}]
Resultatet er
Svar:
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Graf
Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Ligning
For flere forklaringer og eksempler på likninger, se artikkelen Trigonometriske likninger.
c)
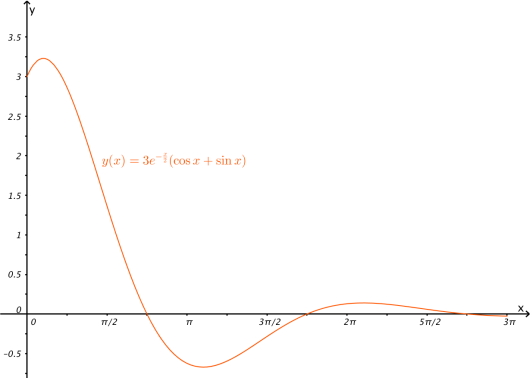
Tegn grafen til for .
Løsningsforslag c)
Jeg tenker
Vi må tegne grafen til funksjonen fra oppgave når er i intervallet .
Vi bruker følgende kommando i GeoGebra for å definere den spesielle løsningenf(x)=3exp(-x/2)(cos(x)+sin(x))
For å tegne denne på intervallet bruker vi deretter:y=Dersom[0 \leq x < 3\pi, f]
Svar:
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Graf
Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Intervall
Pi (π)
Eksponentialfunksjon

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.
d)
Bestem eventuelle nullpunkter til og koordinatene til eventuelle topp- og bunnpunkter på grafen til når .
Løsningsforslag d)
Jeg tenker
Nullpunktene til en funksjon er nøyaktig de -verdiene som tilfredsstiller . Topp- og bunnpunkter er punkter der funksjonen verken vokser eller avtar. Altså må et topp- eller bunnpunkt tilfredsstille .
Vi begynner med å finne nullpunktene ved å kreve at disse punktene tilfredsstiller . Det gir og siden ikke kan ha skyld i at funksjonen er null, må Ved å dividere begge sider av likhetstegnet med kan likningen omgjøres til kravet som betyr at
(Hvis du ikke har sett funksjonen før er det antageligvis fordi du har lært å heller skrive , som betyr det samme.)
Nullpunktene i intervallet er altså For å finne topp- og bunnpunkter deriverer vi først funksjonen
Deretter finner vi mulige ekstremalpunkter ved å kreve at . Det gir og siden aldri kan bli null må Ved å dividere begge sider av likhetstegnet med og løse for kan vi skrive som løses av
der . Ved enten å sette inn vilkårlige verdier mellom nullpunktene, eller å se på grafen i oppgave , finner vi at funksjonen har toppunkter og bunnpunkt i Dette finner vi ved å se at veksler mellom å være positiv og negativ mellom hvert nullpunkt, og at den begynner som positiv. Nullpunktene til er
Bunnpunktet er og toppunktene er .
Numerisk løsning:
Bruk følgende kommandoer geoGebras grafdel:f(x) = Dersom[0 \leq x < 3\pi, 3exp( -x/2 ) (cos(x) + sin(x))]
NP_1:=Nullpunkt[f, \pi/2,\pi]
NP_2:=Nullpunkt[f, 3\pi/2,2\pi]
NP_3:=Nullpunkt[f, 5\pi/2,3\pi]
BP_1:=Ekstremalpunkt[f, \pi, 2\pi]
TP_1:=Ekstremalpunkt[f, 0, \pi]
TP_2:=Ekstremalpunkt[f, 3\pi/2, 5\pi/2]
Resultatet er punktene
Svar: Tilnærmede, numeriske verdier er
Mer om
Denne oppgaven er om Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt . Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Nullpunkt

Toppunkt

Bunnpunkt

Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Eksponentialfunksjon

Derivasjon
For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.
Oppgave 3 (8 poeng) Nettkode: E-4DFP
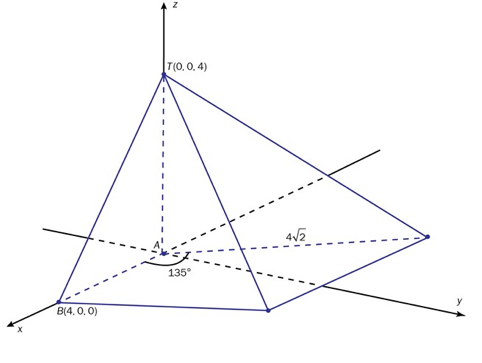
En pyramide er gitt på figuren ovenfor. Pyramiden settes inn i et tredimensjonalt koordinatsystem slik at koordinatene til , og er gitt ved , , . Punktene og ligger i -planet.
a)
Vi setter og . Vis at har koordinatene .
Løsningsforslag a)
Jeg tenker
Vi må finne koordinatene til et punkt når vi kjenner punktets avstand fra Origo, og vinkelen mellom punktet og -aksen. Det kan vi gjøre ved å benytte regneregler for trigonometri.
Vi kan først merke oss at ligger i -planet og at vi derfor må ha . Siden vinkelen mellom punktet -aksen og er , er vinkelen mellom -aksen og lik . Siden avstanden fra Origo, , til , som er , er hypotenusen i en likebenet og rettvinklet trekant må katetene ha lik lengde, . Denne lengden må ifølge Pythagoras læresetning tilfredsstille . Altså må kateten ha lengde . Siden den ene kateten ligger i positiv -retning og den andre i negativ -retning må koordinatene til være .
Alternativ løsning
Vi kan først merke oss at ligger i -planet og at vi derfor må ha . Punktene langs en sirkel med radius er gitt ved koordinatene , der er vinkelen mellom -aksen og punktet. Siden er et punkt på denne sirkelen, med vinkel fra -aksen, er koordinatene til gitt av
Svar: Koordinatene til er
Mer om
Denne oppgaven er om Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se Koordinatsystem I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B. Den horisontale aksen i et koordinatsystem. Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter. Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter. Pytagoras læresetning sier at: I en likebeint trekant er to sider like lange og to vinkler like store. En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.Koordinat
Punkt

x-akse

Kalles også førsteakse.Hypotenus

Katet

Pytagoras læresetning

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.Likebeint trekant

Rett vinkel

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Eksakte verdier.
Visste du at
Ved å huske at diameteren i et kvadrat med sidelengder har lengde og at vinkelen mellom -aksen og er kunne vi med en gang sett at koordinatene til må ha tallverdi . Siden ligger i andre kvadrant må -koordinaten være negativ, men -koordinaten være positiv. Altså er koordinatene til lik .
b)
Punktet er slik at . Vis at har koordinatene .
Løsningsforslag b)
Jeg tenker
For å finne koordinatene til må vi først finne et uttrykk for vektorene og .
Siden punktet må tilfredsstille , og koordinatvektoren til er
kan det være lettere å ta utgangspunkt i
Siden ligger i Origo har vektorene og samme koordinater som punktene og . Det betyr at
Koordinatvektoren til er da gitt av
Altså kan vi skrive koordinatene til som
Svar: Koordinatene til er
Mer om
Denne oppgaven er om En vektor er en størrelse med en retning. I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren. Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = . Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se KoordinatsystemVektor

Koordinat
For flere forklaringer og eksempler på vektorer, se artikkelen Addisjon av vektorer.
c)
Punktene , og ligger i et plan .
Vis at likningen for er
Løsningsforslag c)
Jeg tenker
For å finne likningen for et plan må man i første rekke ha en vektor som står normalt på alle vektorer mellom to punkter i planet. Dersom og er vektorer mellom punkter i planet må peke i samme retning som normalvektoren.
Vi begynner med å finne uttrykk for og , som er to vektorer mellom punkter i planet . Disse er gitt ved
Deretter beregner vi kryssproduktet ved
Siden vi bare er interessert i retningen til denne vektoren kan vi velge normalvektoren
.
Hvis er koordinatvektoren til et punkt i planet må alle punkter med koordinater i planet tilfredsstille likningen
Ved å velge får vi da at likningen for planet er gitt av
Altså er likningen for planet
Svar:
Mer om
Denne oppgaven er om Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. En normalvektor for et plan står vinkelrett på alle linjer i planet. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Plan
Normalvektor

Ligning
For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.
Visste du at
Vi kunne også funnet normalvektoren til planet ved å ta i bruk et geometrisk argument. Siden og ligger like langt fra Origo og langs henholdsvis -aksen og -aksen, må -koordinaten og -koordinaten til normalvektoren være like.
Hvis punktet hadde hatt koordinater måtte alle koordinatene vært like. Siden lengden av normalvektoren ikke har noe å si kunne vi da valgt koordinatene . har imidlertid koordinatene , noe som betyr at vektoren er dobbelt så lang i -retning som den er i -retning. Altså må normalvektoren være dobbelt så lang i -retning som den er i -retning. Dette betyr at vi kan velge som normalvektor til planet .
d)
Volumet av pyramiden kalles og volumet av pyramiden kalles .
Bestem forholdet .
Løsningsforslag d)
Jeg tenker
For å bestemme forholdet må vi først finne et uttrykk for og . For å gjøre dette kan vi bruke formelen for volumet av en pyramide utspent av vektorene , og .
Siden begge pyramidene innholder punktene , og kan vi bruke kryssproduktet vi beregnet i oppgave : . Ettersom en pyramide utspent av tre vektorer , og har volum , kan vi uttrykke volumene og ved
Alt vi trenger er altså å finne uttrykk for vektorene . Siden og er koordinatvektoren til følger det at . Videre finner vi ved
Altså har vi
og
Det betyr at
Svar:
Mer om
Denne oppgaven er om Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3). En vektor er en størrelse med en retning. I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren. Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .Volum

Vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt - areal og volum.
Oppgave 4 (6 poeng) Nettkode: E-4DFV
Et fotballmål har lengde m. En fotballspiller løper med ballen langs linjestykket , slik figuren nedenfor viser. Punktet ligger m fra punktet . Han vil skyte på mål når er størst mulig. avhenger av lengden .
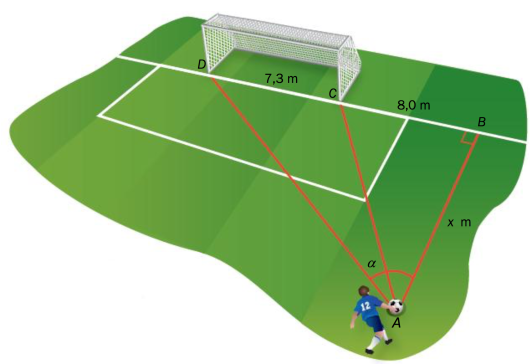
Vi setter og og lar
a)
Bruk formelen til å vise at
Løsningsforslag a)
Jeg tenker
Før vi bruker formelen ovenfor må vi ved å se på figuren beregne og . Det kan vi gjøre ved å huske at i en rettvinklet trekant er tangens til en vinkel alltid lik forholdet mellom motstående katet og hosliggende katet.
Siden er rettvinklet må Siden også er rettvinklet må vi ha
Fra formelen i oppgaveteksten følger det da at
som er det vi ønsket å vise.
Mer om:
Denne oppgaven er om Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten. En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Trigonometriske funksjoner
Rett vinkel

Trekant

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Mer kompliserte likninger.
</divb)
Bestem den største verdien for og tilhørende verdi for .
Løsningsforslag b)
Jeg tenker
Den største verdien for er enten en av endepunktene, som i denne sammenhengen er utelukket, eller et punkt der går fra å vokse til å avta.
For å finne den største verdien for må vi først beregne , for deretter å kreve at på en slik måte at går fra å være positiv til å være negativ i punktet . Fra brøkregelen for derivasjon følger det at Siden nevneren aldri blir uendelig stor må bety at Ettersom vi ikke er interessert i situasjonen der fotballspilleren har løpt langt forbi målet velger vi bare den positive løsningen, altså . Siden disse er de eneste nullpunktene til , er positiv og er negativ må være det eneste toppunktet til . Verdien av er da tilnærmet lik
Svar:
Mer om
Denne oppgaven er om En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen. Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Derivasjon
Ekstremalpunkter
Brøk

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.
c)
Vi vet at har sin største verdi når har sin største verdi.
Bestem .
Løsningsforslag c)
Jeg tenker
Vi må finne slik at er størst mulig.
Siden er maksimal når er maksimal holder det å finne slik at er maksimal. I oppgave fant vi den største verdien for , og siden dette også gir maksimal kan har vi allerede funnet at Det betyr at Altså er den maksimale verdien av lik radianer, eller grader.
Svar:
Mer om
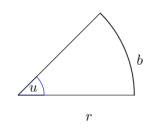
Denne oppgaven er om Det absolutte vinkelmålet til vinkelen er tallet der er buelengden og er radien. Legg merke til at siden både og er lengder, vil lengdebenevningene forkortes mot hverandre i brøken , slik at det absolutte vinkelmålet blir et ubenevnt tall. Likevel sier vi ofte at er målt i radianer. I en sirkel med radius er omkretsen lik . Det er derfor naturlig å si at en runde i sirkelen tilsvarer radier eller radianer. Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.Radianer
Trigonometriske funksjoner
For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Sinus, cosinus og tangens.
Visste du at
At den maksimale vinkelen fotballspilleren må treffe innenfor er radianer betyr at hvis han på dette punktet skyter ballen i en helt vilkårlig retning vil han treffe mål av gangene.
Oppgave 5 (6 poeng) Nettkode: E-4DFZ
Et plan er gitt ved likningen
a)
Bestem likningen for den kuleflaten som har sentrum i punktet og som har som tangentplan.
Løsningsforslag a)
Jeg tenker
Punktene på en kuleflate med sentrum er alle punkter som har avstand fra .
Ifølge Pythagoras læresetning må punktene på en kuleflate med sentrum i punktet og radius tilfredsstille Siden er et tangentplan for kuleflaten må radien, , være avstanden fra til planet . For å finne denne avstanden trenger vi først et punkt i . Her kan vi for eksempel velge punktet . Vektoren fra dette punktet til kulens sentrum, , er da gitt ved
Videre gir koeffisientene i likningen i oppgaveteksten at normalvektoren til planet er . Avstanden mellom og planet er da gitt som
siden gir lengden av den komponenten vektoren har i retningen . Likningen for kuleflaten er altså
Alternativ løsning
Ved å ta i bruk avstandsformelen kan vi finne avstanden fra punktet til planet ved Da følger det at likningen for kuleflaten med sentrum i og tangentplan er
Svar:
Mer om
Denne oppgaven er om En normalvektor for et plan står vinkelrett på alle linjer i planet. Pytagoras læresetning sier at: Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet. Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.Normalvektor

Pytagoras læresetning

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.Tangent

Plan
For flere forklaringer og eksempler på vektorer, se artikkelen Likning for en kule.
b)
Bestem koordinatene til tangeringspunktet mellom kuleflaten og planet .
Løsningsforslag b)
Jeg tenker
Vi må finne koordinatene til det punktet som både er en del av planet og den del av kuleflaten.
Siden tangeringspunktet er det punktet i som er nærmest punktet betyr det at må stå normalt på planet . Altså må det finnes en konstant slik at , der er normalvektoren til planet . Vi har da at koordinatvektoren til punktet er må tilfredsstille både
og
Ved å sette koordinatene til som funksjon av inn i likningen for planet finner vi
Altså er koordinatene til tangeringspunktet
Svar:
Mer om
Denne oppgaven er om Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se KoordinatsystemPlan
Ligning
Koordinat
For flere forklaringer og eksempler på vektorer, se artikkelen Parallelle vektorer.
c)
Et plan er gitt ved
Dette planet skjærer kuleflaten langs en sirkel.
Bestem radien i denne sirkelen.
Løsningsforslag c)
Jeg tenker
Sentrum i sirkelen som består av skjæringspunktene mellom planet og kuleflaten må være nøyaktig det punktet i som er nærmest punktet .
Som i oppgave finner vi avstanden mellom punktet og planet ved først å velge et punkt i for deretter å beregne
.
Siden likningen for ikke har noe konstantledd ligger i . Det betyr at
Hvis er det punktet i planet som er nærmest og er et annet punkt i vil alltid være rettvinklet. Siden alle punkter på kuleflaten har avstand fra følger det fra pythagoras læresetning at radien i sirkelen er
Svar:
Mer om
Denne oppgaven er om Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. Sirkel brukes i to betydninger: 1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets. Areal: En vektor er en størrelse med en retning. I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren. Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = . Pytagoras læresetning sier at: Plan
Sirkel

2) Flaten som sirkellinjen begrenser.
Omkrets: Vektor

Pytagoras læresetning

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.
Visste du at
Siden planet og planet har samme normalvektor er planene parallelle. Siden Origo ligger i og avstanden fra til Origo må være én, følger det videre at avstanden mellom planene og er én. Derfor må avstanden fra til være .




