Hanois tårn

Utstyr

• 2 bord til å ha de små Hanois tårn-oppgavene på.

• Lite Hanois tårn (elevene kan lage på sløyden):

3 pinner, ca 0,5 cm i diameter, 7 cm lange
1 plate
lim
finérplater, skjært opp i små kvadrater

• Stort Hanois tårn:

isoporplater (10 cm tykke, eventuelt 2 x 5 cm som limes sammen)
maling
kontaktpapir
2 m gjerdestolpe (sylinderformet)
stor finérplate
3 planker, hver på ca. 180 cm

I snekkerboden – utstyret blir til

Små Hanois tårn: Bor tre hull i platen som er like langt fra hverandre. Beregn plass nok til at det største og nest største kvadratet kan ligge ved siden av hverandre. Hvert tårn trenger seks brikker. Størrelser: 7 x 7 cm, 6 x 6 cm, 5 x 5 cm, ...., 2 x 2 cm. Bor hull i hver av brikkene. Hullene må være så store at brikkene kan tres ned på pinnene.

Små Hanois tårn

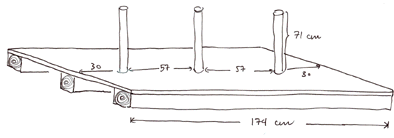
Store Hanois tårn:

Isoporplatene skjæres til som sirkler, en med diameter 60 cm, en med 50 cm og så videre ned til 10 cm. Alle sirkelplatene må ha et sirkulært hull i midten som er stort nok til at de glir lett ned på pinnene på selve brettet. Skivene males i forskjellige farger. Etter at malingen har tørket legges det kontaktpapir på skivene for å forsterke dem.

Matematikken i aktiviteten

Tårnet ligger stablet på venstre pinne. Målet er å flytte hele tårnet over til høyre pinne ved hjelp av pinnen i midten. Bare en skive skal flyttes av gangen. En større skive kan aldri ligge oppå en mindre. Hvor mange flytt trenger vi? Prøv selv før du leser videre!

Systemet avsløres: Med n ringer trenger en $2^n-1$ antall flytt.

Hvordan differensiere?

Spør barna selv hvor mange skiver de vil starte med. Det kan være lurt å prøve med 3 skiver først. De fleste kommer relativt raskt fram til at de trenger 7 flytt for å løse oppgaven. Hele aktiviteten går ut på å søke etter mønster og system. En kan sammen med barna sette opp en hypotese. Hypotesen testes, og etter prøving og feiling kommer en frem til et resultat. De eldste elevene kan komme fram til en formel for det minste antall flytt som trengs når det er n skiver i tårnet.