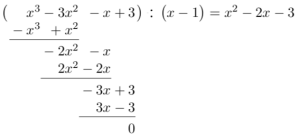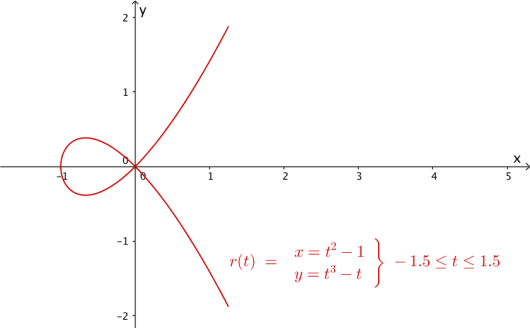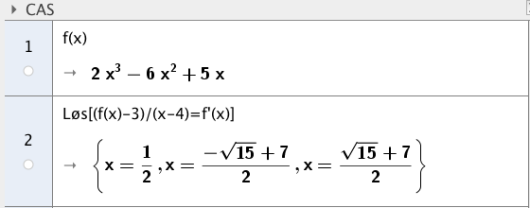Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3022 2017 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timer:

Del 1 skal leveres inn etter 3 timer.

Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler på Del 1:

Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Hjelpemidler på Del 2:

Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:

Del 1 har 7 oppgaver. Del 2 har 4 oppgaver.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen:

Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
vurderer om svar er rimelige

DEL 1 Uten hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4QXO

Deriver funksjonene.

a)

$f (x) = 2 x^{3} - 5 x + 4$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Funksjonen $f$ er en sum av funksjoner på formen $a x^{n}$ , der $a$ og $n$ er konstanter. For den deriverte av en sum har vi at den deriverte er lik summen av de deriverte.

Når vi har en sum kan vi derivere hvert av leddene og summere sammen. $f' (x) = (2 x^{3} - 5 x + 4)' = (2 x^{3})' - (5 x)' + (4)'$ Nå kan vi bruke derivasjonsregelen til den deriverte av en potensfunksjon, at $(a x^{n})' = n a x^{n - 1}$ . Den deriverte til en konstant er lik $0$ . Da får vi $f' (x) = 3 \cdot 2 x^{2} - 5 + 0 = 6 x^{2} - 5$

Svar: $f' (x) = 6 x^{2} - 5$

Mer om:

Denne oppgaven handler om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler, se artikkelen Derivasjonsregler.

For å øve mer, se dette oppgavesettet om derivasjon fra Treningsleiren.

b)

$g (x) = x^{2} e^{x}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Funksjonen $g (x)$ er et produkt av to funksjoner, $x^{2}$ og $e^{x}$ . Da kan vi bruke produktregelen.

Vi kan bruke produktregelen $(u \cdot v)' = u' v + u v'$ for å derivere funksjonen. Vi setter $u = x^{2}$ og $v = e^{x}$ . Da får vi at $\begin{matrix} g' (x) & = & (x^{2} e^{x})' \\ = & (u \cdot v)' \\ = & u' v + u v' \\ = & 2 x e^{x} + x^{2} e^{x} \\ = & x (2 + x) e^{x} \end{matrix}$

Svar: $g' (x) = x (2 + x) e^{x}$

Mer om:

Denne oppgaven handler om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler, se artikkelen Derivasjonsregler.

For å øve mer, se dette oppgavesettet om derivasjon fra Treningsleiren.

c)

$h (x) = \sqrt{x^{2} - 3}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Funksjonen $h (x)$ er en sammensatt funksjon, der $h (x)$ kan skrives som $h (x) = k (u (x))$ og vi kan bruke kjerneregelen.

Vi har en sammensatt funksjon $h (x) = \sqrt{x^{2} - 3}$ som kan skrives som $k (u (x))$ , der $k (u) = \sqrt{u}$ og kjernen $u (x) = x^{2} - 3$ . Nå kan vi bruke kjerneregelen som gir $h' (x) = (k (u (x)))' = k' (u) \cdot u' (x)$ Vi kan derivere hver av funksjonene, og ved å bruke derivasjonsreglene får vi $k' (u) = (\sqrt{u})' = \frac{1}{2 \sqrt{u}}$ og $u' (x) = (x^{2} - 3)' = 2 x$ . Fra kjerneregelen får vi da at $h' (x) = (k (u (x)))' = k' (u) \cdot u' (x) = \frac{1}{2 \sqrt{u}} \cdot 2 x = \frac{2 x}{2 \sqrt{x^{2} - 3}} = \frac{x}{\sqrt{x^{2} - 3}}$

Svar: $h' (x) = \frac{x}{\sqrt{x^{2} - 3}}$

Mer om:

Denne oppgaven handler om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler, se artikkelen Kjerneregelen.

For å øve mer, se dette oppgavesettet om derivasjon fra Treningsleiren.

Oppgave 2 (4 poeng) Nettkode: E-4QXS

Skriv så enkelt som mulig

a)

$\frac{x^{2} - 3}{x^{2} - 9} + \frac{1}{x + 3} + \frac{5}{x - 3}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å forenkle uttrykket kan vi finne fellesnevner og sette på samme brøkstrek. Videre kan vi se om vi kan forkorte uttrykket.

Vi kan begynne med å finne fellesnevner. De to siste leddene har førstegradsuttrykk i nevneren, så disse kan vi ikke faktorisere. Det første leddet har nevneren $x^{2} - 9$ . Dette kan vi skrive som $x^{2} - 3^{2}$ og vi kan bruke konjugatsetningen til å faktorisere uttrykket. Da får vi at $x^{2} - 9 = x^{2} - 3^{2} = (x - 3) (x + 3) .$ Faktorene i nevneren her er de samme som faktorene i de to andre leddene, så $(x - 3) (x + 3)$ er fellesnevneren for uttrykket. Nå kan vi utvide de to andre leddene slik at vi får samme nevner. Vi utvider det andre leddet med $\frac{x - 3}{x - 3}$ og det tredje leddet med $\frac{x + 3}{x + 3}$ . Da får vi $\frac{x^{2} - 3}{(x - 3) (x + 3)} + \frac{1 (x - 3)}{(x + 3) (x - 3)} + \frac{5 (x + 3)}{(x - 3) (x + 3)} .$ Videre kan vi sette på fellesnevner og regne ut:

$\begin{matrix} \frac{x^{2} - 3 + 1 (x - 3) + (5 (x + 3))}{(x - 3) (x + 3)} & = & \frac{(x^{2} - 3) + (x - 3) + (5 x + 15)}{(x - 3) (x + 3)} \\ = & \frac{x^{2} - 3 + x - 3 + 5 x + 15}{(x - 3) (x + 3)} \\ = & \frac{x^{2} + 6 x + 9}{(x - 3) (x + 3)} \end{matrix}$

Telleren i dette uttrykket kan vi faktorisere ved å bruke første kvadratsetning. Vi kan skrive $x^{2} + 6 x + 9 = x^{2} + 2 \cdot 3 \cdot x + 3^{2} = (x + 3)^{2}$ Setter vi dette inn i uttrykket vi fant over ser vi at vi har $(x + 3)$ som felles faktor i teller og nevner, og kan forkorte. Da får vi $\frac{(x + 3)^{2}}{(x - 3) (x + 3)} = \frac{x + 3}{x - 3}$

Svar: $\frac{x + 3}{x - 3}$

Mer om:

Denne oppgaven handler om

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetningen

For flere forklaringer og eksempler, se artikkelen Faktorisering av andregradsuttrykk.

For å øve mer, se dette oppgavesettet om forenkling av sammensatte rasjonale uttrykk.

b)

$2 \ln (a^{- 3} b^{2}) - 3 \ln (\frac{b}{a^{2}})$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Dette er et uttrykk med logaritmer. Da må vi bruke reglene for å regne med logaritmer.

Vi har et uttrykk som består av to ledd hvor vi tar logaritmen til et produkt av to faktorer og logaritmen til en brøk. For logaritmen til produkter og brøker har vi logaritmeregler som sier at $\ln (a \cdot b) = \ln a + \ln b$ og at $\ln \frac{c}{d} = \ln c - \ln d$ . Vi har også en logaritmeregel som sier at $\ln a^{n} = n \ln a$ . Ved å bruke disse reglene kan vi forenkle uttrykket ledd for ledd og se om vi etterhvert kan trekke sammen noen ledd.
Vi begynner med det første leddet. Her får vi ved å bruke logaritmeregelen for produkt at $2 \ln (a^{- 3} b^{2}) = 2 (\ln a^{- 3} + \ln b^{2}) = 2 \ln a^{- 3} + 2 \ln b^{2} .$ Videre kan vi bruke regelen for potenser. Det gir $2 \ln a^{- 3} + 2 \ln b^{2} = 2 \cdot (- 3) \ln a + 2 \cdot 2 \ln b = - 6 \ln a + 4 \ln b$ . I det andre leddet bruker vi regelen for brøk og regelen for potenser og får at $3 \ln (\frac{b}{a^{2}}) = 3 (\ln b - \ln a^{2}) = 3 \ln b - 3 \cdot 2 \ln a = 3 \ln b - 6 \ln a$ Nå kan vi sette inn i det opprinnelige uttrykket og regne ut. $\begin{matrix} 2 \ln (a^{- 3} b^{2}) - 3 \ln (\frac{b}{a^{2}}) & = & - 6 \ln a + 4 \ln b - (3 \ln b - 6 \ln a) \\ = & - 6 \ln a + 4 \ln b - 3 \ln b + 6 \ln a \\ = & \ln b \end{matrix}$

Svar: $\ln b$

Mer om:

Denne oppgaven handler om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer

For flere forklaringer og eksempler, se artikkelen Den Briggske logaritmen.

For å øve mer, se dette oppgavesettet om logaritmer fra Treningsleiren.

Oppgave 3 (4 poeng) Nettkode: E-4QXV

Tre punkt $A (- 1, 6), B (2, 1)$ og $C (4, 4)$ er gitt.

a)

Bestem $\vec{A B}$ og $\vec{A C}$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vektoren mellom to punkter $P (x_{1}, y_{1})$ og $S (x_{2}, y_{2})$ er gitt ved $\vec{P S} = [x_{2} - x_{1}, y_{2} - y_{1}]$

Ved vanlig vektorregning finner vi at vektoren $\vec{A B}$ mellom punktene $A (- 1, 6)$ og $B (2, 1)$ er gitt ved $\vec{A B} = [2 - (- 1), 1 - 6] = [3, - 5]$ og vektoren $\vec{A C}$ mellom punktene $A (- 1, 6)$ og $C (4, 4)$ er gitt ved $\vec{A C} = [4 - (- 1), 4 - 6] = [5, - 2]$ .

Svar: $\vec{A B} = [3, - 5]$ og $\vec{A C} = [5, - 2]$ .

Alternativ løsning

Vi har at $\vec{A B} = \vec{A O} + \vec{O B}$ og tilsvarende for $\vec{A C}$ . Disse vektorene kjenner vi, siden vi kjenner koordinatene til $A$ , $B$ og $C$ .Vi har at at posisjonsvektorene til et punkt $P (a, b)$ , er gitt ved $\vec{O P} = [a, b]$ , og at $\vec{O P} = - \vec{P O}$ . Da får vi $\vec{A B} = \vec{A O} + \vec{O B} = - [- 1, 6] + [2, 1] = [1, - 6] + [2, 1] = [1 + 2, - 6 + 1] = [3, - 5]$ og $\vec{A C} = \vec{A O} + \vec{O C} = [1, - 6] + [4, 4] = [1 + 4, - 6 + 4] = [5, - 2]$

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler, se artikkelen Vektorer mellom to punkter.

b)

Et punkt $D$ er gitt slik at

$\vec{A B} + \vec{C D} = \vec{0}$

Bestem koordinatene til $D$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan la $D$ være punktet gitt ved koordinatene $[x, y]$ og finne et uttrykk for $\vec{C D}$ og løse likningene slik at begge koordinatene er lik $0$ .

Vi lar $D$ være punktet gitt ved $D (x, y)$ . Vi kan nå finne et uttrykk for $\vec{C D}$ . $\vec{C D} = [x - 4, y - 4] .$ Når vi summerer to vektorer summerer vi de koordinatvis. Da får vi at $\vec{A B} + \vec{C D} = [3, - 5] + [x - 4, y - 4] = [3 + (x - 4), - 5 + (y - 4)] = [x - 1, y - 9] .$ Fra likningen vi får oppgitt vil vi ha at begge koordinatene er lik $0$ , altså at $x - 1 = 0$ og at $y - 9 = 0$ . Ved å løse disse likningen får vi $x = 1 og y = 9 .$ Dermed har vi funnet koordinatene til $D$ , $D (1, 9)$ .

Svar: $x = 1, y = 9$

Mer om:

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler, se artikkelen Addisjon av vektorer.

Oppgave 4 (6 poeng) Nettkode: E-4QXY

Funksjonen $P$ er gitt ved

$P (x) = 2 x^{3} - 6 x^{2} - 2 x + 6$

a)

Begrunn at $(1, 0)$ er et vendepunkt på grafen til $P$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For at $(1, 0)$ skal være et vendepunkt for grafen, må vi ha at $P (1) = 0$ , $P ″ (1) = 0$ og at $P'' (x)$ skifter fortegn i dette punktet.

Vi vil bestemme om $(1, 0)$ er et vendepunkt for grafen til $P (x)$ . Først sjekker vi at punktet faktisk ligger på grafen, altså at $P (1) = 0$ . Vi setter inn i for $x = 1$ i uttrykket. Da får vi $P (1) = 2 (1)^{3} - 6 \cdot 1 - 2 \cdot 1 + 6 = 2 - 6 - 2 + 6 = 0$ . Det betyr at punktet ligger på grafen.
For at punktet skal være et vendepunkt må vi ha at $P ″ (1) = 0$ og at $P''$ skifter fortegn i $x = 1$ . For å se om dette stemmer begynner vi med å derivere funksjonen to ganger. $\begin{matrix} P' (x) & = & (2 x^{3} - 6 x^{2} - 2 x + 6)' & = & 2 \cdot 3 x^{2} - 6 \cdot 2 x - 2 & = & 6 x^{2} - 12 x - 2 \\ P ″ (x) & = & (6 x^{2} - 12 x - 2)' & = & 6 \cdot 2 x - 12 & = & 12 x - 12 \end{matrix}$

Hvis vi setter inn for $x = 1$ i uttrykket for den andrederiverte får vi $P ″ (1) = 12 \cdot 1 - 12 = 0$ . Uttrykket til den andrederiverte $P ″ (x) = 12 x - 12$ er likningen til ei rett linje. Da vet vi også at den vil skifte fortegn i nullpunktet sitt, og $(1, 0)$ er et vendepunkt for grafen til $P$ .

Mer om:

Denne oppgaven er om

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Andrederiverte

Den andrederiverte til en funksjon $f (x)$ er funksjonen derivert to ganger og skrives $f'' (x)$ eller $f^{(2)} (x)$ . Kalles også annenderiverte eller dobbeltderiverte.

annenderiverte

For flere forklaringer og eksempler, se artikkelen Vendepunkt og vendetangent.

b)

Faktoriser $P (x)$ i lineære faktorer.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Linære faktorer er uttrykk på formen $(a x + b)$ . Fra oppgave a) vet vi at $x = 1$ er et nullpunkt til $P (x)$ og kan dermed faktorisere ut faktoren $(x - 1)$ . Vi kan da utføre en polynomdivisjon for å finne de andre faktorene.

Siden $(1, 0)$ er et punkt på grafen til $P$ vet vi at $(x - 1)$ er en faktor. Vi kan nå bruke polynomdivisjon for å finne de resterende faktorene. For enkelhets skyld faktoriserer vi ut $2$ før vi gjennomfører polynomdivisjonen. Da får vi

$P (x) = 2 x^{3} - 6 x^{2} - 2 x + 6 = 2 (x^{3} - 3 x^{2} - x + 3) .$

Vi regner da $x^{3} - 3 x^{2} - x + 3 : x - 1 .$

Det betyr at vi kan skrive $2 (x^{3} - 3 x^{2} - x + 3) = 2 (x - 1) (x^{2} - 2 x - 3)$ $x^{2} - 2 x - 3$ er ikke en lineær faktor, så denne må vi faktorisere videre. For å faktorisere dette andregraduttrykket bruker vi abc-formelen til å finne nullpunktene som vi kan vi bruke til å faktorisere. Da får vi $\begin{matrix} x & = & \frac{- b^{\pm} \sqrt{b^{2} - 4 a c}}{2 a} \\ = & \frac{- (- 2) \pm \sqrt{2^{2} - 4 \cdot 1 \cdot (- 3)}}{2 \cdot 1} \\ = & \frac{2 \pm \sqrt{4 + 12}}{2} \\ = & \frac{2 \pm 4}{2} \end{matrix}$

Nullpunktene til $x^{2} - 2 x - 3$ er $x = \frac{2 + 4}{2} = 3, x = \frac{2 - 4}{2} = - 1$ og vi har at $x^{2} - 2 x - 3 = (x - 3) (x - (- 1))$ .
Dermed kan vi faktorisere $2 (x^{3} - 3 x^{2} - x + 3) = 2 (x - 1) (x^{2} - 2 x - 3) = 2 (x - 1) (x + 1) (x - 3)$

Svar: $2 (x - 1) (x + 1) (x - 3)$

Mer om:

Denne oppgaven handler om

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynomer

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

For flere forklaringer og eksempler, se lynkurset Polynomdivisjon.

c)

Løs likningen

$2 e^{3 x} - 6 e^{2 x} - 2 e^{x} + 6 = 0$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi har at $e^{3 x} = {(e^{x})}^{3}$ . Nå kan bruke oppgave b) til å faktorisere uttrykket og finne når faktorene er $0$ .

I oppgave b) så vi at vi kunne faktorisere $2 (x^{3} - 3 x^{2} - x + 3) = 2 (x - 1) (x + 1) (x - 3)$ . Vi kan merke oss at $e^{3 x} = (e^{x})^{3}$ , og $e^{2 x} = (e^{x})^{2}$ . Nå kan vi skrive $2 e^{3 x} - 6 e^{2 x} - 2 e^{x} + 6 = 2 (e^{x})^{3} - 6 (e^{x})^{2} - 2 e^{x} + 6$ og vi kan faktorisere slik at vi får $2 (e^{x})^{3} - 6 (e^{x})^{2} - 2 e^{x} + 6 = 2 ({(e^{x})}^{3} - 3 {(e^{x})}^{2} - e^{x} + 3) = 2 (e^{x} - 1) (e^{x} + 1) (e^{x} - 3)$ For at vi skal ha $2 (e^{x} - 1) (e^{x} + 1) (e^{x} - 3) = 0$ må en av faktorene være lik $0$ .
Vi kan se på faktorene hver for seg. Vi får likningen $e^{x} - 1 = 0, e^{x} + 1 = 0$ og $e^{x} - 3 = 0$ som gir $e^{x} = 1, e^{x} = - 1$ og $e^{x} = 3$ . Her kan vi bruke den naturlige logaritmen til å løse likningen. Den har den egenskapen at $\ln e^{x} = x$ . Vi begynner med $e^{x} = 1$ , og tar vi $\ln$ på begge sider av likhetstegnet får vi at $\ln e^{x} = \ln 1 \Rightarrow x = 0$ Siden $e^{x} > 0$ kan vi se bort i fra den andre likningen, $e^{x} = - 1$ .
Til slutt ser vi på $e^{x} = 3$ , og igjen tar vi logaritmen på begge sider av likhetstegnet. Da får vi $\ln e^{x} = \ln 3 \Rightarrow x = \ln 3$ Det betyr at løsningen til likningen $2 e^{3 x} - 6 e^{2 x} - 2 e^{x} + 6 = 0$ er $x = 0 og x = \ln 3$

Svar: $x = 0 og x = \ln 3$

Mer om:

Denne oppgaven handler om

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkter

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer

For flere forklaringer og eksempler om logaritmer, se artikkelen Den naturlige logaritmen.

Oppgave 5 (6 poeng) Nettkode: E-4QY2

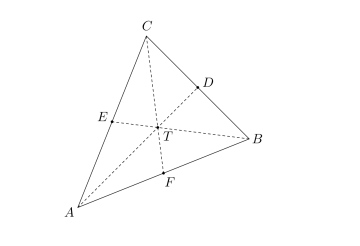
Trekant ABC. F er midtpunkt på AB, D er midtpunkt på BC, og E er midtpunkt på AC.

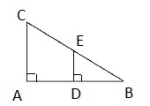
Hjørnene i en trekant er $A (1, 0), B (6, 2)$ og $C (3, 5)$ .

Midtpunktene på sidene i trekanten er $D$ , $E$ og $F$ . Se figuren.

a)

Forklar at koordinatene til punktene $D$ , $E$ og $F$ er

$D (\frac{9}{2}, \frac{7}{2}), E (2, \frac{5}{2}) og F (\frac{7}{2}, 1)$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan finne punktkoordinatene til $D, E$ og $F$ ved å se på posisjonsvektorene $\vec{O D}, \vec{O E}$ og $\vec{O F}$ .

For å finne koordinatene til $D, E$ og $F$ kan vi se på posisjonsvektorene $\vec{O D}, \vec{O E}$ og $\vec{O F}$ . Vi begynner med å finne koordinatene til $D$ . Da ser vi på $\vec{O D}$ , den kan vi skrive som en sum av vektorene $\vec{O B}$ og $\vec{B D}$ , altså har vi at $\vec{O D} = \vec{O B} + \vec{B D} .$ Vi har at $\vec{O B} = [6, 2]$ og siden $D$ er midtpunktet på $\vec{B C}$ får vi at $\vec{B D} = \frac{1}{2} \vec{B C} = \frac{1}{2} [3 - 6, 5 - 2] = [\frac{- 3}{2}, \frac{3}{2}] .$ Nå kan vi regne ut $\vec{O D}$ ; $\vec{O D} = [6, 2] + [\frac{- 3}{2}, \frac{3}{2}] = [6 - \frac{3}{2}, 2 + \frac{3}{2}] = [\frac{9}{2}, \frac{7}{2}],$

som gir $D (\frac{9}{2}, \frac{7,}{2})$ .

På tilsvarende måte får vi at $\vec{O E} = \vec{O A} + \vec{A E}$ der $\vec{O A} = [1, 0]$ og $\vec{A E} = \frac{1}{2} \vec{A C} = \frac{1}{2} [3 - 1, 5 - 0] = [1, \frac{5}{2}] .$ Da får vi $\vec{O E} = [1, 0] + [1, \frac{5}{2}] = [2, \frac{5}{2}],$

som gir $E (2, \frac{5}{2})$ .

Til slutt finner vi koordinatene til $F$ ved å se på $\vec{O F} = \vec{O A} + \vec{A F}$ der $\vec{A F} = \frac{1}{2} \vec{A B} = \frac{1}{2} [6 - 1, 2 - 0] = [\frac{5}{2}, 1]$ som gir at $\vec{O F} = [1, 0] + [\frac{5}{2}, 1] = [\frac{7}{2}, 1],$

og $F (\frac{7}{2}, 1)$

Da har vi at $D, E og F$ har punktkoordinatene $D (\frac{9}{2}, \frac{7}{2})$ , $E (2, \frac{5}{2})$ og $F (\frac{7}{2}, 1)$ .

Mer om:

Denne oppgaven handler om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler, se artiklene Stedvektor (posisjonsvektorer) og Addisjon av vektorer.

b)

Skjæringspunktet mellom medianene i trekanten er $T$ .

Forklar at vi kan skrive $\vec{A T}$ på to måter:

$\vec{A T} = s \cdot \vec{A D}$

$\vec{A T} = \vec{A B} + t \cdot \vec{B E}$

der $s$ og $t$ er reelle tall.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å komme fra $A$ til $C$ kan vi enten gå direkte eller vi kan gå via $B$ .

Det er flere muligheter for å gå fra $A$ til $C$ . Vi kan gå direkte fra $A$ til $T$ , og siden $\vec{A T}$ er parallell med $\vec{A D}$ har vi at $\vec{A T} = s \cdot \vec{A D},$ der $s$ er et reellt tall.
Vi kan også finne $\vec{A T}$ ved å gå via $B$ . Da har vi at $\vec{A T} = \vec{A B} + \vec{B T},$ og siden $\vec{B T}$ er parallell med $\vec{B E}$ kan vi skrive $\vec{B T} = t \cdot \vec{B E}$ , der $t$ er et reellt tall. Det medfører at $\vec{A T} = \vec{A B} + t \cdot \vec{B E} .$

Mer om:

Denne oppgaven handler om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler, se artikkelen Parallelle vektorer.

c)

Bruk vektorlikningene i oppgave b) til å bestemme $s$ og $t$ . Bestem koordinatene til $T$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi har to uttrykk for $\vec{A T}$ som vi kan sette lik hverandre.

Fra oppgave b) har vi at $\vec{A T} = s \cdot \vec{A D}$ og $\vec{A T} = \vec{A B} + t \cdot \vec{B E}$ og det betyr at vi må ha $s \cdot \vec{A D} = \vec{A B} + t \cdot \vec{B E} .$ Vi har at $\vec{A B} = [5, 2]$ , $\vec{A D} = [\frac{9}{2} - 1, \frac{7}{2} - 0] = [\frac{7}{2}, \frac{7}{2}]$ og at $\vec{B E} = [2 - 6, \frac{5}{2} - 2] = [- 4, \frac{1}{2}] .$

Setter vi inn i likningen over får vi at

$\begin{matrix} s \cdot [\frac{7}{2}, \frac{7}{2}] & = & [5, 2] + t \cdot [- 4, \frac{1}{2}] \\ [\frac{7}{2} s, \frac{7}{2} s] & = & [5 - 4 t, 2 + \frac{1}{2} t] \end{matrix}$

For at likningen må stemme må både førstekoordinatene og andre koordinatene være lik hverandre, så da får vi to likninger:
$[\begin{matrix} \frac{7}{2} s = 5 - 4 t \\ \frac{7}{2} s = 2 + \frac{1}{2} t \end{matrix}]$

Fra den andre likningen får vi at $s = \frac{2}{7} (2 + \frac{1}{2} t) = \frac{4}{7} + \frac{1}{7} t .$ Setter vi inn for $s$ i den første likningen får vi

$\begin{matrix} \frac{7}{2} (\frac{4}{7} + \frac{1}{7} t) & = & 5 - 4 t \\ 2 + \frac{1}{2} t & = & 5 - 4 t \\ \frac{9}{2} t & = & 3 \\ t & = & \frac{2}{9} \cdot 3 \\ t & = & \frac{2}{3} . \end{matrix}$

Nå kan vi løse for $s$ og får at $s = \frac{4}{7} + \frac{1}{7} \cdot \frac{2}{3} = \frac{12 + 2}{21} = \frac{14}{21} = \frac{2}{3} .$

Vi får at $s = \frac{2}{3}$ og at $t = \frac{2}{3}$ . For å finne koordinatene til $T$ kan vi se på $\vec{O T} = \vec{O A} + \vec{A T} = \vec{O A} + s \vec{A D} .$ Vi har at $s \vec{A D} = \frac{2}{3} [\frac{7}{2}, \frac{7}{2}] = [\frac{7}{3}, \frac{7}{3}]$ som medfører at $\vec{O T} = [1, 0] + [\frac{7}{3}, \frac{7}{3}] = [\frac{10}{3}, \frac{7}{3}] .$

Svar: $T (\frac{10}{3}, \frac{7}{3})$ .

Mer om:

Denne oppgaven handler om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

For flere forklaringer og eksempler på likningssystemer, se lynkurset Lineære likninger med flere ukjente.

Oppgave 6 (4 poeng) Nettkode: E-4QYA

En fabrikk produserer lyspærer. Alle lyspærene blir kontrollert. I kontrollen blir $8, 0 %$ av lyspærene forkastet. Nærmere undersøkelser viser at

- $92, 0 %$ av de forkastede lyspærene er defekte

- $2, 0 %$ av de godkjente lyspærene er defekte

a)

Vis at sannsynligheten er $9, 2 %$ for at en tilfeldig produsert lyspære er defekt.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

En defekt pære kan enten bli godkjent eller forkastet i kontroll. Vi kan bruke produktsetningen for å finne sannsynligheten for at en pære er både defekt og godkjent, eller både defekt og forkastet. For å finne den totale sannsynligheten for at en pære er defekt kan vi bruke addisjonsregelen.

Vi kan se på hendelsene

D: Lyspæren er defekt
G: Lyspæren blir godkjent i kontrollen

Vi har to mulige hendelser for defekte pærer, at den er defekt og godkjent, $G \cap D$ , og at den er defekt og ble forkastet, $\bar{G} \cap D$ . Disse hendelsene er disjunkte, så fra addisjonssetningen får vi at $P (D) = P (G \cap D) + P (\bar{G} \cap D) .$ Vi kan bruke produktsetningen til å finne $P (D \cap G)$ og $P (D \cap \bar{G})$ . Fra produktsetningen får vi at $P (G \cap D) = P (G) \cdot P (D | G)$ $P (\bar{G} \cap D) = P (\bar{G}) \cdot P (D | \bar{G}) .$ Fra oppgaveteksten vet vi at sannsynligheten for at en lyspære ikke blir godkjent, $P (\bar{G}) = 8 % = 0, 08,$ og siden det er komplementet til at en lyspære blir godkjent, må vi ha $P (G) = 1 - P (\bar{G}) = 1 - 0, 08 = 0, 92 .$ Vi får også vite at $92 %$ av de forkastede lyspærene er defekte. Det betyr at $P (D | \bar{G}) = 92 % = 0, 92 .$ I tillegg får vi vite at $2 %$ av de godkjente lyspærene er godkjent. Det betyr at $P (D | G) = 2 % = 0, 02 .$ Nå kan vi finne sannsynligheten for at en lyspære er defekt ved å sette dette inn i likningene over

$\begin{matrix} P (D) & = & P (G \cap D) + P (\bar{G} \cap D) \\ = & P (G) \cdot P (D | G) + P (\bar{G}) \cdot P (D | \bar{G}) \\ = & 0, 92 \cdot 0, 02 + 0, 08 \cdot 0, 92 \\ = & 0, 92 (0, 02 + 0, 08) = 0, 92 \cdot 0, 1 \\ = & 0, 092 = 9, 2 % \end{matrix}$

som var det vi ville vise.

Mer om:

Denne oppgaven handler om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

Disjunkte hendelser

A og B kalles disjunkte dersom de ikke har noen felles elementer. Dette betyr at $A \cap B = \emptyset$ , altså at det ikke er noen elementer som er både i A og i B.

disjunkte hendelser

For flere forklaringer og eksempler, se artiklene Betinget sannsynlighet og produktsetningen og Addisjonssetningen.

b)

Bruk Bayes’ setning til å bestemme sannsynligheten for at en defekt lyspære blir forkastet i kontrollen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi vil finne den betingede sannsynligheten for at en lyspære blir forkastet, gitt at den er defekt, altså $P (\bar{G} | D)$ .

I denne oppgaven skal vi bruke Bayes’ setning til å finne sannsynligheten for at en defekt pære blir forkastet, altså $P (\bar{G} | D)$ . Fra Bayes’ setning har vi at $P (\bar{G} | D) = \frac{P (\bar{G}) \cdot P (D | \bar{G})}{P (D)} .$ Disse sannsynlighetene fant vi i a) og kan sette inn i uttrykket. Da får vi $P (\bar{G} | D) = \frac{0, 08 \cdot 0, 92}{0, 092} = 0, 08 \cdot 10 = 0, 8 = 80 % .$

Svar: Sannsynligheten er $80 %$ .

Mer om:

Denne oppgaven handler om

Betinget sannsynlighet

Den betingede sannsynligheten $P (A | B)$ er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.

$P (A | B) = \frac{P (A \cap B)}{P (B)}$ .

betinget sannsynlighet

Bayes' setning

Bayes' setning sier at $P (A | B) = \frac{P (B | A) P (A)}{P (B)} .$

Bayes' setning

For flere forklaringer og eksempler, se artikkelen Bayes-setningen.

Oppgave 7 (7 poeng) Nettkode: E-4QYD

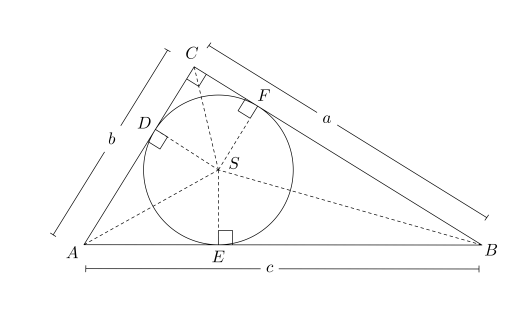
En rettvinklet $Δ A B C$ der $∠ C = 9 0^{\circ}$ er gitt. Den innskrevne sirkelen har sentrum $S$ og radius $r$ . Sirkelen tangerer trekanten i punktene $D$ , $E$ og $F$ . Vi setter $A C = b$ , $B C = a$ og $A B = c$ . Du får oppgitt at $B F = B E$ og $A D = A E$ .

a)

Bruk figuren til å forklare at $a = B F + r$ og $b = A D + r$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Lengden til $a$ må være lik $C F + B F$ og $b$ må være $C D + A D$ , så vi må vise at $C F = C D = r$ . Da kan vi bruke $□ C D S F$ .

Vi kan skrive $a = C F + B F$ og $b = C D + A D$ , og vil vise at $C F = C D = r$ . Da kan vi se på $□ C D S F$ . $D S$ og $F S$ er radier i sirkelen med sentrum $S$ og dermed har vi at

$D S = F S = r .$

Fra figuren ser vi at $□ C D S F$ har tre rette vinkler og fra vinkelsummen til en firkant vet vi at de siste vinkelen også må være $90^{\circ}$ . Det betyr at vi har et kvadrat, så $C D = C F = D S = F S = r$ og $a = r + B F og b = r + A D$ som var det vi ville vise.

Mer om:

Denne oppgaven handler om

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkelen

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Rettvinklet trekant

En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.

rettvinklede trekanter

For flere forklaringer og eksempler, se lynkurset Geometri - vinkler og figurer.

b)

Av figuren ser vi dessuten at $c = A E + B E$ .

Vis at $a + b - c = 2 r$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke uttrykkene for $a, b$ vi fant i oppgave a) og at $c = A E + B E$ .

Fra oppgave a) har vi at $a = B F + r$ og at $b = A D + r$ . I tillegg har vi at $c = A E + B E$ . I oppgaveteksten får vi vite at $A D = A E$ og $B F = B E$ , som betyr at vi kan skrive $c = A D + B F$ .
Skriver vi inn uttrykkene for $a, b$ og $c$ får vi da $a + b - c = (B F + r) + (A D + r) - (A D + B F) = 2 r + B F + A D - A D - B F = 2 r$ som var det vi ville vise.

Mer om:

Denne oppgaven handler om

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

For flere forklaringer og eksempler, se lynkurset om Algebra.

c)

Forklar at vi kan skrive arealet $T$ av trekanten på to måter:

$T = \frac{1}{2} \cdot a \cdot b$ og $T = \frac{1}{2} \cdot r \cdot (a + b + c)$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Arealet til en trekant er gitt ved formelen $A = \frac{1}{2} g \cdot h$ , der $g$ er grunnlinjen og $h$ er høyden til trekanten. For å finne arealet til $△ A B C$ kan vi enten se på arealet til hele trekanten med en gang, eller vi kan dele den opp i mindre trekanter.

Vi begynner med å se på hele trekanten. Arealet til en trekant med grunnlinje $g$ og høyde $h$ er gitt ved $\frac{1}{2} g \cdot h$ . For $△ A B C$ har vi at $B C$ står vinkelrett på $A C$ , så vi kan skrive $g = B C = a$ og $h = A C = b$ . Det betyr at arealet er gitt ved $T = \frac{1}{2} \cdot a \cdot b .$ Da har vi vist den første formelen.

Vi kan også se at $△ A B C$ kan deles opp i tre trekanter, $△ B S C, △ A S C$ og $△ A S B$ , med henholdsvis $a, b$ og $c$ som grunnlinje. Alle de tre trekantene har en radius stående vinkelrett på, så trekantene har høyde $r$ . Da har vi at arealet til $△ B S C$ er gitt ved $A_{1} = \frac{1}{2} \cdot a \cdot r$ , arealet til $△ A S C$ er gitt ved $A_{2} = \frac{1}{2} \cdot b \cdot r$ og arealet til $△ A S B$ er gitt ved $A_{3} = \frac{1}{2} \cdot c \cdot r$ . Arealet til $△ A B C$ er summen av disse, så vi har at

$\begin{matrix} T & = & A_{1} + A_{2} + A_{3} \\ = & \frac{1}{2} \cdot a \cdot r + \frac{1}{2} \cdot b \cdot r + \frac{1}{2} \cdot c \cdot r \\ = & \frac{1}{2} \cdot r \cdot (a + b + c) & . \end{matrix}$

Dette viser den andre formelen vi skulle vise.

Mer om:

Denne oppgaven handler om

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekanter

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

For flere forklaringer og eksempler, se artikkelen En trekant.

d)

Bruk resultatene du fant i oppgavene b) og c) til å utlede Pytagoras' setning.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

I $△ A B C$ har vi at $a$ og $b$ er kateter og $c$ er hypotenusen, så vi vil frem til at $a^{2} + b^{2} = c^{2}$ .

Pytagoras læresetning sier at for en rettvinklet trekant med kateter $a$ og $b$ og hypotenus $C$ har vi at $a^{2} + b^{2} = c^{2}$ . Så det er dette uttrykket vi vil frem til. I oppgave c) har vi at $T = \frac{1}{2} \cdot a \cdot b$ og $T = \frac{1}{2} \cdot r \cdot (a + b + c)$ . Det betyr at vi må ha $\frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot r \cdot (a + b + c) .$ Vi vet også fra oppgave b) at $a + b - c = 2 r$ , som gir at $r = \frac{1}{2} (a + b - c)$ . Vi kan sette inn for $r$ i likningen. Da får vi $\frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot \frac{1}{2} (a + b - c) \cdot (a + b + c) .$ Videre kan multiplisere med $4$ og multiplisere ut parentesene.

$\begin{matrix} 2 a b & = & (a + b - c) \cdot (a + b + c) \\ = & a^{2} + a b + a c + b a + b^{2} + b c - c a - c b - c^{2} \\ = & a^{2} + b^{2} - c^{2} + 2 a b & . \end{matrix}$

Subtraherer vi $2 a b$ fra begge sider og flytter $c^{2}$ over står vi igjen med $c^{2} = a^{2} + b^{2}$ som var det vi ville frem til.

Mer om:

Denne oppgaven handler om

Rettvinklet trekant

En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.

rettvinklede trekanter

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

For flere forklaringer og eksempler, se artikkelen Pytagoras læresetning.

DEL 2 Med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4QYS

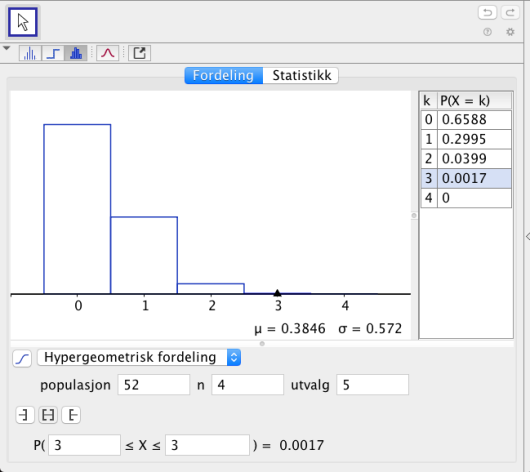
I en kortstokk er det $52$ kort. Kortene er fordelt på de fire fargene hjerter, ruter, spar og kløver. Hver farge har $13$ kort fordelt på verdiene $2$ til $10$ , knekt, dame, konge og ess. Tenk deg at du skal trekke tilfeldig fem kort fra kortstokken.

a)

Bestem sannsynligheten for at du kommer til å trekke nøyaktig tre kort med verdi $10$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi har en uniform trekning av kort, så sannsynligheten er gitt ved $\frac{antall gunstige}{antall mulige}$ . Dette er også en hypergeometrisk modell, og vi kan bruke sannsynlighetskalkulatoren i GeoGebra. Dette ser vi på i den alternative løsningen.

Vi vil finne sannsynligheten for å trekke nøyaktig $3$ kort med verdi $10$ . Siden sannsynligheten er uniform, kan vi finne den ved å regne $\frac{antall gunstige}{antall mulige}$ . Vi kan begynne med å se på antall mulige. Rekkefølgen vi trekker spiller ingen rolle, så vi har et uordnet utvalg uten tilbakelegging, og vi skal velge $5$ kort av $52$ . Antall utvalg finner vi da ved $(\binom{52}{5}) = 2598960 .$ I kortstokken er det totalt $4$ kort med verdi $10$ og vi skal velge $3$ av de. Det kan vi velge på $(\binom{4}{3})$ ulike måter. I tillegg skal vi trekke $2$ kort som ikke har verdi $10$ , altså må vi velge $2$ kort blant de $48$ kortene som har verdi forskjellig fra $10$ . Det kan vi gjøre på $(\binom{48}{2})$ måter. Hvert enkelt av de $(\binom{4}{3})$ måtene kan kombineres med de $(\binom{48}{2})$ , så antall gunstige utfall er $(\binom{4}{3}) \cdot (\binom{48}{2}) = 4512 .$ Sannsynligheten for nøyaktig $3$ kort med verdi $10$ er dermed $P (tre kort med verdi 10) = \frac{(\binom{4}{3}) \cdot (\binom{48}{2})}{(\binom{52}{5})} = \frac{4512}{2598960} \approx 0, 0017 = 0, 17 % .$

Svar: $0, 17 %$ .

Alternativ løsning

For å finne sannsynligheten for å trekke nøyaktig $3$ kort med verdi $10$ kan vi bruke sannsynlighetskalkulatoren i GeoGebra. I “Vis”-menyen velger vi “Sannsynlighetskalkulator”. Da får vi opp

Vi har et eksempel på et hypergeometrisk forsøk, så da må vi velge sannsynlighetsfordelingen til å være hypergeometrisk i stedet for normalfordeling. Videre må vi fylle inn med tallene fra kortstokken. Populasjon er antall elementer, altså hvor mange kort kan velge mellom, som er 52 og $n$ er antall gunstige elementer, som i vårt tilfelle vil si hvor mange tiere, altså $4$ . Utvalg er hvor mange elementer som trekkes ut som er $5$ . For å finne sannsynligheten for å trekke nøyaktig $3$ kort med verdi $10$ , markerer vi ruten med [-] og skriver inn silk at vi får $P (3 \leq x \leq 3)$ på linja under. Da kan vi se at sannsynligheten blir $0, 0017 = 0, 17 %$ .

Mer om:

Denne oppgaven handler om

Kombinatorikk

Handler om å finne antall mulige kombinasjoner i ulike sammenhenger.

Eksempel: antall måter å kombinere Lotto-tallene på, eller hvor mange ulike antrekk vi kan ha på oss dersom vi har 2 bukser og 3 skjorter.

kombinatorikk

Uordnede utvalg

Når vi trekker objekter fra en samling og rekkefølgen vi trekker i ikke er viktig, sier vi at dette er et uordnet utvalg.

Eksempel: Lottotrekning.

uordnede utvalg

Sannsynlighet

sannsynlighet

Hypergeometrisk forsøk

Et hypergeometrisk forsøk har følgende egenskaper:

Det er totalt n gjenstander av to (eller flere) typer.
Antallet gjenstander av type 1 er $n_{1}$ og antallet gjenstander av type 2 er $n_{2}$ , slik at $n_{1} + n_{2} = n$ .
Det skal trekkes et uordnet utvalg uten tilbakelegging av størrelse k.

hypergeometriske forsøk

For flere forklaringer og eksempler, se artiklene Uordnede utvalg uten tilbakelegging og Hvordan finner vi uniform sannsynlighet?.

b)

Bestem sannsynligheten for at du kommer til å trekke nøyaktig tre kort med samme verdi.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

I oppgave a) fant vi sannsynligheten for å finne nøyaktig $3$ kort med verdi $10$ . Sannsynligheten for å trekke nøyaktig $3$ kort med en annen verdi vil være den samme.

Sannsynligheten for å trekke nøyaktig tre kort med samme verdi er den samme for alle verdier, og fra oppgave a) vet vi $\frac{(\binom{4}{3}) \cdot (\binom{48}{2})}{(\binom{52}{5})} .$ Det er $13$ forskjellige kortverdier, så vi kan trekke tre kort med samme verdi på $13$ måter. Da får vi $P (tre kort med samme verdi) = 13 \cdot \frac{(\binom{4}{3}) \cdot (\binom{48}{2})}{(\binom{52}{5})} \approx 0, 023 = 2, 3 % .$

Svar: $2, 3 %$

Mer om:

Denne oppgaven handler om

Sannsynlighet

sannsynlighet

Addisjonssetningen

Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.

$P (A \cup B) = P (A) + P (B) - P (A \cap B)$

addisjonssetningen

For flere forklaringer og eksempler, se lynkurset Sannsynlighet (del II).

c)

Bestem sannsynligheten for at alle kortene du kommer til å trekke, har samme farge.

Figur 1: Ett mulig utfall i oppgave a)

Figur 2: Ett mulig utfall i oppgave b)

Figur 3: Ett mulig utfall i oppgave c)

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi har fortsatt en uniform trekning av kort, så sannsynligheten er gitt ved $\frac{antall gunstige}{antall mulige}$ . Vi kan velge fem kort i samme farge på fire måter, en for hver farge.

Vi skal fortsatt trekke $5$ kort fra kortstokken, så antall mulige utvalg er det samme som i oppgave a), $(\binom{52}{5})$ . Antall gunstige utfall er nå annerledes. Vi vil trekke $5$ kort med samme farge. Utfra Figur 3, antar vi at de med farge skiller mellom ruter og hjerter, og kløver og spar. I kortstokken er det $13$ kort av hver farge, og vi skal velge $5$ . Det kan vi gjøre på $(\binom{13}{5}) = 1287$ måter. Vi kan velge disse kortene på $4$ forskjellige måter, en for hver av fargene. Dermed er $P (fem kort i samme farge) = 4 \cdot \frac{(\binom{13}{5})}{(\binom{52}{5})} = 4 \cdot \frac{1287}{2598960} \approx 0, 002 = 0, 2 % .$

Svar: $0, 2 %$

Mer om:

Denne oppgaven handler om

Kombinatorikk

Handler om å finne antall mulige kombinasjoner i ulike sammenhenger.

Eksempel: antall måter å kombinere Lotto-tallene på, eller hvor mange ulike antrekk vi kan ha på oss dersom vi har 2 bukser og 3 skjorter.

kombinatorikk

Uordnede utvalg

Når vi trekker objekter fra en samling og rekkefølgen vi trekker i ikke er viktig, sier vi at dette er et uordnet utvalg.

Eksempel: Lottotrekning.

uordnede utvalg

og uniform sannsynlighet.

For flere forklaringer og eksempler, se artikkelen Hvordan finner vi uniform sannsynlighet?.

Oppgave 2 (6 poeng) Nettkode: E-4QYW

Posisjonsvektoren til en partikkel er gitt ved

$\vec{r} (t) = [t^{2} - 1, t^{3} - t]$

a)

Tegn grafen til $\vec{r}$ når $t \in [- \frac{3}{2}, \frac{3}{2}]$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen til $\vec{r}$ .

For å tegne grafen til $\vec{r}$ kan vi bruke kommandoen Kurve[<Uttrykk>,<Uttrykk>, <Parametervariabel>, <Start>, <Slutt>] i GeoGebra. Da skriver vi inn
$𝚛 = 𝚔 𝚞 𝚛 𝚟 𝚎 [𝚝^{\land} 2 - 1, 𝚝^{\land} 3 - 𝚝, 𝚝, - 3 / 2, 3 / 2] .$
Vi husker å sette navn på aksene.

Svar:

Mer om:

Denne oppgaven handler om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Vektorfunksjon

En vektorfunksjon $\vec{r (t)}$ er en funksjon av en variabel t som gir en vektor fra origo for hver t:

$\vec{r (t)} = [x (t), y (t)]$

vektorfunksjoner

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

grafer

For flere forklaringer og eksempler på grafer, se artikkelen Parametriserte kurver.

b)

Bestem fartsvektoren $\vec{v} (t)$ og akselerasjonsvektoren $\vec{a} (t)$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi finner fartsvektoren, $\vec{v} (t)$ ved å derivere posisjonsvektoren $\vec{r} (t)$ og akselerasjonsvektoren $\vec{a} (t)$ ved å derivere $\vec{v} (t)$ .

Fart er endring i posisjon per tidsenhet og akselerasjon er endring i fart per tidsenhet. For å finne fartsvektoren $\vec{v} (t)$ kan vi derivere $\vec{r} (t)$ , og for å finne akselerasjonsvektoren kan derivere fartsvektoren $\vec{v} (t)$ . Vi kan bruke CAS til å derivere. For å se hvordan vi kan gjøre det ved regning, se alternativ.
Vi velger “CAS” i “Vis”-menyen i GeoGebra. Fartsvektoren finner vi ved å skrive inn $𝚟 (𝚝) := 𝚛' (𝚝)$ og akselerasjonsvektoren ved å skrive $𝚊 (𝚝) := 𝚟' (𝚝) .$ Da får vi

Svar: $\vec{v} (t) = [2 t, 3 t^{2} - 1]$ og $\vec{a} (t) = [2, 6 t]$ .

Alternativ løsning

Vi kan også finne fartsvektoren og akselerasjonsvektoren ved regning. Når vi skal derivere vektorene, deriverer vi $x$ - og $y$ -komponentene hver for seg. Vi begynner med fartsvektoren, som vi kan finne ved å derivere posisjonsvektoren. Da får vi $\vec{v} (t) = \vec{r}' (t) = [(t^{2} - 1)', (t^{3} - t)'] = [2 t, 3 t^{2} - 1] .$ Akselerasjonsvektoren finner vi ved å derivere fartsvektoren, $\vec{a} (t) = \vec{v}' (t) = [(2 t)', (3 t^{2} - 1)'] = [2, 6 t] .$

Mer om:

Denne oppgaven handler om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Vektorfunksjon

En vektorfunksjon $\vec{r (t)}$ er en funksjon av en variabel t som gir en vektor fra origo for hver t:

$\vec{r (t)} = [x (t), y (t)]$

vektorfunksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler, se artikkelen Parametriserte kurver.

c)

Bruk CAS til å bestemme den minste banefarten til partikkelen.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi finner banefarten ved å ta absoluttverdien av $\vec{v} (t)$ . Vi kan se på funksjonen $f (t) = | \vec{v}' (t) |$ , og finne bunnpunktet til $f (t)$ .

Banefarten er gitt ved absoluttverdien til fartsvektoren. Vi kan betegne banefarten som $f$ , og får da at $f (t) = | \vec{v}' (t) |$ er en funksjon for banefart. For å bestemme den minste banefarten til partikkelen kan vi finne bunnpunktet til $f$ . Vi kan begynne med å definere $f$ i CAS. Fortsetter vi i samme CAS-vindu som i oppgave b), der vi allerede har definert $v (t)$ kan vi skrive inn
$𝚏 (𝚝) := 𝚊 𝚋 𝚜 (𝚟 (𝚝))$
Bunnpunkter til en funksjon er et ekstremalpunkt, og nå kan vi bruke kommandoen ekstremalpunkt for å finne bunnpunktet til $f$ . Da skriver vi inn
$𝙴 𝚔 𝚜 𝚝 𝚛 𝚎 𝚖 𝚊 𝚕 𝚙 𝚞 𝚗 𝚔 𝚝 [𝚏]$ .

Her kan vi se at $f$ har tre ekstremalpunkt, for $t = - \frac{1}{3}, t = 0$ og $t = \frac{1}{3}$ , der $f (0) = 1$ og $f (\frac{1}{3}) = f (- \frac{1}{3}) = 2 \frac{\sqrt{2}}{3}$ . Vi vil finne det ekstremalpunktet som har minst verdi, og har at $2 \frac{\sqrt{2}}{3} \approx 0, 943 < 1$ . Det betyr at banefarten er minst for $t = \frac{1}{3}$ og $t = - \frac{1}{3}$ , og da er den $2 \frac{\sqrt{2}}{3} \approx 0, 94$ .

Svar: Den minste banefarten til partikkelen er omtrent $0, 94$ .

Mer om:

Denne oppgaven handler om vektorfunksjoner og ekstremalpunkter.

For flere forklaringer og eksempler i CAS, se artikkelen CAS.

Oppgave 3 (4 poeng) Nettkode: E-4QZ0

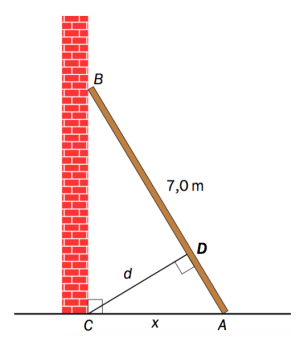
En stige på $7, 0$ m er stilt opp langs en vegg. Stigen danner sammen med veggen og bakken en rettvinklet $Δ A B C$ . Se figuren.

Vi setter $A C = x$ . Den korteste avstanden fra $C$ til stigen er $d$ meter.

a)

Vis at $d = \frac{x \sqrt{49 - x^{2}}}{7}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi har at $△ A B C$ og $△ A C D$ er formlike, og da er forholdet mellom tilsvarende sider konstant.

Vi kan begynne med å se på de to trekantene $△ A B C$ og $△ A C D$ . Begge trekantene har $∠ A$ til felles og begge har en rett vinkel. Det betyr at $△ A B C \sim △ A C D$ . I formlike trekanter er forholdet mellom tilsvarende sider konstant, og det betyr at vi har at $\frac{C D}{B C} = \frac{A C}{A B .}$ Vi har at $C D = d, A C = x$ og $A B = 7$ . For å finne et uttrykk for $B C$ kan vi se på $△ A B C$ og bruke Pytagoras læresetning. Da har vi at

$\begin{matrix} A B^{2} & = & A C^{2} + B C^{2} \\ B C & = & \sqrt{A B^{2} - A C^{2}} \\ B C & = & \sqrt{7^{2} - x^{2}} & . \end{matrix}$

Nå kan vi sette inn uttrykk for sidene og da får vi at $\frac{d}{\sqrt{7^{2} - x^{2}}} = \frac{x}{7} \Rightarrow d = \frac{x \sqrt{7^{2} - x^{2}}}{7} = \frac{x \sqrt{49 - x^{2}}}{7}$ som var det vi ville vise.

Mer om:

Denne oppgaven handler om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

Pytagoras læresetning

For flere forklaringer og eksempler, se artikkelen Formlikhet og kongruens.

b)

Bestem $x$ slik at $d$ blir lengst mulig.

Hvor lang er $d$ for denne verdien av $x$ ?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

I oppgave a) fant vi et uttrykk for $d$ gitt ved $x$ . For å finne den lengste verdien til $d$ kan vi se på funksjonen $d (x)$ og finne toppunktet til denne funksjonen.

Vi kan bruke uttrykket vi fant i oppgave a) til å skrive $d$ som en funksjon av $x$ , $d (x) = \frac{x \sqrt{49 - x^{2}}}{7}$ . Vi vil finne når denne funksjonen har størst verdi, og da kan vi bruke CAS. Først definerer vi funksjonen ved å skrive inn
$𝚍 (𝚡) := 𝚡 * 𝚜 𝚚 𝚛 𝚝 (49 - 𝚡^{\land} 2) / 7$
Vi finner ekstremalpunktene til $d$ ved å bruke kommandoen Ekstremalpunkt, og skriver
$𝙴 𝚔 𝚜 𝚝 𝚛 𝚎 𝚖 𝚊 𝚕 𝚙 𝚞 𝚗 𝚔 𝚝 [𝚍]$
og får opp

Vi har to ekstremalpunkter, ett i x = $- \frac{7}{\sqrt{2}}$ og ett i x = $\frac{7}{\sqrt{2}}$ . Den negative x-verdien kan vi utelukke siden vi ikke kan ha negative lengder.

Vi bruke 2. derivert test ved hjelp av CAS i Geogebra for å sjekke om $\frac{7}{\sqrt{2}}$ er toppunkt. I ekstremalpunktene er den deriverte lik null. Dersom 2. deriverte er negativ i et ekstremalpunkt, så er den deriverte avtagende og vil skifte fortegn i dette punktet. Den går fra å være posetiv til å være negativ. Grafen ser dermed konkav ut og punktet er et toppunkt.

Vi skriver inn påstanden $d'' (\frac{7}{\sqrt{2}}) < 0$ i CAS og sjekker om vi får "true" eller "false" i retur.

Det gir at $d$ har toppunkt for $x = \frac{7}{\sqrt{2}}$ . Den maksimale lengden til $d$ er dermed gitt ved $d (\frac{7}{\sqrt{2}}) = \frac{7}{2} = 3, 5$ .

Svar: d er lengst når $x = \frac{7}{\sqrt{2}} \approx 4, 95$ m og da er d = 3,5 m.

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

For flere forklaringer og eksempler, se artikkelen Topp- og bunnpunkter.

Oppgave 4 (8 poeng) Nettkode: E-4QZ7

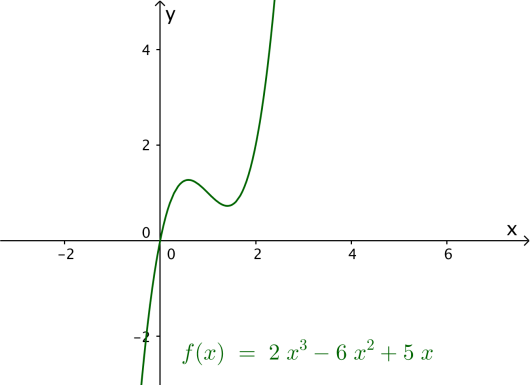
Funksjonen $f$ er gitt ved

$f (x) = 2 x^{3} - 6 x^{2} + 5 x$

a)

Bruk graftegner til å tegne grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen til $f$ .

Vi tegner grafen til $f$ ved hjelp av GeoGebra. Da skriver vi inn
$𝚏 (𝚡) = 2 𝚡^{\land} 3 - 6 𝚡^{\land} 2 + 5 𝚡$
i Skriv-inn-feltet og setter navn på aksene. Resultatet er som vist under.

Svar:

Mer om:

Denne oppgaven handler om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Graf

grafer

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler, se artikkelen Graftegner.

b)

Grafen til $f$ har tre tangenter som går gjennom punktet $A (4, 3)$ .

Forklar at $x$ -koordinaten til tangeringspunktene må være løsning av likningen

$\frac{f (x) - 3}{x - 4} = f^{'} (x)$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

En tangent er en rett linje på formen $y = a x + b$ . Stigningstallet til en tangent i punktet $(x, f (x))$ er $f' (x)$ .

Vi skal se på tangeringspunktene, $(x, f (x))$ , hvis tangent går gjennom punktet $A (4, 3)$ . Stigningstallet til tangenten gjennom $(x, f (x))$ er gitt ved $f' (x)$ . Vi kan også finne stigningstallet ved å se på forholdet mellom endring i $y$ -verdi og endring i $x$ -verdi, og siden tangenten går gjennom punktene $(4, 3)$ og $(x, f (x))$ også være gitt ved $\frac{f (x) - 3}{x - 4}$ , det betyr at vi må ha $f' (x) = \frac{f (x) - 3}{x - 4}$ og $x$ -koordinaten i disse tangeringspunktene må tilfredstille likningen over.

Mer om:

Denne oppgaven handler om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangenter

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

For flere forklaringer og eksempler, se artikkelen Å finne tangenten - introduksjon.

c)

Bruk CAS til å løse denne likningen. Bestem likningen til hver av tangentene.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke Løs-kommandoen i CAS for å finne hvilke $x$ -verdier som løser likningen, og kommandoen Tangent for å finne likningen til hver av tangentene.

Vi kan bruke samme GeoGebra-vindu som i oppgave a), og velger CAS i “Vis”-menyen. Først kan vi skrive inn $𝚏 (𝚡)$ for å sjekke at funksjonen får er definert. Videre kan vi bruke Løs kommandoen for å løse likningen fra oppgave c). Da skriver vi inn $𝙻 ø 𝚜 [(𝚏 (𝚡) - 3) / (𝚡 - 4) = 𝚏' (𝚡)$ ] . Da får vi opp punktene $x = \frac{1}{2}, x = \frac{- \sqrt{15} + 7}{2} og x = \frac{\sqrt{15} + 7}{2} .$

Det betyr at vi vil finne tangenten gjennom punktene $(\frac{1}{2}, f (\frac{1}{2})), (\frac{- \sqrt{15} + 7}{2}, f (\frac{- \sqrt{15} + 7}{2})) og (\frac{\sqrt{15} + 7}{2}, f (\frac{\sqrt{15} + 7}{2}))$ Nå kan vi bruke kommandoen Tangent[ $<$ Punkt $>$ , $<$ Funksjon $>$ ] for hvert av punktene. Da skriver vi inn
$𝚃 𝚊 𝚗 𝚐 𝚎 𝚗 𝚝 [(1 / 2, 𝚏 (1 / 2)), 𝚏]$
$𝚃 𝚊 𝚗 𝚐 𝚎 𝚗 𝚝 [(𝚜 𝚚 𝚛 𝚝 (15) + 7) / 2, 𝚏 (𝚜 𝚚 𝚛 𝚝 (15) + 7) / 2)), 𝚏]$
$𝚃 𝚊 𝚗 𝚐 𝚎 𝚗 𝚝 [(- 𝚜 𝚚 𝚛 𝚝 (15) + 7) / 2, 𝚏 ((- 𝚜 𝚚 𝚛 𝚝 (15) + 7) / 2)), 𝚏]$
Trykker vi på $\approx$ -knappen får vi en avrundet likning for tangenten.

Likningen til tangentene som går gjennom $A (4, 3)$ er
$\begin{matrix} y & = & \frac{1}{2} x + 1 \\ y & = & 0, 91 x - 0, 62 \\ y & = & 117, 09 x - 465, 38 \end{matrix}$

Svar: $y = \frac{1}{2} x + 1, y = 0, 91 x - 0, 62 og y = 117, 09 x - 465, 38$ .

Mer om:

Denne oppgaven handler om

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangenter

og CAS.

For flere forklaringer og eksempler fra CAS, se artikkelen CAS.

d)

La $P (a, b)$ være et punkt i planet.

Hva er det maksimale antallet tangenter grafen til $f$ kan ha som går gjennom $P$ ?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

I stedet for å se på punktet $A (4, 3)$ ser vi på punktet $P (a, b)$ . Da kan vi erstatte $4$ med $a$ og $3$ med $b$ i likningen fra oppgave b).

Vi kan bruke likningen fra oppgave b), men vi setter inn $a$ og $b$ i stedet for $4$ og $3$ . Da får vi at de punktene på $f$ som har tangent som går gjennom $P (a, b)$ har $x$ -koordinat som tilfredstiller likningen $\frac{f (x) - b}{x - a} = f' (x) \Rightarrow f (x) - b - f' (x) (x - a) = 0 .$ Vi har at $f (x)$ er en tredjegradsfunksjon og $f' (x)$ må være en andregradsfunksjon som vi multipliserer med en lineær faktor. Det betyr at dette må være en tredjegradslikning, og den kan maksimalt ha tre løsninger, som betyr at grafen til $f$ kan maksimalt ha tre tangenter som går gjennom $P$ .

Svar: $3$ tangenter.

Mer om:

Denne oppgaven handler om tangenter, derivasjon og polynomlikninger.

REA3022 2017 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4QXO

a)

Løsningsforslag a)

Derivasjon

b)

Løsningsforslag b)

Derivasjon

c)

Løsningsforslag c)

Derivasjon

Oppgave 2 (4 poeng) Nettkode: E-4QXS

a)

Løsningsforslag a)

Faktorisering

Fellesnevner

Konjugatsetningen

b)

Løsningsforslag b)

Logaritme

Oppgave 3 (4 poeng) Nettkode: E-4QXV

a)

Løsningsforslag a)

Alternativ løsning

Vektor

b)

Løsningsforslag b)

Vektor

Oppgave 4 (6 poeng) Nettkode: E-4QXY

a)

Løsningsforslag a)

Vendepunkt

Andrederiverte

b)

Løsningsforslag b)

Polynom

Faktorisering

c)

Løsningsforslag c)

Faktorisering

Nullpunkt

Logaritme

Oppgave 5 (6 poeng) Nettkode: E-4QY2

a)

Løsningsforslag a)

Vektor

b)

Løsningsforslag b)

Vektor

c)

Løsningsforslag c)

Vektor

Ligningssett

Oppgave 6 (4 poeng) Nettkode: E-4QYA

a)

Løsningsforslag a)

Sannsynlighet

Produktsetningen

Disjunkte hendelser

b)

Løsningsforslag b)

Betinget sannsynlighet

Bayes' setning

Oppgave 7 (7 poeng) Nettkode: E-4QYD

a)

Løsningsforslag a)

Sirkel

Kvadrat

Rettvinklet trekant

b)

Løsningsforslag b)

Algebra

c)

Løsningsforslag c)

Trekant

Areal