Formlikhet og kongruens
Hva betyr det at to figurer er formlike? Her skal vi se på to eksempler på hvordan vi anvender formlikhet i en praktisk sammenheng. I tillegg tar vi en titt på begrepet kongruens.
To figurer er formlike dersom de har nøyaktig samme form, men ikke nødvendigvis samme størrelse.
I to formlike figurer er forholdet mellom to samsvarende lengder konstant.
Eksempel 1.
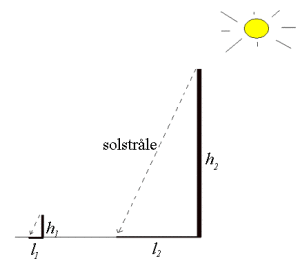
Vi skal bruke en pinne, et målebånd og sola til å måle høyden på et stort tårn.
Vi har en pinne med høyde , som vi plasser loddrett. Så måler vi lengdene og av skyggene som pinnen og tårnet kaster på bakken. La oss si vi fikk , og .
Vi ser at vi har to formlike trekanter, og da er forholdet mellom de samsvarende sidene likt:
Vi multipliserer med på begge sider av likhetstegnet og får
Så ved å måle lengden av en pinne og to skygger kan vi regne ut høyden til et meter høyt tårn!
For å bruke formlikhet, må vi selvsagt forsikre oss om at figurene virkelig er formlike. For to trekanter er det tilstrekkelig å vise at to av vinklene er parvis like store. Siden vinkelsummen i en trekant alltid er , må da også den tredje vinkelen være den samme i begge trekantene, og trekantene må ha samme form.
Eksempel 2.
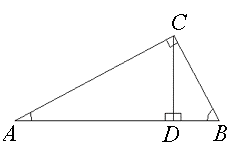
På figuren ser vi tre trekanter: , og . Disse trekantene er formlike når vi forutsetter at og at er en normal ned på .
er formlik med , fordi er felles og . Da er , og trekantene formlike.
På samme måte finner vi at er formlik med , fordi er felles og .
Siden både og er formlike med , må også og være formlike med hverandre.
Av dette kan vi trekke ut at forholdet mellom og er likt forholdet mellom og , altså
Dette gir oss at .
Dette betyr at i et rektangel med sidelengder og , er arealet til rektanglet like stort som arealet til kvadratet med sidelengder , når er fremkommet som på figuren foran. Lengden kalles mellomproporsjonalen mellom de to andre lengdene.
Generelt for tall:
Hvis tre tall , og er slik at , kalles mellomproporsjonalen mellom og .
Kongruens
Hvis vi har to formlike figurer som også er like store, sier vi at figurene er kongruente. Kongruente figurer dekker hverandre helt.
For trekanter kan vi sette opp kriterier som garanterer kongruens. Det betyr at to trekanter er kongruente dersom ett av disse kravene er oppfylt:
1. Sidene i de to trekantene er parvis like lange.
2. To sider og den mellomliggende vinkelen er like store.
3. To vinkler og den mellomliggende siden er parvis like store.
Dette betyr også at hvis ett av kriteriene er oppfylt, kan trekanten konstrueres på én måte. Den er med andre ord entydig bestemt.
Del på Facebook
Begrep
-
Formlike trekanter
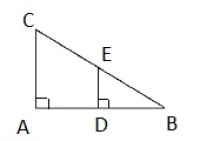
To trekanter er formlike hvis de har parvis like store vinkler.
Eksempel: , det leses trekant ABC er formlik med trekant DBE.
-
Høyde
Lengden av et linjestykke som står normalt på ei linje eller en flate.
-
Kongruens
Brukes både i algebra og i geometri.
I geometri: om figurer, for eksempel trekanter, som har parvis like vinkler og sider.
I algebra: om tall, for eksempel i regning modulo, et tall k om to tall som har samme rest etter divisjon med k.
-
Lengde
Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
-
Likhetstegn
Likhetsteget har symbolet "".
Likhetstegnet forteller at det som står til venstre for likhetstegnet har samme verdi som det som står til høyre.
Eksempel:
-
Normal
En linje som står 90 grader på en annen linje.
-
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
-
Vinkel
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.