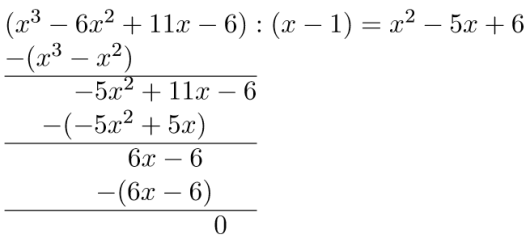Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3022 2013 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4CVE
Deriver funksjonene
a)
b)
c)
Oppgave 2 (3 poeng) Nettkode: E-4CVI
Polynomfunksjonen er gitt ved
a)
Vis at divisjonen går opp, uten å utføre divisjonen.
b)
Utfør polynomdivisjonen og løs ulikheten .
Oppgave 3 (2 poeng) Nettkode: E-4CVL
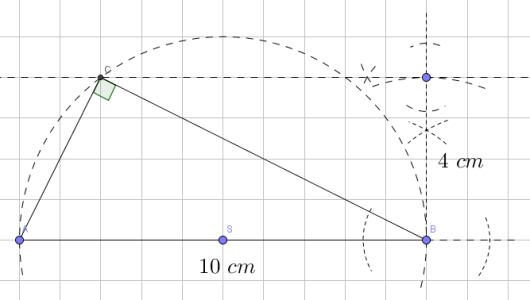
I er cm og . Høyden fra til er cm.
Konstruer gitt at er den lengste kateten. Forklar hva du har gjort.
Oppgave 4 (2 poeng) Nettkode: E-4CVN
En elev skulle løse en likning og begynte slik:
Fullfør løsningen av likningen.
Oppgave 5 (4 poeng) Nettkode: E-4CVP
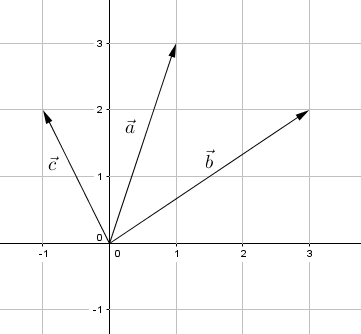
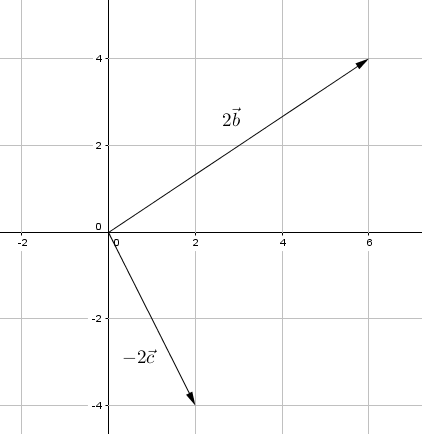
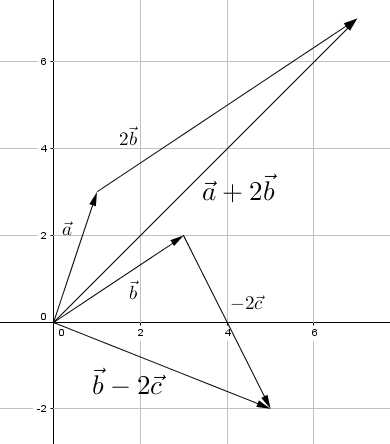
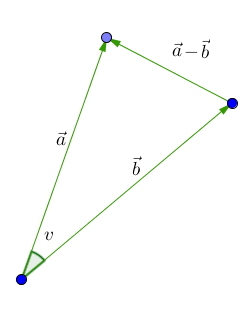
Vi har gitt vektorene , og .
a)
Tegn vektorene og i et koordinatsystem.
b)
Avgjør ved regning om .
Oppgave 6 (5 poeng) Nettkode: E-4CVS
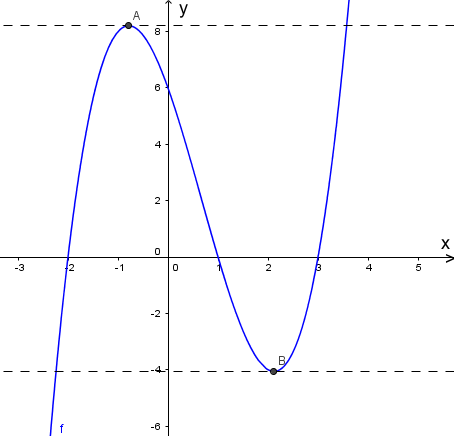
En funksjon er gitt ved
a)
Bestem og .
b)
Bestem koordinatene til eventuelle topp-, bunn- og vendepunkter på grafen til .
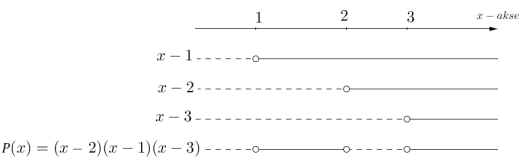
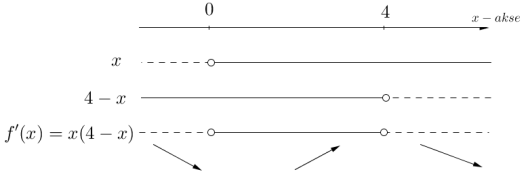
c)
Lag en skisse av grafen til . Bruk denne til å avgjøre for hvilke -verdier og samtidig .
Oppgave 7 (3 poeng) Nettkode: E-4CVW
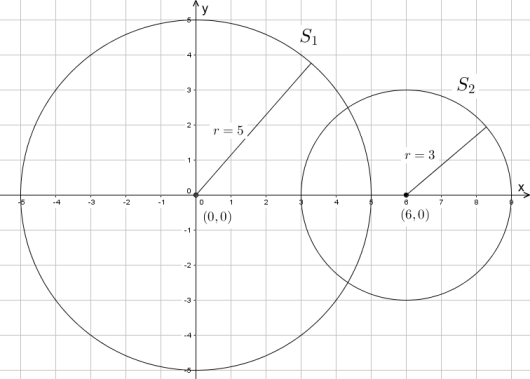
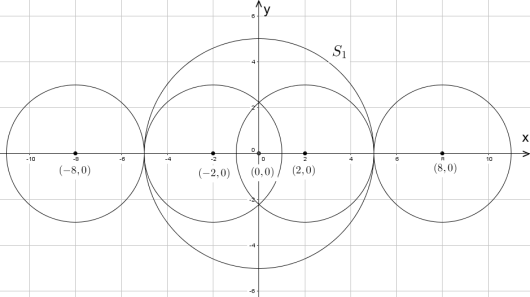
To sirkler og er gitt ved
a)
Tegn sirklene i et koordinatsystem når .
b)
For hvilke verdier av vil sirklene tangere hverandre?
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-4CW0
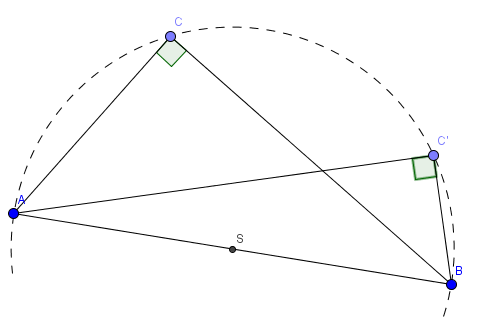
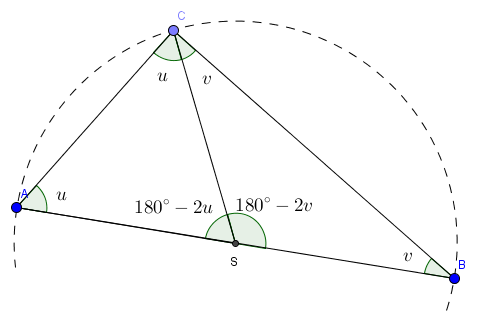
Når grafen til en polynomfunksjon tangerer x-aksen i , har funksjonen minst to like (sammenfallende) nullpunkter i .
a)
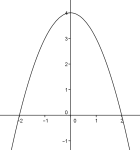
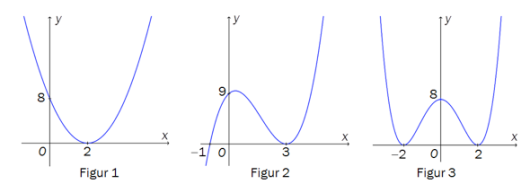
Grafen til en andregradsfunksjon er vist på figur 1. Grafen tangerer -aksen i .
Forklar at
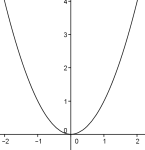
b)
Grafen til en tredjegradsfunksjon er vist på figur 2. Grafen tangerer -aksen i .
Forklar at funksjonsuttrykket til kan skrives på formen
Bestem k.
c)
Grafen til en fjerdegradsfunksjon er vist på figur 3. Grafen tangerer -aksen i og i .
Bestem funksjonsuttrykket .
Oppgave 2 (4 poeng) Nettkode: E-4CW4
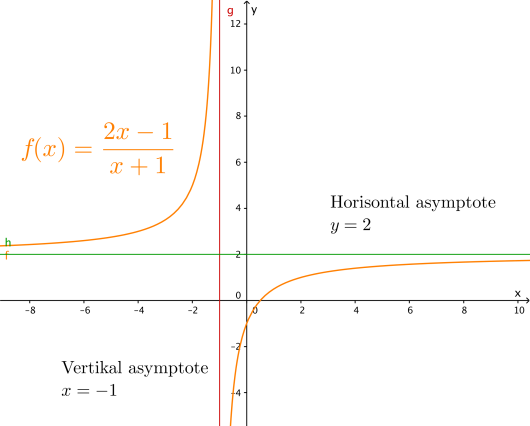
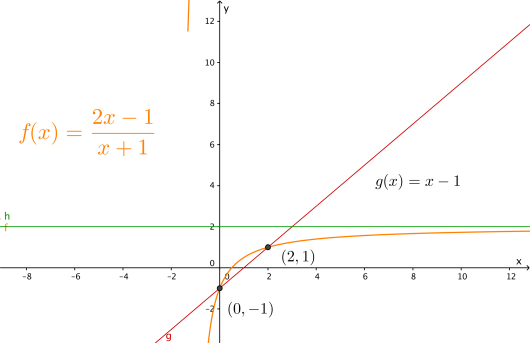
Funksjonen er gitt ved
\
a)
Bestem asymptotene til . Tegn grafen til med asymptoter.
b)
Funksjonen er gitt ved
Bestem skjæringspunktene mellom grafene til og ved regning.
Oppgave 3 (6 poeng) Nettkode: E-4CW8
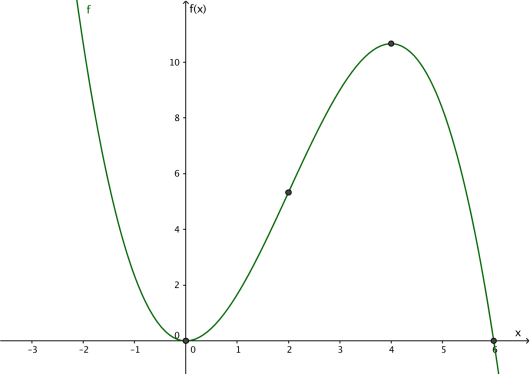
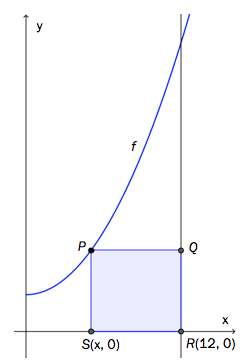
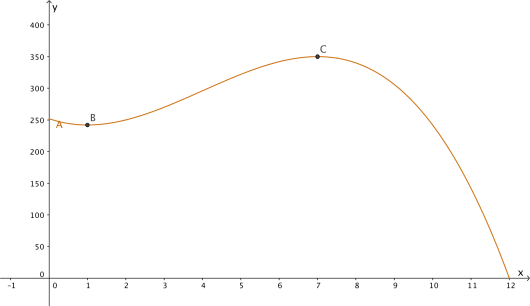
Figuren til høyre viser grafen til funksjonen gitt ved
Rektangelet lages slik at ligger på grafen til , punktene og ligger på -aksen, og og har førstekoordinat . Punktet ligger mellom origo og .
a)
Forklar at arealet av rektanglet kan skrives som
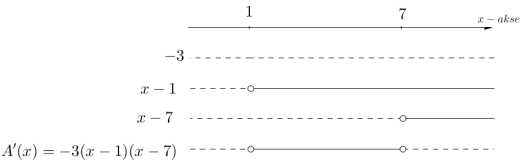
b)
Bestem og bruk denne til å bestemme største og minste verdi som arealet av rektanglet kan ha.
c)
Tegn grafen til , og kontroller om svarene dine fra oppgave b) stemmer.
Oppgave 4 (4 poeng) Nettkode: E-4CWD
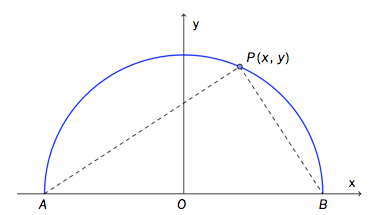
En sirkel med radius og sentrum i origo er gitt ved
Punktet er et vilkårlig punkt på den øvre halvsirkelen. Se skissen nedenfor.
a)
Bestem koordinatene til punktene og uttrykt ved .
Bestem vektorkoordinatene til og .
b)
Vis ved vektorregning at .
Oppgave 5 (6 poeng) Nettkode: E-4CWG
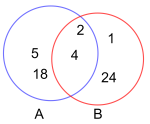
Ved en videregående skole skal elevene velge fag. Hendelsene og definerer vi slik:
: Eleven velger matematikk.
: Eleven velger fysikk.
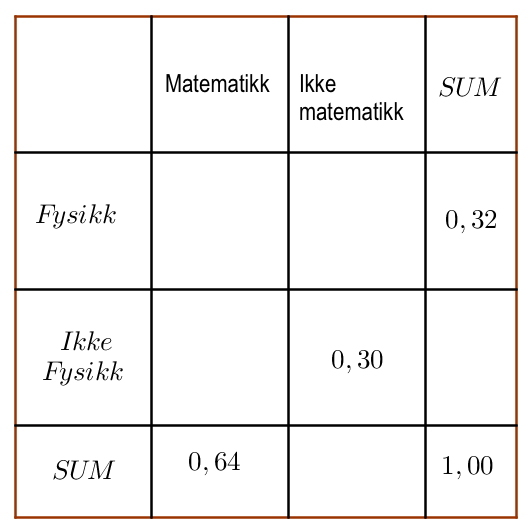
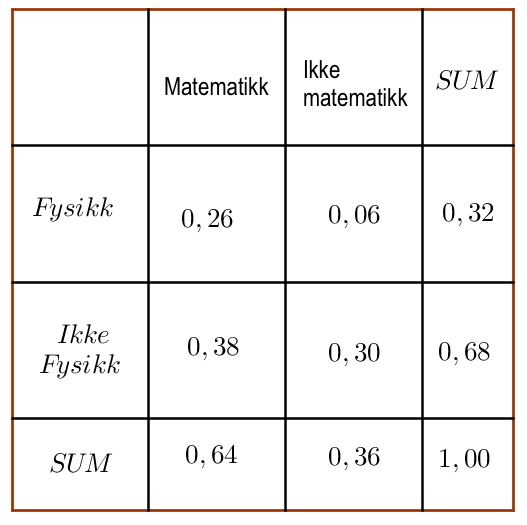
Vi får opplyst at , og .
a)
Bestem og .
b)
Bestem . Undersøk om hendelsene og er uavhengige.
c)
Bruk Bayes’ setning til å bestemme .
Oppgave 6 (8 poeng) Nettkode: E-4CWK
I et koordinatsystem har vi gitt punktene , og .
a)
Bestem og arealet av .
b)
Et punkt er gitt ved at og .
Bestem ved regning koordinatene til .
c)
En parameterframstilling for linjen som går gjennom og , er gitt ved
Et punkt har koordinatene .
Bestem ved regning en verdi for slik at ligger på .
d)
Bestem koordinatene til punktet når .
Oppgave 7 (2 poeng) Nettkode: E-4CWP
Løs likningen med hensyn på