Addisjon av vektorer
For å forstå vektoraddisjon, kan det være greit å tenke vektorer som forflytning mellom punkter. Spiller det noen rolle hvilken vektor kommer først i summen?
MatRIC: Vektorregning
Rettighetshaver: Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC /
ADDISJON AV VEKTORER
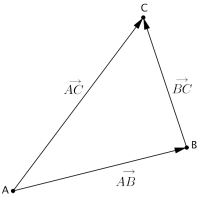
Addisjon av vektorene og :
ADDISJON AV VEKTORER PÅ KOORDINATFORM
La og være to vektorer. Vi adderer vektorer koordinatvis, det vil si
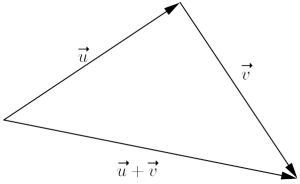
Vi har altså addert -verdiene og -verdiene hver for seg, og fått en ny vektor. Geometrisk tilsvarer dette å flytte slik at den starter der slutter, med samme retning og lengde som før vi flyttet den. Summen er nå pilen som starter der starter og ender der ender.
Vektoraddisjon kan tolkes som å først bevege seg langs den ene vektoren, så langs den andre vektoren.
Eksempel 1
Vi skal addere vektorene . Vi kan tenke at vi først beveger oss langs , det vil si ett steg i -retningen og fem steg i -retningen. Så beveger vi oss langs , elleve steg i -retningen og tre steg i -retningen. Den totale forflytningen blir dermed tolv steg i -retning og åtte steg i -retning, vektoren . Vi kan kalle den nye vektoren for og skriver
Eksempel 2
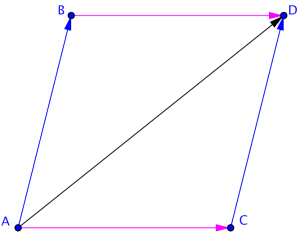
Vektoraddisjon er kommutativ
Leddenes rekkefølge spiller ingen rolle.
Det spiller ingen rolle hvilken vektor som kommer først i summen. Dette ser vi tydelig på figuren til høyre:
- , likheter på grunn av lik lengde og retning.
- Det er det samme om vi først forflytter oss langs og så langs , eller om vi først forflytter oss langs og så langs , summen av vektoren i begge tilfellene.
Del på Facebook
Lynkurs 11.-13.trinn
Vektorer
Består av:
- Hva er en vektor?
- Like vektorer
- Vektorer mellom to punkter
- Vektorer i tre eller flere dimensjoner
- Nullvektor
- Stedvektor (posisjonsvektor)
- Parallelle vektorer
- Lengden til en vektor
- Addisjon av vektorer
- Subtraksjon av vektorer
- Skalarmultiplikasjon
- Prikkprodukt og norm
- Vinkelen mellom to vektorer
- Ortogonale vektorer
- Enhetsvektor og normalisering
- Projeksjon
- Kort om matriser og determinanter
- Kryssprodukt av to vektorer
- Retningsvektor
- Parameterframstilling av en rett linje
- Parametriserte kurver
- Likning til et plan
- Avstand mellom et punkt og et plan
- Likning for en kule
- Kryssprodukt - areal og volum
- Vektorregning med eksempler