Overflatearealet til en terning
Vi skal regne ut overflatearealet til en terning.
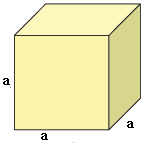
En terning er satt sammen av seks kvadrater, og alle vinkler mellom naboflater er . La oss kalle størrelsen på sidekantene for :
Vi skal regne ut arealet til alle sideflatene. Én sideflate har areal . Legger vi sammen arealet til alle seks sideflatene, får vi overflatearealet til hele terningen.
| Formel |
| En terning med sidekanter med lengde a har overflateareal . |
Eksempel
Per ønsker seg et glassakvarium som passer inn i hyllen hans. Hyllen er kvadratisk med sidelengden . Hvor mye glass trengs når akvariet skal lages?
Vi setter inn for sidekantene i formelen for overflate av en terning:
Vi vet at , og derfor kan vi også skrive .
Vi kunne godt ha regnet med direkte og også på den måten fått samme svar:
Vi trenger altså kvadratmeter med glass for å lage akvariet.
Del på Facebook
Lynkurs, 8.-10.trinn
Geometri - areal og volum
Består av:
- Tom forteller om areal
- Et kvadrat
- Et rektangel
- En trekant
- Et parallellogram
- Et trapes
- Tom forteller om overflatearealer
- Overflatearealet til en terning
- Tom forteller om volum
- Et rett prisme
- En sylinder
- Pyramider og kjegler
- En kule
- Pytagoras læresetning
- Tom forteller om formlikhet og Pytagoras læresetning
- Test deg selv i geometri (areal og volum)!
- Test deg selv i tallet π (PI)
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Overflate
Med overflate av en tredimensjonal figur, for eksempel et prisme eller en sylinder, menes summen av arealene til alle flatene som den tredimensjonale figuren er satt sammen av.
-
Terning
Se Kube