
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2014 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Melk: http://www.melk.no/meierifakta/ (02.10.2014)
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4C0Y
Regn ut og skriv svaret på standardform
Løsningsforslag
Jeg tenker:
Først skriver vi alle enkelttallene i
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Vi skriver alle tallene i brøken som
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Svar:
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n gangerStandardform
Brøk

For flere eksempler og forklaringer se artiklene Tall på standardform og Rask gjennomgang av regneregler for potens og røtter.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Oppgave 2 (1 poeng) Nettkode: E-4C10
Prisen for en vare er satt opp med 25 %. Nå koster varen 250 kroner. Hva kostet varen før prisen ble satt opp?
Løsningsforslag
Jeg tenker:
Denne oppgaven er om regning med
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
La oss si at varen kostet kroner før prisen ble satt opp. Den ble satt opp , så den nye prisen ble . Men vi vet allerede at den nye prisen er kroner; derfor er En annen måte å sette opp den samme likningen på, er å se at er det samme som en fjerdedel. Det betyr at prisen på varen ble satt opp med , så den nye prisen er , eller (Dette er den samme likningen som før, fordi .) Vi vil altså finne tallet som passer inn i ligningen over. Derfor multipliserer vi med på hver side av likhetstegnet, og forkorter. Da får viVi regner ut at Dermed kostet varen kroner.
Alternativ løsning
Varen ble satt opp til av sin forrige pris, så av den opprinnelige prisen var . Dermed er av prisen lik og da er av den originale prisen .
Svar:
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Prosent
Ligning
For flere eksempler og forklaringer om regning med prosent se artikkelen Regneregeler. For mer om hvordan løse en førstegradslikning se artikkelen Lineære likninger.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 3 (2 poeng) Nettkode: E-4C12
En bunke med ark er høy.
Hvor mange ark vil det være i en bunke som er m høy?
Skriv svaret på standardform.
Løsningsforslag
Jeg tenker:
Vi ser at hvis vi finner ut hvor mange bunker på cm det er i en bunke på m, kan vi multiplisere dette med for å få svaret på oppgaven. Husk å skrive svaret som
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Vi finner først ut hvor mange bunker på cm det er i en bunke på m. Vi vet at , og vi vet at en bunke på vil ha ark i seg. Det trengs slike bunker oppå hverandre for å få en bunke på m. Siden vi har en bunke på ark, er det dermed ark i. Vi regner om til standardform:altså millioner ark.
Svar: Det er ark i bunken.
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: Potens
Eksempel: Standardform
For flere eksempler og forklaringer se artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Oppgave 4 (1 poeng) Nettkode: E-4C14
Regn ut
Løsningsforslag
Jeg tenker:
Her regner vi med
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Subtraksjon
En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen.
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.
Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
Vi regner ut hvert ledd for seg. Får å regne ut brøken , husker vi at er det samme som , at og at vi kan “flytte” en potens opp fra
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Nå skal vi regne ut . Den enkleste måten å gjøre dette på, er å se at , så . Vi kan også regne det ut ved å se at . Da får vi .
Nå kan vi regne ut hele uttrykket. Ved å sette inn det vi har regnet ut i det opprinnelige uttrykket, får vi
Svar:
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Brøk

For flere eksempler og forklaringer se artikkelen Potenser med samme grunntall.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 5 (4 poeng) Nettkode: E-4C1F
I 2014 er det 350 elever ved en skole. Anta at det vil være 275 elever ved skolen i 2029, og at antall elever avtar lineært i denne perioden.
a)
Bestem en modell som viser hvor mange elever det vil være ved skolen år etter 2014.
Løsningsforslag a)
Jeg tenker:
I denne oppgaven er en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi er ute etter å finne de
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Svar:.
Mer om:
Denne oppgaven er om
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Å lage en matematisk modell.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
Visste du at:
I denne oppgaven passer den lineære modellen vår helt eksakt med dataene, altså og . Men hva om vi skulle se på elevantallet på flere skoler, vi hadde fått oppgitt antallet elever ved alle skolene i hvert år? Da kunne vi for eksempel hatt flere forskjellige verdier i , så den lineære modellen vår ville ikke vært eksakt. I stedet for å finne den rette linjen som går gjennom alle punktene (en slik linje finnes nemlig ikke), så kan vi prøve å finne den rette linjen som har minst avstand fra dataene. Dette kalles lineær
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
b)
Hvor mange elever vil det være ved skolen i 2024 ifølge modellen i oppgave a)?
Løsningsforslag b)
Jeg tenker:
Året er år etter . Derfor representerer året . Nå kan vi bruke modellen vi fant i deloppgave a).
Tallet er antallet elever ved skolen år etter , i følge den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Svar: elever
Mer om:
Denne oppgaven er om Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner er funksjoner som er skrevet på formen .Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
c)
Ved en annen skole antar ledelsen at funksjonen gitt ved
kan brukes som modell for antall elever ved skolen x år etter 2014.
Hva kan du si, uten å gjøre beregninger, om antall elever ved denne skolen ut fra modellen?
Løsningsforslag c)
Jeg tenker:
Vi ser at er en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
er en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Antall elever ved skolen i er , og antallet øker med hvert år etter det.
Mer om:
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Eksponentialfunksjon

Prosent
For flere eksempler og forklaringer se artiklene Typer av funksjoner og Eksponentiallikninger.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleieren.
Oppgave 6 (3 poeng) Nettkode: E-4C1K
I september 2014 ble en mobilapplikasjon lastet ned 1500 ganger. Antall nedlastinger har økt med 8 % per måned det siste året, og vi antar at denne utviklingen vil fortsette.
a)
Sett opp et uttrykk som du kan bruke til å bestemme hvor mange ganger mobilapplikasjonen vil bli lastet ned i desember 2014.
Løsningsforslag a)
Jeg tenker:
Antall nedlastninger øker med en viss prosentandel hver måned, så utviklingen kan modelleres med en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Utviklingen der antall nedlastninger øker med en viss prosentandel hvert år kan modelleres med en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar:
Mer om:
Denne oppgaven er om En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Ligning
Vekstfaktor
Prosent
Eksponentialfunksjon

For flere eksempler og forklaringer se artiklene Typer av funksjoner og Renter.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleieren.
b)
Sett opp et uttrykk som du kan bruke til å bestemme hvor mange ganger mobilapplikasjonen til sammen ble lastet ned i juli, august, september og oktober 2014.
Løsningsforslag b)
Jeg tenker:
Vi vet at antall nedlastninger kan modelleres med en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vi vil finne den
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: ganger
Mer om:
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Prosent
Funksjon
Potens
Eksempel:
For flere eksempler og forklaringer se artiklene Typer av funksjoner og Rask gjennomgang av regneregler for potens og røtter.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleieren.
Visste du at:
Det kan virke unaturlig at vi kan sette inn negative eksponenter for å få antall nedlastninger i månedene før september. Her er et bevis for at det faktisk er slik. La oss si at antall nedlastninger i juli var , der er et eller annet heltall. I følge teksten skal antall nedlastninger øke med de neste månedene, så antall nedlastninger i august er , og antall nedlastninger i september er . Men vi vet allerede at antall nedlastninger i september var , og derfor er . Dette er en ligning, og vi vil finne tallet som passer inn i den. Vi multipliserer med på hver side av likhetstegnet, og bruker potensreglene til å forkorte. Da får viMen nå har vi funnet at antall nedlastninger i juli er , akkurat det vi får ved å sette inn i modellen vår over. Det samme gjelder for alle de andre månedene.
Oppgave 7 (4 poeng) Nettkode: E-4C20
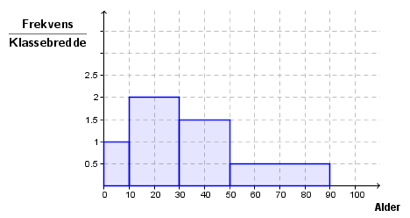
Histogrammet ovenfor viser aldersfordelingen blant de besøkende på en kinoforestilling.
a)
Forklar at det var 30 besøkende mellom 30 og 50 år.
Løsningsforslag a)
Jeg tenker:
I et
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Husk hva som skiller et
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.
Svar: Arealet av den relevante søylen er .
Mer om:
Denne oppgaven er om søylediagram, Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Histogram
Statistikk
For flere eksempler og forklaringer se artikkelen Histogram.
b)
Hvor mange prosent av de besøkende var mellom 0 og 10 år?
Løsningsforslag b)
Jeg tenker:
Dette kan vi gjøre på to måter. Enten kan vi regne ut hvor mange besøkende det var totalt og hvor mange det var mellom og år, eller så kan vi se på arealet av søylen tilhørende klassen til år, og det totale arealet.
Vi viser her den raskeste måten å løse oppgaven på - se på arealet av søylen tilhørende klassen til år, og det totale arealet. I alternativ løsning kan du se hvordan du kan løse oppgaven ved å regne ut antall besøkende totalt og hvor mange det var mellom og år.
Vi teller antall ruter det er i søylene, og ser på antall ruter i søylen for besøkende mellom og år i forhold til det totale antallet. Vi ser først at den første søylen, altså den tilhørende aldersgruppen til år, inneholder ruter. De neste søylene inneholder henholdsvis , og ruter. Antall ruter til sammen er , og siden av disse rutene var fra aldersgruppen til år, var av de besøkende i denne gruppen, akkurat som før.
Grunnen til at vi kun trenger å se på antall ruter i hver søyle i stedet for arealet, er at vi er ute etter en prosentandel. Én rute tilsvarer mennesker, så om vi multipliserer antall ruter i en søyle med , så får vi antall mennesker i denne aldersgruppen. For eksempel hadde den første søylen ruter, så det var besøkende i denne kategorien. Når vi ser på andelen av noe i forhold til noe annet, har det ikke noe å si om vi ser på de faktiske tallene, eller alle tallene dividert med .
Alternativ løsning
Vi starter med å regne ut hvor mange besøkende det var totalt og hvor mange som var mellom og år. Denne metoden vil ta lengst tid.
Først regner vi ut hvor mange av de besøkende som var mellom og år. Denne søylen har høyde og bredde , så det var besøkende i denne kategorien. Dette er regnet ut som i forrige oppgave. På tilsvarende måte regner vi ut hvor mange av de besøkende som var i de andre kategoriene:Totalt var det dermed besøkende, hvorav stykker var mellom og år. Derfor var av de besøkende mellom og år.
Svar: .
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Prosent
Histogram
Statistikk
For flere eksempler og forklaringer se lynkurset Prosent og Statistikk (del II).
c)
Bestem gjennomsnittsalderen blant de besøkende.
Løsningsforslag c)
Jeg tenker:
Når vi her beregner
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi jobber med gruppert materiale, og da antar vi at aldrene er uniformt/jevnt fordelt. Dette vil si at gjennomsnittsalderen i hver gruppe er i midten av aldersgruppen. For eksempel antar vi at gjennomsnittsalderen i aldesgruppen til år, er midt mellom og , altså år. Når vi beregner gjennomsnitt av alle de besøkende, er dette det samme som å anta at alle personene i en aldersgruppe er like gamle som gjennomsnittsalderen.
Som i deloppgave b), kan vi løse dette problemet på to måter. Den ene måten går ut på å bruke de faktiske besøkstallene, som for eksempel at det er stykker som er mellom og år og så videre. I stedet gjør vi som vi viste sist i forrige oppgave: Vi later som om antallet mennesker i hver kategori, er lik antall ruter i søylen til den kategorien. Derfor antar vi at det var 2 besøkende mellom og år, besøkende mellom og år og så videre. Siden vi jobber med gruppert materiale, antar vi også at alle de besøkende i aldersgruppen til år var år, at alle i gruppen til var år, og så videre. Med dette har vi derfor besøkende på år, besøkende på år, besøkende på år og besøkende på år. Gjennomsnittet av disse er
Vi kunne også ha regnet ut dette med å bruke de faktiske tallene. Det ville sett slik ut.
Svar: år
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Histogram
Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Oppgave 8 (3 poeng) Nettkode: E-4C28
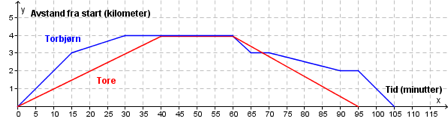
Torbjørn og Tore padler fra Flekkefjord til Torsøy. Der går de i land og tar en pause før de padler tilbake. Ovenfor ser du en forenklet grafisk framstilling av padleturen til Torbjørn (blå graf) og padleturen til Tore (rød graf).
a)
Hvem kommer først til Torsøy?
Hvor lenge er hver av de to guttene på Torsøy?
Løsningsforslag a)
Jeg tenker:
Vi ser nøye på
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi antar at guttene padler i retning rett mot Torsøy og deretter rett tilbake til Flekkefjord. Når de tar en pause på Torsøy, så er de på samme sted over en lengre periode, og grafen skal ikke gå opp eller ned. Dette ser vi skje der , og spørsmålet er hvem som kommer frem til der først.
Ut i fra grafen ser vi at Flekkefjord er cirka kilometer fra Torsøy. Vi er ute etter hvem som padler de kilometerene først. Vi ser at grafen til Torbjørn kommer seg til når , altså på minutter, mens Tore bruker minutter. Derfor kom Torbjørn fram først. Videre ser vi at begge grafene begynner å synke igjen der , så minutter etter start begynner de å padle tilbake igjen. Derfor var Torbjørn på Torsøy i minutter, mens Tore var der i minutter.
Svar: Torbjørn kom fram først, og var der i minutter. Tore var der i minutter.
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Funksjon
Graf
For flere eksempler og forklaringer se artikkelen Hvorfor ser grafen ut som den gjør?.
b)
Hvor fort padler Tore på vei ut til Torsøy?
Løsningsforslag b)
Jeg tenker:
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Der grafen til Tore er en rett linje, betyr det at Tore padler i konstant fart. Tore padler til Torsøy på minutter, og han holder konstant fart. Fra grafen ser vi at Torsøy er kilometer fra Flekkefjord; dette ser vi fordi den lange pausen på Flekkefjord er der . Dermed vet vi at Tore padler kilometer på minutter. Det gir en fart på . Vi vet at minutter er to tredjedeler av en time, så vi kan skrive farten som
Svar: .
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Fart er tilbakelagt distanse per tidsenhet. Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund. Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.Funksjon
Graf
Fart
For flere eksempler og forklaringer se artiklene Rette linjer (lineære funksjoner) og se også eksempel om Vei, fart og tid i artikkelen Hvorfor regne med bokstaver?.
For å øve mer, se oppgavesettene om vei, fart og tid og lineære funksjoner i Treningsleieren.
c)
Hva kan du si om hjemturen ut fra grafene ovenfor?
Løsningsforslag c)
Jeg tenker:
Tore padler hjem igjen med konstant fart, mens Torbjørn er mer ujevn.
Svar: Hjemveien begynner der . Tores graf er en rett linje herfra, så han padler med jevn fart. Torbjørns graf begynner først å avta fortere enn Tores, og det betyr at han starter med høyere fart enn Tore. Etter det står grafen hans stille, så han hviler litt, før han begynner å padle litt sakte igjen. Etter en stund hviler han nok en gang, før han til slutt padler fort med en brått synkende graf. Kanskje var Torbjørn sliten etter å ha padlet fort til Torsøy, og klarte ikke å holde samme fart på tilbakeveien, så han måtte ta det litt roligere en stund. Han kom tilbake minutter etter Tore.
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Funksjon
Graf
For flere eksempler og forklaringer se artikkelen Grafen til en funksjon.
Oppgave 9 (5 poeng) Nettkode: E-4C2D
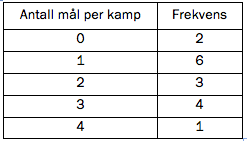
Oda spiller ishockey. Tabellen ovenfor viser hvor mange mål hun skåret per kamp i løpet av forrige sesong.
a)
Bestem gjennomsnittet og medianen.
Løsningsforslag a)
Jeg tenker
Her må vi huske hva
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Husk at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Nå skal vi finne medianen. Den kan vi faktisk finne veldig fort ved å se at Oda skåret eller færre mål i av kampene, og eller flere mål i de resterende kampene. Det betyr at medianen er gjennomsnittet av 1 og 2, altså . Vi kan også se dette ved å skrive opp antall mål Oda skåret i kampene i stigende rekkefølge. Som over vet vi at hun skåret mål i av kampene, mål i av kampene og så videre, så listen vår ser slik ut:Vi vil finne det miderste tallet i denne listen, eller eventuelt gjennomsnittet av de to midterste. Listen kan deles i to mellom 1 og 2:Nå ser vi at medianen må bli gjennomsnittet av og , altså .
Svar: Gjennomsnittet er , og medianen er .
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Medianen er den verdien som vi finner i midten av et rangert datamateriale. Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4. Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer. Se frekvenstabell Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Median
Frekvens
Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.
For å øve mer, se oppgavesettet om median og gjennomsnitt i Treningsleieren.
b)
Bestem den kumulative frekvensen for to mål per kamp.
Løsningsforslag b)
Jeg tenker:
Vi må huske hva
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Den
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Svar:
Mer om:
Denne oppgaven er om Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer. Se frekvenstabell Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere. Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien. Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Frekvens
Kumulativ frekvens

Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
c)
Bestem den relative frekvensen for tre mål per kamp.
Løsningsforslag c)
Jeg tenker
Vi må huske hva den
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Den
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Svar: eller
Mer om:
Denne oppgaven er om Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde. Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer. Se frekvenstabell Antall observasjoner av en spesiell hendelse dividert på antall observasjoner. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Brøk

Frekvens
Relativ frekvens
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
d)
Forklar hva svarene i b) og c) forteller om antall mål Oda skåret denne sesongen.
Løsningsforslag d)
Jeg tenker:
Her må vi tenke på hva
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Den kumulative frekvensen for to mål per kamp var . Det betyr at i av kamper, altså de fleste kampene, så skåret Oda to mål eller færre. Den relative frekvensen for tre mål per kamp var , og det betyr at Oda skåret tre mål i av kampene.
Svar: Oda skåret to mål eller færre i av de kampene, og i av kampene skåret hun mål.
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer. Se frekvenstabell Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere. Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien. Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer. Antall observasjoner av en spesiell hendelse dividert på antall observasjoner. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Prosent
Frekvens
Kumulativ frekvens

Relativ frekvens
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
DEL 2 Med hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4C2J
I kroppsøvingstimen kastet Svein spyd seks ganger. Nedenfor ser du hvor langt han kastet i hvert av de seks kastene.
23,5 m 26,1 m 18,4 m 22,8 m 25,1 m 20,3 m
a)
Bestem gjennomsnittet og standardavviket.
Løsningsforslag a)
Jeg tenker
Vi husker hva
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Svein kastet spyd seks ganger med de oppgitte lengdene. Gjennomsnittet av kastene er
Vi kan også gjøre dette i et regneark, og da er det lettere å finne standardavviket. Det første vi gjør er å legge inn kastelengdene.
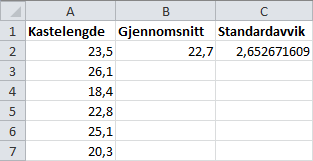
Her har vi lagt verdiene i rute A2 til rute A7. For å regne ut gjennomsnittet av dette, skriver vi i rute 2B
=GJENNOMSNITT(A2:A7)Standardavviket er like enkelt, og i 2C skriver vi
=STDAV.P(A2:A7)Resultatet ligger i bildet over. Dermed har vi funnet ut at Svein kastet i gjennomsnitt med et standardavvik på cirka . Vi bruker STDAV.P fordi vi vil regne ut standardavviket for hele datasettet. Hvis vi hadde brukt STDAV, ville vi fått estimerte verdier basert på utvalg.
Svar: Gjennomsnittet er , og standardavviket er cirka .
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Standardavvik
Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt og Varians og standardavvik.
For å øve mer, se opppgavesettet om gjennomsnitt i Treningsleieren.
b)
Kjell kastet også spyd seks ganger. Standardavviket for kastene til Kjell var 3,2 m.
Hva kan du ut fra dette si om kastene til Kjell sammenliknet med kastene til Svein?
Løsningsforslag b)
Jeg tenker:
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Svar:
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Mer om:
Denne oppgaven er om Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Standardavvik
Statistikk
For flere eksempler og forklaringer se artikkelen Varians og standardavvik.
Oppgave 2 (5 poeng) Nettkode: E-4C2M
En tankbil med gift har vært innblandet i en ulykke. Noe av giften har havnet i en innsjø. Innsjøen brukes som drikkevannskilde.
Giftkonsentrasjonen mg/L i drikkevannet døgn etter ulykken er gitt ved
a)
Bestem giftkonsentrasjonen i drikkevannet rett etter ulykken.
Hvor mange prosent avtar giftkonsentrasjonen i drikkevannet per døgn?
Løsningsforslag a)
Jeg tenker:
Rett etter ulykken har det gått døgn. Derfor er giftkonsentrasjonen på dette tidspunktet lik .
Ulykken skjer der . Derfor får vi giftkonsentrasjonen rett etter ulykken ved å sette inn i uttrykket for – med andre ord regner vi ut . Vi får Dermed var giftkonsentrasjonen rett etter ulykken.
Videre ser vi at uttrykket er en potensuttrykk med
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Giftkonsentrasjonen rett etter ulykken var , og den avtar per døgn.
Mer om
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
For flere eksempler og forklaringer se artiklene Typer av funksjoner, Johannes viser eksponential- og logaritmefunksjoner og Eksponentiallikninger.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleieren.
b)
Hvor mye avtok giftkonsentrasjonen i drikkevannet i gjennomsnitt per døgn den første uken etter ulykken?
Løsningsforslag b)
Jeg tenker:
Etter en uke er . Vi skal finne den
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
Giftkonsentrasjonen rett etter ulykken er , og etter en uke er den . Vi vet allerede hva er fra forrige oppgave. Vi regner ut : Dermed har giftkonsentrasjonen avtatt fra til , som er en negativ endring på Denne endringen skjer over dager. Giftkonsentrasjonen avtar derfor i gjennomsnitt per døgn den første uken.
Svar: Cirka per døgn.
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: En funksjon har gjennomsnittlig vekstfart mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Gjennomsnittlig vekstfart
Eksponentialfunksjon

Funksjon
For flere eksempler og forklaringer se artikkelen Hvorfor ser grafen ut som den gjør?.
c)
Når giftkonsentrasjonen kommer under 0,40 mg/L, er det ikke lenger farlig å drikke vannet.
Hvor mange døgn tar det før vannet igjen kan drikkes?
Løsningsforslag c)
Jeg tenker:
Vi vil finne hvor mange døgn det går før giftkonsentrasjonen er under . Det er det samme som å finne punktet der krysser linjen , og dette kan vi gjøre grafisk i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi velger å løse likningen grafisk i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
f(x) = 1.42*0.87^xog
y = 0.4i “Skriv inn”-vinduet i GeoGebra. Deretter tilpasser vi aksene slik at vi ser skjæringspunktet. Vi bruker verktøyet “Skjæring mellom to objekt” og får at koordinatene er , som vist under.
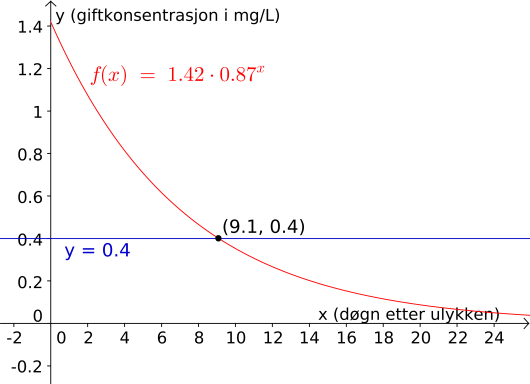
Det betyr at , altså at det etter cirka døgn er gift i drikkevannet. Dermed kan vannet drikkes igjen etter litt over døgn.
Svar: Vannet kan drikkes etter døgn.
Mer om:
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Skjæringspunkt

Linje
Graf
Funksjon
Ligning
Eksponentialfunksjon

For flere eksempler og forklaringer se Grafisk løsning av likninger og Fra en funksjon til en graf.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.
Visste du at:
I denne oppgaven løser vi ligningen grafisk. Vi kan også løse likningen ved regning, og da har vi bruk for det som heter . Vi vet at og at , men hva skal vi opphøye 10 i for å få 50? Tallet slik at er kalt logaritmen til 50, og vi skriver . Altså er , eller mer genereltfor alle positive tall . Logaritmer kan vi regne ut på datamaskin eller kalkulator, akkurat som vi gjør med kvadratrøtter eller potenser. En veldig fin egenskap med logaritmer, er at vi kan “flytte” eksponenter ned på denne måten:for alle positive tall og alle tall . For eksempel er . Ved hjelp av disse logaritmene kan vi løse ligningenved regning. Det første vi gjør er å få potensen med alene på venstre side, og dette gjør vi ved å dividere med og forkorte. Da får viNå kan vi bruke logaritmene våre. Hvis er et tall som passer inn i likningen over, er tallet på venstre side det samme tallet som det på høyre side, og da må logaritmene deres også være de samme. Derfor kan vi ta logaritmen av hver side, og vi fårNå kan vi bruke eksponentregelen vår, og flytte -en ned. Vi har at . Nå er likningen vårAlt vi trenger å gjøre nå, er å dividere med på begge sider og forkorte. Da får viVi kan regne ut på kalkulator atakkurat som vi fant i oppgaven. Hvis du vil vite mer om logaritmer se artikkelen Mer om logaritmer.
Oppgave 3 (4 poeng) Nettkode: E-4C2Q
Da Mads og Malin ble konfirmert, opprettet de hver sin konto i banken. Begge satte inn 25 000 kroner. Renten er 2,25 % per år.
a)
Hvor mye vil Mads ha på kontoen 10 år etter konfirmasjonen dersom han lar pengene stå urørt?
Hvor mange prosent har beløpet på kontoen hans til sammen økt i denne perioden?
Løsningsforslag a)
Jeg tenker:
Når et beløp øker med , så er det nye beløpet lik det opprinnelige multiplisert med . Tallet er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Etter ett år har Mads på kontoen sin. Etter to år har han på kontoen sin, og så videre. Etter 10 ti år har Mads dermedpå kontoen sin. Dette gir en total
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Etter 10 år vil beløpet være , som er en økning på cirka .
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefotPotens
Eksempel: Prosent
Vekstfaktor
Rente
For flere eksempler og forklaringer se artikkelen Renter.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
b)
Malin lar pengene stå urørt i 5 år. Så setter hun inn 25 000 kroner til på kontoen sin.
Hvor mye vil Malin ha på kontoen 10 år etter konfirmasjonen?
Løsningsforslag b)
Jeg tenker:
Her deler vi problemet opp i to femårsperioder. Hver periode kan løses på tilsvarende måte som i deloppgave a). Vi regner igjen med
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Ved tilsvarende argumenter som i forrige oppgave, vet vi at Malin etter år har i banken. Så setter hun inn til, som gir en total på Disse pengene samler renter i år til. Etter dette er det på kontoen.
Svar: Cirka .
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefot En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Prosent
Vekstfaktor
Rente
Potens
Eksempel:
For flere eksempler og forklaringer se artikkelen Banksparing over flere år.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 4 (4 poeng) Nettkode: E-4C2U
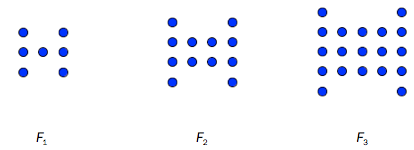
Ole lager figurer av runde perler. Ovenfor ser du tre figurer , og .
a)
Følg samme mønster, og tegn figuren .
Løsningsforslag a)
Jeg tenker:
Figurene består av et «
Kvadrat
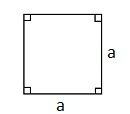
En firkant der alle sider er like lange og alle vinkler 90°.
Figuren består av én perle i midten, med to kolonner av tre perler på hver side. Neste figur består av fire perler i et kvadrat i midten, altså et kvadrat med sidelengde to, med to kolonner med fire perler på hver side. Helt tilsvarende består av et kvadrat med sidelengde tre i midten, og to kolonner med lengde fem på hver side. Kvadratet i midten øker med én i sidelengde for hver figur, og kolonnene øker med én i høyde. Derfor skal det være et kvadrat med sidelengde fire i , og på sidene skal det være to kolonner med lengde seks. Det vil se ut som under.
Svar: 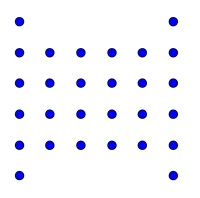
Mer om:
Denne oppgaven er om En firkant der alle sider er like lange og alle vinkler 90°. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.Kvadrat

Linje
For flere eksempler og forklaringer se artikkelen Et kvadrat.
b)
Sett opp en modell som viser hvor mange perler det vil være i figur uttrykt ved .
Løsningsforslag b)
Jeg tenker:
En modell i denne sammenhengen, er et uttrykk eller en
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Vi kan løse denne oppgaven på flere måter. For en matematisk forståelse for problemet, se alternativ løsning. Her løser vi ved å bruke
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi vet allerede hvor mange perler de fire første figurene inneholder; dette kan vi legge inn som en liste med punkter i GeoGebra. Videre skal vi finne en passende funksjon. Måten figurene er bygget opp på indikerer at antall perler vokser som et polynom av grad . Dette kan vi se ved å se at hvis hver figur bestod av et kvadrat med perler i hver side, så er antall perler , altså et andregradspolynom. Derfor skriver vi
RegPoly[Liste1, 2]
i “Skriv inn”-vinduet. Resultatet er vist under.
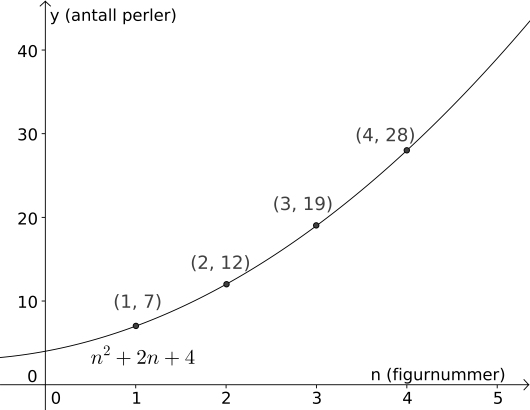
Dermed ser vi at er en god modell for antall perler.
Alternativ løsning
I deloppgave a) fant vi ut av hva systemet for å lage nye figurer var. I denne oppgaven skal vi bruke dette systemet til å finne ut hvor mange perler det er i figur , der er et hvilket som helst heltall større enn . I forrige oppgave fant vi ut at hver figur består av et “kvadrat”, pluss to “linjer” på siden.
I figur hadde kvadratet sidelengde , og linjene hadde lengde . I figur hadde kvadratet sidelengde , og linjene lenge . Det ser ut til at i figur , så har kvadratet i midten sidelengde , og linjene lengde . Dette stemmer også med figurene og . En linje med lengde bidrar med perler i figuren. I figur har vi to slike linjer, og antall perler i disse linjene til sammen erEt kvadrat med sidelengde bidrar med perler. (Dette er arealet av kvadratet.) Nå har vi funnet ut hvor mange perler det er i hver av delene av figur , og legger vi dem sammen, får vi svaret vi er ute etter. Det blir
Svar: Antall perler i figur er .
Mer om:
Denne oppgaven er om En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En firkant der alle sider er like lange og alle vinkler 90°.Linje
Kvadrat

For flere eksempler og forklaringer se artiklene Regresjon 1 ogAndregradslikninger.
c)
Bruk modellen til å bestemme hvor mange perler det vil være i figuren .
Løsningsforslag c)
Jeg tenker:
Vi kan bruke
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
I figur er det perler. I figur er det derfor perler.
Svar: perler
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk. Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.Funksjon
Formel
For flere eksempler og forklaringer se artikkelen Typer av funksjoner.
Oppgave 5 (4 poeng) Nettkode: E-4C2Z
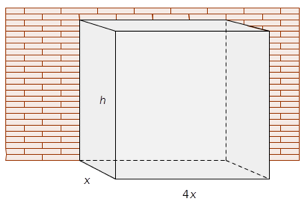
Du skal lage et fuglebur av hønsenetting. Buret skal ha form som et rett, firkantet prisme. Buret skal bygges langs en mur slik at muren utgjør den ene veggen. Buret skal stå på bakken og trenger ikke bunn.
Sett bredden av buret lik meter og høyden lik meter. Buret skal være fire ganger så langt som det er bredt. Se skissen ovenfor.
a)
Vis at overflaten m2 som skal lages av hønsenetting, er gitt ved
Løsningsforslag a)
Jeg tenker:
Fire sider av buret skal bestå av hønsenetting, nemlig taket, siden nærmest oss (hvis vi ser på buret som vist i tegningen), og de to sideflatene. Vi skal legge sammen arealet av disse.
Dimensjonene av figuren er vist under.
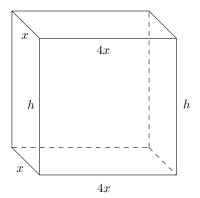
Taket av buret er et rektangel med sidelengder og . Arealet av taket er derfor . Fronten av buret er et rektangel med sidelengder og , og har dermed areal . De to sideflatene er rektangler med sidelengder og , og hver av dem har derfor areal . Det totale overflatearealet til den delen av buret som skal lages av hønsenetting, er derfor
Svar: .
Mer om:
Denne oppgaven er om Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og . Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°. Omkrets: Areal
Noen måleenheter for areal er m2, dm2 og cm2.Polynom
Rektangel

Areal:
For flere eksempler og forklaringer se artikkelen Overflatearealet til en terning.
For å øve mer, se oppgavesettet om overflateareal i Treningsleieren.
b)
Du skal bruke m2 hønsenetting.
Vis at høyden meter av buret da er gitt ved
Løsningsforslag b)
Jeg tenker:
Vi kjenner til uttrykket for overflatearealet til den dele av buret som skal lages og vi vet nøyaktig hvor mye høsenetting skal brukes.
Overflatearealet til den delen av buret som skal lages av hønsenetting, er og vi skal bruke nøyaktig hønsenetting. Nå har vi to uttrykk som bestemmer det samme tallet, og da må de uttrykkene være de samme. Derfor har vi at .
Vi vil finne den verdien for som passer inn i likningen . Det er to ukjente i likningen, både og ; siden vi er ute etter å finne uttrykt ved hjelp av , så bare antar vi at er et vanlig tall og at vi skal løse dette som en førstegradslikning (
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
Svar: Hvis vi løser ligningen for , så får vi at .
Mer om:
Denne oppgaven er om Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og . En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Areal
Noen måleenheter for areal er m2, dm2 og cm2.Polynom
Ligning
Funksjon
For flere eksempler og forklaringer se artikkelen Lineære likninger.
For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleieren.
c)
Hvordan må du lage buret for at volumet skal bli størst mulig?
Løsningsforslag c)
Jeg tenker:
Vi må finne et uttrykk for
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Buret har form som et rett
Prisme
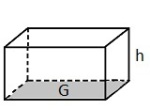
Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.
Har et prisme grunnflate G og høyde h, er volumet lik G · h.
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).

Dermed er volumet til buret lik . Dette er det vanskelig å lage en graf ut av, siden uttrykket avhenger av både og . Heldigvis fant vi i forrige oppgave at ; derfor er volumet av buret gitt ved Her ser vi at volumet bare avhenger av tallet . Nå kan vi tegne grafen i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
V(x) = 4*x^2*(40 - 4*x^2)/(6x)Vi drar til aksene slik at vi ser den interessante delen av
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Ekstremalpunkt[V, 0, 3]i “Skriv inn”-vinduet. Vi velger grensene og fordi vi ser at toppunktet ligger mellom disse -verdiene. Vi får dermed toppunktet som vist under.
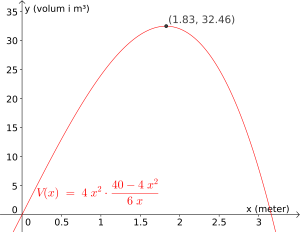
Dette betyr at når , så er volumet av buret lik , og dette er det største mulige volumet. Fra forrige oppgave får vi at høyden av buret må være
Svar: Buret får størst volum når og ; da er volumet .
Mer om:
Denne oppgaven er om Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3). Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Volum

Areal
Noen måleenheter for areal er m2, dm2 og cm2.Toppunkt

Funksjon
For flere eksempler og forklaringer se artiklene Tom forteller om volum og Topp- og bunnpunkter.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleieren.
Oppgave 6 (8 poeng) Nettkode: E-4C45
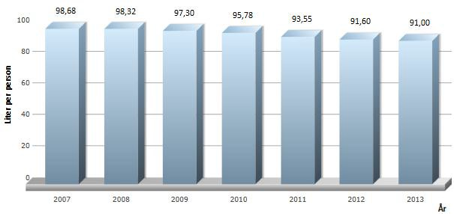
Diagrammet ovenfor viser hvor mange liter melk hver person i Norge drakk i gjennomsnitt hvert år i perioden 2007-2013.
Sett i 2007, i 2008 og så videre.
a)
Bruk opplysningene i diagrammet til å bestemme
- en lineær funksjon som viser hvordan forbruket av melk har endret seg i denne perioden
- en andregradsfunksjon som viser hvordan forbruket av melk har endret seg i denne perioden
Løsningsforslag a)
Jeg tenker:
Her skal vi bruke
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi skal finne funksjonsuttrykkene ved hjelp av
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
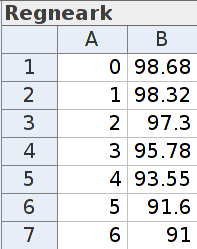
Deretter lager vi en liste med punkter ut i fra tabellen. Det gjør vi ved å markere tabellen, høyreklikke, og velge “Liste med punkt” i “Lag”-menyen. Listen blir hetende Liste1. Vi er først bedt om å lage en lineær funksjon som passer med dataene. Det gjør vi ved å skrive
f(x) = RegLin[Liste1]i “Skriv inn”-menyen. Vi høyreklikker på den resulterende funksjonen og klikker “Likning ” for å få funksjonsuttrykket på en mer kjent form.

Det er det samme når vi skal finne andregradsfunksjonen, bare at vi skriver
f(x) = RegPoly[Liste1, 2]i stedet.

Svar: Den lineære funksjonen er , mens andregradsfunksjonen er .
Mer om:
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og . En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen: Likningen kan løses ved hjelp av abc-formelen. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Regresjon
Polynom
Andregradslikning
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Regresjon 1. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
b)
Tegn grafene til funksjonene du fant i oppgave a) i et koordinatsystem for .
Løsningsforslag b)
Jeg tenker:
Vi bruker GeoGebra-filen fra deloppgave a).
Det eneste vi gjør er å justere aksene i filen fra deloppgave a). Vi husker å gi passende navn og enheter til aksene. Resultatet er vist under.
Svar: 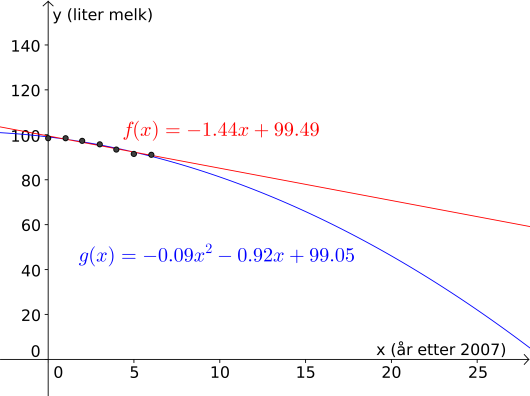
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Graf
Funksjon
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Koordinatsystem.
c)
Hvor mange liter melk vil hver person i Norge i gjennomsnitt drikke hvert år om ti år ifølge hver av de to funksjonene?
Løsningsforslag c)
Jeg tenker
«I år» betyr , så «om ti år» er i . Det tilsvarer .
Vi kalte den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
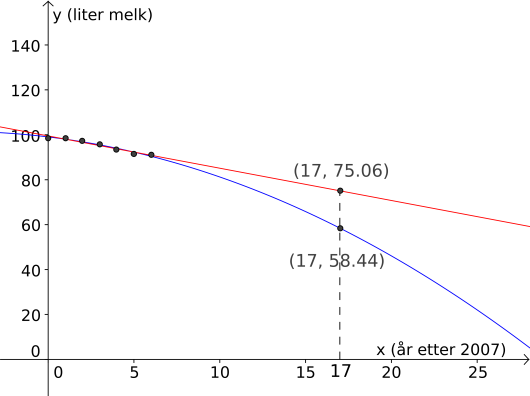
Her ser vi at antall liter er i følge den lineære modellen, og i følge andregradsmodellen.
Svar: i følge den lineære modellen, og i følge andregradsmodellen.
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Graf
Funksjon
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Hvorfor ser grafen ut som den gjør?. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
d)
Hvor mange liter vil forbruket per person avta med per år om ti år ifølge hver av de to funksjonene?
Løsningsforslag d)
Jeg tenker:
I den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
I den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
For andregradsfunksjonen må vi finne
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
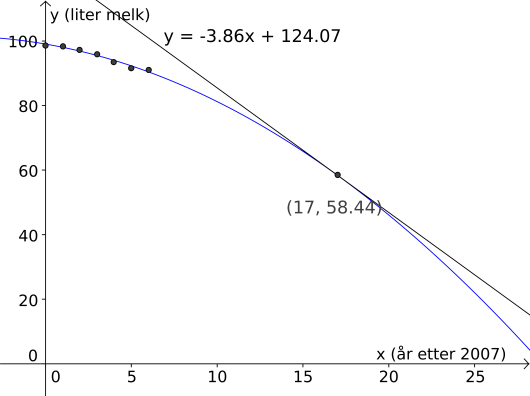
Stigningstallet til linjen er , så i følge denne modellen vil forbruket avta med per år i .
Svar: I følge den lineære modellen vil forbruket avta med per år i . I følge andregradsmodellen vil det avta med .
Mer om:
Denne oppgaven er om Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2. En funksjon har gjennomsnittlig vekstfart mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet. Lineære funksjoner er funksjoner som er skrevet på formen . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Stigningstall

Gjennomsnittlig vekstfart
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Tangent

Derivasjon
For flere eksempler og forklaringer se artiklene Å finne tangenten og Introduksjon til derivasjon - gjennomsnittlig og momentan vekstfart.
For å øve mer, se oppgavesettet om veksthastighet i Treningsleieren.
Oppgave 7 (8 poeng) Nettkode: E-4C6W
I displayet på en tredemølle kan farten justeres mellom 0 km/h og 20 km/h. Det er mistanke om at båndet på tredemøllen går for fort i forhold til farten som angis i displayet (angitt fart). En gruppe 2P-elever får i oppgave å undersøke dette.
Elevene måler at løpebåndet på tredemøllen er 3,25 meter langt. Når båndet har gått én runde, har man altså løpt 3,25 meter. For å undersøke sammenhengen mellom angitt fart og reell fart teller elevene antall runder båndet går i løpet av ett minutt ved ulike fartsangivelser.
| Angitt fart km/h | Antall runder i løpet av ett minutt | Reell fart km/h |
|---|---|---|
a)
Skriv av tabellen ovenfor i besvarelsen din, gjør beregninger, og fyll inn verdiene for reell fart i kolonnen til høyre.
Løsningsforslag a)
Jeg tenker
For hver runde båndet går, så har det beveget seg . Når vi har antall runder båndet går per minutt, kan vi dermed finne hvor fort båndet beveger seg. Vi kan gjøre oppgaven lettere ved å se at fart og antall runder per minutt er
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Det første vi gjør er å skrive av den oppgitte tabellen.
| Angitt fart km/h | Antall runder i løpet av ett minutt | Reell fart km/h |
|---|---|---|
I kolonnen til høyre skal vi skrive hvor fort båndet går, når antall runder per minutt står i kolonnen i midten. Vi viser to måter å gjøre dette på. De to måtene er essensielt like, men den første metoden sier litt mer om hvorfor utregningene er som de er, og den andre er raskere. Vi kan spare en del tid ved å bruke proposjonale størrelser, og denne metoden viser vi senere.
I den andre raden står det at båndet går runder på et minutt. Hver runde er , så runder tilsvarerDette gir en fart på per minutt. Vi skal omregne dette til kilometer per time. Før det første er , fordi det er meter i én kilometer. For det andre er ett minutt lik time. Derfor har vi
Derfor fyller vi inn på riktig plass i tabellen.
| Angitt fart km/h | Antall runder i løpet av ett minutt | Reell fart km/h |
|---|---|---|
Dette skal vi gjøre for de andre radene også. Det kan ta litt tid å gjøre disse utregningene om og om igjen, men det trenger vi ikke. Det som tar mest tid er å regne om fra meter per minutt til kilometer per time. For å konvertere, multipliserte vi først antall meter med for å få antall kilometer, og deretter dividerte vi antall minutter med for å få antall timer. Fordi brøken var i telleren, “flyttet” vi opp. Sluttresultatet er at vi multipliserte den opprinnelige farten med , og på denne måten kan vi konvertere all fart på formen m/min til km/t. For eksempel er 400 m/min lik .
Nå kan vi fortsette med tabellen vår. I den tredje raden står det 65 runder per minutt. Siden hver runde er meter langt, er 65 runder meter. Det gir en fart på meter per minutt, og av diskusjonen over vet vi at meter per minutt erkilometer per time. Derfor fyller vi inn i tredje rad.
| Angitt fart km/h | Antall runder i løpet av ett minutt | Reell fart km/h |
|---|---|---|
På tilsvarende måte regner vi ut at runder per minutt gir og runder per minutt gir Dette fyller vi inn i tabellen i henholdsvis fjerde og femte rad.
| Angitt fart km/h | Antall runder i løpet av ett minutt | Reell fart km/h |
|---|---|---|
Vi kan også løse problemet ved å se at antall runder per minutt og reell fart er proposjonale størrelser. Det betyr at
der er en konstant. Dette betyr at I tabellen ser vi at 18 runder per minutt gir i reell fart, så konstanten er Det betyr at antall runder per minutt tilsvarer farten . For eksempel gir 10 runder per minutt . Ut i fra dette finner vi tallene som skal inn i tabellen.Dette er de samme tallene som vi fikk over.
Svar:
| Angitt fart km/h | Antall runder i løpet av ett minutt | Reell fart km/h |
|---|---|---|
Mer om:
Denne oppgaven er om Proporsjon betyr at to forhold er like. Eksempel: a forholder seg til b som c forholder seg til d, Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Fart er tilbakelagt distanse per tidsenhet. Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund. Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.Proporsjon
Tabell

Fart
For flere eksempler og forklaringer se artikkelen Proporsjonalitet.
b)
Elevene vil lage en modell som viser den reelle farten km/h som funksjon av den angitte farten km/h.
Bestem den lineære funksjonen som passer best som modell for denne sammenhengen.
Bestem den potensfunksjonen som passer best som modell for denne sammenhengen.
Hvilken av disse to modellene mener du elevene bør velge? Begrunn svaret.
Løsningsforslag b)
Jeg tenker:
Den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
Her kan vi bruke både Excel og
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
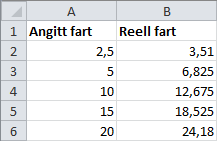
Vi vil ha tabellen inn i et
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
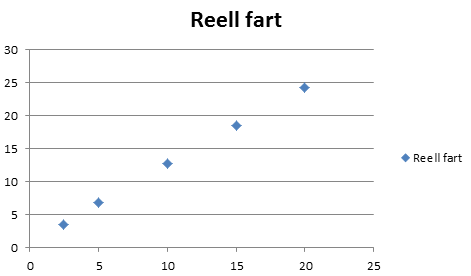
For å utføre
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
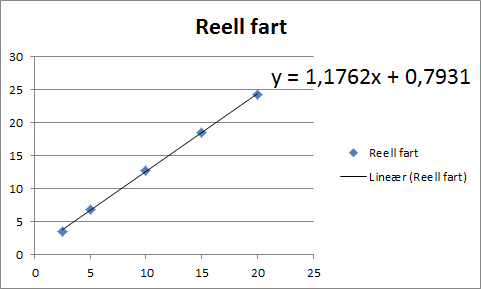
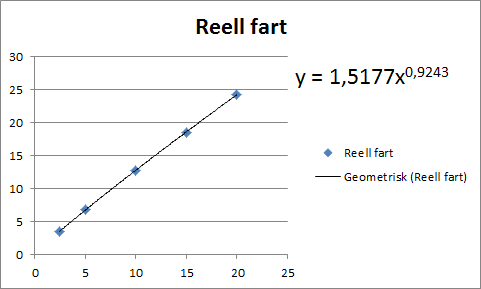
Dermed har vi funnet ut at den beste lineære funksjonen er og at den beste potensfunksjonen er Vi kan tegne funksjonene inn i GeoGebra for å sammenligne dem.
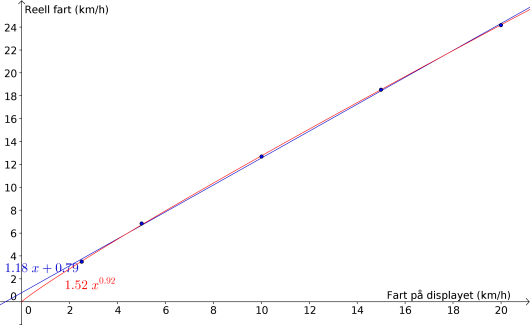
Her ser vi at funksjonene er nesten helt like overalt. Det største unntaket er at potensfunksjonen går gjennom origo, og at den lineære funksjonen ikke gjør det. Fordi funksjonene er ganske like ellers, er det lurt å la dette bestemme hvilken som passer best. Hvis displayet viser at man beveger seg i rundt når båndet står står stille, så passer den lineære funksjonen best, men hvis displayet starter på er potensfunksjonen best. Det er sannsynlig at tredemøllen starter på , så vi velger potensfunksjonen.
Svar: Den beste lineære funksjonen erog den beste potensfunksjonen erPotensfunksjonen er sannsynligvis best, fordi den starter i origo.
Mer om:
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner er funksjoner som er skrevet på formen .Regresjon
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Regresjon 2: Hva betyr det at en kurve "passer til dataene"?.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleieren.
c)
Henrik vil løpe i 15 km/h.
Hvilken fart bør han angi i displayet på tredemøllen ifølge modellen du valgte i oppgave b)?
Løsningsforslag c)
Jeg tenker:
Vi velger potensfunksjon som modell. Vi må finne ut hva skal være for at .
Vi valgte potensfunksjonen som modell. Vi har . Hvis er farten som er vist på displayet, så er den egentlige farten (i følge modellen vår). Vi vil finne ut hva displayet må vise () hvis den egentlige farten () skal være lik . Med andre ord må vi finne en slik at . Det kan gjøres grafisk i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
y = 15i “Skriv inn”-vinduet, og bruke skjæringsverktøyet for å finne skjæringspunktet mellom denne linjen og grafen. Prosedyren er for øvrig helt lik dersom vi hadde valgt den lineære funksjonen som modell. Under viser vi skjæringspunktene med begge grafene.
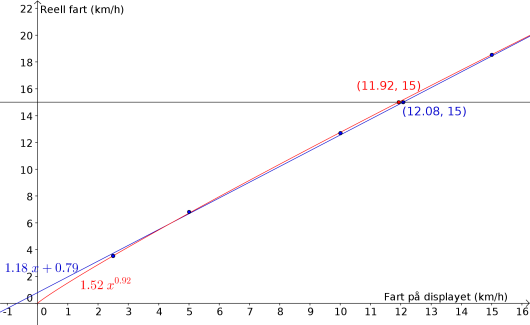
Det er det røde skjæringspunktet vi er interessert i. Der står det at ; det betyr at hvis vi vi skal jogge i , så skal det stå på displayet. Hadde vi valgt den lineære modellen, skulle det stått .
Svar: I følge potensfunksjonen skal det stå , og den lineære funksjonen gir . (Svaret avhenger av hvilken funksjon man valgte i forrige oppgave.)
Mer om:
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Lineære funksjoner er funksjoner som er skrevet på formen . Fart er tilbakelagt distanse per tidsenhet. Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund. Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.Skjæringspunkt

Graf
Linje
Potens
Eksempel: Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Fart
For flere eksempler og forklaringer se artikkelen Grafisk løsning av likningssett.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.
d)
Elevene vil lage et oppslag som skal henge ved siden av tredemøllen, slik at de som løper, kan finne den reelle farten.
Lag et forslag til oppslag.
Løsningsforslag d)
Jeg tenker:
Her skal vi lage et grafisk oppslagsverk som gjør det lett å se hvilken fart man skal ha. Vi kan for eksempel lage en graf eller en tabell.
Vi lager en
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Svar: 
Mer om:
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Tabell

Graf
Funksjon
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).




