Grafen til en funksjon
En av de enkleste metodene for å forstå en funksjon, er å tegne grafen til funksjonen. Vi tegner da hva slags verdier funksjonen får i et koordinatsystem og får et godt bilde av hvordan den oppfører seg.
Den enkleste – om ikke akkurat den mest elegante – metoden å tegne grafen til en funksjon på, gjennomgås allerede på ungdomsskolen:
|
Tegning av grafen til en funksjon .
|
Kurven vi får på denne måten, blir en god tilnærming til grafen. Desto flere
punkter vi velger, jo mer nøyaktig blir grafen. I de fleste tilfeller vi ser på er det imidlertid
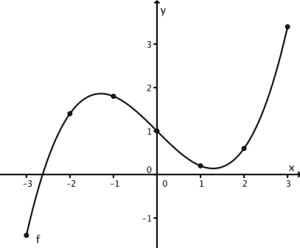
mer enn nok å ta med 7-8 punkter. På figuren under har vi tegnet grafen til funksjonen
over intervallet . Som tabellen viser, har vi valgt -verdiene .
I lynkurset "Funksjonsdrøfting" kan du lese mer om hvordan vi kan tegne grafer mer effektivt og få mer informasjon om funksjonen.
Del på Facebook