
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

Mat1015 2013 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Fotball: http://www.vg.no/sport/fotball/norsk/artikkel.php?artid=10078823 (12.02.2013)
- Tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4BQD
I en klasse er det 20 elever. Nedenfor ser du hvor mange dager hver av elevene var borte fra skolen i løpet av et skoleår.
0 3 2 7 2 0 0 11 4 3 28 1 0 3 2 1 1 0 0 32
a)
Bestem gjennomsnitt, median og typetall for elevenes fravær dette skoleåret.
Løsningsforslag a)
Jeg tenker
Her må vi huske hva
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
For å finne
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Videre skal vi finne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Det er 20 elever til sammen. Gjennomsnittet er derfor
(Her har vi telt at det var 3 elever som hadde 1 fraværsdag, 3 som hadde 2 fraværsdager, og så videre.)
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Svar: Medianen er , gjennomsnittet er og typetallet er 0.
Mer om statistikk
Denne oppgaven er om
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Flere forklaringer og eksempler om median finner vi i artikkelen Median, om gjennomsnitt finner vi i artikkelen Gjennomsnitt, og om typetall finner vi i artikkelenTypetall.
For å øve mer, se oppgavesettet om media, gjennomsnitt og typetall i Treningsleieren.
b)
Dersom du skulle presentere et sentralmål for klassens fravær dette skoleåret, ville du da brukt gjennomsnitt eller median? Forklar hvorfor.
Løsningsforslag b)
Jeg tenker
Meningen med et sentralmål er at det skal fungere som en god estimator på fremtidig fravær. Vi kan velge mellom
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Svar: To av elevene hadde veldig høyt fravær, som drar
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Mer om statistikk
Denne oppgaven er om
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Flere forklaringer og eksempler om median finner man i lynkurset Median, om gjennomsnitt finner man i lynkurset Gjennomsnitt, og om typetall finner man i lynkurset Typetall.
For å øve mer, se oppgavesettene om median, gjennomsnitt og typetall i Treningsleieren.
Oppgave 2 (1 poeng) Nettkode: E-4BQG
Regn ut og skriv svaret på standardform
Løsningsforslag
Jeg tenker
Vi skal finne produktet av to
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Vi kan bytte om på rekkefølgen i produktet. Vi vil ha alle tierpotenser for seg selv. Da kan vi skrive tallet som Potensreglene sier at vi kan legge sammen eksponenter hvis potensene har samme grunntall. Derfor får vi . Nå kan vi skrive tallet som , og dette er nesten på standardform. Vi ser at ; tallet foran tierpotensen i er ikke mellom 1 og 10, så vi må faktorisere ut en tier. Vi ser at , så vi får og dette er på standardform.
Svar: .
Mer om potenser
Denne oppgaven er om standardform,
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
For flere eksempler og forklaringer se artikkelen Tall på standardform, for potensregeler se artikkelen Potenser med samme grunntall, og mer om faktorisering finner du i artikkelen Primtall og faktoriserin.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Oppgave 3 (3 poeng) Nettkode: E-4BQI
Skriv så enkelt som mulig
a)
Løsningsforslag a)
Jeg tenker
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Vi husker at . Når vi skal forenkle potensuttrykk, er det lurt å gjøre om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Svar: 4
Mer om
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
For flere eksempler og forklaringer på potenser se artikkelen Rask gjennomgang av regneregler for potens og røtter.
For å øve mer, se oppgaveteksten om potenser i Treningsleieren.
b)
Løsningsforslag b)
Jeg tenker
Vi skal regne med
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Vi starter med . Vi kan multiplisere
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Svar: .
Mer om
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
For flere eksempler og forklaringer på potenser se lynkurset Potenser og røtter, og for brøk se lynkurset Brøk.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 4 (2 poeng) Nettkode: E-4BQL
Per satte inn 200 000 kroner i banken 1. januar 2008. Renten har vært 4,65 % per år.
Sett opp et uttrykk som viser hvor mye penger Per har fått i rente i løpet av de fem årene fra 1. januar 2008 til 1. januar 2013.
Løsningsforslag
Jeg tenker
Hvis noe øker med , så er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Her skal vi bruke
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Rente
Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.
Se renteformel og rentefot
Svar: , eller .
Mer om
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Rente
Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.
Se renteformel og rentefot
For flere eksempler og forklaringer på prosent se lynkurset Prosent, og for rente se lynkurset Rente.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 5 (6 poeng) Nettkode: E-4BQN
Ifølge en undersøkelse kan et 20 måneder gammelt barn i gjennomsnitt 300 ord. Et 50 måneder gammelt barn kan i gjennomsnitt 2100 ord.
a)
Framstill opplysningene ovenfor som punkter i et koordinatsystem med måneder som enhet langs - aksen og ord som enhet langs - aksen.
Trekk en rett linje gjennom punktene.
Løsningsforslag a)
Jeg tenker
Her skal vi tegne et
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Det første vi gjør, er å tegne et
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
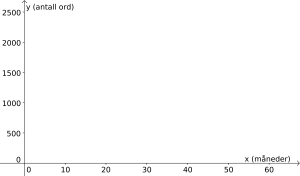
Nå skal vi tegne inn punktene. Et barn på 20 måneder kan i gjennomsnitt 300 ord, og det tilsvarer punktet i koordinatsystemet. Tilsvarende tegner vi inn punktet .

Til slutt tegner vi den rette streken mellom punktene med linjal. Resultatet er vist under.
Svar: 
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Førstekoordinat
Førstekoordinat er et punkts verdi langs første-aksen, eller x-aksen i koordinatsystemet. Når et punkt beskrives med et tallpar (7,3), er førstekoordinaten det første tallet i tallparet, 7 i dette eksempelet.
Andre koordinat
Andre koordinat er et punkts verdi langs andreaksen i koordinatsystemet.
Når et punkt beskrives med et tallpar (5,3), er andrekoordinaten det andre tallet i tallparet, 3 i dette eksempelet.
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
For flere eksempler og forklaringer på funksjoner se artiklene Koordinatsystem og Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
Visste du at
Hvis en rett linje går gjennom de to forskjellige punktene og , så er likningen til linjen Formelen over kalles topunktsformelen. I denne oppgaven gir topunktsformelen at likningen til linjen er og vi kunne brukt den for å løse neste oppgave.
b)
Linjen i oppgave a) kan brukes som modell for sammenhengen mellom et barns alder og hvor mange ord barnet kan.
Bruk linjen til å anslå hvor mange ord et 35 måneder gammelt barn i gjennomsnitt kan.
Løsningsforslag b)
Jeg tenker
Vi skal finne ut hvor den loddrette linjen krysser linjen fra deloppgave a). Vi skal finne
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Vi finner i koordinatsystemet vårt, og går loddrett oppover til vi treffer linjen. Da er
Andre koordinat
Andre koordinat er et punkts verdi langs andreaksen i koordinatsystemet.
Når et punkt beskrives med et tallpar (5,3), er andrekoordinaten det andre tallet i tallparet, 3 i dette eksempelet.

Vi ser at koordinaten til skjæringspunktet er .
Svar: ord
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Førstekoordinat
Førstekoordinat er et punkts verdi langs første-aksen, eller x-aksen i koordinatsystemet. Når et punkt beskrives med et tallpar (7,3), er førstekoordinaten det første tallet i tallparet, 7 i dette eksempelet.
Andre koordinat
Andre koordinat er et punkts verdi langs andreaksen i koordinatsystemet.
Når et punkt beskrives med et tallpar (5,3), er andrekoordinaten det andre tallet i tallparet, 3 i dette eksempelet.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
For flere eksempler og forklaringer på funksjoner se lynkurset om Rette linjer (lineære funksjoner) og Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
c)
Bestem et matematisk uttrykk for modellen. Kommenter modellens gyldighetsområde.
Løsningsforslag c)
Jeg tenker
Dette er en rett linje. Vi kjenner det generelle funksjonsuttrykket til en rett linje (lineær funksjon). Vi må finne
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Funksjonsuttrykket til en rett linje er på formen . Vi kan finne dette uttrykket ved å finne
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Formelen er ikke gyldig der den gir negative -verdier, altså der , fordi det ikke er mulig å kunne et negativt antall ord.
Svar: Likningen til linjen er . Grafen gjelder ikke der , altså der .
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Førstekoordinat
Førstekoordinat er et punkts verdi langs første-aksen, eller x-aksen i koordinatsystemet. Når et punkt beskrives med et tallpar (7,3), er førstekoordinaten det første tallet i tallparet, 7 i dette eksempelet.
Andre koordinat
Andre koordinat er et punkts verdi langs andreaksen i koordinatsystemet.
Når et punkt beskrives med et tallpar (5,3), er andrekoordinaten det andre tallet i tallparet, 3 i dette eksempelet.
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
For flere eksempler og forklaringer på funksjoner se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
Oppgave 6 (2 poeng) Nettkode: E-4BQS
| Lommepenger (kroner) | Antall elever |
Tabellen ovenfor viser hvor mye lommepenger elevene ved en skole får en måned.
Hvor mye får elevene ved skolen i gjennomsnitt i lommepenger denne måneden?
Løsningsforslag
Jeg tenker
Vi jobber med gruppert informasjon. Da antar vi at tallene er jevnt fordelt utover gruppene, slik at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Det er 30 elever som fikk mellom 0 og 300 kroner i lommepenger. Vi antar at elevene fikk lommepenger jevnt fordelt utover dette intervallet, slik at de
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
| 1 | 5 | 4 | 5 | 0 | = | 6 | 7 | 5 | 0 | |||
| 0 | 0 | |||||||||||
| 7 | 5 | |||||||||||
| 6 | 0 | |||||||||||
| 6 | 7 | 5 | 0 |
Vi regner ut telleren i uttrykket for gjennomsnittet.
| 4 | 5 | 0 | 0 | ||
| + | 6 | 7 | 5 | 0 | |
| + | 3 | 7 | 5 | 0 | |
| = 1 | 5 | 0 | 0 | 0 |
Nevneren er , så gjennomsnittet blir
Svar: 300 kroner, gitt at informasjonen er jevnt fordelt i klassene.
Mer om
Denne oppgaven er om
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere eksempler og forklaringer på gjennomsnitt se lynkurset Gjennomsnitt, og for statistikk se lynkurset Statistikk. For flere forklaringer og eksempler om addisjon og multiplikasjon se artiklene Addisjon og Multiplikasjon.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Oppgave 7 (2 poeng) Nettkode: E-4BQU
Beskriv en praktisk situasjon der funksjonen gitt ved kan brukes som modell.
Løsningsforslag
Jeg tenker
Dette er en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Funksjonen er en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Prosentfaktor
En prosentfaktor er et prosenttall skrevet om til et desimaltall.
Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Én situasjon er der er antall radioaktive isotoper i et stoff etter år. En annen situasjon er der er mengden væske i en tank etter måneder, og at av væsken fordamper hver måned. Det kan også tenkes at er verdien til et produkt (for eksempel en bil) i år etter man kjøpte den.
Mer om
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
For flere eksempler og forklaringer se artikkelen Eksponentiallikning og lynkursene Potenser og Prosent.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 8 (4 poeng) Nettkode: E-4BQW
Viktig kommentar: Omforming til og fra binære tall er ikke lenger med i læreplanen for 2P.
a)
Skriv tallene 11, 22 og 44 i totallsystemet.
Løsningsforslag a)
Jeg tenker
(NB! Omforming til og fra binære tall er ikke lenger med i læreplanen for 2P.) Hvis vi har tallet , der , , og er enten 1 eller 0, så er tallet på binærform. For eksempel har tallet binærform 1001. Alle tall kan skrives på denne måten.
Vi starter med 11. Vi vet at og at . Vi kan skrive tallet på formen . Derfor består binærformen av 11 av fire sifre, der det første sifferet er 1. Videre kan vi skrive 3 som . Totalt kan vi skrive 11 som , som er tallet 1011 i totallsystemet.
Videre prøver vi oss på 22. Vi vet at er en største toerpotensen som er mindre enn 22. Vi har , og 6 kan skrives som , så vi kan skrive 22 som , eller . I totallsystemet er dette 10110.
Vi gjør det samme med 44. Vi har at , og , så . I totallsystemet er dette 101100.
Svar:, , og .
Mer om
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
For flere eksempler og forklaringer på potenser se lynkurset Potenser, for tallsystemer se lynkurset Tallsystemer, og for totallssystemet se lynkurset Totallssystemet.
b)
Formuler en regel for hvordan vi dobler et tall i totallsystemet.
Løsningsforslag b)
Jeg tenker
(NB! Omforming til og fra binære tall er ikke lenger med i læreplanen for 2P.) Vi skrev doblede tall på totallsystemet i forrige oppgave, og vi kan se om det er et system der.
I forrige oppgave regnet vi ut at , , og . Hver gang vi doblet tallet, altså hver gang vi multipliserte tallet med 2, la vi bare på en null i totallsystemet. Dette er det samme som å multiplisere med 10 i titallsystemet – vi har at , , og så videre. Effekten er den samme fordi .
Svar: Hvis man dobler et tall i totallsystemet, legger man til en null på slutten av tallet.
Mer om
For flere eksempler og forklaringer på potenser se artikkelen Potenser med samme grunntall, for tallsystemer se artikkelen Tallsystemet vårt - og andre tallsystemer, og for totallssystemet se artikkelen 2-tallsystem (binært system), og for titallsystemet se artikkelen Titallsystemet.
Visste du at
Det binære tallsystemet, altså totallsystemet, er veldig nyttig. Vi bruker det binære tallsystemet i datamaskiner. Det er (blant annet) fordi tall i en datamaskin bare er forskjellige elektriske spenninger, og det er mye mer robust å dele spenningsspektret inn i to deler (0 og 1) enn å dele det inn i 10. Men totallsystemet er ikke bare fryd og gammen; tallet har nemlig ikke en endelig desimalutvikling i totallsystemet. Mer spesifikt er lik (Dette skriver vi noen ganger som .) Det betyr at vi ikke kan representere det enkle tallet eksakt på datamaskin, i hvert fall ikke hvis vi ikke bruker andre løsninger enn direkte representasjon. Grunnen til at vi kan skrive med endelig antall desimaler i titallsysemet, er fordi er en brøk med 5 i nevneren, og 5 har bare faktorer som dividerer 10. Derimot har ikke 5 noen faktorer som deler 2. Derfor kan vi heller ikke skrive , , og så videre, med endelig antall desimaler i totallsystemet. Vi kan heller ikke skrive eller med endelig antall desimaler i titallsystemet.
c)
Tallene og er skrevet i tretallsystemet.
Hvilket tall i tretallsystemet er tre ganger så stort som tallet ? Hvilket tall i tretallsystemet er en tredjedel av tallet ?
Løsningsforslag c)
Jeg tenker
(NB! Omforming til og fra binære tall er ikke lenger med i læreplanen for 2P.) På samme måte som at fordobling i totallsystemet legger til en 0, så vil tredobling i tretallsystemet også legge til en 0.
Da vi doblet et tall i totallsystemet, la vi på en 0 på slutten av tallet. På tilsvarende måte kan vi ta bort en 0 hvis vi dividerer med . Dette skjer også med multiplikasjon og divisjon med 10 i titallsystemet; og . Det er det samme med tretallsystemet og multiplikasjon og divisjon med 3. Hvis vi multipliserer med 3 vil vi derfor få , og hvis vi dividerer med 3 får vi .
Svar: Hvis vi multipliserer med 3 får vi , og hvis vi dividerer med 3 får vi .
Mer om
For flere eksempler og forklaringer på tallsystemer se lynkurset Tallsystemet vårt - og andre tallsystemer.
DEL 2 Med hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4BR1

Ovenfor ser du hvor mange utenlandske spillere som spilte i den norske eliteserien hvert år i perioden 2000–2012.
Bestem gjennomsnitt og standardavvik for dette datamaterialet.
Løsningsforslag
Jeg tenker
Her kan vi bruke regneark.
Vi bruker Excel. Det første vi gjør er å legge inn all informasjonen fra tabellen. I tabellen under har vi ikke tatt med hvilket år som antallet spillere tilsvarer, for dette er ikke nødvendig informasjon når vi skal regne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
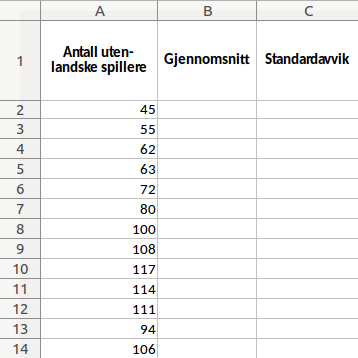
All informasjonen ligger nå i rutene fra og med A2 til og med A14. For å regne gjennomsnitt, skriver vi
=GJENNOMSNITT(A2:A14)og for å finne standardavviket, skriver vi
=STDAV.P(A2:A14)Vi bruker STDAV.P fordi vi vil regne ut standardavviket for hele datasettet. Hvis vi hadde brukt STDAV, ville vi fått estimerte verdier basert på utvalg. Nå ser tabellen vår slik ut.
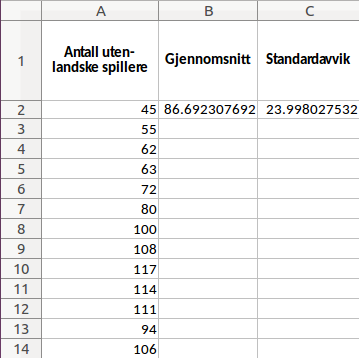
Dermed er gjennomsnittet av antall utenlandske spillere i perioden 2000–2012 lik cirka , mens standardavviket er rundt 24.
Svar: Gjennomsnittet er cirka , mens standardavviket er rundt 24.
Mer om
Denne oppgaven er om
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere eksempler og forklaringer på gjennomsnitt se lynkurset Gjennomsnitt, og for standardavvik se lynkurset Varians og standardavvik . Lynkurset om regneark er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Oppgave 2 (2 poeng) Nettkode: E-4BRX
| Antall elever | |
| Går | 4 |
| Sykler | 7 |
| Kjøre privat bil | 3 |
| Tar buss | 10 |
| Tar tog | 6 |
I tabellen ovenfor ser du hvordan elevene i en klasse kommer seg til og fra skolen. Bruk et sektordiagram til å presentere datamaterialet fra tabellen.
Løsningsforslag
Jeg tenker
Her kan vi bruke regneark.
Vi bruker Excel. Det første vi gjør er å kopiere av tabellen til regnearket.

Nå kan vi lage sektordiagrammet. Vi går i “Sett inn”-menyen og velger sektordiagram.
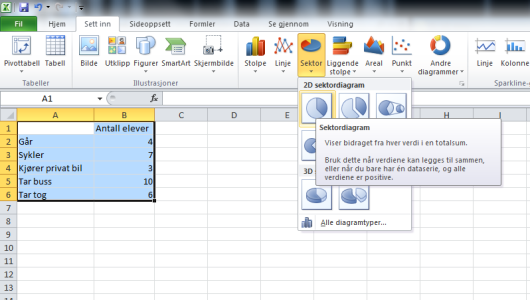
Resultatet er vist under.
Svar: 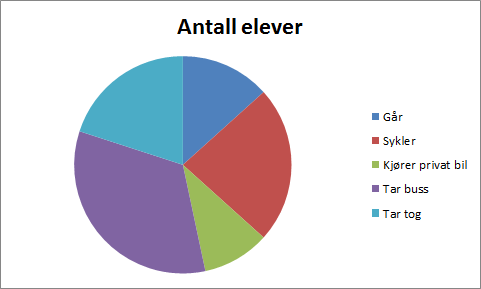
Mer om
Denne oppgaven er om regneark,
Sektordiagram
Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere eksempler og forklaringer på sektordiagram se lynkurset Sektordiagram. Lynkurset om regneark er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om presentasjonsformer i Treningsleieren.
Oppgave 3 (4 poeng) Nettkode: E-4BS9
I et atomkraftverk omdannes radioaktive atomkjerner. I omdanningen forsvinner noe av massen fra atomkjernene, og energi blir frigitt.
Når massen kilogram forsvinner fra atomkjernene, er den frigitte energien, Joule (J), gitt ved
Konstanten har verdien
a)
Hvor mye energi blir frigitt når en masse på kg forsvinner fra atomkjernene?
Løsningsforslag a)
Jeg tenker
Her skal vi sette inn verdier i
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Vi har , der er massen i kilogram, og . Tallet er den frigitte energien i Joule (J) når massen forsvinner fra atomkjernene. I vårt tilfelle er , så energien i J blir
Svar: .
Mer om
Denne oppgaven er om potenser med
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
For flere eksempler og forklaringer på potenser se lynkurset Potenser.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Visste du at
Likningen er kjent som masseenergiloven, og den ble utledet av Einstein i 1905. Konstanten er et veldig stort tall, og likningen viser hvor enormt mye energi som ligger i massen rundt oss. Det er altså dette prinsippet som ligger bak atomkraft.
b)
En norsk husholdning har et årlig energiforbruk på J
Hvor mye masse må forsvinne for å gi nok energi til en norsk husholdning i et år?
Løsningsforslag b)
Jeg tenker
Her skal vi finne den massen som skal til for å få .
Vi vil finne tallet energien som blir sluppet løs fra materie blir lik . Dermed skal vi finne tallet som passer inn i ligningen Her er bare en konstant, og da kan vi dividere med og forkorte. Vi får Nå kan vi sette inn . Da får vi Vi trenger altså masse for å gi nok energi til en norsk husholdning i et år. Det er én tusendels gram.
Svar: .
Mer om
Denne oppgaven er om potenser med
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
For flere eksempler og forklaringer på potenser se lynkurset Potenser med samme grunntall.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 4 (10 poeng) Nettkode: E-4BSK
| Årstall | 1985 | 1990 | 1995 | 2000 | 2005 | 2010 |
|
Prosent mannlige røykere |
42 | 37 | 34 | 31 | 25 | 19 |
Tabellen ovenfor viser hvor mange prosent av norske menn i alderen 16–74 år som røykte hver dag noen år i perioden 1985–2010.
Sett i 1985, i 1990 og så videre, og bruk opplysningene i tabellen til å bestemme
a)
1) en lineær modell som viser hvordan andelen mannlige røykere har endret seg
2) en eksponentiell modell som viser hvordan andelen mannlige røykere har endret seg
Løsningsforslag a)
Jeg tenker
Vi kan bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Først må vi legge inn punktene i et regneark i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
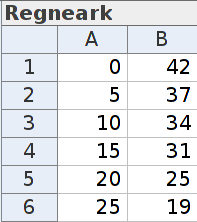
Videre markerer vi tabellen vår, høyreklikker, og velger “Liste med punkt” under “Lag liste”-menyen. Listen blir hetende Liste1. Vi tilpasser aksene slik at vi ser alle punktene. Nå skal vi lage en lineær modell og en eksponentiell modell. Det gjør vi ved å skrive henholdsvis
f = RegLin[Liste1]og
g = RegEksp[Liste1]i “Skriv inn”-vinduet. (Vi hadde ikke trengt å navngi funksjonene, men det er beleilig når vi skal bruke dem.) Nedenfor viser vi henholdsvis den lineære og den eksponentielle modellen. For å få den lineære modellen på en kjent form, høyreklikker vi på den og velger “Likning ”.


Her ser vi at den lineære modellen er , mens den eksponentielle modellen er .
Svar: Den lineære modellen er , mens den eksponentielle modellen er .
Mer om
Denne oppgaven er om
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
For flere eksempler og forklaringer se artikkelen Hva er matematisk modellering?.
For å øve mer, se oppgavesettet om modellering i Treningsleieren.
b)
Hvor mange prosent av norske menn i alderen 16–74 år vil være røykere i 2020 ifølge hver av de to modellene i oppgave a)?
Løsningsforslag b)
Jeg tenker
Vi må finne funksjonsverdiene til modellene våre i 2020.
Dette regner vi ut i fra funksjonene vi fant i forrige oppgave. Vi kan gjøre det på kalkulator, men det tar kortere tid å bare bruke GeoGebra-filen fra forrige oppgave. Året 2020 tilsvarer . Vi kalte den lineære og den eksponentielle funksjonen for henholdsvis og , og da er alt vi trenger å gjøre å skrive
f(35)for å finne verdien for den lineære modellen, og tilsvarende for . Vi kan som nevnt også gjøre det med kalkulator, og resultatene blir de samme: og Derfor gir den lineære modellen at cirka av mennene røyker hver dag i 2020, mens den eksponentielle modellen angir cirka .
Svar: Den lineære modellen gir cirka , og den eksponentielle gir cirka .
Mer om
Denne oppgaven er om
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere eksempler og forklaringer på matematiske modeller se artikkelen Å lage en matematisk modell.
For å øve mer, se oppgavesettet om modellering i Treningsleieren.
c)
Når vil andelen mannlige røykere bli lavere enn 5 % ifølge hver av de to modellene i oppgave a)?
Løsningsforslag c)
Jeg tenker
Hvis vi skal finne ut når den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vi vil finne ut hvor og krysser linjen . Vi bruker GeoGebra-filen fra de forrige oppgavene, og tar begge funksjonene på én gang. Først lager vi linjen ved å skrive
y = 5i “Skriv inn”-vinduet. Vi finner skjæringspunktene ved å klikke på punktene der linjen treffer de to grafene.

Her ser vi at den lineære modellen krysser linjen der , og den eksponentielle funsjonen krysser linjen der . Den lineære modellen sier derfor at det går cirka år før røykingen når under , mens den eksponentielle modellen sier at det vil gå cirka 73 år. Det gir årstall på henholdsvis 2027 og 2058.
Svar: Den lineære modellen gir cirka 2027, og den eksponentielle modellen gir cirka 2058.
Mer om
Denne oppgaven er om
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
or flere eksempler og forklaringer på matematiske modeller se artikkelen Hva er matematisk modellering?, og for funksjoner se lynkurset Funksjoner (del II).
For å øve mer, se oppgavesettet om modellering i Treningsleieren.
d)
Kommenter modellenes gyldighetsområde.
Løsningsforslag d)
Jeg tenker
Her skal vi finne ut av hvilke tidsperioder de forskjellige modellene gir mest mening.
Den lineære modellen gjelder åpenbart ikke der den går under -aksen, for vi kan ikke ha et negativt antall røykere. Videre vil det nok ikke være 0 røykere rundt år 2035, som modellen antyder, med mindre vi får nye lovgivninger. Derfor gir nok gyldighetsområdet for den lineære modellen seg i god tid før .
Den eksponentielle modellen viser en utflatning av røykere, i stedet for en brå slutt. I naturen er slike modeller ofte gode, og det er vanskelig å si noe på gyldighetsområdet uten å spekulere i fremtidige lovgivninger eller trender.
Svar: Den lineære modellen gir en for rask nedgang i røyking, og har et mindre gyldighetsområdet enn den eksponentielle modellen.
Mer om
Denne oppgaven er om
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Definisjonsmengde
En funksjon tar verdier fra en bestemt mengde, og denne mengden kalles definisjonsmengden til funksjonen.
Eksempel:
har definisjonsmengde . Merk at funksjonen ikke kan være definert i fordi vi ikke kan dele på .
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer på funksjoner se lynkurset Funksjoner (del II), og for matematiske modeller se artikkelen Hva er matematisk modellering?.
Oppgave 5 (6 poeng) Nettkode: E-4BSX
Runar observerer en bakteriekultur i to døgn. Når han begynner observasjonene, er det 1000 bakterier i bakteriekulturen. Det viser seg at antall bakterier dobles hver sjette time. Etter 6 h er det 2000 bakterier i bakteriekulturen, etter 12 h er det 4000 bakterier i bakteriekulturen, osv.
a)
Hvor mange bakterier vil det være i bakteriekulturen etter 24 h?
Løsningsforslag a)
Jeg tenker
Antallet bakterier dobles hver sjette time, så antallet skal dobles to ganger i perioden fra 12 timer til 24 timer.
Etter 12 timer er det 4 000 bakterier i bakteriekulturen, og antallet skal dobles hver sjette time. Derfor er det bakterier etter 18 timer, og bakterier etter 24 timer.
Svar: 16 000 bakterier
Mer om
Denne oppgaven er om
Doble
Doble betyr å legge til like mye som en allerede har. Det er det samme som å multiplisere med 2.
For flere eksempler og forklaringer på eksponentialfunksjoner se artikkelen Johannes viser eksponential- og logaritmefunksjoner.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleieren.
b)
Sett opp en modell som viser hvordan antall bakterier endrer seg i løpet av de to døgnene.
Løsningsforslag b)
Jeg tenker
Dette kan vi gjøre med
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi kan finne modellen med hjelp fra GeoGebra.
La være antall timer som har gått, og la være antall bakterier etter timer. Vi vet at når , så er , og at dobler seg hver gang øker med 6. Da har vi at og så videre. Vi kan legge dette inn i et regneark i GeoGebra. Vi velger “Regneark” i “Vis”-menyen, og skriver -verdier i første kolonne og -verdier i andre kolonne.
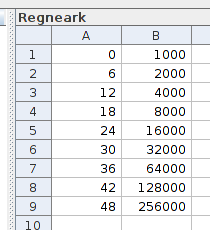
Vi har fylt ut -verdier helt opp til 48 fordi eksperimentet går over to døgn. Videre lager vi en liste ut av disse punktene; det gjør vi ved å markere tabellen, høyreklikke og velge “Liste med punkt” i “Lag”-menyen. Listen blir hetende Liste1. Nå kan vi finne den eksponentielle modellen ved å skrive
RegEksp[Liste1]i “Skriv inn”-vinduet. Da får vi følgende funksjon.

Funksjonsuttrykket til funksjonen er , og dette er modellen vår. Denne funksjonen passer nøyaktig inn med punktene vi har; det er fordi veksten til antall bakterier er eksponentiell (altså at den øker med en viss prosentandel ved hver tidsenhet), og modellen vår er også eksponentiell.
Svar: , hvis er antall bakterier etter timer.
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
For flere eksempler og forklaringer på matematiske modeller se lynkurset Kultur og modellering, for funksjoner se lynkurset Funksjoner (del II), og for regresjon se lynkurset Regresjon.
Visste du at
Vi kan også finne modellen med regning. La være antall bakterier i bakteriekulturen etter timer. (Det vil si at når øker med 1, så går vi 6 timer fram i tid.) Vi vet at bakteriekulturen starter med 1 000, så . Videre skal bakteriekulturen doble seg for hver . Siden det gir en
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
c)
Hvor mange prosent øker antall bakterier med per time?
Løsningsforslag c)
Jeg tenker
Vi kan bruke modellen fra deloppgave b) og vi skal se på
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Fra deloppgave b) vet vi at antallet bakterier etter timer er . Tallet er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar:
Mer om
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
For flere eksempler og forklaringer på prosent se lynkurset Prosent, for funksjoner se lynkurset Funksjoner og for potenser se lynkurset Potenser.
d)
Hvor mange bakterier vil det være i bakteriekulturen etter 40 h?
Etter hvor mange timer vil det være 50 000 bakterier i bakteriekulturen?
Løsningsforslag d)
Jeg tenker
Dette bruker vi modellen vår til. Vi skal finne
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
I følge modellen vår vil det være bakterier etter timer; det betyr at det etter 40 timer vil være bakterier. Dette tallet kan vi finne ved å skrive
B(40)i GeoGebra-filen vår. Da får vi cirka .
Videre skal vi finne ut når det er 50 000 bakterier i bakteriekulturen, altså finne den -en slik at . Det gjør vi ved å finne skjæringspunktet mellom grafen til og linjen . Vi lager linjen ved å skrive
y=50000Vi finner
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

Her ser vi at skjæringspunktet har koordinater på cirka . Det betyr at , så etter cirka 34 timer vil det være 50 000 bakterier i bakteriekulturen. Vi merker oss at i de 6 timene mellom 34 og 40, så øker bakteriekulturen fra cirka 50 000 til cirka 100 000, og det passer med at bakteriekulturen dobles hver sjette time.
Svar: Etter 40 timer er det bakterier, og etter cirka 34 timer er det 50 000 bakterier.
Mer om
Denne oppgaven er om
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer på funksjoner se lynkurset En video om funksjoner og artikkelen Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.
Oppgave 6 (6 poeng) Nettkode: E-4BT5
I en undersøkelse ble 30 elever spurt om hvor lang tid de bruker på å komme seg til og fra skolen hver dag. Elevene oppga tiden i minutter. Resultatet av undersøkelsen er vist nedenfor.
28 56 12 16 34 78 64 18 10 21
32 26 54 62 64 70 50 44 70 86
16 20 38 14 80 24 20 32 14 10
a)
Lag et klassedelt materiale av tallene ovenfor. La den første klassen starte i 10, og la alle klassene ha klassebredde 10.
Løsningsforslag a)
Jeg tenker
Vi skal lage en liste over hvor mange som bruker mellom 10 og 20 minutter for å komme seg til skolen, hvor mange som bruker mellom 20 og 30 minutter, og så videre.
Vi skal lage et klassedelt materiale, der den første klassen starter i 10, og alle klassene har klassebredde 10. Det gir klassene , , og så videre, opp til , siden ingen bruker flere enn 90 minutter. Vi skal skrive opp hvor mange som faller innenfor de diverse klassene. For å gjøre det, kan vi for eksempel gå gjennom hvert tall og finne ut hvilken klasse tallet tilhører.
Vi er kun ute etter hvor mange som er i hver kategori. Nå kan vi sette opp det klassedelte materialet som under.
Svar:
Mer om
Denne oppgaven er om
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere eksempler og forklaringer på statistikk se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om datainnsamling i Treningsleieren.
b)
Ta utgangspunkt i det klassedelte materialet i a), og bestem gjennomsnittet.
Løsningsforslag b)
Jeg tenker
I klassedelt materiale, antar vi at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi antar at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
og ut i fra den klassedelte informasjonen vi fant i forrige oppgave, får vi Gjennomsnittet er altså cirka minutter.
Svar: Cirka minutter, gitt at gjennomsnittet i hver klasse ligger på klassemidtpunktet.
Mer om
Denne oppgaven er om
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
For flere eksempler og forklaringer på statistikk se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Visste du at
Det faktiske gjennomsnittet er minutter. Estimatet vi fant er derfor ganske godt.
c)
Bruk det klassedelte materialet til å avgjøre hvor stor andel av elevene som trenger mindre enn 60 min på å komme seg til og fra skolen.
Løsningsforslag c)
Jeg tenker
Her skal vi legge sammen antallet personer i klassen og under.
Vi skal finne ut hvor mange elever som bruker mindre enn 60 minutter på å komme seg til skolen. For å finne dette må vi legge sammen antallet som bruker mellom 10 og 20 minutter, de som bruker mellom 20 og 30 minutter, helt opp til 60. Altså skal vi legge sammen antallet personer i klassen og under. Det er det samme som den
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Svar: Cirka .
Mer om
Denne oppgaven er om
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere eksempler og forklaringer på statistikk se lynkurset Gjennomsnitt, for prosent se lynkurset Prosent.
Oppgave 7 (6 poeng) Nettkode: E-4BTF
Ved opptak til Politihøgskolen rangeres søkerne etter poeng.
Reglene for poengberegning er:
- Gjennomsnittet av karakterene fra videregående skole multipliseres med 10.
- Fullført førstegangstjeneste gir 2 poeng.
- Det gis ekstrapoeng for realfag/språkfag, maksimalt 4 poeng.
- Det gis også alderspoeng, 2 poeng for hvert år etter fylte 20 år, maksimalt 8 poeng.
Poengene til søkeren er summen av poengene fra de fire punktene ovenfor.
Mathias er 22 år. Han har fullført førstegangstjenesten.
Nedenfor ser du karakterene til Mathias fra videregående skole.
2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 6
Mathias får 1,5 ekstrapoeng for realfag/språkfag.
Mathias søker Politihøgskolen.
a)
Hvor mange poeng har han ifølge reglene ovenfor?
Løsningsforslag a)
Jeg tenker
Her må vi gå gjennom reglene, punkt for punkt, og finne ut hvor mange poeng Mathias får.
Vi starter med
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
så Karakterene skal multipliseres med 10 for å få poengene, så Mathias får poeng fra karaktersnittet sitt. Neste punkt på listen er førstegangstjenesten – det har Mathias fullført, så han får 2 ekstrapoeng. Videre får han poeng for realfag og språkfag. Det siste punktet er alderspoeng. Mathias er 22 år, og han skal få 2 poeng for hvert år etter fylte 20 år. Det blir poeng. Totalt får Mathias poeng.
Svar: poeng.
Mer om
Denne oppgaven er om
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
For flere eksempler og forklaringer på gjennomsnitt se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
b)
Mathias kom ikke inn på Politihøgskolen i Oslo. Der var poenggrensen 47,7
For å være sikker på å komme inn neste år vil Mathias prøve å forbedre karakterene i noen fag, slik at han til sammen får 50,7 poeng neste år.
Hva må gjennomsnittet av karakterene til Mathias være neste år for at han til sammen skal ha 50,7 poeng?
Løsningsforslag b)
Jeg tenker
Vi må regne ut hvor mange ekstrapoeng Mathias får, og deretter kan vi finne ut hvor mange poeng fra karaktersnittet han trenger.
Neste år vil Mathias være ett år eldre, og dermed vil han ha mottatt 2 ekstra alderspoeng. Han har ekstrapoeng fra før, så han har totalt tilleggspoeng. Nå er det bare poengene fra karakterene som står igjen. La være antall poeng Mathias må få fra karakterene for å få en poengsum på . Da må . Vi trekker fra på begge sider av likhetstegnet. Da får vi Snittkarakteren kan regnes ut ved å dividere karakterpoengene med 10, så Mathias må ha i karaktersnitt for å få poeng.
Svar:
Mer om
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
For flere eksempler og forklaringer se artikkelen Lineære likninger, og for gjennomsnitt se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleieren.
c)
Mathias regner med at han skal klare å gå opp én karakter i de fagene han velger å ta opp igjen.
Hvor mange fag må han da ta opp igjen for å klare 50,7 poeng?
Løsningsforslag c)
Jeg tenker
Hver karakter bidrar med til
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Mathias’ karaktersum før han tar opp fag er 95. Hvis han tar opp fag og går opp i én karakter i hver av dem, blir karaktersummen . Gjennomsnittet av karakterene er da , så hvert fag han tar opp bidrar med til karaktersnittet. Vi vil at karaktersnittet skal bli minst , så vi må finne det heltallet som gjør at karaktersnittet blir lik , altså Denne likningen kan vi løse med regning. Først multipliserer vi med 25 på begge sider for å få bort brøkstreken. Nå kan vi trekke 95 fra begge sider. Da får vi Dermed får vi at . Det betyr at Mathias må ta opp 8 fag.
Vi kunne også løst det på denne måten. Hver karakter bidrar med til snittet, og det forrige snittet var . Da løser vi likningen og vi får .
Svar: 8 fag
Mer om
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
For flere eksempler på likninger se artikkelen Lineære likninger, og for gjennomsnitt se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleieren.




