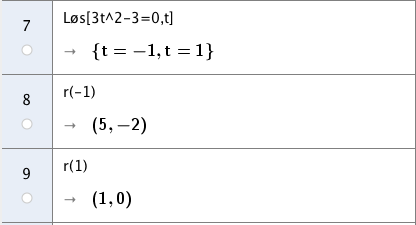Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3022 2016 HØST

Del 1
Del 2
Eksamensinformasjon

Eksamenstid
5 timer: 
Del 1 skal leveres inn etter 3 timer. 
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler på Del 1
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler

Hjelpemidler på Del 2
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte
Del 1 har 8 oppgaver. Del 2 har 5 oppgaver.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen
Poeng i del 1 og del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse  
gjennomfører logiske resonnementer  
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner  
kan bruke hensiktsmessige hjelpemidler  
vurderer om svar er rimelige  
forklarer framgangsmåter og begrunner svar  
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger
Kilder for bilder, tegninger osv. 

Alle grafer og figurer: Utdanningsdirektoratet

DEL 1 uten hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4P1K

Deriver funksjonene

a)

$f (x) = 2 x^{2} - 5 x - 6$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Funksjonen $f (x)$ er en sum av funksjoner på formen $a x^{n}$ der $a$ og $n$ er konstanter. Den deriverte av en sum er summen av de deriverte.

Vi kan finne den deriverte ved å derivere hvert av leddene og summere. Da får vi

$f' (x) = (2 x^{2} - 5 x - 6)' = (2 x^{2})' - (5 x)' - (6)'$

Vi bruker derivasjonsreglene til den deriverte av en potensfunksjon, som gir at $(a x^{n})' = n a x^{n - 1}$ og at den deriverte av en konstant er $0$ . Da kan vi skrive

$(2 x^{2})' - (5 x)' - (6)' = 2 \cdot 2 x^{1} + (- 5) = 4 x - 5$

Svar: $f' (x) = 4 x - 5$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynomer

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

b)

$g (x) = x \ln x$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

$g (x)$ er et produkt av to funksjoner $x$ og $\ln x$ . Da kan vi bruke produktregelen.

Vi kan bruke produktregelen

$(u \cdot v)' = u' \cdot v + u \cdot v'$

for å derivere funksjonen.

Vi setter $u = x$ og $v = ln x$ . Da blir

$\begin{matrix} g' (x) & = & (x \cdot \ln x)' \\ = & (u \cdot v)' \\ = & u' \cdot v + u \cdot v' \\ = & (x)' \cdot \ln x + x \cdot (\ln x)' \\ = & 1 \cdot \ln x + x \cdot \frac{1}{x} \\ = & \ln x + 1 \end{matrix}$

Svar: $g' (x) = ln x + 1$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

c)

$h (x) = \frac{e^{2 x}}{x - 3}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

$h (x)$ er en brøk med $e^{2 x}$ i teller og $x - 3$ i nevner. For å derivere $h (x)$ kan vi bruke brøkregelen. For å derivere $e^{2 x}$ er en sammensatt funksjon, og da kan vi bruke kjerneregelen.

Vi bruker brøkregelen for derivasjon med $u = e^{2 x}$ og $v = x - 3$ .

Da får vi

$\begin{matrix} h' (x) & = & (\frac{e^{2 x}}{x - 3})' = (\frac{u}{v})' = \frac{u' \cdot v - u \cdot v'}{v^{2}} \\ = & \frac{(e^{2 x})' \cdot (x - 3) - (e^{2 x}) \cdot (x - 3)'}{(x - 3)^{2}} \end{matrix}$

Telleren $e^{2 x}$ er en sammensatt funksjon. Vi lar $f (x) = e^{2 x}$ , og velger $z = 2 x$ som kjerne,

$f (z) = e^{z}$ der $z = 2 x$ .

$(e^{z})' = e^{z}$ og $z' = 2$ .

Av kjerneregelen får vi $f' (x) = e (z)' \cdot z' = (e^{z}) \cdot z' = e^{z} \cdot 2 = 2 e^{2 x}$

Nå kan vi derivere alle leddene i brøken over og da kan vi regne ut

$\begin{matrix} h' (x) & = & \frac{(e^{2 x})' \cdot (x - 3) - (e^{2 x}) \cdot (x - 3)'}{(x - 3)^{2}} \\ = & \frac{2 e^{2 x} \cdot (x - 3) - e^{2 x} \cdot 1}{(x - 3)^{2}} \\ = & \frac{2 {x e}^{2 x} - 6 e^{2 x} - e^{2 x}}{(x - 3)^{2}} \\ = & \frac{2 {x e}^{2 x} - 7 e^{2 x}}{(x - 3)^{2}} \\ = & \frac{e^{2 x} (2 x - 7)}{(x - 3)^{2}} \end{matrix}$

Svar: $h' (x) = \frac{e^{2 x} (2 x - 7)}{(x - 3)^{2}}$

Mer om:

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av sammensatte uttrykk.

Oppgave 2 (5 poeng) Nettkode: E-4P2H

En funksjon $f$ er gitt ved

$f (x) = {(x + 1)}^{2} (x - 2)$

a)

Bestem nullpunktene til $f$ .  

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal finne ut når $f (x) = 0$ . Da kan vi finne når faktorene til $f$ er lik $0$ .

Dersom en av faktorene til $f (x)$ er lik $0$ , så vil $f (x) = 0$ . Derfor starter vi med å faktorisere $f (x)$ .

$f (x) = (x + 1)^{2} (x - 2) = (x + 1) (x + 1) (x - 2)$

Faktorene til $f$ er $(x + 1)$ og $(x - 2)$ .

Den første faktoren, $(x + 1) = 0$ når $x = - 1$ , og den andre faktoren, $(x - 2) = 0$ når $x = 2$ . Da har vi at $f (x) = 0$ når $x = - 1$ og når $x = 2$

Svar: Nullpunktene er $(- 1, 0)$ og $(2, 0)$

Mer om

Denne oppgaven er om

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Faktorisering av uttrykk

Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.

Eksempel: $x^{2} + 4 x + 3 = (x + 1) (x + 3)$

faktorisering av uttrykk i x

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkt

For flere forklaringer og eksempler på nullpunkt, se artikkelen Nullpunktsetningen - når går divisjonen opp?

b)

Bestem eventuelle topp- og bunnpunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan finne eventuelle topp- og bunnpunkter ved å derivere $f$ , og finne når $f' (x) = 0$ . For å bestemme topp- og bunnpunkt, og eventuelle

Terassepunkt

Et terassepunkt for en funksjon $f (x)$ er et stasjonært punkt $a$ (et punkt der den deriverte er null), som verken er et topp- eller bunnpunkt.

terassepunkt

kan det være lurt å lage et f

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.

ortegnsskjema

for

f' (x)

Vi begynner med å derivere $f (x)$ . Da kan vi bruke produktregelen, med $u = (x + 1)^{2}$ og $v = x - 2$ . Da får vi

$\begin{matrix} f' (x) & = & ((x + 1)^{2} (x - 2))' = (u \cdot v)' = u' \cdot v + u \cdot v' \\ = & ((x + 1)^{2})' \cdot (x - 2) + (x + 1)^{2} \cdot (x - 2)' \end{matrix}$

For å derivere $(x + 1)^{2}$ kan vi bruke kjerneregelen med $u (x) = x + 1$ som kjerne. Da blir $u' (x) = 1$ , og vi får

$((x + 1)^{2})' = (u^{2})' \cdot u' = 2 u \cdot 1 = 2 (x + 1)$

Vi bruker dette til å regne $f' (x)$

$\begin{matrix} f' (x) & = & ((x + 1)^{2})' \cdot (x - 2) + (x + 1)^{2} \cdot (x - 2)' \\ = & 2 (x + 1) (x - 2) + (x + 1)^{2} \cdot 1 \end{matrix}$

For å kunne tegne fortegnsskjema må vi faktorisere $f' (x)$

$\begin{matrix} f' (x) & = & 2 (x + 1) (x - 2) + (x + 1)^{2} \\ = & (x + 1) (2 x - 4) + (x + 1)^{2} \\ = & (x + 1) ((2 x - 4) + (x + 1)) \\ = & (x + 1) (2 x - 4 + x + 1) \\ = & (x + 1) (3 x - 3) \end{matrix}$

$x + 1$ er negativ når $x < - 1$ og positiv når $x > - 1$ , og $3 x - 3$ er negativ når $x < 1$ og positiv når $x > 1$ , da får vi fortegnsskjemaet

Når $f' (x)$ er positiv vokser $f (x)$ , og når $f' (x)$ er negativ avtar $f (x)$ , Så vi har toppunkt når $x = - 1$ og bunnpunkt når $x = 1$ .
For å finne $y$ -koordinatene til topp- og bunnpunktene, må vi finne $f (1)$ og $f (- 1)$ . Siden vi vet fra a) vet at $- 1$ er et nullpunkt, får vi

$f (- 1) = 0$ .

Vi regner også ut

$f (1) = (1 + 1)^{2} (1 - 2) = 4 (- 1) = - 4$

Svar: $(- 1, 0)$ er toppunktet og $(1, - 4)$ er bunnpunktet til $f$ .

Mer om

Denne oppgaven er om

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.

fortegnskjema

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

c)

Lag en skisse av grafen til f.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Fra deloppgave a) har vi nullpunktene til $f$ , og fra deloppgave b) har vi toppunkt og bunnpunkt. I deloppgave b) fant vi når grafen stiger og når grafen avtar. Dette kan vi bruke til å skissere grafen til $f$ .

Vi kan begynne med å tegne inn punktene vi allerede kjenner fra deloppgave a) og b). Fra a) vet vi at grafen har nullpunkt når $x = - 1$ og $x = 2$ , så $(- 1, 0)$ og $(2, 0)$ er to punkter på grafen, og fra b) vet vi at $(- 1, 0)$ er et toppunkt, og at $(1, - 4)$ er et bunnpunkt.

Fortegnsskjemaet vi lagde i b) viser at grafen stiger mot høyre når $x < - 1$ , og $x > 1$ , for $- 1 < x < 1$ vil grafen avta.

Vi bruker dette til å skissere grafen

Mer om

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

Oppgave 3 (3 poeng) Nettkode: E-4P2E

a)

Skriv så enkelt som mulig

$\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal skrive uttrykket så enkelt som mulig, da kan vi faktorisere og finne

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

Vi kan begynne med å faktorisere leddene i uttrykket. Da får vi

$\begin{matrix} \frac{2 x + 10}{x^{2} + 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10} & = & \frac{2 (x + 5)}{(x + 5) (x - 5)} + \frac{x}{x + 5} - \frac{2 \cdot 2}{2 (x - 5)} \\ = & \frac{2 (x + 5)}{(x + 5) (x - 5)} + \frac{x}{x + 5} - \frac{2}{x - 5} \end{matrix}$

Da får vi at den minste fellesnevneren er gitt ved $(x + 5) (x - 5)$ .

Dermed har vi at vi at

$\begin{matrix} \frac{2 x + 10}{x^{2} + 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10} & = & \frac{2 (x + 5)}{(x + 5) (x - 5)} + \frac{x}{x + 5} - \frac{2}{x - 5} \\ = & \frac{2 (x + 5)}{(x + 5) (x - 5)} + \frac{x (x - 5)}{(x + 5) (x - 5)} - \frac{2 (x + 5)}{(x + 5) (x - 5)} \\ = & \frac{(2 x + 10) + (x^{2} - 5 x) - (2 x + 10)}{(x + 5) (x - 5)} \\ = & \frac{2 x + 10 + x^{2} - 5 x - 2 x - 10}{(x + 5) (x - 5)} \\ = & \frac{x^{2} - 5 x}{(x + 5) (x - 5)} \\ = & \frac{x (x - 5)}{(x + 5) (x - 5)} \\ = & \frac{x}{x + 5} \end{matrix}$

Svar: $\frac{2 x + 10}{x^{2} + 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10} = \frac{x}{x + 5}$

Mer om:

Denne oppgaven er om

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetningen

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

For flere forklaringer og flere eksempel, se artikkelen Faktorisering av andregradsuttrykk.

b)

Løs ligningen

$\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} = \frac{4}{2 x - 10}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke svaret vi fant i deloppgave a). Vi har $\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} = \frac{4}{2 x - 10}$ . Dersom vi flytter uttrykket på høyre side på andre siden av likhetstegnet får vi $\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10} = 0$ , og dette forenklet vi i deloppgave a)

Vi har at

$\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} = \frac{4}{2 x - 10}$

kan skrives som

$\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10} = 0$

Fra deloppgave a) har vi at

$\frac{2 x + 10}{x^{2} - 25} + \frac{x}{x + 5} - \frac{4}{2 x - 10} = \frac{x}{x + 5}$ .

Vi kan da regne ut

$\frac{x}{x + 5} = 0$

Dette gir oss at $x = 0$ .

Svar: $x = 0$

Mer om

Denne oppgaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

For flere forklaringer og eksempler på likninger, se artikkelen Rasjonale likninger.

Oppgave 4 (4 poeng) Nettkode: E-4P25

Løs ligningene

a)

$2^{3 x - 2} - 13 = 3$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi har $2^{3 x - 2}$ på venstre side av likningen, altså har vi en

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentiallikning

. Slike likninger løser vi vanligvis ved å ta logaritmen på begge sider. Men, vi kan også prøve å få toerpotens på begge sider og sette eksponentene lik hverandre.

Vi har

$\begin{matrix} 2^{3 x - 2} - 13 & = & 3 \\ 2^{3 x - 2} & = & 16 \\ 2^{3 x - 2} & = & 2^{4} \end{matrix}$

Eksponentene må være lik hverandre, så da kan vi løse ligningen

$\begin{matrix} 3 x - 2 & = & 4 \\ 3 x & = & 6 \\ x & = & 2 \end{matrix}$

Svar: $x = 2$

Mer om

Denne oppgaven er om

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentiallikninger

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger

eksponenter

For flere forklaringer og eksempler på eksponentiallikninger, se artikkelen Eksponentiallikninger.

b)

$(lg x)^{2} + \lg x - 2 = 0$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Dette er en andregradslikning med logaritmer. Vi kan uttrykke likningen ved hjelp av $u = \lg x$ og bruke $a b c$ -formelen for å finne $u$ . Da kan vi også finne verdien av løsningene $x$ .

Vi kan sette $u = \lg x$ . Da får vi

$(\lg x)^{2} + \lg x - 2 = u^{2} + u - 2 = 0$

Denne kan vi løse for $u$ ved å bruke

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

. Da har vi at

a = 1

b = 1

c = - 2

, og vi kan sette inn i formelen

$u = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Da får vi:

$\begin{matrix} u & = & \frac{- 1 \pm \sqrt{1^{2} - 4 \cdot 1 \cdot (- 2)}}{2 \cdot 1} \\ = & \frac{- 1 \pm \sqrt{1 - (- 8)}}{2} \\ = & \frac{- 1 \pm \sqrt{9}}{2} \\ = & \frac{- 1 \pm 3}{2} \end{matrix}$

Da får vi $u_{1} = \frac{- 1 + 3}{2}$ og $u_{2} = \frac{- 1 - 3}{2}$ .

Regner vi ut disse ligningen får vi at

$u_{1} = 1$ og $u_{2} = - 2$

Vi vil finne løsningene for $x$ så da setter vi inn for $u$

$u_{1} = \log x_{1} = 1$

Nå kan vi løse denne ligningen med hensyn på $x$

$\begin{matrix} 10^{\log x_{1}} & = & 10^{1} \\ x_{1} & = & 10 \end{matrix}$

og tilsvarende kan vi gjøre for $u_{2} = \log x_{2}$

$\begin{matrix} \log x_{2} & = & - 2 \\ 10^{\log x_{2}} & = & 10^{- 2} \\ x_{2} & = & \frac{1}{10^{2}} \\ = & 0, 01 \end{matrix}$

Svar: $x_{1} = 10$ og $x_{2} = 0, 01$

Mer om

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

For flere forklaringer og eksempler, se artikkelen Logaritmelikninger.

Oppgave 5 (6 poeng) Nettkode: E-4P37

I et koordinatsystem har vi punktene $A (- 3, - 2)$ , $B (3, 4)$ og $C (- 4, 5)$ .  En linje $l$ går gjennom punktet $C$ og er parallell med $A B$ .

a)

Sett opp en parameterframstilling for $l$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må huske hvordan parameterstilling en rett linje har. Linjen $l$ skal være parallell med $A B$ , så $l$ må ha samme

Retningsvektor

En linje $l$ går gjennom punktet $A (x_{0}, y_{0})$ og er parallell med vektoren $\vec{v} = [a, b]$ . Vektoren $\vec{v}$ kalles for retningsvektoren for linja.

retningsvektor

som

A B

En parameterfremstilling for en rett linje gjennom punktet $A (x_{1}, y_{1})$ som har retningsvektor $[a, b]$ har parameterfremstilling

$l : {\begin{matrix} x = x_{1} + a t \\ y = y_{1} + b t \end{matrix}$

Linjen $l$ skal være parallell med $A B$ , og vil ha samme retningsvektor som $\vec{A B}$ . Vi kan finner vektoren fra $A (- 3, - 2)$ til $B (3, 4)$ ved

$\vec{A B} = [3 - (- 3), 4 - (- 2)] = [6, 6] = 6 [1, 1]$

Linjen $l$ skal være parallell med $\vec{A B}$ og ha retningsvektor $[1, 1]$ . Linjen $l$ skal også gå gjennom punktet $C (- 4, 5)$ . Da får vi at parameterfremstillingen er

$l : {\begin{matrix} x = - 4 + 1 t \\ y = 5 + 1 t \end{matrix}$

Svar: $l : {\begin{matrix} x = - 4 + t \\ y = 5 + t \end{matrix}$

Mer om

Denne oppgaven er om

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".

parallell

Vektorfunksjon

En vektorfunksjon $\vec{r (t)}$ er en funksjon av en variabel t som gir en vektor fra origo for hver t:

$\vec{r (t)} = [x (t), y (t)]$

vektorer

Retningsvektor

En linje $l$ går gjennom punktet $A (x_{0}, y_{0})$ og er parallell med vektoren $\vec{v} = [a, b]$ . Vektoren $\vec{v}$ kalles for retningsvektoren for linja.

retningsvektor

For flere forklaringer og eksempler på linjer, se artikkelen Parameterframstilling av en rett linje.

b)

Linjen $l$ skjærer $x$ -aksen i punktet $D$ .

Bestem koordinatene til $D$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Alle punkter på $x$ -aksen vil være på formen $(x, 0)$ , der $x$ er et tall, så vi må finne det punktet på linja $l$ der $y = 0$ .

For at $D$ skal ligge på linja $l$ må det være på formen til parameterfremstillingen vi fant i deloppgave a). Linja $l$ krysser $x$ -aksen når $y = 0$ . Fra deloppgave a) har vi at $y = 5 + t$ , og vi kan regne ut

$y = 0 \Rightarrow 5 + t = 0 \Rightarrow t = - 5$

Vi setter inn $t = - 5$ i uttrykket for $x$ fra deloppgave a) og får

$x = - 4 + (- 5) = - 9$

Linja $l$ skjærer $x$ -aksen i $D (- 9, 0)$ .

Svar: $D (- 9, 0)$

Mer om

Denne oppgaven er om

x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.

x-akse

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på linjer, se artikkelen Parameterframstilling av en rett linje.

c)

Bestem koordinatene til et punkt $E$ på linjen $l$ slik at ∠BAE = 90°.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Nå vi har $∠ B A E = 90^{\circ}$ betyr det at vektorene $\vec{A B}$ står vinkelrett på $\vec{A E}$ . Skalarproduktet til to vektorer som står vinkelrett på hverandre er lik $0$ .

Dersom $\vec{A B}$ står vinkelrett på $\vec{A E}$ er $\vec{A B} \cdot \vec{A E} = 0$ . Vi kjenner $A (- 3, - 2)$ og $B (3, 4)$ .

Punktet $E$ ligger på $l$ , så $E$ har koordinater $(- 4 + t, 5 + t)$ for en verdi av $t$ . Fra deloppgave a) har vi at $\vec{A B} = [6, 6]$ .

Vi finner $\vec{A E}$ :

$\vec{A E} = [- 4 + t - (- 3), 5 + t - (- 2)] = [- 1 + t, 7 + t]$

Vi regner ut skalarproduktet av $\vec{A B}$ og $\vec{A E}$

$\begin{matrix} \vec{A B} \cdot \vec{A E} & = & [6, 6] \cdot [- 1 + t, 7 + t] \\ = & 6 (- 1 + t) + 6 (7 + t) \\ = & - 6 + 6 t + 42 + 6 t \\ = & 36 + 12 t \end{matrix}$

$\vec{A B}$ og $\vec{A E}$ skal stå vinkelrett på hverandre så $\vec{A B} \cdot \vec{A E} = 0$ . Da får vi at

$\begin{matrix} 36 + 12 t & = & 0 \\ 12 t & = & - 36 \\ t & = & \frac{- 36}{12} \\ t & = & - 3 \end{matrix}$

Vektorene står vinkelrett på hverandre når $t = - 3$ .Vi kan sette inn for $t = - 3$ i $E$ . Da får vi at $E$ er punktet

$(- 4 + t, 5 + t) = (- 4 + (- 3), 5 + (- 3)) = (- 4 - 3, 5 - 3) = (- 7, 2)$

Svar: $E (- 7, 2)$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler, se artikkelen Ortogonale vektorer.

Oppgave 6 (4 poeng) Nettkode: E-4P22

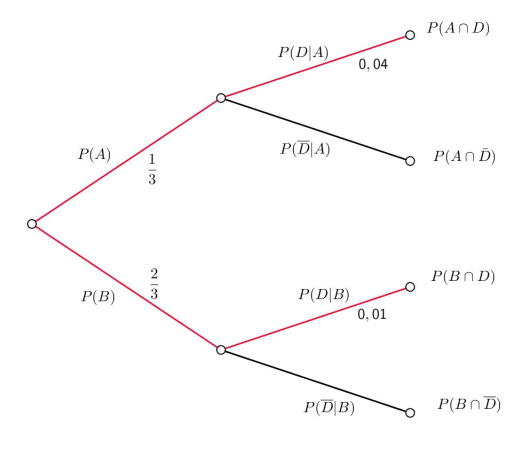
I en fabrikk er det to maskiner, maskin A og maskin B, som produserer samme type nøkler.

- 4 % av nøklene fra maskin A er defekte.  
- 1 % av nøklene fra maskin B er defekte.  
- Maskin B produserer dobbelt så mange nøkler som maskin A.

a)

En nøkkel blir valgt tilfeldig fra lageret.  

Bestem sannsynligheten for at nøkkelen er defekt.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

De mulige utfallene som gir at vi trekker en defekt nøkkel er enten at vi trekker en nøkkel fra $A$ , og den er defekt, $D$ , som er hendelsen $A \cap D$ eller vi trekker en nøkkel fra $B$ og den er defekt, $D$ , hendelsen $B \cap D$ . Vi kan finne sannsynligheten for disse hendelsene, $P (A \cap D)$ og $P (B \cap D)$ , ved å bruke produktregelen. Sannsynligheten for at vi trekker en defekt nøkkel er summen av disse to.

Vi kan begynne med å skrive opp den informasjonen vi får gitt i oppgaveteksten.
Vi ser på hendelsene

$A$ = “nøkkelen fra maskin $A$ ”
$B$ = “nøkkel fra maskin $B$ ”
$D$ = “nøkkelen er defekt”

Det første vi får informasjonen om er at $4 %$ av nøklene fra maskin $A$ er defekte, dette forteller oss at gitt at vi har en nøkkel fra maskin $A$ , er sannynligheten $0, 04$ for at nøkkelen er defekt altså

$P (D | A) = 0, 04$

Gitt at vi trekker en nøkkel fra maskin $B$ , er sannsynligheten $0, 01$ for at nøkkelen er defekt

$P (D | B) = 0, 01$

Maskin $B$ produserer dobbelt så mange nøkler som maskin $A$ , da blir sannsynligheten for å trekke en nøkkel fra $B$ ,

$P (B) = \frac{2}{3}$

og sannsynligheten for å trekke en nøkkel fra $A$

$P (A) = \frac{1}{3}$

Vi skal finne sannsynligheten for at vi trekker en nøkkel som er defekt. Mulighetene vi har er at vi enten trekker en nøkkel fra maskin $B$ óg den er defekt, eller vi trekker en nøkkel fra maskin $A$ og den er defekt, altså hendelsene $A \cap D$ og $B \cap D$ . Vi kan finne sannsynligheten for disse hendelsene ved å bruke produktregelen. Da får vi at

$P (A \cap D) = P (A) \cdot P (D | A) = \frac{1}{3} \cdot 0, 04 = \frac{0, 04}{3}$

$P (B \cap D) = P (B) \cdot P (D | B) = \frac{2}{3} \cdot 0, 01 = \frac{0, 02}{3}$

For å finne sannsynligheten for å trekke en defekt nøkkel kan vi bruke addisjonssetningen, og siden disse er disjunkte hendelser, får vi

$P (D) = P (A \cap D) + P (B \cap D) = \frac{0, 04}{3} + \frac{0, 02}{3} = \frac{0, 06}{3} = 0, 02$

Alternativ

For å få oversikt over de ulike sannsynlighetene kan vi lage et valgtre. For å få sannsynlighetene for hendelsene på ytterst på grenene multipliserer vi sammen sannsynlighetene langs grenene.

Vi finner sannsynligheten til hendelsen $D$ , $P (D)$ ved å regne ut og summere de røde grenene;

$P (A \cap D) = P (A) \cdot P (D | A) = \frac{1}{3} \cdot 0, 04 = \frac{0, 04}{3}$

$P (B \cap D) = P (B) \cdot P (D | B) = \frac{2}{3} \cdot 0, 01 = \frac{0, 02}{3}$

$P (D) = P (A \cap D) + P (B \cap D) = \frac{0, 04}{3} + \frac{0, 02}{3} = \frac{0, 06}{3} = 0, 02$

Alternativ

Vi kan også bruke setningen for total sannsynlighet som slår sammen produktregelen og addisjonsregelen i ett steg. Den sier at

$\begin{matrix} P (D) & = & P (A) \cdot P (D | A) + P (B) \cdot P (D | B) \\ = & \frac{1}{3} \cdot 0, 04 + \frac{2}{3} \cdot 0, 01 \\ = & \frac{0, 04}{3} + \frac{0, 02}{3} \\ = & \frac{0, 06}{3} \\ = & 0, 02 \end{matrix}$

Svar: Sannynligheten for at nøkkelen er defekt er $2 %$ .

Mer om

Denne oppgaven er om

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

Disjunkte hendelser

A og B kalles disjunkte dersom de ikke har noen felles elementer. Dette betyr at $A \cap B = \emptyset$ , altså at det ikke er noen elementer som er både i A og i B.

disjunkte hendelser

Addisjonssetningen

Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.

$P (A \cup B) = P (A) + P (B) - P (A \cap B)$

addisjonssetningen

For flere forklaringer og eksempler, se artikkelen Betinget sannsynlighet og produktregelen.

b)

Det viser seg at den valgte nøkkelen er defekt. 

Bestem sannsynligheten for at nøkkelen ble produsert av maskin $A$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi vil finne sannsynligheten for at nøkkelen er fra maskin $A$ , gitt den er defekt, $P (A | D)$ . Da kan vi bruke Bayes’ setning.

Vi vil finne $P (A | D)$ , og fra deloppgave a) kjenner vi $P (D | A)$ , $P (A)$ og $P (D)$ . Da kan det være nyttig å bruke Bayes’ setning som sier

$P (A | D) = \frac{P (A) \cdot P (D | A)}{P (D)}$

Nå kan vi sette inn for sannsynligheten vi fant i a). Dette gir $P (A | D) = \frac{\frac{1}{3} \cdot 0, 04}{0, 02} = \frac{1}{3} \cdot 2 = \frac{2}{3} = 0, 67$

Svar: Sannsynligheten for at nøkkelen er fra $A$ er $67 %$ .

Mer om

Denne oppgaven er om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

Bayes' setning

Bayes' setning sier at $P (A | B) = \frac{P (B | A) P (A)}{P (B)} .$

Bayes’ setning

For flere forklaringer og eksempler, se artikkelen Bayes-setningen.

Oppgave 7 (6 poeng) Nettkode: E-4P29

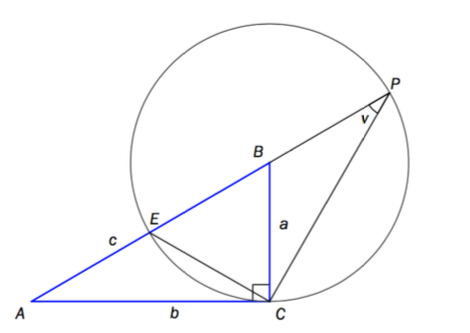
En rettvinklet $Δ A C B$ med sidelengdene $B C = a$ , $A C = b$ og $A B = c$ er gitt. Vi tegner en sirkel med sentrum i $B$ og radius $a$ . Linjen gjennom $A$ og $B$ skjærer sirkelen i $E$ og $P$ . Vi setter $∠ B P C = v$ . Se figuren nedenfor.

a)

Vis at $∠ A C E = v$ og $Δ A C P \sim Δ A C E$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

To trekanter er formlike dersom de har to parvis like vinkler.

Vi skal vise at $∠ A C E = v$ . Vi kan begynne med å se på $∠ A C P$ .

Som vi kan se er

$∠ A C P = ∠ A C E + ∠ E C P = ∠ A C B + ∠ B C P$ .

Vi har fått oppgitt at $∠ A C B = 90^{\circ}$ , og $∠ E C P$ er en periferivinkel som spenner over samme bue som sentralvinkelen $∠ E B P = 180^{\circ}$ . Dermed er $∠ E C P = 90^{\circ}$ . Da har vi

$∠ A C P = ∠ A C E + 90^{\circ} = 90^{\circ} + ∠ B C P$ ,

så $∠ A C E = ∠ B C P$ .

Linjestykkene $B C$ og $B P$ er lik radius til sirkelen, så $Δ B C P$ er en likebeint trekant. Da er $∠ B P C = ∠ B C P = v$ , og da må også $∠ A C E = v$ .

$Δ A C P \sim Δ A C E$ dersom vi har to parvis like vinkler. $∠ C A E = ∠ C A P$ er felles i trekantene, og vi har vist at $∠ A C E = ∠ A P C = v$ . Da har vi to parvis like vinkler, og da må også den siste vinkelen være lik i de to trekantene, og $Δ A C P \sim Δ A C E$ .

Svar: Vi har to parvise like store vinkler, så da er trekantene formlike.

Mer om:

Denne oppgaven er om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

Likebeint trekant

I en likebeint trekant er to sider like lange og to vinkler like store.

likebeinte trekanter

For flere forklaringer og eksempler på formlikhet, se artikkelen Formlikhet og kongruens.

b)

Forklar at $A E = c - a$ , og at $A P = c + a$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Siden $B$ er sentrum i sirkelen er $B P$ og $B E$ lik radiusen, og må dermed være lik $B C$ .

Vi begynner med å se på $A E$ . Lengden vil være

$A E = A B - B E$

Vi har fått oppgitt at $A B = c$ . Vi vet også at $B E$ er lik radius til sirkelen, så $B E$ må være lik $B C = a$ . Setter vi inn dette i uttrykket for $A E$ over får vi

$A E = A B - B E = c - a$ .

På tilsvarende måte kan vi skrive

$A P = A B + B P$ .

Også $B P$ er lik radius, så $B P = a$ , og $A B = c$ , så da har vi

$A P = A B + B P = c + a$ .

Mer om

Denne oppgaven er om

Lengde

Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.

lengde

Radius

Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.

radius

For flere forklaringer og eksempler på sirkler, se artikkelen Alt om sirkel.

c)

Bruk formlikheten i oppgave a) til å vise at

$\frac{c + a}{b} = \frac{b}{c - a}$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

I formlike trekanter er forholdene mellom samsvarende sider det samme. I $Δ A C P$ og $Δ A C E$ må $A P$ og $A C$ , $C P$ og $C E$ , og $A C$ og $A E$ være samsvarende sider.

Siden $Δ A C P \sim Δ A C E$ må forholdet mellom de samsvarende sidene være det samme, dermed må forholdene mellom $A P$ og $A C$ være likt forholdet mellom $A C$ og $A E$ . Det vil si at

$\frac{A P}{A C} = \frac{A C}{A E}$

I deloppgave b) fant vi at $A P = c + a$ og $A E = c - a$ , dersom vi setter inn dette får vi

$\frac{A P}{A C} = \frac{A C}{A E} = \frac{c + a}{b} = \frac{b}{c - a}$ .

Mer om

Denne oppgaven er om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

For flere forklaringer og eksempler, se artikkelen Tom forteller om formlikhet og Pytagoras læresetning.

d)

Bruk resultatet i oppgave c) til å vise at Pytagoras setning gjelder.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Pytagoras setning sier at for en rettvinklet trekant hvor $a$ og $b$ er kateter, og $c$ er hypotenusen har vi at $a^{2} + b^{2} = c^{2}$ . I $Δ A B C$ har vi nettopp dette.
Vi vil bruke resultatet i deloppgave c) og ved regning se om vi kan få det på formen til Pytagoras setning.

Vi vil gjøre om på likningen $\frac{c + a}{b} = \frac{b}{c - a}$ fra deloppgave c) og se om vi kan få den på formen $a^{2} + b^{2} = c^{2}$ .

Vi kan begynne med å multiplisere med $b$

$\begin{matrix} b \cdot \frac{c + a}{b} & = & b \cdot \frac{b}{c - a} \\ c + a & = & \frac{b^{2}}{c - a} \end{matrix}$

Videre kan vi multiplisere med $c - a$

$\begin{matrix} (c + a) (c - a) & = & (c - a) \frac{b^{2}}{c - a} \\ (c + a) (c - a) & = & b^{2} \end{matrix}$

Ved konjugatsetningen får vi at $(c + a) (c - a) = c^{2} - a^{2}$ .

Dermed får vi

$\begin{matrix} (c + a) (c - a) & = & b^{2} \\ c^{2} - a^{2} & = & b^{2} \\ a^{2} + b^{2} & = & c^{2} \end{matrix}$

som er Pytagoras setning, der $a$ er kateter, og $c$ er hypotenusen i $Δ A B C$ .

Mer om:

Denne oppgaven er om

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

For flere forklaringer og eksempler, se artikkelen Pytagoras læresetning.

Oppgave 8 (3 poeng) Nettkode: E-4P3C

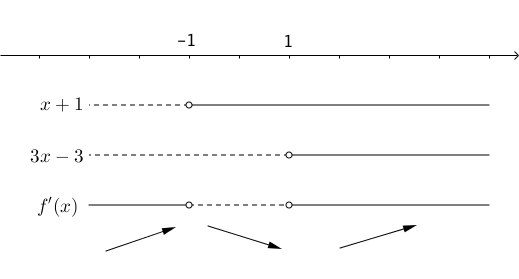
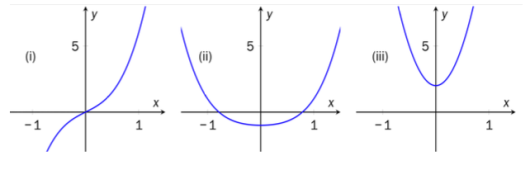
Nedenfor er det laget skisser av grafene til en funksjon f, den deriverte f' og den
andrederiverte f''.

Avgjør hva som er grafen til f, hva som er grafen til f', og hva som er grafen til f''.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Den deriverte forteller noe om stigningstallet til en funksjon, og den dobbeltderiverte forteller noe om krumningen til funksjonen. Dersom den deriverte er lik $0$ , vil vi ha stasjonære punkter, og når den dobbeltderiverte skrifter fortegn vil vi ha et vendepunkt.

Vi kan begynne med (i). Denne grafen er monotont voksende, altså må den deriverte alltid være positiv. Dersom denne er grafen til f passer det da at (iii) som alltid er positiv er den deriverte til $f$ .

Vi må sjekke om (ii) kan være den dobbeltderiverte til $f$ , dersom (i) er skissen av grafen til $f$ . Grafen (i) har den hule siden ned når $x < 0$ og den hule siden opp når $x > 0$ , så $f ″ (x)$ skulle i dette tilfellet vært negativ når $x < 0$ , og positiv når $x > 0$ , men dette stemmer ikke for (ii), så den kan ikke være den dobbeltderiverte til $f$ , dersom (i) viser grafen til $f$ .

Vi kunne se at det passer at (iii) viser den deriverte til (i), men (ii) passer ikke til å være den dobbeltderiverte til (i). Vi kan sjekke om (ii) viser grafen til $f$ , og om (i) kan være den deriverte til (ii).

(ii) har bunnpunkt i $x = 0$ , så her må den deriverte være lik 0, det stemmer med skisse (i). I (ii) så er grafen avtagende får $x < 0$ , og da må den deriverte være negativ, og voksende for $x > 0$ , da må vi den deriverte være positiv. Dette stemmer med (i), den er negativ for $x < 0$ og positiv for $x > 0$ , så (i) kan være den deriverte til (ii). (i) er konveks, så $f ″$ skal være positiv, dette passer med at $f ″$ er tegnet i (iii). Hvis (iii) var $f$ , måtte $f ″$ være positiv mellom $- 1$ og $1$ . Det stemmer verken for grafen i (i) eller (ii).

Da kan vi konkludere med at (ii) er grafen til $f$ , (i) er grafen til $f'$ og (iii) er grafen til $f ″$

Svar: (ii) er $f$ , (i) er $f'$ og (iii) er $f ″$

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Andrederiverte

Den andrederiverte til en funksjon $f (x)$ er funksjonen derivert to ganger og skrives $f'' (x)$ eller $f^{(2)} (x)$ . Kalles også annenderiverte eller dobbeltderiverte.

annenderiverte

For flere forklaringer og eksempler, se lynkurset Funksjonsdrøfting.

DEL 2 med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4P3E

I pengespillet Lotto legges $34$ kuler i en beholder. Hver kule er nummerert med ett av tallene fra $1$ til $34$ . Sju kuler trekkes tilfeldig uten tilbakelegging. Tallene på de sju kulene er vinnertallene.

a)

Når du spiller Lotto, krysser du av sju av tallene fra $1$ til $34$ på en kupong.

På hvor mange måter kan du velge ut sju av de $34$ tallene?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Utvalget er

Uordnede utvalg

Når vi trekker objekter fra en samling og rekkefølgen vi trekker i ikke er viktig, sier vi at dette er et uordnet utvalg.

Eksempel: Lottotrekning.

uordnet

Uten tilbakelegging

Dersom vi ikke legger tilbake den første gjenstanden før vi trekker neste, sier vi at et forsøk er gjort uten tilbakelegging.

Eksempel: Lottotrekning.

uten tilbakelegging

, da kan vi bruke

Binomialkoeffisient

Binomialkoeffisienten

$(\begin{matrix} n \\ m \end{matrix}) = \frac{n!}{m! (n - m)!}$

hvor $n! = n \cdot (n - 1) \cdot \cdot \cdot 2 \cdot 1$ ,

forteller hvor mange måter det kan trekkes m objekter ut fra en samling av n gjenstander uten tilbakelegging.

binomialkoeffisienten

(\binom{n}{k})

for å finne antall måter å velge på.

Vi skal velge $7$ tall blant $34$ tall. Rekkefølgen for tallene spiller ingen rolle, og det er ingen tilbakelegging. Da kan vi regne $(\binom{34}{7})$ . $(\binom{34}{7}) = \frac{34 \cdot 33 \cdot 32 \cdot 31 \cdot 30 \cdot 29 \cdot 28}{7!} = \frac{34 \cdot 33 \cdot 32 \cdot 31 \cdot 30 \cdot 29 \cdot 28}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 5379616$

Svar: 5 379 616 måter

Mer om

Denne oppgaven er om

Kombinatorikk

Handler om å finne antall mulige kombinasjoner i ulike sammenhenger.

Eksempel: antall måter å kombinere Lotto-tallene på, eller hvor mange ulike antrekk vi kan ha på oss dersom vi har 2 bukser og 3 skjorter.

kombinatorikk

Uordnede utvalg

Når vi trekker objekter fra en samling og rekkefølgen vi trekker i ikke er viktig, sier vi at dette er et uordnet utvalg.

Eksempel: Lottotrekning.

uordnede utvalg

Uten tilbakelegging

Dersom vi ikke legger tilbake den første gjenstanden før vi trekker neste, sier vi at et forsøk er gjort uten tilbakelegging.

Eksempel: Lottotrekning.

uten tilbakelegging

og binomialkoeffisient.

For flere forklaringer og eksempler, se artikkelen Uordnede utvalg uten tilbakelegging.

b)

Tore har levert inn en lottokupong der han har krysset av tallene

$3$ , $5$ , $11$ , $18$ , $21$ , $25$ , $32$

Bestem sannsynligheten for at Tore får nøyaktig $5$ rette.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi har en uniform trekning av kuler, så da kan vi finne sannsynligheten ved å regne $\frac{antall gunstige}{antall mulige}$ .

Dette er et eksempel på en hypergeometrisk modell, og da kan vi bruke sannsynlighetskalkulatoren i GeoGebra. Se alternativ.

Vi skal finne sannsynligheten for å trekke nøyaktig fem rette. Sannsynligheten er uniform, så for å finne sannsynligheten kan vi regne $\frac{antall gunstige}{antall mulige}$ .

I deloppgave a) fant vi at antall mulige måter er $(\binom{34}{7}) = 5379616$

Vi må finne hvor mange av utfallene som er gunstige, for å velge nøyaktig fem rette tall. Det er $7$ vinnertall, så vi må velge $5$ tall av de $7$ vinnertallene. Dette kan vi velge på $(\binom{7}{5})$ måter.

De to siste tallene må vi velge blant de tallene som ikke er vinnertall, som er $34 - 7 = 27$ tall. Da har vi $(\binom{27}{2})$ måter å velge disse på.

Hvert enkelt av de $(\binom{7}{5})$ måtene å velge $5$ rette tall på kan kombineres med de $(\binom{27}{2})$ måtene å velge de $2$ siste tallene. Til sammen kan vi derfor velge $5$ rette tall på $(\binom{7}{5}) \cdot (\binom{27}{2})$ måter. Dette er antall gunstige utvalg.
Dermed er

$P (5 rette) = \frac{(\binom{7}{5}) \cdot (\binom{27}{2})}{(\binom{34}{7})} = \frac{21 \cdot 351}{5379616} \approx 0, 0014 = 0, 14 %$

Alternativ

For å finne sannsynligheten for at Tore får $5$ rette kan vi bruke sannsynlighetskalkulatoren i GeoGebra. I "Vis"-menyen velger vi "Sannsynlighetskalkulator". Da får vi opp

Vi har et eksempel på et hypergeometrisk forsøk, så da må vi velge sannsynlighetsfordelingen til å være hypergeometrisk i stedet for normalfordeling.

Videre må vi fylle inn med tallene fra Lottotrekningen. Populasjon er antall elementer, altså hvor mange tall Tore kan velge mellom, som er $34$ , $n$ er antall gunstige elementer, som i Tores tilfelle er $7$ , og utvalg er hvor mange elementer som trekkes ut, som også er $7$ .

Vi skal finne hvor stor sannsynligheten er for at Tore får nøyaktig $5$ rette. Da markerer vi ruten med $[-]$ , og skriver inn slik at vi får $P (5 \leq x \leq 5)$ på den nederste linja. Da får vi rett ut at sannsynligheten for $5$ rette er $0, 0014 = 0, 14 %$ .

Svar: $0, 14 %$

Mer om

Denne oppgaven er om uniform sannsynlighet,

Utfall

Mulig resultat av en hendelse.

Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.

utfall

Gunstig utfall

Et gunstig utfall er den hendelsen som er interessant for oss.

Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.

Se Hendelse

gunstige utfall

For flere forklaringer og eksempler, se artikkelen Hvordan finner vi uniform sannsynlighet?.

c)

Tore ser lottotrekningen på TV. Etter at det er trukket ut fire tall, går strømmen, og TV-en går i svart. Tallene som til da er trukket ut, er $5$ , $21$ , $3$ og $11$ .

Bestem sannsynligheten for at Tore får sju rette på lottokupongen sin.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke samme fremgangsmåte som i deloppgave b), men vi må endre antall gunstige og antall mulige.

Det er trukket ut 4 tall, altså er det gjenstår det å trekke $3$ tall. Disse kan trekkes blant $30$ tall.
Antall mulige måter å trekke de siste $3$ tallene på er

$(\binom{30}{3}) = \frac{30 \cdot 29 \cdot 28}{3!} = \frac{30 \cdot 29 \cdot 28}{3 \cdot 2 \cdot 1} = 4060$

Siden det bare gjenstår $3$ tall og Tore mangler $3$ tall, kan de siste tallene bare bli trukket på én gunstig måte. De tre gjenstående tallene må trekkes. Antall gunstige er altså $1$ . Da får vi

$P (7 rette) = \frac{1}{4060} \approx 0, 0002 = 0, 02 %$

Svar: $0, 02 %$

Mer om

Denne oppgaven er om uniform sannsynlighet,

Utfall

Mulig resultat av en hendelse.

Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.

utfall

Gunstig utfall

Et gunstig utfall er den hendelsen som er interessant for oss.

Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.

Se Hendelse

gunstige utfall

Binomialkoeffisienter

De koeffisientene man får når en opphøyer (x+y) i et naturlig tall.

binomialkoeffisienter

For flere forklaringer og eksempler om sannsynlighet, se artikkelen Hvordan finner vi uniform sannsynlighet?.

Oppgave 2 (6 poeng) Nettkode: E-4P3I

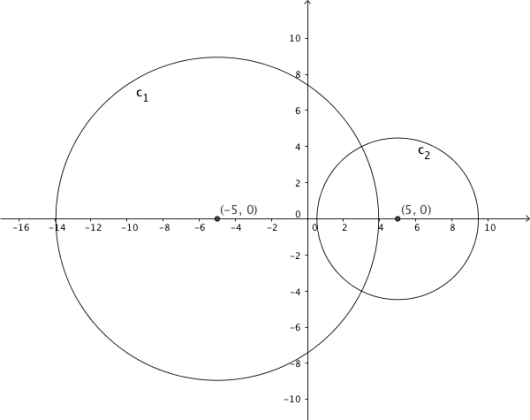
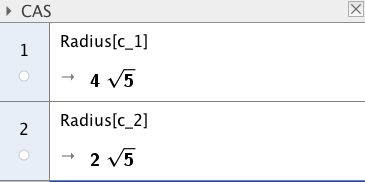
To sirkler $c_{1}$ og $c_{2}$ med sentrum i henholdsvis $S_{1}$ og $S_{2}$ er gitt ved

$c_{1} : {(x + 5)}^{2} + y^{2} = 80$
$c_{2} = x^{2} - 10 x + y^{2} + 5 = 0$

a)

Bestem sentrum og radius i sirklene $c_{1}$ og $c_{2}$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra som verktøy for å tegne sirklene og finne både sentrum og radius. Vi kan også bruke at alle sirkler kan skrives på formen $(x - x_{0})^{2} + (y - y_{0})^{2} = r^{2}$ , der $(x_{0}, y_{0})$ er sentrum av sirkelen, og r er radiusen.

Vi kan finne sentrum og radius av sirklene ved å bruke GeoGebra. For $c_{1}$ skriver vi i “Skriv inn”-feltet

$𝚌_1 : (𝚡 + 5)^{\land} 2 + 𝚢^{\land} 2 = 80$

Vi kan se på figuren at sentrum er i $(- 5, 0)$ , men for å være helt sikker kan vi bruke “Midtpunkt eller sentrum”-vertøyet og velge $c_{1}$ .

Da får vi at sentrum er $(- 5, 0)$ . For å finne radiusen kan vi skrive Radius [c_1] i CAS. Da får vi den eksakte løsningen. Radius til $c_{1}$ er lik $4 \sqrt{5}$ .

Vi kan gjøre det tilsvarende for $c_{2}$ . Da skriver vi

$𝚌_2 : 𝚡^{\land} 2 - 10 𝚡 + 𝚢^{\land} 2 + 5 = 0$

Bruker vi “Midtpunkt eller sentrum”-verktøyet på $c_{2}$ får vi at sentrum til $c_{2}$ er (5,0). Vi skriver Radius [c_1] i CAS, og får at radius til $c_{2}$ er $2 \sqrt{5}$ .

Alternativ

Alle sirkler kan skrives som likninger på formen $(x - x_{0})^{2} + (y - y_{0})^{2} = r^{2}$ .

Vi kan prøve å skrive likningene $c_{1}$ og $c_{2}$ om til denne formen, og bestemme sentrum og radius utfra den.

Likningen til $c_{1}$ er nesten på formen vi ønsker, det som mangler er at vi har $(x + 5)^{2}$ og at høyresiden ikke er kvadrert. Dersom vi skriver $(x + 5) = (x - (- 5))$ og $80 = {\sqrt{80}}^{2}$ får vi

$c_{1} : (x + 5)^{2} + y^{2} = 80 \Rightarrow (x - (- 5))^{2} + (y - 0)^{2} = {\sqrt{80}}^{2}$

kan vi se at $c_{1}$ har sentrum i $(- 5, 0)$ og har en radius $\sqrt{80} = \sqrt{16 \cdot 5} = 4 \sqrt{5}$ .

For å få $c_{2}$ på formen må vi lage et fullstendig kvadrat. Vi vil bruke andre kvadratsetning, der

$a^{2} - 2 a b + b^{2} = (a - b)^{2}$

Vi har $x^{2} - 10 x$ , og må finne hva vi må legge til for å fullføre kvadratet. Hvis vi sammenligner med ligningen over har vi $a = x$ , og vi har at $2 a b = 2 b x = 10 x$ , så $b = 5$ . Vi må legge til $5^{2} = 25$ . Dette må vi gjøre på begge sider av likhetstegnet, og da får vi

$\begin{matrix} x^{2} - 10 x + y^{2} + 5 & = & 0 \\ x^{2} - 10 x + 25 + y^{2} & = & - 5 + 25 \\ (x - 5)^{2} + y^{2} & = & 20 \\ (x - 5)^{2} + (y - 0)^{2} & = & {\sqrt{20}}^{2} \end{matrix}$

Nå kan vi se at $c_{2}$ må ha sentrum i $(5, 0)$ og radius lik $\sqrt{20} = \sqrt{4 \cdot 5} = 2 \sqrt{5}$

Svar: $c_{1}$ har sentrum i $(- 5, 0)$ og har radius $4 \sqrt{5}$ og $c_{2}$ har sentrum i $(5, 0)$ og radius $2 \sqrt{5}$

Mer om

Denne oppgaven er om

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Radius

Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.

radius

Fullføre kvadratet

Omskriving av et andregradsuttrykk slik at det likner mest mulig på et fullstendig kvadrat, altså få uttrykket på formen $a x^{2} + b x + c$ til ${(\cdot \cdot \cdot)}^{2} + r$ der $r$ er en konstant, kalles å fullføre kvadratet.

fullføre kvadrater

For flere forklaringer og eksempler på å fullføre kvadrater, se artikkelen Å fullføre kvadratet.

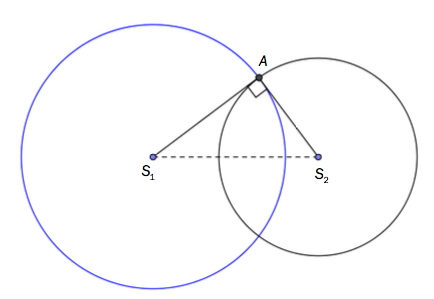
b)

La A være et av skjæringspunktene mellom sirklene. Sirklene $c_{1}$ og $c_{2}$ kalles ortogonale
dersom $\vec{A S_{1}}$ ⊥ $\vec{A S_{2}}$ . Se skissen nedenfor.

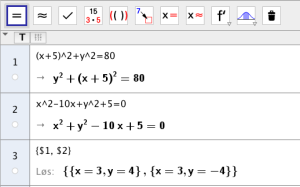
Bestem skjæringspunktene mellom sirklene $c_{1}$ og $c_{2}$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke GeoGebra til å finne skjæringspunktene mellom sirklene. Vi kan også finne dem ved regning, ved å løse de to likningene som et likningssett.

Vi begynner å se hvordan vi kan finne skjæringspunktene ved hjelp av GeoGebra. Vi tegner inn $c_{1}$ ved å skrive

$𝚌_1 : (𝚡 + 5)^{\land} 2 + 𝚢^{\land} 2 = 80$

i “Skriv inn”-feltet og $c_{2}$ ved å skrive

$𝚌_2 : 𝚡^{\land} 2 - 10 𝚡 + 𝚢^{\land} 2 + 5 = 0$

For å finne skjæringspunktene skriver vi

$𝚂 𝚔 𝚓 æ 𝚛 𝚒 𝚗 𝚐 [𝚌_1, 𝚌_2]$

Da får vi punktene $(3, 4)$ og $(3, - 4)$ .

Alternativ

Vi kan også finne skjæringspunkene til sirklene ved regning. Vi kan sette det opp som et ligningsett

$\begin{matrix} I & (x + 5)^{2} + y^{2} & = & 80 \\ I I & x^{2} - 10 x + y^{2} + 5 & = & 0 \end{matrix}$

Vi regner ut (x+5)² i ligning $(I)$ som gir

$x^{2} + 10 x + 25 + y^{2} = 80$

Vi kan subtrahere $(I I)$ fra $(I)$ . Da får vi at

$\begin{matrix} x^{2} + 10 x + 25 + y^{2} - (x^{2} - 10 x + y^{2} + 5) & = & 80 - 0 \\ x^{2} + 10 x + 25 + y^{2} - x^{2} + 10 x - y^{2} - 5 & = & 80 \\ 10 x + 10 x & = & 80 - 25 + 5 \\ 20 x & = & 60 \\ x & = & 3 \end{matrix}$

Nå kan vi sette inn for x=3 i $(I)$ og da får vi

$\begin{matrix} (3 + 5)^{2} + y^{2} & = & 80 \\ 64 + y^{2} & = & 80 \\ y^{2} & = & 16 \\ y & = & \pm 4 \end{matrix}$

Vi kan sjekke at dette også stemmer for $(I I)$ . Vi begynner med å sjekke for $y = 4$ .

$3^{2} - 10 \cdot 3 + 4^{2} + 5$

$= 9 - 30 + 16 + 5 = 0$

Vi vil få tilsvarende for $y = - 4$ siden $4^{2} = (- 4)^{2}$ . Skjæringspunktene er altså $(3, 4)$ og $(3, - 4)$ .

Alternativt kan vi løse dette likningsettet i CAS, da skriver vi inn $(x+5)^2+y^2=80$ på den første linjen og $x^2-10x+y^2+5=0$ på den andre linjen.

Deretter skriver vi inn $\{$ 1, $ 2\}$ og velger "Løs" på knappen med "x=".

Da får vi

som gir samme svar som over.

Svar: $(3, 4)$ og $(3, - 4)$ .

Mer om

Denne oppgaven er om

Skjæringspunkt

skjæringspunkter

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

For flere forklaringer og eksempler om likninger, se artikkelen Likningssystemer.

c)

Undersøk ved å bruke vektorregning om sirklene $c_{1}$ og $c_{2}$ er ortogonale.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

To vektorer står normalt på hverandre dersom skalarproduktet er $0$ .

For å finne ut om sirklene er ortogonale må vi finne skalarproduktet mellom $\vec{A S_{1}}$ og $\vec{A S_{2}}$ . Dersom dette er lik $0$ , vil $\vec{A S_{1}} ⊥ \vec{A S_{2}}$ og sirklene er ortogonale.

Fra deloppgave a) vet vi at $S_{1} = (- 5, 0)$ og $S_{2} = (5, 0)$ . $A$ er skjæringspunktet mellom $c_{1}$ og $c_{2}$ , som fra deloppgave b) må være punktet $(3, 4)$ .

Vi begynner med å finne $\vec{A S_{1}}$ og $\vec{A S_{2}}$ .

$\vec{A S_{1}} = [- 5 - 3, 0 - 4] = [- 8, - 4]$

$\vec{A S_{2}} = [5 - 3, 0 - 4] = [2, - 4]$

Skalarproduktet mellom $\vec{A S_{1}}$ og $\vec{A S_{2}}$ er

$\vec{A S_{1}} \cdot \vec{A S_{1}} = [- 8, - 4] \cdot [2, - 4] = - 8 \cdot 2 + (- 4) \cdot (- 4) = - 16 + 16 = 0$

Da er $\vec{A S_{1}} ⊥ \vec{A S_{2}}$ og sirklene er ortogonale.

Svar: $\vec{A S_{1}} ⊥ \vec{A S_{2}}$ så $c_{1}$ og $c_{2}$ er ortogonale.

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

For flere forklaringer og eksempler, se artikkelen Ortogonale vektorer.

Oppgave 3 (4 poeng) Nettkode: E-4P3V

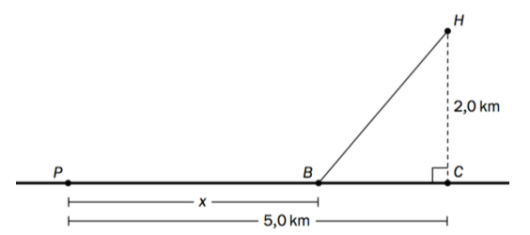
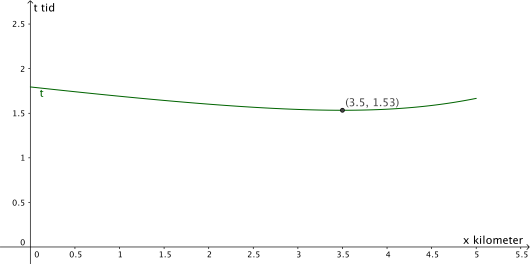
Anne skal på hytta. Hun må sette bilen sin på en parkeringsplass $P$ ved en rettlinjet vei. Punktet $C$ er det punktet på veien som ligger nærmest hytta $H$ . Avstanden fra $P$ til $C$ er $5, 0$ km. Avstanden fra $C$ til $H$ er $2, 0$ km.

Anne vurderer å følge veien fram til et punkt $B$ før hun svinger ut i terrenget og går rett mot hytta. Se figuren nedenfor.

Hun regner med å holde farten $5$ km/h på veien og farten $3$ km/h i terrenget.

a)

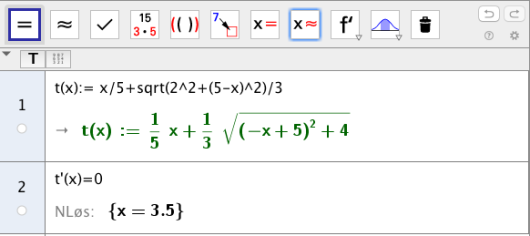
Vi setter $P B = x km$ . Tiden hun bruker fra parkeringsplassen til hytta, målt i timer,

kaller vi for $t (x)$ .

Vis at

$t (x) = \frac{x}{5} + \frac{\sqrt{2^{2} + (5 - x)^{2}}}{3}$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan dele opp strekningen i den hun kjører på vei og den hun går i terrenget. Vi skal finne tiden hun bruker og vi får oppgitt strekning og tid, da kan vi bruke sammenhengen mellom strekning, fart og tid; $s = v \cdot t$ . Siden vi vil finne tiden bruker vi $t = \frac{s}{v}$ .

Vi kan dele opp strekningen Anne skal kjøre i den strekningen som hun kjører på vei, og den delen hun går i terrenget, og se hvor lang tid hun vil bruke på hver av de, og deretter summere de sammen.

Vi kan begynne med å se på hvor lang tid hun bruker på strekningen hun kjører langs veien. Strekningen langs veien er $x$ km, vi har $s_{v} = x$ og farten langs veien er $5$ km/t, $v_{v} = 5$ km/t. Utfra formelen som viser sammenheng mellom strekning, fart og tid, $s = v \cdot t$ , kan vi da regne tiden hun bruker langs veien ved

$t_{v} = \frac{s_{v}}{v_{v}} = \frac{x}{5}$

Dette samsvarer med det første leddet i funksjonen $t$ , så det første leddet er tiden hun bruker langs veien.
Det andre leddet $\frac{\sqrt{2^{2} + (5 - x)^{2}}}{3}$ må da være tiden hun bruker i terrenget. Vi kan finne strekningen hun går, $s_{t}$ ved å bruke Pytagoras læresetning for $Δ B C H$ , der strekningen vil være hypotenusen, $B H$ i den rettvinklede trekanten med kateter $C H = 2, 0 km$ og $B C = 5, 0 - x km$ . Da får vi at

$s_{t}^{2} = 2^{2} + (5 - x)^{2} \Rightarrow s_{t} = \sqrt{2^{2} + (5 - x)^{2}}$

Farten hun holder i terrenget, $v_{t}$ er på $3$ km/t, så da får vi at tiden hun bruker i terrenget,

$t_{t} = \frac{s_{t}}{v_{t}} = \frac{\sqrt{2^{2} + (5 - x)^{2}}}{3}$

som er det samme som det andre leddet i likningen.

Da blir den totale tiden hun bruker

$t = t_{v} + t_{s} = \frac{x}{5} + \frac{\sqrt{2^{2} + {(5 - x)}^{2}}}{3}$

som var det vi ville frem til.

Mer om

Denne oppgaven er om

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

Pytagoras læresetning

For flere forklaringer og eksempler på Pytagoras læresetning, se artikkelen Pytagoras læresetning.

b)

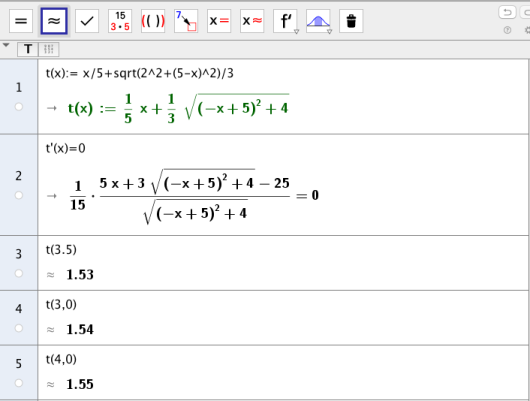
Bestem hvor Anne må velge punktet $B$ for å komme raskest fram til hytta. Hva er den korteste tiden hun kan bruke?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi vil finne når $t$ er minst. Vi kan enten løse oppgaven grafisk, ved hjelp av GeoGebra, hvor vi kan finne bunnpunktet til grafen, eller vi kan regne ut den deriverte til $t$ og finne eventuelle bunnpunkt ved å finne de stasjonære punktene når $t' (x) = 0$ , og finne verdien til $t$ i dette punktet. Her kan CAS være et nyttig hjelpemiddel.

Vi skal se hvordan vi kan løse oppgaven grafisk. I den alternative løsningen ser vi hvordan vi kan løse den ved å bruke CAS og finne den deriverte til $t$ .

Vi begynner med å skrive funksjonen inn i GeoGebra. Vi har at $x$ må ligge mellom $0$ og $5$ . Da skriver vi inn $𝚝 (𝚡) = 𝙵 𝚞 𝚗 𝚔 𝚜 𝚓 𝚘 𝚗 [𝚡 / 5 + 𝚜 𝚚 𝚛 𝚝 (2^{\land} 2 + (5 - 𝚡)^{\land} 2) / 3, 0, 5]$ i “Skriv inn”-feltet.

For å finne bunnpunktet til grafen skriver vi inn Min[t,0,5]. Da får vi opp grafen med punktet $(3, 5, 1, 53)$

Anne vil bruke minst tid når $x = 3, 5$ , altså når hun velger punktet $B$ $3, 5$ km fra $P$ . Da bruker hun $1, 53$ timer, ca $1$ time og $30$ min.

Alternativ

Vi kan også finne den minste verdien til $t$ ved regning. Da kan vi derivere funksjonen $t$ , og finne når $t' (x) = 0$ . For å finne $t' (x)$ kan vi bruke CAS. Vi begynner med å definere $t (x)$ ved å skrive inn

$𝚝 (𝚡) := 𝚡 / 5 + 𝚜 𝚚 𝚛 𝚝 (2^{\land} 2 + (5 - 𝚡)^{\land} 2) / 3$

i CAS. Nå kan vi skrive inn t’(x)=0 som er det vi vil regne ut, og deretter velger vi Løs numerisk.

$t' (x) = 0$ når $x = 3, 5$ , altså er $x = 3, 5$ et stasjonært punkt. Vi kan regne ut hvor lang tid hun brukte når $x = 3, 5$ ved å regne ut $t (3, 5)$ . Dette kan vi bruke CAS til, og da skriver vi inn t(3.5). Velger vi “Numerisk” får vi svaret som et desimaltall. Utregningen i CAS gir da at $t (3, 5) = 1.53$ , altså bruker hun $1, 53$ timer når hun velger $B$ til å være $3, 5$ km fra $P$ .

Vi vet bare at $x = 3, 5$ er gir et stasjonært punkt, og for å forsikre oss om at det er et bunnpunkt kan vi regne ut $t (3)$ og $t (4)$ og sjekke om disse verdiene er større. Dersom vi skriver det i CAS får vi at $t (3) = 1.54$ og $t (4) = 1, 55$ , så $x = 3, 5$ må gi et bunnpunkt.

Svar: Hun må velge punktet $B$ $3, 5$ km fra $P$ , da bruker hun $1, 53$ timer.

Mer om

Denne oppgaven er om

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på bunnpunkter, se artikkelen Topp- og bunnpunkter.

Oppgave 4 (6 poeng) Nettkode: E-4P44

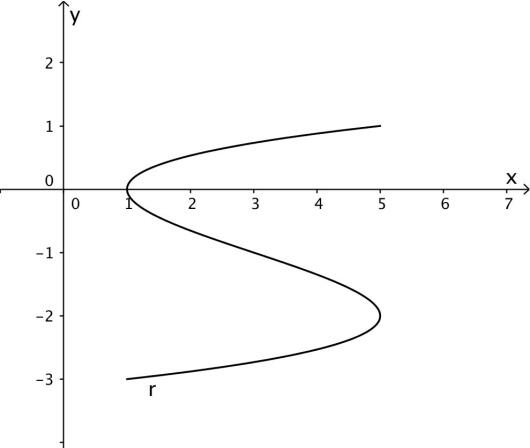
En partikkel beveger seg i en bane gitt ved

$\vec{r} (t) = [t^{3} - 3 t + 3, t - 1], - 2 \leq t \leq 2$

a)

Bruk graftegner til å tegne grafen til $\vec{r}$ i et koordinatsystem.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen til $\vec{r}$ .

For å tegne grafen til $\vec{r}$ kan vi bruke kommandoen Kurve[<Uttrykk>,<Uttrykk>, <Parametervariabel>, <Start>, <Slutt>] i GeoGebra. Da skriver vi inn

$𝚛 = 𝚔 𝚞 𝚛 𝚟 𝚎 [𝚝^{\land} 3 - 3 𝚝 + 3, 𝚝 - 1, 𝚝, - 2, 2]$

i “Skriv inn”-feltet.

Svar:

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Vektorfunksjon

En vektorfunksjon $\vec{r (t)}$ er en funksjon av en variabel t som gir en vektor fra origo for hver t:

$\vec{r (t)} = [x (t), y (t)]$

vektorfunksjoner

Graf

grafer

For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.

b)

Bestem posisjonen, banefarten og akselerasjonen når $t = 1$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan finne posisjonen ved å regne ut $\vec{r} (1)$ . Banefarten er absoluttverdien av fartsvektoren $\vec{v} (t) = \vec{r}' (t)$ . Akselerasjonvektoren $\vec{a} (t) = \vec{v}' (t) = \vec{r} ″ (t)$ finner vi ved å derivere fartsvektoren. Vi finner akselerasjonen ved å ta absoluttverdien av akselerasjonsvektoren.

Vi kan finne posisjon, banefart og akselerasjon når t=1 ved å bruke GeoGebra og CAS. I deloppgave a) definerte vi $\vec{r}$ og vi kan bruker GeoGebra-vindu. .

Posisjonen kan vi finne ved å skrive inn r(1) i “Skriv inn”-feltet i GeoGebra. Da får vi opp punktet A=(1,0).

Posisjonen til partikkelen er i punktet (1,0).

Vi kan finne fartsvektoren ved å bruke CAS. Vi velger “CAS” i “Vis”-menyen i GeoGebra. For å finne fartsvektorene skriver vi inn i CAS

$𝚟 (𝚝) := 𝚛' (𝚝)$

og for å finne når $t = 1$ skriver vi $𝚟 (1)$ . Vi finner banefarten. $| \vec{v (1)} |$ ved å skrive Lengde[v(1)]. Da får vi

Vi kan finne akselerasjonsvektoren ved å skrive $𝚊 (𝚝) := v' (t)$ i CAS. For å finne akselerasjonen skriver vi a(1) og finner $| \vec{a} (1) |$ ved å skrive Lengde[a(1)]. Vi får følgende i CAS

Alternativ

Vi kan finne posisjon, banefart og akselerasjon ved regning.

Vi begynner med posisjonen til partikkelen. Da kan vi sette inn for $t = 1$ i $\vec{r} (t)$ . Da får vi

$\vec{r} (1) = [1^{3} - 3 \cdot 1 + 3, 1 - 1] = [1 - 3 + 3, 0] = [1, 0]$ .

Posisjonen til partikkelen når $t = 1$ er punktet $(1, 0)$ .

For å finne fartsvektoren, $\vec{v} (t)$ når $t = 1$ må vi derivere $\vec{r} (t)$ . Da må vi derivere $x$ - og $y$ -komponenten hver for seg. Dette gir at

$\vec{v} (t) = \vec{r}' (t) = [(t^{3} - 3 t + 3)', (t - 1)'] = [3 t^{2} - 3, 1]$

Vi setter inn for $t = 1$ og får

$\vec{v} (1) = [3 \cdot 1^{2} - 3, 1] = [3 - 3, 1] = [0, 1]$ .

For å finne banefarten regner vi ut absoluttverdien $| \vec{v} (t) |$ .

$| \vec{v} (1) | = | [0, 1] | = \sqrt{1^{2} + 0^{2}} = 1$ .

Banefarten er $1$ .

Akselerasjonsvektoren $\vec{a} (t)$ er den deriverte av $\vec{v} (t)$ , så for å finne akselerasjonsvektoren må vi derivere $\vec{v} (t)$ komponentvis

$\vec{a} (t) = \vec{v}' (t) = [(3 t^{2} - 3)', (1)'] = [6 t, 0]$ .

Vi setter inn for $t = 1$ og får

$\vec{a} (1) = [6 \cdot 1, 0] = [6, 0]$ .

Vi finner akselerasjonen ved å finne absoluttverdien av $\vec{a} (t)$ .

$| \vec{a} (1) | = | [6, 0] | = \sqrt{6^{2} + 0^{2}} = 6$ .

Akselerasjonen er $6$ .

Svar: Posisjonen til partikkelen er $(1, 0)$ , banefarten er $1$ og akselerasjonen er $6$ .

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

Vektorfunksjon

En vektorfunksjon $\vec{r (t)}$ er en funksjon av en variabel t som gir en vektor fra origo for hver t:

$\vec{r (t)} = [x (t), y (t)]$

vektorfunksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på vektorfunksjoner, se artikkelen Derivasjon av vektorfunksjoner 1 - Parameterfremstilling.

c)

Bestem de punktene på grafen der fartsvektoren $\vec{v} (t)$ er parallell med $y$ -aksen

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

To vektorer er parallelle hvis $\vec{u} = k \cdot \vec{v}$ . En retningsvektor til $y$ -aksen er $[0, 1]$ .

Vi vil at fartsvektoren $\vec{v} (t)$ skal være parallell med $y$ -aksen som har retningsvektor $[0, 1]$ . For at de skal være parallelle må vi ha at

$\vec{v} (t) = [3 t^{2} - 3, 1] = k [0, 1]$ .

Vi ser at andre komponenten i begge vektorene er $1$ . For at vektorene skal være parallelle må vi da ha

$3 t^{2} - 3 = 0$ .

Denne likningen kan vi løse i CAS ved kommandoen "Løs[<Likning>,<Variabel>]" og skrive inn 𝙻ø𝚜[3𝚝^{^}2−3=0,𝚝], som gir

t = - 1 og t = 1

. Fartsvektoren er parallell med

y -aksen

i punktene

\vec{r} (- 1)

\vec{r} (1)

. Disse punktene finner vi ved å skrive

𝚛 (- 1)

𝚛 (1)

i samme CAS-vindu som i a) og b). Da får vi punktene

(5, - 2)

(1, 0)

Alternativ

Vi vil løse ligningen for t og da får vi

$\begin{matrix} 3 t^{2} - 3 & = & 0 \\ 3 t^{2} & = & 3 \\ t^{2} & = & 1 \\ t = 1 & \lor & t = - 1 \end{matrix}$

Fartsvektoren er altså parallell med $y$ -aksen når $t = 1$ og når $t = - 1$ . Vi setter inn for $t = - 1$ i $\vec{r} (t)$ og får

$\vec{r} (- 1) = [(- 1)^{3} - 3 (- 1) + 3, - 1 - 1] = [5, - 2]$ .

Fra deloppgave b) vet vi at $\vec{r} (1) = [1, 0]$ .

Svar: I punktene $(1, 0)$ og $(5, - 2)$

Mer om

Denne oppgaven er om

Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".

parallell

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektorer

, og

Retningsvektor

En linje $l$ går gjennom punktet $A (x_{0}, y_{0})$ og er parallell med vektoren $\vec{v} = [a, b]$ . Vektoren $\vec{v}$ kalles for retningsvektoren for linja.

retningsvektor

For flere forklaringer og eksempler på vektorer, se artikkelen Parallelle vektorer.

Oppgave 5 (2 poeng) Nettkode: E-4P4B

Funksjonen $f$ er gitt ved

$f (x) = x^{2} + 2 x - 11$

Noen punkter på grafen til $f$ har avstand $5$ fra origo. Bruk CAS til å bestemme de eksakte verdiene for $x$ -koordinatene til disse punktene.

Løs oppgaven her

Løsningsforslag

Jeg tenker

De punktene som har avstand $5$ fra origo vil skjære en sirkel med sentrum i origo og radius $5$ .

Siden de spør etter eksakte verdier kan vi ikke bruke grafdelen av GeoGebra.

Vi kan finne de punktene på grafen $f$ som har avstand $5$ fra origo ved å finne skjæringspunktene til $f$ og en sirkel $s$ , med sentrum i origo og radius $5$ . En sirkel kan skrives på formen $(x - x_{0})^{2} + (y - y_{0}) = r^{2}$ , der $(x_{0}, y_{0})$ er sentrum og $r$ er radius. Sirkelen $s$ har sentrum $(0, 0)$ og $r = 5$ , og kan da skrives på formen

$s : x^{2} + y^{2} = 5^{2} = 25$

Vi definerer $f (x)$ og $s$ i CAS ved å skrive

$𝚏 (𝚡) := 𝚡^{\land} 2 + 2 𝚡 - 11$

$𝚜 := 𝚡^{\land} 2 + 𝚢^{\land} 2 = 25$

For å finne skjæringspunktene mellom $f$ og $s$ skriver vi Skjæring[f,s]. For at vi skal få eksakte løsninger må vi ha "="-tegnet markert i CAS.

Da får vi

Svar: x-verdiene i disse punktene er $3, - 4, \frac{\sqrt{41} - 3}{2}$ og $\frac{- \sqrt{41} - 3}{2}$

Mer om

Denne oppgaven er om

Skjæringspunkt

skjæringspunkt

Sirkel

Sirkel brukes i to betydninger:

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

For flere forklaringer og eksempler på sirkler, se artikkelen Alt om sirkel.

REA3022 2016 HØST

Del 1

Del 2

Eksamensinformasjon

DEL 1 uten hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4P1K

a)

Løsningsforslag a)

Derivasjon

Polynom

b)

Løsningsforslag b)

Derivasjon

Logaritme

c)

Løsningsforslag c)

Derivasjon

Brøk

Oppgave 2 (5 poeng) Nettkode: E-4P2H

a)

Løsningsforslag a)

Polynom

Faktorisering av uttrykk

Nullpunkt

b)

Løsningsforslag b)

Terassepunkt

Fortegnsskjema

Toppunkt

Bunnpunkt

Fortegnsskjema

Derivasjon

c)

Løsningsforslag c)

Graf

Toppunkt

Bunnpunkt

Oppgave 3 (3 poeng) Nettkode: E-4P2E

a)

Løsningsforslag a)

Fellesnevner

Faktorisering

Konjugatsetningen

Fellesnevner

b)

Løsningsforslag b)

Brøk

Ligning

Faktorisering

Oppgave 4 (4 poeng) Nettkode: E-4P25

a)

Løsningsforslag a)

Eksponentialligning

Eksponentialligning

Eksponent

b)

Løsningsforslag b)

abc-formelen

Logaritme

abc-formelen

Oppgave 5 (6 poeng) Nettkode: E-4P37

a)

Løsningsforslag a)

Retningsvektor

Linje

Parallell

Vektorfunksjon

Retningsvektor

b)

Løsningsforslag b)

x-akse

Skjæringspunkt

Ligning

c)

Løsningsforslag c)

Vektor

Oppgave 6 (4 poeng) Nettkode: E-4P22

a)

Løsningsforslag a)

Alternativ