Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2017 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler på Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Hjelpemidler på Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 12 oppgaver. Del 2 har 7 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som «graftegner» og «CAS» skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4QUY
Regn ut og skriv svaret på standardform
Oppgave 2 (1 poeng) Nettkode: E-4QV0
Regn ut
Oppgave 3 (2 poeng) Nettkode: E-4QV3
Regn ut og skriv svaret så enkelt som mulig
Oppgave 4 (2 poeng) Nettkode: E-4QV5
Løs likningssystemet
Oppgave 5 (2 poeng) Nettkode: E-4QV7
Løs likningen
Oppgave 6 (2 poeng) Nettkode: E-4QV9
Skriv så enkelt som mulig
Oppgave 7 (4 poeng) Nettkode: E-4QVB
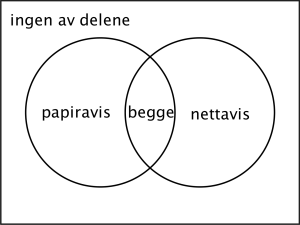
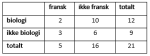
Ved en skole leser av elevene aviser på nett, leser papiraviser, og leser ikke aviser.
a)
Systematiser opplysningene gitt i teksten ovenfor i et venndiagram eller i en krysstabell.
b)
Bestem sannsynligheten for at en tilfeldig valgt elev ved skolen leser både aviser på nett og papiraviser.
c)
En elev ved skolen leser aviser på nett.
Bestem sannsynligheten for at denne eleven ikke leser papiraviser.
Oppgave 8 (2 poeng) Nettkode: E-4QVF
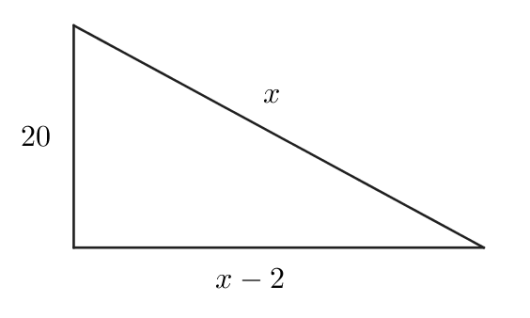
Om en rettvinklet trekant får du vite:
- Lengden av den korteste siden er
- Differansen mellom lengdene av de to andre sidene er
Hvor lang er den lengste siden i denne trekanten?
Oppgave 9 (4 poeng) Nettkode: E-4QVH
En funksjon er gitt ved
a)
Bestem den gjennomsnittlige vekstfarten til i intervallet
b)
Bestem den momentane vekstfarten til når
Oppgave 10 (2 poeng) Nettkode: E-4QVK
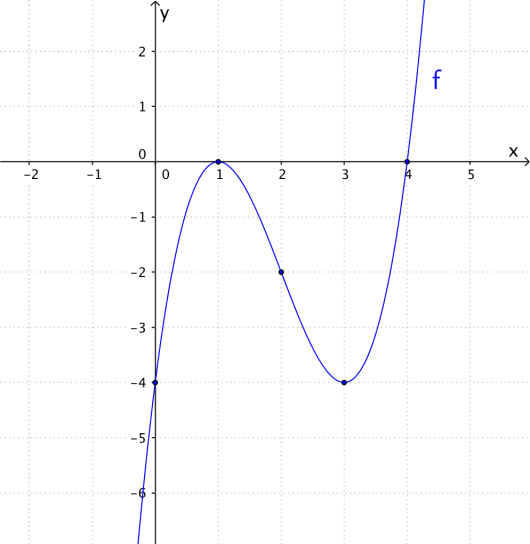
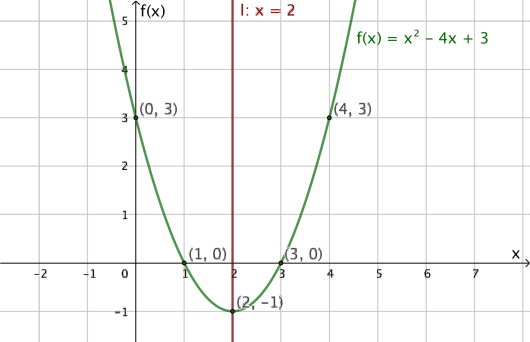
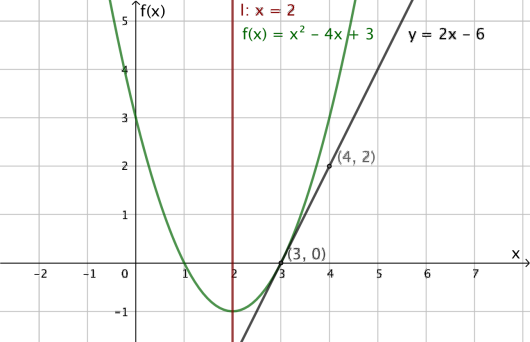
I koordinatsystemet ovenfor har vi tegnet grafen til en tredjegradsfunksjon .
Bruk den grafiske framstillingen til å løse ulikhetene
a)
b)
Oppgave 11 (8 poeng) Nettkode: E-4QVT
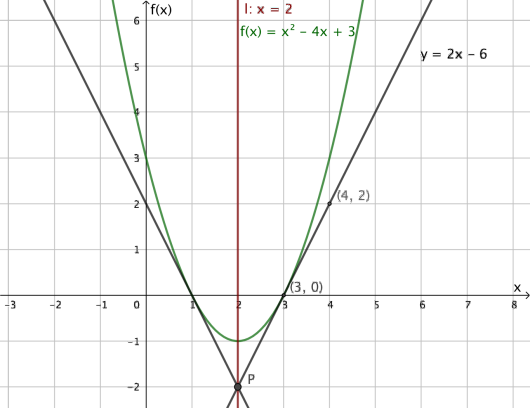
Funksjonen er gitt ved
a)
Bestem nullpunktene til .
b)
Grafen til er symmetrisk om en linje .
Tegn grafen til sammen med linjen i et koordinatsystem.
c)
Grafen til har en tangent med stigningstall .
Bestem likningen for denne tangenten.
Tegn tangenten i det samme koordinatsystemet som du brukte i oppgave b).
d)
Tangenten fra oppgave c) skjærer linjen i punktet . Grafen til har en annen tangent som også går gjennom punktet .
Skisser denne tangenten i samme koordinatsystem som du har brukt tidligere i oppgaven.
Bestem likningen for tangenten grafisk.
e)
Gjør beregninger og avgjør om likningen du fant i oppgave d), er riktig.
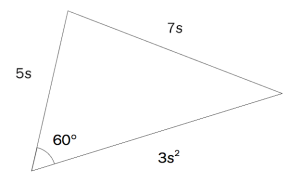
Oppgave 12 (5 poeng) Nettkode: E-4QVZ
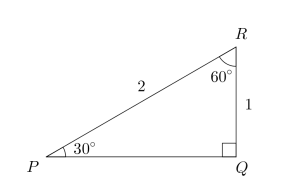
a)
Bruk ovenfor til å vise at
Videre i oppgaven kan du få bruk for noen av disse trigonometriske verdiene.
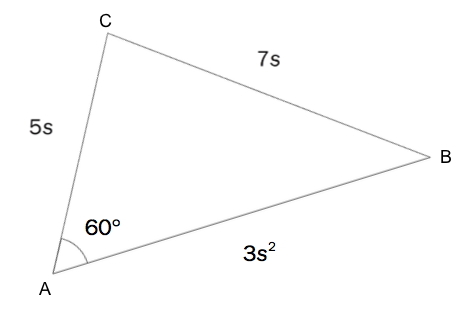
b)
I er og
Bestem arealet av .
c)
Vis at
DEL 2 Med hjelpemidler
Oppgave 1 (7 poeng) Nettkode: E-4QWD
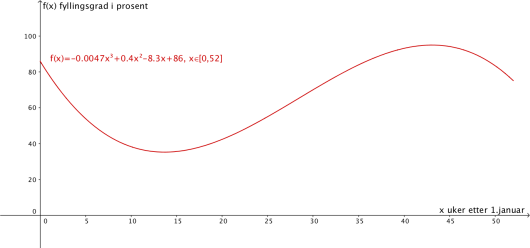
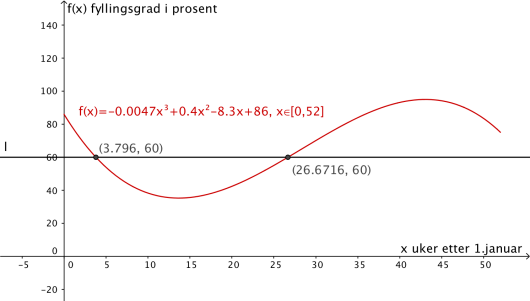
Funksjonen gitt ved
viser fyllingsgraden prosent i et vannmagasin uker etter . januar .
a)
Bruk graftegner til å tegne grafen til .
b)
I hvor mange uker var fyllingsgraden høyere enn ?
c)
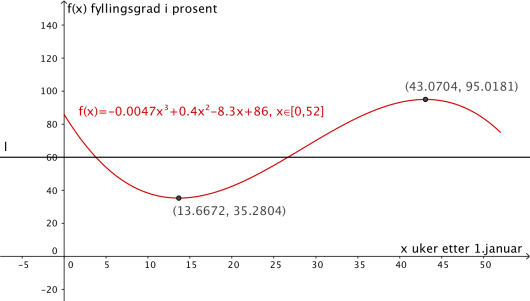
I hvilken uke var fyllingsgraden lavest?
Hvor stor del av vannmagasinet var fylt da?
d)
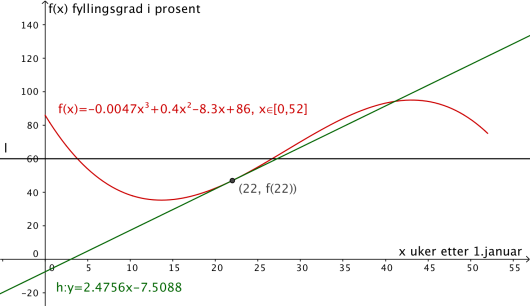
Bestem likningen for tangenten til grafen til i punktet .
Hva forteller stigningstallet til denne tangenten om fyllingsgraden i vannmagasinet?
Oppgave 2 (2 poeng) Nettkode: E-4QWJ
To voksne og tre barn betaler til sammen kroner for billetter til en kinoforestilling. En voksenbillett koster kroner mer enn en barnebillett.
Hvor mye koster en barnebillett, og hvor mye koster en voksenbillett?
Oppgave 3 (2 poeng) Nettkode: E-4QWL
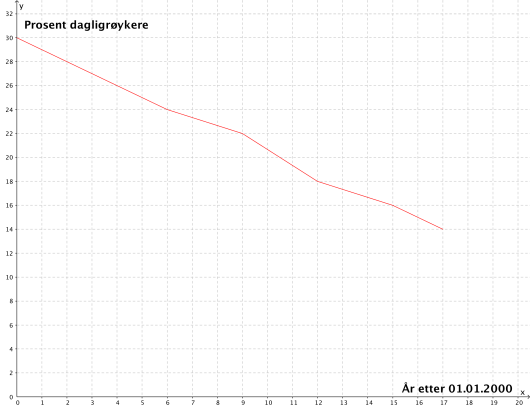
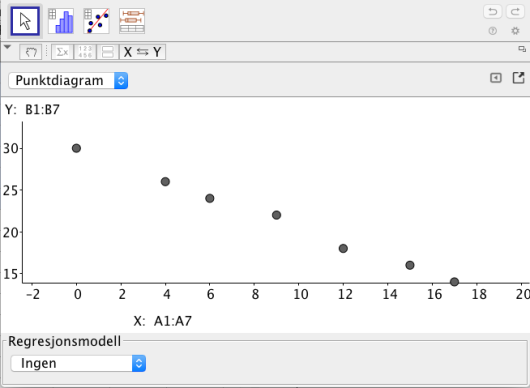
Linjediagrammet ovenfor viser hvordan andelen dagligrøykere ved en bedrift har avtatt i perioden .
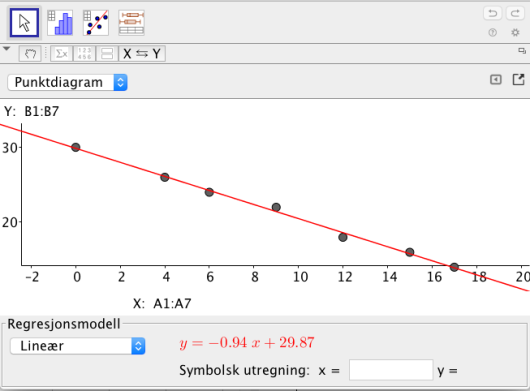
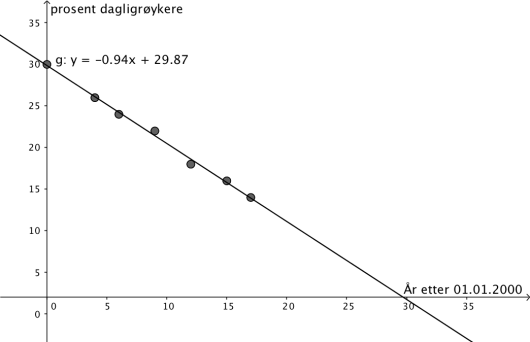
a)
Bestem en lineær modell som tilnærmet beskriver utviklingen.
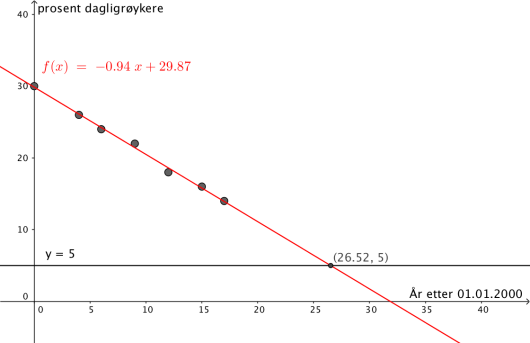
b)
Når vil andelen dagligrøykere ved bedriften være ifølge modellen i oppgave a)?
Oppgave 4 (4 poeng) Nettkode: E-4QWS
Ved et meieri blir det oppdaget en feil ved en av maskinene som skrur korker på kartongene. På kjølelageret er det kartonger med lettmelk og kartonger med helmelk. av kartongene med lettmelk og av kartongene med helmelk har ikke tett kork.
Tenk deg at du skal ta en kartong tilfeldig fra kjølelageret.
a)
Bestem sannsynligheten for at kartongen ikke har tett kork.
b)
Anta at du tar en kartong som ikke har tett kork.
Bestem sannsynligheten for at kartongen inneholder lettmelk.
Oppgave 5 (2 poeng) Nettkode: E-4QX1
Gitt trekanten ovenfor.
Bruk CAS til å bestemme .
Oppgave 6 (3 poeng) Nettkode: E-4QX3
En funksjon er gitt ved
Bruk CAS til å
- vise at grafen til har et nullpunkt og et stasjonært punkt i
- avgjøre om er et toppunkt, et bunnpunkt eller et terrassepunkt
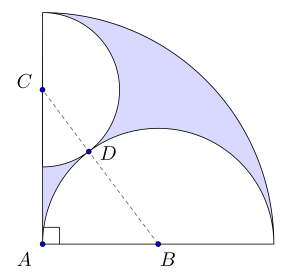
Oppgave 7 (4 poeng) Nettkode: E-4QX7
Figuren ovenfor viser
- en halvsirkel med sentrum i og radius
- en halvsirkel med sentrum i og radius
- en kvart sirkel med sentrum i og radius
De to halvsirklene tangerer hverandre i punktet . Punktet ligger på linjen gjennom og .
a)
Bruk Pytagoras’ setning til å vise at
b)
Bruk CAS til å bestemme arealet av det blå området på figuren uttrykt ved .