Å finne tangenten - introduksjon

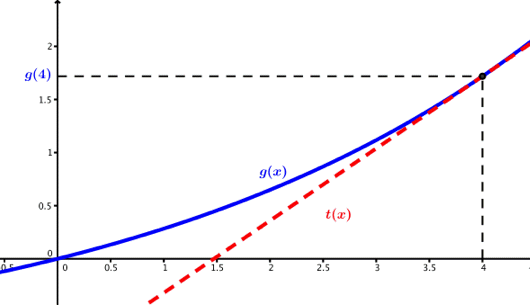
La funksjonen $g\left(x\right)=e^{\frac{x}{4}}-1$ beskrive pengene i sparekontoen din over tid. Du lurer på hvordan summen kommer til å utvikle seg hvis den fortsetter å vokse nøyaktig slik den vokser etter 4. Du vil finne en funksjon som beskriver denne utviklingen. Denne funksjonen skal ha samme stigning som $g\left(x\right)$ har etter 4 måneder og ha samme verdi i det punktet, altså $g\left(x\right)$.

Vi er da ute etter 

$t\left(x\right)$ til $g\left(x\right)$ i $x=4$. Tangenten er en lineær funksjon, så den har formen $t\left(x\right)=ax+b$. Vår oppgave er å finne tallene $a$ og $b$ som gir riktig funksjon.

Vi vet at tangenten skal ha samme stigningstall $a$ som stigningen til $g\left(x\right)$ i $x=4$ (etter 4 måneder), så vi finner den deriverte av $g\left(x\right)$ i 4.

 $g\text{'}\left(x\right)=\frac{1}{4}{e}^{\frac{x}{4}}$

 $g\text{'}\left(4\right)=\frac{1}{4}e\approx 0,68$

så $a=0.68$.

Nå har vi $t\left(x\right)=0,68x+b$. Vi vet at tangenten tangerer $g\left(x\right)$ i $x=4$, altså må $g\left(4\right)=t\left(4\right)$.

 $g\left(4\right)=t\left(4\right)$

 $e^{\frac{4}{4}}-1=\frac{1}{4}e\cdot 4+b$

 $b=-1$

Vi har da funnet tangenten $t\left(x\right)=0,68x-1$ (For å tegne funksjonen holder det å bruke den avrundede verdien for A).

 

Generelt: Vi vil finne tangenten $f\left(x\right)$ til en funksjon $f\left(x\right)$ i et punkt $x=c$.

Tangenten har formen $t\left(x\right)=ax+b$. $a$ er stigningstallet, og det må være den samme som stigningen til $f\left(x\right)$ i punktet $c$. Dermed har vi at

            $a=f\text{'}\left(c\right)$

funksjonene $t\left(x\right)$ og $f\left(x\right)$ skal berøre hverandre i $x=c$, altså har vi

            $f\left(c\right)=t\left(c\right)$

            $a=f\text{'}\left(c\right)$

            $a=f\text{'}\left(c\right)$

            $b=f\left(c\right)-f\text{'}\left(c\right)c$

Nå har vi en generell formel for tangenten $t\left(x\right)$ til en funksjon $f\left(x\right)$ i punktet $x=c$:

            $t\left(x\right)=ax+b$

            $a=f\text{'}\left(c\right)$

            $b=f\left(c\right)-f\text{'}\left(c\right)c$

Eksempel

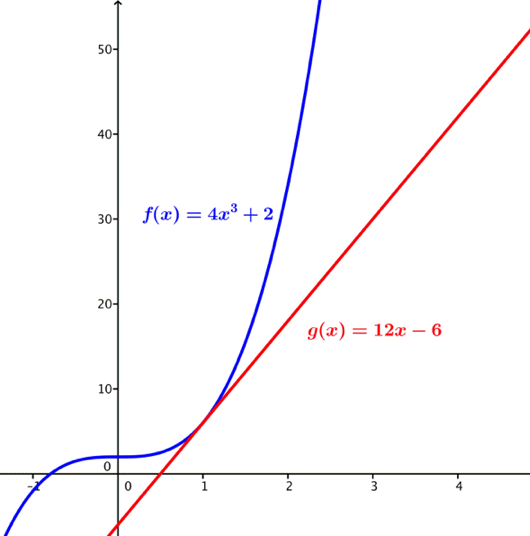
Oppgave. Finn tangenten til $f\left(x\right)=4x^3+2$ i $1$.

Løsning.

Vi starter med å derivere $f$: $f\text{'}\left(x\right)=4\cdot 3x^2$

Vi får altså

$a=f\text{'}\left(1\right)=4\cdot 3\cdot 1^2=12$

$b=f\left(c\right)-f\text{'}\left(c\right)c=6-12=-6$

Så vi får $g\left(x\right)=12x+6$.