Venn-diagram og mengdelære
Hva mener vi med unionen og snittet av to mengder? Hva er et Venn-diagram, og hva brukes det til?
Husk at et utfallsrom består av alle mulige utfall i et forsøk. Tenk at vi tegner opp hele utfallsrommet U som et rektangel, og innholdet i rektangelet skal representere alle elementene i utfallsrommet. Deretter tegner vi begivenheter som sirkler inne i utfallsrommet. Dette kalles et Venn-diagram, og er en abstrakt måte å representere utfall på. Dette betyr at man ikke skal henge seg opp i akkurat hvor ting er plassert, det viktige i et Venn-diagram er at det viser forholdet mellom utfall.
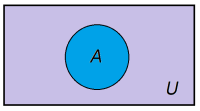
Venn-diagrammet for en begivenhet A ser ut som:
Anta nå at A og B er to begivenheter i utfallsrommet U. Det er lurt å repetere definisjonen av union, snitt, differanse, kompliment og disjunkte mengder. Begrepene kan du finne under Begrep til høyre.
La oss nå se på noen spesielle egenskaper ved blant annet union og snitt.
- Unionen mellom en mengde og hele utfallsrommet er alltid lik utfallsrommet, altså .
- Snittet av en mengde og hele utfallsrommet er alltid lik mengden du startet med, altså .
- En mengde og sitt komplement er alltid disjunkte, og unionen av dem danner hele utfallsrommet. Kort notert: og .
- For disjunkte mengder og er og .
Eksempel.
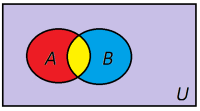
La utfallsrommet være U = {rød, hvit, blå, gul, grønn, svart }, begivenheten A = {rød, gul }, begivenheten B = {blå, gul } og begivenheten C = {hvit }. Vi tegner A og B i et Venn-diagram, der vi lar hvit, grønn og svart representeres samlet ved en lilla farge.
Unionen av A og B er lik det røde, blå og gule området dekket av de to sirklene, {rød, gul, blå }.
Snittet av A og B er det gule området som er i både A og B, {gul }.
Differansen mellom B og A er det området som er med i A, men ikke i B, altså det røde området. {rød }.
Differansen mellom A og B er det området som er med i B, men ikke i A, altså det blå området. {blå }.
Komplementet til A er hele området i utfallsrommet som ikke er A, altså de blå og lilla områdene. Som vi sa består det lilla området av alle utfallene i hele utfallsrommet bortsett fra A og B, det vil si hvit, grønn og svart. Derfor er {blå, hvit, grønn, svart}.
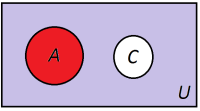
Hvis vi ser på tilsvarende for begivenhetene A og C, ser Venn-diagrammet annerledes ut. Dette skyldes at begivenhetene A og C er disjunkte. Hvis vi nå lar det lilla området representere blå, gul, grønn og svart kan Venn-diagrammet for A og C tegnes som:
Prøv nå selv å finne og .
Svar:
{rød, gul, hvit }
{}
{rød, gul }
{hvit }
{rød, blå, gul, grønn, svart }
{rød, hvit, blå, gul, grønn, svart }
{rød, gul }
Del på Facebook
Lynkurs 11.-13.trinn
Sannsynlighet (del II)
Består av:
- Repetisjon av begreper
- Hvordan finner vi uniform sannsynlighet?
- Venn-diagram og mengdelære
- Addisjonssetningen
- Sannsynlighet ved komplementære hendelser
- Betinget sannsynlighet og produktsetningen
- Bayes-setningen
- Uavhengige hendelser og produktsetningen
- Ikke-uniforme sannsynlighetsmodeller
- Ordnede utvalg
- Uordnede utvalg uten tilbakelegging
- Binomiske forsøk
- Hypergeometriske forsøk
Begrep
-
Differanse (mengder)
Differansen mellom mengden A og mengden B betegnes med og er mengden av alle elementer som er i B men ikke i A.
-
Disjunkte hendelser
A og B kalles disjunkte dersom de ikke har noen felles elementer. Dette betyr at , altså at det ikke er noen elementer som er både i A og i B.
-
Komplement
Komplementet til A, betegnet med , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, .
-
Snitt
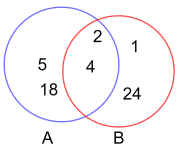
Snittet av to mengder A og B er en ny mengde som består av alle elementer som forekommer både i A og B.
Eksempel:
-
Union

Unionen av to mengder A og B er en ny mengde som består av alle elementer som forekommer i minst en av A og B.
Eksempel: hvis er to mengder, blir unionen .
-
Utfall
Mulig resultat av en hendelse.
Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.
-
Utfallsrom
Alle mulige utfall en hendelse kan ha. Utfallsrom betegnes med .
Eksempel: Karakterer på en matematikkprøve har utfallsrommet .