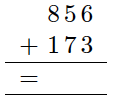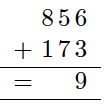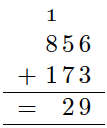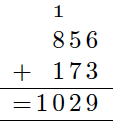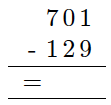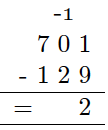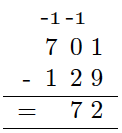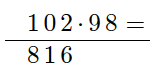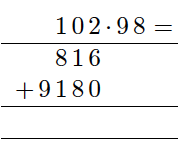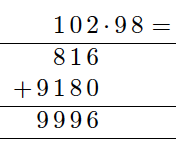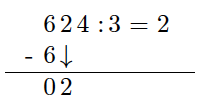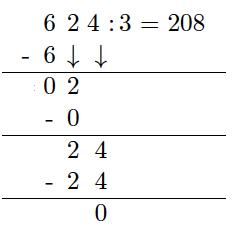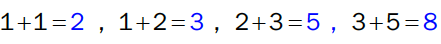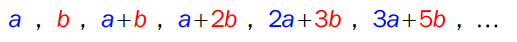Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT0010 2016 VÅR

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:
5 timer totalt. Del 1 og Del 2 skal deles ut samtidig.

Del 1 skal du levere innen 2 timer.

Del 2 skal du levere innen 5 timer.

Hjelpemidler på Del 1:
Ingen hjelpemidler er tillatt, bortsett fra vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Hjelpemidler på Del 2:
Før Del 1 er levert inn, er ingen hjelpemidler tillatt, bortsett fra vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Etter at Del 1 er levert inn, er alle hjelpemidler tillatt, med unntak av Internett eller andre verktøy som tillater kommunikasjon.

Framgangsmåte og forklaring:
Del 1 har 16 oppgaver. Du skal svare på alle oppgavene. Skriv med penn når du krysser av eller fører inn svar i Del 1.

Del 2 har 9 oppgaver. Du skal svare på alle oppgavene.

I regneruter skal du vise hvordan du kommer fram til svaret.

Ved konstruksjon skal du bruke passer, linjal og blyant.

Du skal ikke kladde på oppgavearkene. Bruk egne kladdeark.

På flervalgsoppgavene setter du bare ett kryss per spørsmål.

Eksempel:

Uttrykket $3 \cdot {(1 + 2 \cdot 2)}^{2}$ har verdien:

35 50 62 75

○ ○ ○ ⊗

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Vis hvordan du har kommet fram til svarene.

Før inn nødvendige mellomregninger. Skriv med penn.

I regnearkoppgaver skal du ta utskrift av det ferdige regnearket. Husk å vise hvilke formler du har brukt i regnearket.

Du skal levere utskriften sammen med resten av besvarelsen.

Dersom du bruker en digital graftegner, skal skala og navn på aksene være med på utskriften.

Veiledning om vurderingen:
Den høyeste poengsummen i Del 1 er 24 og den høyeste poengsummen i Del 2 er 36, men den er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering på grunnlag av Del 1 og Del 2. Sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er kreativ og kan anvende fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger: Kildelister for bilder, tegninger mv.:

Hjelpemidler på Del 1 (Utdanningsdirektoratet)
Elektron, sykkel (www.openclipart.com, 5.07.2016)
Passer (www.freeimages.com, 5.07.2016)
Euro, kodelås, bil (www.openclipart.co,. 5.07.2016)
Italienske varmretter: www.ica.no (02.09.2015)
«Det siste måltid»: www.philvaz.com (20.01.2016)
«Den vitruviske mann»: www.world-mysteries.com (20.01.2016)
Palazzo Vendramin-Calergi, Galilei, da Vinci og Fibonacci og andre illustrasjoner: Utdanningsdirektoratet
Andre bilder, tegninger og figurer: Utdanningsdirektoratet

Eksamenstid:
5 timer totalt. Del 1 og Del 2 skal deles ut samtidig.

Del 1 skal du levere innen 2 timer.

Del 2 skal du levere innen 5 timer.

Hjelpemidler på Del 1:
Ingen hjelpemidler er tillatt, bortsett fra vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Framgangsmåte og forklaring:
Del 1 har 16 oppgaver. Du skal svare på alle oppgavene. Skriv med penn når du krysser av eller fører inn svar i Del 1.

Del 2 har 9 oppgaver. Du skal svare på alle oppgavene.

I regneruter skal du vise hvordan du kommer fram til svaret.

Ved konstruksjon skal du bruke passer, linjal og blyant.

Du skal ikke kladde på oppgavearkene. Bruk egne kladdeark.

På flervalgsoppgavene setter du bare ett kryss per spørsmål.

Eksempel:

Uttrykket $3 \cdot {(1 + 2 \cdot 2)}^{2}$ har verdien

35 50 62 75

○ ○ ○ ⊗

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Vis hvordan du har kommet fram til svarene.

Før inn nødvendige mellomregninger. Skriv med penn.

I regnearkoppgaver skal du ta utskrift av det ferdige regnearket. Husk å vise hvilke formler du har brukt i regnearket.

Du skal levere utskriften sammen med resten av besvarelsen.

Dersom du bruker en digital graftegner, skal skala og navn på aksene være med på utskriften.

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er kreativ og kan anvende fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinge

Eksamenstid:
5 timer totalt. Del 1 og Del 2 skal deles ut samtidig.

Del 1 skal du levere innen 2 timer.

Del 2 skal du levere innen 5 timer.

Hjelpemidler på Del 1:
Ingen hjelpemidler er tillatt, bortsett fra vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Framgangsmåte og forklaring:
Del 1 har 16 oppgaver. Du skal svare på alle oppgavene. Skriv med penn når du krysser av eller fører inn svar i Del 1.

Del 2 har 9 oppgaver. Du skal svare på alle oppgavene.

I regneruter skal du vise hvordan du kommer fram til svaret.

Ved konstruksjon skal du bruke passer, linjal og blyant.

Du skal ikke kladde på oppgavearkene. Bruk egne kladdeark.

På flervalgsoppgavene setter du bare ett kryss per spørsmål.

Eksempel:

Uttrykket $3 \cdot {(1 + 2 \cdot 2)}^{2}$ har verdien

35 50 62 75

○ ○ ○ ⊗

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Vis hvordan du har kommet fram til svarene.

Før inn nødvendige mellomregninger. Skriv med penn.

I regnearkoppgaver skal du ta utskrift av det ferdige regnearket. Husk å vise hvilke formler du har brukt i regnearket.

Du skal levere utskriften sammen med resten av besvarelsen.

Dersom du bruker en digital graftegner, skal skala og navn på aksene være med på utskriften.

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er kreativ og kan anvende fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinge

På flervalgsoppgavene setter du bare ett kryss per spørsmål.

Eksempel:

Uttrykket $3 \cdot {(1 + 2 \cdot 2)}^{2}$ har verdien

35 50 62 75

○ ○ ○ ⊗

På flervalgsoppgavene setter du bare ett kryss per spørsmål.

Eksempel:

Uttrykket $3 \cdot {(1 + 2 \cdot 2)}^{2}$ har verdien

35 50 62 75

○ ○ ○ ⊗

På flervalgsoppgavene setter du bare ett kryss per spørsmål.

Eksempel:

Uttrykket $3 \cdot {(1 + 2 \cdot 2)}^{2}$ har verdien

Del 1 uten hjelpemidler

Oppgave 1 (2 poeng) Nettkode: E-4FV8

Regn ut

a)

$856 + 173 =$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Dette er et addisjonsstykke med flersifrede tall.

Vi setter opp tallene:

Vi starter med enerplassen. Summen av $6$ og $3$ er $9$ , så vi setter $9$ på enerplassen:

Vi gjør det samme på tierplassen, men her ser vi at vi får $12$ og da setter vi $2$ på tierplassen og flytter $1$ opp til hundrere:

Vi legger nå sammen alle hundrerne og får:

Svar: $1029$

Mer om

Denne oppgaven er om

Addisjon

Er det samme som å legge til, legge sammen eller plusse sammen.

Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
Tallene 5 og 7 kalles ledd, og resultatet, 12, kalles en sum.
Mellom leddene skrives plusstegn +.

addisjon

Flere forklaringer og eksempler på hvordan man adderer flersifrede tall, finner du i artikkelen Addisjon.

For å øve mer, se oppgavesettet Addisjon i Treningsleieren.

b)

$701 - 129 =$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Dette er et subtraksjonsstykke med store tall.

Vi setter opp tallene over hverandre:

Vi starter med enerplassen. $9$ er større enn $1$ , så vi må ’veksle’ en tier fra tierplassen. Da får vi stykket $11 - 9 = 2$ , så:

På tierplassen blir stykket nå $0 - 3$ , siden $3$ er større enn $0$ må vi ’veksle’ en hundrer fra hundreplassen.

Til slutt regner vi ut hva som skal stå på hundreplassen.

Svar: $572$

Mer om

Denne oppgaven er om

Subtraksjon

En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen.

subtraksjon

Flere forklaringer og eksempler på hvordan man subtraherer med flersifrede tall, finner du i artikkelen Subtraksjon.

For å øve mer, se oppgavesettet Subtraksjon i Treningsleieren.

c)

$102 \cdot 98 =$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Dette er et multiplikasjonsstykke med flersifrede tall.

Vi setter opp regnestykket:

$102 \cdot 98 =$

Vi multipliserer ett og ett siffer fra faktoren til høyre inn i faktoren til venstre. Vi starter med å multiplisere inn $8$ :

Nå multipliserer vi $9$ med faktoren til venstre. Setter en null under sifferet lengst til høyre, for å markere at vi har flyttet oss fra enerplassen til tierplassen:

Nå adderer vi tallene:

Svar: $9996$

Mer om

Denne oppgaven er om

Multiplikasjon

Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".

Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.

Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.

Eksempel: 3 · 4 = 12 og 4 · 3 = 12

Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).

multiplikasjon

Flere forklaringer og eksempler på hvordan man multipliserer, finner du i artikkelen Multiplikasjon.

For å øve mer, se oppgavesettet Multiplikasjon i Treningsleieren.

d)

$624 : 3 =$

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Dette er divisjon med flersifret tall.

Vi setter opp stykket:

$624 : 3 =$

Vi ser på dividenden. Vi kan dividere $6$ med $3$ og vi får $6 : 3 = 2$ . Vi skriver $2$ i resultatet, og trekker fra $6$ :

Vi dividerer $2$ med $3$ , og får $0$ . Vi tar ned siste siffer. Vi ser at $24 : 3 = 8$ og vi setter $8$ i resultatet:

Svar: $208$

Mer om

Denne oppgaven er om

Divisjon

Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.

Eksempel: $6 : 2 = 3$ fordi $2 \cdot 3 = 6$ .

divisjon

Flere forklaringer og eksempler på hvordan man dividerer, finner du i artikkelen Divisjon.

For å øve mer, se oppgavesettet Divisjon i Treningsleieren.

Visste du at?

Når vi dividerer et tall med noe som er mindre enn $1$ , så blir svaret større enn tallet vi startet med! Du kan tenke deg at vi har $5$ meter tau, og alle skal få en halv meter tau hver. Da har vi nok til at $10$ personer får en taubit.

Oppgave 2 (1 poeng) Nettkode: E-4FVD

Gjør om

a)

$4 550 mm =$ ____ $m$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

$1$ meter er $1000$ millimeter. Derfor er $1$ mm det samme som $0, 001$ m.

$4550$ mm $= 4550 \cdot 0, 001$ m $= 4, 55$ m.

Svar: $4550 mm$ er $4, 55 m$ .

Mer om

Denne oppgaven er om

Benevning

En bokstavkode som står etter måltallet. Eksempelvis forteller 25,2 kg, at vi har med masse å gjøre. Benevningen kg er en forkortelse for kilogram. Måltallet (25,2) forteller oss noe om mengden.

Eksempel på andre benevninger:
g, dL, h, km/h, g/cm³

benevning

Lengdeenhet

Måleenheten for lengde er meter med forkortelsen m. Andre lengdemål avledet av meter er: kilometer (km), desimeter (dm), centimeter (cm) og millimeter (mm).

lengdeenhet

Flere forklaringer og eksempler på hvordan man regner mellom lengdeenheter, finner du i artikkelen Lengdeenheter.

For å øve mer, se oppgavesettet Lengdeenheter i Treningsleieren.

b)

$0, 8 kg =$ ____ $g$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

$1$ kg er $1000$ g.

$0, 8$ kg $= 0, 8 \cdot 1000$ g $= 800$ g

Svar: $0, 8 kg$ er $800 g$ .

Mer om

Denne oppgaven er om

Benevning

Eksempel på andre benevninger:
g, dL, h, km/h, g/cm³

benevning

Flere forklaringer og eksempler på hvordan man regner mellom volumenheter, finner du i artikkelen Volumenheter.

For å øve mer, se oppgavesettet Måleneheter i Treningsleieren.

Visste du at?

Kilo er gresk og betyr tusen. Så derfor er et KILOgram lik tusen gram!

Oppgave 3 (0,5 poeng) Nettkode: E-4FVO

Hvilket uttrykk har den laveste verdien?

${(- 3)}^{2}$
$\frac{20}{2 + 3}$
$2 + 2^{2}$
$- 2^{2} + 6$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi må regne ut og finne hvilket uttrykk har svar med lavest verdi.

$(- 3)^{2} = (- 3) \cdot (- 3) = 9$

Neste uttrykk er lik:

$\frac{20}{2 + 3} = \frac{20}{5} = 20 : 5 = 4$

Nest siste uttrykk er det samme som:

$2 + 2^{2} = 2 + 2 \cdot 2 = 2 + 4 = 6$

Og siste uttrykk er lik:

$- 2^{2} + 6 = - 2 \cdot 2 + 6 = - 4 + 6 = 2$

Svar: $- 2^{2} + 6$

Mer om

Denne oppgaven er om

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$

potens

Flere forklaringer og eksempler på hvordan man regner med potenser, finner du i lynkurset Potenser.

For å øve mer, se oppgavesettet Potenser i Treningsleieren.

Oppgave 4 (1 poeng) Nettkode: E-4FVY

Regn ut, og skriv svaret som en mest mulig forkortet brøk:

a)

$\frac{1}{6} + \frac{2}{6} =$ ____

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Brøkene har fellesnevner, så vi kan skrive felles brøkstrek og addere tellerne.

Først lager vi felles brøkstrek og adderer

$\frac{1}{6} + \frac{2}{6} = \frac{1 + 2}{6} = \frac{3}{6}$

Så forkorter vi brøken:

$\frac{3}{6} = \frac{3}{3 \cdot 2} = \frac{1}{2}$

Svar: $\frac{1}{2}$

Mer om

Denne oppgaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

, forkorting av brøk,

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

nevner

Teller

Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.

Eksempel: I brøken $\frac{5}{9}$ , er det 5 som er telleren. 9 kalles nevner.

teller

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

fellesnevner

Flere forklaringer og eksempler på hvordan man regner med brøk, finner du i artikkelen Addisjon og subtraksjon med brøk.

For å øve mer, se oppgavesettet Brøkregning - fellesnevneren i Treningsleieren.

b)

$\frac{4}{5} - 0, 4 =$ ____

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her har vi en brøk og et desimaltall. Fordi vi skal oppgi svaret som en brøk, må vi først gjøre desimaltallet om til brøk. Deretter må vi finne fellesnevner ved å utvide brøkene. Husk alltid å sjekke om en av nevnerne kan være fellesnevner.

$0, 4$ er det samme som $\frac{4}{10}$ . Fordi $10 = 5 \cdot 2$ , er $10$ fellesnevner.

Vi utvider brøken $\frac{4}{5}$ ved å multiplisere med $2$ over og under brøkstreken, og subtraherer tellerne:

$\frac{4}{5} - \frac{4}{10} = \frac{4 \cdot 2}{5 \cdot 2} - \frac{4}{10} = \frac{8 - 4}{10} = \frac{4}{10}$

Så fortkorter vi brøken:

$\frac{4}{10} = \frac{2 \cdot 2}{2 \cdot 5} = \frac{2}{5}$

Svar: $\frac{2}{5}$

Mer om

Denne oppgaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

Brøk

, Forkorte brøk,

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

Nevner

Teller

Fellesnevner

Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.

Eksempel: $\frac{2}{21} + \frac{1}{6} = \frac{4}{42} + \frac{7}{42}$ , 42 er fellesnevner for disse to brøkene.

Fellesnevner

Flere forklaringer og eksempler på hvordan man regner med brøk, finner du i artiklene Addisjon og subtraksjon med brøk og Forkorte og utvide brøk.

For å øve mer, se oppgavesettene Brøkregning - utvidelse og Brøkregning - forkorting i Treningsleieren.

Oppgave 5 (0,5 poeng) Nettkode: E-4FW1

Hvilket tall har den høyeste verdien?

$0, 9$
$0, 10$
$0, 89$
$0, 1980$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Alle tallene er desimaltall. Husk at jo større tall står nærmest kommaet, desto nærmere er desimaltallet tallet $1$ .

ener		tidel	hundredel	tusendel	titusendel
0	,	9
0	,	1	0
0	,	8	9
0	,	1	9	8	0

Vi sammenligner siffrene på tidelsplassen. Tallet med høyest verdi har siffer med høyest verdi på denne plassen. Det er derfor $0, 9$ .

(Legg merke til at $0, 10$ og $0, 1980$ har $1$ på tidelsplassen. For å finne ut hvilket av disse har høyest verdi, ser vi på neste plass, hundredeler. Sifferet for hundredeler er $0 i 0, 10 og 9 i 0,198$ . Derfor har $0, 1980$ høyere verdi enn $0, 10$ .)

Oppsumert: $0, 10 < 0, 1980 < 0, 89 < 0, 9$

Svar: $0, 9$

Mer om

Denne oppgaven er om

Desimaltall

Desimaltall er tall som inneholder komma.

Eksempel: 2,34 og 18,001

Sifrene som følger etter komma, kalles desimaler.

desimaltall

Flere forklaringer og eksempler finner du i artikkelen Addisjon og subtraksjon av desimaltall.

For å øve mer, se oppgavesettet Desimaltall i Treningsleieren.

Oppgave 6 (0,5 poeng) Nettkode: E-4FW3

Massen til et elektron er ca. $0, 000 000 000 000 000 000 000 000 000 000 91 kg$

På standardform skriver vi dette tallet som

$91 \cdot 10^{- 33} kg$
$91 \cdot 10^{32} kg$
$9, 1 \cdot 10^{31} kg$
$9, 1 \cdot 10^{- 31} kg$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Standardform betyr å skrive tallet som produkt av et tall mellom $0$ og $10$ , og en tierpotens.

Vi flytter komma til vi bare har ett siffer foran komma, og multipliserer med like mange tiere som antallet plasser vi flyttet komma. Men legg merke til at massen er veldig lite desimaltall og derfor multipliserer vi her med en negativ potens av $10$ .

Husk at for eksempel $3 \cdot 10^{2} = 3 \cdot 100 = 300$ , mens $3 \cdot 10^{- 2} = 3 \cdot 0, 01 = 0, 03 .$

Vær lur og tell først alle nullene som står mellom komma og $91$ . Det er $30$ av disse og derfor først skriver vi:

$0, 00000000000000000000000000000091 = 0, 91 \cdot 10^{- 30}$

Men standardform betyr at tallet er mellom $0$ og $10$ og derfor er: $0, 00000000000000000000000000000091 = 0, 91 \cdot 10^{- 30} = 9, 1 \cdot 10^{- 31}$

Svar: $9, 1 \cdot 10^{- 31} kg$

Mer om

Denne oppgaven er om

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

standardform

Flere forklaringer og eksempler på standardform finner du i artikkelen Tall på standardform.

For å øve mer, se oppgavesettet Tall på standardform i Treningsleieren.

Oppgave 7 (2 poeng) Nettkode: E-4FWD

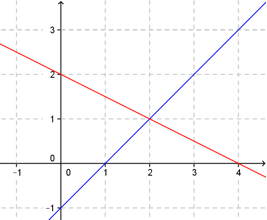
Skriv funksjonsuttrykket til $f$ og $g$

$f (x) =$ ____

$g (x) =$ ____

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ser at begge grafene er rette linjer. Dette betyr at funksjonsuttrykkene er på formen $a x + b$ der $a$ er stigningstall og $b$ er der funksjonen skjærer $y$ -aksen.

Vi begynner med funksjonen $g (x)$ (den røde). Vi ser at grafen skjærer $y$ - aksen i punktet $(0, 2)$ . Dette betyr at $b = 2$ og vi kan derfor skrive $g (x) = a x + 2$ . Grafen skjærer $x - a k s e n$ i punktet $(4, 0)$ . Så når $g = 0$ er $x = 4$ . Vi setter inn disse verdiene funksjonsuttrykket og løser likningen med hensyn på $a$ : $a \cdot 4 + 2 = 0$

$4 a + 2 = 0$

$4 a + 2 - 2 = 0 - 2$

$4 a = - 2$ $a = - \frac{2}{4}$

$a = - \frac{1}{2}$

Da har vi at $g (x) = - \frac{1}{2} x + 2$ .

På tilsvarende måte finner vi uttrykket for $f$ (den blå). Vi vet at vi kan skrive $f$ som $f (x) = a x + b$ . vi må finne $a$ og $b$ . Her ser vi at $f$ skjærer $y$ - aksen i $(0, - 1)$ og det betyr at $b = - 1$ og $f (x) = a x - 1$ . For å finne $a$ , ser vi at grafen skjærer $x$ -aksen i $(1, 0)$ . Dette betyr at når $x = 1$ er $f = 0$ . Da kan vi skrive dette som en likning:

$a \cdot 1 - 1 = 0$

$a - 1 + 1 = 0 + 1$

$a = 1$

Funksjonen $f (x) = 1 \cdot x - 1 = x - 1$ .

Svar: $g (x) = - \frac{1}{2} x + 2$ og $f (x) = x - 1$

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Flere forklaringer og eksempler på forholdet mellom grafer og funksjoner finner du i artikkelen Fra en graf til en funksjon.

For å øve mer, se oppgavesettet Lineære funksjoner i Treningsleieren.

Oppgave 8 (1 poeng) Nettkode: E-4FWG

En sykkel koster $3 500 kr$ . Du får $20 %$ rabatt (prisavslag).

Hvor mye koster sykkelen etter at rabatten er trukket fra prisen?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Rabatt betyr prisavslag, altså at vi betaler mindre. Først må vi finne ut hvor mye $20 %$ av $3500$ kr er og deretter må vi trekke dette fra $3500$ kr.

$20 %$ av $3500$ kroner er det samme som

$3500 kr \cdot 20 % = 3500 kr \cdot \frac{20}{100}$

Vi vet at $\frac{20}{100} = \frac{2}{10} = \frac{1}{5}$ og vi får da at

$3500 kr \cdot \frac{1}{5} = \frac{3500}{5} kr = 700 kr$

Dette betyr at prisavslaget var på $700$ kroner. Derfor trekker vi det fra $3500 kr$ og vi får prisen som ble betalt for sykkelen: $3500 kr - 700 kr = 2800 kr$

Svar: $2800 kr$

Mer om

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Flere forklaringer og eksempler på hvordan man regner med prosent finner du i artikkelen Reglereglene.

For å øve mer, se oppgavesettet Prosentregning i Treningsleieren.

Oppgave 9 (0,5 poeng) Nettkode: E-4FWK

Vi skal kaste én terning.

Sannsynligheten for at terningen vil vise $5$ eller $6$ øyne, er

$\frac{1}{6}$
$\frac{2}{6}$
$\frac{5}{6}$
$\frac{6}{6}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Når vi kaster en terning, har vi seks mulige resultater (1, 2, 3, 4, 5 eller 6 øyne).

$Sannsynlighet = \frac{Antall gunstige utfall}{Antall mulige utfall}$

Hver av utfallene har samme sannsynlighet, altså $\frac{1}{6}$ .

Totalt er det $6$ mulige utfall. Vi skal ha 5 øyne eller 6 øyne, altså $2$ gunstige ufall:

$P (5 ø y n e e l l e r 6 ø y n e) = \frac{2}{6} = \frac{1}{3}$

Alternativ løsning

Sannsynligheten for å få 5 øyne er lik

$P (5 ø y n e) = \frac{1}{6}$

Tilsvarende gjelder for 6 øyne:

$P (6 ø y n e) = \frac{1}{6}$

Sannsynligheten for å få 5 eller 6 øyne er derfor:

$P (5 ø y n e) + P (6 ø y n e) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$

Svar: Sannsynligheten for å få $5$ eller $6$ øyne er $\frac{1}{3}$ .

Mer om

Denne oppgaven er om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

Utfall

Mulig resultat av en hendelse.

Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.

utfall

Gunstig utfall

Et gunstig utfall er den hendelsen som er interessant for oss.

Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.

Se Hendelse

gunstig utfall

Flere forklaringer og eksempler på hvordan man finner sannsynlighet, finner du i artikkelen Hvordan finner vi sannsynligheten?.

For å øve mer, se oppgavesettet Sannsynlighetsregning i Treningsleieren.

Oppgave 10 (0,5 poeng) Nettkode: E-4FWN

Vi skal kaste to terninger.

Sannsynligheten for at terningene vil vise til sammen 10 øyne, er

$\frac{1}{36}$
$\frac{2}{36}$
$\frac{3}{36}$
$\frac{10}{36}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kaster nå to terninger. Hver av disse har seks mulige utfall. Vi skal finne sannsynligheten for at summen er 10 øyne.

Husk at $Sannsynlighet = \frac{Antall gunstige utfall}{Antall mulige utfall}$

Hvilke kast gir oss en sum på $10$ ? Jo, $4 + 6$ , $6 + 4$ og $5 + 5$ .

Sannsynligheten for å få $4$ øyne og $6$ øyne er lik:

$P (4 + 6) = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36}$

Tilsvarende får vi at

$P (6 + 4) = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36}$

Og sannsynligheten for den siste muligheten er

$P (5 + 5) = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36}$

Derfor er sannsynligheten for tilsammen å få $10$ øyne lik:

$P (10) = \frac{1}{36} + \frac{1}{36} + \frac{1}{36} = \frac{3}{36} = \frac{1}{12}$

Svar: Sannsynligheten for at terningene vil vise tilsammen $10$ øyne er $\frac{1}{12}$ .

Mer om

Denne oppgaven er om

Sannsynlighet

sannsynlighet

Flere forklaringer og eksempler på sannsynlighetsregning, finner du i artkkelen Hvordan finner vi sannsynligheten?.

For å øve mer, se oppgavesettet Sannsynlighet i Treningsleieren.

Oppgave 11 (1,5 poeng) Nettkode: E-4FWQ

Løs likningene

a)

$4 x - 3 = x$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her er det en førstegradslikning der den ukjente $x$ står på begge sider av likhetstegnet.

Vi begynner med å trekke fra $4 x$ på begge sider av likhetstegnet og på denne måten samler vi alle ledd med $x$ på høyresiden av likningen:

$4 x - 3 = x$

$4 x - 3 - 4 x = x - 4 x$

$- 3 = - 3 x$

For å få den ukjente $x$ alene på høyresiden av likhetstegnet, dividerer vi med $- 3$ alle ledd på begge sider av likningen og forkorter:

$\frac{- 3}{- 3} = \frac{- 3 x}{- 3}$

$1 = x$

Sett likningen på prøve med $x = 1$ for å forsikre deg om at svaret er riktig:

Venstresiden: $4 x - 3 \Rightarrow 4 \cdot 1 - 3 = 4 - 3 = 1$

Høyresiden: $x \Rightarrow 1$

Venstresiden $=$ Høyresiden

Svar: $x = 1$

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

førstegradslikninger

Flere forklaringer og eksempler på likninger, finner du i artikkelen Løs en førstegradslikning.

For å øve mer, se oppgavesettet Førstegradslikninger i Treningsleieren.

b)

$\frac{x - 1}{2} - x = 3$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her har vi en førstegradslikning med én ukjent, $x$ . Alle ledd med den ukjente er allerede samlet på en og samme side, men vi har en brøk på venstre siden av likhetstegnet.

Vi begynner med å multiplisere hele likningen (alle ledd på begge sider) med $2$ slik at vi kan forkorte og slippe og regne med brøker:

$\frac{x - 1}{2} - x = 3$

$\frac{x - 1}{2} \cdot 2 - x \cdot 2 = 3 \cdot 2$

Vi forkorter og får at:

$x - 1 - 2 x = 6$

Vi trekker sammen ledd med den ukjente og legger til $1$ på begge sider av likningen: $- x - 1 + 1 = 6 + 1$ $- x = 7$

For å få den ukjente alene på venstresiden, må vi multiplisere med $- 1$ (husk begge sider av likningen): $- x \cdot (- 1) = 7 \cdot (- 1)$ $x = - 7$

Vi setter svaret på prøve med $x = - 7$ .

Venstresiden: $\frac{x - 1}{2} - x \Rightarrow \frac{- 7 - 1}{2} - (- 7) = - 4 + 7 = 3$

Høyresiden: $3$

Venstresiden $=$ Høyresiden

Svar: $x = - 7$

Mer om

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

lineære likninger

Flere forklaringer og eksempler på førstegradslikninger, finner du i artikkelen Løs en førstegradslikning.

For å øve mer, se oppgavesettet Førstegradslikninger II i Treningsleieren.

Oppgave 12 (1,5 poeng) Nettkode: E-4FWT

Skriv så enkelt som mulig

a)

$- a + 2 a + 3 a$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her skal vi regne med bokstaver. Alle ledd er like og derfor kan vi trekke ut fellesfakoren $a$ og legge sammen resten.

$- a + 2 a + 3 a = a (- 1 + 2 + 3) = 4 a$

Svar: $4 a$

Mer om

Denne oppgaven er om

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

Flere forklaringer og eksempler på hvordan man regner med bokstaver, finner du i artikkelen Regnereglene.

For å øve mer, se oppgavesettet Algebra i Treningsleieren.

b)

$\frac{1}{a - 1} - \frac{1}{a + 1}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her ser vi at bokstavene er i nevneren. For å kunne trekke sammen disse to brøkene, må vi først finne fellesnevner.

Når vi har to tallbrøker som ikke har fellesfaktorer, finner vi fellesnevneren ved å multiplisere sammen nevnere. Det samme gjør vi her. Fellesnevneren er derfor $(a - 1) (a + 1)$ . Vi utvider brøkene før vi setter dem på fellesbrøkstrek:

$\frac{1}{(a - 1)} - \frac{1}{(a + 1)} = \frac{1 \cdot (a + 1)}{(a - 1) (a + 1)} - \frac{1 \cdot (a - 1)}{(a - 1) (a + 1)} = \frac{(a + 1)}{(a - 1) (a + 1)} - \frac{(a - 1)}{(a - 1) (a + 1)}$

Nå setter vi det på fellesbrøkstrek og trekker sammen: $\frac{(a + 1) - (a - 1)}{(a - 1) (a + 1)} = \frac{a + 1 - a + 1}{(a - 1) (a + 1)} = \frac{2}{(a - 1) (a + 1)}$

På fellesnevneren kan vi bruke konjugatsetningen og derfor skrive brøken som: $\frac{2}{a^{2} - 1}$

Svar: $\frac{2}{a^{2} - 1}$

Mer om

Denne oppgaven er om

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetning

Flere forklaringer og eksempler på hvordan man regner med bokstaver, finner du i artikkelen Fortegn foran parenteser og Konjugatsetning.

For å øve mer, se oppgavesettet Forenkling av rasjonale uttrykk i Treningsleieren.

Oppgave 13 (1 poeng) Nettkode: E-4FWW

En pose inneholder $6 kg$ hundekjeks. En hund spiser i gjennomsnitt $0, 2 kg$ hundekjeks per dag.

Hvor mange dager varer posen med hundekjeks? Vis utregningen din.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi vet hvor mye én pose inneholder og vi vet hvor mye en hund spiser i løpet av én dag.

Hundekjeks i en pose: $6$ kg

En hund spiser i snitt: $0, 2$ kg

Antall dager en pose varer: $6$ kg $: 0, 2$ kg= $30$

Svar: $30$ dager

Mer om

Denne oppgaven er om

Divisjon

Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.

Eksempel: $6 : 2 = 3$ fordi $2 \cdot 3 = 6$ .

divisjon

For flere forklaringer og eksempler på divisjon, se artikkelen Divisjon.

For å øve mer, se oppgavesettet Divisjon i Treningsleieren.

Oppgave 14 (0,5) Nettkode: E-4FX0

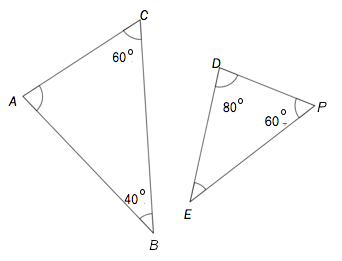
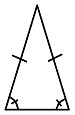
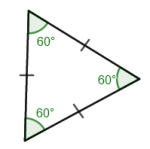
Hvilken påstand er riktig om trekantene som er tegnet?

$Δ A B C$ er en likesidet trekant
$Δ D E F$ er en likebent trekant
$Δ A B C ≅ Δ D E F$ (kongruente trekanter)
$Δ A B C \sim Δ D E F$ (formlike trekanter)

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ser nøye på vinklene på trekantene. Husk at vinkelsummen i en trekant er $180$ grader.

I en likesidet trekant er alle tre vinklene like store, altså $60$ grader. Trekantene er ikke likesidet.

I en likebeint trekant er de to vinklene som står ovenfor de likebeinte sidene like store, mens den tredjevinkelen er forskjellig fra de to andre. Trekantene er ikke likebeinte.

To trekanter er kongruente når de er formlike og like store. Trekantene er ikke like store og derfor er de heller ikke kongruente.

To trekanter er formlike hvis de har nøyaktig samme form, men ikke nødvendigvis størrelse. Vinkelsummen i en trekant er $180$ grader. Derfor er $∠ A = 180 - 40 - 60 = 80$ grader. Vi vet også med en gang at $∠ E = 40$ . Du kan regne den ut på samme måte som vi fant $∠ A$ , men det er ikke nødvendig. Bare se at trekanten $E F D$ har to like vinkler med trekanten $A B C$ og dermed må den siste vinkelen også være like stor. Dette forteller oss også at trekantene er formlike.

Svar: Trekantene er formlike (alternativ 4).

Mer om

Denne oppgaven er om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

Kongruens

Brukes både i algebra og i geometri.

I geometri: om figurer, for eksempel trekanter, som har parvis like vinkler og sider.

I algebra: om tall, for eksempel i regning modulo, et tall k om to tall som har samme rest etter divisjon med k.

kongruens

Likebeint trekant

I en likebeint trekant er to sider like lange og to vinkler like store.

likebent trekant

Fere forklaringer og eksempler på geometri finner du i artiklene Formlikhet og kongruens.

For å øve mer, se oppgavesettet Formlikhet og kongruens i Treningsleieren.

Oppgave 15 (0,5 poeng) Nettkode: E-4FX3

Et tog går fra Oslo kl. $22.46$ . Toget er framme i Trondheim kl. $06.34$ morgenen etter.

Da har toget brukt ____ $h$ ____ $\min$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Husk at det er 60 minutter i en time.

Toget drar fra Oslo kl.22.46.

Til kl.23 bruker toget 14 minutter og frem til midnatt bruker det tilsammen 1 time og 14 minutter. Fra midnatt til kl.06.34 er det 6 timer og 34 minutter.

Vi legger sammen og får at det er 7 timer og 48 minutter toget bruker fra Oslo til Trondheim

Svar: Da har toget brukt $7$ timer og $48$ minutter.

Mer om

Denne oppgaven er om

Tidsenhet

Det grunnleggende tidsmålet er sekund. Andre tidsenheter er minutt, time og døgn.
Sammenhengen mellom tidsenhetene er ikke basert på 10-tallsystemet, slik vi er vant til fra lengde og vekt.

tidsenhet

Flere forklaringer og eksempler på hvordan man regner med tid, finner du i artiklene 60-tallsystem. Artikkelen om tidsenheter er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet Timer, minutter og sekunder i Treningsleieren.

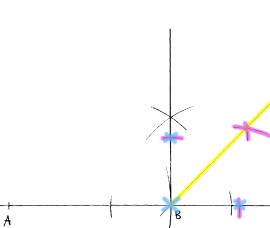
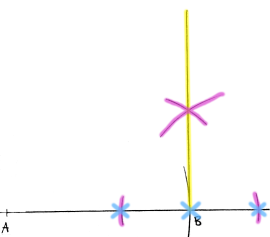
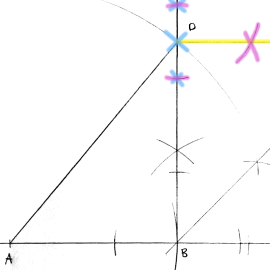
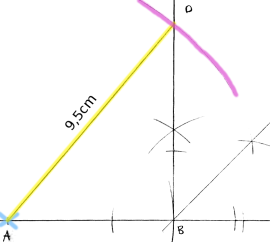
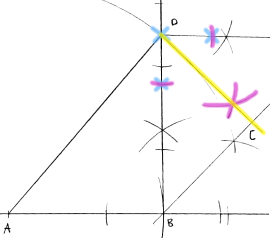
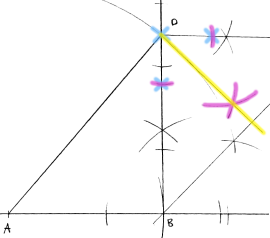
Oppgave 16 (2 poeng) Nettkode: E-4FX8

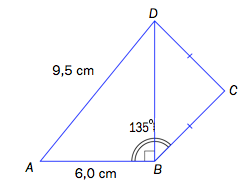
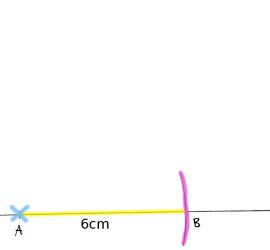
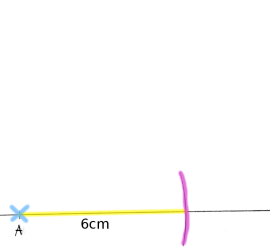
Nedenfor ser du en hjelpefigur med følgende mål:

$A B = 6, 0 cm, A D = 9, 5 cm, ∠ A B D = 90 °, B C = B D$ og

$∠ A B C = 135 °$

Konstruer figuren.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Dette er en konstruksjonsoppgave, og vi må bruke passer og linjal for å konstruere figuren.

Konstruksjonsforklaring:

1. Vi markerer et punkt $A$ på en rett linje, og setter av et punkt $B 6, 0 cm$ fra $A$ .

2. Vi konstruerer $90 °$ i $B$ på høyre side av punktet, og halverer vinkelen.

3. Vi slår en sirkel med radius $9, 5 cm$ om punktet $A$ , og kaller punktet der sirkelen møter vinkelbenet til $B$ for $D$ .

4. Vi onstruerer $90 °$ i $D$ og halverer vinkelen.

5. Vi setter av punktet $C$ der vinkelbena til $B$ og $D$ møtes.

Nedenfor viser vi skritt for skritt hvordan figuren er konstruert. I din eksamensbesvarelse vil alle trinnene bli vist i en og samme figur. Sett passerspissen i det blå krysset, slå de lilla linejene med passere og trekk de gule linjene med blyant og linjal.

1. Vi markerer et punkt $6, 0 cm$ fra punktet $A$ .

2. Vi kaller punktet for $B$ .

3. Vi konstruerer $90 °$ i $B$ .

4. Vi halverer vinkelen.

5. Vi slår en sirkel med radius $9, 5 cm$ om punktet $A$ og kaller skjæringspunktet $D$ .

6. Vi konstruerer $90 °$ i $D$ .

7. Vi halverer vinkelen.

8. Vi kaller punktet der vinkelbena møtes $C$ .

Mer om

Denne oppgaven er om

Vinkel

En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.

vinkler

Rettvinklet trekant

En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.

rettvinklede trekanter

Flere forklaringer og eksempler på hvordan man konstruerer vinkler, finner du i artikkelen Konstruksjon av figurer.

For å øve mer, se oppgavesettet Konstruksjon i Treningsleieren.

Oppgave 17 (0,5 poeng) Nettkode: E-4FXA

Hvis $A = \frac{g \cdot h}{2}$ , da er:

$h = 2 \cdot A \cdot g$
$h = \frac{2 \cdot g}{A}$
$h = \frac{A}{2 \cdot g}$
$h = \frac{2 \cdot A}{g}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ønsker å ha $h$ alene på venstresiden av likhetstegnet. Vi skriver om uttrykket i oppgaveteksten.

Vi ser på uttrykket

$A = \frac{g \cdot h}{2}$

som en likning. Derfor multipliserer vi begge sider med $2$ :

$A \cdot 2 = \frac{g \cdot h}{2} \cdot 2$

Vi forkorter og får at:

$2 A = g \cdot h$

Vi skal ha $h$ alene på en side og derfor dividerer vi begge sider med $g$ :

$\frac{2 A}{g} = \frac{g \cdot h}{g}$

Vi forkorter og får at:

$\frac{2 A}{g} = h$

Svar: $h = \frac{2 \cdot A}{g}$

Mer om

Denne oppgaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

Flere forklaringer og eksempler på hvordan man regner om formler, finner du i artikkelen Regnereglene. For flere forklaringer og eksempler på førstegradslikninger se artikkelen Løs en førstegradslikning!

For å øve mer, se oppgavesettet Førstegradslikning i Treningsleieren.

Oppgave 18 (2 poeng) Nettkode: E-4FXH

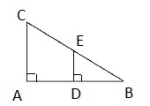
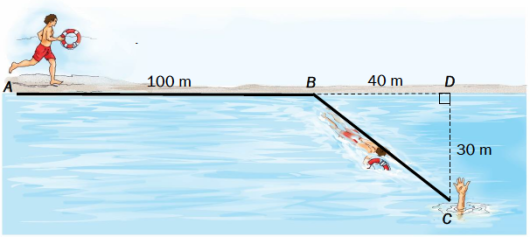
En badevakt løper fra $A$ til $B$ og svømmer videre fra $B$ til $C$ for å hjelpe en person i nød. Se skissen nedenfor.

a)

Vis ved regning at $B C = 50 m$ .

Løs oppgaven her

Løsningsforslag a)

Tanker

Vi ser på skissen at trekanten $C D B$ er rettvinklet. Dette betyr at vi kan bruke Pytagoras læresetning til å finne hypotenusen $B C$ .

Ifølge Pytagoras læresetning er $B D^{2} + C D^{2} = B C^{2} .$

Vi setter inn og får at:

$B C^{2} = 40^{2} + 30^{2}$

$B C = \sqrt{1600 + 900}$

$B C = \sqrt{2500}$

$B C = 50$

Svar: $B C = 50$

Mer om

Denne oppgaven er om

Rettvinklet trekant

En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.

rettvinklet trekant

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

Flere forklaringer og eksempler på hvordan man regner med Pytagoras setning, finner du i artikkelen Pytagoras' læresetning.

For å øve mer, se oppgavesettet Pytagoras læresetning i Treningsleieren.

b)

Badevakten løper i $20 s$ og svømmer i $1 \min$ . Regn ut forholdet mellom farten han har når han løper, og farten han har når han svømmer.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Først må vi finne farten når badevakten løper og når han svømmer. Deretter ser vi på forholdet mellom disse to tallene.

Farten er lik avstanden dividert på tiden.

Badevakten løper fra $A$ til $B$ som utgjør $100$ meter. Tiden han bruker på denne avstanden er $20$ sekunder. Derfor er farten hans når han løper lik:

$\frac{100 m}{20 s} = 5 \frac{m}{s}$

Badevakten svømmer avstanden $B C$ og bruker 1 minutt, altså 60 sekunder. Derfor er farten hans når han svømmer lik:

$\frac{50 m}{60 s} = \frac{5}{6} \frac{m}{s}$

Forholdet mellom farten når han løper og farten når han svømmer er det samme som:

$\frac{løpefart}{svæmmefart} = \frac{5}{\frac{5}{6}} = \frac{30}{5} = 6$

Forholdet er derfor $6 : 1$ .

Svar: $6 : 1$

Mer om

Denne oppgaven er om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proporsjon

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

Flere forklaringer og eksempler på hvordan man finner forhold, finner du i lynkurset Målestokk og forholdsregning.

For å øve mer, se på oppgavesettene Målestokk og Vei, fart og tid i Treningsleieren.

Oppgave 19 (2,5 poeng) Nettkode: E-4FXM

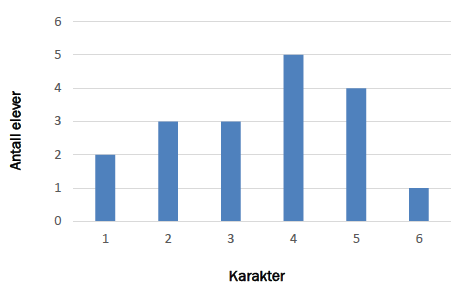
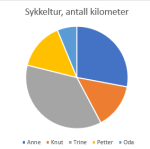
På en matematikkprøve fordeler karakterene seg slik i en klasse med $18$ elever:

a)

Typetallskarakteren er ____.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Typetallskarakter er den karakteren som forekommer oftest.

Vi leser av diagrammet at den høyeste stolpen er den som gir hva størst antall elever fikk. Den høyeste stolpen er karakteren 4.

Svar: $4$

Mer om

Denne oppgaven er om

Typetall

Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.

Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.

typetall

Flere forklaringer og eksempler på hvordan man finner typetall finner du i artikkelen Typetall.

For å øve mer, se oppgavesettet Typetall i Treningsleieren.

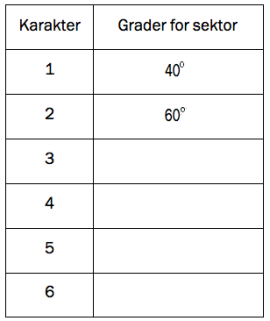
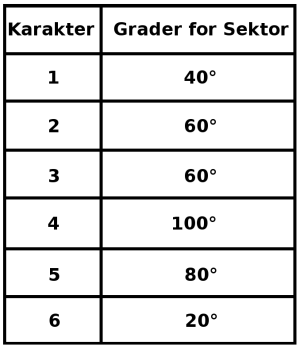
b)

Gjør beregninger, og fyll inn det som mangler i tabellen nedenfor.

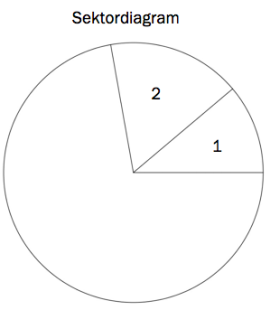
Lag ferdig sektordiagrammet som viser karakterfordelingen i klassen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Hele sektordiagrammet er alle elevene, altså 18 elever. Vi må først finne hvor mange grader i sektordiagrammet svarer til 1 elev.

1 elev er det samme som $360 : 18 = 20$ grader. Vi kan også finne dette ut i fra tabellen siden det står at karakter 1 svarer til $40$ grader og vi ser at det er $2$ elever som fikk karakter 1. Karakter 3 var det 3 elever som fikk og derfor svarer det til $3 \cdot 20 = 60$ grader.

Karakter 4 var det 5 elver som fikk og det er det samme som $5 \cdot 20 = 100$ grader.

Karakter 5 var det 4 elever som fikk og det er det samme som $4 \cdot 20 = 80$ grader.

Karakter 6 fikk 1 elev og det er $20$ grader.

Karakter 2 og 3 skal være like store på sektrodiagrammet. Karakter 4 skal være størst, mens karakter 6 skal være minst. Vi vet også at karakter 1, 2, 3 og 6 utgjør halvparten av sirkelen, mens 4 og 5 er den andre halvparten.

Mer om

Denne oppgaven er om

Stolpediagram

Et søylediagram uten bredde på søylene.

Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.

Se Søylediagram

stolpediagram

Sektordiagram

Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.

sektordiagram

Flere forklaringer og eksempler på hvordan man lager diagrammer, finner du i artikkelen Sektordiagram.

For å øve mer, se oppgavesettet Sektordiagram i Treningsleieren.

c)

Gjennomsnittskarakteren er ____ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Gjennomsnittskarakter finner vi ved å legge sammen alle karakterene og dividere på $18$ elever.

Vi legger sammen alle karakterene:

$1 \cdot 2 + 2 \cdot 3 + 3 \cdot 3 + 4 \cdot 5 + 5 \cdot 4 + 6 = 63$

Gjennomsnittskarakteren er derfor:

$63 : 18 = 3, 5 .$

Svar: $3, 5$

Mer om

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data

Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1) $2 + 2 + 4 + 3 = 11$
2) antall data er 4. $11 : 4 = 2, 75$

gjennomsnitt

Flere forklaringer og eksempler på hvordan man finner gjennomsnittet, finner du i artikkelen Gjennomsnitt.

For å øve mer, se oppgavesettet Gjennomsnitt i Treningsleieren.

Oppgave 20 (0,5 poeng) Nettkode: E-4FXX

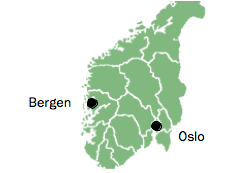
Den korteste avstanden mellom Bergen og Oslo er ca. $300 km$ (i luftlinje).

På et kart er denne avstanden $2, 0 cm$ .

Målestokken for dette kartet er

$1 : 30 000$
$1 : 150 000$
$1 : 3 000 000$
$1 : 15 000 000$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Målestokk er det samme som forhold. For å finne det, må vi finne ut hvor mange enheter i virkeligheten svarer til $1$ enhet på kartet.

Målestokken er oppgitt i centimeter. Og avstanden på kartet er $2, 0$ cm. $300$ km er det samme som $300 \cdot 100000$ cm og det er det samme som $30000000$ cm. Dette betyr at $1$ cm er det samme som $30000000 : 2$ cm og dette gir oss målestokk $1 : 15000000$ .

Svar: $1 : 15000000$

Mer om

Denne oppgaven er om

Målestokk

Målestokken angir hva en måleenhet på for eksempel kartet svarer til i terrenget.

Eksempel:
Et kart har målestokken 1 : 25000 (leses: en til tjuefemtusen)

Dette betyr for eksempel at:

-	1 cm på kartet tilsvarer 25000 cm i terrenget (25000 cm = 250 m)
-	1 dm på kartet tilsvarer 25000 dm i terrenget
-	4 cm på kartet er 25000 · 4 cm i terrenget (25000 · 4 cm = 100000 cm = 1000m = 1 km).

Eller mer generelt:
1 bestemt måleenhet på kartet er 25000 slike måleenheter i terrenget.

målestokk

Flere forklaringer og eksempler på målestokk finner du i artikkelen Målestokk.

For å øve mer, se oppgavesettet Målestokk i Treningsleieren.

Oppgave 21 (2 poeng) Nettkode: E-4FY0

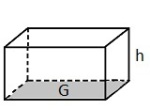
En hermetikkboks har tilnærmet form som en sylinder (med topp og bunn).

Regn ut overflaten av hermetikkboksen. Du kan bruke at $π \approx 3$ .

Løs oppgaven her

Løsningsforslag

Jeg tenker

Hermetikkboksen har form til en sylinder. Vi vet at overflaten til en sylinder er to sirkler og et rektangel.

Diameteren for bunn og topp er $20, 0$ cm. Dette gir radius lik $10, 0$ cm. Da er arealet til topp og bunn lik: $A_{1} = π r^{2} \cdot 2 \approx 3 \cdot 10 cm \cdot 10 cm \cdot 2 = 600 {cm}^{2}$

Arealet av et rektangel er høyden multiplisert med bredden. Her er høyden $h = 24 cm$ og bredden er omkretsen av hermetikkboksen, $b = O = 2 \cdot π \cdot r$ .

$A_{2} = h \cdot b = h \cdot O = (2 \cdot π \cdot r \cdot 24) {cm}^{2} = 1440 {cm}^{2}$

Overflaten av sylinderen er $A_{1} + A_{2}$ :

$A = (600 + 1440) {cm}^{2} = 2040 {cm}^{2} = 20, 40 {dm}^{2}$

Svar: $2040 {cm}^{2}$ eller $20, 40 {dm}^{2} .$

Mer om

Denne oppgaven er om

Likesidet trekant

I en likesidet trekant er alle sidene like lange og alle vinklene 60°.

likesidet trekant

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

Potens

potens

Flere forklaringer og eksempler på hvordan man finner areal, finner du i artikkelen En sylinder.

For å øve mer, se oppgavesettet Overflate i Treningsleieren.

Del 2 med hjelpemidler

Oppgave 1 (2 poeng) Nettkode: E-4FYE

I denne oppgaven ser vi bort fra vekslingsgebyr.

a)

En familie skal reise til Italia. En dag kjøper familien disse eurosedlene i en norsk bank:

1 € (euro) koster 9,3165 norske kroner i banken.

Hvor mange norske kroner betaler familien for eurosedlene?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi vet hvor mye 1 euro koster. Vi må først finne ut hvor mange euro familien kjøpte totalt.

La oss se på denne skritt for skritt.

Vi adderer de ulike sedlene og finner ut at familien kjøpte:

$(10 + 20 + 50 + 100 + 200 + 500) euro$

Tilsammen er dette lik $880$ euro.

Vi vet at $1$ euro koster $9, 3165$ NOK og derfor koster $880$ euro

$(880 \cdot 9, 3165) NOK = 8198, 52 NOK$

Svar: $8199 NOK$

Mer om

Denne oppgaven er om

Valutakurs

Valutakursen forteller hvilken verdi pengene i to land har i forhold til hverandre.

Denne kursen bestemmes fra dag til dag i de enkelte land.

valutakurs

Gjeldende siffer

Vi definerer antall gjeldene siffer som det totale antall siffer med unntak av eventuelle nuller til venstre.

Eks:
30 000 har fem gjeldende siffer
30,001 har fem gjeldene siffer
0,0001 har ett gjeldende siffer
0,0300 har tre gjeldende siffer

Tall på formen b · 10ª der a er et helt tall og 1 ≤ b < 10 har like mange gjeldende siffer som det er gjeldende siffer i b.

Eksempel: 2,83 · 10² har tre gjeldende siffer.

gjeldende siffer

Lynkurs om valutakurs er under utarbeidelse.

For å øve mer, se oppgavesettet Norske penger og andre valuta i Treningsleieren.

b)

En valutakalkulator på Internett viser at du får 1389,78 € for 13 000 norske kroner.

Hvor mye koster 1 € ifølge valutakalkulatoren?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

$1389, 78$ euro koster $13000$ NOK. Vi skal finne $1$ euro.

Vi vet at $1389, 78 euro = 13 000 NOK$

Ser vi på dette som en likning, vet vi at vi får euro alene hvis vi dividerer med $1389, 78$ begge sider av likhetstegnet:

$\frac{1389, 78 EUR}{1389, 78} = \frac{13 000 NOK}{139, 78}$

$1 EUR = 9, 353998$ NOK

Svar: $1 EUR = 9, 353998 NOK$

Mer om:

Denne oppgaven er om

Valutakurs

Valutakursen forteller hvilken verdi pengene i to land har i forhold til hverandre.

Denne kursen bestemmes fra dag til dag i de enkelte land.

valutakurs

, forholdsregning (finnes ikke) og

Gjeldende siffer

gjeldende siffer

Lynkurset med dette tema er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet Norske penger og andre valuta i Treningsleieren.

Oppgave 2 (8 poeng) Nettkode: E-4FYM

a)

Familien bruker kofferter med kodelås. Koden består av fire sifre fra 0 til 9.

Hvor mange forskjellige koder kan familien lage med en slik kodelås?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

En kodelås med ett siffer fra $0$ til $9$ har ti ulike muligheter. En kodelås med to siffer fra $0$ til $9$ vil ha ti muligheter hver og alle kombinasjonene av disse.

I en kodelås med fire sifre gir hvert siffer ti muligheter og derfor vil vi til sammen ha:

$10 \cdot 10 \cdot 10 \cdot 10 \cdot = 10^{4} = 10000$ mulige kombinasjoner.

Svar: Det er $10 000$ mulige kombinasjoner.

Mer om:

Denne oppgaven er om

Kombinatorikk

Handler om å finne antall mulige kombinasjoner i ulike sammenhenger.

Eksempel: antall måter å kombinere Lotto-tallene på, eller hvor mange ulike antrekk vi kan ha på oss dersom vi har 2 bukser og 3 skjorter.

kombinatorikk

For flere forklaringer og eksempler se artikkelen Kombinasjoner.

For å øve mer, se oppgavesettet Kombinatorikk I i Treningsleieren.

b)

Far har glemt koden til sin kodelås. Han husker at to av sifrene er $7$ , og at de to andre sifrene er $3$ , men han husker ikke rekkefølgen.

Skriv opp de ulike kombinasjonene.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Kodelåsen har fire siffer. To av sifrene er $3$ og to av sifrene er $7$ .

For å finne mulige kombinasjoner med disse sifrene, skriver vi disse i alle mulige ulike rekkefølge.

Svar: De mulige kombinasjonene er

$\begin{matrix} 3377 \\ 3737 \\ 3773 \\ 7373 \\ 7733 \\ 7337 \end{matrix}$

Mer om

Denne oppgaven er om

Kombinatorikk

Handler om å finne antall mulige kombinasjoner i ulike sammenhenger.

Eksempel: antall måter å kombinere Lotto-tallene på, eller hvor mange ulike antrekk vi kan ha på oss dersom vi har 2 bukser og 3 skjorter.

kombinatorikk

For flere eksempler og forklaringer se artikkelen Kombinasjoner.

For å øve mer, se oppgavesettet Kombinasjoner II i Treningsleieren.

Visste du at?

Læren om forskjellige kombinasjoner heter kombinatorikk. Kombinatorikk brukes nesten overalt, særlig i termodynamikken. Termodynamikken er læren om hvordan varme, energi og arbeid henger sammen. Det regnes for eksempel på sannsynligheten for at et stoff er i gass- eller væskeform, der man bruker nøyaktighet helt ned på atomnivå.

Det er vanskelig å måle tilstanden til hvert eneste atom i et stoff, fordi det finnes mange milliarder av dem. Derfor regner man ut hvor mange forskjellige tilstander atomene kan være i, og den tilstanden det finnes flest kombinasjoner av, er den mest sannsynlige. Da sier man at stoffet er i den tilstanden.

c)

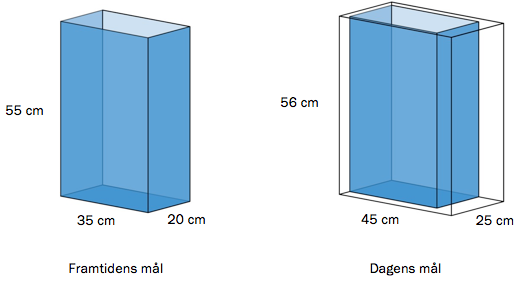
I framtiden kan målene på tillatt håndbagasje på fly bli mindre.

Bestem volumet av håndbagasjen etter framtidens mål og etter dagens mål.

Løs oppgaven her

Løsningsforslag c)

Tanker:

Håndbagasjen er en prisme med høyde $h$ , bredde $b$ og lengde $l$ . Volumet er lik $V = h \cdot b \cdot l$ .

Framtidens håndbagasjen er en prisme med høyde $55$ cm, bredde $35$ cm og dybde $20$ cm. Volumet er lik

$V_{f r a m t i d e n s} = h \cdot b \cdot l = (55 \cdot 20 \cdot 35) {cm}^{3} = 38500 {cm}^{3} = 38, 5 {dm}^{3}$ .

Dagens håndbagasje er en prisme med høyde $56$ cm, bredde $25$ cm og dybde $45$ cm. Volumet er lik

$V_{d a g e n s} = h \cdot b \cdot l = (56 \cdot 25 \cdot 45) {cm}^{3} = 63000 {cm}^{3} = 63 {dm}^{3}$ .

Svar: Volum av håndbagasjen etter framtidens mål er $38, 5 {dm}^{3}$ mens dagens er $63 {dm}^{3}$ .

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Prisme

Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.

Har et prisme grunnflate G og høyde h, er volumet lik G · h.

prisme

For flere forklaringer og eksempler om hvordan finne volum av prismer, se artikkelen Et rett prisme.

For å øve mer, se oppgavesettet Volum i Treningsleieren.

d)

Avisen Aftenposten skriver at endringen av målene betyr at største tillatte volum for håndbagasje vil bli nesten $40 %$ mindre enn i dag.

Kontroller om det stemmer.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi må sjekke om framtidens volum er det samme som $40$ % av dagens volum. Vi bruker svaret vi fant i oppgave c) og gjør det om til prosent.

Framtidens er $38 500 {cm}^{3}$ , mens dagens er $63 000 {cm}^{3}$ . I prosent er dette

$\frac{38500 \cdot 100 %}{63000} = 61, 1 %$

Framtidens volum av håndbagasjen er det samme som 61% av dagens. Dette betyr at den største tillatte volum i framtidens volum minker med rundt $40$ %.

Svar: Det stemmer at framtidens tillatte volum for håndbagasje er nesten $40 %$ mindre enn i dag.

Mer om

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosentregning

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

For flere forklaringer og eksempler se artiklene Prosent av hva da?.

For å øve mer, se oppgavesettet Prosentregning i Treningsleieren.

Oppgave 3 (4 poeng) Nettkode: E-4FYT

Familien leier en bil i Venezia, og planlegger å kjøre disse tre strekningene i Italia:

a)

Bilen bruker i gjennomsnitt $0, 45 L$ bensin per mil. Bensinprisen er 1,65 € per liter.

Hvor mange euro koster bensinen til sammen hvis familien bare kjører de tre strekningene som er vist ovenfor?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Først må vi finne den totale strekningen, så antall liter bensin bilen bruker på den totale strekningen og til slutt multiplisere denne med prisen per liter.

Den totale strekningen er:

$(287 + 83 + 371) km = 741 km$

Bilen bruker i gjennomsnitt $0, 45$ L bensin per mil. Før vi kan finne det totale bensinforbruket for turen, gjør vi først om den totale strekningen til mil: $741 : 10 = 74, 1$ mil

Det totale bensinforbruket er: $74, 1 mil \cdot 0, 45 \frac{L}{mil} = 33, 345 L$

Prisen per liter er $1, 65$ euro og den totale prisen er derfor:

$33, 345 L \cdot 1, 65 \frac{EUR}{L} = 55, 03 EUR$

Svar: Bensinen for alle tre strekningene koster $55, 03 EUR$ .

Mer om

Denne oppgaven er om

Benevning

Eksempel på andre benevninger:
g, dL, h, km/h, g/cm³

benevning

Addisjon

Er det samme som å legge til, legge sammen eller plusse sammen.

Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
Tallene 5 og 7 kalles ledd, og resultatet, 12, kalles en sum.
Mellom leddene skrives plusstegn +.

addisjon

Multiplikasjonstegn

Regnetegnet for multiplikasjon er · .
Noen ganger kan du se multiplikasjonstegnet skrevet som x.

Eksempel: 2 · 3 eller 2 x 3

multiplikasjon

For flere forklaringer og eksempler se artikklene Addisjon og Multiplikasjon.

For å øve mer, se oppgavesettet De fire regneartene i Treningsleiren.

b)

Familien kjører mer enn de tre strekningene. Leie av bilen koster 640 € pluss 0,35 € per kilometer. Når ferien er slutt, betaler familien til sammen 948 € for leie av bilen.

Hvor mange kilometer har familien faktisk kjørt?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi vet at totalprisen er det samme som billeien i tillegg til kostnad per kilometer. Ved å trekke billeie fra totalprisen, får vi hvor mye reisestrekningen kostet.

Prisen for antall tilbakelagte kilometer:

$948 - 640 = 308$

Vi vet at de betaler $0, 35$ euro per kilometer. Derfor er antall tilbakelagte kilometer lik:

$308 : 0, 35 = 880$ km

Svar: Familien har faktisk kjørt $880 km.$

Alternativ løsning

Vi setter det opp som en likning. Vi vet at prisen de betalte er lik billeien pluss antall kilometer multiplisert med prisen per kilometer. Vi kaller antall kilometer for $x$ og skriver:

$948 = 640 + 0, 35 x$

Dette er en linær likning med en ukjent. Vi trekker først fra $640$ på begge sider av likhetstegnet og deretter dividerer med $0, 35$ på begge sider av likhetstegnet:

$948 - 640 = 640 + 0, 35 x - 640$

$308 = 0, 35 x$

$\frac{308}{0, 35} = \frac{0, 35 x}{0, 35}$

$x = \frac{308}{0, 35}$

$x = 880$

Mer om

Denne oppgaven er om

Subtraksjon

En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen.

subtraksjon

Divisjon

Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.

Eksempel: $6 : 2 = 3$ fordi $2 \cdot 3 = 6$ .

divisjon

eller

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

lineær likning

For flere forklaringer og eksempler se artikler Subtraksjon, Divisjon og Løs en førstegradslikning!

For å øve mer, se oppgavesettene De fire regneartene II og Førstegradslikninger i Treningsleieren.

Oppgave 4 (4 poeng) - REGNEARK Nettkode: E-4FYY

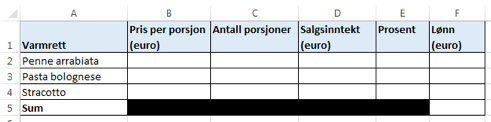
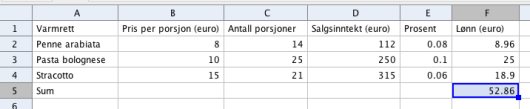
I Firenze møter familien Gina, som er servitør på en restaurant. En del av lønnen hennes er bestemt av hvor mye hun selger av tre typer varmretter. For hver av disse tre varmrettene får Gina en viss prosent av salgsinntekten som lønn.

Nedenfor ser du: pris per porsjon, antall porsjoner som Gina selger og hvor mange prosent av salgsinntektene Gina får i lønn for hver av de tre varmrettene en bestemt dag.

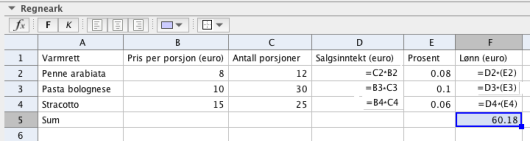
a)

Bruk regneark til å vise at Gina får til sammen 60,18 € i lønn for salget av varmrettene denne dagen. Vis hvilke formler du har brukt.

Løs oppgaven her

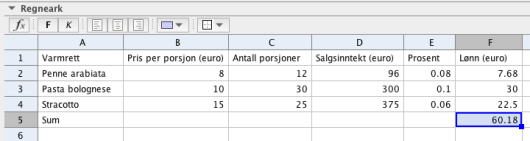
b)

En annen dag selger Gina $14$ porsjoner penne arrabiata, $25$ porsjoner pasta bolognese og $21$ porsjoner stracotto. Prisene og prosentene er uendret.

Bruk regnearket til å bestemme hvor mye Gina får i lønn til sammen denne dagen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her legger vi inn de nye tallene under Antall porsjoner i regnearket i GeoGebra for å finne hvor mye Gina får i lønn den dagen.

Svar: Hun tjener $52, 8$ euro.

Mer om:

Denne oppgaven er om bruk av regneark (i GeoGebra).

Lynkurset med temaet er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet Regneark II i Treningsleieren.

Oppgave 5 (4 poeng) Nettkode: E-4FZB

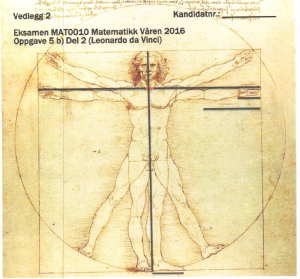
I nærheten av Firenze ble kunstneren og vitenskapsmannen Leonardo da Vinci født.

To av hans mange berømte kunstverk «Det siste måltid» og «Den vitruviske mann».

Vedlegg 1 og 2 finner du i høyrespalten. Bruk disse til å besvare spørsmålene under. (Vedleggene måtte leveres inn som en del av besvarelsen.)

a)

Bruk vedlegg 1. Tegn perspektivlinjer. Marker hvor forsvinningspunktet på kunstverket er.

Løs oppgaven her

b)

Bruk vedlegg 2. Ta mål av mannen når han står med bena samlet og armene rett ut, og avgjør om disse påstandene er riktige:

Lengden fra langfingertupp til langfingertupp (armspennet) er lik høyden til mannen.
Lengden av en hånd er lik $\frac{1}{10}$ av høyden til mannen.
Lengden fra albuen til langfingertuppen er lik $\frac{1}{5}$ av høyden til mannen.
Forholdet mellom lengden av en fot og høyden til mannen er $1 : 7$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Nå sjekker vi om påstandene 1. til 4. er riktige.

Vi måler og finner ut følgende:

Høyden til mannen er lik $13, 0$ cm. Lengden til armspenne er også $13, 0$ cm. Påstanden er riktig.

Lengden til hånden er $1, 3$ cm, mens $\frac{1}{10}$ av høyden til mannen svarer til $1, 3 cm.$ Påstanden stemmer.

Lengden fra albuen til langfingertuppen er $3, 3$ cm. Mens $\frac{1}{5}$ av høyden er lik $\frac{1}{5} \cdot 13 = 2, 6$ cm. Påstanden er ikke riktig.

Lengden til foten er $1, 8$ cm. Dette gir at $13 : 1, 8 = 7, 22$ og forholdet er tilnærmet lik $1 : 7 .$

Svar: Påstandene 1, 2 og 4 stemmer.

Mer om:

Denne oppgaven er om

Målestokk

Målestokken angir hva en måleenhet på for eksempel kartet svarer til i terrenget.

Eksempel:
Et kart har målestokken 1 : 25000 (leses: en til tjuefemtusen)

Dette betyr for eksempel at:

-	1 cm på kartet tilsvarer 25000 cm i terrenget (25000 cm = 250 m)
-	1 dm på kartet tilsvarer 25000 dm i terrenget
-	4 cm på kartet er 25000 · 4 cm i terrenget (25000 · 4 cm = 100000 cm = 1000m = 1 km).

Eller mer generelt:
1 bestemt måleenhet på kartet er 25000 slike måleenheter i terrenget.

målestokk

og regning med forhold.

For flere forklaringer og eksempler se lynkurset Målestokk og forholdsregning.

For å øve mer, se oppgavesettet Målestokk i Treningsleieren.

Oppgave 6 (4 poeng) Nettkode: E-4FZO

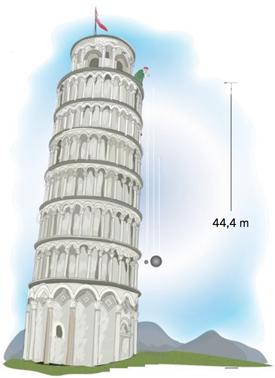
Familien stopper ved Det skjeve tårn i Pisa.

Det blir fortalt at Galileo slapp tunge blykuler fra den laveste siden av tårnet.

Hele fallhøyden er 44,4 m. Se figuren nedenfor.

Hvis vi slipper en kule fra toppen og ser bort fra luftmotstanden, vil kulen falle $h$ meter på

$t$ sekunder. Galileo viste at

$h = 4, 9 t^{2}$

a)

Vi setter $h = 44, 4 m$ . Vis ved regning at det tar ca. $3 s$ fra vi slipper kulen til den treffer bakken.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi vet at funksjonsuttrykket er $h = 4, 9 t^{2}$ og $h = 44, 4$ m. Vi skal vise at tiden det tar kula å treffe bakken er $3$ s. Vi kan sette inn $3$ for $t$ i uttrykket og vise at $h = 44, 4$ eller vi kan sette inn for $h$ og løser det som en likning med hensyn på $t$ .

Vi viser begge løsningsmetoder, så husk å se på alternativ løsning under.

Vi setter inn $3$ for $t$ i uttrykket:

$h = 4, 9 t^{2}$

$h = 4, 9 \cdot 3^{2}$

$h = 4, 9 \cdot 9$

$h = 44, 1$

Svar: Vi har derfor vist at kula treffer bakken etter $3$ s.

Alternativ løsning

Vi setter inn $44, 4$ for $h$ og løser likningen med hensyn på $t$ :

$h = 4, 9 t^{2}$

$44, 4 = 4, 9 t^{2}$

Vi dividerer med 4,9 begge sider av likningen:

$\frac{44, 4}{4, 9} = \frac{4, 9 t^{2}}{4, 9}$

$\frac{44, 4}{4, 9} = t^{2}$

Nå tar vi roten på begge siden av likhetstegnet:

$\sqrt{\frac{44, 4}{4, 9}} = \sqrt{t^{2}}$

$\sqrt{\frac{44, 4}{4, 9}} = t$

$t = 3, 01$

Mer om:

Denne oppgaven er om

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

For flere forklaringer på fart, tid og strekning se artikkelen Hvorfor regne med bokstaver og Målingsforhold.

For å øve mer, se oppgavesettet Måling - fart I i Treningsleieren.

b)

Vis ved regning at kulen faller ca. $25 m$ i løpet av det siste sekundet.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi finner først hvor langt ned kulen faller etter $2$ sekunder og trekker det fra den totale avstanden som er $44, 4$ meter.

Vi setter inn $2$ for $t$ :

$h = 4, 9 t^{2}$

$h = 4, 9 \cdot 2^{2}$

$h = 4, 9 \cdot 4$

$h = 19, 6$

Den totale høyden er $44, 4$ og derfor er avstanden det siste sekundet likt:

$44, 4 m - 19, 6 m = 24, 8 m$

Svar: Herved har vi vist at kula faller ca. $25 m$ i løpet av det siste sekundet.

Mer om

Oppgven er om

Fart

Fart er tilbakelagt distanse per tidsenhet.

Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.

Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.

vei, fart og tid

Algebra

Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.

Et algebrauttrykk kan være:

n + n + n + n + n = 5n

Her har vi lagt sammen n til sammen 5 ganger.

algebra

For flere forklaringer og eksempler se artiklene Hvorfor regne med bokstaver? og Målingsforhold.

For å øve mer, se oppgavesettet Måling - fart II i Treningsleieren.

Oppgave 7 (4 poeng) - GRAFTEGNER Nettkode: E-4FZS

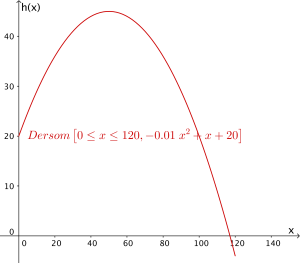
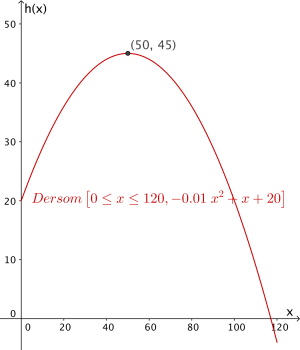
Galileo viste at kanonkuler går i en bane som vi kaller en parabel. Se skissen nedenfor.

Banen til en kanonkule kan beskrives ved hjelp av funksjonen $h$ gitt ved

$h (x) = {- 0, 01 x}^{2} + x + 20$

Her viser $h (x)$ hvor mange meter kanonkulen er over havet når den har kommet $x$ meter fra

kanonen, målt langs havoverflaten.

a)

Bruk graftegner til å tegne grafen til $h$ for $x$ -verdier fra og med $0$ til og med $120$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her bruker vi funksjonen Funksjon[ <Funksjon>, <Start>, <Slutt> ] i GeoGebra og tegner grafen.

Vi skriver inn i Geogebra: Funksjon[ $- 0, 01 x^{2} + x + 20$ , $0$ , $120$ ]

Svar:

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

grafer

. Vi bruker graftegner i GeoGebra.

For flere forklaringer og eksempler på funksjoner og grafer, se artikkelen Fra funksjon til graf eller lynkurset Funksjoner. Lynkurset om GeoGebra og graftegner er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet Funksjoner i Treningsleieren.

b)

Bruk graftegner til å bestemme hvor høyt over havet kanonkulen er på sitt høyeste.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi bruker funksjonen Ekstremalpunkt[ <Funksjon>, <Start>, <Slutt> ] i GeoGebra og finner toppunktet.

Vi skriver inn i Geogebra: Ekstremalpunkt[ $- 0, 01 x^{2} + x + 20$ , $0$ , $120$ ]

Svar: Etter $50$ meter er kanonkulen $45$ meter over havet.

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

. Vi bruker graftegner i GeoGebra.

For flere forklaringer og eksempler se lynkurset Funksjoner. Lynkurset om graftegning i GeoGebra er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet Funksjoner II i Treningsleieren.

Oppgave 8 (4 poeng) Nettkode: E-4FZX

Fibonacci-tallene har fått navn etter Leonardo Fibonacci fra Pisa (ca. 1170–ca. 1250).

Fibonacci-tallene er en tallfølge der de to første tallene er 1. Hvert av de neste tallene er summen av de to tallene foran:

og så videre.

De åtte første Fibonacci-tallene er

a)

Skriv opp de neste fire Fibonacci-tallene i tallfølgen ovenfor.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

I en tallfølge finner vi alltid et mønster. Her får vi vite at hvert av de neste tallene er summen av de to tallene foran.

De neste fire Fibonacci-tallene finner vi ved å legge sammen de to siste tallene i tallfølgen og slik fortsetter vi:

$13 + 21 = 34$

$21 + 34 = 55$

$34 + 55 = 89$

$55 + 89 = 144$

Svar: De neste fire tallene er $34, 55, 89 og 144 .$

Mer om

Denne oppgaven er om tallfølger og

Fibonacci-tallene

Tallfølgen 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,... kalles Fibonacci-tallene. Det neste tallet i følgen finner vi ved å ta summen av de to foregående tallene. Det neste tallet er 34 + 55 = 89.

Fibonacci-tallene forekommer ofte i naturen, for eksempel i forbindelse med spiraler i kongler og solsikker.

Fibonacci-tallene

For flere forklaringer og eksempler på tallfølger, se lynkurset Følger og rekker og den matematiske teksten Fibonaccitallene.

For å øve mer, se oppgavesettet Tallfølger i Treningsleieren.

Visste du at?

Leonardo Fibonacci var en italiensk matematiker fra Pisa. Selvom Fibonacci-tallrekken er oppkalt etter ham, var det ikke han som oppfant den. Den ble beskrevet av matematikere allerede 200 år f.Kr. Fibonacci er også kjent for å ha introdusert de arabiske tallene i den vestlige verden.

b)

I tallfølgen nedenfor er de to første leddene a og b. Hvert av de neste leddene er summen av de to leddene foran.

Skriv opp de fire neste leddene i denne tallfølgen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi ser nøye på tallene foran $a$ og så tallene foran $b$ . Hva skjer?

Det vi ser er at faktorene foran $a$ og $b$ følger Fibonacci-tallfølgen.

Derfor vil de neste leddene være:

$5 a + 8 b$

$8 a + 13 b$

$13 a + 21 b$

$21 a + 34 b$

Svar: De neste leddene er $5 a + 8 b$ , $8 a + 13 b$ , $13 a + 21 b$ og $21 a + 34 b$ .

Mer om

Oppgaven er om tallfølger og

Fibonacci-tallene

Tallfølgen 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,... kalles Fibonacci-tallene. Det neste tallet i følgen finner vi ved å ta summen av de to foregående tallene. Det neste tallet er 34 + 55 = 89.

Fibonacci-tallene forekommer ofte i naturen, for eksempel i forbindelse med spiraler i kongler og solsikker.

Fibonacci-tallene

For å lese mer om Fibonacci-tallene, se den matematiske teksten Fibonaccitallene.

For å øve mer, se oppgavesettet Tallfølger II i Treningsleieren.

Visste du at

Det finnes ulike tallfølger. En type heter aritmetiske tallfølger, mens en annen heter geometriske tallfølger. Les mer om disse i lynkurset Følger og rekker.

Oppgave 9 (2 poeng) Nettkode: E-4G0B

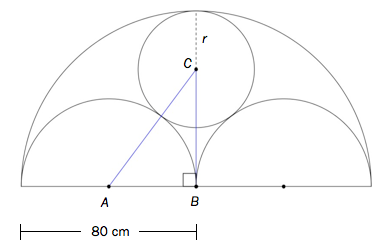
Bildet viser en del av bygningen Palazzo Vendramin-Calergi i Venezia. Nedenfor ser du en skisse av den øvre delen av vinduene. Skissen viser tre halvsirkler og én sirkel. Sirkelen tangerer alle de tre halvsirklene.

Punktet $B$ er sentrum i den store halvsirkelen.

Punktet $A$ er sentrum i en av de små halvsirklene.

Punktet $C$ er sentrum i sirkelen.

Linjestykket $r$ er radius i sirkelen.

Regn ut lengden av radien $r$ .

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi vet at radiusen i den største halvsirkelen (med sentrum $B$ ) er $r_{s t o r} = 80$ cm. Avstanden $A B = 40$ cm og trekanten $A B C$ er rettvinklet.

Lengden til $r$ er lik $80 - B C$ cm. Hvis vi klarer å finne sidelengedene i trekanten, kan vi bruke Pytagoras læresetning og finne ut lengden til $B C$ og deretter $r$ .

Vi vet at $A B = 40$ cm og vi vet at $B C = 80 - r$ . Hypotenusen ${A C}^{} = 40 + r$ . Da kan vi bruke Pytagoras læresetning:

$(40 + r)^{2} = 40^{2} + (80 - r)^{2}$

$(40 + r) (40 + r) = 1600 + (80 - r) (80 - r)$

$1600 + 80 r + r^{2} = 1600 + 6400 - 160 r + r^{2}$

Vi kan trekke fra $1600$ og $r^{2}$ fra begge sider av likhetstegnet:

$1600 + 80 r + r^{2} - 1600 - r^{2} = 1600 + 6400 - 160 r + r^{2} - 1600 - r^{2}$

$80 r = 6400 - 160 r$

Nå legger vi til $160 r$ til begge sider av likhetstegnet:

$80 r + 160 r = 6400 - 160 r + 160 r$

$240 r = 6400$

Dividerer vi med $240$ på begge sider, får vi:

$\frac{240 r}{240} = \frac{6400}{240}$

$r = \frac{6400}{240}$

$r = 26, 6666$

Svar: Radien er ca. $27 cm.$

Mer om

Denne oppgaven er om

Pytagoras læresetning

Rettvinklet trekant

En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.

rettvinklet trekant

Radius

Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.

radius

For flere forklaringer og eksempler se artikkelen Pytagoras læresetning, En trekant og Alt om sirkel.

For å øve mer, se oppgavesettet Geometri- Pytagoras læresetning i Treningsleieren.

MAT0010 2016 VÅR

Del 1

Del 2

Eksamensinformasjon

Del 1 uten hjelpemidler

Oppgave 1 (2 poeng) Nettkode: E-4FV8

a)

Løsningsforslag a)

Addisjon

b)

Løsningsforslag b)

Subtraksjon

c)

Løsningsforslag c)

Multiplikasjon

d)

Løsningsforslag d)

Divisjon

Oppgave 2 (1 poeng) Nettkode: E-4FVD

a)

Løsningsforslag a)

Benevning

Lengdeenhet

b)

Løsningsforslag b)

Benevning

Oppgave 3 (0,5 poeng) Nettkode: E-4FVO

Løsningsforslag

Potens

Oppgave 4 (1 poeng) Nettkode: E-4FVY

a)

Løsningsforslag a)

Brøk

Nevner

Teller

Fellesnevner

b)

Løsningsforslag b)

Brøk

Nevner

Teller

Fellesnevner

Oppgave 5 (0,5 poeng) Nettkode: E-4FW1

Løsningsforslag

Desimaltall

Oppgave 6 (0,5 poeng) Nettkode: E-4FW3

Løsningsforslag

Standardform

Oppgave 7 (2 poeng) Nettkode: E-4FWD

Løsningsforslag

Funksjon

Lineære funksjoner

Oppgave 8 (1 poeng) Nettkode: E-4FWG

Løsningsforslag

Prosent

Oppgave 9 (0,5 poeng) Nettkode: E-4FWK

Løsningsforslag

Alternativ løsning

Sannsynlighet

Utfall

Gunstig utfall

Oppgave 10 (0,5 poeng) Nettkode: E-4FWN

Løsningsforslag

Sannsynlighet

Oppgave 11 (1,5 poeng) Nettkode: E-4FWQ

a)

Løsningsforslag a)

Ligning

Lineære ligninger

b)

Løsningsforslag b)

Ligning

Lineære ligninger

Oppgave 12 (1,5 poeng) Nettkode: E-4FWT

a)

Løsningsforslag a)

Algebra

b)

Løsningsforslag b)

Algebra