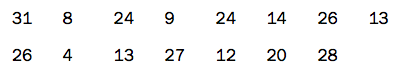Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1015 2016 Høst

Del 1
Del 2
Eksamensinformasjon

Eksamenstid
5 timer: 
Del 1 skal leveres inn etter 2 timer.
 Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler på Del 1
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Hjelpemidler på Del 2
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Fremgangsmåte
Du skal svare på alle oppgavene i Del 1 og Del 2.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse  
gjennomfører logiske resonnementer  
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner  
kan bruke hensiktsmessige hjelpemidler  
forklarer framgangsmåter og begrunner svar  
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger  
vurderer om svar er rimelige

Andre opplysninger
Kilder for bilder, tegninger osv.

Bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet

DEL 1 uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4OUA

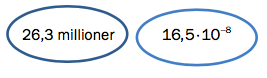
Skriv tallene nedenfor på standardform

Løs oppgaven her

Løsningsforslag

Jeg tenker

Én million er det samme som $1 000 000$ . Vi skal skrive som et tall på

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

standardform

1)
Et tall på standardform er formen $a \cdot 10^{n}$ , der $a$ er et tall mellom $1$ og $10$ , og $n$ er et helt tall.
Vi har at $1$ million er $1 000 000 = 10^{6}$ , så $26, 3$ millioner er $26, 3 \cdot 10^{6}$ . For at tallet skal være på standardform må tallet før tierpotensen være mellom $1$ og $10$ , så dette er ikke helt på standardform. Vi vet at $26, 3 = 2, 63 \cdot 10$ , så tallet på standardform er

$26, 3 \cdot 10^{6} = 2, 63 \cdot 10 \cdot 10^{6} = 2, {63 \cdot 10}^{7}$

2)
$16, 5 \cdot 10^{- 8}$ er nesten på standardform, bortsett fra at $16, 5$ ikke er mellom $1$ og $10$ , men igjen vet vi at $16, 5 = 1, 65 \cdot 10$ , så

$16, 5 \cdot 10^{- 8} = 1, 65 \cdot 10 \cdot 10^{- 8} = 1, 65^{\cdot} 10^{- 7}$

Svar: $2, 63 \cdot 10^{7}$ og $1, 65 \cdot 10^{- 7}$

Mer om:

Denne oppgaven er om

Standardavvik

Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.

tall på standardform

Heltall

Heltall er de tallene vi oftest teller: 0, 1, 2, 3, 4... De hele tallene inkluderer også de negative tallene; -1, -2, -3...

Symbolet for mengden av hele tall er ℤ.

heltall

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$

potens

For flere eksempler og forklaringer se artikkelen Tall på standardform.

For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.

Oppgave 2 (1 poeng) Nettkode: E-4OUF

Regn ut og skriv tallet som desimaltall

$\frac{3, 5 \cdot 10^{8}}{7, 0 \cdot 1 0^{5} \cdot 0, 5 \cdot 10^{6}}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ser en brøk med

Potens

potenser

i både

Teller

Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.

Eksempel: I brøken $\frac{5}{9}$ , er det 5 som er telleren. 9 kalles nevner.

teller

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

nevner

. Potensene har samme

Grunntall

En potens består av et grunntall og en eksponent.

Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.

grunntall

og da kan vi bruke potensreglene.

Vi kan flytte opp tall fra nevneren dersom vi bytter fortegn på

Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger

eksponenten

. Da får vi

$\frac{3, 5 \cdot 10^{8}}{7, 0 \cdot 10^{5} \cdot 0, 5 \cdot 10^{6}} = \frac{3, 5 \cdot 10^{8} \cdot 10^{- 5} \cdot 10^{- 6}}{7, 0 \cdot 0, 5}$

I nevneren får vi $7, 0 \cdot 0, 5 = 3, 5$ . I telleren kan vi addere eksponentene til potensene med samme grunntall. Da får vi

$\frac{3, 5 \cdot 10^{8 + (- 5) + (- 6)}}{3, 5} = \frac{3, 5 \cdot 10^{8 - 5 - 6}}{3, 5} = \frac{3, 5 \cdot 10^{- 3}}{3, 5} = \frac{10^{- 3}}{1}$

Vi kan flytte $10^{- 3}$ ned i telleren, men da må vi huske å bytte fortegn. Da ser vi at det kan skrives som

$\frac{1}{10^{3}} = \frac{1}{1000} = 0, 001$

Svar: $0, 001$

Mer om:

Denne oppgaven er om

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

tall på standardform

og potens.

For flere forklaringer og eksempler på standardform, se artikkelen Potenser med samme grunntall.

For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.

Oppgave 3 (1 poeng) Nettkode: E-4OUH

Ved en skole er det $135$ jenter og $115$ gutter.

Hvor mange prosent av elevene er jenter?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi skal finne ut hvor stor

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosentandel

av alle elevene på skolen som er jenter, da må vi se på hvor mange jenter det er i forhold til det totale antall elever.

Vi skal finne ut hvor stor prosentandel av alle elevene som er jenter. Det totale antallet elever på skolen er $135 + 115 = 250$ .

$\frac{135}{250}$ av elevene på skolen er jenter. Prosent betyr del av hundre. Vi kan utvide brøken slik at vi først får 1000 i nevner, også kan vi deretter forkorte til 100 i nevneren.

$\frac{135 \cdot 4}{250 \cdot 4} = \frac{540}{1000} = \frac{54}{100} = 54 %$

Svar: $54 %$ er jenter.

Mer om:

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler på prosent, se artikkelen Prosent av hva da?.

For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.

Oppgave 4 (2 poeng) Nettkode: E-4OUJ

En vare kostet like mye i butikk $A$ og butikk $B$ . Så ble prisen endret.

I butikk $A$ ble prisen først satt opp med $10 %$ . Senere ble prisen satt ned med $10 %$ .
I butikk $B$ ble prisen først satt ned med $10 %$ . Senere ble prisen satt opp med $10 %$ .

Avgjør hvilken av de tre påstandene nedenfor som er riktig.

Påstand 1: Varen koster nå minst i butikk $A$ .
Påstand 2: Varen koster nå minst i butikk $B$
Påstand 3: Varen koster like mye i de to butikkene.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Når en vare blir satt opp med $10 %$ kan vi finne ny pris ved å multiplisere orginalpris med $1, 1$ , og når en vare blir satt ned med $10 %$ kan vi finne ny pris ved å multiplisere med $0, 9$ .

Varen hadde samme originalpris i butikk $A$ og $B$ . Vi kan se på endringen på prisen i de ulike butikkene.
Vi begynner med butikk $A$ . Her ble prisen først satt opp med $10 %$ . Vi kan finne ny pris ved å multiplisere med $1, 1$ . Ny pris av varen ble da

$ny pris A = originalpris \cdot 1, 1$

Den nye prisen ble så satt ned med $10 %$ , da kan vi multiplisere med $0, 9$ for å finne den nyeste prisen

$nyeste pris A = ny pris A \cdot 0, 9 = originalpris \cdot 1, 1 \cdot 0, 9$

Den siste prisen i butikk $A$ er altså $originalpris \cdot 1, 1 \cdot 0, 9$ .

Tilsvarende får vi i butikk $B$ . Der ble prisen først satt ned med $10 %$ . Etter den første prisendringen var prisen da

$ny pris B = originalpris \cdot 0, 9$

Prisen blir deretter satt opp igjen med $10 %$ , den nyeste prisen i butikk $B$ blir da

$nyeste pris B = ny pris B \cdot 1, 1 = originalpris \cdot 0, 9 \cdot 1, 1$

Rekkefølgen til faktorene spiller ingen rolle, så vi ser at prisen på varen vil være $originalpris \cdot 0, 9 \cdot 1, 1$ i begge butikkene, så påstand $3$ stemmer.

Svar: Påstand $3$ er riktig

Mer om:

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler se artiklene Prosent av hva da? og Regneregler.

For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.

Oppgave 5 (2 poeng) Nettkode: E-4OUL

Tenk deg at du har $1024$ kroner. Hver uke framover bruker du halvparten av de pengene du har igjen.

Skriv $1024$ som en potens med grunntall $2$ , og regn med potenser for å bestemme hvor mye du vil ha igjen etter $7$ uker.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi skal skrive $1024$ som

Potens

potens

med

2

som

Grunntall

En potens består av et grunntall og en eksponent.

Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.

grunntall

. Altså må vi finne ut hvor mange ganger

2

må multipliseres med seg selv for å få

1024

For å kunne skrive $1024$ som potens med $2$ som grunntall må vi finne hvor mange ganger $2$ er multiplisert med seg selv for å få $1024$ . Vi vil ha det på formen $2^{n}$ der $n$ er et heltall.
Vi kan begynne med å se at $1024 = 512 \cdot 2$ . Videre kan vi se at $512 = 256 \cdot 2$ , altså er $1024 = 512 \cdot 2 = 256 \cdot 2 \cdot 2 = 256 \cdot 2^{2}$ Vi kan fortsette sånn til vi kun står igjen med $2$ .

$\begin{matrix} 1024 & = & 512 \cdot 2 \\ = & 256 \cdot 2 \cdot 2 & = & 256 \cdot 2^{2} \\ = & 128 \cdot 2 \cdot 2^{2} & = & 128 \cdot 2^{3} \\ = & 64 \cdot 2 \cdot 2^{3} & = & 64 \cdot 2^{4} \\ = & 32 \cdot 2 \cdot 2^{4} & = & 32 \cdot 2^{5} \\ = & 16 \cdot 2 \cdot 2^{5} & = & 16 \cdot 2^{6} \\ = & 8 \cdot 2 \cdot 2^{6} & = & 8 \cdot 2^{7} \\ = & 4 \cdot 2 \cdot 2^{7} & = & 4 \cdot 2^{8} \\ = & 2 \cdot 2 \cdot 2^{8} & = & 2^{10} \end{matrix}$

1024 kan altså skrives som en potens med grunntall $2$ som $2^{10}$ .

Vi bruker halvparten av pengene hver uke, det vil si at vi dividerer pengene vi har på $2$ for hver uke som går. Etter en uke har vi $\frac{1024}{2}$ kroner igjen, etter to uker har vi $\frac{1024}{2 \cdot 2}$ kroner igjen, så etter 7 uker har vi

$\frac{1024}{2^{7}} = \frac{2^{10}}{2^{7}} = 2^{10} \cdot 2^{- 7} = 2^{10 - 7} = 2^{3} = 2 \cdot 2 \cdot 2 = 8$

Alternativ

For å finne ut hvordan vi kan skrive $1024$ som en potens med grunntall $2$ , kan vi også gå motsatt vei fra den over; vi kan multiplisere $2$ med seg selv eller med potenser med $2$ som grunntall. Vi kan begynne med

$2^{2} = 2 \cdot 2 = 4$

I stedet for å multiplisere med $2$ hver gang, kan vi nå finne $2^{4}$ ved å multiplisere $2^{2} \cdot 2^{2}$

$2^{4} = 2^{2 + 2} = 2^{2} \cdot 2^{2} = 4 \cdot 4 = 16$

Vi kan finne $2^{8}$ på samme måte

$2^{8} = 2^{4 + 4} = 2^{4} \cdot 2^{4} = 16 \cdot 16 = 256$

Nå vokser taller fortere når vi multipliserer med $2$ , så nå kan vi fortsette med $2^{9}$

$2^{9} = 2^{8} \cdot 2 = 256 \cdot 2 = 512$

Dersom vi multipliserer dette med $2$ får vi

$2^{10} = 2^{9} \cdot 2 = 512 \cdot 2 = 1024$

1024 kan altså skrives som en potens med grunntall $2$ som $2^{10}$ .

Svar: Vi har $8$ kroner igjen.

Mer om:

Denne oppgaven er om

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

tall på standardform

Potens

potenser

For flere forklaringer og eksempler se artikkelen Tall på standardform.

For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.

Oppgave 6 (4 poeng) Nettkode: E-4OUP

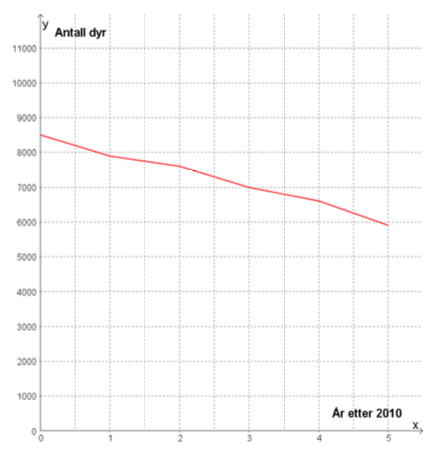
Linjediagrammet ovenfor viser hvordan antall dyr av en art har avtatt innenfor et bestemt område i perioden $2010 - 2015$ .

a)

Bestem en lineær funksjon som tilnærmet beskriver utviklingen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineær funksjon

kan skrives på formen

f (x) = a x + b

. Grafen til en lineær funksjon vil være en rett linje.

Vi skal bestemme en lineær funksjon til linjediagrammet. Da må vi finne en funksjon på formen $f (x) = a x + b$ , der $a$ er

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstallet

til grafen, og

b

er konstantleddet, som passer til linjediagrammet. Vi må bestemme konstantene

a

b

. Konstantleddet,

b

, er der linjen krysser

y

-aksen. Det kan vi lese av grafen. Vi ser at i

2010

, når linjediagrammet starter, er det omtrent

8500

dyr. Da får vi at

$b = 8500$

Antall dyr har sunket fra $8500$ i $2010$ til $6000$ i $2015$ , altså har antall dyr sunket med $8500 - 6000 = 2500$ dyr på $5$ år. Hvert år har det sunket med $\frac{2500}{5} = 500$ dyr, og vi har en vekst på $- 500$ dyr per år. Stigningstallet til $f$ er lik $a = - 500$ . Den lineære funksjonen er da

$f (x) = - 500 x + 8500$

Svar $f (x) = - 500 x + 8500$

Mer om:

Denne oppgaven er om

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).

koordinatsystem

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineær funksjon

og matematiske modeller.

For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.

b)

Hvor mange dyr av arten vil det være i området i $2018$ ifølge funksjonen fra oppgave a)?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Funksjonen vi fant i deloppgave a) forteller oss hvor mange dyr det er $x$ år etter $2010$ . Vi kan sette inn for $x = 8$ i likningen.

I forrige oppgave fant vi ut at antall dyr $x$ år etter $2010$ vil være $f (x) = - 500 x + 8500$ . For å finne ut hvor mange dyr det er i $2018$ kan vi sette inn for $x = 8$ i likningen. Da får vi

$f (8) = - 500 \cdot 8 + 8500 = - 4000 + 8500 = 4500$

Svar: I $2018$ vil det være $4500$ dyr av arten i området.

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.

c)

Hvor mange år vil det gå før det ikke er flere dyr av arten igjen i området ifølge funksjonen fra oppgave a)?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må finne ut når funksjonsuttrykket i deloppgave a) er lik $0$ .

Vi skal finne ut etter hvor mange år det vil gå før det ikke er flere dyr av arten igjen i området. Vi vil altså finne ut når funksjonssuttrykket vi fant i deloppgave a) er lik 0. Da må vi løse likningen

Da får vi

$\begin{matrix} - 500 x + 8500 & = & 0 \\ - 500 x & = & - 8500 \\ x & = & \frac{- 8500}{- 500} \\ x & = & 17 \end{matrix}$

Etter $17$ år vil det ikke være flere dyr av arten igjen i området.

Svar: $17$ år

Mer om:

Mer om
Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere eksempler og forklaringer se artikkelen Lineære likninger.

For å øve mer, se oppgavesettet om lineære likninger i Treningsleieren.

Oppgave 7 (4 poeng) Nettkode: E-4OUV

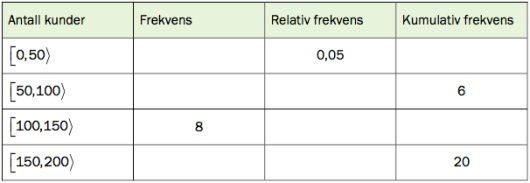
Sondre solgte frukt og grønnsaker på torget 20 lørdager i løpet av 2016. Hver av de 20 lørdagene skrev han opp hvor mange kunder han hadde. Han laget også en tabell. Tabellen ser du nedenfor, men her mangler noen av tallene Sondre satte inn.

a)

Tegn av tabellen ovenfor, og fyll inn tallene som mangler.
Gjør beregninger eller forklar hvordan du tenker.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her må vi huske på definisjonene av frekvens,

Relativ frekvens

Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.

Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.

relativ frekvens

Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.

Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.

Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.

kumulativ frekvens

Frekvensen til et intervall er antall dager som hadde antall kunder i intervallet. Siden frekvensen til $[100, 150 ⟩$ er $8$ , var det $8$ dager det var mellom $100$ og $150$ kunder.
Den relative frekvensen til et intervall er hvor stor andel av dagene som hadde antall kunder i dette intervallet. At den relative frekvensen til $[0, 50 ⟩$ er $0, 05$ betyr at $0, 05 = 5 %$ av dagene hadde mellom $0$ og $50$ kunder.

Kumulativ frekvens for et intervall er antall dager det var antall kunder i intervallet, eller et lavere intervall. At den kumulative frekvensen for $[50, 100 ⟩$ er $6$ , betyr at $6$ av dagene var mellom $0$ og $100$ kunder.
Vi kan begynne med å skrive inn tabellen som den er:

Antall kunder	Frekvens	Relativ frekvens	Kumulativ frekvens
$[0, 50 ⟩$		$0, 05$
$[50, 100 ⟩$			$6$
$[100, 150 ⟩$	$8$
$[150, 200 ⟩$			$20$

Det kan være lurt å begynne å fylle inn tabellen øverst, og jobbe seg nedover. Vi vet at den relative frekvensen til $[0, 50 ⟩$ er $0, 05$ , det betyr at $5 %$ av dagene hadde mellom $0$ og $50$ kunder.

$5 % = \frac{5}{100} = \frac{1}{20}$

$5 %$ er det samme som $1$ av $20$ , så frekvensen til intervallet $[0, 50 ⟩$ er $1$ .

Ingen dager hadde færre antall kunder i intervallet, så den kumulative frekvensen er også $1$ .

Da har vi den første raden, og vi kan fylle inn

Antall kunder	Frekvens	Relativ frekvens	Kumulativ frekvens
$[0, 50 ⟩$	$1$	$0, 05$	$1$
$[50, 100 ⟩$			$6$
$[100, 150 ⟩$	$8$
$[150, 200 ⟩$			$20$

Vi fortsetter med det neste intervallet, $[50, 100 ⟩$ . Den kumulative frekvensen til $[50, 100 ⟩$ er $6$ , så det var seks dager med mellom $0$ og $100$ kunder, men vi vet at det var $1$ dag med mellom $0$ og $50$ kunder, så da står vi igjen med $6 - 1 = 5$ . Frekvensen til intervallet er da lik $5$ . Det er totalt $20$ dager, så den relative frekvensen blir lik $\frac{5}{20} = \frac{1}{4} = 0, 25$ . Vi fyller inn.

Antall kunder	Frekvens	Relativ frekvens	Kumulativ frekvens
$[0, 50 ⟩$	$1$	$0, 05$	$1$
$[50, 100 ⟩$	$5$	$0, 25$	$6$
$[100, 150 ⟩$	$8$
$[150, 200 ⟩$			$20$

Frekvensen til intervallet $[100, 150 ⟩$ er $8$ . Den relative frekvensen blir da $\frac{8}{20} = \frac{4}{10} = 0, 40$ . Den kumulative frekvensen er hvor mange dager det var mellom $0$ og $150$ kunder, og vi vet at det var $6$ dager med mellom $0$ og $100$ , så den kumulative frekvensen blir $6 + 8 = 14$ . Vi fyller inn i tabellen.

Antall kunder	Frekvens	Relativ frekvens	Kumulativ frekvens
$[0, 50 ⟩$	$1$	$0, 05$	$1$
$[50, 100 ⟩$	$5$	$0, 25$	$6$
$[100, 150 ⟩$	$8$	$0, 40$	$14$
$[150, 200 ⟩$			$20$

Da gjenstår bare den siste raden. Av de $20$ dagene hadde $14$ av disse mellom $0$ og $150$ kunder. Antall dager som hadde mellom $150$ og $200$ kunder blir da $20 - 14 = 6$ . Frekvensen til intervallet $[150, 200 ⟩$ er lik $6$ . Den relative frekvensen blir $\frac{6}{20} = \frac{3}{10} = 0, 30$ . Nå kan vi fylle inn den siste raden i tabellen.

Antall kunder	Frekvens	Relativ frekvens	Kumulativ frekvens
$[0, 50 ⟩$	$1$	$0, 05$	$1$
$[50, 100 ⟩$	$5$	$0, 25$	$6$
$[100, 150 ⟩$	$8$	$0, 40$	$14$
$[150, 200 ⟩$	$6$	$0, 30$	$20$

Svar:

Antall kunder	Frekvens	Relativ frekvens	Kumulativ frekvens
$[0, 50 ⟩$	$1$	$0, 05$	$1$
$[50, 100 ⟩$	$5$	$0, 25$	$6$
$[100, 150 ⟩$	$8$	$0, 40$	$14$
$[150, 200 ⟩$	$6$	$0, 30$	$20$

Mer om:

Denne oppgaven er om

Frekvenstabell

En frekvenstabell er en opptelling og ordning av dataene i en datasamling.

Se frekvens

frekvenstabell

Relativ frekvens

Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.

Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.

relativ frekvens

Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.

Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.

Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.

kumulativ frekvens

Statistikk

Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.

statistikk

For flere eksempler og forklaringer se artikkelen Frekvens.

b)

Nedenfor ser du listen der Sondre har skrevet opp hvor mange kunder han hadde hver av de 20 lørdagene. Tre av tallene er skjult under flekker.

Foreslå tre mulige tall som kan stå under de tre flekkene slik at de $20$ verdiene ovenfor gir resultatene i tabellen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne ut hvilke intervall det mangler tall i.

Vi kan begynne å sjekke intervallet $[0, 50 ⟩$ . Vi må huske forskjellen på [ og $⟩$ . Når det står $[0, 50 ⟩$ betyr det at intervallet går fra $0$ og opp til $50$ , men $50$ er ikke med. $50$ er med i intervallet $[50, 100 ⟩$ . Når vi ser gjennom tallene har vi ingen tall i dette intervallet. Tabellen vår forteller at vi skal ha ett tall i dette intervallet, så da kan vi foreslå et vilkårlig tall mellom $0$ og $49$ , f.eks. $30$ .

Av tallene Sondre har skrevet ned er $50$ , $60$ , $75$ , $88$ og $96$ i intervallet $[50, 100 ⟩$ . Fra tabellen vet vi at dette intervallet har frekvens $5$ , så her mangler ingen tall.

I det neste intervallet $[100, 150 ⟩$ har Sondre skrevet ned $100, 105, 116, 120, 125, 125, 133 og 140$ . Fra tabellen vet vi at frekvensen til dette intervallet er $8$ , så her mangler heller ingen tall.

I det siste intervallet $[150, 200 ⟩$ har Sondre skrevet opp tallene $150, 169, 175 og 185$ . Altså fire tall, men frekvensen for intervallet er $6$ . Dermed mangler det to tall, f. eks. $162$ og $192$ .

Svar: Mulige tall er $30$ , $162$ og $192$ .

Mer om:

Denne oppgaven er om

Data

Opplysninger som vi samler inn kalles data.

Data kan for eksempel være 3, 5, 10, 41 og 41, som er alderen i en familie bestående av fem personer. Data kan også være blå, grønn, gul, som er farger på biler.

data

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

Frekvens

Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.

Se frekvenstabell

frekvens

For flere forklaringer og eksempler se artikkelen Data, populasjon og utvalg.

Oppgave 8 (2 poeng) Nettkode: E-4OUZ

Siri har kjøpt bil. Hun antar at verdien av bilen $x$ år etter at hun kjøpte den, vil være gitt
ved

$V (x) = 250 000 \cdot {0, 9}^{x}$

a)

Hva forteller tallene $250 000$ og $0, 9$ i dette funksjonsuttrykket om verdien av Siris bil?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Dette er en

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

En eksponentialfunksjon kan skrives på formen $f (x) = a \cdot r^{x}$ , der a er funksjonsverdien når $x = 0$ , og $r$ er vekstfaktoren. Når $r$ er mindre enn $1$ , vil størrelsen avta eksponentielt, og den avtar med en viss prosentandel.

Verdien til bilen vil være gitt ved $V (x) = 250 000 \cdot 0, 9^{x}$ , og da har vi at $a = 250000$ , så det første året til bilen være verdt 250 000 kr. $r = 0, 9$ , så $0, 9$ er vekstfaktoren. Den forteller oss at verdien avtar med en viss prosentandel hvert år. Vi kan finne denne prosentandelen ved å se på vekstfaktoren. Vekstfaktoren kan skrives som $1 - \frac{p}{100}$ , og vi vet at denne er lik $0, 9$ , da må vi ha at $0, 9 = 1 - 0, 1 = 1 - \frac{10}{100}$ , som forteller at verdien vil avta med $10 %$ .

Svar: $250 000$ forteller oss hvor mye bilen var verdt opprinnelig, og $0, 9$ forteller oss at verdien vil avta med $10 %$ i året.

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Vekstfaktor

Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.

Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.

vekstfaktor

, prosent og matematiske modeller.

For flere eksempler og forklaringer se artikkelen Eksempel: Antall bakterier i en gryte.

For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleiren.

b)

Hva vil bilens verdi være ett år etter at Siri kjøpte den?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan løse likningen for $V (1)$ .

For å finne verdien til bilen etter $1$ år, kan vi løse likningen for $x = 1$ . Da setter vi inn

$V (1) = 250 000 \cdot 0, 9^{1} = 250 000 \cdot 0, 9$

Vi regner ut

Alternativ

Vi vet at verdien bilen vil avta med $10 %$ i løpet av det første året. $10 %$ av $250 000$ er $250 000 \cdot \frac{10}{100} = 250 000 \cdot 0, 1 = 25 000$ Så etter $1$ år har bilen sunket i verdi med $25 000$ kr, da vil verdien være $250 000 - 25 000 = 225 000$

Svar: Etter $1$ år vil bilen være verdt $225 000$ kr.

Mer om:

Denne oppgaven er om

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentiallikninger

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere eksempler se artikkelen Eksponentiallikninger.

Oppgave 9 (3 poeng) Nettkode: E-4OV3

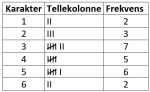
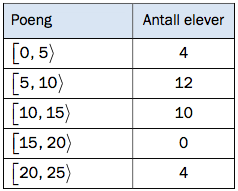
Tabellen nedenfor viser hvor mange poeng hver av de $30$ elevene i en 2P-gruppe fikk på
en matematikkprøve.

a)

Bestem gjennomsnittet for det klassedelte datamaterialet.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

I denne oppgaven behandler vi gruppert informasjon. Da kan vi anta at

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data

Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1) $2 + 2 + 4 + 3 = 11$
2) antall data er 4. $11 : 4 = 2, 75$

gjennomsnittet

for hver gruppe ligger midt i gruppen.

Vi antar at gjennomsnittet i hvert poengintervall ligger midt i intervallet, for eksempel i intervallet $[0, 5 ⟩$ antar vi at elevene i gjennomsnitt fikk $2, 5$ poeng hver. Tilsvarende antar vi at elevene gjennomsnittlig poengsum i intervallet $[5, 10 ⟩$ var $7, 5$ poeng, i intervallet $[10, 15 ⟩$ var $12, 5$ , i $[15, 20 ⟩$ antar vi $17, 5$ og i $[20, 25 ⟩$ antar vi $22, 5$ poeng.
Gjennomsnittlig poengsum er forholdet mellom totale antall poeng og antall elever, så nå kan vi legge sammen alle poengsummene og dividere på antall elever

$\begin{matrix} Gjennomsnitt & = & \frac{antall poeng}{antall elever} \\ = & \frac{2, 5 \cdot 4 + 7, 5 \cdot 12 + 12, 5 \cdot 10 + 17, 5 \cdot 0 + 22, 5 \cdot 4}{30} \\ = & \frac{10 + 90 + 125 + 90}{30} \\ = & \frac{315}{30} \\ = & \frac{300}{30} + \frac{15}{30} \\ = & 10 + 0, 5 \\ = & 10, 5 \end{matrix}$

Svar: Gjennomsnittet var $10, 5$ poeng.

Mer om:

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

Statistikk

statistikk

For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.

For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleiren.

b)

Per var en av elevene som hadde prøven. Han fikk $10$ poeng og påstår at han var blant den beste halvdelen av elevene.

Kan Per bruke medianen for datamaterialet til å begrunne påstanden sin?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å finne medianen ordner vi poengsummene i stigende rekkefølge. Dersom antallet obervasjoner er et oddetall er medianen det midterste, mens dersom antallet observasjoner er et partall, er medianen gjennomsnittet av de to poengsummene nærmest midtpunktet.

Det er $30$ poengsummer og medianen er gjennomsnittet av den $15$ . og $16$ . poengsummen. Poengsummene er ordnet i tabellen vår. Vi kan ikke si nøyaktig hva medianen i klasserommet er, men fra tabellen kan vi se at de må ligge i intervallet $[5, 10 ⟩$ .
Per, med sine $10$ poeng, vil ligge i neste intervall og dersom han bruker medianen kan han si at han var den beste halvdelen i klassen.

Svar: Ja, Per kan bruke medianen til å begrunne påstanden.

Mer om:

Denne oppgaven er om

Median

Medianen er den verdien som vi finner i midten av et rangert datamateriale.

Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

median

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

Statistikk

statistikk

For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.

For å øve mer, se oppgavesettet om median og gjennomsnitt i Treningsleiren.

Oppgave 10 (4 poeng) Nettkode: E-4OVM

Nedenfor har vi beskrevet fire ulike situasjoner.

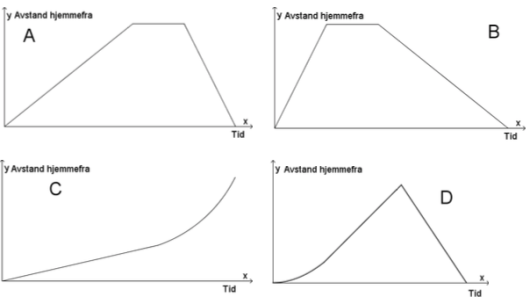
Nedenfor ser du grafiske framstillinger som beskriver sammenhengen mellom tid og Elines avstand hjemmefra for hver av de fire situasjonene.

Hvilken graf passer til situasjon $1$ ?
Hvilken graf passer til situasjon $2$ ?
Hvilken graf passer til situasjon $3$ ?
Hvilken graf passer til situasjon $4$ ?

Begrunn svarene dine.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Når grafen stiger er Eline på vei fra hjemmet, når grafen er flat står hun i ro, og når grafen avtar er Eline på vei hjemmover. Jo brattere grafen stiger, jo høyere er farten til Eline.

Vi tar for oss hver av grafene og ser hvilken situasjon den kan passe. Vi begynner med A.
Grafen begynner å stige, da er Eline på vei fra hjemmet. Grafen stiger jevnt, så hun holder samme fart. Når grafen flater ut, er konstant, stopper Eline opp. Deretter begynner grafen å avta, da er Eline på vei hjemover igjen. Grafen er brattere nå enn når hun var på vei fra hjemmet, så Eline holder en høyere fart på vei hjem. Dette passer til Situasjon $3$ .

Graf B begynner med å stige jevnt og raskt, så Eline må holde en høy fart før hun stopper opp når grafen er konstant. Etter en liten pause begynner grafen å avta, men slakere enn på vei fra hjemmet, og Eline må ha en roligere fart nå enn på vei hjemmefra. Dette passer til situasjon $2$ .

I graf C stiger grafen hele veien. Den begynner med en slak stigning, før den etterhvert blir brattere. Eline starter med en rolig fart. Når grafen blir brattere øker farten til Eline. Dette beskriver situasjon $4$ .

Graf D. Grafen begynner å stige, og den stiger brattere etterhvert. Da er Eline på vei hjemmefra, med en fart som øker. Eline snur uten pause, og har en høy fart hjemover. Dette passer situasjon $1$ .

Svar: A og situasjon $3$ , B og situasjon $2$ , C og situasjon $4$ , og D og situasjon $1$ .

Mer om:

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

For flere forklaringer og eksempler se artikkelen Hvorfor ser grafen ut som den gjør?.

For å øve mer, se oppgavesettet om grafisk fremstilling i Treningsleiren.

DEL 2 med hjelpemidler

Oppgave 1 (2 poeng) Nettkode: E-4OVO

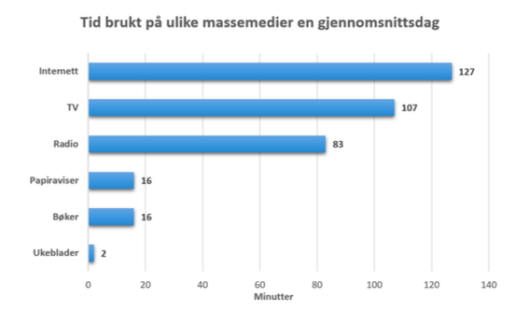
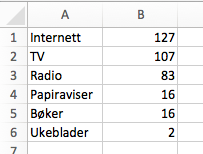
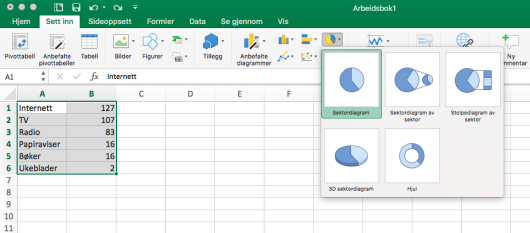
Diagrammet ovenfor viser hvor mange minutter personer i Norge brukte på ulike massemedier en gjennomsnittsdag i 2015.

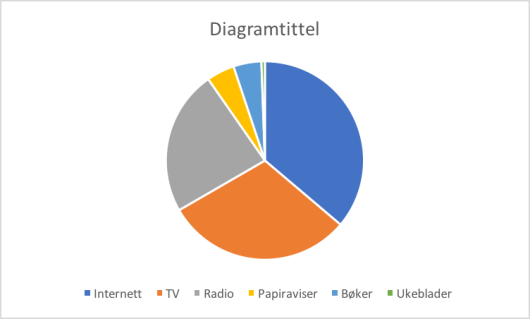
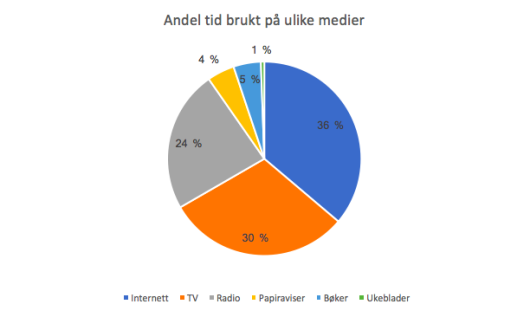
Lag et sektordiagram som viser hvor stor andel av tiden som ble brukt på hvert av de ulike massemediene.

Løs oppgaven her

Oppgave 2 (3 poeng) Nettkode: E-4OZ9

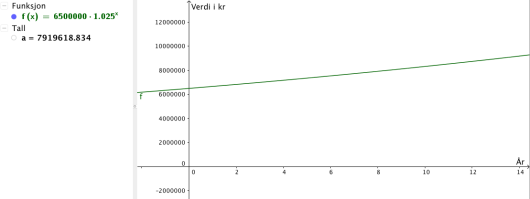
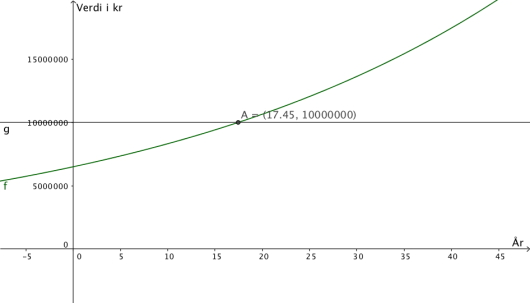
Verdien av en eiendom har økt med $2, 5 %$ per år fram til nå. Anta at verdien vil fortsette å
øke med $2, 5 %$ per år framover. I dag er eiendommen verd $6 500 000$ kroner.

a)

Hva vil verdien av eiendommen være om $8$ år?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Dette er en

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

der eiendommens verdi øker med

2, 5 %

per år.

Eiendommen øker med $2, 5 %$ i verdi, så

Vekstfaktor

Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.

Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.

vekstfaktoren

til verdiøkningen er

$1 + \frac{2, 5}{100} = 1, 025$

Vi kan sette dette opp som en eksponentialfunksjon på formen $f (x) = a \cdot b^{x}$ , der $a$ er verdien når $x = 0$ og $b$ er vekstfaktoren. $b$ har vi funnet at er $1, 025$ . $a$ er funksjonsverdien når $x = 0$ . Vi lar $x$ være lik $0$ i dag, så $a = 6500000$ .

Da har vi funksjonen

$f (x) = 6 500 000 \cdot 1, 025^{x}$

som gir oss verdien til eiendommen etter $x$ år. Vi skal finne verdien etter $8$ år, og da kan vi sette inn for $x = 8$ i funksjonen

$f (8) = 6 500 000 \cdot 1, 025^{8} \approx 7 919 619$

$1$ million er $1 000 000$ , så $7 919 619 = 7, 919 619 millioner \approx 7, 92 millioner$ .

Alternativ

Man kan også bruke funksjonen vi fant over til å løse denne oppgaven i

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

. I “Skriv inn”-feltet kan vi skrive

$𝚏 (𝚡) = 6 500 000 * {1.025}^{\land} 𝚡$

For å finne verdien etter $8$ år kan man skrive f(8) i “Skriv inn”-feltet. Da får vi $a = 7 919 618, 83$ , som er det samme som over.

Svar: Etter $8$ år er eiendommen verdt $7 919 618 kr \approx 7, 92 millioner kr$

Mer om:

Denne oppgaven er om

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentialfunksjoner

Vekstfaktor

Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.

Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.

vekstfaktor

For flere eksempler og forklaringer se artikkelen om Typer av funksjoner.

b)

Hva var verdien av eiendommen for $8$ år siden?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan løse det som en eksponentialfunksjon på formen $f (x) = a \cdot b^{x}$

Eiendommen har steget i verdi med $2, 5 %$ frem til i dag, så vekstfaktoren til verdien til eiendommen har vært den samme frem til i dag som den er i dag. Vi kan bruke funksjonen vi fant i deloppgave a) for å finne hva verdien til eiendommen var for $8$ år siden.

Da må vi ha at $x = - 8$ . Vi setter inn for dette i funskjonen og får

$f (- 8) = 6 500 000 \cdot 1, 025^{- 8} \approx 5 334 853$

$1$ million er $1 000 000$ , så $5 334 853 = 5, 334853 millioner \approx 5, 33 millioner$ .

Alternativ

Vi kan bruke GeoGebra-filen fra den alternative løsningen i deloppgave a), og skrive inn f(-8) i “Skriv inn”-feltet.

Da får vi at $b = 5 334 852, 71$ .

Svar: Verdien til eiendommen var omtrent $5, 33 millioner kr$ .

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Vekstfaktor

Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.

Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.

vekstfaktor

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentiallikninger

For flere forklaringer og eksempler se artikkelen Typer av funksjoner.

c)

Når vil verdien av eiendommen passere $10 000 000$ kroner?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan løse ligningen grafisk ved hjelp av GeoGebra.

For å finne når verdien til eiendommen passerer $10 000 000$ kr kan vi bruke GeoGebra. Vi skriver inn funksjonen fra deloppgave a)

$𝚏 (𝚡) = 6 500 000 * {1.025}^{\land} 𝚡$

i “Skriv inn”-feltet. Vi skal finne når verdien til eiendommen passerer $10 000 000$ . Da kan vi lage en linje for $y = 10 000 000$ , så da skriver inn y=10000000 i “Skriv inn”-feltet. I algebrafeltet kan vi se at linja får navnet $g$ . Når grafen krysser linja vil eiendommen ha en verdi på $10 000 000$ . Vi kan finne skjæringspunktet mellom grafen og linja $g$ ved å skrive inn $𝚂 𝚔 𝚓 æ 𝚛 𝚒 𝚗 𝚐 [𝚏, 𝚐]$ .

Da får vi skjæringspunktet $(17, 45, 10 000 000)$ .

Dette forteller at etter $17, 45$ år vil eiendommen være verdt mer enn $10 000 000$ .

Svar: Etter $17, 45$ år.

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere forklaringer og eksempler se artikkelen Grafisk løsning av likninger.

For å øve mer, se oppgavesettet om skjæringspunkt i Treningsleiren.

Oppgave 3 (8 poeng) Nettkode: E-4OZJ

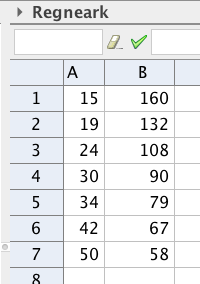
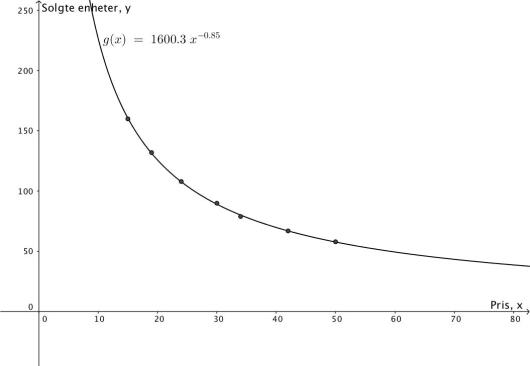
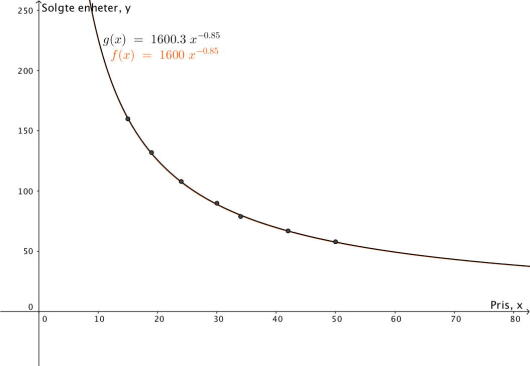
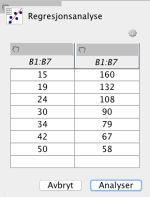
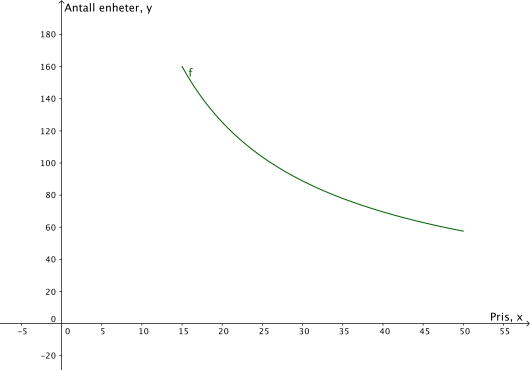
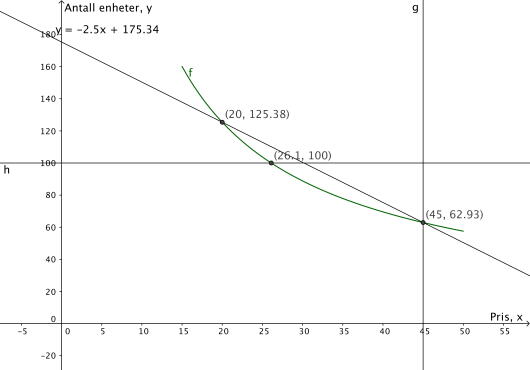
Tabellen nedenfor viser pris og antall solgte enheter av en vare.

a)

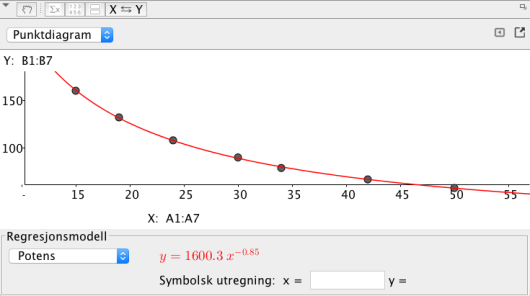
Bruk regresjon til å vise at funksjonen $f$ gitt ved

$f (x) = 1600 \cdot x^{- 0, 85}$

er en god modell for sammenhengen mellom pris $x$ og antall solgte enheter av varen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan finne en modell som passer til tabellen ved

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

i GeoGebra, og sjekke om den passer med den gitte funksjonen.

Funksjonen $f (x)$ ser vi er en potensfunksjon, fordi variabelen $x$ er grunntall i potensen. Potensfunksjoner kan skrives på formen $f (x) = a \cdot x^{b}$ , der $a$ og $b$ er konstanter. Dersom variabelen hadde vært eksponenten i potensen, altså at vi hadde hatt $b^{x}$ , ville det vært en eksponentialfunksjon.

Vi finner en

Matematisk modell

Matematiske modeller brukes ofte for å beskrive fenomener i naturen.

Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.

modell

for enheter ved å bruke regresjon i GeoGebra. Vi begynner med å skrive inn tabellen i et regneark. For å få opp regneark velger vi “Regneark” i “Vis”-menyen. Vi fyller inn informasjonen fra tabellen.

Vi markerer tabellen, høyreklikker og velger “Liste med punkt” i “Lag”-menyen. Listen blir hetende Liste1. Nå skal vi lage en modell ved regresjon, og vi skal sammenlikne den med funksjonen, f, som er gitt. f er en potensfunksjon, altså på formen $f (x) = a \cdot x^{b}$ , så vi vil gjøre regresjon med samme type funksjon. Derfor skriver vi

$𝚐 = 𝚁 𝚎 𝚐 𝙿 𝚘 𝚝 [𝙻 𝚒 𝚜 𝚝 𝚎 1]$

i “Skriv inn”-feltet. Vi setter navn på aksene ved å høyreklikke i grafikkfeltet og velge xAkse og yAkse inne på innstillinger. Da får vi følgende funksjon

Vi kan se at funksjonen $g = 1600, 3 \cdot x^{- 0, 85}$ er nesten lik den gitte modellen, ved $f = 1600 \cdot x^{(- 0.85)}$ . Vi kan også se det ved å tegne inn $f$ i samme GeoGebra vindu. Da skriver vi $𝚏 = 1600 * 𝚡^{\land} - 0, 85$ i “Skriv inn”-feltet. Vi ser at de to grafene nesten sammenfaller helt, og punktene fra tabellen ligger svært nær grafene, så den gitte funksjonen må være en god modell.

Alternativ

GeoGebra har også et regresjonsanalyse-verktøy vi kan bruke. Da skriver vi inn tabellen i regnearket på samme måte som over. Vi kan nå markere tabellen og velge “Regresjonsanalyse”. Det finner vi ved å trykke på den lille pilen på knappen med histogram på.

Da får vi opp følgende vindu og velger analyser

Nå får vi opp punktene tegnet inn i et koordniatsystem, og under “Regresjonsmodell” kan vi velge Potens, og da vil vi får den best tilpassede potensfunksjonen til punktene som er

$y = 1600, 3 x^{- 0, 85}$

Denne funksjonen er tilnærmet lik den gitte funksjonen, så $f (x)$ må være en god modell.

Svar: Den gitte funksjonen $f$ er en god modell for sammenhengen mellom pris $x$ og antall solgte enheter.

Mer om:

Denne oppgaven er om

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

, potensfunksjoner og

Matematisk induksjon

En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:

Bevis påstanden for n =1.
Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).

Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).

matematiske modeller

For flere forklaringer og eksempler se artikkelen Regresjon I.

b)

Bruk graftegner til å tegne grafen til $f$ for $15 \leq x \leq 50$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen.

Vi kan bruke GeoGebra til å tegne grafen til f. Vi skriver inn

$𝚏 = 𝙵 𝚞 𝚗 𝚔 𝚜 𝚓 𝚘 𝚗 [1600 * 𝚡^{\land} (- 0.85), 15, 50]$

i “Skriv-inn”-feltet. Vi drar i aksene ved å trykke på shift-knappen og bruke musepekeren slik at $x$ -aksen viser fra $0$ til $50$ , og $y$ -aksen slik at vi kan se hele grafen. For å sette navn på aksene høyreklikker vi i grafikkfeltet og går inn på innstillinger. Under xAkse og yAkse kan vi sette navn på aksene.

Svar:

Mer om:

Denne oppgaven er om graf,

Koordinatsystem

koordinatsystem

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Intervall

Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).

Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.

intervall

For flere eksempler og forklaringer se artikkelen Fra en funksjon til en graf.

Lynkurset om GeoGebra er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.

c)

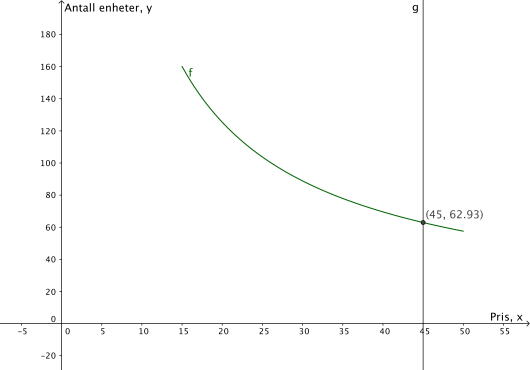
Bestem antall solgte enheter når prisen er $45$ kroner.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke GeoGebra og grafen vi tegnet i deloppgave b)

Vi skal finne solgte enheter når prisen er $45$ kroner. Da kan vi tegne en linje $x = 45$ , og se hvor linja og grafen krysser. Skriver inn x=45 i “Skriv inn”-feltet, og ser at linja får blir hetende $g$ . Vi kan finne

Skjæringspunkt

skjæringspunktet

ved å bruke skjæringsverktøyet,

, og velge $f$ og $g$ .

Vi får opp punktet $A = (45, 62, 93)$ . Det betyr at når prisen er på $45$ kroner blir det solgt $63$ enheter.

Svar: Det selges $63$ enheter når prisen er $45$ kroner.

Mer om:

Denne oppgaven er om

Graf

graf

Skjæringspunkt

skjæringspunkt

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere eksempler og forklaringer se Grafisk løsning av likninger.

For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.

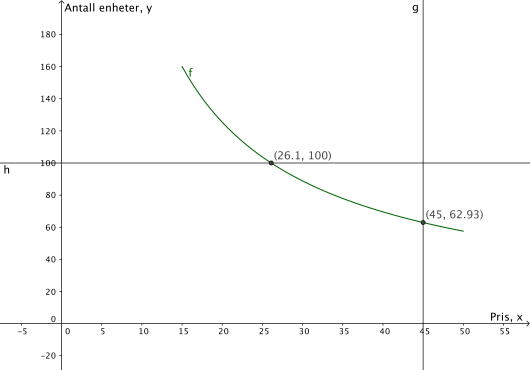
d)

Bestem prisen når antall solgte enheter er $100$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi kan se hvor grafen fra deloppgave b) krysser linja $y = 100$ .

Vi skal finne prisen når antall solgte enheter er $100$ . Da kan vi tegne inn en linje $y = 100$ , og se hvor denne linja krysser grafen til $f$ . Skriver inn y=100 i samme GeoGebra fil som deloppgave b) og c). Linja blir hetende $h$ . Vi bruker skjæringsverktøyet til å finne hvor og $h$ krysser.

Da får vi opp skjæringspunktet $B = (26, 1, 100)$ . Dette viser at når det blir solgt $100$ enheter er er prisen på $26$ kroner per enhet.

Svar: Prisen er $26$ kroner per enhet.

Mer om
Denne oppgaven er om graf,

Skjæringspunkt

skjæringspunkt

Koordinatsystem

koordinatsystem

For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger.

For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.

e)

Bestem den gjennomsnittlige vekstfarten for funksjonen f fra $x = 20$ til $x = 45$ .
Hva forteller svaret om antall solgte enheter?

Løs oppgaven her

Løsningsforslag e)

Jeg tenker

Gjennomsnittlig vekstfart mellom to punkter kan vi finne ved å se på stigningstallet mellom punktene.

Vi kan enten finne den gjennomsnittlige vekstfarten ved å bruke GeoGebra eller ved regning.
Vi begynner med å regne ut. Den gjennomsnittlige vekstfarten er farten funksjonen ville steget i dersom den steg like raskt hele veien. Når prisen er $20$ kr blir det solgt $f (20)$ enheter. Dette kan vi regne ut ved å skrive $f (20)$ i “Skriv inn”-feltet i GeoGebra. Da får vi at

$f (20) = 125, 38$

Når prisen var på $20$ kroner ble det solgt omtrent $125$ enheter, Når prisen var $45$ kr ble det solgt

$f (45) = 62, 93$

enheter, altså omtrent $63$ enheter. Antall enheter har da avtatt fra $125$ enheter til $63$ enheter når prisen har økt med $45 - 20 = 25$ kr; det gir en gjennomsnittlig vekstfart på

$\frac{63 - 125}{25} \approx - 2, 5$

enheter per krone.

Alternativ

Vi kan også finne den gjennomsnittlige vekstfarten ved å se på stigningstallet til linja som går gjennom punktene på grafen når $x = 20$ og $x = 45$ . For å finne disse punktene skriver vi inn (20,f(20) og (45, f(45). Vi finner linja mellom disse punktene ved å velge Linje,

og trykke på de to punktene på grafen. For å få linja på formen $y = a x + b$ , høyreklikker vi på linja og velger Likning y=ax+b. Da kan vi se at funksjonen til linja er på formen $y = - 2, 5 x + 175, 34$ .

Linjer på formen $y = a x + b$ har stignigstall $a$ , så linja vår har stigningstall $- 2, 5$ og da er dette gjennomsnittlig vekstfart per krone.
Dette forteller oss at dersom prisen øker fra $20$ kroner til $45$ kroner vil antall solgte enheter minke med $2, 5$ enheter per krone i gjennomsnitt.

Svar: Gjennomsnittlig vekstfart er -2,5 enheter per krone. Det forteller at i snitt avtar antall solgte enheter med 2,5 enheter for hver krone prisen øker med mellom 20 og 45 kr.

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Graf

grafer

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Gjennomsnittlig vekstfart

En funksjon $f (x)$ har gjennomsnittlig vekstfart

$\frac{Δ y}{Δ x} = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$

mellom $x_{2}$ og $x_{1}$ . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.

gjennomsnittlig vekstfart

For flere forklaringer og eksempler på lineære funksjoner, se artikkelen Rette linjer (lineære funksjoner).

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.

Oppgave 4 (6 poeng) Nettkode: E-4OZL

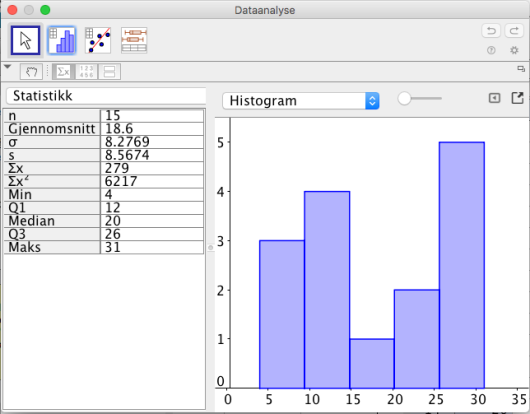
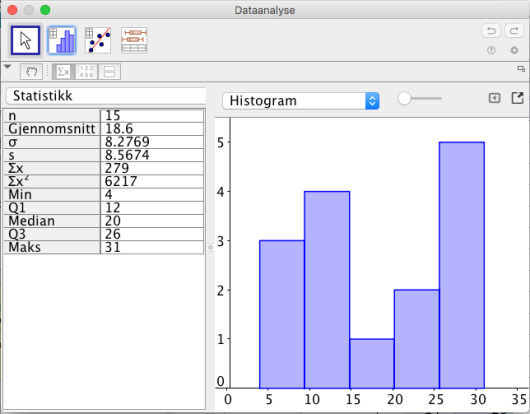
Klasse 2A har hatt matematikkprøve. De $15$ elevene i klassen fikk disse poengsummene:

a)

Bestem gjennomsnittet og medianen for poengsummene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å finne

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnittet

Median

Medianen er den verdien som vi finner i midten av et rangert datamateriale.

Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

medianen

for poengsummen.

Vi skriver inn alle poengsummene i et regneark i GeoGebra. Det får vi opp ved å trykke på Regneark i “Vis”-menyen. Vi marker tallene vi har skrevet og høyreklikker. Vi velger og velger “Liste” i “Lag”-menyen. Listen blir hetende Liste1.

For å finne gjennomsnittet skriver vi inn kommandoen Gjennomsnitt[Liste1]. Da finner den gjennomsnittet til tallene i listen. Da får vi opp et tall, $a = 18, 6$ . Gjennomsnittet er altså $18, 6$ poeng.
Vi finner medianen ved å bruke kommandoen Median[Liste1]. Da får vi opp $b = 20$ , altså er medianen $20$ .

Alternativ

GeoGebra har også et eget statistikkverktøy som kan brukes. Da skriver vi tallene inn i et regneark, markerer alle tallene og velger "Analyse av en variabel"-verktøyet ved å klikke på knappen med et histogram. I vinduet som kommer opp velger vi "Analyser". Da får vi opp et histogram. For å få opp informasjon om dataen kan vi trykke på knappen det står $Σ x$ på. Da får vi opp dette bildet:

I tabellen til venstre kan vi lese av at gjennomsnittet er $18, 6$ og medianen er $20$ .

Svar: Gjennomsnittet er $18, 6$ og medianen er $20$ .

Mer om:

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

Median

Medianen er den verdien som vi finner i midten av et rangert datamateriale.

Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

median

For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.

For å øve mer, se oppgavesettet om gjennomsnitt og median i Treningsleiren.

b)

Påstand $1$ : Gjennomsnittet er $7, 0 %$ lavere enn medianen.
Påstand $2$ : Medianen er $7, 5 %$ høyere enn gjennomsnittet.

Avgjør om hver av påstandene ovenfor er riktige.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi skal først finne hva gjennomsnittet er i forhold til medianen, og deretter medianen i forhold til gjennomsnittet.

En generell fremgangsmåte for å finne ut hvor stor prosentandel et tall a er av et annet tall $b$ , er å se på forholdet mellom de to: tallet $a$ er $\frac{a}{b} \cdot 100 %$ av $b$ .

Vi ser først på påstand $1$ . Her skal vi skal finne ut om gjennomsnittet er $7, 0 %$ lavere enn medianen. Vi skal se på hvor stor prosentandel gjennomsnittet er av medianen. Da får vi

$\frac{Gjennomsnitt}{Median} \cdot 100 % = \frac{18, 6}{20} \cdot 100 % = 93 %$

Gjennomsnittet er $93 %$ av medianen, altså $7 %$ lavere, så pastanden stemmer.

Vi sjekker påstand $2$ . Her skal vi se på medianen i forhold til gjennomsnitt. Da får vi

$\frac{Median}{Gjennomsnitt} \cdot 100 % = \frac{20}{18, 6} \cdot 100 % = 107, 5 %$

Medianen er $7, 5 %$ større enn gjennomsnittet, og påstanden stemmer.

Svar: Påstandene stemmer.

Mer om:

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

Median

Medianen er den verdien som vi finner i midten av et rangert datamateriale.

Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

median

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler på prosent se artikkelen Prosent av hva da?.

For å øve med, se oppgavesettet om prosentregning i Treningsleiren.

c)

Bestem standardavviket for poengsummene.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke GeoGebra til å finne

Standardavvik

Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.

standardavviket

Vi kan bruke regnearket som vi lagde i deloppgave a). Der laget vi en liste, Liste1, som inneholdt alle poengsummene. For å finne standardavviket for poengsummene bruker vi kommandoen Standardavvik[Liste1]. Da får vi opp at $c = 8, 28$ . Standardavviket for poengsummene er $8, 28$ .

Alternativ

Vi kan bruke samme statistikkverktøyet som vi brukte i alternativ løsning på deloppgave a). Da fikk vi opp

Her kan vi også finne standardavviket. Her bruker GeoGebra symbolet $σ$ . Så da kan vi se at standardavviket, $σ$ , er $8, 2769$ .

Svar: Standardavviket er $8, 28$ .

Mer om:

Denne oppgaven er om

Standardavvik

Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.

standardavvik

For flere forklaringer og eksempler se artikkelen Varians og standardavvik.

d)

$15$ elever fra klasse 2B har hatt samme prøve. I denne klassen ble gjennomsnittet for poengsummene $18, 6$ og standardavviket $5, 9$ .

Hva kan du si om poengsummene i 2B sammenliknet med poengsummene i 2A?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Standardavviket er et mål på hvor spredt informasjonen er.

Begge klassene hadde samme gjennomsnitt, men standardavviket er større for 2A enn for 2B. Det forteller oss at i klasse 2B var poengsummene mer samlet rundt gjennomsnittet, mens poengsummene i klasse 2A varierer mer.

Svar: Dette forteller oss at resultatene i klasse 2A varierer mer enn i 2B.

Mer om:

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

og standardavvik.

For flere forklaringer og eksempler se artiklene Gjennomsnitt, median og typetall og Varians og standardavvik.

Oppgave 5 (5 poeng) Nettkode: E-4P07

Når en pasient har tatt en tablett, vil virkestoffet i tabletten brytes ned i kroppen. Konsentrasjonen av virkestoffet i blodet vil avta eksponentielt med tiden. 

Tabellen nedenfor viser konsentrasjonen i mikrogram per milliliter (μg/mL) av virkestoffet i blodet $1$ time etter og $24$ timer etter at pasienten har tatt tabletten.

a)

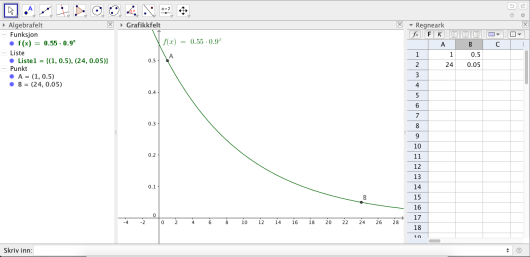
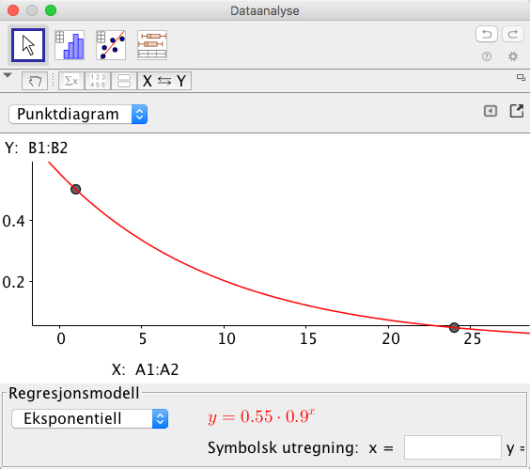
Bruk opplysningene i tabellen til å bestemme en eksponentiell modell $f (x)$ for konsentrasjonen av virkestoffet i blodet $x$ timer etter at pasienten har tatt en tablett.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

En eksponentiell modell for konsentrasjonen av virkestoffet i blodet er en funksjon på formen $f (x) = a \cdot b^{x}$ som passer med dataene vi har. Vi kan bruke GeoGebra for å bestemme denne modellen ved

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

Vi vil ha en funksjon $f$ , slik at $f (x)$ er mikrogram per milliliter ( $μ$ g/mL) av virkestoffet i blodet $x$ timer etter at pasienten har tatt tabletten, for eksempel skal $f (5)$ være $μ$ g/mL av virkestoffet i blodet etter $5$ timer.
Vi kan finne en slik modell ved regresjon i GeoGebra. Vi begynner med å velge Regneark i “Vis”-menyen. I regnearket skriver vi inn $1$ og $24$ i den første kolonnen, og $0.50$ og $0.050$ i den andre kolonnen. Vi markerer rutene med tall i, høyreklikker og velger “Liste med punkter” i “Lag”-menyen.

Listen blir hetende Liste1. Vi drar i aksene slik at vi får opp punktene $(1, 0, 50)$ og $(24, 0, 050)$ i grafikkfeltet. Vi vil ha en eksponentialfunksjon som går gjennom disse punktene. Da kan vi skrive RegEksp[Liste1]. Da får vi opp funksjonen $f (x) = 0, 55 \cdot 0, 9^{x}$ som går gjennom de to punktene våre. Dette er regresjonsmodellen vår, og vi ser at grafen går gjennom de to punktene.

Alternativ

Vi kan også bruke GeoGebra sitt regresjonsverktøy, slik vi gjorde i oppgave 3. Da skriver vi tallene inn i regnearket som over, markerer rutene og velger "Regresjonsanalyse"-verktøyet. Det finner vi ved å trykke på den lille pilen i venstre hjørnet i ruten med histogram i. Vi velger "Analyser" i vinduet som kommer opp. Da får vi opp et koordinatsystem hvor de to punktene er tegnet inn. For å finne en eksponentiell modell som passer til punktene velger vi "Eksponentiell" i dropvinduet under "Regresjonsmodell".

Da får vi opp følgende bilde

som viser at $y = 0, 55 \cdot 0, 9^{x}$ er en eksponentiell modell som passer til informasjonen vi har.

Svar: En eksponentiell modell for konsentrasjonen av virkestoff i blodet x timer etter pasienten har tatt en tabtett er $f (x) = 0, 55 \cdot 0, 9^{x}$

Mer om:

Denne oppgaven er om matematiske modeller,

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

For flere forklaringer og eksempler se artikkelen Regresjon 1.

For å øve mer, se oppgavesettet eksponentialfunksjoner i Treningsleiren.

b)

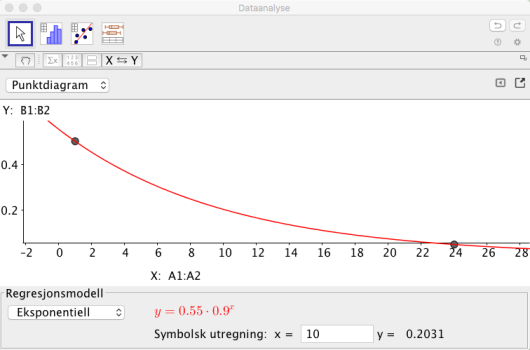
Bruk modellen fra oppgave a) til å bestemme konsentrasjonen av virkestoffet i blodet $10$ timer etter at pasienten har tatt en tablett.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke den eksponentielle modellen $f (x)$ vi fant i deloppgave a) for konsentrasjon av virkestoffet etter $x$ timer, og finne for $x = 10$ .

Vi kan finne ut hvor mye virkestoff som er i blodet ved å regne ut $f (10)$ . Funksjonen $f (x)$ fra deloppgave a) gir konsentrasjonen av virkestoff i blodet etter $x$ timer.

Når vi skal finne konsentrasjonen av virkestoff etter $10$ timer har vi at $x = 10$ , og vi kan regne ut for $f (10)$

$f (10) = 0, 55 \cdot 0, 9^{10} \approx 0, 1917$

Dette kan vi runde av vil $0, 2$ μg/mL.

Alternativ

Vi kan også finne konsentrasjonen av virkestoff grafisk ved å bruke GeoGebra. Da kan vi finne ut hvor grafen krysser linja $x = 10$ . Vi skriver inn x=10. Linja blir hetende $g$ . For å finne skjæringspunktet mellom linja $g$ og grafen til $f$ skriver vi inn Skjæring[f,g].

Da får vi opp punktet $(10, 0, 2)$ . Etter $10$ timer vil det være $0, 2$ $μ$ g/mL virkestoff i blodet.

Alternativ

Et annet alternativ er å bruke regresjonsverktøyet som vi brukte i den alternative løsningen i deloppgave a). I vinduet vi fikk opp stod det "Symbolsk utregning". Her kan vi skrive inn $x$ -verdien, så får vi den $y$ -verdien modellen gir. Altså kan vi skrive inn $10$ , og da får vi at når $x = 10$ så er $y = 0, 2031$ .

Svar: Etter $10$ timer var det $0, 2$ $μ$ g/mL virkestoff i blodet.

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Potens

potens

For flere eksempler og forklaringer om potensregning se artikkelen Rask gjennomgang av regneregler for potens og røtter.

For å øve mer, se oppgavesettet om potensregning i Treningsleiren.

c)

En pasient begynner å ta tabletter. Han tar én tablett klokka $08 : 00$ hver morgen og én tablett klokka $20 : 00$ hver kveld.

Bruk modellen fra oppgave a) til å bestemme konsentrasjonen av virkestoffet i blodet $30$ timer etter at pasienten tok den første tabletten.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Pasienten vil ta en ny tablett hver $12$ . time, og da vil konsentrasjonen i blodet øke med den konsentrasjonen av virkestoff som er i en tablett.

Vi kan bruke modellen i deloppgave a) til å finne hvor mye virkestoff som er i en tablett. Da kan vi regne $f (0) = 0, 55 \cdot 0, 9^{0} = 0, 55$ . Hver tablett inneholder altså $0, 55$ $μ$ g/mL.

I løpet av $30$ timer vil pasienten ta $3$ tabletter. Han tar første tablett klokka $08 : 00$ om morgenen. Etter $12$ timer, klokka $20 : 00$ , vil han ta en ny tablett. Klokka $08 : 00$ dagen etter, $24$ timer etter første tablett vil han ta en tredje tablett. $6$ timer etter pasienten tar tredje tablett har det totalt gått $30$ timer siden han tok første tablett. Vi vil altså finne konsentrasjonen $6$ timer etter pasienten tar tredje tablett.

Etter $12$ timer vil konsentrasjonen av virkestoff etter den første tabletten være

$0, 55 \cdot 0, 9^{12} \approx 0, 1553$

Når pasienten tar den andre tabletten vil virkestoffet øke til

$0, 1553 μ g/mL + 0, 55 μ g/mL = 0, 7053 μ g/mL$

Konsentrasjonen avtar fortsatt med $10 %$ for hver time, så konsentrasjonen av virkestoff i blodet x timer etter den andre tabletten vil være

$0, 7053 \cdot 0, 9^{x}$

$12$ timer etter pasienten fikk andre tablett, $24$ timer etter første tablett, vil den nye konsentrasjonen ha avtatt til

$0, 7053 \cdot 0, 9^{12} \approx 0, 1992$

Nå tar pasienten den tredje tabletten og konsentrasjonen vil øke med $0, 55$ $μ$ g/mL. Da får vi at den nye konsentrasjon er

$0, 1992 μ g/mL + 0, 55 μ g/mL = 0, 7492 μ g/mL$

$6$ timer etter pasienten har tatt den $3$ . tabletten vil det ha gått totalt $30$ timer.

Konsentrasjonen av virkestoffet i blodet vil når være

$0, 7492 \cdot 0, 9^{6} \approx 0, 3981 \approx 0, 4$

Etter 30 timer vil konsentrasjonene av virkestoffet i blodet være $0, 4$ $μ$ g/mL.

Alternativ

$30$ timer etter at pasienten fikk første tablett, har det gått $18$ timer siden han fikk den andre, og $6$ timer siden han fikk den tredje tabletten. Vi kan finne konsentrasjonen av virkestoff i blodet ved å regne

\begin{matrix} f (30) + f (18) + f (6) & = & 0, 55 \cdot 0, 9^{30} + 0, 55 \cdot 0, 9^{18} + 0, 55 \cdot 0, 9^{6} \\ = & 0, 023 + 0, 083 + 0, 292 \\ = & 0, 398 \approx 0, 4 \end{matrix}

Konsentrasjonen at virkestoffet vil være på $0, 4 μ g/mL$ .

Svar: Konsentrasjonen vil være $0, 4 μ g/mL$ g/mL $30$ timer etter pasienten tar første tablett.

Mer om:

Denne oppgaven er om eksponentialfunksjoner og potenser.

For flere forklaringer og eksempler se Rask gjennomgang av regneregler for potens og røtter.

For å øve mer, se oppgavesettet om potensregning i Treningsleiren.

Oppgave 6 (6 poeng) Nettkode: E-4P0F

$1$ . september $2016$ kjøpte Monica en hytte. Hun lånte da $1 000 000$ kroner av foreldrene.

De inngikk følgende avtale:

- Renten på lånet skal være $2, 5 %$ per år.  
- Tilbakebetalingen skal skje ved at Monica overfører $100 000$ kroner til foreldrenes konto $1$ . september hvert år til lånet er nedbetalt.  
- Første overføring skal skje $1$ . september $2017$ .  

I denne oppgaven skal du lage et regneark som viser  

- hvor mye Monica skylder foreldrene etter hver overføring fram til lånet er nedbetalt  
- hvor mye Monica betaler i renter, og hvor mye hun betaler i avdrag hvert år  
- hvor mye Monica totalt vil ha betalt i renter i løpet av nedbetalingstiden

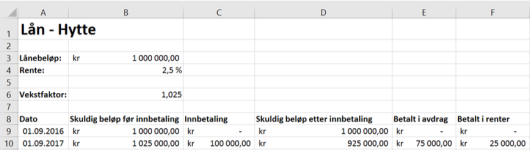
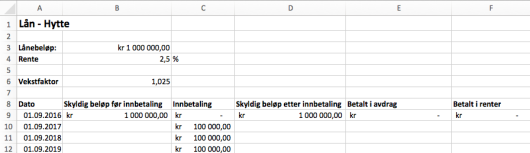
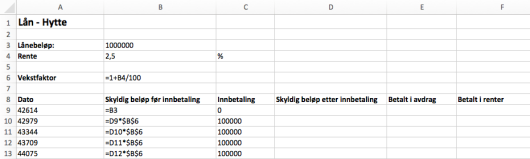
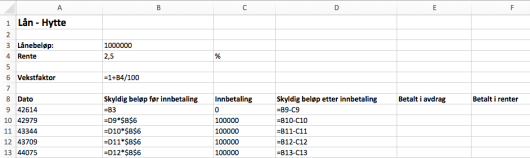
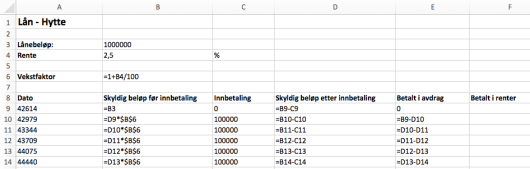
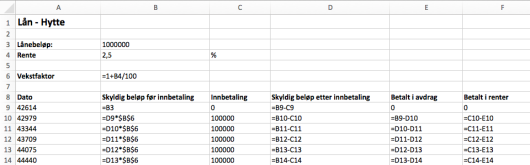
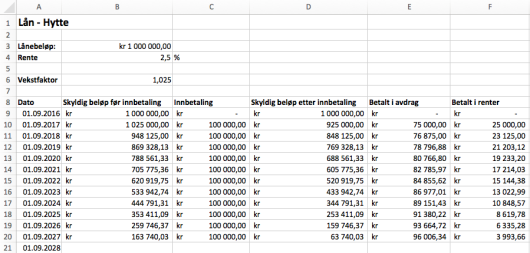
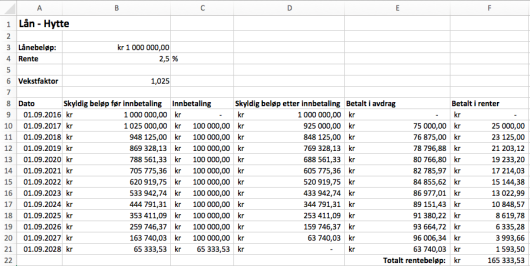
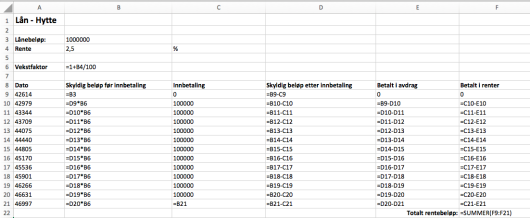
 Nedenfor ser du et eksempel på hvordan de første radene i regnearket kan se ut. 

Husk at du i størst mulig grad skal benytte formler, slik at løsningen blir dynamisk, og at formlene som er brukt, skal komme klart fram i besvarelsen din.  

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan bruke Excel for å lage regnearket.

Vi kan bruke eksempelet for de første radene som er gitt i oppgaven, og skriver det inn i et regneark. Øverst skriver vi opp den informasjonen vi får gitt i oppgaven; lånebeløp og renter. Vekstfaktoren er $1 + \frac{p}{100}$ , der $p$ er den prosentvise økningen, i vårt tilfelle $2, 5 %$ , så vekstfaktoren kan vi finne ved å skrive =1+B4/100

I første rad for oversikten ov nedbetaling skriver vi inn det opprinnelige lånebeløpet. Det første året betaler Monica ingen innbetaling, så den er $0$ kr, hun har da ikke ikke betalt verken avdrag eller renter. Innbetalingen er fast på $100 000$ kr hvert år, så lenge ikke lånebeløpet er lavere.

På grunn av renter stiger lånet hvert år med en vekstfaktor på 1,025. For å finne hva Monica skylder før innbetaling må vi multiplisere vekstfaktoren med det beløpet Monica skylder etter innbetaling året før.

Skyldig beløp før innbetaling i 2017, i celle B10, blir skyldig beløp etter innbetaling i $2016$ multiplisert med vekstfaktoren, altså =D9*B6. Tilsvarende blir det for neste år, i celle B11 må vi ha =D10*B6 i og så videre.

Formelen “kopieres” til cellen under ved å markere cellen dra i firkanten i høyre hjørnet og dra nedover. Når vi sier at formelen “kopieres”, er det regneoperasjonen som kopieres, men hvilke celler som inngår endres. Når vi kopierer formelen til cellen under, vil også cellene som inngår i formelen endres til den under. Dersom vi kopierer formelen i celle B11 til B12 vil vi få =D11*B7. For at hver celle skal multipliseres med vekstfaktoren låser vi celle B6. Da kan vi skrive i celle B10 = D9*$B$6, når vi kopierer formelen til cellen under vil vi få B11= D10*$B$6 og så videre.

Innbetalingen er $100 000$ kr hvert år, så den trenger vi ikke gjøre noe med enda. Når Skyldig beløp før innbetaling er mindre enn $100 000$ kr må vi endre denne.
For å finne Skyldig beløp etter innbetaling subtraherer vi beløpet Monica betaler inn fra Skyldig beløp før innbetaling. I celle D9 får vi da =B9-C9. Vi kan kopiere formelen på samme måte som over. Da får vi som vist i regnearket under:

Betalt i avdrag blir den delen av innbetalingen som betaler ned på lånesummen. Vi kan finne ut hvor mye som blir betalt i avdrag ved å finne differansen mellom beløpet Monica skyldte etter innbetaling året før og hva hun skylder etter innbetaling i år. Etter første innbetaling kan vi finne ut hvor mye Monica betalte i avdrag ved å subtrahere Skyldig beløp etter innbetaling i $2017$ fra Skyldig beløp etter innbetaling i $2016$ , og vi kan skrive =B9-D10 i celle E10. Vi kan kopiere denne formelen til cellene under i kolonnen.

Av de $100 000$ kr som hun betaler hvert år har vi funnet den delen av innbetalingen som går til å betale avdrag. Den resterende summen er det Monica betaler i renter. Så for å finne hvor mye som blir betalt i renter kan vi subtrahere det beløpet som blir betalt i avdrag fra innbetalingsbeløpet. Etter innbetaling i $2017$ kan vi finne ut hvor mye av innbetalingen som er betalt i renter, i celle F10, ved å bruke formelen =C10-E10. Det blir samme formel for F11; C11-E11, så vi kan kopiere formelen ved å dra i den grønne ruten på celle F10.

Når vi har regnet beløpene frem til og med $2027$ vil regnearket se slik ut:

Før innbetaling i $2028$ kan vi se at det resterende beløpet er $65 333, 53$ kr, så dette året trenger ikke Monica å betale $100 000$ kr, men kun det resterende beløpet.
Vi skal også finne ut hvor mye Monica totalt har betalt i renter i løpet av nedbetalingstiden kan vi bruke formelen SUMMER, og summere over alle cellene under Betalt i renter. Da får vi =SUMMER(F9:F21). Regnearket vil da se slik ut:

Regnearket under viser hvordan det ser ut med formler.

Svar:

Mer om:

Denne oppgaven er om regneark,

Rente

Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.

Se renteformel og rentefot

rente

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere eksempler og forklaringer se artiklene Renter og Banksparing over flere år.

For å øve mer på prosentregning, se oppgavesettet om prosentregning i Treningsleiren.

Oppgave 7 (6 poeng) Nettkode: E-4P0U

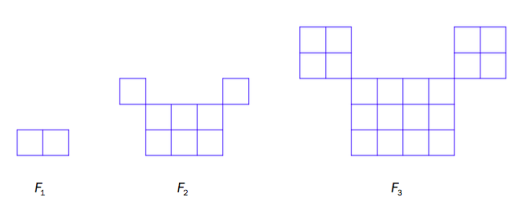
Snorre lager figurer av kvadratiske klosser etter et fast mønster.
Ovenfor ser du figur $F_{1}$ , $F_{2}$ og $F_{3}$ .

a)

Hvor mange klosser trenger Snorre for å lage $F_{4}$ og for å lage $F_{5}$ ?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å finne neste figur må man øke med en klosse i lengden og en i bredden for bunnen på figuren, og “ørene” vil være kvadrater med en ekstra klosse i bredden og en ekstra i høyden.

I $F_{4}$ vil bunnen bestå av et rektangel med $5$ klosser i lengden og $4$ klosser i bredden, totalt $5 \cdot 4 = 20$ klosser. Hvert av “ørene” vil være et kvadrat der hver side består av $3$ klosser, hvert “øre” vil altså bestå av $3 \cdot 3 = 9$ klosser. Vi har to “ører”, så vi vil totalt ha $18$ klosser. Hele figuren vil da bestå av $20 + 18 = 38$ klosser.

$F_{5}$ vil ha en bunn bestående av et rektangel med $6$ klosser i lengden og $5$ i bredden, totalt $6 \cdot 5 = 30$ , og kvadratiske ører med $4$ klosser i hver side, hvert “øre” vil bestå av $4 \cdot 4 = 16$ klosser. Det totale antall klosser i “ørene” vl være $32$ . $F_{5}$ vil bestå av $30 + 32 = 62$ klosser.

Alternativ

Det går også å tegne opp figurene og telle klosser.

F_4:

Når vi teller ser vi at figuren har $38$ klosser.

F₅:

Her kan vi telle at figuren er bygget opp av $62$ klosser.

Svar: $F_{4}$ består av $38$ klosser og $F_{5}$ består av $62$ klosser.

Mer om:

Dette er en oppgave om

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

For flere forklaringer og eksempler se artiklene Et kvadrat og Et rektangel.

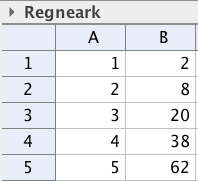
b)

Bestem et uttrykk for antall klosser i figur $F_{n}$ uttrykt ved $n$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne ut hvordan vi kan uttrykke de ulike delene av figuren ved $n$ .

Vi skal finne et uttrykk for antall klosser i figur $F_{n}$ uttrykt ved $n$ . Dette kan vi gjøre med regning. Det kan også gjøres ved regresjon, se da alternativ løsning. Figuren består av et rektangel og to kvadrater.

Vi kan begynne å finne et uttrykk for rektangelet i bunn. Fra de gitte figurene kan vi se at lengden til hver figur består av en kloss mer enn nummeret til figuren, for eksempel består lengden av rektangelet i $F_{1}$ av $1 + 1 = 2$ klosser og lengden til rektangelet i $F_{3}$ består av $3 + 1 = 4$ klosser. Lengden til rektangelet i $F_{n}$ må da bestå av $n + 1$ klosser.

Bredden til rektangelet i hver figur er den samme som nummeret til figuren. Eksempelvis har rektangelet i $F_{1}$ $1$ kloss i bredden og rektangelet i $F_{3}$ har $3$ klosser. Rektangelet i $F_{n}$ må da ha bredde på $n$ klosser.

Rektangelet i bunn av figur $F_{n}$ består da av

$(n + 1) \cdot n = n^{2} + n$

klosser.

Kvadratene i figurene har sider med en mindre rute enn nummeret til figuren. $F_{2}$ har kvadrater bestående av $1$ rute og $F_{3}$ sine kvadrater består av sider med $3 - 1 = 2$ klosser. Figur $F_{n}$ har kvadrater med side bestående av $n - 1$ klosser. Hvert kvadrat består da av $(n - 1) (n - 1) = (n - 1)^{2}$ klosser. Vi har to kvadrater, så totalt utgjør disse

$2 (n - 1)^{2} = 2 (n - 1) (n - 1) = 2 (n^{2} - n - n + 1) = 2 (n^{2} - 2 n + 1) = 2 n^{2} - 4 n + 2$

klosser.

Antall klosser i figur $F_{n}$ kan uttrykkes ved å addere antall klosser i rektangelet og antall klosser i kvadratene. Da får vi

$2 n^{2} - 4 n + 2 + n^{2} + n = 3 n^{2} - 3 n + 2$

Alternativ

Vi kan også finne et uttrykk for figur $F_{n}$ ved å bruke regresjon i GeoGebra.
Vi vet hvor mange klosser de fire fem første figurene inneholder. Dette legger vi inn som en liste med punkter i et regneark i GeoGebra. Vi velger “Regneark” i “Vis”-menyen og fyller inn

Vi lager en liste ved å markere rutene, høyreklikke og velge “Liste med punkt” i “Lag”-menyen. Listen blir hetende Liste1
Måten figuren er bygget opp på indikerer at antall klosser vokser som et polynom av grad $2$ . Dette kan vi se blant annet ved at kvadratene i $F_{n}$ består av $n - 1$ klosser i hver side, så antall klosser i kvadratet er $(n - 1)^{2}$ , altså et andregradspolynom. Derfor skriver vi

$𝚁 𝚎 𝚐 𝙿 𝚘 𝚕 𝚢 [𝙻 𝚒 𝚜 𝚝 𝚎 1, 2]$

i “Skriv inn”-feltet. Da får vi resultatet som vist under

Funksjonen for antall klosser i figur med nummer x er

$f (x) = 3 x^{2} - 3 x + 2$

Svar: Antall klosser i $F_{n}$ kan uttrykkes ved $3 n^{2} - 3 n + 2$

Mer om:

Denne oppgaven er om

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

For flere eksempler og forklaringer se artiklene Andregradslikninger og Regresjon 1.

c)

Snorre har 1000 klosser. Han vil lage en figur som er så stor som mulig.

Bruk formelen fra oppgave b) til å bestemme hvor mange klosser han får til overs når han har laget figuren.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke uttrykket vi fant i b) og se på grafen til uttrykket i GeoGebra

I deloppgave b) fant vi ett uttrykk for antall klosser til figur $F_{n}$ . Vi kan skrive dette uttrykket inn i GeoGebra. Da får vi en graf som viser hvor mange klosser som trengs for figur $F_{n}$ når $n = x$ . Vi skriver inn uttrykket i GeoGebra, men erstatter n med x; $3 𝚡^{2} - 3 𝚡 + 2$ Da får vi opp funksjonen $f (x) = 3 x^{2} - 3 x + 2$

Vi vil finne ut hvor stor figur Snorre kan lage med $1000$ klosser. Vi kan lage en linje for $y = 1000$ , og finner når linjen skjærer grafen til uttrykket. For å få linjen i GeoGebra skriver vi inn y=1000. Linjen blir da hetende $g$ . For å finne skjæringspunktet mellom linja $g$ og $f$ bruker vi kommandoen Skjæring[f,g]. Vi får opp punktet $(18, 75, 1000)$ .

Med $1000$ klosser kan Snorre lage figur $F_{18}$ .

Vi skal finne ut hvor mange klosser Snorre har til overs etter å ha bygget figuren. Da kan vi bruke uttrykket vårt til å finne ut hvor mange klosser Snorre må bruke for å lage figur $F_{18}$ . Da er n= 18 i uttrykket, og vi regner ut

$3 n^{2} - 3 n + 2 = 3 \cdot 18^{2} - 3 \cdot 18 + 2 = 920$

Dette kan vi og finne ved å skrive f(18) i “Skriv inn”-feltet i GeoGebra.

Snorre bruker altså $920$ klosser til å bygge figuren, da har han $1000 - 920 = 80$ klosser igjen.

Svar: Snorre har $80$ klosser igjen etter å ha bygget $F_{18}$ .

Mer om:

Denne oppgaven er om

Graf

graf

Skjæringspunkt

skjæringspunkt

, andregradsuttrykk og

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinat

For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger.

MAT1015 2016 Høst

Del 1

Del 2

Eksamensinformasjon

DEL 1 uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4OUA

Løsningsforslag

Standardform

Standardavvik

Heltall

Potens

Oppgave 2 (1 poeng) Nettkode: E-4OUF

Løsningsforslag

Potens

Teller

Nevner

Grunntall

Eksponent

Standardform

Oppgave 3 (1 poeng) Nettkode: E-4OUH

Løsningsforslag

Prosent

Prosent

Oppgave 4 (2 poeng) Nettkode: E-4OUJ

Løsningsforslag

Prosent

Oppgave 5 (2 poeng) Nettkode: E-4OUL

Løsningsforslag

Potens

Grunntall

Alternativ

Standardform

Potens

Oppgave 6 (4 poeng) Nettkode: E-4OUP

a)

Løsningsforslag a)

Lineære funksjoner

Stigningstall

Stigningstall

Koordinatsystem

Lineære funksjoner

b)

Løsningsforslag b)

Funksjon

Ligning

c)

Løsningsforslag c)

Funksjon

Ligning

Oppgave 7 (4 poeng) Nettkode: E-4OUV

a)

Løsningsforslag a)

Relativ frekvens

Kumulativ frekvens

Frekvenstabell

Relativ frekvens

Kumulativ frekvens

Statistikk

b)

Løsningsforslag b)

Data

Intervall

Frekvens

Oppgave 8 (2 poeng) Nettkode: E-4OUZ

a)

Løsningsforslag a)

Eksponentialfunksjon

Eksponentialfunksjon

Vekstfaktor

b)

Løsningsforslag b)

Alternativ

Eksponentialligning

Prosent

Oppgave 9 (3 poeng) Nettkode: E-4OV3

a)

Løsningsforslag a)

Gjennomsnitt

Gjennomsnitt

Statistikk