
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3024 2016 HØST
Eksamenstid
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler på del 1
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler
Hjelpemidler på del 2
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte
Del 1 har 7 oppgaver. Del 2 har 4 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen
Poeng i del 1 og del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger
Kilder for bilder, tegninger osv.:
- Befolkning: www.dagbladet.no (06.05.2016)
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 uten hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4PBT
Deriver funksjonene
Løsningsforslag
Jeg tenker
er en konstant multiplisert med en cosinusfunksjon med kjerne . Da kan vi bruke kjerneregelen for derivasjon.
Vi har som er en sammensatt funksjon. Da kan vi bruke kjerneregelen for derivasjon som sier at den deriverte av en sammensatt funksjon Vi kan sette .
Når vi regner ut ved å bruke kjerneregelen får vi
Svar:
Mer om
Denne oppgaven er om
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av sammensatte uttrykk.
b)
Løsningsforslag b)
Jeg tenker
Dette er en sammensatt funksjon, og vi kan sette kjernen og bruke kjerneregelen.
Vi kan bruke kjerneregelen da kan vi velge som kjerne. Kjerneregelen gir da
Svar:
Mer om
Denne oppgaven er om
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen - tre eksempler.
c)
Løsningsforslag c)
Jeg tenker
Vi skal derivere en brøk med funksjoner i både teller og nevner. Da kan vi bruke brøkregelen.
Brøkregelen for derivasjon sier at for to deriverbare funksjoner og er
Vi kan sette og . Vi har at og . Da følger det at
Svar:
Mer om
Denne oppgaven er om
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av sammensatte uttrykk.
Oppgave 2 (5 poeng) Nettkode: E-4PBX
Bestem integralene
a)
Løsningsforslag a)
Jeg tenker
Et intergral av en sum er det samme som summen av integralene til hvert av leddene, så vi kan integrere hvert ledd for seg.
Vi kan integrere leddene i polynomet hver for seg, så vi kan skrive
Når C er en konstant kan vi skrive , da får vi
Integralet av en funksjon er .
Nå kan vi regne ut
Her har vi satt .
Svar:
Mer om
Denne oppgaven er om
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
For flere forklaringer og eksempler, se artikkelen Delvis integrasjon.
b)
Løsningsforslag b)
Jeg tenker
Vi skal finne integralet til produktet av og . Vi kjenner den integrerte til som er , og blir lettere når vi deriverer den, så da kan det være lurt å bruke delvis integrasjon.
Delvis integrasjon sier at hvis vi har to deriverbare funksjoner og så er
Ved å sette og får vi og . Da har vi at
der
Svar:
Mer om
Denne oppgaven er om
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklaringer og eksempler, se artikkelen Delvis integrasjon.
c)
Løsningsforslag c)
Jeg tenker
Her ser vi at sinusfunksjonen i integranden har en kjerne, . I tillegg er en faktor i integranden. Det kan tyde på at vi bør prøve å integrere ved hjelp av substitusjon.
Vi kan prøve å løse integralet ved å bruke substitusjon. Regelen for intergrasjon sier at dersom vi har og er deriverbar, så er
Sinusfunksjonen har en kjerne , så vi kan prøve med . Da blir , og vi får følgende utregning:
Nå kan vi sette inn . Resultatet av integrasjonen blir da
Svar:
Mer om
Denne oppgaven er om
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklaringer og eksempler på integrasjon, se artikkelen Integrasjon ved substitusjon.
Oppgave 3 (4 poeng) Nettkode: E-4PC1
En rett linje går gjennom og der og er to positive tall.
a)
Bestem ligningen for linjen, uttrykt ved og .
Løsningsforslag a)
Jeg tenker
Vi vil ha en ligning på formen , der er stigningstallet, og er konstantleddet som sier hvor linjen krysser -aksen.
Linjen går gjennom , så den krysser -aksen i , så .
Stigningstallet kan vi finne ved å dividere hvor mye grafen vokser i -retning, , på hvor mye den vokser i -retning, , da finner vi får vi
Svar:
Mer om
Denne oppgaven er om
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner).
b)
Linjestykket roteres om -aksen. Vi får da et omdreiningslegeme.
Bestem et uttrykk for volumet til omdreiningslegemet.
Hva slags legeme har du regnet ut volumet til?
Løsningsforslag b)
Jeg tenker
Formelen til volumet av et omdreiningslegeme, rotert om -aksen er I deloppgave b) fant vi et uttrykk, for linjestykket .
I deloppgave b) fant vi at linjen gjennom punktene og
kan uttrykkes ved .
Nå skal vi bare se på linjestykket . Det avgrenses av og . For å finne volumet til omdreiningslegemet, bruker vi at og får
Siden er en konstant, kan vi trekke den utenfor integralet. Vi kan bruke regelen for integralet til er og da kan vi finne volumet ved å regne ut
Volumet til omdreiningslegemet kan uttrykkes ved .
Dette er formelen for volumet til en kjegle. Den vil ha toppunkt i , høyde og akse langs -aksen.
Svar: og er volumet til en kjegle.
Mer om
Denne oppgaven er om
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Kjegle
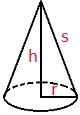
En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.
Kjeksen til en kroneis har form som en kjegle.
Volum : V =
Overflate : A =
For flere forklaringer og eksempler på volum, se artikkelen Halvar utleder formler for volum til kuler og kjegler.
Oppgave 4 (6 poeng) Nettkode: E-4P7A
En funksjon er gitt ved
a)
Bestem perioden til .
Løsningsforslag a)
Jeg tenker
En funksjon har periode dersom er det minste positive tall slik at
for alle . En periodisk funksjon kan ikke ha begrenset definisjonsmengde, så funksjonen i oppgaven er ikke periodisk. Vi antar i oppgave a) at for å kunne beregne en periode. Vi vet at
har periode.
Funksjonen er på formen
med . Perioden er derfor
.
Svar: Perioden til er .
Mer om
Denne oppgaven er om
Trigonometriske funksjoner
Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
For flere forklaringer og eksempler på funksjoner, se artikkelen Periodiske funksjoner.
b)
Bestem ekstremalverdiene og .
Løsningsforslag b)
Jeg tenker
Verdien til sinusfunksjon svinger mellom og . Funksjonen vil ha ekstremverdier der dersom det kan oppnås innenfor .
Siden vil den harmoniske funksjonen gjennomløpe fulle perioder, og dermed oppnå ekstremalverdienen
.
Dette gir .
Svar:
Mer om
Denne oppgaven er om
Ekstremalpunkter
Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
For flere forklaringer og eksempler på sinus, se artikkelen Grafene til sin x, cos x og tan x.
c)
Forklar hvorfor grafen vil ha alle sine vendepunkter på likevektlinjen. Bestem koordinatene til vendepunktene.
Løsningsforslag c)
Jeg tenker
Likevektslinjen til funksjonen er . Vendepunktene til er når den annenderiverte er og skifter fortegn.
Vendepunktene til kan vi finne ved å finne ut når .
Da kan vi begynne med . For å derivere kan vi bruke kjerneregelen, med som kjerne. Utregning gir da
Vi kan derivere dette uttrykket igjen for å finne . Da kan vi bruke samme kjerne.
når . For at dette skal være tilfelle må vi ha
Da må -koordinaten til vendepunktet være . Siden må vi ha .
For å finne -verdien til vendepunktene setter vi inn for i
Sinusuttrykket blir da lik , og -verdiene til koordinatene til vendepunktene er og dermed ser vi at alle vendepunktene ligger på likevektslinjen.
Svar: Vendepunktene har koordinater , der
Mer om
Denne oppgaven er om
Vendepunkt

Et vendepunkt for en funksjon er et punkt , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte fortegn.
Andrederiverte
Den andrederiverte til en funksjon er funksjonen derivert to ganger og skrives eller . Kalles også annenderiverte eller dobbeltderiverte.
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere forklaringer og eksempler vendepunkt, se artikkelen Vendepunkt og vendetangent.
d)
Lag en skisse av grafen til .
Løsningsforslag d)
Jeg tenker
Vi kan bruke den informasjonen vi har funnet i de tidligere deloppgavene. Da har vi funnet og , likevektslinjen til og perioden.
Fra deloppgave c) vet vi at likevektslinjen til er . Vi vet også at . Denne verdien fikk vi når , for eksempel hvis så . Siden perioden har vi når , altså for og . Minimumspunktene, når vil ligge midt i mellom to maksimumspunkt, så vi når , altså og . I tillegg vet vi at vi har vendepunkt i , for . Nå kan vi tegne inn de punktene vi har og skissere grafen som går gjennom disse punktene.
Svar: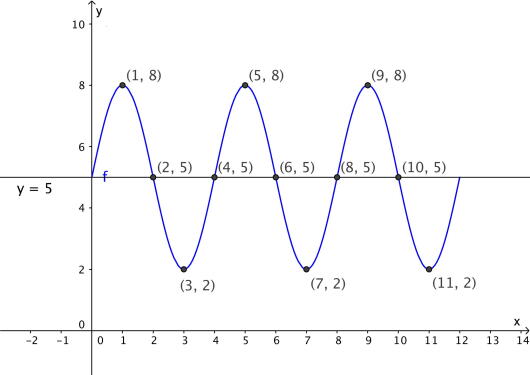
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Vendepunkt

Et vendepunkt for en funksjon er et punkt , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte fortegn.
Ekstremalpunkt

Vi sier at et punkt er et ekstremalpunkt for en funksjon hvis det enten er et toppunkt eller bunnpunkt for funksjonen.
For flere forklaringer og eksempler om grafer, se artikkelen Grafen til en funksjon.
Oppgave 5 (5 poeng) Nettkode: E-4PC4
Vi har gitt differensialligningen
a)
Vis at er en løsning til differensiallikningen når .
Løsningsforslag a)
Jeg tenker
For å finne ut om er en løsning av differensiallikningen kan vi sette inn for i ligningen.
Dersom er en løsning av ligningen , må vi ha at .
Vi kan derivere ved å bruke kjerneregelen med som kjerne. Det gir at
.
Tilsvarende får vi
.
Nå kan vi sette inn i ligningen
.
Ved å faktorisere ut får vi
.
Siden må også som betyr at er en løsning av ligningen.
Svar: er en løsning.
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere forklaringer og eksempler om differensiallikninger, se artikkelen Andre ordens differensiallikninger.
b)
Bestem den generelle løsningen til differensialligningen.
Løsningsforslag b)
Jeg tenker
Dette er en andre ordens differensiallikning med karakteristisk likning , så for å finne den generelle løsningen må vi finne løsningene til den karakteristiske likningen.
Siden er den karakteristiske likningen til differensiallikningen, vil vi finne for hvilken denne likningen stemmer. Da kan vi bruke andregradsformelen
med , og .
Det gir
og
Den karakteristiske ligningen har to reelle røtter, så da er den generelle løsningen på formen
Setter vi inn for og får vi
Svar:
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
For flere forklaringer og eksempler på differensiallikninger, se artikkelen Andre ordens differensiallikninger.
c)
Bestem den spesielle løsningen som tilfredsstiller betingelsene og .
Løsningsforslag c)
Jeg tenker
Vi må finne konstantene og slik at betingelsene er tilfredstilt. Da kan vi regne ut og og finne hva og må være.
Den første betingelsen gir at . I deloppgave b) fant vi den generelle løsningen. Nå kan vi sette inn
Dersom den første betingelsen skal være tilfredstilg må .
Den andre betingelse gir at . Da må vi begynne med å finne hva er. Vi bruker kjerneregelen med og som kjerner, og da får vi
Videre kan vi sette inn for som gir
Skal den andre betingelsen være tilfredsstilt må vi ha at .
De to betingelsene gir ligningsettet
Den andre ligningen gir .
Setter vi dette inn i den første ligningen får vi
Det gir
Nå har vi funnet ut hva og må være for at betingelsene skal holde, og da blir løsningen av ligningen
Svar:
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
For flere forklaringer og eksempler, se artikkelen Andre ordens differensiallikninger.
Oppgave 6 (5 poeng) Nettkode: E-4PC8
Brøken er definert ved at telleren er summen av de første oddetallene, mens nevneren er summen av de neste oddetallene.
a)
Regn ut , og .
Forkort svarene.
Løsningsforslag a)
Jeg tenker
Her skal vi regne ut og forkorte brøkene.
Vi skal regne ut , og . Da får vi
Svar:
Mer om
Denne oppgaven er om
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
For flere forklaringer og eksempler på brøk, se artikkelen Forkorte og utvide brøk.
b)
Vis at summen av de første oddetallene kan skrives .
Løsningsforslag b)
Jeg tenker
Vi kan vise at ved induksjon. Da må vi vise at det stemmer for og at hvis det stemmer for så må det også stemme for .
Vi kan skrive det 'te oddetallet som .
For å vise at kan vi bruke induksjon. Det første vi må vise er at formelen stemmer for . Da sier påstanden at
Formelen stemmer for .
Nå antar vi at påstanden stemmer for . Vi kan skrive det -te oddetallet som .
Da er altså
Videre må vi vise at formelen stemmer for , altså summen av de minste oddetallene. Da må vi addere det neste oddetallet, til summen .
Antagelsen vår sier at , dermed blir summen
Summen av de (k+1) minste oddetallene er altså lik og formelen stemmer for . Ved å anta at stemmer følger det at også stemmer. Da stemmer for alle ved induksjon.
Alternativ
Vi kan også bruke formelen for sum av en aritmetisk rekke for å vise at dette stemmer.
Summen, av en aritmetisk rekke er gitt ved .
For oddetallene blir og er det 'te oddetallet, og kan skrives som .
Nå kan vi fylle inni formelen
og får det vi ville ha.
Svar: Vi har ved induksjon vist at stemmer for alle
Mer om
Denne oppgaven er om
Oddetall
Tallene 1, 3, 5, 7, 9 og 11 er eksempler på oddetall.
Oddetall er heltall hvor svaret ikke blir et heltall når de deles med 2.
Alle oddetall kan skrives på formen 2n+1, der n er et helt tall.
Et heltall som ikke er oddetall er partall.
Matematisk induksjon
En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:
- Bevis påstanden for n =1.
- Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).
Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).
For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.
c)
Forklar at . Regn ut denne brøken.
Løsningsforslag c)
Jeg tenker
er summen av de første oddetallene. Vi kan bruke summen fra deloppgave b) til å regne ut brøken.
I er telleren summen av de første oddetallene, mens nevneren er summen av de neste oddetallene. I deloppgave b) skrev vi summen av de første oddetallene som , så telleren må være lik . I nevneren vil vi ha de neste oddetallene. Dersom vi tar summen vil vi få de første oddetallene og trekker vi fra første, sitter vi igjen med de neste oddetallene. Dermed kan skrives som .
Vi skal nå regne ut denne brøken. Da kan vi bruke resultatet fra deloppgave b), at . Setter vi inn for i får vi
Dette stemmer også med svarene vi fikk i deloppgave a)
Svar:
Mer om
Denne oppgaven er om
Sum
Resultatet av en addisjon.
Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.
Oddetall
Tallene 1, 3, 5, 7, 9 og 11 er eksempler på oddetall.
Oddetall er heltall hvor svaret ikke blir et heltall når de deles med 2.
Alle oddetall kan skrives på formen 2n+1, der n er et helt tall.
Et heltall som ikke er oddetall er partall.
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
For flere forklaringer og eksempler rekker , se artikkelen Aritmetiske rekker.
Oppgave 7 (7 poeng) Nettkode: E-4PCC
Ligningen til en kuleflate er gitt ved
a)
Vis at punktet ligger på kuleflaten.
Løsningsforslag a)
Jeg tenker
Vi kan sette inn for , og i ligningen til kuleflaten. Dersom ligningen stemmer ligger punktet på kuleflaten.
I punktet har vi koordinatene , og . For å finne ut om punktet ligger på kuleflaten kan vi sette inn for , og i ligningen for kuleflaten. Dersom likningen stemmer vil punktet ligge på kuleflaten.
Svar: Ligningen til kuleflaten stemmer for , så punktet ligger på kuleflaten.
Mer om
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Koordinat
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.
Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.
Se Koordinatsystem
Kule
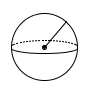
Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.
b)
Vis at kulen har sentrum i . Bestem radien til kulen.
Løsningsforslag b)
Jeg tenker
En kule med radius og sentrum i har likningen , så vi må omforme likningen slik at den blir på denne formen. Dette kan vi gjøre ved hjelp av fullstendige kvadrater.
Vi vil få ligningen på formen , med , og , altså på formen . Da må vi lage fullstendige kvadrater. Vi kan begynne med å samle alle leddene med til et fullstendig kvadrat
Tilsvarende kan vi gjøre for alle leddene med
og til slutt også for alle leddene med
Vi ser at ligningen nå er på den ønskede formen, med sentrum i og radius
Svar: Sentrum er i og radius, , er .
Mer om
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
Radius
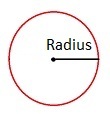
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
For flere forklaringer og eksempler, se artikkelen Likning for en kule.
c)
Bestem ligningen for tangentplanet til kuleflaten i punktet .
Løsningsforslag c)
Jeg tenker
Vektoren fra kulens sentrum til punktet , vil stå normalt på tangentplanet, så vi kan bruke til å finne ligningen til tangentplanet.
Kulens sentrum er og ligger på kuleflaten. Vektoren
går gjennom sentrum i kulen og står normalt på kuleflaten i punktet . Tangentplanet i punktet består av alle punkter innholdt i en linje som tangerer kulen i punktet , vil stå normalt på alle linjene i dette planet, og vil være en normalvektor. Det betyr at alle vektorer mellom to punkter i planet må stå vinkelrett på og da må . Siden ligger i tangentplanet må alle punkter som også ligger i tangentplanet tilfredstille Vi kan uttrykke
.
Da får vi
Siden , så tilfredstiller alle punktene i tangentplanet i likningen som da er likningen til planet.
Svar:
Mer om
Denne oppgaven er om
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Vektor

En vektor er en størrelse med en retning.
I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.
Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .
Normalvektor
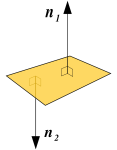
En normalvektor for et plan står vinkelrett på alle linjer i planet.
Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
For flere forklaringer og eksempler på plan, se artikkelen Likning til et plan.
d)
Et annet plan går gjennom og og står normalt på .
Bestem ligningen til .
Løsningsforslag d)
Jeg tenker
Når planene og står normalt på hverandre, vil også normalvektorene, og , stå normalt på hverandre, og .
Siden normalvektorene og vil står normalt på hverandre og vi vil ha Fra deloppgave c) vet vi at . Vi kan uttrykke . Da kan vi regne
.
Denne ligningen sier ingenting om , så kan være et vilkårlig tall. Planet går gjennom , så ligningen til kan uttrykkes
Siden punktet også ligger i planet må ligningen tilfredsstille
Nå har vi at
Ingen av ligningene sier at , og vi kan sette . Fra den nederste av de to ligningene får vi . Nå kan vi sette inn for i den øverste, dette gir
Sette vi inn i ligningen for får vi
Alternativ
Planene og står normalt på hverandre, så normalvektorene, og , vil også stå normalt på hverandre. Normalvektoren til vil også stå normalt på vektoren , som ligger i . Vi kan finne en slik normalvektor ved å finne vektorproduktet . Før vi regner vektorproduktet finner vi at Fra deloppgave b) har vi at er en normalvektor til , så nå kan vi finne vektorproduktet mellom disse.
Nå har vi en normalvektor og et punkt i planet , så da kan vi finne likningen til planet ved Mulitpliserer vi med på begge sider av likhetstegnet ser vi at vi får samme svar som i den andre løsningen.
Svar:
Mer om
Denne oppgaven er om
Normalvektor

En normalvektor for et plan står vinkelrett på alle linjer i planet.
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
For flere forklaringer og eksempler på plan, se artikkelen Likning til et plan.
DEL 2 med hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4PCH

Ved inngangen til var folketallet i Norge . I en modell for befolkningsveksten antar vi at
- netto innvandring per år vil være
- antall som blir født per år, vil være av folketallet
- antall som dør per år, vil være av folketallet
Vi lar folketallet være , der er antall år etter .
a)
Forklar at vi kan skrive
Løsningsforslag a)
Jeg tenker
Befolkningsveksten, er endringen i folketall og endringen bestemmes av antall mennesker som blir født, dør og av netto innvandring.
Befolkningsveksten påvirkes av netto innvandring, og fødsler og død. Vi får oppgitt at antall som blir født hvert år er av folketallet, og antall som dør er . I tillegg må vi også ta hensyn til netto innvandring som vil være på .
Befolkningsveksten vil da kunne uttrykkes ved
Siden vi ser på , der er antall år etter 2015, vil være folketallet i 2015, altså .
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere forklaringer og eksempler på differensialfunksjoner, se artikkelen Første ordens lineære differensiallikninger.
b)
Løs differensialligningen.
Løsningsforslag b)
Jeg tenker
Dette er en lineær førsteordens differensiallikning. Denne kan vi enten løse ved regning, og da kan vi multiplisere med en integrerende faktor, eller vi kan løse den ved hjelp av CAS.
Vi kan enten løse likningen for hånd, eller ved hjelp av CAS. Løsningsforslag for å løse oppgaven for hånd ligger under Alternativ.
Vi kan bruke CAS til å løse differensialligningen ved å bruke kommandoen “LøsODE[<Likning>, <Punkt på f>]”.
Ligningen vi vil løse er , og punktet er for å bestemme konstanten.
Vi vet at , så da er et punkt på y.
Da skriver vi inn
LøsODE[y’-0.003y=44000, (0,5200000)].

Her er både eksakt og avrundet løsning.
Alternativ
For å løse likningen ved regning kan vi starte med å flytte begge leddene som avhenger av på samme side av likhetstegnet. Slik at vi får
Videre nå kan vi introdusere en integrerende faktor som vi multipliserer med på begge sider av ligningen. Da får vi
Venstre side av ligningen er nå lik
så nå har vi
Nå kan vi integrere begge sider, og da bruker vi at . Det gir
Nå kan vi dividere på på begge sider som gir
For å finne konstanten , bruker vi at vi vet at . Om vi setter inn for i ligningen over får vi
Videre kan vi løse ligningen
Løsningen på differensialligningen blir da
Svar:
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Eksponentialligning
En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.
Eksempel med som ukjent: eller
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
For flere forklaringer og eksempler, se artikkelen Separable differensiallikninger.
c)
Når vil folketallet passere millioner ifølge denne modellen?
Hvor stor er vekstfarten i folketallet da?
Løsningsforslag c)
Jeg tenker
Vi kan løse ligningen
Denne oppgaven kan vi løse grafisk ved hjelp av GeoGebra. Vi kan tegne inn grafen til funksjonen ved å skrive inn
,
og for å finne når folketallet passerer millioner, kan vi finne ut når grafen til krysser linja . Da må vi skrive inn , og finne skjæringspunkt mellom de to grafene.

Da får vi punktet , som forteller oss at folketallet passerer millioner nesten år etter 2015, i slutten av år .
Befolkningsveksten kan vi da finne ved å sette inn i likningen fra deloppgave a).
Det gir som forteller at befolkningsveksten vil være en økning på innbyggere i året.
Alternativ
Vi vil finne når folketallet, passerer 7 millioner. Siden folketallet er gitt ved
kan vi løse
I følge modellen vil folketallet passere millioner år etter , altså i på slutten av .
Befolkningsveksten da kan vi finne ved å sette inn ligningen fra deloppgave a) med . Da får vi
Befolkningsveksten vil være en økning på innbyggere i året.
Svar: Mot slutten av 2043, og da vil befolkningsveksten være en økning på innbyggere i året.
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
For flere forklaringer og eksempler på funksjoner, se artikkelen Johannes viser eksponential- og logaritmefunksjoner.
Oppgave 2 (8 poeng) Nettkode: E-4PDI
Funksjonen er gitt ved
a)
Bruk graftegner til å tegne grafen til .
Løsningsforslag a)
Jeg tenker
Vi kan bruke GeoGebra til å tegne funksjonen.
For å tegne grafen til funksjonen i GeoGebra skriver vi inn
Svar: 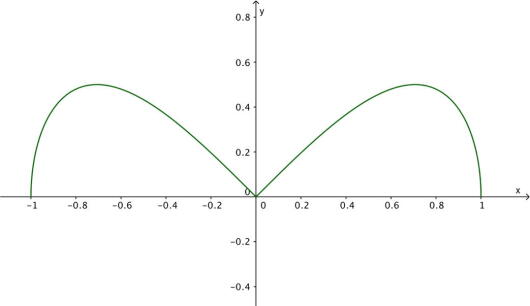
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.
b)
Bruk CAS til å bestemme de eksakte koordinatene til toppunktene på grafen til .
Løsningsforslag b)
Jeg tenker
For å finne ekstremalpunktene til grafen kan vi finne når og for å sjekke om vi har toppunkt kan vi sjekke om .
Vi begynner med å definere funksjonen i CAS. Da skriver vi inn
For å finne kan vi skrive

Da får vi at
når
Vi kan sjekke at dette er toppunkt ved å sjekke om
og
Dersom det stemmer har vi et toppunkt. Da skriver vi inn og i CAS.

Da får vi
og
Dette forteller oss at vi har toppunkt når og .
Videre må vi finne verdien til i toppunktene. Da skriver vi i CAS og , som gir og .

Toppunktene til grafen er og .
Svar: Toppunktene til grafen er og .
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Andrederiverte
Den andrederiverte til en funksjon er funksjonen derivert to ganger og skrives eller . Kalles også annenderiverte eller dobbeltderiverte.
For flere eksempler og forklaringer om ekstremalpunkt, se artikkelen Topp- og bunnpunkter.
c)
Bestem det samlede arealet av områdene som er avgrenset av grafen til og -aksen.
Løsningsforslag c)
Jeg tenker
For å finne arealet mellom grafen til og -aksen-aksen kan vi integrere . Før vi regner dette ut må vi se om noe av området under grafen til vil ligge under -aksen.
Først kan vi se at . På intervallet vil vi alltid ha , så vi får kvadratroten av et ikke-negativt tall. Når er utenfor intervallet vil ikke funksjonen være definert.
Arealet under grafen til f er det samme som å finne integralet til fra til . Dersom vi bruker samme GeoGebravindu som i deloppgave a), er funksjonen allerede definert, hvis ikke kan vi definere ved å skrive .
Nå kan vi finne arealet ved å bruke kommandoen Integral i CAS og skrive .

Da får vi .
Alternativ
Vi begynner med å se hvordan vi kan regne arealet mellom grafen til
og -aksen. I alternativ løsning vil vi se hvordan vi kan gjøre det uten hjelp av CAS.
Først kan vi se at . På intervallet vil vi alltid ha , så vi får kvadratroten av et positivt tall. Når er utenfor intervallet vil ikke integralet være definert. Skjæringspunktene mellom og -aksen finner vi ved å finne nullpunktene til , med andre ord når .
Det betyr at og er nullpunkter, og siden er positiv på hele intervallet, altså ligger hele området over -aksen. Da kan vi finne areal under grafen ved å regne
Funksjonen er symmetrisk om , det vil si at
på hele intervallet vårt, og dette medfører at og at
Vi kan faktorisere og regne ut
For å løse dette integralet kan vi bruke substitusjon ved å sette . Da får vi
De nye integrasjonsgrensene blir
og
Da kan vi regne ut
Arealet under grafen til vil være .
Svar: Arealet er .
Mer om
Denne oppgaven er om
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.
d)
Grafen til roteres om -aksen. Bestem volumet av omdreiningslegemet som da framkommer.
Løsningsforslag d)
Jeg tenker
Volumet av omdreiningslegemeet til en funksjon kan skrives som et integral av sylindere med høyde og grunnflate , og vi kan finne volumet ved formelen
For å finne volumet til omdreningslegemet kan vi bruke formelen
og CAS. I CAS skriver vi inn
, der er definert som i deloppgave b).

Alternativ
Fra deloppgave c) har vi at
på grunn av symmetrien til .
Volumet til omdreiningslegemet kan vi finne ved å regne ut dette integralet.
Svar: Volumet er
Mer om
Denne oppgaven er om
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Omdreiningslegeme
Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
For flere forklaringer og eksempler på integrasjon, se artikkelen Volum av et omdreiningslegeme.
Oppgave 3 (7 poeng) Nettkode: E-4PDW
To plan og er gitt ved
a)
Vis at punktet ligger i begge planene.
Løsningsforslag a)
Jeg tenker
Vi kan sette inn for og i ligningene for planene, og dersom ligningene stemmer, er et punkt i planet.
Dersom punktet ligger i planene vil det tilfredstille likningen til hvert av planene. Med andre ord kan vi sette inn for , og i likningene og om likningen stemmer ligger punktet i planet.
og
Vi ser at likningen til begge planene stemmer når vi setter inn for koordinatene til , altså ligger i planene.
Svar: Punktet ligger i begge planene
Mer om
Denne oppgaven er om
Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
Koordinat
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.
Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.
Se Koordinatsystem
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
For flere forklaringer og eksempler, se artikkelen Likning til et plan.
b)
Bestem slik at vinkelen mellom og blir .
Løsningsforslag b)
Jeg tenker
Et plan med ligning vil ha normalvektor . Når vinkelen mellom normalvektorene til planene er vil også vinkelen mellom planene være .
Normalvektoren, , til vil være og normalvektoren, til vil være . For å finne vinkelen mellom normalvektorene kan vi bruke skalarproduktet. Når vinkelen mellom vektorene er er skalarproduktet gitt ved
Nå kan vi regne ut
Vi vet at . og vi kan regne ut og
Vi kan nå sette inn i skalarproduktet og løse ligningen med hensyn på
Svar: Vi må ha for at vinkelen mellom planene skal være .
Mer om
Denne oppgaven er om
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Vektor

En vektor er en størrelse med en retning.
I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.
Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .
Normalvektor

En normalvektor for et plan står vinkelrett på alle linjer i planet.
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
Vinkel
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklaringer og eksempler om vektorer, se artikkelen Vinkelen mellom to vektorer.
c)
Hvilken verdi for vil gi den minste vinkelen mellom og ? Hvor stor er vinkelen?
Løsningsforslag c)
Jeg tenker
Vi kan bruke skalarproduktet til å finne en funksjon for , der er vinkelen mellom og .
I deloppgave b) brukte vi skalarproduktet
mellom normalvektorene og vi fant at
og
Når vi setter inn dette får vi
som gir
Vi kan finne maksimumsverdien for ved hjelp av CAS. Da kan vi definere som en funksjon, , slik at
Denne definerer vi i CAS ved å skrive inn
For å finne ut når har ekstremalpunkt må vi finne for hvilken vi har . Dette kan vi finne ved å skrive Løs[f’(p)]=0 i CAS. Da får vi at gir et ekstremalpunkt for .
Videre kan vi sjekke
for å se om er maksimums- eller minimumspunkt. I CAS skriver vi f”(0), og får som forteller oss at vi har et maksimumspunkt.

Vi har altså funnet ut for hvilken som gir , og dermed også , størst verdi, og som gir at vinkelen vil være minst mulig. Setter vi inn for får vi at , og vinkelen .
Alternativ
Vi kan også se at for er og , så når har vi at jo større er, dess mindre er vinkelen , med andre ord vil vi ha størst mulig.
I uttrykket har vi i nevneren, og vi vil velge slik at dette uttrykket blir størst mulig. Da vil vi ha minst mulig nevner, og det får vi når vi velger . Dersom vi velger vil brøken, og bli mindre, og vinkelen større.
Så da må og vi vil få at , som gir at vinkelen .
Svar: vil gi den minste vinkelen, og da er vinkelen .
Mer om
Denne oppgaven er om
Vektor

En vektor er en størrelse med en retning.
I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.
Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Ekstremalpunkt

Vi sier at et punkt er et ekstremalpunkt for en funksjon hvis det enten er et toppunkt eller bunnpunkt for funksjonen.
For flere forklaringer og eksempler på ekstremalpunkt, se artikkelen Topp- og bunnpunkter.
d)
De to planene skjærer hverandre langs en linje . Bestem en parameterframstilling for uttrykt ved .
Løsningsforslag d)
Jeg tenker
Vi har at ligger i begge planene og da vil normalvektoren til både og stå normalt på linjen. Ved å finne kryssproduktet mellom normalvektorene, og , til planene, vil vi finne en vektor som står normalt på begge vektorene.
Retningsvektoren til vil stå normalt på både og siden ligger i begge planene. Vi kan finne en vektor som står normalt på både og ved å finne kryssproduktet mellom dem.
For å finne kryssproduktet kan vi bruke CAS.
Først definerer vi normalvektorene ved å skrive og . CAS bruker kommandoen Vektorprodukt for å finne kryssproduktet, så vi kan skrive .Da får vi vektoren , som vil være retningsvektor til linjen .

For å finne parameterfremstillingen til trenger vi også et punkt på linjen. Fra a) vet vi at punktet ligger i begge planene, og må da også ligge på linjen. Nå har vi både retningsvektor og et punkt på linjen, og da kan vi finne parameterfremstillingen:
Svar: En parameterfremstilling er gitt ved
Mer om
Denne oppgaven er om
Vektor

En vektor er en størrelse med en retning.
I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.
Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .
Normalvektor

En normalvektor for et plan står vinkelrett på alle linjer i planet.
Retningsvektor
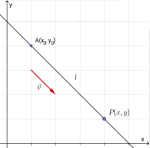
En linje går gjennom punktet og er parallell med vektoren . Vektoren kalles for retningsvektoren for linja.
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
For flere forklaringer og eksempler på vektorer, se artikkelen Parameterfremstilling av en rett linje.
Oppgave 4 (4 poeng) Nettkode: E-4PE0
Om en uendelig geometrisk rekke vet vi at
- summen er
- summen av de tre første leddene er
a)
Sett opp et ligningssystem som uttrykker opplysningene ovenfor.
Løsningsforslag a)
Jeg tenker
I en geometrisk rekke kan hvert ledd, uttrykkes ved der er en kvotienten. Siden summen av den uendelige rekker er 8, vet vi at den konvergerer, og at , da er summen av en uendelig geometrisk rekke er gitt ved formelen .
Vi får oppgitt at summen av den geometrisk rekken er 8, altså konvergerer den. Siden summen, , av en uendelig geometrisk rekke som konvergerer kan gis ved formelen
har vi at
Det andre vi får oppgitt er at summen av de tre første leddene er 7, altså har vi at
Siden vi har en geometrisk rekke kan hvert av leddene uttrykkes ved det første, . Da får vi at og . Altså kan vi skrive
Nå har vi et ligningsett med to ligninger og to ukjente:
Svar:,
Mer om
Denne oppgaven er om
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Uendelige rekker
En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.
Eksempel :
( ∞ er tegnet for uendelighet )
For flere forklaringer og eksempler på rekker, se artikkelen Uendelig rekker.
b)
Bruk CAS til å bestemme kvotienten og det første leddet i rekken.
Løsningsforslag b)
Jeg tenker
Vi kan bruke “Løs”-kommandoen i CAS.
For å løse ligningssettet i CAS kan vi bruke kommandoen “Løs”. Da skriver vi
Løs[{a_1/(1-k)=8, a_1(1+k+k^2)=7}, {a_1,k}]
i CAS-vinduet. Da vil CAS løse ligningsettet fra deloppgave a) med hensyn på og .

Utregningen fra CAS viser at og
Svar: og
Mer om
Denne oppgaven er om
Trigonometrisk rekke
En rekke der hvert ledd er en potens av en trigonometrisk funksjon.
Eksempel:
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Kvotient
Resultatet av en divisjon kalles en kvotient.
Eksempel: , her er 4 en kvotient.
Ledd
I en addisjon kalles tallene som legges sammen for ledd.
Eksempel: , her kalles tallene 8, 3 og 5 for ledd.
For flere forklaringer og eksempler på rekker, se artikkelen Geometrisk rekke.




