
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2015 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 10 oppgaver. Del 2 har 7 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Jordkloden (www.openclipart.org, 5.07.2016)
- Varmekilder: http://www.tu.no/kraft/2015/01/14/her-fyrer-man-mest-med-ved-i-norge (25.02.2015)
- Nina: http://www.vg.no/nyheter/innenriks/vaer-og-uvaer/her-blaaste-nina-mest/a/23371898/ (11.01.2015)
- BSU: https://www.sparebank1.no (26.02.2015)
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4CMV
Prisen på en vare er satt ned med 30 %. I dag koster varen 280 kroner.
Hvor mye kostet varen før prisen ble satt ned?
Løsningsforslag
Jeg tenker:
Hvis varen ble satt ned til , så er lik av den opprinnelige prisen.
La betegne prisen på varen i kroner, før den ble satt ned. Da varen ble satt ned med , må den da ha kostet kroner. Vi vet allerede at varen kostet etter den ble nedsatt, så vi har at , eller der vi har brukt at
Prosentfaktor
En prosentfaktor er et prosenttall skrevet om til et desimaltall.
Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.
Svar:
Mer om:
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
For flere eksempler og forklaringer om prosentregning se artikkelen Regneregeler. For mer om likninger se artikkelen Lineære likninger.
For å øve mer, se oppgavesettet om prosentregning og førstegradslikninger i Treningsleieren.
Oppgave 2 (1 poeng) Nettkode: E-4CMX
Regn ut og skriv svaret på standardform
Løsningsforslag
Jeg tenker:
Her må vi huske på at vi kan bytte om rekkefølgene på
Faktor
I en multiplikasjon kalles tallene faktorer. Resultatet kalles et produkt.
Eksempel: 5 · 3 = 15. Her er 5 og 3 er faktorer. Tallet 15 er produktet. Vi kan si at 15 består av faktorene 5 og 3.
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Faktor
I en multiplikasjon kalles tallene faktorer. Resultatet kalles et produkt.
Eksempel: 5 · 3 = 15. Her er 5 og 3 er faktorer. Tallet 15 er produktet. Vi kan si at 15 består av faktorene 5 og 3.
Svar:
Mer om:
Denne oppgaven er om Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.Standardform
Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n ganger
For flere eksempler og forklaringer se artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Oppgave 3 (1 poeng) Nettkode: E-4CMZ
Regn ut
Løsningsforslag
Jeg tenker:
Vi ser
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Først regner vi ut
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Svar:
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Brøk

For flere eksempler og forklaringer se artikkelen Potenser med samme grunntall.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 4 (2 poeng) Nettkode: E-4CN1
For 10 år siden vant Lea i Lotto. Hun opprettet en konto i banken og satte inn hele gevinsten. Beløpet har stått urørt på kontoen siden. Renten har hele tiden vært 3,2 % per år.
I dag har Lea 500 138 kroner på kontoen.
Sett opp et uttrykk som du kan bruke til å regne ut hvor stor gevinsten til Lea var.
Løsningsforslag
Jeg tenker
Vi skal finne det opprinnelige beløpet når vi vet hvor mye penger som er i banken etter år. Dette kan vi gjøre ved å betegne det opprinnelige beløpet med , og sette opp et uttrykk for hvor mye penger det er i banken ti år etter.
Hvis det står et beløp i banken med i rente, kan vi finne ut hvor mange penger som står i banken etter år (nemlig grunnbeløpet multiplisert med ). Denne oppgaven går ut på å gjøre det motsatte, nemlig å finne det opprinnelige beløpet når vi vet hvor mange penger som er i banken etter 10 år.
La betegne antall kroner Lea vant i Lotto. Etter ett år i banken, har beløpet vokst til , og etter to år har det vokst til , og så videre. Etter år er beløpet . Men vi vet allerede nøyaktig hva dette beløpet er – for Lea hadde i banken etter år. Nå har vi to uttrykk for det samme tallet, og da må de to være like. Altså har vi Vi vil finne tallet for som passer inn her, så vi vil gjøre om ligningen til å ha alene på én side. Dette kan vi gjøre ved å dividere med på begge sider – eller tilsvarende, å multiplisere med på begge sider. Vi fårNå har vi funnet et uttrykk for hvor mange penger Lea vant. (Dette er for øvrig lik cirka .)
Svar: Hvis er antall kroner Lea vant, er .
Mer om
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefot En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Prosent
Rente
Ligning
Potens
Eksempel:
For flere eksempler og forklaringer se artiklene Prosent av hva da? og Renter.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 5 (2 poeng) Nettkode: E-4CN4

Omkretsen av jordkloden ved ekvator er ca. 40 000 km. Tenk deg at voksne og barn står hånd i hånd og danner en ring rundt jordkloden. Hver person favner i gjennomsnitt 1,6 m.
Omtrent hvor mange personer må stå hånd i hånd for å nå rundt jordkloden ved ekvator? Skriv svaret på standardform.
Løsningsforslag
Jeg tenker
Her må vi se på
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Forholdet mellom
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi husker at . Det betyr at jordklodens omkrets er cirka Vi skriver dette som et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Svar: Cirka mennesker
Mer om
Denne oppgaven er om Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Standardform
Potens
Eksempel:
For flere eksempler og forklaringer se artiklene Tall på standardform og Oppsummering av regneregler for potenser.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Visste du at
Det er cirka milliarder mennesker på jordkloden per , eller på standardform. Det betyr at hvis alle menneskene holdt hverandre i hendene rundt jordkloden ved ekvator, så hadde vi nådd cirkaaltså nesten ganger, rundt kloden.
Oppgave 6 (3 poeng) Nettkode: E-4CN7
| Alder | Bedrift A Frekvens |
Bedrift B Frekvens |
| 52 | 35 | |
| 36 | 45 | |
| 12 | 20 | |
| Sum | 100 | 100 |
Hver av de to bedriftene A og B har 100 ansatte. Tabellen ovenfor viser aldersfordelingen for de ansatte i bedriftene.
a)
I hvilken bedrift er medianalderen lavest? Grunngi svaret.
Løsningsforslag a)
Jeg tenker:
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Vi kan ikke si nøyaktig hva
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Vi starter med bedrift A. Medianen er altså
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: Medianalderen i bedrift A er lavest.
Mer om:
Denne oppgaven er om Medianen er den verdien som vi finner i midten av et rangert datamateriale. Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Median
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.
For å øve mer, se oppgavesettet om median og gjennomsnitt i Treningsleieren.
b)
Bestem gjennomsnittsalderen for de ansatte i bedrift B.
Løsningsforslag b)
Jeg tenker:
Vi arbeider med gruppert informasjon. Da antar vi at dataene vi har er jevnt fordelt innenfor gruppene. For eksempel antar vi at gjennomsnittalderen av alle som er i intervallet , er .
Vi antar at gjennomsnittsalderen til hver gruppe er midt i intervallet. For å regne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Divisjon
Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.
Eksempel: fordi .
Vi regner ut at , og , så dette blir Dette betyr at gjennomsnittsalderen i bedrift B er år.
Svar: Gjennomsnittsalderen i bedrift B er år.
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Oppgave 7 (3 poeng) Nettkode: E-4CNE
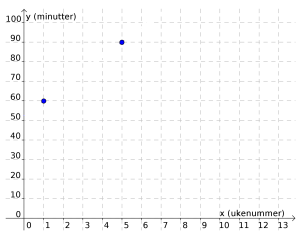
I koordinatsystemet ovenfor har Liv markert hvor mange minutter hun trente i uke 1 og i uke 5. Liv har som mål at antall minutter hun trener, skal øke lineært for hver uke.
a)
Bestem en modell som Liv kan bruke for å regne ut hvor mange minutter hun må trene hver uke framover.
Løsningsforslag a)
Jeg tenker
At noe er
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Vi vil finne likningen til linjen vist på bildet under.
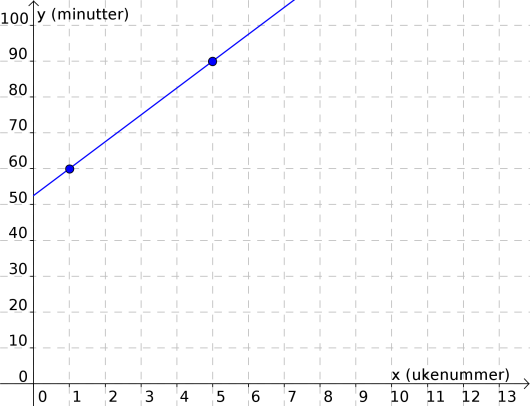
Altså vil vi finne
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Svar: Hvis er antall minutter Liv må trene i uke , så er .
Mer om
Denne oppgaven er om Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2. Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). Ligninger der alle de ukjente opptrer i første grad. Eksempel: En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Lineære funksjoner er funksjoner som er skrevet på formen . Den loddrette aksen i et koordinatsystem. Stigningstall

Koordinatsystem

Lineære ligninger
Linje
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.y-akse

Kalles også andreaksen.
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
b)
Hvor mange timer må hun trene i uke 40 ifølge denne modellen?
Løsningsforslag b)
Jeg tenker
Alt vi trenger å gjøre er å sette inn i likningen vi har funnet i deloppgave a).
Fra forrige oppgave vet vi at Liv må trene i uke nummer . Setter vi inn , får vi at hun må trene timer i uke . Vi ser at , så hun må trene i minutter. Det er timer og minutter.
Svar: Hun må trene i minutter, som er det samme som timer og minutter.
Mer om
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Funksjon
Ligning
For flere eksempler og forklaringer se artiklene Grafen til en funksjon og Lineære likninger.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
Oppgave 8 (2 poeng) Nettkode: E-4CNI
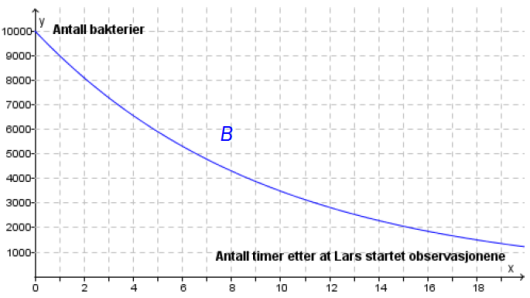
Lars observerer en bakteriekultur. Fra han startet observasjonene, har antall bakterier avtatt eksponentielt. Se grafen til funksjonen ovenfor.
Bestem vekstfaktoren og sett opp utrykket for
Løsningsforslag
Jeg tenker:
At bakteriekulturen avtar
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
På grafen ser vi at vi startet med bakterier, og etter time avtok bakteriekulturen til bakterier, altså av det vi opprinnelig hadde. Derfor er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Prosentfaktor
En prosentfaktor er et prosenttall skrevet om til et desimaltall.
Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.
Nå kan vi finne uttrykket for . Vi vet at det er på formen der er antall bakterier ved start. Vi startet med bakterier, så ; dermed har vi
Svar: Vekstfaktoren er , og uttrykket for er .
Mer om:
Denne oppgaven er om Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Vekstfaktor
Eksponentialfunksjon

Potens
Eksempel:
For flere eksempler og forklaringer se artikkelen Johannes viser eksponential- og logaritmefunksjoner. For mer om prosentregning se lynkurset Prosent.
For å øve mer, se oppgavesettet om eksponentialfunskjoner i Treningsleieren.
Oppgave 9 (5 poeng) Nettkode: E-4CNL
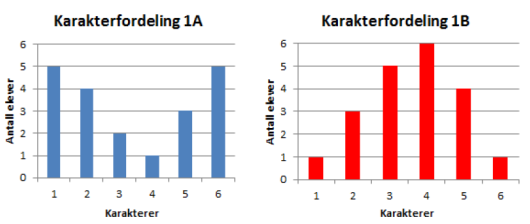
Diagrammene ovenfor viser hvordan karakterene i klasse 1A og 1B fordelte seg ved forrige matematikkprøve.
a)
Bestem gjennomsnittskarakteren i hver av de to klassene.
Løsningsforslag a)
Jeg tenker:
For å bestemme
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi starter med klasse 1A. Karakterene står vannrett nederst, mens antallet som har fått denne karakteren står loddrett oppover. Stolpen som står over “” på den vannrette linjen, når opp til “” på den loddrette linjen, og det betyr at det er elever som har fått karakteren . Summen av disse karakterene er . Tilsvarende er det elever som har fått karakteren , og summen av disse karakterene er , og så videre. Summen av alle karakterene blir dermedVi må også finne ut hvor mange elever det er. Det gjør vi ved å legge sammen antallet elever som har fått hver karakter, og det blirGjennomsnittskarakteren i klasse 1A er derfor
Vi ser at , så dette er gjennomsnittskarakteren i 1A.
Det er helt tilsvarende å regne ut gjennomsnittskarakteren i 1B. Vi får at gjennomsnittskarakteren blir
Svar: Gjennomsnittskarakteren i 1A og 1B er henholdsvis og .
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleiren.
b)
I hvilken klasse er standardavviket for karakterfordelingen størst? Grunngi svaret.
Løsningsforslag b)
Jeg tenker:
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi kunne ha regnet ut
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: 1A
Mer om:
Denne oppgaven er om Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Standardavvik
Statistikk
For flere eksempler og forklaringer se artikkelen Varians og standardavvik.
c)
Bestem den kumulative frekvensen for karakteren 3 i hver av de to klassene.
Løsningsforslag c)
Jeg tenker:
Den
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Vi starter med klasse 1A. Der var det elever som fikk karakteren , elever som fikk og elever som fikk karakteren . Det er totalt , og dette er den
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
I klasse 1B var det , og som fikk henholdsvis karakterene , og . Den kumulative frekvensen er dermed .
Svar: Den kumulative frekvensen for 1A og 1B er henholdsvis og .
Mer om:
Denne oppgaven er om Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere. Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien. Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Kumulativ frekvens

Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
d)
Bestem den relative frekvensen for karakteren 6 i hver av de to klassene.
Løsningsforslag d)
Jeg tenker:
Den
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner. Relativ frekvens
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Svar: Den relative frekvensen for karakteren i henholdsvis klasse 1A og klasse 1B, er og .
Mer om:
Denne oppgaven er om Antall observasjoner av en spesiell hendelse dividert på antall observasjoner. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Relativ frekvens
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
Oppgave 10 (4 poeng) Nettkode: E-4CNS
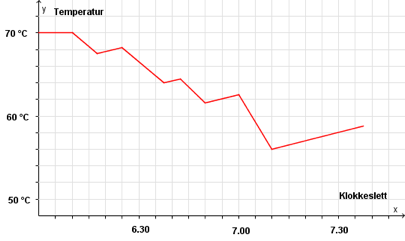
Hos familien Vassdal er termostaten i varmtvannstanken satt til 70 °C . Når familien bruker varmtvann fra tanken, renner kaldt vann inn, og gjennomsnittstemperaturen på vannet i tanken avtar. Varmeelementet slår seg da automatisk på, og vannet varmes opp igjen.
Grafen ovenfor viser hvordan temperaturen i tanken varierte en morgen. Det varme vannet ble bare brukt til å dusje.
a)
Hvor mange familiemedlemmer dusjet denne morgenen?
Løsningsforslag a)
Jeg tenker:
Hver gang
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Når noen dusjer, så blir temperaturen i varmtvannstanken kaldere, og
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Svar: stykker
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Graf
Funksjon
For flere eksempler og forklaringer se artikkelen Fra en funksjon til en graf.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
b)
Datteren Vanda var den som brukte lengst tid i dusjen.
Hvor lenge dusjet hun?
Løsningsforslag b)
Jeg tenker:
Lengden på dusjingen kan vi se på hvor langt
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
Vi legger merke til at mellomrommet mellom hvert hakk på -aksen er minutter.
Klokken begynner grafen å avta, og den slutter å avta kl. . Det betyr at den som startet dusjingen klokken dusjet i minutter. På denne måten kan vi se hvor lenge alle dusjingene pågikk. Vanda dusjet mellom og ca. , for dette er det største intervallet som grafen avtar på. Hun dusjet i minutter og sekunder.
Svar: I minutter og sekunder
Mer om:
Denne oppgaven er om Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. Den horisontale aksen i et koordinatsystem. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Intervall
x-akse

Kalles også førsteakse.Graf
Funksjon
For flere eksempler og forklaringer se artikkelen Hvorfor ser grafen ut som den gjør?.
For å øve mer, se oppgavesettet funksjoner i praktiske situasjoner i Treningsleieren.
c)
Da familien forlot hjemmet klokka 7.30, var temperaturen i varmtvannstanken 58 °C .
Hvor lang tid tok det før temperaturen var steget til 70 °C igjen?
Løsningsforslag c)
Jeg tenker:
Vi må finne ut hvor fort temperaturen i tanken stiger.
Vi ser på
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
Klokken var temperaturen på , og klokken var temperaturen . Det betyr at temperaturen i tanken økte med på minutter, eller på minutter. Vi vil finne ut hvor lang tid det tar fra kl. , da tanken hadde en temperatur på , til den hadde temperatur på . Det er en økning på , og siden det tar minutter å øke temperaturen med , så tar det å varme opp tanken igjen.
Svar: minutter, eller timer
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Lineære funksjoner er funksjoner som er skrevet på formen . Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.Graf
Linje
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Stigningstall

For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.
DEL 2 Med hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4CNX
| Oslo | Østlandet for øvrig |
Sør- Norge |
Vestlandet | Mdit-Norge | Nord-Norge | |
| Elektriske ovner |
59,7% | 36,6% | 30,4% | 32,4% | 34,2% | 36,5% |
| Varmepumpe | 8,3% | 18,0% | 25,5% | 33,2% | 33,8% | 27,7% |
| Vannbåren varme |
7,3% | 9,3% | 8,1% | 6,4% | 4,0% | 5,0% |
| Sentralvarme | 12,6% | 4,8% | 3,1% | 2,8% | 0,4% | 7,5% |
| Vedfyring | 5,3% | 26,8% | 28,3% | 19,9% | 19,6% | 22,0% |
| Annet eller vet ikke |
6,8% | 4,5% | 4,6% | 5,3% | 8,0% | 1,3% |
Tabellen ovenfor gir en oversikt over de viktigste varmekildene for husstander i ulike deler av Norge.
Bruk regneark til å lage ett diagram der du presenterer opplysningene i tabellen på en oversiktlig måte.
Løsningsforslag
Jeg tenker
Vi setter opp den samme tabellen i et regneark, for eksempel Excel, og finne et passende diagram.
Først skriver vi inn all informasjonen i regnearket. Vi har brukt Excel.
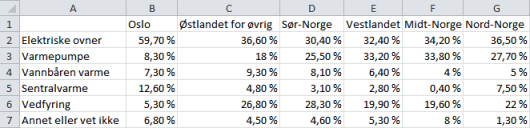
Vi vil lage et diagram ut av dette, og derfor markerer vi alt vi har skrevet ned og velger “Sett inn”. Der har vi en rekke forskjellige typer diagrammer vi kan velge mellom; vi velger et
Stolpediagram
Et søylediagram uten bredde på søylene.
Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.
Se Søylediagram
Stolpediagram
Et søylediagram uten bredde på søylene.
Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.
Se Søylediagram
Resultatet er vist under. Vi kunne også ha brukt en annen type diagram.
Svar: 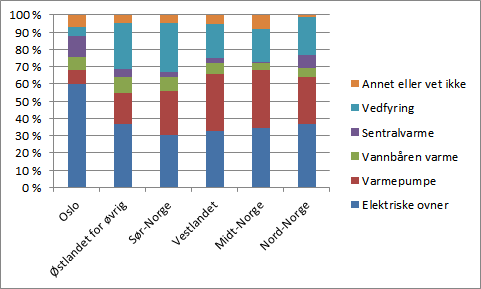
Mer om
Denne oppgaven er om Et søylediagram uten bredde på søylene. Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak. Se Søylediagram Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirennStolpediagram
Tabell

For flere eksempler og forklaringer se artikkelen Søyle og stolpediagram.
For å øve mer, se oppgavesettet om søylepediagram i Treningsleiren.
Oppgave 2 (7 poeng) Nettkode: E-4CNZ
Funksjonene og gitt ved
viser hvordan vekten til to babyer, Geir og Janne, utviklet seg det første leveåret.
Geir veide kilogram, og Janne veide kilogram måneder etter fødselen.
a)
Bruk graftegner til å tegne grafen til og grafen til i samme koordinatsystem.
Løsningsforslag a)
Jeg tenker
Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Vi skal tegne to
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Funksjon[ <Funksjon>, <Start>, <Slutt> ]på begge to. Vi skriver det følgende i «Skriv inn»-feltet:
G = Funksjon[0.003*x^3 - 0.088*x^2 + 1.17*x + 3.7, 0, 12]
F = Funksjon[0.0017*x^3 - 0.057*x^2 + 0.93*x + 3.7, 0, 12]Deretter drar vi
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Svar: 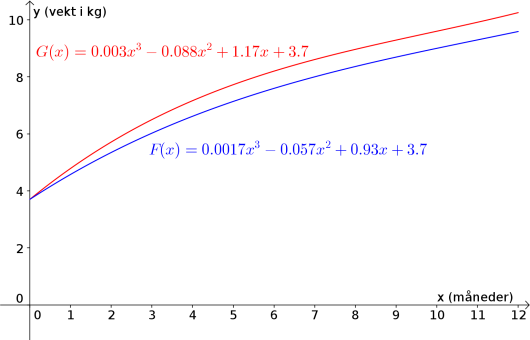
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. Den horisontale aksen i et koordinatsystem. Den loddrette aksen i et koordinatsystem. Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Graf
Intervall
x-akse

Kalles også førsteakse.y-akse

Kalles også andreaksen.Koordinatsystem

Funksjon
For flere eksempler og forklaringer se artikkelen Grafen til en funksjon.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
b)
Hvor mange kilogram la hver av de to babyene på seg i løpet av det første leveåret?
Løsningsforslag b)
Jeg tenker
Vekten til Geir og Janne i slutten av det første leveåret, er henholdsvis og . Dette kan vi bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
For å finne ut hva babyene la på seg i vekt, må vi finne ut hva de veide da de var født og i slutten av det første leveåret. Begge to startet på , fordi det er
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
G(12)i «Skriv inn»-feltet, og tilsvarende med . Da får vi henholdsvis cirka og , så Geir og Janne veide henholdsvis og ved slutten av deres første leveår. Begge startet på , så Geir har lagt på segog Janne la på seg
Svar: Geir og Janne la på seg henholdsvis cirka og .
Mer om
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Funksjon
For flere eksempler og forklaringer se artikkelen Johannes forteller deg om polynomfunksjoner.
c)
Hvor mange måneder gikk det før hver av de to babyene hadde doblet fødselsvekten sin?
Løsningsforslag c)
Jeg tenker
Vi må finne ut når hver av babyene hadde i vekt, altså må vi løse
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi kan løse likningene og grafisk ved å finne skjæringspunktene mellom og med linjen . Vi skriver det følgende i «Skriv inn»-feltet.
y = 7.4Nå kan vi finne løsningene ved å finne Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.Skjæringspunkt

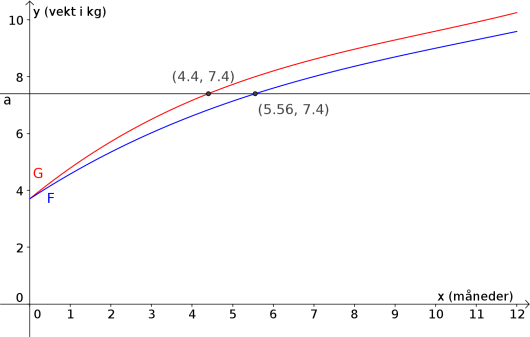
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se KoordinatsystemKoordinat
Svar: Geir og Janne brukte henholdsvis måneder og cirka måneder på å doble vekten sin.
Mer om
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se Koordinatsystem En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Skjæringspunkt

Linje
Koordinat
Graf
For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om skjæringspunkt i Treningsleiren.
d)
Bestem og
Hva forteller disse svarene om vekten til Geir?
Løsningsforslag d)
Jeg tenker
Vi kan finne brøkene ved å bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi regner ut brøkene ganske lett ved å skrive det følgene i «Skriv inn»-feltet i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
(G(12)-G(0))/12
(G(2)-G(0))/2Vi får at dette blir henholdsvis cirka og cirka .
Så skal vi tolke dette. Tallet er hvor mange kilogram Geir veide etter måneder, og er hvor mye han veide da han ble født. Derfor er hvor mye han økte i vekt i løpet av disse månedene. Dette regnet vi ut i b). Så dividerer vi tallet med . Det betyr at vi ser på gjennomsnittlig vektøkning per måned de første månedene, og den er på cirka . Det betyr at Geir la på seg i
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: og . Det betyr at Geir vokste i gjennomsnitt per måned de første månedene, og per måned de første månedene.
Mer om
Denne oppgaven er om Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Brøk

Funksjon
Graf
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artiklene Gjennomsnitt og Introduksjon til derivasjon - gjennomsnittlig og momentan vekstfart.
For å øve mer, se opogavesettet om veksthastighet i Treningsleiren.
Oppgave 3 (6 poeng) Nettkode: E-4CO9
Tabellen nedenfor viser hvor mange nye elbiler som ble solgt i Hordaland i 2010 og 2014.
| År | 2010 | 2014 |
| Antall nye elbiler | 26 | 2962 |
a)
La være antall år etter 2010. Bruk opplysningene i tabellen til å bestemme en eksponentiell modell for elbilsalget i Hordaland.
Løsningsforslag a)
Jeg tenker
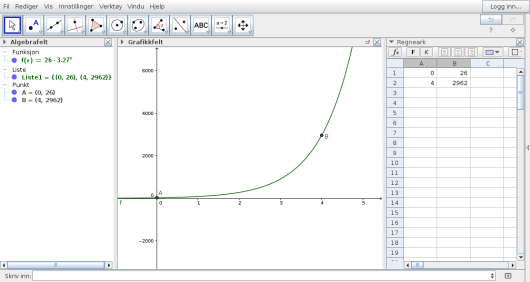
En eksponentiell modell for bilsalget er en eksponentialfunksjon som passer med dataene vi har. Vi kan lage denne modellen med
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi vil ha en funksjon slik at er antall elbiler solgt i året år etter . For eksempel skal være antall solgte elbiler i .
Først viser vi hvordan vi lager modellen med
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
regeksp[Liste1]i «Skriv inn»-feltet. Resultatet er en funksjon , som går gjennom de to punktene vi har. Dette er
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
Alternativ løsning
Vi kan også lage modellen ved hjelp av regning. La være antall solgte elbiler i året år etter . For eksempel er antallet solgte elbiler i , og antallet solgte elbiler i . For å finne funksjonen , må vi finne konstanten og vekstfaktoren . Vi vet allerede at , så . (Dette kan vi gjøre mer rigorøst ved å se at .)
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Det kunne vært hensiktsmessig å la være antall år etter i stedet for antall fireårsperioder. Siden av en fireårsperiode er år, er alt vi trenger å gjøre for å oppnå dette å erstatte med i ligningen over. Da får vi
Dette er det samme som vi fikk i GeoGebra.
Svar: Hvis er antall solgte biler i året år etter , så er .
Mer om
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Regresjon
Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Graf
For flere eksempler og forklaringer se artiklene Å lage en matematisk modell og Typer av funksjoner.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleiren.
b)
Hvor mange prosent steg elbilsalget per år i perioden fra 2010 til 2014 ifølge modellen fra oppgave a)?
Løsningsforslag b)
Jeg tenker
Vi kan brukte
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Vi har fra deloppgave a) at er antall solgte bilder i året år etter .
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Cirka hvert år
Mer om
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Prosent
Vekstfaktor
Eksponentialfunksjon

For flere eksempler og forklaringer se artikkelen Regneregler.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
c)
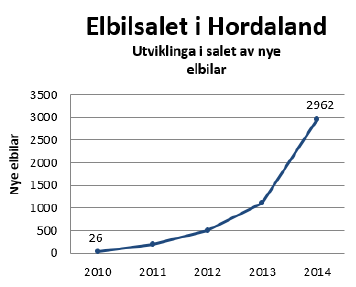
Diagrammet ovenfor viser utviklingen i salget av nye elbiler i Hordaland i perioden 2010–2014.
Gjør beregninger og vurder om modellen fra oppgave a) er en god modell for å beskrive denne utviklingen.
Løsningsforslag c)
Jeg tenker
Vi må sammenligne verdiene i modellen vår opp mot de faktiske verdiene i , og .
Nedenfor har vi markert salgsverdiene i de forskjellige årene i
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
(1, f(1))og så videre i «Skriv inn»-feltet.
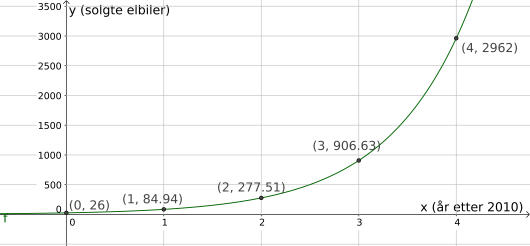
Se tolkningen av dette nedenfor.
Svar: Vi ser at modellen vår viser ganske lave salgstall for , og , men modellen beskriver selve utviklingen helt greit: Salget øker lite i begynnelsen, men mer og mer etter hvert som tiden går. En eksponentiell modell er nok fornuftig i perioden mellom og , men akkurat den modellen vi har valgt er ikke den beste; vi skulle helst ha gjort en regresjon med mer data. Etter er nok ikke modellen så god, da den forutser at det blir solgt rundt elbiler i .
Mer om
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Regresjon
Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Graf
For flere eksempler og forklaringer se artiklene Typer av funksjoner og Regresjon 1.
Oppgave 4 (4 poeng) Nettkode: E-4COE
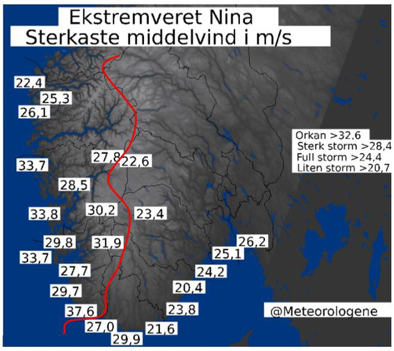
Figuren ovenfor viser sterkeste middelvind ulike steder i Sør-Norge under ekstremværet
«Nina» i januar 2015.
Vi lar den røde streken være skillet mellom Vestlandet og Sør-Østlandet.
a)
Bruk regneark til å bestemme gjennomsnitt og standardavvik for sterkeste middelvind på Vestlandet og sterkeste middelvind på Sør-Østlandet.
Løsningsforslag a)
Jeg tenker:
Først setter vi opp informasjonen på en oversiktlig måte i et regneark. Deretter kan vi regne ut
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Vi bruker Excel. Først setter vi opp tallene i en tabell. Vi må huske å skille på Vestlandet og Sør-Østlandet.
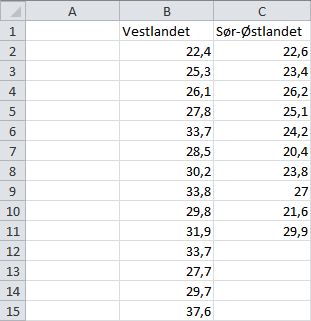
Her har vi gjort plass i A-søylen for å legge til
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Vi skal regne ut gjennomsnittet av hver av kolonnene i tabellen vår. Dette kan vi gjøre «manuelt» ved å legge sammen alle tallene og dividere på antallet, eller vi kan bruke gjennomsnitts-kommandoen i regnearket. Hvis vi vil regne ut gjennomsnittet manuelt, for eksempel for Vestlandet, skriver vi
=SUMMER(B2:B15)/14i en passende rute. Her summerer vi opp alle tallene i B-kolonnen fra og med rad til og med rad , og dividerer på antall rader vi har valgt. For Sør-Østlandet skulle vi ha skrevet
=SUMMER(C2:C11)/10Alternativt kunne vi skrevet
=GJENNOMSNITT(B2:B15)for Vestlandet og
=GJENNOMSNITT(C2:C11)for Sør-Østlandet. Videre skal vi finne standardavviket. Dette kan vi også gjøre manuelt, men det er såpass mer innviklet at vi velger å bruke innebygde funksjoner. For Vestlandet skriver vi
=STDAV.P(B2:B15)Vi bruker STDAV.P fordi vi vil regne ut standardavviket for hele datasettet. Hvis vi hadde brukt STDAV, ville vi fått estimerte verdier basert på utvalg. Sør-Østlandet er tilsvarende. Resultatet er vist under.
Svar:
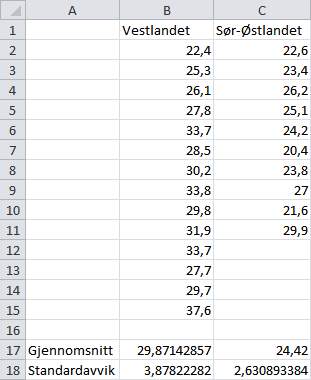
Mer om
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Tabell

Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Standardavvik
Statistikk
For flere eksempler og forklaringer se artikkelen Varians og standardavvik.
b)
Hva forteller svarene i oppgave a) om sterkeste middelvind på Vestlandet sammenliknet med sterkeste middelvind på Sør-Østlandet?
Løsningsforslag b)
Jeg tenker:
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
I deloppgave a) fant vi at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Svar: Vindstyrken var generelt sterkere og mer variert på Vestlandet.
Mer om:
Denne oppgaven er om Fart er tilbakelagt distanse per tidsenhet. Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund. Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s. Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Fart
Standardavvik
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleiren.
Oppgave 5 (4 poeng) Nettkode: E-4COJ

Tenk deg at du oppretter en BSU-konto 1. januar neste år og setter inn 25 000 kroner. Du setter inn 25 000 kroner 1. januar de neste sju årene også. Renten er 4,7 % per år.
a)
Lag et regneark som gir en oversikt over hvor mye du vil ha på kontoen ved slutten av hvert år disse åtte årene.
Løsningsforslag a)
Jeg tenker
Her skal vi regne ut
Rente
Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.
Se renteformel og rentefot
Det aller første vi gjør er å finne et måte å sette opp informasjonen vi har, slik at vi kan regne ut
Rente
Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.
Se renteformel og rentefot
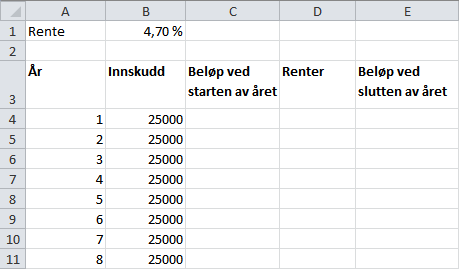
Det første året er representert i rad . Her setter vi inn kroner. Beløpet ved starten av det første året er dermed også , så vi skriver
=B4i rute C4. Renten er på , så for å finne renten det første året kan vi skrive
=C4*B1Her legger vi merke til at B1 er renten på . Vi skriver kommandoen over i ruten D4. Beløpet i slutten av året er summen av rentene og beløpet i starten av året, så vi skriver
=C4 + D4i rute E4. Det blir stående som renter og som beløp ved slutten av året.
Nå begynner vi på rad 5. Fra det første året hadde vi på kontoen, og vi setter inn igjen. Det betyr at vi har i starten av året (dette tallet er lik ). Derfor skriver vi
=E4 + B5i rute C5. Rentene dette året skal regnes ut i fra det beløpet vi hadde i begynnelsen av året, så rentene blir , helt tilsvarende som før. Totalbeløpet er summen av startbeløpet og rentene.
I de neste radene gjør vi det samme som vi gjørde i rad . I rute CN skal det stå
=E(N-1) + BNI rute DN skal det stå
=CN*B1og i rute EN skal det stå
=CN + DN(Her er N nummeret på raden vi er i.) Sluttresultatet er vist under.
Svar: 
Mer om
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Prosent
For flere eksempler og forklaringer se artiklene Regneregler og Banksparing over flere år.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
b)
Hvor mye vil du få til sammen i renter i løpet av disse åtte årene?
Løsningsforslag b)
Jeg tenker
Her kan vi legger vi sammen alle renteinntektene fra regnearket.
Vi utformet regnearket slik at vi så hvor mye
Rente
Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.
Se renteformel og rentefot
=SUMMER(D4:D11)i en passende rute i regnearket vårt.
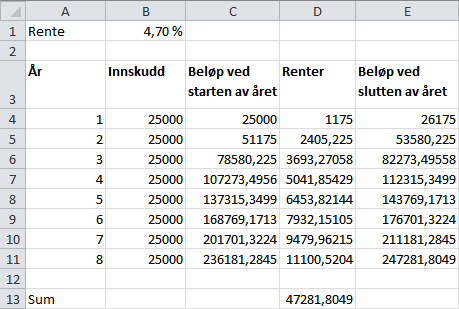
Her ser vi at vi fikk cirka i renter.
Hvis vi ikke hadde satt opp renteinntektene hvert år, kunne vi gjort følgende. Vi vet at vi sitter igjen med rundt i slutten av år 8. Vi hadde derimot kun satt inn i banken, og da må vi ha fått i renter.
Svar: Cirka
Mer om
Denne oppgaven er om regneark, Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefot Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Rente
Prosent
For flere eksempler og forklaringer se artikkelen Renter.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
Oppgave 6 (6 poeng) Nettkode: E-4COO
Tenk deg at du har lånt penger i banken og vil betale tilbake lånet med termin én gang i året.
Sett
- lånesummen lik L kroner
- renten lik p prosent per år, slik at vekstfaktoren blir
Dersom du betaler tilbake lånet i løpet av terminer, er terminbeløpet kroner gitt ved
Du tar opp et lån på 1 000 000 kroner med rente 3,5 % per år.
a)
Vis at terminbeløpet er gitt ved
Løsningsforslag a)
Jeg tenker
Vi har allerede fått oppgitt en
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Vi må sette inn tall for verdiene og i formelen
Tallet er lånebeløpet i kroner, så . Videre er renten på , så vekstfarten er dermed Vi setter inn dette i formelen . Da får vi Dette er nesten det vi ville ha. Vi regner ut at og da får vi akkurat som vi skulle ha.
Svar: Sett inn og i den oppgitte formelen.
Mer om
Denne oppgaven er om Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde. En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk. Eksempel: , er en formel for flateinnholdet av en sirkel med radius r. Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefotBrøk

Formel
Rente
For flere eksempler og forklaringer se artikkelen Renter.
b)
Bruk graftegner til å tegne grafen til for
Løsningsforslag b)
Jeg tenker
Dette kan vi gjøre i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi skal tegne
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
T = Funksjon[35000*1.035^x/(1.035^x-1), 1, 70]Vi må også huske å sette passende navn på
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Svar: 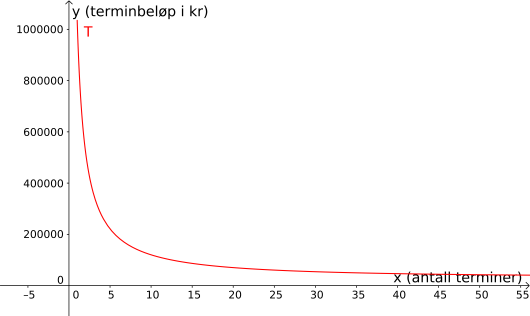
Mer om
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Eksponentialfunksjon

Graf
For flere eksempler og forklaringer se artikkelen Grafen til en funksjon.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
c)
Bestem terminbeløpet dersom du vil betale tilbake lånet i løpet av 20 terminer.
Løsningsforslag c)
Jeg tenker
Terminbeløpet vil være på kroner hvis vi vil betale i løpet av 20 terminer.
Vi må regne ut . Det kan vi ganske enkelt gjøre ved å skrive
T(20)i «Skriv inn»-feltet i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi kunne også regnet ut dette på kalkulator ved å regne ut Dette blir det samme som over.
Svar: Terminbeløpet er på .
Mer om
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Brøk

For flere eksempler og forklaringer se artikkelen Rask gjennomgang av regneregler for potens og røtter.
For å øve mer, se oppgavesettet om potensregning i Treningsleiren.
d)
Hvor lang tid vil det ta å betale tilbake lånet dersom du betaler 50 000 kroner hver termin?
Løsningsforslag d)
Jeg tenker
Vi vet at terminbeløpet i kroner, altså , er . Vi må finne en et antall terminer, , som gjør at . Dette kan vi gjøre i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi må finne en slik at Dette kan vi gjøre
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
y = 50000i «Skriv inn»-feltet i GeoGebra-filen fra deloppgave b). Den krysser grafen til i ett punkt; vi drar til aksene slik at vi ser krysningspunktet bedre. Vi klikker på punktet for å finne
Koordinat
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.
Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.
Se Koordinatsystem
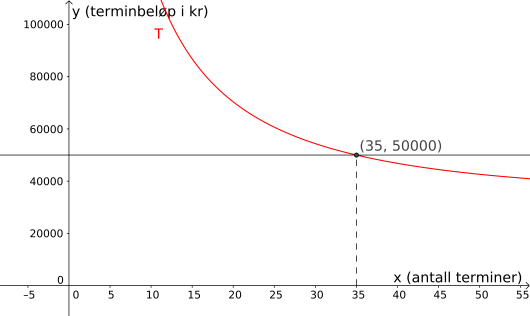
Det betyr at , altså at vi bruker terminer på å tilbakebetale hvis terminbeløpet er .
Svar: terminer.
Mer om
Denne oppgaven er om En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Ligning
Graf
Skjæringspunkt

Eksponentialfunksjon

For flere eksempler og forklaringer se artiklene Eksponentiallikninger og Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleiren.
Oppgave 7 (6 poeng) Nettkode: E-4CP8
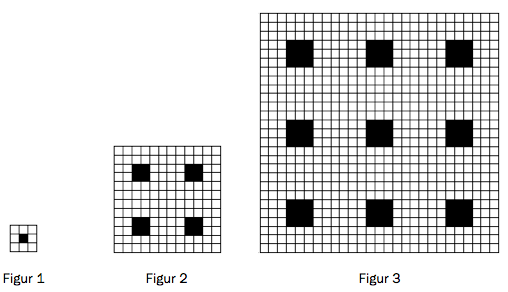
Ovenfor ser du de tre første figurene i en serie som kan fortsettes. De store kvadratene er sammensatt av hvite og svarte kvadrater. Hvert av de hvite kvadratene har areal lik 1. De svarte kvadratene har areal som øker i størrelse.
a)
Bestem det totale arealet av de svarte kvadratene i den neste figuren, figur 4.
Løsningsforslag a)
Jeg tenker
Her må vi finne ut av hvor mange svarte kvadrater det skal være i figur , og hvor store hver av dem er.
Før det første ser vi at hver av de svarte kvadratene øker med i sidelengde for hver figur. I figur , og er sidelengdene i kvadratene henholdsvis , og . Derfor må sidelengdene til de svarte kvadratene i figur ha som sidelengde. Arealet av hvert av de svarte kvadratene i den nye figuren er derfor .
Nå må vi finne ut hvor mange svarte kvadrater som skal være med i figur 4. I figur 1 er det svart kvadrat. I figur er det svarte kvadrater, og i figur er det svarte kvadrater. Derfor ser det ut til at det skal være svarte kvadrater i figur . Legg merke til at arealet til et kvadrat er det samme som antall svarte firkanter i den figuren.
Nå kan vi regne ut det totale arealet av de svarte kvadrater i figur . Figur har kvadrater med i areal, så det totale arealet blir .
Svar: Arealet er .
Mer om
Denne oppgaven er om Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En firkant der alle sider er like lange og alle vinkler 90°.Areal
Noen måleenheter for areal er m2, dm2 og cm2.Kvadrat
For flere eksempler og forklaringer se artikkelen Et kvadrat.
b)
Sett opp et uttrykk som viser det totale arealet av de svarte kvadratene i figur uttrykt ved .
Løsningsforslag b)
Jeg tenker
Her kan vi gjøre framgangsmåten i deloppgave a) mer generell.
Fra forrige oppgave vet vi at i figur , så er arealet av de svarte kvadratene lik , og det er slike kvadrater. Det totale arealet til disse kvadratene er . (For eksempel er det svarte kvadrater i figur , hver av dem med areal , så det totale arealet er .)
Svar: Det totale arealet av de svarte kvadratene i figur er .
Mer om
Denne oppgaven er om Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En firkant der alle sider er like lange og alle vinkler 90°. Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.Areal
Noen måleenheter for areal er m2, dm2 og cm2.Kvadrat

Andregradsuttrykk
For flere eksempler og forklaringer se artikkelen Johannes forteller deg om polynomfunksjoner.
c)
Antall hvite kvadrater i den nederste raden i hver figur kan uttrykkes med et andregradsuttrykk
Bestem
Løsningsforslag c)
Jeg tenker:
Her kan det lønne seg å se på figurene som sammensatt av kvadrater av samme størrelse som de svarte områdene i figurene.
Figur er satt sammen av totalt kvadrater av den minste typen, altså - kvadrater slik som det svarte kvadratet i midten.
Figur er satt sammen av - kvadrater stablet til et stort kvadrat. I nederste linje er det slike kvadrater, siden det er kvadrater for hvert av de nederste sorte kvadratene.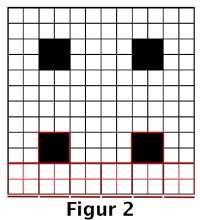
Figur er satt sammen av - kvadrater og det er slike i nederste linje siden det er hvite - kvadrater for hvert av de tre nederste sorte.

Figur n er satt sammen av - kvadrater. Det vil være sorte kvadrater i nest nederste linje, og for hver av dem er det hvite - kvadrater i nederste linje.
Totalt er det ganger (antall sorte kvadrater i nest nederste linje) ganger (antall små hvite kvadrater i nederste linje av hvert av -kvadratene) små hvite kvadrater i nederste linje av -te figur. Dette blir hvite kvadrater totalt.
Alternativ løsning
Vi teller figurene og ser at fordi det er små kvadrater i nederste rad på Figur 1. På tilsvarende måte finner vi ut av at . Dette betyr at punktene ligger på grafen til
Nå prøver vi regresjon i GeoGebra for å finne en andregradsfunksjon som har en graf som går gjennom de tre punktene. Vi vet at hvis vi har to punkter i koordinatsystemet, så går det nøyaktig én linje gjennom dem. På tilsvarende vis er det slik at dersom punkter i koordinatsystemet har forskjellige - koordinater, så finnes det nøyaktig én andregradsfunksjon som har alle tre punktene på sin graf.
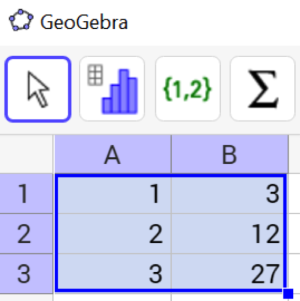
Vi legger inn punktene i regnearket i GeoGebra:
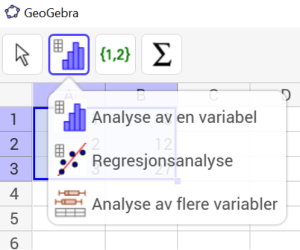
Deretter klikker vi på ikonen i verktøylinjen og velger Regresjonsanalyse:
I neste vindu velger vi regresjonsmodellen polynom av grad :
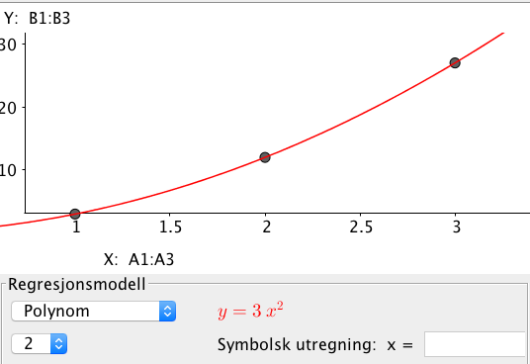
Modellen kommer opp i rød skrift og er altså . Med våre navn på variablene blir dette .
Svar: .
Mer om:
Denne oppgaven er om En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En firkant der alle sider er like lange og alle vinkler 90°. Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.Linje
Kvadrat

Andregradsuttrykk
For flere eksempler og forklaringer se artikkelen Andregradsfunksjoner.
d)
Sett opp et uttrykk for det totale arealet av de hvite kvadratene i figur uttrykt ved .
Løsningsforslag d)
Jeg tenker:
Antallet hvite kvadrater i en figur, er arealet av hele figuren, bortsett fra arealet til de svarte kvadratene.
Vi har atHver figur er et kvadrat, og sidelengden i kvadratet er . Derfor er arealet av hver figur lik . Videre skal vi trekke fra arealet til de svarte kvadratene, som vi fra b) vet at er . Dermed har vi
Svar: Antall hvite kvadrater i figur er , dette blir også det totale arealet av de hvite kvadratene.
Mer om:
Denne oppgaven er om Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En firkant der alle sider er like lange og alle vinkler 90°.Areal
Noen måleenheter for areal er m2, dm2 og cm2.Kvadrat





