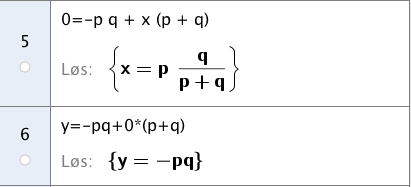Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2016 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler på Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Hjelpemidler på Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Om oppgaven krever en bestemt løsningsmetode, vil en alternativ metode kunne gi lav/ingen uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er kreativ og kan anvende fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4QCV
Løs likningssystemet
Oppgave 2 (2 poeng) Nettkode: E-4QCX
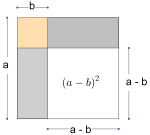
Skriv så enkelt som mulig
Oppgave 3 (2 poeng) Nettkode: E-4QCZ
Løs ulikheten
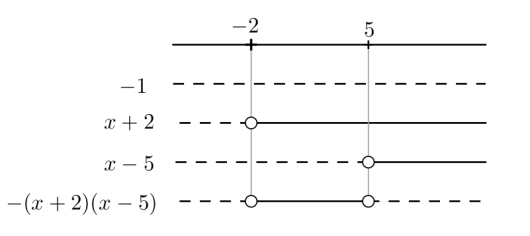
Oppgave 4 (2 poeng) Nettkode: E-4QD1
Løs likningen
Oppgave 5 (1 poeng) Nettkode: E-4QD3
Løs likningen
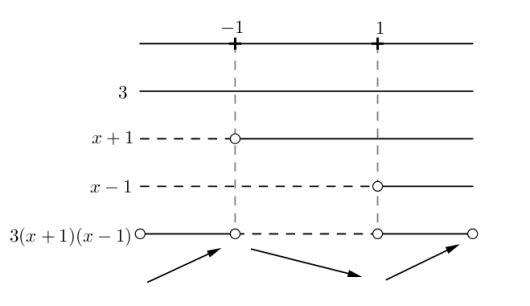
Oppgave 6 (2 poeng) Nettkode: E-4QD5
Skriv så enkelt som mulig
Oppgave 7 (2 poeng) Nettkode: E-4QD7
Skriv så enkelt som mulig
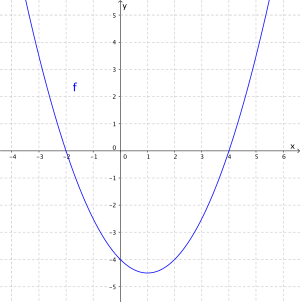
Oppgave 8 (2 poeng) Nettkode: E-4QD9
I koordinatsystemet ovenfor har vi tegnet grafen til en andregradsfunksjon . Bestem funksjonsuttrykket .
Oppgave 9 (8 poeng) Nettkode: E-4QDB
Funksjonen er gitt ved
a)
Bestem nullpunktene til .
b)
Vis at
c)
Bestem og bruk den deriverte til å bestemme eventuelle topp- og bunnpunkt på grafen til .
d)
Bestem likningen for tangenten til i punktet .
e)
Vis at grafen til ikke har andre tangenter som er parallelle med tangenten du fant i oppgave d).
Oppgave 10 (2 poeng) Nettkode: E-4QDH
En likesidet trekant har omkrets .
Vis at arealet av trekanten er .
Oppgave 11 (1 poeng) Nettkode: E-4QDP
Om en vinkel får du vite:
-
-
Bestem .
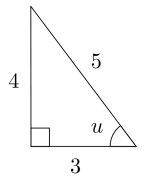
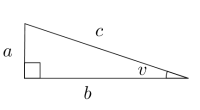
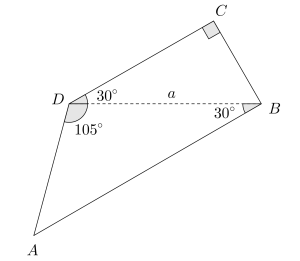
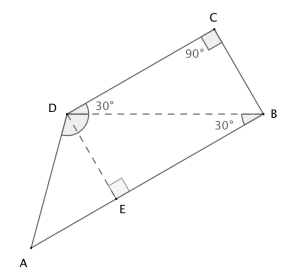
Oppgave 12 (3 poeng) Nettkode: E-4QDX
a)
Gitt trekanten ovenfor.
Vis at
b)
Bruk trekanten ovenfor til å vise at for alle
Oppgave 13 (3 poeng) Nettkode: E-4QE0
I en eske er det fire blå og fire røde nisser. Tenk deg at du skal ta tre nisser tilfeldig fra eksen. Du skal ta én nisse om gangen, og du skal sette dem på en rekke fra venstre mot høyre.
a)
Bestem sannsynligheten for at rekken vil bli som vist på bildet nedenfor.
b)
Bestem sannsynligheten for at det vil bli én blå og to røde nisser i rekken.
c)
Bestem sannsynligheten for at det vil bli minst én blå nisse i rekken.
Oppgave 14 (4 poeng) Nettkode: E-4QE4
Sirkelbuene på figuren ovenfor er halvsirkler. Linjestykket har lengden , og linjestykket har lengden .
a)
Bestem omkretsen av det blå området på figuren uttrykt ved .
b)
Bestem arealet av det blå området på figuren uttrykt ved .
DEL 2 Med hjelpemidler
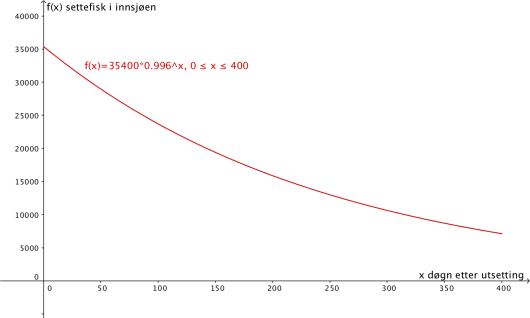
Oppgave 1 (5 poeng) Nettkode: E-4QEC
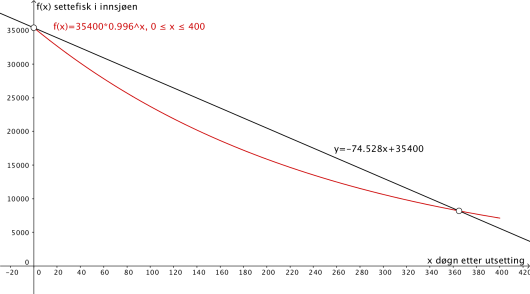
En jakt- og fiskeforening vil sette ut fisk i en innsjø. Fisk som blir satt ut, kaller vi settefisk. Foreningen går ut fra at funksjonen er gitt ved
viser hvor mange settefisk det vil være igjen i innsjøen døgn etter utsettingen.
a)
Bruk graftegner til å tegne grafen til .
b)
Hva forteller tallene og i funksjonsutrykket om antall settefisk i innsjøen?
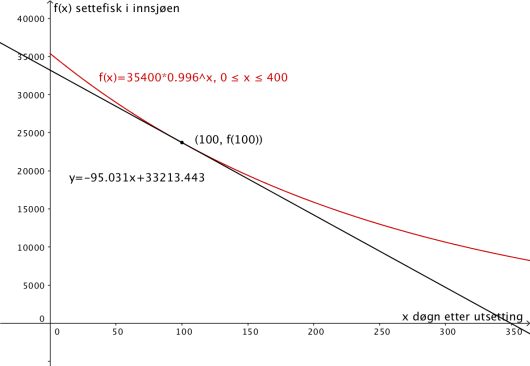
c)
Bestem ved å tegne en tangent til grafen i .
Hva forteller denne verdien om antall settefisk i innsjøen?
d)
Bestem gjennomsnittlig vekstfart for antall settefisk det første året etter utsettingen.
Oppgave 2 (4 poeng) Nettkode: E-4QEJ
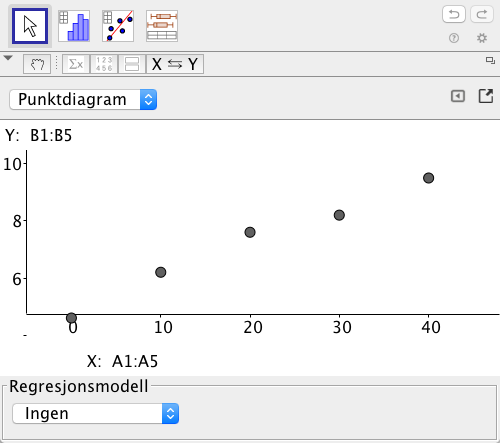
| År | |||||
|
Kilogram sjokolade per person |
Tabellen ovenfor viser hvor mange kilogram sjokolade hver person i Norge i gjennomsnitt spiste i årene .
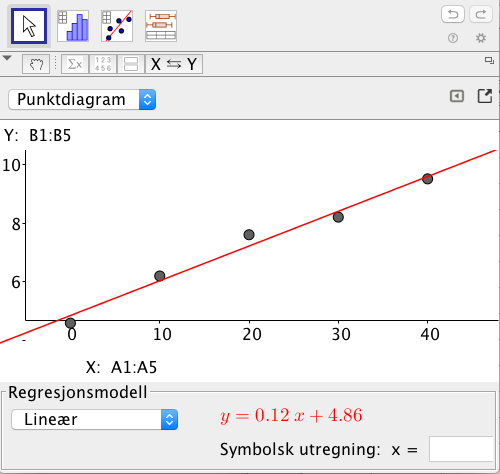
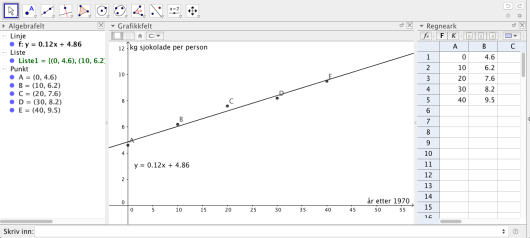
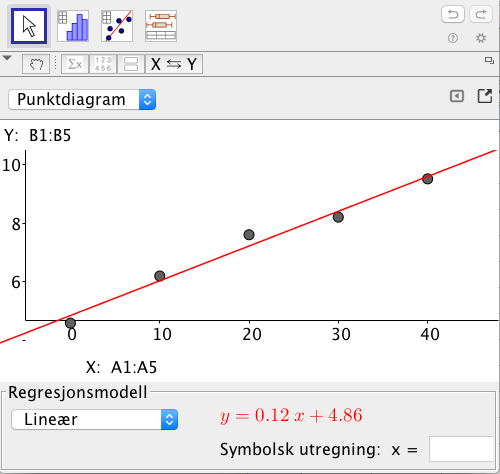
a)
La være antall år etter , og bruk regresjon til å bestemme en lineær funksjon som kan beskrive utviklingen i perioden .
b)
Hva forteller stigningstallet til funksjonen ?
c)
Hvor mange gram sjokolade vil hver person i Norge i gjennomsnitt spise i ifølge funksjonen ?
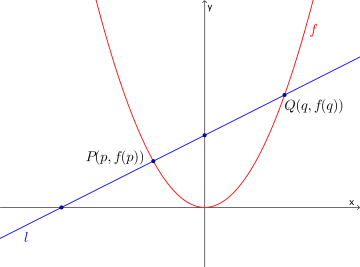
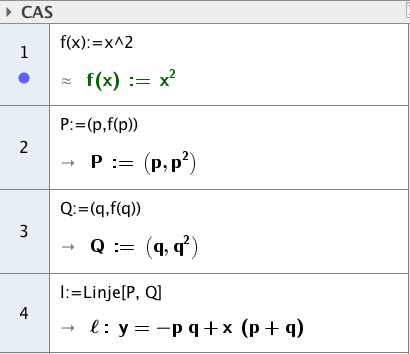
Oppgave 3 (4 poeng) Nettkode: E-4QEN
Funksjonen er gitt ved
Linja skjærer grafen til i punktene .
Se koordinatsystemet.
a)
Vis at linja har stigningstall .
b)
Bruk CAS til å bestemme skjæringspunktene mellom linja og koordinataksene.
Oppgave 4 (4 poeng) Nettkode: E-4QEQ
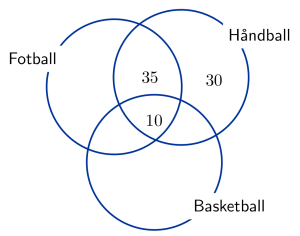
En idrettsklubb har tre aktiviteter: fotball, håndball og basketball. Noen av medlemmene deltar i én aktivitet, noen i to aktiviteter og noen i alle tre aktivitetene. Idrettsklubben har totalt medlemmer.
Tabellen nedenfor viser hvor mange medlemmer som deltar i hver aktivitet.
| Aktivitet | Medlemmer |
| Fotball | |
| Håndball | |
| Basketball |
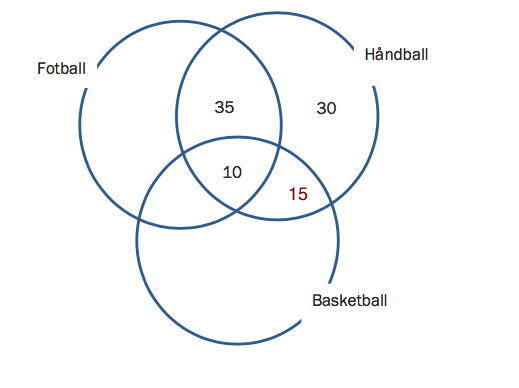
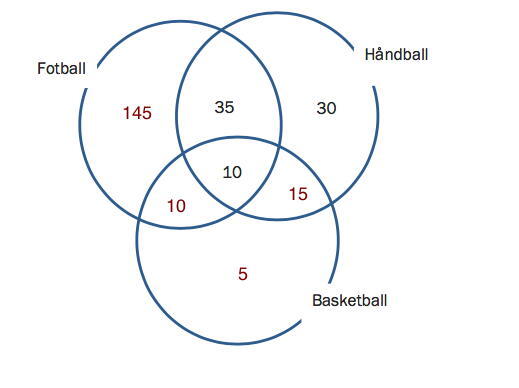
a)
Tegn et venndiagram som vist nedenfor. Gjør beregninger, og sett inn tallene som mangler.
b)
Vi skal velge et medlem tilfeldig fra klubben.
Bestem sannsynligheten for at vi kommer til å velge et medlem som deltar i alle tre aktivitetene.
c)
Tenk deg at vi har valgt et medlem som spiller håndball.
Bestem sannsynligheten for at dette medlemmet også spiller fotball.
Oppgave 5 (3 poeng) Nettkode: E-4QEU
En funksjon er gitt ved
Bruk CAS til å vise at grafen til har et terrassepunkt.
Bestem koordinatene til terrassepunktet uttrykt ved .
Oppgave 6 (4 poeng) Nettkode: E-4QEW
Gitt ovenfor.
a)
Vis at
b)
Vis at arealet av er