Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1013 2013 Høst

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:

Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Hjelpemidler på Del 2:

Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Du skal svare på alle oppgavene.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger:

Kilder for bilder, tegninger osv.

Fisk (www.freeimages.com , 5.07.2016)
Tegninger, grafer og figurer: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4B6H

Regn ut og skriv svaret på standardform

$7, 5 \cdot 10^{12} \cdot 4, 0 \cdot 10^{- 4}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi har to tall på

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

standardform

. Rekkefølgen til faktorene spiller ingen rolle når vi multipliserer, så vi kan først multiplisere desimaltallene og deretter bruke potensreglene.

Når vi skal multipliserer spiller ikke faktorenes rekkefølge noen rolle, så vi kan begynne med å multiplisere desimaltallene:

$7, 5 \cdot 10^{12} \cdot 4, 0 \cdot 10^{- 4} = 7, 5 \cdot 4, 0 \cdot 10^{12} \cdot 10^{- 4} = 30 \cdot 10^{12} \cdot 10^{- 4}$ .

Fra potensreglene vet vi at for å multipliserer potensene med grunntall $10$ kan vi addere eksponentene.

Da får vi

$30 \cdot 10^{12 + (- 4)} = 30 \cdot 10^{8}$

Men dette er ikke på standardform, fordi $30$ ikke er i intervallet $[1, 10)$ . Vi skriver derfor $30 = 3 \cdot 10$ og får at

$30 \cdot 10^{8} = 3 \cdot 10 \cdot 10^{8} = 3, 0 \cdot 10^{9}$

som er på standardform.

Svar: $3, 0 \cdot 10^{9}$

Mer om

Denne oppgaven er om

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

standardform

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$

potenser

Flere forklaringer og eksempler på hvordan man finner tall på standardform finner du i artikkelen Tall på standardform.

For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.

Oppgave 2 (4 poeng) Nettkode: E-4B6K

Siv har fire blå og seks svarte bukser i skapet. Én av de blå og tre av de svarte buksene passer ikke lenger.

a)

Tegn av tabellen nedenfor, og fyll inn tall i de hvite rutene.

	Blå bukser	Svarte bukser	Sum
Bukser som passer
Bukser som ikke passer
Sum

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må fylle inn rutene med tall som passer både kolonnen og raden som ruten er i. I oppgaveteksten finner vi antall blå bukser som ikke passer. For eksempel skal vi i den øverste ruten til venstre skrive antall blå bukser (fordi vi er i "Blå bukser-kolonnen) som passer (fordi vi er i "Bukser som passer"-raden).

Vi begynner med å skrive av tabellen som gitt i oppgaven.

	Blå bukser	Svarte bukser	Sum
Bukser som passer
Bukser som ikke passer
Sum

Vi kan begynne med å fylle inn informasjonen vi har fått direkte fra oppgaveteksten. For det første får vi vite at Siv har $4$ blå bukser og $6$ svarte. Dette kan vi skrive inn i nederste rad.

	Blå bukser	Svarte bukser	Sum
Bukser som passer
Bukser som ikke passer
Sum	4	6

Videre får vi vite at $1$ blå bukse og $3$ svarte bukser ikke passer. Dette kan vi skrive inn "Bukser som ikke passer"-raden.

	Blå bukser	Svarte bukser	Sum
Bukser som passer
Bukser som ikke passer	1	3
Sum	4	6

For å finne antallet blå bukser som passer, kan vi trekke antallet blå bukser som ikke passer fra det totale antallet blå bukser. Det gir $4 - 1 = 3$ , så det er $3$ blå bukser som passer. På samme måte må det være $6 - 3 = 3$ svarte bukser som passer. Nå ser tabellen slik ut:

	Blå bukser	Svarte bukser	Sum
Bukser som passer	3	3
Bukser som ikke passer	1	3
Sum	4	6

Nå må vi fylle ut den siste kolonnen i tabellen, Sum. I en rute i denne kolonnen skriver vi summen av de to andre tallene i den samme raden.

Totalt antall bukser som passer er $3 + 3 = 6$ og totalt antall bukser som ikke passer er $3 + 1 = 4$ .

I den siste ruten – som er det totale antallet bukser – må vi på samme måte skrive $4 + 6 = 10$ .

Svar:

	Blå bukser	Svarte bukser	Sum
Bukser som passer	3	3	6
Bukser som ikke passer	1	3	4
Sum	4	6	10

Mer om

Denne oppgaven er om

Tabell

Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.

Eksempel: rutetabell for buss, resultatliste for skirenn

tabeller

For flere forklaringer og eksempler se artikelene Data, populasjon og utvalg.

b)

Siv tar tilfeldig én bukse fra skapet.

Bestem sannsynligheten for at buksen passer.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi bruker krysstabellen vår. Sannsynlighet vil være antall

Gunstig utfall

Et gunstig utfall er den hendelsen som er interessant for oss.

Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.

Se Hendelse

gunstige utfall

dividert med antall mulige utfall.

Siv velger en tilfeldig bukse, så sannsynligheten for å trekke en gitt bukse er like stor uansett hvilken bukse det er snakk om. Da er sannsynligheten lik

$\frac{antall gunstige utfall}{antall mulige utfall}$ .

Fra krysstabellen vet vi at Siv har ti bukser, hvorav seks passer, altså har vi ti mulige og seks gunstige utfall. Da er sannsynligheten for å buksen passer

$\frac{antall gunstige}{antall mulige} = \frac{6}{10} = \frac{3}{5}$ .

Svar: Sannsynligheten for at buksen passer er $\frac{3}{5}$ .

Mer om

Denne oppgaven er om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

Gunstig utfall

Et gunstig utfall er den hendelsen som er interessant for oss.

Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.

Se Hendelse

gunstig utfall

For flere forklaringer og eksempler se artikkelen Repetisjon av begreper i lynkurset Sannsynlighet (del II).

c)

Siv har tatt en bukse som passer.

Bestem sannsynligheten for at denne buksen er blå.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må igjen finne

Sannsynlighet

sannsynligheten

ved å finne antall

Gunstig utfall

Et gunstig utfall er den hendelsen som er interessant for oss.

Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.

Se Hendelse

gunstige utfall

(antall blå bukser) og antall mulige utfall (antall bukser som passer).

Vi vet at det er seks bukser som passer, så Siv må ha trukket en av dem. Blant de seks er det tre som er blå. Det betyr at det er seks mulige utfall hvorav tre av dem er gunstige. Da har vi:

$P (blå bukse|buksen passer) = \frac{antall gunstige}{antall mulige} = \frac{3}{6} = \frac{1}{2}$ .

Svar: Sannsynligheten for at det er en blå bukse er $\frac{1}{2}$ .

Mer om

Denne oppgaven er om

Sannsynlighet

sannsynlighet

Flere forklaringer på hvordan man finner sannsynligheten finner du i artikkelen Hvordan finner vi uniform sannsynlighet? og Betinget sannsynlighet i lynkurset Sannsynlighet (del II).

Oppgave 3 (2 poeng) Nettkode: E-4B6O

Skriv så enkelt som mulig

$\frac{2 x^{2} - 18}{x^{2} + 6 x + 9}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi har en brøk med andregradsuttrykk i teller og nevner. For å forkorte en brøk må vi ha samme faktor i

Teller

Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.

Eksempel: I brøken $\frac{5}{9}$ , er det 5 som er telleren. 9 kalles nevner.

telleren

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

nevneren

så vi kan faktorisere teller og nevner og se om de har felles faktorer.

Først faktoriserer vi telleren og nevneren hver for seg for å se om de har noen felles faktorer.

Vi begynner med å faktorisere telleren, da kan vi begynne med å faktorisere

$2 x^{2} - 18 = 2 (x^{2} - 9)$ .

For den andre faktoren i telleren ser det ut til at vi kan bruke

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetningen

. Vi har at

$2 (x^{2} - 9) = 2 (x^{2} - 3^{2}) = 2 (x + 3) (x - 3)$ .

Nevneren kan vi faktorisere ved å bruke

Første kvadratsetning

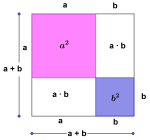
Første kvadratsetning sier at

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .

første kvadratsetning

, som sier

$(x + a)^{2} = (x + a) (x + a) = x^{2} + 2 a x + a^{2}$ .

Hvis vi setter $a = 3$ her, får vi $(x + 3)^{2} = x^{2} + 6 x + 9$ , som er nevneren.

Vi kan skrive brøken som

$\frac{2 x^{2} - 18}{x^{2} + 6 x + 9} = \frac{2 (x + 3) (x - 3)}{(x + 3)^{2}}$

Her ser vi at vi har en felles faktor $(x + 3)$ . Vi forkorter brøken med denne, altså dividerer med den telleren og nevneren.

$\frac{2 x^{2} - 18}{x^{2} + 6 x + 9} = \frac{2 (x + 3) (x - 3)}{(x + 3)^{2}} = \frac{2 (x + 3) (x - 3)}{(x + 3) (x + 3)} = \frac{2 (x - 3)}{(x + 3)}$ .

Alternativ løsning

Både teller og nevner er

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

. Vi kan faktorisere disse ved å bruke

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

som sier at likningen

a x^{2} + b x + c = 0

har løsningene

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

Telleren faktoriserer vi ved å løse likningen $2 x^{2} - 18 = 0$ der $a = 2$ , $b = 0$ , $c = - 18$ . Løsningene er da

$x = \frac{- 0 \pm \sqrt{0^{2} - 4 \cdot 2 \cdot (- 18)}}{2 \cdot 2} = \pm \frac{\sqrt{144}}{4} = \pm \frac{12}{4} = \pm 3$ .

Telleren kan vi da skrive som $2 x^{2} - 18 = 2 (x - 3) (x + 3)$ .

Vi faktoriserer nevneren ved å løse likningen $x^{2} + 6 x + 9 = 0$ der er $a = 1$ , $b = 6$ , og $c = 9$ . Løsningene er

$x = \frac{- 6 \pm \sqrt{6^{2} - 4 \cdot 1 \cdot 9}}{2 \cdot 1} = \frac{- 6 \pm \sqrt{0}}{2} = - 3$ .

Da kan vi skrive nevneren som $x^{2} + 6 x + 9 = (x + 3)^{2}$ .

Vi kan skrive brøken som

$\frac{2 x^{2} - 18}{x^{2} + 6 x + 9} = \frac{2 (x + 3) (x - 3)}{(x + 3)^{2}}$

Felles faktoren er $x + 3$ . Vi forkorter brøken ved å dividere telleren og nevneren med den felles faktoren.

$\frac{2 x^{2} - 18}{x^{2} + 6 x + 9} = \frac{2 (x + 3) (x - 3)}{(x + 3)^{2}} = \frac{2 (x + 3) (x - 3)}{(x + 3) (x + 3)} = \frac{2 (x - 3)}{(x + 3)}$

Svar: $\frac{2 (x - 3)}{x + 3}$

Mer om

Denne oppgaven er om

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

Første kvadratsetning

Første kvadratsetning sier at

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .

første kvadratsetning

Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:

$(a + b) (a - b) = a^{2} - b^{2}$ .

konjugatsetningen

For flere eksempler og forklaringer se artikkelen Paranteser og Faktorisering, abc-formelen og videoen Hvordan bruke kvadratsetningene?.

For å øve mer, se oppgavesettet om faktorisering i Treningsleiren.

Oppgave 4 (2 poeng) Nettkode: E-4B6Q

Regn ut og skriv svaret så enkelt som mulig

$\frac{\sqrt{2} \cdot 2^{0} \cdot 2^{- 1}}{8^{\frac{1}{2}} \cdot 2^{- 2}}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Her er det best å forenkle telleren og nevneren hver for seg først. Vi får bruk for

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$
potens

reglene. Vi prøver å skrive alle faktorer som toerpotenser.

Vi vil forenkle uttrykket mest mulig, og begynner med å se på teller og nevner for seg. Vi kan bruke potensreglene.

Vi begynner med å se på telleren

$\sqrt{2} \cdot 2^{0} \cdot 2^{- 1}$ .

Vi vil bruke potensregler for å skrive denne enklest mulig.

Da kan vi bruke potensregelene som gir at

$\sqrt{a} = a^{\frac{1}{2}}$ for positive tall $a$ og at $a^{0} = 1$ .

Dette gir oss at $\sqrt{2} = 2^{\frac{1}{2}}$ og $2^{0} = 1$ .

Når vi skal multiplisere potenser med samme grunntall, kan vi addere eksponentene.

Da kan vi skrive telleren som

$\sqrt{2} \cdot 2^{0} \cdot 2^{- 1} = 2^{\frac{1}{2}} \cdot 1 \cdot 2^{- 1} = 2^{\frac{1}{2} + (- 1)} = 2^{- \frac{1}{2}}$ .

Videre ser vi på nevneren

$8^{\frac{1}{2}} \cdot 2^{- 2}$ .

Vi kan skrive $8 = 2 \cdot 2 \cdot 2 = 2^{3}$ og kan bruke at ${(a^{m})}^{n} = a^{m \cdot n}$ som gir at $8^{\frac{1}{2}} {= (2^{3})}^{\frac{1}{2}} = 2^{\frac{3}{2}}$ .

Da får vi at nevneren kan skrives som

$8^{\frac{1}{2}} \cdot 2^{- 2} = 2^{\frac{3}{2}} \cdot 2^{- 2} = 2^{\frac{3}{2} - 2} = 2^{- \frac{1}{2}}$ .

Vi har nå forenklet uttrykket til

$\frac{2^{- \frac{1}{2}}}{2^{- \frac{1}{2}}} = 1$ .

Svar: $1$

Mer om

Denne oppgaven er om potenser.

For flere eksempler og forklaringer se artikkelen Rask gjennomgang av regneregler med potenser og røtter i lynkurset Potenser og røtter.

For å øve mer, se oppgavesettet om potenser i Treningsleiren.

Oppgave 5 (2 poeng) Nettkode: E-4B6S

Løs likningen

$2 \log (x) - 8 = 5 \log (x) + 1$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi har en likning med

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer

. og vi husker at

10^{\log x} = x

Vi begynner med å samle alle leddene med logaritmer på én side av likningen:

$\begin{matrix} 2 \log (x) - 8 & = & 5 \log (x) + 1 \\ 2 \log (x) - 5 \log (x) & = & 1 + 8 \\ - 3 \log (x) & = & 9 \\ \log (x) & = & - 3 \end{matrix}$

Hvis $a = b$ , så er $10^{a} = 10^{b}$ , og vi kan skrive om likningen til

$10^{\log (x)} = 10^{- 3}$ .

Vi vet at $10^{\log (x)} = x$ , og da er

$x = 10^{- 3}$

$x = \frac{1}{1000} = 0, 001$ .

Svar: $x = 10^{- 3} = 0, 001$

Mer om

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritmer

For flere eksempler og forklaringer om logaritmelikninger, se artikkelen Logaritmelikninger. Flere forklaringer og eksempler på logaritmeregning finner du i lynkurset Logaritmer.

Oppgave 6 (2 poeng) Nettkode: E-4B6U

En rett linje går gjennom punktene $(1, 2)$ og $(3, 5)$ .

Bestem likningen for linjen.

Løs oppgaven her

Løsningsforslag

Jeg tenker

En rett linje kan skrives som $y = a x + b$ . Ved hjelp av de gitte punktene finner vi

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstallet

a

Konstant

En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.

Eksempel: $A = π r^{2}$ , $π$ er en konstant og $r$ er en variabel.

Se Variabel

konstantleddet

b

I likningen for en linje, $y = a x + b$ er $a$ stigningstallet. Den må være lik $\frac{endring i y - retning}{endring i x - retning}$ . Dette kan vi se ved å sette inn koordinatene til to punkter $(x_{1}, y_{1})$ og $(x_{2}, y_{2})$ på linja i likningen $y = a x + b$ . Denne likningen må oppfylles av begge punktene. Det gir oss:

$\begin{matrix} y_{1} = & a x_{1} + b & (1) \\ y_{2} = & a x_{2} + b & (2) \end{matrix}$

Trekker vi nå likning (2) fra likning (1), får vi:

$\begin{matrix} y_{1} - y_{2} & = & a x_{1} - a x_{1} + b - b \\ y_{1} - y_{2} & = & a (x_{1} - x_{2}) \\ a & = & \frac{y_{1} - y_{2}}{x_{1} - x_{2}} \end{matrix}$

Linjen vi skal finne likningen til, går gjennom punktene $(1, 2)$ og $(3, 5)$ . Dette gir at stigningstallet er

$a = \frac{5 - 2}{3 - 1} = \frac{3}{2}$ .

Nå kan vi finne $b$ ved å sette inn $a = \frac{3}{2}$ og koordinatene til et av punktene i likningen til linja. Vi velger å sette inn for punktet $(1, 2)$ , der $x = 1 og y = 2$ , og får

$2 = \frac{3}{2} \cdot 1 + b$

$b = \frac{1}{2}$ .

Da har vi både funnet stigningstallet og konstantleddet til linja, og kan sette opp likningen til linja gjennom de to punktene.

Svar: $y = \frac{3}{2} x + \frac{1}{2}$

Alternativ løsning

Linjen går gjennom punktene $x = 1, y = 2$ og $x = 3, y = 5$ . Vi setter inn disse verdiene i uttrykket for linjen:

$x = 1 og y = 2$ gir $2 = a \cdot 1 + b$ .

$x = 3 og y = 5$ gir $5 = a \cdot 3 + b$ .

Nå har vi et likningssett med to ukjente:

$\begin{matrix} (I) & a + b = 2 \end{matrix}$

$\begin{matrix} (II) & 3 a + b = 5 \end{matrix}$

Vi løser likningssettet med substitusjon. Likning (I) gir oss $b = 2 - a$ . Vi setter inn $b = 2 - a$ i likning (II).

$\begin{matrix} 3 a + (2 - a) = 5 \end{matrix}$

$2 a = 3$

$a = \frac{3}{2}$

Vi setter inn $a = \frac{3}{2}$ i likning (I) for å finne $b$ . Vi får det samme svaret om vi bruker likning (II) og det må du gjerne sjekke selv.

$b = 2 - a = 2 - \frac{3}{2}$
$b = \frac{1}{2}$

Vi setter inn for $a og b$ i likningen for linjen $y = a x + b = \frac{3}{2} x + \frac{1}{2}$ .

Mer om

Denne oppgaven er om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystemer

For flere eksempler og forklaringer se Rette linjer (lineære funksjoner). Flere eksempler på hvordan man løser et sett med likninger finner du i lynkurset Lineære likninger med flere ukjente, og forklaringer på funksjonsuttrykk finner du i lynkurset Funksjoner (del II).

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.

Oppgave 7 (2 poeng) Nettkode: E-4B6W

Løs likningssystemet

$[\begin{matrix} - x + y = 2 \\ - 2 x^{2} + y^{2} = 4 \end{matrix}]$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ser et likningssystem med to likninger med to ukjente, $x$ og $y$ . Likningene er av ulik grad og vi kan derfor kun bruke substitusjonsmetoden. Andregradslikningen kan også ha to løsninger for hver av de to ukjente.

For lettere å holde orden på likningene, nummererer vi disse:

$\begin{matrix} - x + y & = 2 & (1) \\ - 2 x^{2} + y^{2} & = 4 & (2) \end{matrix}$

Fordi likning (2) er en andregradslikning, er ikke addisjonsmetoden aktuell å bruke. Vi bruker substitusjons- eller innsettingsmetoden.

Vi bruker (1) til å uttrykke $y$ avhengig av $x$ :

$\begin{matrix} - x + y & = 2 \\ y & = 2 + x \end{matrix}$

Nå substituerer vi for $y = 2 + x$ for i (2):

$\begin{matrix} - 2 x^{2} + y^{2} & = 4 \\ - 2 x^{2} + (2 + x)^{2} & = 4 \\ - 2 x^{2} + 2^{2} + 2 \cdot 2 x + x^{2} & = 4 \\ - 2 x^{2} + 4 + 4 x + x^{2} & = 4 \\ 4 x - x^{2} & = 0 \end{matrix}$

Vi har en andregradslikning med én ukjent, $x$ . Vi kan løse likningen med

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

abc-formelen

, men i dette tilfellet kan det gjøres enklere. Begge leddene på høyresiden har en faktor

x

, som vi kan faktorisere utenfor en parentes. Dette gir

$4 x - x^{2} = x (4 - x) = 0$ .

For at et produkt $a b$ skal være $0$ , må vi ha $a = 0$ eller $b = 0$ (eller begge deler). Da må vi ha enten $x = 0$ eller $4 - x = 0$ . Dette gir enten $x = 0 eller x = 4 .$ Nå vil vi finne tilsvarende $y$ slik at likningene er tilfredsstilt.

Vi setter $x = 0$ i likning $(1)$ :

$- 0 + y = 2$

$y = 2$

(Du kan sjekke selv at $x = 0$ i likning $(2)$ gir samme svar.)

Vi setter så inn for $x = 4$ i likning (1):

$- 4 + y = 2$

$y = 6$

(Du kan selv sjekke at $x = 4$ i likning $(2)$ gir samme svar.)

Likningssystemet har to løsninger:

$x = 0$ og $y = 2$

$x = 4$ og $y = 6$ .

Svar: Likningssettet har to løsninger, $x = 0, y = 2$ og $x = 4, y = 6$

Mer om

Denne oppgaven er om

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystemer

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikninger

Flere forklaringer og eksempler se artiklene Substitusjonsmetoden og Likningssystemer.

Visste du at?

Disse to likningene beskriver to kurver i planet ved at et punkt $(x_{0}, y_{0})$ ligger på kurven hvis $x_{0}, y_{0}$ oppfyller likningen. De kan for eksempel tegnes med GeoGebra. Det vi har gjort nå, er å finne ut hvor de to kurvene har skjæringspunkter. En kurve beskrevet av en $n$ -tegradslikning kalles en $n$ -tegradskurve, så dette er en førstegradskurve (eller en linje) og en andregradskurve (også kalt et kjeglesnitt). De har to skjæringspunkter, og man kan lure på om det er noen sammenheng mellom antall skjæringspunkter og gradene til kurvene. Det er det – en $n$ -tegradskurve og en $m$ -tegradskurve kan ikke ha flere enn $n \cdot m$ skjæringspunkter.

Oppgave 8 (6 poeng) Nettkode: E-4B6Y

Funksjonen $f$ er gitt ved

$f (x) = x^{3} - 3 x^{2}, D_{f} = ℝ$

a)

Bestem koordinatene til eventuelle ekstremalpunkter (topp- og bunnpunkter) på grafen til $f$ ved regning.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi finner

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunktene

ved å

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivere

f

og finne

x

-verdiene der

f' (x) = 0

Vi begynner med å derivere funksjonen, og siden $f$ er et flerleddet uttrykk, kan vi derivere ledd for ledd. Da får vi at

$f' (x) = (x^{3} - 3 x^{2})' = (x^{3})' - ({3 x}^{2})' = 3 x^{2} - 3 \cdot 2 x = 3 x^{2} - 6 x$ .

For å finne ekstremalpunktene, løser vi likningen:

$\begin{matrix} f' (x) & = & 0 \\ 3 x^{2} - 6 x & = & 0 \\ x^{2} - 2 x & = & 0 \\ x (x - 2) & = & 0 \end{matrix}$

Vi kan ikke dividere med $x$ på begge sider på samme måte som vi gjorde med $3$ , fordi vi ikke vet om $x \neq 0$ . Produktet $x (x - 2) = 0$ har nullpunktene $0$ og $2$ , siden det er nullpunktene til $x$ og $x - 2$ henholdsvis.

Vi setter inn for $x = 0$ og får

$f (0) = 0^{3} - 3 \cdot 0^{2} = 0$ .

Deretter setter vi inn for $x = 2$ og får

$f (2) = (2)^{3} - 3 \cdot (2)^{2} = 8 - 12 = - 4$ .

Ekstremalpunktene er $(0, 0)$ og $(2, - 4)$ . Vi vet at $D_{f}$ ikke har endepunkter, og $f$ er deriverbar overalt, så dette er de eneste

Kritisk punkt

De kritiske punktene til en funksjon $f (x)$ for $x \in [a, b]$ er

1. Punkter der $f' (x) = 0$ .

2. Punkter der $f' (x)$ ikke er definert.

3. Endepunktene til intervallet, $a$ og $b$ .
kritiske punktene

. Men vi må forsikre oss om at ingen av dem er terrassepunkt. Det kan vi gjøre ved å tegne en fortegnslinje. Vi kan faktorisere

f' (x)

som

f' (x) = 3 x (x - 2)

. Vi ser at

3 x

er negativ for

x < 0

, og positiv for

x > 0

. Den andre faktoren

x - 2

er negativ for

x < 2

og positiv for

x > 2

. Fortegnslinjen vår blir:

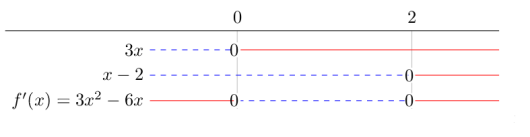
Vi ser at den deriverte endrer fortegn når den går forbi punktene vi fant, så de er ekstremalpunkter.

Svar: Ekstremalpunktene er $(0, 0)$ og $(2, - 4)$ . $(0, 0)$ er toppunkt og $(2, - 4)$ er bunnpunkt.

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

For flere eksempler og forklaringer om fortegnsskjema og ekstremalpunkter se lynkurset Funksjonsdrofting.

For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleiren.

b)

Forklar at $f (x) = x^{2} \cdot (x - 3)$ , og bruk dette til å bestemme nullpunktene til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her kan vi faktorisere funksjonsuttrykket. Nullpunktene finner vi ved å finne for hvilke $x$ -verdier vi får at $f (x) = 0$ .

I funksjonsuttrykket vårt $f (x) = x^{3} - 3 x^{2}$ har vi at begge leddene har $x^{2}$ som faktor, og da kan vi sette det utenfor en parantes. Da kan vi skrive

$f (x) = {x^{3} - {3 x}^{2} = x}^{2} (x - 3)$

som var det vi ville ha.

For å finne nullpunktene må vi finne ut for hvilke $x$ -verdier vi får at $f (x) = 0$ , altså vil vi se på når

$x^{2} (x - 3) = 0$ .

Et produkt er lik $0$ hvis og bare hvis minst en av faktorene er det. Derfor er $f (x) = 0$ hvis $x^{2} = 0$ eller $x - 3$ = 0. Nullpunktene er i $x = 0$ eller $x = 3$ .

Svar: Nullpunktene for $f (x)$ er $0$ og $3$ .

Mer om

Denne oppgaven er om

Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering

faktorisering

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkter

Flere forklaringer og eksempler på faktorisering se artikkelen Parenteser og faktorisering. For flere eksempler og forklaringer om hvordan man finner nullpunkter og ekstremalpunkter se lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettene faktorisering og nullpunkt i Treningsleiren.

c)

Lag en skisse av grafen til $f$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

For å skissere en graf, bruker vi et koordinatsystem der vi gir setter navn på aksene. Vi må finne punkter som ligger på grafen. Ekstremalpunktene og nullpunktene fra deloppgave a) og b) kan vi markere i koordinatsystemet. Vi finner enda et par punkter ved å lage en tabell med $x$ -verdier og tilhørende $f (x)$ -verdier.

Vi har funnet $f (x)$ for tre $x$ -verdier (ekstremalpunkter og nullpunkter):

$x$	$f (x)$
0	0
2	-4
3	0

Før vi kan skissere grafen trenger vi noen flere punkter på grafen.

Da finner vi velger vi noen andre $x$ -verdier – vi tar $x = 1$ og $x = - 1$ – og regner ut $f (x)$ for disse. Da får vi

$f (1) = 1^{2} (1 - 3) = - 2$

$f (- 1) = {(- 1)}^{2} (- 1 - 3) = - 4$

Da blir tabellen vår:

$x$	$f (x)$
0	0
2	-4
3	0
1	-2
-1	-4

Nå tegner vi et koordinatsystem og navngir aksene. Vi tegner inn punktene fra tabellen, og skisserer grafen gjennom punktene.

Svar: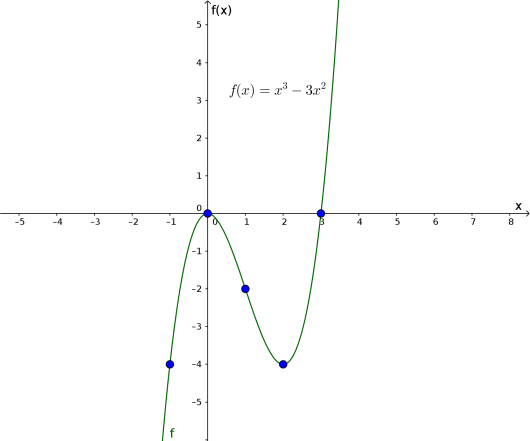

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

For flere eksempler og forklaringer se artikkelen Grafen til en funksjon i lynkurset Funksjon (del II) og lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleieren.

Oppgave 9 (1 poeng) Nettkode: E-4B72

Gitt $Δ A B C$ der $∠ B = 90^{\circ}$ og $\sin A = \frac{3}{7}$ .

Bestem $\cos C$ .

Løs oppgaven her

Løsningsforslag

Jeg tenker

$△ A B C$ er rettvinklet og da kan vi bruke definisjonen av cosinus til å bestemme $\cos C$ . Det kan være lurt å tegne en hjelpefigur.

Vi har at $∠ B = 90^{\circ}$ så $△ A B C$ er rettvinklet, med hypotenus $A C$ . Vi kan tegne dette inn i en hjelpefigur.

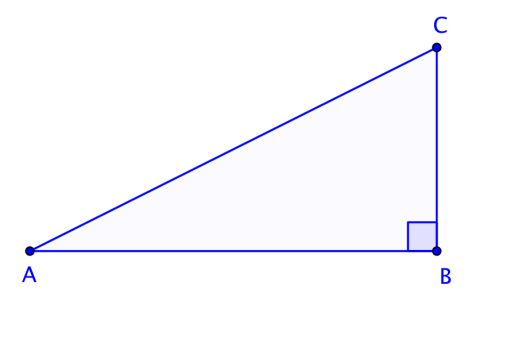
Vi har fått oppgitt at $\sin A = \frac{3}{7}$ . Sinus til $∠ A$ er definert ved

$\sin A = \frac{motstående katet}{hypotenus} = \frac{B C}{A C}$ .

Vi vil finne $\cos C$ . Fra definisjonen til cosinus har vi at

$\cos C = \frac{hosliggende katet}{hypotenus} = \frac{B C}{A C}$ ,

som betyr at

$\cos C = \sin A = \frac{3}{7}$ .

Svar: $\cos C = \frac{3}{7}$

Mer om

Denne oppgaven er om

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Flere forklaringer og eksempler på sinus og cosinus finner du i artikkelen Sinus, cosinus og tangens i lynkurset Trigonometri.

For å øve mer, se oppgavesettet om vinkelberegninger ved hjelp av sinus, cosinus og tangens i Treningsleiren.

Oppgave 10 (2 poeng) Nettkode: E-4B75

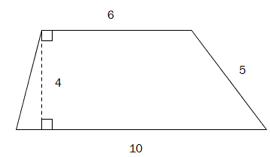
En firkant har form som vist på figuren ovenfor.

Vis at omkretsen av firkanten er $21 + \sqrt{17}$ .

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi finner omkretsen til trapeset ved å summere alle sidelengdene, så da må vi finne den siste sidelengden. Da kan vi se på den rettvinklede trekanten til venstre, med den stiplede linjen og den ukjente sidelengden som to av sidene, og bruke

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

For å lettere ha oversikt over hvilke sidelengder vi jobber med tegner vi av figuren og setter navn på punktene:

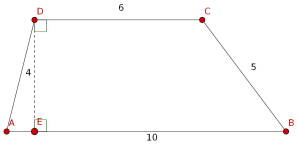
Vi vil altså finne lengden til $A D$ , og for å gjøre det vil vi bruke

Pytagoras læresetning

på

△ A D E

. Men, da må vi må først finne lengden av

A E

, som er lik

A B - B E

For å finne $B E$ feller vi en normal fra $C$ ned på $A B$ og kaller skjæringspunktet for $F$ . Nå har vi at $B E = B F + F E$ og vil bestemme lengdene til $F E og B F$ .

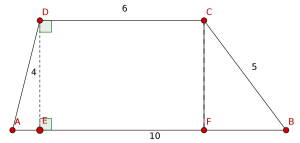
Siden vi har et trapes må $A B$ og $D C$ være parallelle og $□ E F C D$ er et rektangel, og derfor må $F E = D C = 6$ .

Vi har også at $△ B F C$ en rettvinklet trekant, så da kan vi bruke Pytagoras læresetning. Så da har vi at

$B C^{2} = B F^{2} + C F^{2}$ .

Vi setter inn for $B C = 5 og C F = 4$ , og får:

$\begin{matrix} 5^{2} & = & B F^{2} + 4^{2} \\ 25 & = & B F^{2} + 16 \\ {B F}^{2} & = & 9 \\ B F & = & 3 \end{matrix}$

Siden vi vil finne en sidelengde tar vi bare den positive løsningen av likningen ${B F}^{2} = 9$ .

Nå har vi funnet både $B F$ og $E F$ og har da at $B E = 6 + 3 = 9$ . Vi vet $A B = 10$ , og da får vi at

$A E = A B - B E = 10 - 9 = 1$ .

Da kan vi endelig bestemme $A D$ ved å bruke Pytagoras setning på $△ A E D$ . Vi har da at

$\begin{matrix} {A D}^{2} & = & {A E}^{2} + {D E}^{2} \\ {A D}^{2} & = & 1^{2} + 4^{2} \\ {A D}^{2} & = & 1 + 16 \\ A D & = & \sqrt{17} & . \end{matrix}$

Nå kjenner vi alle sidelengdene og kan beregne omkretsen $O$ :

$O = A B + B C + C D + D A = 10 + 5 + 6 + \sqrt{17} = 21 + \sqrt{17}$

Mer om

Denne oppgaven er om

Geometri

Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.

geometri

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

Pytagoras læresetning

Pytagoras' setning

Flere eksempler på hvordan man kan finne sidelengder finner du i artikkelen Pytagoras' setning.

For å øve mer, se oppgavesettet om Pytagoras læresetning i Treningsleiren.

DEL 2 Med hjelpemidler

Oppgave 1 (8 poeng) Nettkode: E-4B78

Funksjonen $f$ gitt ved

$f (x) = 3 x^{3} - 48 x^{2} + 162 x + 300$

viser hvor mange tonn fisk $f (x)$ det var i en fiskebestand $x$ år etter år 2000.

a)

Tegn grafen til $f$ for $x \in [0, 10] .$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan tegne funksjonsgrafen med

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

I GeoGebra kan vi bruke følgende kommando for å tegne grafen av en funksjon definert over et gitt intervall:

Funksjon[ <Funksjon>, <Start>, <Slutt> ].

Vi vil tegne grafen for $x \in [0, 10]$ og skriver da inn

f = Funksjon[ 3x^3-48x^2+162x+300, 0 , 10 ]

Vi tilpasser aksene og setter på navn.

Svar: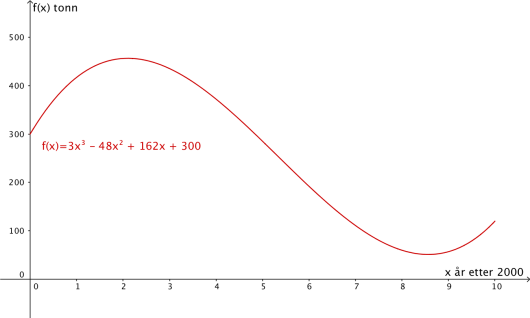

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Graf

grafer

Flere forklaringer og eksempler på hvordan man tegner en graf finner du i artikkelen Grafen til en funksjon.

For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.

b)

Bestem grafisk når fiskebestanden var minst. Hvor mange tonn fisk var det i fiskebestanden da?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Fiskebestanden er minst der funksjon har et

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

. I

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

gir kommandoen Ekstremalpunkt[<Funksjon>]

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

topp

- og

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkter

. Vi må sjekke hvilket av punktene er et bunnpunkt.

I GeoGebra kan vi bruke kommandoen

Ekstremalpunkt[<Funksjon>, <Start>, <Slutt>]

som gir oss både topp- og bunnpunkter.

Vi definerte funksjonen vår i GeoGebra i a), og kan nå skrive

Ekstremalpunkt[f, 0, 10].

Da får vi opp punktene som markert på grafen under:

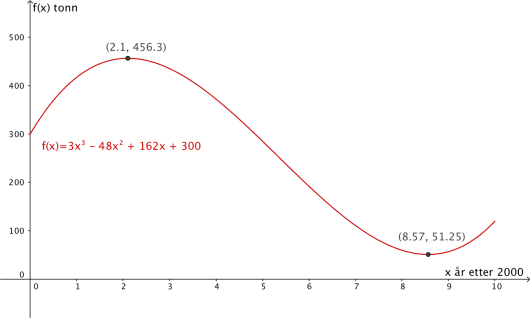
Vi får punktene $(2.1, 456.3) og (8.57, 51.25)$ . Bunnpunktet er punktet med minst funksjonsverdi, altså $B = (8.57, 51.25)$ . Første koordinaten forteller oss etter hvor lang tid fiskebestanden er minst, mens den siste forteller hvor stor den var på det tidspunktet. Vi har da at fiskebestanden var minst $8, 57$ år etter år $2000$ , så på sommeren i år $2008$ , og da var den på $51, 25$ tonn.

Svar: Fiskebestanden var minst på sommeren i år $2008$ , og da var den på $51, 25 tonn$ .

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Graf

grafer

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkter

For flere eksempler og forklaringer om hvordan man finner ekstremalpunkter se lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleiren.

Visste du at

0,57 år er tidsperioden fra midnatt mellom nyttårsaften og første nyttårsdag til 1:11 om natten 28. juli (i et år som ikke er skuddår).

c)

Finn svarene i oppgave b) ved regning.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Bunnpunktet er der deriverte funksjonen har nullpunkter (eller den kan være i endepunktene av intervallet). Vi bruker CAS i GeoGebra.

Vi vil finne bunnpunktet til $f$ . Siden $f$ er definert på et lukket intervall, kan det være at funksjonen har et bunnpunkt i et av endepunktene. Men vi har allerede tegnet funksjonsgrafen, og ser at endepunktene ikke er globale bunnpunkter.

For å finne bunnpunktet til $f$ vil vi finne ut når $f' (x) = 0$ . Da kan vi bruke CAS.

Vi åpner CAS i "Vis"-menyen og skriver inn funksjonen $f$ ved å skrive inn

f(x):= 3x^3-48x^2+162x+300

og på denne måten definerer vi f i CAS.

For å finne den deriverte skriver vi inn "f'(x)" eller vi kan trykke på knappen i verktøylinjen med "f'". Videre skriver vi inn

"f'(x)=0" og får at $x = 2, 1$ og $x = 8, 57$ .

Nå vet vi ikke om disse punktene er topp- eller bunnpunkt, så da må vi finne funksjonsverdien for $x = 2, 1$ og $x = 8, 57$ . Da kan vi skrive inn "f(2.1)" og "f(8.57)" i CAS og får $f (2, 1) = 456, 3 og f (8, 57) = 51, 25$ . Så $x = 8, 57$ er et potensielt bunnpunkt. For å forsikre at $x = 8, 57$ er et bunnpunkt, og ikke et terrassepunkt sjekker vi at den deriverte endrer fortegn fra negativt til positivt i dette punktet. Da sjekker vi den deriverte i et punkt $2, 1 < x < 8, 57$ , for eksempel $x = 8, 5$ , og et punkt $x > 8, 57$ , for eksempel $x = 8, 6$ . Vi skriver da "f'(8.5)" og "f'(8.6)" inn i CAS. Da ser vi at den deriverte endrer fortegn, og $(8, 57, 51, 25)$ er et bunnpunkt.

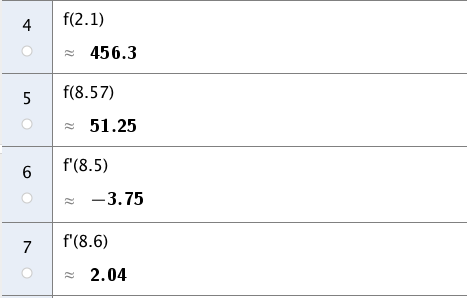
Det betyr at fiskebestanden var minst $8, 57$ år etter år $2000$ , det vil si på sommeren $2008$ , og da var den på $51, 25$ tonn

Svar: Bestanden var på sitt minste sommeren $2008$ , med $51, 25$ tonn fisk.

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.

nullpunkter

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkter

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler se artikkelen Topp- og bunnpunkter.

For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleiren.

d)

Regn ut $f (5)$ . Bestem den momentane vekstfarten når $x = 5$ . Hva forteller disse to svarene om fiskebestanden?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi bruker CAS i

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

for å regne ut

f (5)

og den

Momentan vekstfart

Den momentane vekstfarten til funksjonen $f (x)$ i et punkt $x = a$ , er stigningstallet til tangenten til kurven i punktet.

momentane vekstfarten

. Den momentane vekstfarten i et punkt, er det samme som den deriverte i punktet, så vi kan altså finne

f' (5) .

Vi kan bruke CAS til regne ut $f (5)$ . Vi kan fortsette i samme CAS-vindu som i c), der funksjonen vår alt er definert.

For å regne ut $f (5)$ skriver vi "f(5)" i CAS. Da får vi at

$f (5) = 285$ .

Når vi skal finne den momentane vekstfarten når $x = 5$ , finner vi den deriverte i punktet, så vi vil regne ut $f' (5)$ . Da skriver vi i "f'(5)", og får at

$f' (5) = - 93$ .

Dette betyr at etter $5$ år var bestanden på $285$ tonn fisk, og at den akkurat da avtok med en hastighet på $93$ tonn i året.

Svar: Etter $5$ år var det $285$ tonn fisk i bestanden, og den momentane vekstfarten var $- 93$ tonn fisk i året.

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

deriverte

Flere forklaringer og eksempler på hvordan man deriverer finner du i lynkurset Derivasjon.

For å øve mer, se oppgavesettet om veksthastighet i Treningsleiren.

Visste du at

I denne fasiten har vi antatt at funksjonen $f$ kan deriveres uten å kommentere det. Men det finnes funksjoner som ikke er deriverbare. Et enkelt eksempel er funksjonen gitt ved $f (x) = \sqrt{x^{2}}$ , som ikke kan deriveres i $0$ . For å se hvorfor, prøv å tegne funksjonsgrafen og se hva skjer for negative $x$ og rundt $0$ .

Oppgave 2 (4 poeng) Nettkode: E-4B7D

I en dam er det $20 000$ L vann. Vannmengden minker med $8$ % hvert døgn.

a)

Hvor mye vann vil det være igjen i dammen etter ett døgn?

Hvor mye vann vil det være igjen i dammen etter ti døgn?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Først må vi finne et uttrykk for vannmengden som en funksjon av antall døgn. Fordi vannmengden avtar med en prosentandel, er dette en

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Vannmengden avtar med $8 %$ per døgn, altså er

Vekstfaktor

Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.

Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.

vekstfaktoren

lik

$1 - 8 % = 1 - \frac{8}{100} = \frac{92}{100} = 0, 92$

Hvis vannstanden er $S$ liter på et tidspunkt, vil den være $S \cdot 0, 92 L$ døgnet etter. To døgn etter vil den altså være $S \cdot 0, 92^{2} L$ , og etter $x$ døgn vil den være $S \cdot 0, 92^{x} L$ . Siden vannmengden ved starten (altså for $x = 0$ ) er $20 000 L$ , blir funksjonsuttrykket:

$f (x) = 20 000 \cdot 0, 92^{x}$

For å finne vannstanden etter $1$ døgn kan vi sette inn for $x = 1$ . Da får vi $f (1) = 20 000 \cdot 0, 92^{1} = 18 400$ ,

og for å finne etter $10$ døgn setter vi inn for $x = 10$ og får

$f (10) = 20 000 \cdot 0, 92^{10} \approx 8 687, 8$ .

Svar: Etter et døgn er det igjen $18 400$ liter, og etter ti døgn vil det være ca. $8 688$ liter igjen.

Mer om

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Momentan vekstfart

Den momentane vekstfarten til funksjonen $f (x)$ i et punkt $x = a$ , er stigningstallet til tangenten til kurven i punktet.

vekstfart

Flere eksempler og forklaringer på hvordan man setter opp en matematisk modell finner du i lynkurset Kultur og modellering.

For å øve mer, se oppgavesettet om modellering i Treningsleiren.

b)

Hvor mange døgn vil det gå før det er $5 000$ L vann igjen i dammen?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi har fått oppgitt vannmengden og skal nå finne $x$ slik at $f (x) = 5000$ . Vi må løse en

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentiallikning

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

Eksponentiallikningen

vi skal løse er

$20 000 \cdot 0, 92^{x} = 5000$

Vi kan begynner med å dividere med $20 000$ på begge sider. Da får vi at

${0, 92}^{x} = 0, 25$

For å løse likningen kan vi ta logaritmen av begge sider, og bruke logaritmeregelen som sier at $\log (a^{b}) = b \log (a)$ .

$\begin{matrix} 0, 92^{x} & = & 0, 25 \\ \log (0, 92^{x}) & = & \log (0, 25) \\ x \log (0, 92) & = & \log (0, 25) \\ x & = & \frac{\log (0, 25)}{\log (0, 92)} \\ x & \approx & 16, 63 & . \end{matrix}$

Svar: Det vil gå litt over $16$ og et halvt døgn før det er $5000$ L vann igjen i dammen.

Alternativ løsning

Vi kan løse denne likningen ved å bruke CAS. Da kan vi bruke kommandoen Nløs[<Likning>]. Da vil CAS løse likningen og gi oss et svar i desimaltall, men som kan være avrundet fra den eksakte løsningen.

Vi skriver inn

Nløs[20000*0.92^x=5000].

Da får vi at $x \approx 16, 63$ som forteller oss at etter litt over $16$ og et halvt døgn vil det være $5000$ L igjen i dammen.

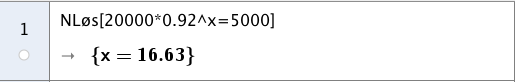
Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Eksponentialligning

En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.

Eksempel med $x$ som ukjent: $2 \cdot 10^{x} = 4$ eller ${1, 03}^{x} = 2$

eksponentiallikning

Flere forklaringer og eksempler finner du i artikkelen Eksponentiallikninger og Inger Christin løser eksponentiallikninger.

For å øve mer, se oppgavesettet om eksponentiallikninger i Treningsleiren.

Oppgave 3 (6 poeng) Nettkode: E-4B7G

En undersøkelse har vist at $20 %$ av alle syklistene i en by sykler uten lys i mørket. Vi velger tilfeldig ti syklister fra denne byen.

a)

Bestem sannsynligheten for at minst én av de ti sykler uten lys i mørket.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan anta at det er nok syklister til at antallet syklister som allerede er valgt, ikke påvirker sannsynligheten vår for å velge en syklist med lys. Vi husker at summen av alle mulige utfall alltid er lik én og at $1 - " alle ikke gunstige utfall " = " alle gunstige utfall "$ .

Vi har to mulige

Hendelse

En hendelse eller begivenhet er en delmengde av utfallsrommet. En hendelse består av ett eller flere utfall.

Se Gunstig utfall

hendelser

$L$ : "én tilfeldig valgt syklist har lys",

og den

Komplement

Komplementet til A, betegnet med $A^{c}$ , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, $A^{c} = U ∖ A$ .

komplementære

hendelsen

$U$ : "én tilfeldig valgt syklist har ikke lys".

Da vet vi at

$P (U) = 20 % = \frac{1}{5}$

$P (L) = 1 - P (U) = 80 % = \frac{4}{5}$

Det er ikke helt enkelt å direkte regne ut sannsynligheten for at minst en av de ti valgte syklistene ikke har lys - da måtte vi ha regnet ut et tall for hvert eneste mulige måte å få minst en syklist uten lys blant de ti vi velger ut. Derfor er det lettere å regne ut sannsynligheten for den komplementære hendelsen, nemlig at alle av de ti syklistene har lys.

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

Produktsetningen

sier da at sannsynligheten for dette er:

$P (alle har lys)^{} = (\frac{4}{5})^{10} \approx 0, 107$ .

Så sannsynligheten for at alle av de ti syklistene har lys, er $0, 107$ . Da må sannsynligheten for at minst én av de ti sykler uten lys være

$P (minst én uten lys) = 1 - 0, 107 = 0, 893 = 89, 3 %$ .

Svar: Sannsynligheten er $89, 3 %$ for at minst en syklist ikke har lys.

Mer om

Denne oppgaven er om

Sannsynlighet

sannsynlighet

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetning

Komplement

Komplementet til A, betegnet med $A^{c}$ , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, $A^{c} = U ∖ A$ .

komplement

Flere forklaringer og eksempler se artiklene Sannsynlighet ved komplementære hendelser og Uavhengige hendelser og produktsetningen i lynkurset Sannsynlighet (del II).

For å øve mer, se oppgavesettet om produksetningen i Treningsleiren.

b)

Bestem sannsynligheten for at bare den første, den fjerde og den tiende syklisten vi velger, sykler uten lys i mørket.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Her antar vi at utfallene er uavhengige og vi bruker produktsetningen.

Vi bruker samme notasjon som i (a). Vi skal altså ha denne rekken av utfall: $U L L U L L L L L U$ . Det gir at sannsynligheten for at kun den første, fjerde og tiende syklisten sykler uten lys blir:

$P (U) \cdot P (L) \cdot P (L) \cdot P (U) \cdot P (L) \cdot P (L) \cdot P (L) \cdot P (L) \cdot P (L) \cdot P (U) = P (U)^{3} P (L)^{7}$

$= {(\frac{1}{5})}^{3} {(\frac{4}{5})}^{7} = \frac{16384}{9765625} \approx 0, 002 = 0, 2 %$ .

Når vi multipliserer har ikke rekkefølgen på faktorene noe å si, så sannsynligheten for enhver rekkefølge med tre syklister som sykler uten lys vil være $0, 2 %$ .

Svar: Sannsynligheten denne rekkefølgen er ca. $0, 2 %$ .

Mer om

Denne oppgaven er om

Uavhengige hendelser

To begivenheter A og B kalles uavhengige dersom utfallet i den ene ikke påvirker utfallet i den andre.

uavhengige hendelser

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

Flere forklaringer og eksempler på hvordan man finner sannsynlighet finner du i artikkelen Uavhengige hendelser og produktsetningen.

For å øve mer, se oppgavesettet om produktsetningen i Treningsleiren.

c)

Denne oppgaven tar for seg binomisk fordeling som ikke lenger er pensum på læreplanen i 1T.

Bestem sannsynligheten for at nøyaktig tre av de ti sykler uten lys i mørket.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Dette gir et

Binomisk forsøk

Et binomisk forsøk må tilfredsstille følgende krav:

Antall delforsøk n er fast.
Alle delforsøkene er uavhengige.
For hvert delforsøk er det kun to mulige utfall. Det utfallet vi er interessert i kalles for suksess, mens det andre er kalt for fiasko.
For hvert delforsøk er sannsynligheten for suksess lik p.

binomisk forsøk

. Da må vi finne ut på hvor mange måter vi kan velge tre syklister ut av ti på.

I oppgave b) fant vi ut at sannsynligheten for at tre syklister i en bestemt rekkefølge, den første, fjerde og tiende syklisten, sykler uten lys er ${(\frac{1}{5})}^{3} \cdot {(\frac{4}{5})}^{7} = 0, 2 %$ .

Dersom de tre syklistene uten lys hadde skullet komme andre steder i rekken av de ti syklistene, ville tilsvarende regning som i a) fortsatt gitt sannsynligheten ${(\frac{1}{5})}^{3} \cdot {(\frac{4}{5})}^{7}$ fordi $3$ av faktorene i produktethadde vært $\frac{1}{5}$ og resten $\frac{4}{5}$ .

Antallet slike måter å velge tre fra en mengde på ti syklister, er gitt ved binomialkoeffisienten $(\begin{matrix} 10 \\ 3 \end{matrix}) = \frac{10!}{3! (10 - 3)!} = 120$ . Altså har vi at sannsynligheten for at nøyaktig tre av ti sykler uten lys er

$P (tre uten lys av ti) = 120 \cdot {(\frac{1}{5})}^{3} {(\frac{4}{5})}^{7} \approx 0.201 = 20, 1 %$

Svar: Sannsynligeheten for at nøyaktig tre av de ti syklistene mangler lys er ca. $20, 1 %$ .

Mer om

Denne oppgaven er om

Binomisk forsøk

Et binomisk forsøk må tilfredsstille følgende krav:

Antall delforsøk n er fast.
Alle delforsøkene er uavhengige.
For hvert delforsøk er det kun to mulige utfall. Det utfallet vi er interessert i kalles for suksess, mens det andre er kalt for fiasko.
For hvert delforsøk er sannsynligheten for suksess lik p.

binomiske forsøk

Binomialkoeffisient

Binomialkoeffisienten

$(\begin{matrix} n \\ m \end{matrix}) = \frac{n!}{m! (n - m)!}$

hvor $n! = n \cdot (n - 1) \cdot \cdot \cdot 2 \cdot 1$ ,

forteller hvor mange måter det kan trekkes m objekter ut fra en samling av n gjenstander uten tilbakelegging.

binomialkoeffisient

Sannsynlighet

sannsynlighet

Flere eksempler på hvordan man finner binomialkoeffisienten finner du i artikkelen Binomiske forsøk.

For å øve mer, se oppgavesettet om binomisk sannsynlighet i Treningsleiren.

Oppgave 4 (2 poeng) Nettkode: E-4B7K

Per, Pål og Espen har til sammen 198 mynter. Per har seks ganger så mange mynter som Pål og tre ganger så mange mynter som Espen.

Hvor mange mynter har hver av de tre guttene?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi bruker informasjonen til å sette oppe et

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

Vi lar antallet mynter Pål har være $x$ .

Vi vet at Per har seks ganger så mange mynter som Pål, så Per må ha $6 x$ mynter.

Per har tre ganger så mange mynter som Espen, så Espen har en tredel av Pers antall. Da må Espen ha $\frac{6 x}{3} = 2 x$ mynter.

Tilsammen har guttene da $x + 6 x + 2 x = 9 x$ mynter. Vi får vite at de tilsammen har $198$ mynter, så vi må ha:

$9 x = 198$

$x = \frac{198}{9} = 22$

Det betyr at Pål har 22 mynter. Vi kan nå også regne ut at Per har $6 x = 6 \cdot 22 = 132$ mynter, og Espen har $2 x = 2 \cdot 22 = 44$ mynter.

Svar: Pål har 22 mynter, Espen har 44 mynter og Per har 132 mynter.

Alternativ løsning

Vi kan også løse oppgave på denne måten. La Per ha $m$ , Pål $n$ og Espen $r$ mynter. Den oppgitte informasjonen gjør at vi kan sette opp likningssystemet:

$\begin{matrix} m & = & 6 n \\ 3 r & = & m \\ m + n + r & = & 198 \end{matrix}$

Nå kan vi bruke CAS til å løse likningssystemet, og da bruker vi kommandoen

Løs[ <Liste med likninger>, <Liste med variabler> ].

I dette tilfellet må vi skrive

Løs[{m=6n, 3r=m, m+n+r=198} , {m,n,r}]

som gir svaret

{{m = 132, n = 22, r = 44}}.

Mer om

Denne oppgaven er om

Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.

likningssystem

Flere forklaringer og eksempler på likningssystemer finner du i lynkurset Lineære likninger med flere ukjente.

For å øve mer, se oppgavesettet om likningssystemer i Treningsleiren.

Oppgave 5 (2 poeng) Nettkode: E-4B7M

Vis at det finnes to ulike trekanter som tilfredsstiller de tre kravene nedenfor.

- En side i trekanten skal være $5, 0 cm$

- En side i trekanten skal være $8, 0 cm$

- Arealet av trekanten skal være $17, 5 {cm}^{2}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi får oppgitt trekantens areal og to av sidelengdene. Det tyder på at vi kan bruke

Arealsetningen

For en trekant $△ A B C$ er arealet gitt ved $A = \frac{sin (∠ A) \cdot A B \cdot A C}{2}$ .

arealsetningen

. Husk at vinklene i en trekant kan være både spiss, stump og rett.

Vi vet at to av sidelengdene er $5, 0$ cm og $8, 0$ cm. Vi lar disse være sidene $A B$ og $A C$ i en trekant $△ A B C$ . Vi skriver $A_{△ A B C}$ for arealet av $△ A B C$ , som vi vet er $17, 5 {c m}^{2}$ . Arealsetningen forteller oss at vi har

$A_{△ A B C} = \sin (∠ A) \frac{A B \cdot A C}{2}$

Vi setter inn informasjonen vi har og får

$17, 5 {cm}^{2} = \sin (∠ A) \frac{5, 0 cm \cdot 8, 0 cm}{2}$

$17, 5 {cm}^{2} = \sin (∠ A) \cdot 20, 0 {cm}^{2}$

$\sin (∠ A) = \frac{17, 5 {cm}^{2}}{20, 0 {cm}^{2}} = 0, 875$

$∠ A = \sin^{- 1} (0, 875) \approx 61^{\circ}$

Men, siden $\sin (v) = \sin (180^{\circ} - v)$ , kan også at $∠ A = 180^{\circ} - 61^{\circ} = 119^{\circ}$ . Det betyr at $∠ A$ kan ha to størrelser - den kan enten være spiss eller stump.

Mer om

Denne oppgaven er om

Trigonometri

Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.

trigonometri

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Flere forklaringer og eksempler på hvordan man regner med disse finner du i lynkurset Trigonometri.

For å øve mer, se oppgavesettet om vinkelberegninger ved hjelp av sinus, cosinus og tangens i Treningsleiren.

Oppgave 6 (6 poeng) Nettkode: E-4B7O

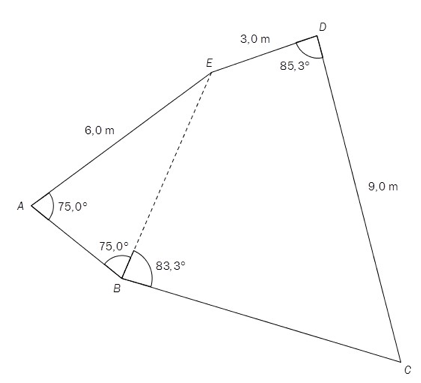
Et område $A B C D E$ har form som vist på figuren ovenfor.

a)

Bestem arealet av $Δ A B E$ ved regning.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å finne en trekants areal kan vi bruke

Arealsetningen

For en trekant $△ A B C$ er arealet gitt ved $A = \frac{sin (∠ A) \cdot A B \cdot A C}{2}$ .

arealsetningen

. Da må vi kjenne to sidelengder i trekanten og vinkelen mellom dem.

Vi vil bruke arealsetningen for å finne arealet til $△ A B E$ . Da må kjenne lengden til to av sidene og vinkelen mellom dem.

$△ A B E$ er en

Likebeint trekant

I en likebeint trekant er to sider like lange og to vinkler like store.

likebeint trekant

med

∠ E A B = ∠ A B E = 75^{\circ}

. Da må vi også ha at

A E = B E = 6, 0 m

. I tillegg vet vi at vinkelsummen i en trekant er

180^{\circ}

, som betyr at

$∠ A B E + ∠ E A B + ∠ B E A = 180^{\circ}$ . Altså er $∠ B E A = 180^{\circ} - ∠ E A B - ∠ A B E .$

Nå setter vi inn for $∠ E A B = ∠ A B E = 75^{\circ}$ , og får at $∠ B E A = 180^{\circ} {- 75^{\circ} - 75^{\circ} = 30}^{\circ}$ .

Da har vi all informasjonen vi trenger, og kan bruke arealsetningen.

$A_{△ A B E} = \sin (∠ B E A) \frac{A E \cdot B E}{2} = \sin (30^{\circ}) \frac{6, 0 m \cdot 6, 0 m}{2} = \frac{1}{2} \cdot 18, 0 m^{2} = 9, 0 m^{2}$ .

Svar: Trekanten $Δ A B E$ har areal $9, 0 m^{2}$ .

Mer om

Denne oppgaven er om

Trigonometri

Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.

trigonometri

Likebeint trekant

I en likebeint trekant er to sider like lange og to vinkler like store.

likebente trekanter

Flere forklaringer og eksempler på hvordan man bruker trigonometri finner du i artikkelen Arealsetningen.

For å øve mer, se oppgavesettet om areal i Treningsleiren.

b)

Bestem lengden $C E$ ved regning.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi trekker linjestykket $C E$ , og får en $△ C D E$ , hvor vi kjenner to sider og en vinkel. Da kan vi bruke

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$

cosinussetningen

Vi trekker linjestykket $C E$ .

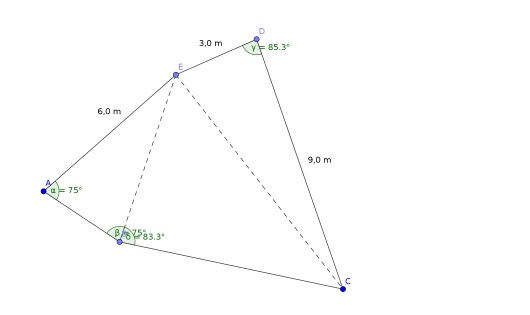
Nå har vi en trekant $△ C D E$ der vi kjenner to av sidelengdene og en vinkel, og skal finne den siste sidelengden. Da kan vi bruke

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$

cosinussetningen

. Den sier i vårt tilfelle at vi har:

$C E^{2} = D E^{2} + C D^{2} - 2 \cdot D E \cdot C D \cdot \cos (∠ C D E)$

Vi setter inn $D E = 3, 0 m$ , $C D = 9, 0 m$ og $∠ C D E = 85, 3^{\circ}$ , og får:

$C E^{2} = (3, 0 m)^{2} + (9, 0 {m)}^{2} - 2 \cdot (3, 0 m) \cdot (9, 0 m) \cdot \cos (85, 3^{\circ})$

$C E = \sqrt{(3, 0 m)^{2} + (9, 0 m)^{2} - 2 \cdot (3, 0 m) \cdot (9, 0 m) \cdot \cos (85, 3^{\circ})}$

$C E \approx \sqrt{85, 6 m^{2}}$

$C E \approx 9, 25 m$ .

Svar: $C E$ har en lengde på ca. $9, 25 m$ .

Alternativ løsning

Vi kan komme litt raskere frem til svaret med CAS. Her kan vi bruke kommandoen

Nløs[<Likning>, <Variabel>].

Vi skriver inn

NLøs[ CE^2 = 3.0^2+9.0^2-2*3.0*9.0*cos(85.3°), CE ].

Her er det viktig å huske $^{\circ}$ -symbolet – den trengs for å fortelle GeoGebra at vi måler vinklene i grader. Vi bruker kommandoen NLøs i stedet for Løs for å få ut et omtrentlig svar. Den gir oss

CE = (-9.25), CE = 9.25.

Men, en side kan ikke ha negativ lengde, så vi må ha $C E = 9, 25$ .

Mer om

Denne oppgaven er om

Trigonometri

Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.

trigonometri

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Flere forklaringer og eksempler på hvordan man kan finne sidelengder finner du i artikkelen Cosinussetningen.

For å øve mer, se oppgavesettet om cosinussetningen i Treningsleiren.

c)

Bestem lengden $B C$ ved regning.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi skal igjen finne en ukjent sidelengde i en trekant der vi kjenner to sidelengder og en vinkel. Da kan vi bruke

Cosinussetningen

La $A B C$ være en trekant. Anta at vi kjenner sidene $A B$ , $A C$ og $∠ A$ mellom dem. Da er

$B C^{2} = A C^{2} + A B^{2} - 2 (A B \cdot A C) \cos ∠ A .$

cosinussetningen

igjen.

Vi kjenner alt vi trenger, og skriver opp cosinussetningen:

$C E^{2} = B C^{2} + B E^{2} - 2 \cdot B C \cdot B E \cdot \cos (∠ E B C)$

Denne gangen er det $B C$ som er ukjent. Fra a) og b) vet vi at $C E = 9, 25 m og B E = 6, 0 m$ , og vi har fått oppgitt at $∠ E B C = {83, 3}^{\circ}$ . Da setter vi inn i uttrykket og får

$(9, 25 m)^{2} = B C^{2} + (6, 0 m)^{2} - 2 \cdot B C \cdot (6, 0 m) \cdot \cos (83, 3^{\circ})$

Dette kan vi løse i CAS, ved å bruke kommandoen

Nløs[<Likning>, <Variabel>],

så for å finne $B C$ skriver vi :

NLøs[9.25^2 = BC^2 + 6.0^2 - 2*BC*6.0*cos(83.3°), BC]

Her er det viktig å huske $^{\circ}$ -symbolet – den trengs for å vise at vi måler vinklene i grader. Vi bruker kommandoen NLøs i stedet for Løs for å få ut et omtrentlig svar.

Da får vi at

${B C = - 6, 36, B C = 7, 77}$ .

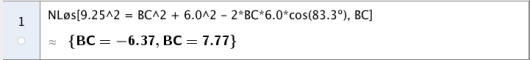
Siden en side ikke kan ha negativ lengde, så det er bare $7, 77 m$ er riktig lengde.

Svar: $B C$ har en lengde på ca. $7, 8 m$ .

Mer om

Denne oppgaven er om

Trigonometri

Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.

trigonometri

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikning

For eksempler og forklaringer se artikkelen Cosinussetningen. Flere forklaringer og eksempler på hvordan man løser andregradslikninger finner du i artikkelen Løs en andregradslikning.

For å øve mer, se oppgavesettet om cosinussetningen i Treningsleiren.

Oppgave 7 (8 poeng) Nettkode: E-4B7Z

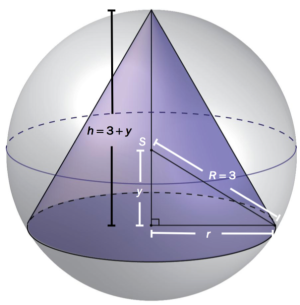
En kjegle er innskrevet i en kule. Kulen har sentrum i $S$ og radius $R = 3$ . Grunnflaten i kjeglen har radius r. Høyden i kjeglen er $h = 3 + y$ , der $y$ er avstanden fra $S$ til grunnflaten i kjeglen. Se skissen ovenfor.

Sett $r = 2$

a)

Hvor høy er kjeglen?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Høyden er gitt ved $h = 3 + y$ , så vi må finne $y$ . Da kan vi se på trekanten med sider $R, r og y$ , og bruke

Pytagoras læresetning

Vi kan tenke oss at vi tar et tverrsnitt av sirkelen med kjeglen. Da får vi som vist på figuren under.

Høyden i kjeglen er gitt ved $h = 3 + y$ , så vi vil regne ut $y$ . Vi har en rettvinklet trekant med sidelengder $y, r, R$ , så ved å bruke Pytagoras læresetning har vi at

$y^{2} + r^{2} = R^{2}$

$y = \sqrt{R^{2} - r^{2}}$ .

Nå kan vi sette inn for $R = 3$ og $r = 2$ og får at

$y = \sqrt{3^{2} - 2^{2}} = \sqrt{5}$ .

Det gir at $h = y + 3 = \sqrt{5} + 3$ .

Svar: Kjeglens høyde er $3 + \sqrt{5}$ .

Mer om

Denne oppgaven er om

Kjegle

En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.

Kjeksen til en kroneis har form som en kjegle.

Volum : V = $\frac{π r^{2} h}{3}$
Overflate : A = $π r^{2} + π r s$

kjegler

Pytagoras læresetning

Flere forklaringer og eksempler på hvordan man regner på kjegler finner du i artikkelen Pyramider og kjegler.

For å øve mer, se oppgavesettet om Pytagoras læresetning i Treningsleiren.

b)

Volumet av en kjegle er gitt ved $V = \frac{1}{3} π r^{2} h$

Bestem volumet av kjeglen ved regning.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi setter inn størrelsene vi vet inn i formelen for volumet av en kjegle.

Vi kan finne volumet til kjeglen ved den gitte formelen $V = \frac{1}{3} π r^{2} h$ . I kjeglen vår har vi $r = 2$ og $h = 3 + \sqrt{5}$ . Setter vi dette inn i formelen får vi

$V = \frac{1}{3} π \cdot 2^{2} \cdot (3 + \sqrt{5}) = \frac{π (12 + 4 \sqrt{5)}}{3} \approx 21, 9$ .

Det kan være nyttig å ha den nøyaktige formen for høyden, men her tillater vi oss å runde av.

Svar: Kjeglens volum er ca. $21, 9$ .

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Hvordan vi finner volumet av en kjegle finner du i artikkelen Pyramider og kjegler.

For å øve mer, se oppgavesettet om volum i Treningsleiren.

c)

Sett nå $r = x$ .

Vis at volumet av kjeglen da er gitt ved

$f (x) = \frac{1}{3} π \cdot x^{2} \cdot (3 + \sqrt{9 - x^{2}})$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi må uttrykke størrelsene vi ikke får opplyst med $x$ og deretter sette inn i formelen for volumet.

Vi begynner med å finne et uttrykk for $h$ .

Fra a) vet vi at

$y^{2} + r^{2} = R^{2}$ ,

og nå har vi at $r = x$ og $R = 3$ , så det gir

$x^{2} + y^{2} = 3^{2}$

$y = \sqrt{9 - x^{2}}$ .

Høyden i kjeglen er gitt ved $h = y + 3$ som betyr at $h = \sqrt{9 - x^{2}} + 3$ .

Nå kan vi sette inn for $h = \sqrt{9 - x^{2}} + 3$ og $r = x$ . Da får vi:

$V = \frac{1}{3} π \cdot x^{2} \cdot (\sqrt{9 - x^{2}} + 3)$

Volumet er nå avhengig av $x$ , så vi kan tolke $V$ som en funksjon av $x$ . Derfor velger vi å skrive $f (x)$ for $V$ . Det gir

$f (x) = \frac{1}{3} π x^{2} (3 + \sqrt{9 - x^{2}})$

som var det vi skulle fram til.

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Pytagoras læresetning

For flere forklaringer og eksempler om funksjoner se lynkurset Funksjoner (del II).

For å øve mer, se oppgavesettet om volum i Treningsleiren.

d)

Hvor stor må radius og høyde i den innskrevne kjeglen være for at volumet av kjeglen skal bli størst mulig? Hvor stort blir volumet?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi vet hva volumet er som en funksjon $f$ av radien $x$ . Det betyr at volumet av kjeglen er størst der $f$ har et maksimumspunkt.

Spørsmålet spør også om hvor stor høyden i kjeglen må være. Men vi fant ut i løpet av forrige deloppgave at høyden $h$ også er en funksjon av $x$ , så vi trenger bare finne den $x$ -verdien som gir et maksimumspunkt for $f$ . Dette gjør vi ved å finne

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunktene

til

f

. Det går an å gjøre dette for hånd, ved å derivere funksjonen

f

, men vi bruker CAS-systemet i GeoGebra.

Vi skriver i CAS:

f(x):= (1/3)* $π$ *x^2*(3+sqrt(9-x^2))

Merk at her bruker vi

:= og ikke =.

Dette gjør vi for å definere $f$ til å være funksjonen gitt ved $f (x) = \frac{1}{3} π x^{2} (3 + \sqrt{9 - x^{2}})$ .

Da kan vi skrive

Ekstremalpunkt[f] for å finne ekstremalpunktene.

Vi får svaret:

{(((-2) * sqrt(2)), (32 * $π$ / 3)), (0, 0), ((2 * sqrt(2)), (32 * $π$ / 3))}

Ekstremalpunktene er altså:

$(- 2 \sqrt{2}, \frac{32 π}{3}), (0, 0), (2 \sqrt{2}, \frac{32 π}{3})$

En negativ $x$ -verdi gir ikke mening, fordi $x$ er en lengde. Det er også klart at $x = 0$ gir et volum på 0, så det kan heller ikke være riktig svar. Da er det bare $(2 \sqrt{2}, \frac{32 π}{3})$ igjen. Vi må vite at dette er et toppunkt, og det kan vi gjøre ved å tegne grafen og finne punktet $(2 \sqrt{2}, \frac{32 π}{3})$ på den.

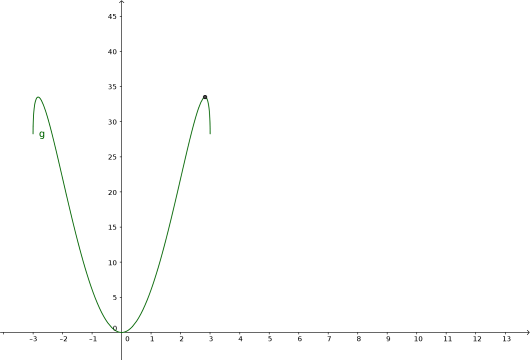
Så $f (x)$ har et maksimumspunkt i $(x, f (x)) = (2 \sqrt{2}, \frac{32 π}{3})$ . Vi vet fra oppgave (c) at $h = 3 + \sqrt{9 - x^{2}}$ . Setter vi inn $x = 2 \sqrt{2}$ der, får vi $h = 3 + \sqrt{9 - (2 \sqrt{2})^{2}} = 3 + \sqrt{9 - 8} = 4$ . Da er volumet $\frac{32 π}{3}$ .

Svar: Volumet er størst når radien i den innskrevne kjeglen er lik $2 \sqrt{2}$ .

Da er høyden $4$ og volumet $\frac{32 π}{3}$ .

Mer om

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Forklaringer på hvordan man finner toppunkt finner du i artikkelen Topp- og bunnpunkter lynkurset Funksjonsdrøfting.

Visste du at?

I denne oppgaven kunne for eksempel volumet som er $\frac{32 π}{3}$ rundes av. Men om man skriver $\frac{32 π}{3}$ er det helt nøyaktig. Runder vi av til $33, 5$ kutter vi uendelig mange desimaler. Det kan ofte være konstruktivt å runde av hvis det gjør svaret lettere å forstå, men vær bevisst på at svaret blir mindre presist.

MAT1013 2013 Høst

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4B6H

Løsningsforslag

Standardform

Standardform

Potens

Oppgave 2 (4 poeng) Nettkode: E-4B6K

a)

Løsningsforslag a)

Tabell

b)

Løsningsforslag b)

Gunstig utfall

Sannsynlighet

Gunstig utfall

c)

Løsningsforslag c)

Sannsynlighet

Gunstig utfall

Sannsynlighet

Oppgave 3 (2 poeng) Nettkode: E-4B6O

Løsningsforslag

Teller

Nevner

Konjugatsetningen

Første kvadratsetning

Alternativ løsning

Andregradsuttrykk

abc-formelen

Faktorisering

abc-formelen

Første kvadratsetning

Konjugatsetningen

Oppgave 4 (2 poeng) Nettkode: E-4B6Q

Løsningsforslag

Potens

Oppgave 5 (2 poeng) Nettkode: E-4B6S

Løsningsforslag

Logaritme

Logaritme

Oppgave 6 (2 poeng) Nettkode: E-4B6U

Løsningsforslag

Stigningstall

Konstant

Alternativ løsning

Lineære funksjoner

Ligning

Ligningssett

Oppgave 7 (2 poeng) Nettkode: E-4B6W

Løsningsforslag

abc-formelen

Ligningssett

Andregradslikning

Oppgave 8 (6 poeng) Nettkode: E-4B6Y

a)

Løsningsforslag a)

Ekstremalpunkter

Derivasjon

Kritisk punkt

Funksjon

Ekstremalpunkt

b)

Løsningsforslag b)

Faktorisering

Nullpunkt

c)

Løsningsforslag c)

Funksjon

Graf

Oppgave 9 (1 poeng) Nettkode: E-4B72

Løsningsforslag

Cosinus

Oppgave 10 (2 poeng) Nettkode: E-4B75

Løsningsforslag

Pytagoras læresetning

Pytagoras læresetning