Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1011 2017 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timar:

Del 1 skal leverast inn etter 2 timar.

Del 2 skal leverast inn seinast etter 5 timar.

Hjelpemiddel på Del 1:

Vanlege skrivesaker, passar, linjal med centimetermål og vinkelmålar.

Hjelpemiddel på Del 2:

Alle hjelpemiddel er tillatne, med unntak av Internett og andre verktøy som tillèt kommunikasjon.

Framgangsmåte:

Del 1 har 9 oppgåver. Del 2 har 8 oppgåver.

Der oppgåveteksten ikkje seier noko anna, kan du fritt velje framgangsmåte. Om oppgåva krev ein bestemt løysingsmetode, vil ein alternativ metode kunne gi låg/noko utteljing.

Bruk av digitale verktøy som grafteiknar og rekneark skal dokumenterast med utskrift eller gjennom ein IKT-basert eksamen.

Rettleiing om vurderinga:

Poeng i Del 1 og Del 2 er berre rettleiande i vurderinga. Karakteren blir fastsett etter ei samla vurdering. Det betyr at sensor vurderer i kva grad du

viser rekneferdigheiter og matematisk forståing
gjennomfører logiske resonnement
ser samanhengar i faget, er oppfinnsam og kan ta i bruk fagkunnskap i nye situasjonar
kan bruke formålstenlege hjelpemiddel
forklarer framgangsmåtar og grunngir svar
skriv oversiktleg og er nøyaktig med utrekningar, nemningar, tabellar og grafiske framstillingar
vurderer om svar er rimelege

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4QPL

Du har $15$ L saft. Du skal helle saften over i beger. I hvert beger er det plass til $2$ dL. Hvor mange beger kan du fylle?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi skal fordele $15$ L saft over i mindre begre, som hvert rommer $2$ dL, og da kan vi dividere volumet av saften på volumet til begrene. Før vi dividerer må vi passe på at vi har samme enhet for volum.

Det første vi kan merke oss er at volumet til saften og volumet til begrene er oppgitt i forskjellige enheter. Vi kan begynne med å finne volumet til saften gitt i dL. Vi har at $1 L = 10 dL$ som betyr at $15 L = 150 dL$ . For å finne antall begre vi kan fylle med saft, dividerer vi $150$ dL på $2$ dL. Nå dividerer vi to tall med samme benevning, så enhetene vil kansellere hverandre. Vi får da $150 dL : 2 dL = 75$ som betyr at vi kan fylle opp $75$ begre.

Svar: Vi kan fylle opp $75$ begre.

Mer om:

Denne oppgaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Divisjon

Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.

Eksempel: $6 : 2 = 3$ fordi $2 \cdot 3 = 6$ .

divisjon

.

For flere eksempler og forklaringer, se artikkelen Divisjon med brøk.
For å øve mer, se oppgavesettet om brøk i Treningsleiren.

Oppgave 2 (1 poeng) Nettkode: E-4QPN

I $2006$ var indeksen for en vare $125$ . Varen kostet da $1000$ kroner. I $2016$ var indeksen for den samme varen $150$ .

Hvor mye kostet varen i $2016$ dersom prisen har fulgt indeksen?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Dersom en vare har fulgt indeksen, betyr det at forholdet mellom indeks og pris er konstant. Dette kan vi bruke for å bestemme prisen på varen i $2016$ .

Siden forholdet mellom indeks og pris er konstant har vi at $\frac{pris i 2006}{indeks i 2006} = \frac{pris i 2016}{indeks i 2016} .$ Oppgaveteksten oppgir pris og indeks i $2006$ , samt indeksen i $2016$ . Vi kan sette inn for disse størrelsene i likningen over. Da får vi $\frac{1000 kr}{125} = \frac{pris i 2016}{150} .$ Nå har vi en likning der den ukjente er pris i $2016$ . For å løse likningen kan vi multiplisere med $150$ på begge sider av likhetstegnet og forkorte. $\begin{matrix} \frac{1000 kr}{125} \cdot 150 & = \frac{pris i 2016}{150} \cdot 150 \\ pris i 2016 & = \frac{1000}{125} \cdot 150 \end{matrix}$ Nå må vi regne ut $\frac{1000 kr}{125} \cdot 150 = 1000 kr \cdot \frac{150}{125}$ . Nå kan vi faktorisere og forkorte, og får at prisen er $pris i 2016 = 1000 kr \cdot \frac{25 \cdot 6}{25 \cdot 5} = (200 \cdot 5) kr \cdot \frac{6}{5} = 200 kr \cdot 6 = 1200 kr$

Svar: Varen kostet $1200$ kroner i 2016.

Mer om:

Denne oppgaven er om konsumprisindeks, forhold og brøk.

For flere forklaringer og eksempler på regning med forhold, se artikkelen Målingsforhold. Oraklet har forklart hva konsumprisindeks er her.

Oppgave 3 (3 poeng) Nettkode: E-4QPP

I Norge måler vi temperatur i grader celsius ( $^{\circ} C$ ). I USA blir temperatur målt i grader fahrenheit ( $^{\circ} F$ ). Når temperaturen er $x^{\circ} C$ , er den $y^{\circ} F$ , der

$y = \frac{9}{5} x + 32$

a)

Bruk formelen ovenfor til å regne om $1 5^{\circ} C$ til grader fahrenheit.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal bestemme hvor mange grader $15^{\circ}$ $C$ er i fahrenheit, som betyr at vi kan sette inn for $x = 15$ i formelen som er gitt i oppgaven.

Vi skal regen om $15^{\circ}$ $C$ til $y^{\circ}$ F. Fra oppgaveteksten så har vi at når temperaturen er $15^{\circ}$ $C$ så kan vi sette inn for $x = 15$ i formelen, og får da at $y = \frac{9}{5} \cdot 15 + 32 = \frac{9 \cdot 15}{5} + 32 = 9 \cdot 3 + 32 = 27 + 32 = 59 .$ Det betyr at $15^{\circ}$ $C$ er det samme som $59^{\circ}$ F.

Svar: $15^{\circ}$ $C$ tilsvarer $59^{\circ}$ F.

Mer om:

Denne oppgaven er om

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

lineære likninger

For flere forklaringer og eksempler, se lynkurset Førstegradslikninger.

For å øve mer, se oppgavesettet om førstegradslikninger i Treningleiren.

b)

Løs likningen

$x = \frac{9}{5} x + 32$

Hva forteller løsningen du fikk?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan løse likningen som en vanlig likning med en ukjent.

Vi begynner med å løse likningen med hensyn på $x$ :

$\begin{matrix} x & = & \frac{9}{5} x + 32 \\ x - \frac{9}{5} x & = & 32 \\ \frac{5 x}{5} - \frac{9 x}{5} & = & 32 \\ \frac{- 4 x}{5} & = & 32 \\ x & = & 32 \cdot \frac{5}{- 4} \\ x & = & - 8 \cdot 5 \\ x & = & - 40 \end{matrix}$

Dersom vi sammenlikner denne likningen med formelen gitt i oppgaven, har vi at $y = x$ , som betyr at grader i celsius og fahrenheit er likt, altså at når vi har $- 40^{\circ}$ $C$ , så har vi også $- 40^{\circ}$ F.

Svar: Vi får $x = - 40$ som betyr at $- 40^{\circ} C = - 40^{\circ}$ F.

Mer om:

Denne oppgaven er om

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

lineære likninger

For flere forklaringer og eksempler, se artikkelen Førstegradslikninger.

For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleiren.

Oppgave 4 (2 poeng) Nettkode: E-4QPS

Et taxiselskap har en fast pris på turer fra Oslo sentrum til Gardermoen. Ofte tar flere personar taxi sammen. Taxiselskapet vil lage en tabell som viser sammenhengen mellom antall personer som er med i én taxi, og beløpet hver person må betale for turen.

Se nedenfor.

a)

Skriv av og fyll ut tabellen.

Oslo-Gardermoen
Personer	$1$	$2$	$3$	$4$
Beløp å betale per person (kroner)			$260$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi vet at det er fast pris på turer til Gardermoen. Vi vet også hvor mye hver person må betale dersom det er $3$ personer i taxien. Da kan vi finne ut hvor mye en tur til Gardermoen koster.

En taxitur til Gardermoen har fast pris. Dersom det er tre personer i taxien må hver person betale $260$ kr. Det betyr at en tur til Gardermoen koster $3 \cdot 260 kr = 780 kr .$ For å fylle ut tabellen kan vi dividere fast pris på antall personer i taxien. Dersom det er én person blir prisen $780 kr$ . For $2$ personer blir prisen $780 kr : 2 = 390 kr$ For $4$ personer blir prisen $780 kr : 4 = 195 kr$ Nå kan vi fylle inn denne informasjonen inn i tabellen som blir seende slik ut:

Oslo-Gardermoen
Personer	$1$	$2$	$3$	$4$
Beløp å betale per person (kroner)	780	390	$260$	195

Mer om:

Denne oppgaven er om

Divisjon

Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.

Eksempel: $6 : 2 = 3$ fordi $2 \cdot 3 = 6$ .

divisjon

For flere forklaringer og eksempler, se artikkelen Divisjon.

b)

Forklar at antall personer og beløpet hver person må betale, er omvendt proporsjonale størrelser.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

To størrelser er omvendt proporsjonale dersom produktet av samsvarende tall er konstant.

For at antall personer og beløpet hver person må betale skal være omvendt proporsjonale størrelser må vi har at produktet mellom samsvarende størrelser er konstant, altså at $antall personer \cdot beløpet hver person må betale = taxipris$ der taxiprisen er konstant. Vi vet at taxiprisen er fast på $780$ kr, så vi har at $antall personer \cdot beløpet hver person må betale = 780 kr$ Det betyr at produktet av antall personer og beløpet hver person må betale er konstant, så de er omvendt proporsjonale størrelser.

Mer om:

Denne oppgaven er om omvendt proporsjonale størrelser.

For flere forklaringer og eksempler, se artikkelen Proporsjonalitet.

For å øve mer, se oppgavesettet om omvendt proporsjonalitet i Treningsleiren.

Oppgave 5 (3 poeng) Nettkode: E-4QPV

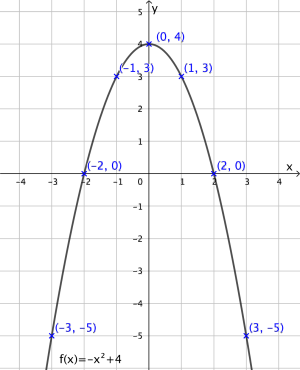
En funksjon $f$ er gitt ved

$f (x) = - x^{2} + 4$

a)

Skriv av og fyll ut verditabellen nedenfor.

$x$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$
$f (x)$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan sette inn for de ulike $x$ -verdiene i verditabellen i funksjonen $f (x)$ . Vi kan legge merke til at i funksjonen $f$ har vi kun et ledd med $x$ , og det er $x^{2}$ . Siden $x^{2} = (- x)^{2}$ har vi at $f (x) = f (- x)$ . Vi kan også merke oss at $- x^{2} \neq ({- x}^{2})$ .

For å fylle inn i verditabellen må vi bestemme $f (x)$ for de $x$ -verdiene i tabellen. Når vi nærmere på funksjonsuttrykket $f (x) = - x^{2} + 4$ , forekommer $x$ kun i leddet $- x^{2}$ . Det betyr at for eksempel for $x = - 3$ og $x = 3$ får vi $- (3)^{2} = - (- 3)^{2}$ , så $f (x) = f (- x)$ og vi trenger kun å sette inn for noen av verdiene for $x$ . Da får vi for $x = 0$ $f (0) = - (0)^{2} + 4 = 4 .$ For $x = - 1$ og $x = 1$ $f (- 1) = f (1) = - (1)^{2} + 4 = - 1 + 4 = 3 .$ For $x = - 2$ og $x = 2$ får vi $f (- 2) = f (2) = - (2)^{2} + 4 = 0$ og til slutt få vi for $x = - 3$ og $x = 3$ $f (- 3) = f (3) = - (3)^{2} + 4 = - 9 + 4 = - 5$ Nå kan vi sette inn i verditabellen:

$x$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$
$f (x)$	$- 5$	$0$	$3$	$4$	$3$	$0$	$- 5$

Mer om:

Denne oppgaven er om

Verditabell

En tabell med verdier av en variabel, for eksempel $x$ , og tilhørende funksjonsverdier, for eksempel $y$ , kalles for en verditabell.

Verditabellen gir oss oversikt over verdier som hører sammen. Den hjelper oss enten med å finne punkter som ligger på grafen til en funksjon eller funksjonsuttrykket til en graf.

verditabell

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

.

For flere forklaringer og eksempler, se artikkelen Andregradsfunksjoner.

For å øve mer, se oppgavesettet om kvadratiske funksjoner i Treningsleiren.

b)

Tegn grafen til $f$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke verditabellen fra a) til å tegne inn koordinater til punkt som ligger på grafen til $f$ , og bruke disse til å tegne grafen til funksjonen.

I verditabellen fra oppgave a) kan vi se at $f (x) = - 5$ når $x = - 3$ som betyr at grafen til $f$ går gjennom punktet $(- 3, - 5)$ . På tilsvarende måte kan vi finne punkt for hver kolonne i verditabellen som grafen til $f$ vil gå gjennom. Disse punktene kan vi tegne inn i et koordinatsystem. Fra verditabellen ser vi at verdiene for $x$ varierer fra $- 3$ til $3$ og for $f (x)$ fra $4$ til $- 5$ og da vet vi omtrentlig hvor stort koordinatsystem vi må tegne. Vi begynner med å føre inn punktene vi får fra verditabellen:

Det gir oss et ganske godt inntrykk av hvordan grafen til $f$ skal se ut, så da kan vi bare tegne den inn slik at den går gjennom punktene.

Svar:

Mer om:

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

grafer

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

.

For flere forklaringer og eksempler, se artikkelen Funksjonsgrafer for andregradsfunksjoner.

For å øve mer, se oppgavesettet om Grafisk fremstilling i Treningsleiren.

Oppgave 6 (4 poeng) Nettkode: E-4QPY

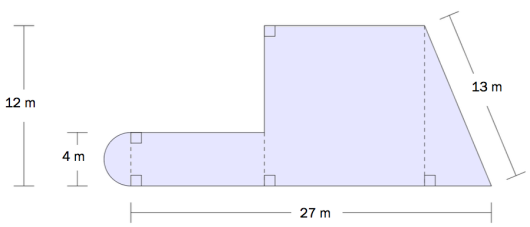
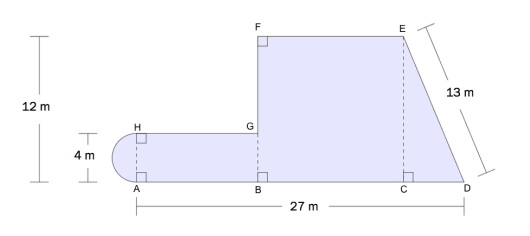
Området som er markert med blått ovenfor, er satt sammen av en halv sirkel, et rektangel, et kvadrat og en rettvinklet trekant.

Sett $π \approx 3$ og regn ut tilnærmede verdier for omkretsen og for arealet av området.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi har en sammensatt figur. For å finne arealet av hele figuren kan vi finne

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

arealet

til hver av figurene den er sammensatt av og addere dem.

Vi skal regne ut omkretsen og arealet av en sammensatt figur som består av en halv sirkel, et rektangel, et kvadrat og en trekant. For å gjøre det lettere å vite hvilke sider og figurer vi snakker om begynner vi med å sette navn på figuren.

Vi ser nå på

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkretsen

først.

Omkrets

Omkretsen er summen av de heltrukne yttersidene til figuren. Det første vi må gjøre er å finne lengdene til de ukjente sidene. For å bestemme omkretsen på halvsirkelen fra $A$ til $H$ bruker vi formelen for omkrets til en sirkel, som er $O = π \cdot d$ , der $d = A H = 4 m$ er diameteren. Siden vi bare har en halvsirkel må vi dividere med $2$ . Da får vi at omkretsen er $O_{A H} = \frac{3 \cdot 4 m}{2} = 6 m .$ Vi vet at $A D = 27 m$ og $D E = 13 m$ . $F E$ er en side i kvadratet $B C E F$ , som betyr at $E F = 12 m$ . $F G = B F - A H = 12 m - 4 m = 8 m$ . Nå gjenstår bare lengden på rektangelet $A B G H$ . Vi har at $H G = A D - F E - C D$ . Vi kan bestemme lengden til $C D$ ved

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

. Fra den får vi at

$\begin{matrix} C D^{2} + C E^{2} & = & D E^{2} \\ C D^{2} & = & (13 m)^{2} - (12 m)^{2} \\ C D^{2} & = & 169 m^{2} - 144 m^{2} \\ C D & = & \sqrt{25 m^{2}} \\ C D & = & 5 m \end{matrix}$

og da får vi at $H G = 27 m - 12 m - 5 m = 10 m$ . Nå kan vi finne omkretsen ved å legge sammen alle sidelengdene

$\begin{matrix} O & = & A D + D E + E F + F G + G H + O_{A H} \\ = & 27 m + 13 m + 12 m + 8 m + 10 m + 6 m \\ = & 76 m \end{matrix}$

Den sammensatte figuren har en omkrets på $76 m$ . Vi fortsetter med å se på arealet til figuren.

Areal

For å finne arealet til hele figuren kan vi begynne med å finne arealet til hver av figurene den er satt sammen av.
Vi ser først på arealet av halvsirkelen med diameter $A H$ . Radiusen til denne halvsirkelen er $\frac{4 m}{2} = 2 m$ . Arealet til en sirkel er gitt ved $A = π \cdot r^{2}$ , og siden vi bare har en halvsirkel må vi dividere på $2$ . Da får vi at arealet til halvsirkelen er $A_{H} = \frac{π \cdot (2 m)^{2}}{2} = \frac{3 \cdot 4 m^{2}}{2} = 6 m^{2} .$

Vi kan fortsette med å finne arealet til rektangelet $A B G H$ . Arealet til et rektangel er gitt ved formelen $A = l \cdot b$ , der $l$ er lengden og $b$ er bredden til rektangelet. Da får vi at $A_{R} = A B \cdot A H = 10 m \cdot 4 m = 40 m^{2} .$

Arealet til et kvadrat er gitt ved $A = s \cdot s = s^{2}$ der $s$ er siden til kvadratet. Kvadratet $B C E F$ har da areal $A_{K} = B C^{2} = (12 m)^{2} = 144 m^{2}$ Før vi kan finne arealet til hele figuren gjenstår bare å finne arealet til trekant $C D E$ . Arealet til en trekant finner vi ved formelen $A = \frac{g \cdot h}{2}$ der $g$ er grunnlinjen og $h$ er høyden i trekant. Ved denne formelen får vi at arealet til trekant $C D E$ er gitt ved $A_{T} = \frac{C D \cdot C E}{2} = \frac{5 m \cdot 12 m}{2} = 30 m^{2} .$ Nå kan vi finne arealet til hele figuren ved å summere arealene over. Da får vi

$\begin{matrix} A & = & A_{H} + A_{R} + A_{K} + A_{T} \\ = & 6 m^{2} + 40 m^{2} + 144 m^{2} + 30 m^{2} \\ = & 220 m^{2} . \end{matrix}$

Arealet til hele figuren er $220 m^{2}$ .

Svar: Omkretsen er $76 m$ og arealet er $220 m^{2}$ .

Mer om:

Denne oppgaven er om

Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.

Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.

omkrets

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

.

For flere forklaringer og eksempler, se lynkurset Geometri - areal og volum.

For å øve mer, se oppgavesettet om areal og omkrets i Treningsleiren.

Oppgave 7 (2 poeng) Nettkode: E-4QQ0

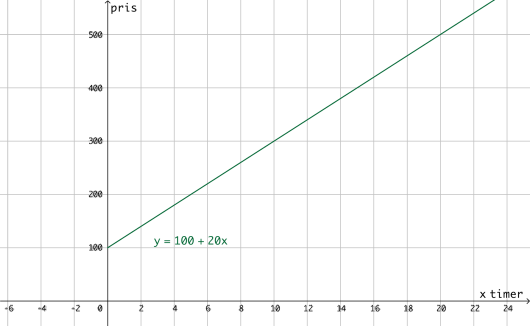
Gi et eksempel på en sammenheng fra virkeligheten som kan beskrives med en lineær funksjon. Bestem funksjonsuttrykket, og lag en skisse av grafen til funksjonen.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineær funksjon

er en funksjon på formen

y = a x + b

, der

a

er stigningstallet og

b

er konstantleddet.

Vi skal finne en sammenheng som kan beskrives med en lineær funksjon på formen $y = a x + b$ der $a$ er stigningstall og $b$ er konstantledd. En sammenheng som kan beskrives på denne måten er prisen for å leie kano, der du betaler $100$ kroner i fast pris, i tillegg til $20$ kroner per time. Prisen for å leie kano i $x$ timer er da gitt ved $y = 20 x + 100$ Grafen til funksjonen vil da være en rett linje, som krysser $y$ -aksen i $y = 100$ og har stigningstall $a = 20$ som betyr at prisen øker med $20$ kr for hver time $x$ vi øker med. Vi skisserer grafen.

Mer om:

Denne oppgaven er om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Graf

grafer

.

For flere forklaringer og eksempler, se artikkelen Fra en funksjon til en graf.

For å øve mer, se oppgavesettet om lineære funksjoner og grafisk fremstilling i Treningsleiren.

Oppgave 8 (4 poeng) Nettkode: E-4QQ2

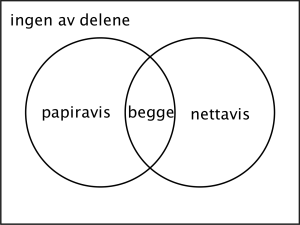
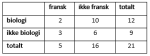
Ved en skole leser $80 %$ av elevene aviser på nett, $50 %$ leser papiraviser, og $2 %$ leser ikke aviser.

a)

Systematiser opplysningene gitt i teksten over i et venndiagram eller i en krysstabell.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Venn-diagram og krysstabell er måter å fremstille informasjonen på. Vi må systematisere opplysningene våre.

Vi ser først på hvordan vi kan systematisere opplysningen i et venndiagram. I den alternative løsningen ser vi på krysstabell.

Vi begynner med å tegne et venn-diagram uten tall som vi kan bruke som hjelpefigur. Da kan vi enklere se hvilke opplysninger vi må finne.

Fra venn-diagrammet ser vi at vi har fire mulige utfall:

leser ingen aviser

leser papiraviser

leser nettaviser

leser både papir- og nettaviser

Fra opplysningene vet vi at $2 %$ av elevene ikke leser aviser. Det betyr at $100 % - 2 % = 98 %$ av elevene leser aviser. Vi kaller andelen elever som leser papiraviser for $P$ og andelen som leser aviser på nett for $N$ . Vi har $P + N = 50 % + 80 % = 130 % .$ Siden det bare er $98 %$ som leser aviser betyr det at $130 % - 98 % = 32 %$ leser både aviser på nett og papiraviser.
Da har vi at $50 % - 32 % = 18 %$ leser kun papiraviser og $80 % - 32 % = 48 %$ leser kun aviser på nett.
Vi kan sjekke at vi har riktig prosentandeler ved å summere opp og se at vi får $100 %$ . Vi har $ingen aviser + papiraviser + nettaviser + begge deler = 2 % + 18 % + 48 % + 32 % = 100 % .$ Da kan vi sette inn i venndiagrammet.

Svar:

Alternativ løsning

Vi kan begynne å sette opp en krysstabell med overskriftene:

	Leser avis på nett	Leser ikke avis på nett	Sum
Leser papiravis
Leser ikke papiravis
Sum

Vi kan begynne å fylle inn den informasjonen vi får direkte fra oppgaveteksten.

	Leser avis på nett	Leser ikke avis på nett	Sum
Leser papiravis			50%
Leser ikke papiravis		$2 %$
Sum	$80 %$		$100 %$

Når vi summerer andelene av de som ikke leser papir avis og de som leser papiravis må vi få $100 %$ , altså må vi ha at $50 %$ ikke leser papiravis. Det samme gjelder når vi summerer andelen som leser avis på nett og de som ikke gjør det, som gir at $20 %$ leser ikke aviser på nett.

	Leser avis på nett	Leser ikke avis på nett	Sum
Leser papiravis			50%
Leser ikke papiravis		$2 %$	50%
Sum	$80 %$	$20 %$	$100 %$

Det betyr at vi må ha $20 % - 2 % = 18 %$ som kun leser papiraviser, og $50 % - 2 % = 48 %$ som kun leser aviser på nett.

	Leser avis på nett	Leser ikke avis på nett	Sum
Leser papiravis		$18 %$	$50 %$
Leser ikke papiravis	$48 %$	$2 %$	$50 %$
Sum	$80 %$	$20 %$	$100 %$

Da gjenstår det bare å fylle inn for de som leser avis både nett og papir, som blir $50 % - 18 % = 32 %$ . Den endelige krysstabellen blir da:

	Leser avis på nett	Leser ikke avis på nett	Sum
Leser papiravis	$32 %$	$18 %$	$50 %$
Leser ikke papiravis	$48 %$	$2 %$	$50 %$
Sum	$80 %$	$20 %$	$100 %$

Mer om:

Denne oppgaven er om venn-diagram og

Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.

krysstabell

.

For flere forklaringer og eksempler, se artikkelen Venn-diagram og mengdelære.

b)

Bestem sannsynligheten for at en tilfeldig valgt elev ved skolen leser både aviser på nett og papiraviser.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke venndiagrammet fra a).

Vi kan se direkte fra venndiagrammet (og krysstabellen) at sannsynligheten for at en tilfeldig valgt elev leser både avis på nett og papiravis er $32 %$ .

Svar: $32 %$

Mer om:

Denne oppgaven er om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

og venn-diagram.

For flere forklaringer og eksempler, se artikkelen Venn-diagram og mengdelære.

c)

En elev ved skolen leser aviser på nett.

Bestem sannsynligheten for at denne eleven ikke leser papiraviser.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi skal finne betinget sannsynlighet, altså at en elev ikke leser papiraviser, gitt at han leser aviser på nett.

Vi vil finne betinget sannsynligheten for at en elev ikke leser papiraviser, gitt at han leser avisen på nett, $P (I k k e p a p i r | N e t t)$ . Vi kan bestemme sannsynligheten ved å se på $\frac{antall gunstige}{antall mulige} .$

La M være antall elever ved skolen. Da er antall mulige 80% av M, altså 0,80M. Antall gunstige er 48% av M, altså 0,48M.

Dermed er $P (\overset{}{I k k e p a p i r} | N e t t) = \frac{0, 48 M}{0, 80 M} = \frac{48}{80} = \frac{6 \cdot 8}{10 \cdot 8} = \frac{6}{10} = 0, 6 = 60 %$

Svar: $60 %$

Mer om:

Denne oppgaven er om uniform sannsynlighet.

For flere forklaringer og eksempler, se artikkelen Hvordan finner vi uniform sannsynlighet.

For å øve mer, se oppgavesettet om sannsynlighet i Treningsleiren.

Oppgave 9 (4 poeng) Nettkode: E-4QQ6

Tenk deg at du skal blande rød og blå maling i forholdet $2 : 5$ .

a)

Hvor mye rød maling må du tilsette dersom du har en boks med $7, 5$ dL blå maling?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

At noe skal blandes i forholdet $2 : 5$ betyr at vi skal ha $2$ deler med den ene tingen og $5$ deler med den andre. For eksempel skal vi blande $2$ dL rød maling med $5$ dL blå maling for å få $7$ dL med blandet maling.

Den blå malingen skal utgjøre $5$ deler. Siden vi har $7, 5$ dL blå maling, betyr det at én del i er, i dL, $\frac{7, 5}{5} = 1, 5 .$ Vi skal ha $2$ deler rød maling. Da trenger vi $2 \cdot 1, 5 dL = 3 dL$ rød maling.

Svar: Vi trenger $3$ dL rød maling.

Mer om:

Denne oppgaven er om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proporsjoner

.

For flere forklaringer og eksempler, se artikkelen Målingsforhold.

b)

Hvor mye rød maling trenger du for å lage $21$ L ferdig blanding?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Ferdig blanding består av $7$ deler, der $2$ er rød maling og $5$ er blå maling.

Iblandingen skal det være totalt $21$ L, som utgjør $7$ deler; $5$ deler blå maling og $2$ deler rød maling. Da har vi at én del er $\frac{21 L}{7} = 3 L$ maling. Vi skal ha $2$ deler rød maling, som betyr at vi trenger $2 \cdot 3 L = 6 L$ maling.

Svar: Vi trenger $6$ L rød maling.

Mer om:

Denne oppgaven er om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proporsjoner

For flere forklaringer og eksempler, se artikkelen Målingsforhold.

c)

Du har $21$ L ferdig blanding i forholdet $2 : 5$ , men ønsker en blanding i forholdet $1 : 3$ . Du vil ordne dette ved å tilsette litt mer av den ene fargen.

Hvilken farge må du tilsette?

Hvor mye må du tilsette av denne fargen?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Forholdet $1 : 3$ er det samme som $2 : 6$ .

Vi har at forholdet er det samme som $2 : 6$ . Sammenlikner vi dette med forholdet $2 : 5$ ser vi at vi vil ha mer blå maling, mer nøyaktig vil vi ha én del til med blå maling. I oppgave b) så vi at én del utgjorde $3$ L, som betyr at vi må tilsette $3$ L blå maling.

Svar: Vi må tilsette $3$ L blå maling.

Denne oppgaven er om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proporsjoner

For flere forklaringer og eksempler, se artikkelen Målingsforhold.

DEL 2 Med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4QQC

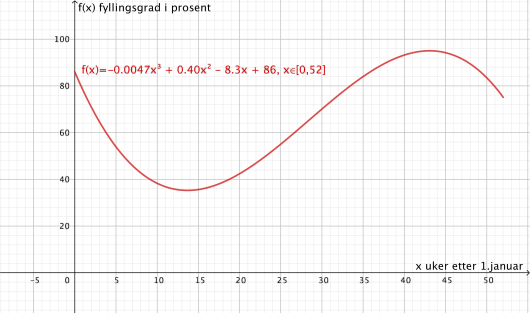
Funksjonen $f$ er gitt ved

$f (x) = - 0, 0047 x^{3} + 0, 40 x^{2} - 8, 3 x + 86, 0 \leq x \leq 52$

viser fyllingsgraden $f (x)$ prosent i et vannmagasin $x$ uker etter $1$ . januar $2016$ .

a)

Bruk graftegner til å tegne grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen til $f$ .

Vi tegner grafen i GeoGebra og da kan vi bruke kommandoen Funksjon[ $<$ Funksjon $>$ , $<$ Start $>$ , $<$ Slutt $>$ ]. Vi vil tegne grafen for $x \in [0, 52]$ og skriver da inn $f (x) = Funksjon [- 0.0047 x^{\land} 3 + 0.40 x^{\land} 2 - 8.3 x + 86, 0, 52]$ Under “Innstillinger” og “Avrunding” kan vi stille inn slik at GeoGebra viser fire desimaler. Vi tilpasser aksene og setter på navn.
Resultatet er vist under.

Svar:

Mer om:

Dette er en oppgave om

Graf

graf

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler, se lynkurset GeoGebra.

b)

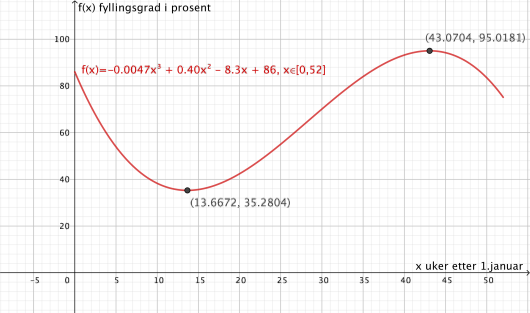
Bestem bunnpunktet på grafen til $f$ .

Hvilken praktisk informasjon gir koordinatene til bunnpunktet?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Bunnpunktet til grafen forteller oss noe om den laveste verdien til funksjonen.

Bunnpunktet er et ekstremalpunkt, og da kan vi bruke kommandoen Ekstremalpunkt[ $<$ Polynom $>$ ]. Vi vil finne bunnpunktet til $f$ , og skriver da inn $Ekstremalpunkt [f] .$

Da får vi opp bunnpunktet $(13.67, 35.28)$ . $x$ -koordinaten til bunnpunktet forteller oss når fyllingsgraden til vannmagasinet var på det laveste, og $y$ -koordinaten forteller hva fyllingsgraden var. Det betyr at fyllingsgrad var lavest i uke $13$ og da var den på omtrent $35, 3 %$ .

Svar: Fyllingsgrad var lavest $13, 7$ uker etter 1. januar, som vil si i begynnelsen av april, og da var den på omtrent $35, 3 %$ .

Mer om:

Dette er en oppgave om

Graf

graf

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

For flere forklaringer og eksempler, se artikkelen topp-og bunnpunkter.

For å øve mer, se dette oppgavesettet om ekstremalpunkter i Treningsleiren.

c)

Hvor mange prosentpoeng avtok fyllingsgraden med i løpet av de fire første ukene i $2016$ ?

Hvor mange prosent avtok fyllingsgraden med i løpet av de fire første ukene i $2016$ ?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Det er viktig å skille mellom forskjellen i prosentpoeng, som er forskjellen mellom to prosenttall, og forskjellen i prosent.

Vi begynner med å finne fyllingsgraden for $x = 0$ og $x = 4$ , som tilsvarer fyllingsgraden i begynnelsen av året, og fire uker ut i $2016$ . Da kan vi bruke funksjonen vår i GeoGebra og skrive inn $f (0)$ og $f (4)$ . Da får vi at $f (0) = 86$ og $f (4) \approx 58, 9$ . Det betyr at i løpet av de første fire ukene i $2016$ avtok fyllingsgraden med $86 - 58, 9 = 27, 1$ prosentpoeng.
For å finne ut hvor stor prosent fyllingsgraden avtok med, må vi finne ut hvor stor prosentandel nedgangen er av den opprinnelige fyllingsgraden, altså hvor stor prosentandel $27, 1$ er av $86$ . Da ser vi på forholdet mellom de to tallene og får at nedgangen på $27, 1 %$ er $\frac{27, 1}{86} \cdot 100 % \approx 31, 5 %$ av $86 %$ .

Svar: Fyllingsgraden avtok med $27, 1$ prosentpoeng, som tilsvarer $31, 5 %$ .

Mer om:

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Prosentpoeng

Prosentpoeng er forskjellen mellom to prosenttall.

Eksempel: Forskjellen mellom $80 %$ og $82 %$ er 2 prosentpoeng.

prosentpoeng

For flere forklaringer og eksempler, se artikkelen prosentpoeng.

For å øve mer, se dette oppgavesettet om prosentregning fra Treningsleiren.

Oppgave 2 (6 poeng) Nettkode: E-4QQG

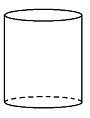
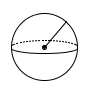
Pedalbøtte Sylinderformet beholder

Til venstre ovenfor ser du en pedalbøtte med lokk. Vi går ut fra at pedalbøtten er satt sammen av en sylinder og en halv kule. Ved siden av ser du den sylinderformede beholderen som er inne i pedalbøtten.

Gå ut fra at alle målene gitt på bildene ovenfor er innvendige mål.

a)

Bestem volumet av den sylinderformede beholderen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan finne volumet til den sylinderformede beholderen ved å multiplisere grunnflaten, som er en sirkel, med høyden.

Volumet til en sylinder er gitt ved $V = G \cdot h$ der $G$ er grunnflaten til sylinderen og $h$ er høyden. Grunnflaten til sylinderen er en sirkel med radius $r = \frac{320 mm}{2} = 160$ mm.

Vi kan regne dette om til ${dm}^{}$ . Vi har at $100 mm = 1 dm$ , så da er $160 mm = 1, 6 dm .$

Arealet til en sirkel er gitt ved $A = π \cdot r^{2}$ , så grunnflaten har et areal på $G = π \cdot (1, 6 dm)^{2} \approx 8, 0425 {dm}^{2} .$

Nå må vi multiplisere dette med høyden til sylinderen som er $535$ mm. Siden vi nå har oppgitt arealet til grunnflaten i dm $^{2}$ , vil vi skrive høyden også i dm. Da kan vi dividere på $100$ som gir $h = 5, 35$ dm. Fra formelen for volumet til en sylinder får vi at beholderen har et volum på $V = 8, 0425 {dm}^{2} \cdot 5, 35 dm \approx 43, 03 {dm}^{3} .$ Vi har også at $1 L = 1 {dm}^{3}$ , så da er volumet til den sylinderformede beholderen $43$ L.

Svar: $43 L$ .

Mer om:

Denne oppgaven handler om

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

For flere forklaringer og eksempler, se artikkelen En sylinder.

For å øve mer, se dette oppgavesettet om volum i Treningsleiren.

b)

Tenk deg at du fyller $40$ L vann i denne beholderen.

Hvor høyt i beholderen vil vannet stå?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi får oppgitt volumet, og fra oppgave a) kjenner vi grunnflaten til sylinderen. Da kan vi gjøre om på formelen for volum for å finne høyden, $h$ .

I oppgave a) brukte vi formelen for volumet til et sylinder $V = G \cdot h$ . Nå vil vi finne ut hvor høyt vannet vil stå i beholderen når volumet er $40$ L. Fra oppgave a) vet vi også at grunnflaten har areal $G \approx 8, 0425 {dm}^{2}$ og at $1 {dm}^{3} = 1 L$ . Da kan vi sette inn for $V = 40 {dm}^{3}$ og $G = 8, 0425 {dm}^{2}$ i formelen for volum, og løse den som en likning med hensyn på $h$ . $\begin{matrix} 40 {dm}^{3} & = & 8, 0425 {dm}^{2} \cdot h \\ h & = & \frac{40 {dm}^{3}}{8, 0425 {dm}^{2}} \\ h & \approx & 4, 97 dm \end{matrix}$

Dersom vi fyller $40$ L i beholderen vil vannet vil stå $4, 97 dm = 497 mm$ høyt.

Svar: $497$ mm.

Mer om:

Denne oppgaven handler om

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

For flere forklaringer og eksempler, se artikkelen Omskriving av formler.

c)

Bestem volumet av pedalbøtten med lokk.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan finne volumet for sylinderen og halvkulen og deretter addere dem sammen. Høyden av hele pedalbøtten er summen av høyden i sylinderen og radius til halvkulen.

Pedalbøtten er satt sammen av en halvkule og en sylinder. For å bestemme volumet kan vi finne volumet til hver av de to delene, og deretter addere dem sammen. Vi begynner med halvkulen.
Volumet til en kule er gitt ved formelen $V = \frac{4}{3} π \cdot r^{3} .$ Volumet til halvkulen er da halvparten av dette $V_{H K} = \frac{1}{2} \cdot \frac{4}{3} π \cdot r^{3} = \frac{2}{3} π \cdot r^{3} .$ Diameteren til pedalbøtten er $400$ mm som betyr at radiusen er $r = 200 mm = 2, 0 dm$ . Vi kan sette inn for $r$ i formelen over og får at volumet til halvkulen er $V_{H K} = \frac{2}{3} π \cdot (2, 0 dm)^{3} \approx 16, 76 {dm}^{3} .$ Nå kan vi finne volumet til sylinderen, som er gitt ved formelen $V = G \cdot h$ . Grunnflaten $G$ er gitt ved $G = π \cdot r^{2} = π \cdot (2, 0 dm)^{2} \approx 12, 57 {dm}^{2} .$ For å bestemme volumet må vi først bestemme høyden av sylinderdelen av bøtten. Da kan vi subtrahere radiusen til halvkulen fra høyden av hele pedalbøtten, og da får vi at $høyden av sylinderen = 755 mm - 200 mm = 555 mm$ . Volumet til sylinderdelen av bøtten er da $V_{S} = 12, 57 {dm}^{2} \cdot 5, 55 dm \approx 69, 76 {dm}^{3} .$ Nå kan vi summere volumene av halvkulen og sylinderen for å finne det totale volumet av pedalbøtten. $V = 16, 76 {dm}^{3} + 69, 76 {dm}^{3} = 86, 52 {dm}^{3} .$ som er det samme som $86, 52$ L.

Svar: Volumet av pedalbøtten er omtrent $86, 52$ L.

Mer om:

Denne oppgaven handler om

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

For flere forklaringer og eksempler, se lynkurset Geometri - areal og volum.

For å øve mer, se dette oppgavesettet om volum i Treningsleiren.

Oppgave 3 (4 poeng) Nettkode: E-4QQL

En nettbutikk selger leverpostei i porsjonspakninger og i bokser. Se nedenfor.

- $22$ g leverpostei i hver

porsjonspakning 

- $6$ porsjonspakninger i hver eske

- $32$ kroner per eske

200

g leverpostei i hver boks

a)

Hva ville en boks med $200$ g leverpostei ha kostet dersom prisen per gram hadde vært den samme som for leverposteien i porsjonspakningene?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må først finne ut prisen per gram for leverposteien i porsjonspakning og deretter bruke denne prisen til å bestemme hva en boks med $200$ g leverpostei ville koste.

Vi begynner med å finne ut prisen per gram for leverposteien i porsjonspakningen. Vi betaler $32$ kr for $6$ porsjonspakninger på $22$ g hver, altså for $6 \cdot 22 g = 132 g$ . Vi kan finne prisen per gram ved å dividere prisen på antall gram; $\frac{32 kr}{132 g} = \frac{32}{132} kr/g$ . Nå kan vi multiplisere denne prisen per gram med antall gram i den andre boksen, altså $200$ g. Dersom prisen per gram hadde vært den samme for leverposteien ville boksen på $200$ g kostet $\frac{32}{132} kr/g \cdot 200 g \approx 48 kr$

Svar: En boks med $200$ g leverpostein ville kostet omtrent $48$ kr.

Mer om:

Denne oppgaven handler om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proporsjoner

For flere forklaringer og eksempler, se artikkelen Målingsforhold.

b)

Boksen med $200$ g leverpostei koster $24$ kroner i nettbutikken.

Hvor mange prosent dyrere per gram er leverposteien i porsjonspakninger sammenliknet med leverposteien i boks?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne forholdet mellom prisen per gram for leverpostein i porsjonspakning og i boks på $200$ g.

Når boksen med leverpostei koster $24$ kr er prisen per gram for boksen $\frac{24 kr}{200 g}$ . Forholdet mellom prisen på leverpostei i porsjonspakning og i boks er da gitt ved $\frac{\frac{32}{132} kr/g}{\frac{24}{200} kr/g} = \frac{0, 2424 kr/g}{0, 12 kr/g} = 2, 02$ som er vekstfaktoren for $102 %$ vekst. Det betyr at leverposteien i porsjonspakning er $102 %$ dyrere sammenliknet med den i boks.

Svar: Leverposteien i porsjonspakning er $102 %$ dyrere.

Mer om:

Denne oppgaven handler om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

forhold

For flere forklaringer og eksempler, se artikkelen Målingsforhold.

Oppgave 4 (3 poeng) Nettkode: E-4QQP

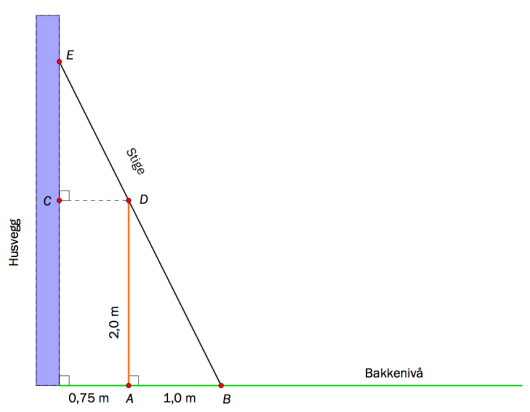
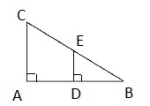
En stige står på skrå mot en husvegg. Stigen berører et gjerde. Gjerdet er $2, 0$ m høyt og står $0, 75$ m fra husveggen. Stigen er plassert $1, 0$ m fra gjerdet. Se figuren ovenfor.

a)

Forklar at $Δ A B D$ og $Δ C D E$ er formlike.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

To trekanter er formlike dersom de har parvis like vinkler, så vi kan sjekke om dette stemmer for $Δ A B D$ og $Δ C D E$ .

Det første vi kan merke oss er at begge trekantene er rettvinklet; i $Δ A B D$ er $∠ B A D = 90^{\circ}$ og i $Δ C D E$ er $∠ D C E = 90^{\circ}$ . I tillegg så er husveggen og gjerdet parallelle, så $A D | | C E$ . Det betyr at begge disse linjene vil gi like store vinkler når de krysses av samme linje, $B E$ , så $∠ C E D = ∠ A D B$ .

Siden vinkelsummen til en trekant alltid er lik $180^{\circ}$ betyr det at $∠ D B A = ∠ E D C$ , og trekantene er formlike.

Mer om:

Denne oppgaven handler om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

For flere forklaringer og eksempler, se artikkelen Formlikhet og kongruens.

For å øve mer, se dette oppgavesettet om formlikhet og kongruens i Treningsleiren.

b)

Hvor lang er stigen?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Lengden til stigen kan vi finne ved å addere $B D$ og $D E$ . Vi kan bruke Pytagoras læresetning for å bestemme $B D$ . Vi har også at i formlike trekanter er forholdet mellom samsvarende sider det samme.

For å finne lengden til stigen, må vi først finne lengden til $B D$ og $D E$ . Vi kan begynne med å finne lengden på $B D$ ved Pytagoras læresetning, og deretter bruke at de er samsvarende sider i de formlike trekantene. $B D$ er hypotenusen i $A B D$ , og ved Pytagoras læresetning har vi at $\begin{matrix} B D^{2} & = & A B^{2} + A D^{2} \\ B D^{2} & = & (1, 0 m)^{2} + (2, 0 m)^{2} \\ B D & = & \sqrt{5, 0} m \end{matrix}$ Fra formlikhet får vi at forholdet mellom samsvarende sider i $Δ A B D$ og $Δ C D E$ vil være likt. Det betyr at $\frac{D E}{C D} = \frac{B D}{A B}$ og vi kjenner verdien til $C D, B D$ og $A B$ . Da kan vi sette inn i likningen over: $\begin{matrix} \frac{D E}{0, 75 m} & = & \frac{\sqrt{5, 0} m}{1, 0 m} \\ D E & = & 0, 75 \cdot \sqrt{5, 0} m \end{matrix}$ Lengden til stigen er finner vi ved $B D + D E = \sqrt{5, 0} m + 0, 75 \sqrt{5, 0} m \approx 3, 9 m$

Svar: Stigen er $3, 9$ m.

Mer om:

Denne oppgaven handler om

Pytagoras læresetning

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

For flere forklaringer og eksempler, se artikkelen Formlike trekanter og kongruens.

For å øve mer, se dette oppgavesettet om formlikhet i Treningsleiren.

Oppgave 5 (4 poeng) Nettkode: E-4QQS

Ved et meieri blir det oppdaget en feil ved en av maskinene som skrur korker på kartongene. På kjølelageret er det $200$ kartonger med lettmelk og $100$ kartonger med helmelk. $\frac{2}{5}$ av kartongene med lettmelk og $\frac{1}{4}$ av kartongene med helmelk har ikke tett kork.

Tenk deg at du skal ta en kartong tilfeldig fra kjølelageret.

a)

Bestem sannsynligheten for at kartongen ikke har tett kork.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi har en uniform sannsynlighetsfordeling og da er sannsynligheten for en hendelse gitt ved $\frac{antall gunstige utfall}{antall mulige utfall}$ . For å kunne bestemme sannsynligheten må vi finne hvor mange av kartongene som ikke har tett kork.

Sannsynligheten for at vi trekker en kartong uten tett kork er gitt ved $P (ikke tett kork) = \frac{antall gunstige utfall}{antall mulige utfall} .$ Antall mulige utfall er det totale antall kartonger, altså $200 + 100 = 300$ kartonger. Antall gunstige utfall er antall melkekartonger uten tett kork. Der har vi at $200 \cdot \frac{2}{5} = 80$ av lettmelkene ikke har tett kork, og at $100 \cdot \frac{1}{4} = 25$ av helmelkene er uten tett kork. Det vil si at vi har $80 + 25 = 105$ kartonger uten tett lokk. Da får vi at $P (ikke tett kork) = \frac{antall gunstige utfall}{antall mulige utfall} = \frac{105}{300} = \frac{35}{100} = 35 % .$

Svar: Sannsynligheten for at kartongen ikke har tett kork er $35 %$ .

Mer om:

Denne oppgaven handler om uniform sannsynlighet.

For flere forklaringer og eksempler, se artikkelen Hvordan finner vi uniform sannsynlighet?.

For å øve mer, se dette oppgavesettet om uniforme sannsynlighetsmodeller i Treningsleiren.

b)

Anta at du tar en kartong som ikke har tett kork.

Bestem sannsynligheten for at kartongen inneholder lettmelk.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Sannsynligheten er fortsatt gitt ved $\frac{antall gunstige utfall}{antall mulige utfall}$ , der mulige utfall er kartongene uten tett lokk, og antall gunstige er antall lettmelk-kartonger uten tett lokk.

Vi finner sannsynligheten for at vi trekker en kartong som inneholder lettmelk, gitt at vi tar en kartong uten tett lokk ved $P (lettmelk | ikke tett kork) = \frac{antall gunstige utfall}{antall mulige utfall} .$ Antall mulige utfall er nå alle kartongene uten tett lokk, som vi fra a) vet er $105$ kartonger. Antall gunstige utfall er antall kartonger med lettmelk som ikke har tett lokk, som er $80$ . Da får vi at $P (lettmelk | ikke tett kork) = \frac{antall gunstige utfall}{antall mulige utfall} = \frac{80}{105} \approx 0, 762 = 76, 2 % .$

Svar: Sannsynligheten for at kartongen inneholder lettmelk er $76, 2 %$ .

Mer om:

Denne oppgaven handler om uniform sannsynlighet.

For flere forklaringer og eksempler, se artikkelen Hvordan finner vi uniform sannsynlighet?.

Oppgave 6 (3 poeng) Nettkode: E-4QQV

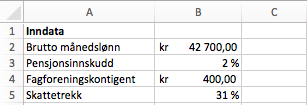
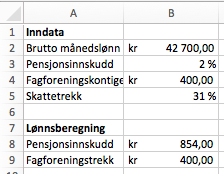
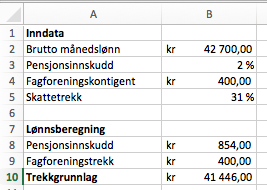
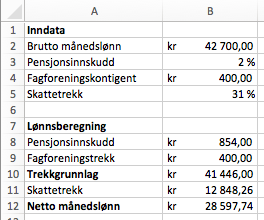
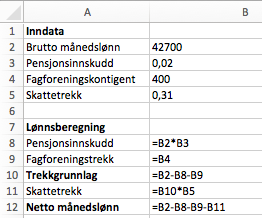
Du får vite følgende om Marte:

- Hun har en fast brutto månedslønn på $42 700$ kroner.

- Hun betaler $2 %$ i pensjonsinnskudd.

- Hun betaler $400$ kroner i fagforeningskontingent hver måned.

- Hun har et prosentkort med et skattetrekk på $31 %$ .

Lag et regneark der du legger inn opplysningene ovenfor på en oversiktlig måte. Bruk regnearket til å bestemme Martes netto månedslønn.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan bruke Excel til å lage regnearket. Netto månedslønn for Marte er lønn etter at pensjonsinnskudd, fagforeningskontigent og skatt er trukket fra.

Det første vi gjør er å føre inn den informasjonen vi får i oppgaven inn i regnearket.

Nå kan vi begynne å beregne hva de ulike trekkene vil bli. Det første er pensjonstrekk, som er på $2 %$ av fast lønn. For å bestemme hvor mye Marte trekkes i pensjon hver måned kan vi multiplisere cellene B2 og B3, så i cellen for Pensjonsinnskudd skriver vi =B2*B3. Fagforeningskontigenten trekkes som et fast beløp, og det vil være =B4.

Før vi kan regne ut skattetrekket må vi finne trekkgrunnlaget som vi beregner skattetrekk ut fra. Det er lønnen vi står igjen med etter vi har trukket fra pensjonsinnskuddet og fagforeningskontigenten. I regnearket vårt kan vi finne trekkgrunnlaget ved å ta =B2-B8-B9.

Skattetrekket kan vi nå finne ved å multiplisere trekkgrunnlaget med skatteprosenten, så ved å skrive inn =B10*B5.

Nå gjenstår bare å subtrahere de ulike trekkene fra brutto månedslønn. Det gjør vi ved å skrive inn =B2-B8-B9-B11.

Dersom vi ser på regnearket med formler, vil det se slik ut:

Mer om:

Denne oppgaven er om regneark,

Brutto månedslønn

Det beløpet du mottar fra arbeidsgiver i måneden, før skatter og avgifter er trukket fra.

brutto

Netto månedslønn

Lønnen du får utbetalt. Da er skatt, fagforeningskontigent og lignende trukket fra bruttolønna.

netto månedslønn

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Skatt

Skatt er en avgift som stat og kommune pålegger den enkelte borger å betale.

skatt

For flere eksempler og forklaringer, se lynkurset Skatt.

Oppgave 7 (5 poeng) Nettkode: E-4QQX

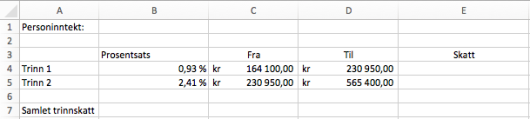
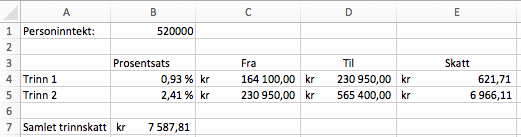
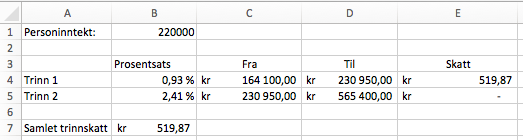
Arbeidstakere som har en personinntekt på over $164 000$ kroner, må betale trinnskatt. Trinnskatten på de to laveste trinnene beregnes slik:

- $0, 93 %$ av den delen av personinntekten som er mellom $164 000$ og

$230 950$ kroner

- $2, 41 %$ av den delen av personinntekten som er mellom $230 950$ og

$565 400$ kroner

Terje har en personinntekt på $220 000$ kroner.

Lise har en personinntekt på $520 000$ kroner.

a)

Hvor mye må hver av dem betale i trinnskatt?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må merke oss at de ikke må betale den oppgitte prosentandelen av hele personinntekten sin, men kun den delen som faller innenfor de ulike trinnene.

Terje har en personinntekt på $220 000$ kr. Det betyr at den delen av inntekten som er over $164 100$ kr, altså $220 000 kr - 164 100 kr = 55 900 kr$ må han betale $0, 93 %$ av i trinnskatt. De medfører at han må betale $55 900 kr \cdot 0, 93 % = 55 900 kr \cdot 0, 0093 = 519, 87 kr \approx 520 kr$ i trinnskatt.

Lise har en personinntekt på $520 000$ kr i året. Hun har $230 950 kr - 164 000 kr = 66 850$ av personinntekten i det laveste trinnet og må betale $0, 93 %$ av dette i trinnskatt. Det tilsvarer $66 850 kr \cdot 0, 0093 = 621, 71 kr \approx 622 kr .$ I tillegg er $520 000 kr - 230 950 kr = 289 050 kr$ i det neste trinnet som hun må betale $2, 41 %$ i skatt av, som tilsvarer $289 050 kr \cdot 0, 0241 = 6966, 11 kr \approx 6966 kr .$ Totalt må hun betale $622 kr + 6966 kr = 7588 kr$

Svar: Terje må betale $520 kr$ og Lise må betale $7588 kr$ i trinnskatt.

Mer om:

Denne oppgaven er om prosent og skatt.

For flere eksempler og forklaringer, se artikkelen Inntektsskatt.

b)

Lag ett regneark som arbeidstakere med en personinntekt på mellom $164 100$ og $565 400$ kroner kan bruke for å beregne hvor mye de må betale i trinnskatt.

Når en arbeidstaker legger inn sin personinntekt, skal regnearket beregne skatt på hvert trinn og samlet trinnskatt.

Bruk regnearket til å kontrollere svarene dine fra oppgave a).

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke Excel til å lage regnearket som beregner trinnskatten. Der kan vi bruke kommandoen ”Hvis” for å bestemme hvor mye av inntekten vi skal betale trinnskatt på for hvert trinn.

Det første vi kan gjøre er å føre opp opplysningene vi har om trinnskatt. Vi må ha en celle hvor vi kan føre inn personinntekten. I tillegg må vi ha en rad for hvert trinn som beregner hvor mye vi må betale i trinnskatt for det trinnet. I trinn 1 betaler vi $0, 93 %$ i trinnskatt for den delen av personinntekten som er mellom $164 100$ kr og $230 950$ kr og i trinn 2 betaler vi $2, 41 %$ i trinnskatt for den delen av personinntekten som er mellom $230 950$ kr og $565 400$ kr. Vi kan føre disse opplysningene inn i regnearket vårt som vist under:

Nå vil vi bruke en formel som beregner hvor mye trinnskatt vi må betale for hvert trinn. Da kan vi bruke “Hvis”-kommando i Excel. Den fungerer slik at vi skriver
Hvis(Betingelse; Hvis betingelsen stemmer så skjer dette ; Hvis betingelsen ikke stemmer skjer dette).
Vi kan begynne med å finne en formel for trinnskatt for trinn 1. Vi betaler trinnskatt for den delen av personinntekten som er mellom $164 100$ kr og $230 950$ kr. Det betyr at dersom personinntekten er lavere enn $230 950$ kr betaler vi trinnskatt av $𝚙 𝚎 𝚛 𝚜 𝚘 𝚗 𝚒 𝚗 𝚗 𝚝 𝚎 𝚔 𝚝 - 164 100$ kr, og dersom inntekten er høyere enn $230 950$ kr betaler vi trinnskatt for $230 950 kr - 164 100 kr$ . Vi kan merke oss at oppgaveteksten sier vi skal lage et regneark for arbeidstakere med en personinntekt på mellom $164 100$ kr og $565 400$ kr.
Dersom vi lar betingelsen i ”Hvis”-kommandoen være at personinntekten, i celle $𝐁 1$ , er mindre enn makssummen for trinn 1, i $𝐃 4$ , må vi betale $(𝐁 1 - 𝐂 4) \cdot 0, 93 %$ i trinnskatt. Siden personinntekten uansett skal være på større enn $164 100$ kr, har vi at hvis betingelsen ikke gjelder, altså at personinntekten er på mer enn $230 950$ kr, må vi betale $(𝐃 4 - 𝐂 4) \cdot 0, 93 %$ i trinnskatt. Formelen for å beregne trinnskatt for trinn 1, som vi kan skrive i celle $𝐄 4$ blir da $= Hvis (𝐁 1 < 𝐃 4; (𝐁 1 - 𝐂 4) * 𝐁 4; (𝐃 4 - 𝐂 4)^{*} 𝐁 4)$ For å betale trinnskatt for trinn 2 må vi ha personinntekten i $𝐁 1$ er over minstegrensen for dette trinnet i $𝐂 5$ , så det kan være betingelsen i ”Hvis”-kommandoen, altså at . Dersom betingelsen er innfridd må vi betale $𝐁 1 - 𝐂 5 \cdot 2, 41 %$ i trinnskatt. Dersom betingelsen ikke gjelder, altså at personinntekten er mindre enn $230 950$ , skal vi ikke betale noe i trinnskatt for trinn 2. Formelen for å beregne trinnskatt på trinn 2 kan vi da skrive inn i $𝐄 5$ som $= Hvis (𝐁 1 > 𝐂 5; (𝐁 1 - 𝐂 5) * 𝐁 5; 0)$ Siden vi vil beregne samlet trinnskatt må vi summere trinnskatt for trinn 1 og trinn 2. Det kan vi gjøre ved å skrive $= 𝐄 4 + 𝐄 5$ . Med disse formlene skrevet inn vil regnearket se slik ut:

Vi skal bruke regnearket til å kontrollere svarene fra oppgave a). Vi kan begynne med å teste det med Lise sin personinntekt. Da skriver vi inn $520 000$ i $𝐁 2$ , og får at regnearket vil se slik ut:

Vi kan se at vi får et øre i forskjell her, fra løsningen i a). Det kommer av at vi avrundet til to desimaler i utregningen i a), mens i Excel regner de med flere desimaler selv om de bare viser to i regnearket.

For å kontrollere Terje sin skatt, skriver vi inn $220 000 kr$ i $𝐁 2$ . Da vil regnearket se slik ut:

som er det samm vi får før avrunding i oppgave a).

Mer om:

Denne oppgaven er om regneark og

Skatt

Skatt er en avgift som stat og kommune pålegger den enkelte borger å betale.

skatt

For flere eksempler og forklaringer, se lynkurset Skatt.

Oppgave 8 (5 poeng) Nettkode: E-4QR0

a)

Vis at du vil bruke $6$ min og $40$ s på å kjøre $1$ mil dersom du holder en fart på $90$ km/h.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke at sammenhengen mellom fart $v$ , strekning $s$ og tid $t$ er gitt ved $v = \frac{s}{t}$ . Vi må passe på å bruke samme enhet for tid og strekning når vi regner.

Vi skal sjekke at vi bruker $6$ min og $40$ s dersom vi holder $90$ km/h på en strekning på $1$ mil.
Sammenhengen mellom fart $v$ , strekning $s$ og tid $t$ er gitt ved $v = \frac{s}{t}$ , som vi kan gjøre om og får at $t = \frac{s}{v}$ .

Før vi kan bruke denne formelen, må vi passe på at vi har samme enhet for tid og strekning. $1$ mil er det samme som $10$ km, så $s = 10$ km. $1$ time er det samme som $60 \cdot 60 s = 3600 s$ . Da kan vi skrive farten $v = \frac{90 km}{1 h} = \frac{90 km}{3600 s}$ . Tiden skal da være gitt ved $t = \frac{s}{v} = \frac{10 km}{\frac{90 km}{3600 s}} = 10 km \cdot \frac{3600 s}{90 km} = 400 s .$

Dette skal være det samme som $6$ min og $40$ s. Gjør vi det om til sekunder får vi at $6 min = 6 \cdot 60 s = 360 s$ , så vi har $360 s + 40 s = 400 s$ , som var det vi ville vise.

Mer om:

Denne oppgaven handler om

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

For flere forklaringer og eksempler, se lynkurset Vei, fart og tid.

Overskriften, tabellen og sitatet nedenfor er hentet fra nettsidene til Norges Automobil-Forbund (NAF).

Opprinnelig fart	Tidsbesparelse per mil om du øker farten til
Opprinnelig fart	$90$ km/h	$100$ km/h	$110$ km/h
$80$ km/h	$50$ s	$1$ min $30$ s	$2$ min $3$ s
$90$ km/h		$40$ s	$1$ min $13$ s
$100$ km/h			$33$ s

Løs oppgaven her

b)

Vis at du sparer ca. $1$ min og $13$ s per mil ved å øke farten fra $90$ km/h til $110$ km/h.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan finne ut hvor lang tid vi bruker på å kjøre $1$ mil i en fart på $110$ km/h.

På tilsvarende måte som i a) kan vi finne tiden vi bruker på å kjøre $1$ mil i $110$ km/h ved $t = \frac{s}{v} = \frac{10 km}{\frac{110 km}{3600 s}} = 10 km \cdot \frac{3600 s}{110 km} \approx 327 s .$ Så med en fart på $110$ km/h bruker vi $327$ s, som betyr at vi sparer $400 - 327 = 73$ sekunder. Det er det samme som $60 + 13$ , altså $1$ min og $13$ s som var det vi ville ha.

Mer om:

Denne oppgaven handler om

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

For flere forklaringer og eksempler, se lynkurset Vei, fart og tid.

c)

Anta at du kjører med en konstant fart på $110$ km/h.

Hvor langt må du kjøre for å spare $15$ min sammenliknet med om du hadde holdt en konstant fart på $90$ km/h?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Fra oppgave b) vet vi at på $1$ mil sparer vi $73$ s.

Vi skal finne ut hvor langt vi må kjøre for å spare $15$ minutter. Det er det samme som $15 \cdot 60 s = 900 s$ . I oppgave b) så vi at på sparte $73$ s/mil. For å spare $15$ min må vi kjøre $\frac{900 s}{73 s/mil} = 12, 3 mil .$

Svar: Vi må kjøre $12, 3$ mil.

Mer om:

Denne oppgaven handler om

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

For flere forklaringer og eksempler, se lynkurset Vei, fart og tid.

MAT1011 2017 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4QPL

Løsningsforslag

Brøk

Divisjon

Oppgave 2 (1 poeng) Nettkode: E-4QPN

Løsningsforslag

Oppgave 3 (3 poeng) Nettkode: E-4QPP

a)

Løsningsforslag a)

Formel

Lineære ligninger

b)

Løsningsforslag b)

Lineære ligninger

Oppgave 4 (2 poeng) Nettkode: E-4QPS

a)

Løsningsforslag a)

Divisjon

b)

Løsningsforslag b)

Oppgave 5 (3 poeng) Nettkode: E-4QPV

a)

Løsningsforslag a)

Verditabell

Funksjon

Andregradsuttrykk

b)

Løsningsforslag b)

Graf

Andregradsuttrykk

Oppgave 6 (4 poeng) Nettkode: E-4QPY

Løsningsforslag

Areal

Omkrets

Pytagoras læresetning

Omkrets

Areal

Kvadrat

Sirkel

Trekant

Rektangel

Oppgave 7 (2 poeng) Nettkode: E-4QQ0

Løsningsforslag

Lineære funksjoner

Lineære funksjoner

Stigningstall

Graf

Oppgave 8 (4 poeng) Nettkode: E-4QQ2

a)

Løsningsforslag a)

Alternativ løsning

Krysstabell

b)

Løsningsforslag b)

Sannsynlighet

c)

Løsningsforslag c)

Oppgave 9 (4 poeng) Nettkode: E-4QQ6

a)

Løsningsforslag a)

Proporsjon

b)

Løsningsforslag b)

Proporsjon

c)

Løsningsforslag c)

Proporsjon

DEL 2 Med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4QQC

a)

Løsningsforslag a)

Graf

GeoGebra

b)

Løsningsforslag b)