Krumningsegenskaper
Nå skal vi se på hvilken vei grafen til en funksjon bøyer seg. Dette kalles å analysere funksjonens krumningsegenskaper.
De matematiske uttrykkene vi skal bruke om dette, er konveks og konkav:
Konveks og konkav
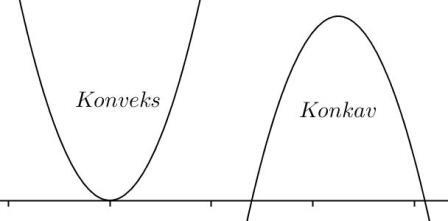
La være en kontinuerlig funksjon. I de intervallene der grafen til åpner seg oppover (som på figuren under), sier vi at er konveks. I de intervallene der grafen åpner seg nedover (som på figuren under), sier vi at er konkav.
Vi ønsker å finne krumningsegenskapene ved regning. Ikke minst ønsker vi å finne punktet der grafen skifter mellom å være konveks og konkav. Dette punktet kaller vi vendepunktet.
Akkurat som den deriverte er utslagsgivende for monotoniegenskapene til , er det den annenderiverte som avgjør krumningen til :
Teorem
Anta at er to ganger deriverbar på intervallet . Da har vi at
for alle er konveks i .
for alle er konkav i .
Punktet der den annenderiverte skifter fortegn kaller vi vendepunktet.
Vi finner som regel vendepunktet ved å sette .
Huskeregel: Hvis er positiv, får vi et smil :), men hvis er negativ, får vi en sur munn :(.
Eksempel
Oppgave. Finn ut hvor funksjonen f er konveks og konkav, når
Løsning. Vi begynner med å derivere to ganger:
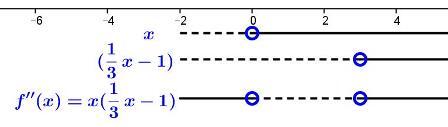
Vi bruker teoremet over som forteller oss at krumningen er avhengig av om den annenderiverte er positiv eller negativ. Vi lager derfor fortegnslinja til .
Vi faktoriserer utrykket ved å trekke ut og får
.
Så kan vi enkelt lage fortegnslinja ved å kombinere de to faktorene:
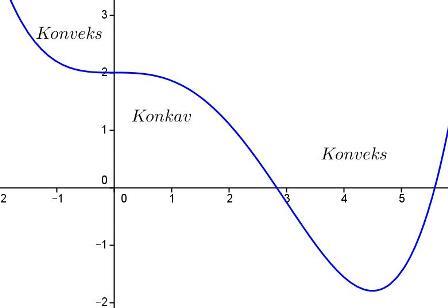
Vi leser av at den annenderiverte er positiv, , på intervallene og . Grafen er altså konveks i disse intervallene. På intervallet er den annenderiverte negativ, og følgelig er grafen konkav her. Grafen under bekrefter det vi har funnet.
Vendepunktene finner vi nå ved å se på fortegnslinja når skifter fortegn. Vi ser at dette skjer i og , så dette er vendepunktene våre.
Grafen til f(x).
Del på Facebook