Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2017 Vår
Eksamenstid
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler på Del 1
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Hjelpemidler på Del 2
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Fremgangsmåte
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
DEL 1 Uten hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4QS3
I en klasse er det elever. Tabellen nedenfor viser hvor mange søsken de elevene har.
| Antall søsken | Frekvens |
Bestem gjennomsnittet, medianen, typetallet og variasjonsbredden .
Oppgave 2 (1 poeng) Nettkode: E-4QS5
Ved en skole er det elever. En dag tok av elevene buss til skolen.
Hvor mange prosent av elevene tok buss til skolen denne dagen?
Oppgave 3 (2 poeng) Nettkode: E-4QS7
Regn ut
Oppgave 4 (2 poeng) Nettkode: E-4QS9
I L vann er det omtrent vannmolekyler.
Hvor mange vannmolekyler er det i dl vann?
Oppgave 5 (3 poeng) Nettkode: E-4QSB
I er verdien av en leilighet kroner.
Per antar at verdien vil stige med kroner hvert år.
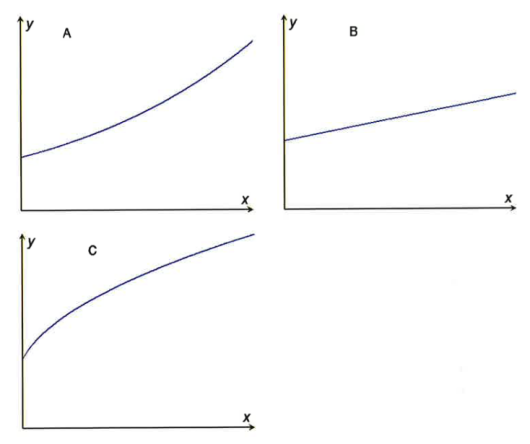
a)
Sett opp en modell som viser verdien av leiligheten år etter dersom det går slik Per antar.
b)
Kari antar at verdien vil stige med hvert år.
Sett opp en modell som viser verdien av leiligheten år etter dersom det går slik Kari antar.
c)
Hvilken av grafene nedenfor kan være grafen til ?
Hvilken av grafene nedenfor kan være grafen til ?
Begrunn svarene dine.
Oppgave 6 (6 poeng) Nettkode: E-4QSF
Et år deltok elever i en konkurranse. Besvarelsene ble vurdert, og lærerne laget en tabell. Tabellen ser du nedenfor, men her mangler noen av tallene lærerne satte inn.
| Poengsum | Frekvens | Relativ frekvens | Klassemidtpunkt |
a)
Tegn av tabellen ovenfor, og fyll inn tallene som mangler.
b)
Bestem gjennomsnittlig poengsum for elevene som deltok i konkurransen.
c)
Et annet år deltok elever i konkurransen. Tabellen nedenfor viser poengfordelingen.
| Poengsum | Frekvens |
Bestem medianen for poengsummene til elevene som deltok i konkurransen dette året.
Oppgave 7 (7 poeng) Nettkode: E-4QSJ
Ovenfor ser du tre figurer. Figurene er satt sammen av små, blå pinner. Hver pinne har lengden cm. Tenk deg at du skal fortsette å lage figurer etter samme mønster.
a)
Hvor mange pinner trenger du for a lage figur ?
Bestem omkretsen av figur .
b)
Bestem et uttrykk for antall pinner i figur uttrykt ved .
c)
Bestem et uttrykk for omkretsen av figur uttrykt ved .
d)
En figur som følger samme mønster som ovenfor, har en omkrets på cm.
Bestem antall pinner i denne figuren .
DEL 2 Med hjelpemidler
Oppgave 1 (8 poeng) Nettkode: E-4QT2
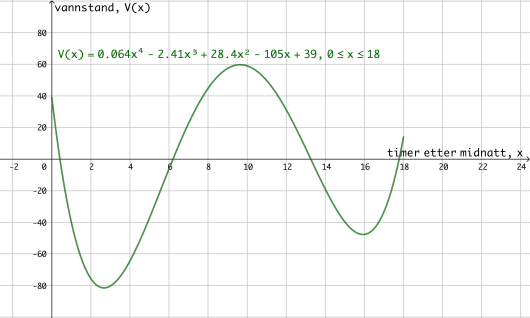
Funksjonen gitt ved
viser vannstanden centimeter over eller under middelvann timer etter midnatt i Tromsø en dag.
a)
Bruk graftegner til å tegne grafen til .
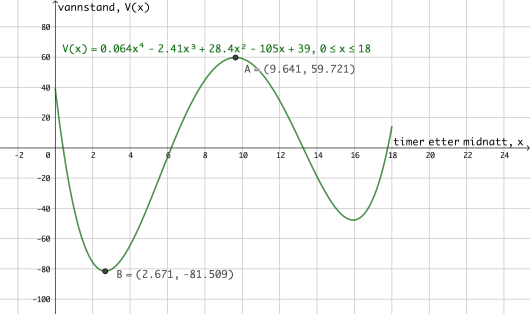
b)
Vis at vannstanden er ca. cm under middelvann én time etter midnatt og ca. cm over middelvann timer etter midnatt.
c)
Bestem forskjellen mellom høyeste og laveste vannstand i perioden fra midnatt og fram til klokka .
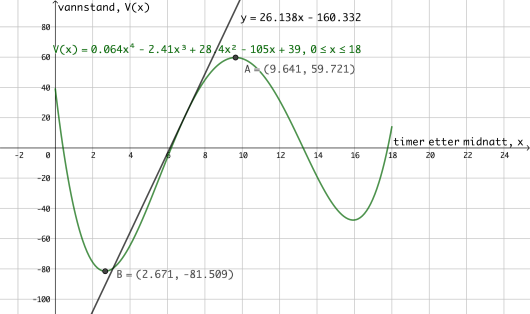
d)
Bestem den momentane vekstfarten til funksjonen klokken .
Gi en praktisk tolkning av dette svaret.
Oppgave 2 (2 poeng) Nettkode: E-4QTB
Emil betalte kroner for en leilighet. Han betalte mer enn prisantydningen.
Hva var prisantydningen for denne leiligheten?
Oppgave 3 (2 poeng) Nettkode: E-4QTD
For år siden arvet Ida penger. Hun satte alle pengene inn på en ny bankkonto.
Hun har fått en fast rente på per år. I dag har hun kroner på kontoen.
Hvor mye penger arvet Ida?
Oppgave 4 (2 poeng) Nettkode: E-4QTJ
Beskriv en praktisk situasjon som passer med grafen ovenfor.
Oppgave 5 (4 poeng) Nettkode: E-4QTO
Ved en skole kom alle elevene som hadde valgt , opp til skriftlig eksamen. Histogrammet nedenfor viser poengfordelingen.
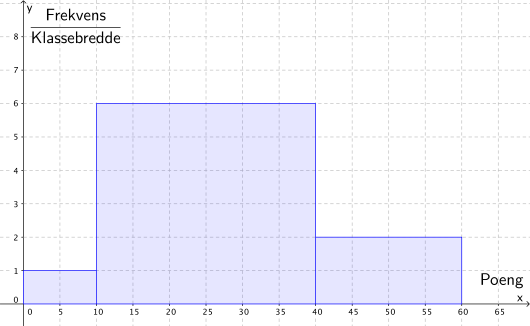
a)
Vis at det til sammen var elever i -gruppene.
b)
Bestem gjennomsnittlig poengsum for elevene.
Oppgave 6 (4 poeng) Nettkode: E-4QTR

Temperaturen blir lavere jo høyere over havet vi kommer. Spiterstulen ligger m over havet. Toppen av Galdhøpiggen ligger m over havet. En dag er temperaturen pa Spiterstulen .
Vi antar at temperaturen , meter over Spiterstulen denne dagen er gitt ved
a)
Hvor høyt over Spiterstulen vil du være når temperaturen er denne dagen?
b)
Bestem temperaturen på toppen av Galdhøpiggen denne dagen.
c)
Hvor mange grader synker temperaturen med per m stigning denne dagen?
Oppgave 7 (5 poeng) Nettkode: E-4QU6
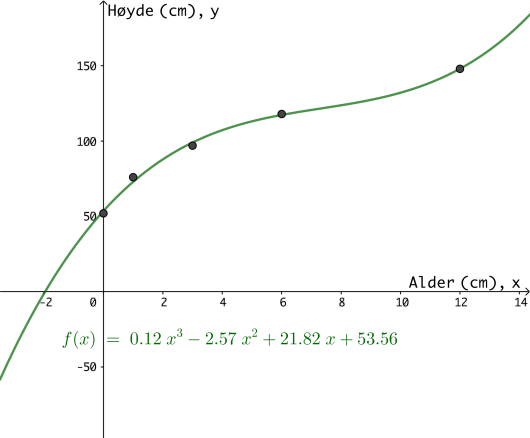
Tabellen nedenfor viser hvor høy Per var og år etter fødselen.
| Alder (år) | 0 | 1 | 3 | 6 | 12 |
| Høyde (cm) | 52 | 76 | 97 | 118 | 148 |
a)
Bruk opplysningene i tabellen til å bestemme en tredjegradsfunksjon som tilnærmet viser høyden til Per de første leveårene.
b)
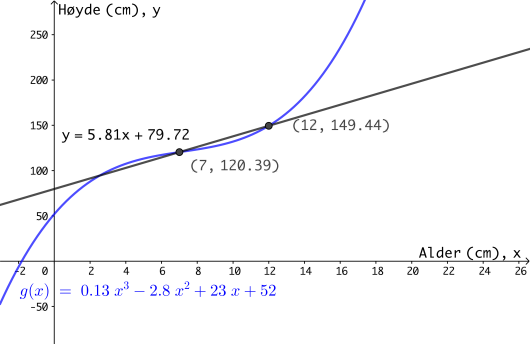
Espen er år. Funksjonen gitt ved
viser høyden hans cm, år etter fødselen.
Bestem Espens gjennomsnittlige vekstfart fra han var år, til han ble år.
c)
Sitatet nedenfor er hentet fra nettsidene til Norsk Helseinformatikk AS.
| "Gutter har en maksimal høydevekst pa ca. cm per år midt i puberteten. Etter vekstspurten i puberteten avtar veksthastigheten ned mot null." |
Anta at Espen kommer i puberteten når han er år. Puberteten varer vanligvis i to-tre år.
Ta utgangspunkt i sitatet ovenfor, og vurder om funksjonen kan brukes til å bestemme høyden til Espen etter at han har fylt år.
Oppgave 8 (4 poeng) Nettkode: E-4QUA
|
|
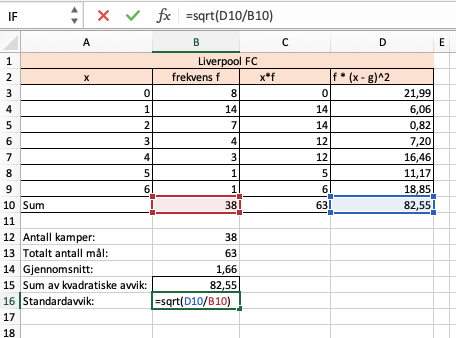
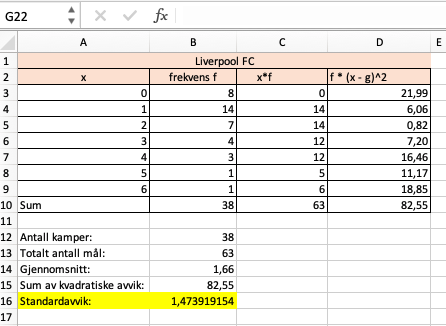
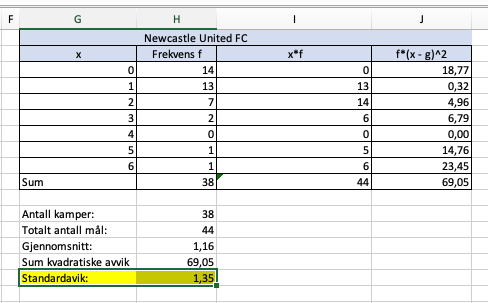
||||||||||||||||||||||||||||||||||||
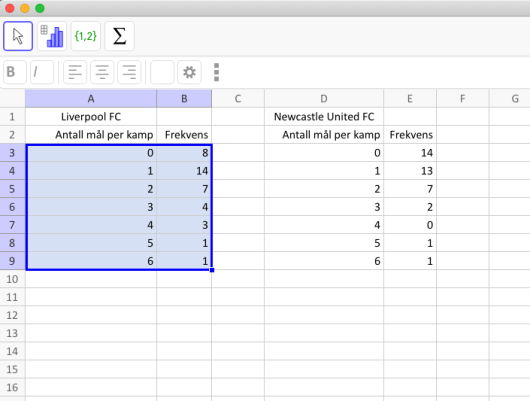
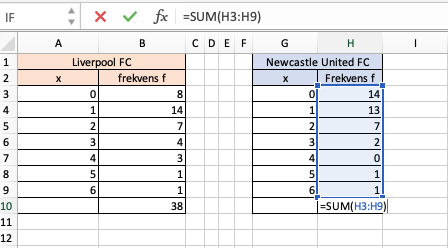
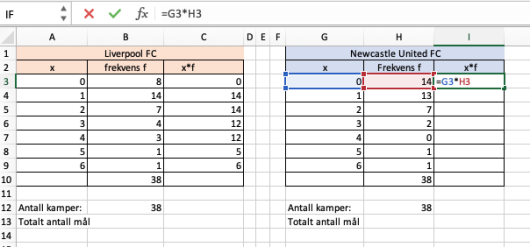
Tabellene ovenfor viser hvor mange mål Liverpool FC og Newcastle United FC skåret per kamp i sesongen .
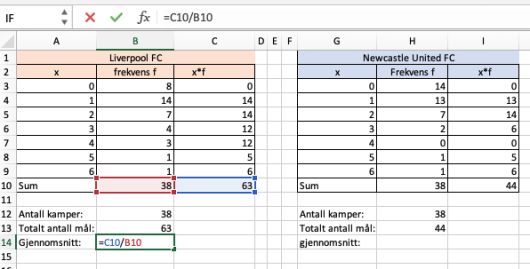
a)
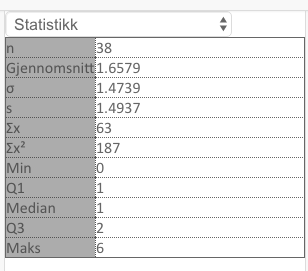
Bestem gjennomsnittet og medianen for antall skårede mål per kamp for begge klubbene.
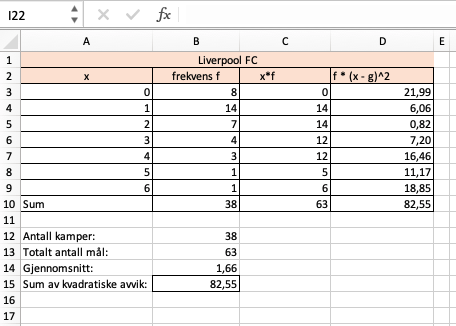
b)
Bestem standardavviket for antall skårede mål per kamp for begge klubbene.
Hva forteller dette oss?
Oppgave 9 (5 poeng) Nettkode: E-4QUD
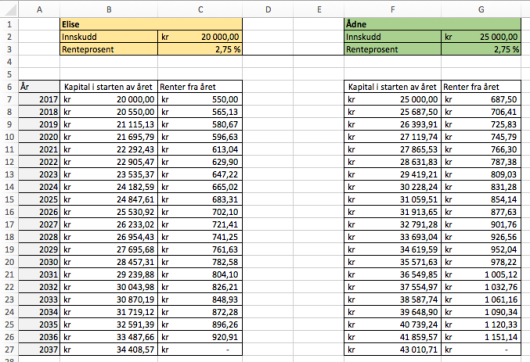
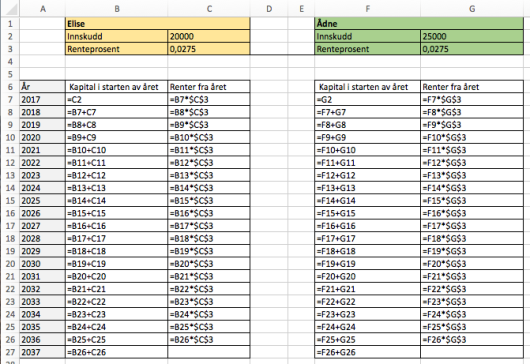
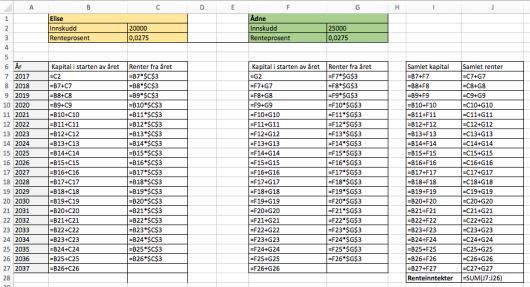
Elise og Ådne opprettet hver sin bankkonto . januar . Elise satte inn kroner. Ådne satte inn kroner. Begge får en rente pa per år, og begge lar pengene stå urørt.
a)
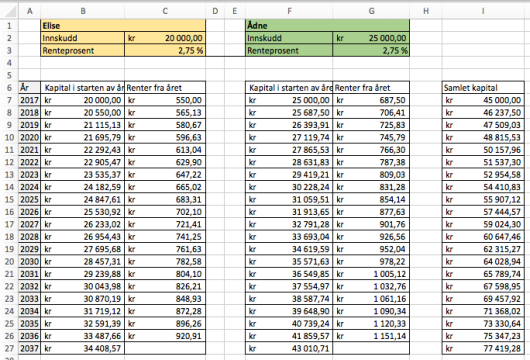
Lag et regneark som gir en oversikt over hvor mye Elise og Ådne vil ha i banken hvert år fram til og med . desember .
b)
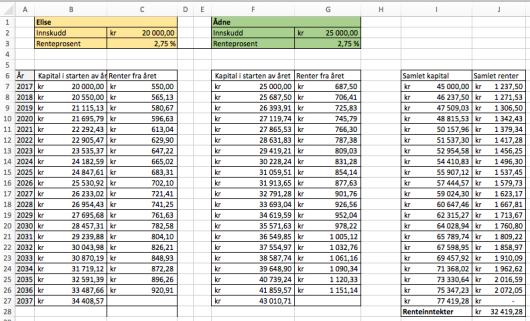
Hvor mange år går det før de har mer enn kroner i banken tilsammen?
c)
Hvor mye vil Elise og Ådne til sammen få i renter disse årene?