
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2015 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 13 oppgaver. Del 2 har 5 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Tegninger, grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4BGE
Regn ut og skriv svaret på standardform
Løsningsforslag
Jeg tenker
Vi skriver om
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Vi skriver først nevneren om til et tall på standardform:
Det gir
For å forenkle brøken kan vi potensreglene
, , og
Da skriver vi at
Fordi svaret er på formen der og , er svaret skrevet på standardform.
Svar:
Mer om
Denne oppgaven handler om
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Flere forklaringer og eksempler på hvordan man skriver tall på standardform finner du i artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.
Visste du at?
Vi bruker tall på standardform for å lettere uttrykke veldig store og veldig små tall. Et eksempel er Placks konstant , som er forholdet mellom energien og frekvensen til lys. Den har verdien . Et annet tall er det ekstremt store stallet ”googol”, som har verdien .
Oppgave 2 (2 poeng) Nettkode: E-4BGG
Løs likningssystemet
Løsningsforslag
Jeg tenker
Dette er et likningssystem med to likninger og to ukjente. Vi kan enten bruke addisjonsmetoden eller substitusjonsmetoden for å løse det.
Vi kan løse likningssystemet enten ved å bruke substitisjonsmetoden, som også er kalt innsetttingsmetoden, eller ved addisjonsmetoden. Under "Alternativ løsning" løser vi den ved addisjonsmetoden.
Vi begynner med å nummerere likningene:
For å løse likningssystemet ved substitusjonsmetoden bruker vi likning til å finne et uttrykk for :
Nå kan vi substituere for i likning slik at vi får en likning med kun én ukjent:
Nå kan vi finne ved å sette inn for i likning :
Svar:
Alternativ løsning
Vi nummererer likningene:
Addisjonsmetoden går ut på å addere hver av sidene i likningen, slik at den ene ukjente faller bort. Ofte må vi først mutliplisere med et passende tall i en eller fler av likningene.
Vi multipliserer likning med tallet . Da får vi likningssystemet:
Nå adderer vi likning og slik at faller bort:
Vi har regnet ut at . Satt inn i gir dette:
Mer om
Denne oppgaven handler om
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Flere forklaringer og eksempler finner du i lynkurset Lineære likninger med flere ukjente.
For å øve mer, se oppgavesettet om likningssystemer i Treningsleiren.
Visste du at?
Ved å skrive om begge likningene som et uttrykk for , får vi at Dette kan vi tenke på som likningen til to rette linjer. Hvis vi tegner disse inn i samme koordinatsystem, finne vi løsningen til likningsystemet, som er skjæringspunktet mellom disse to grafene.
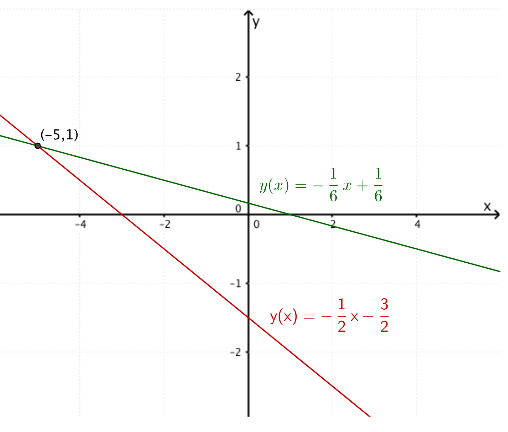
Skjæringspunktet mellom de to linjene er da nøyaktig det settet av verdier og som er løsningen av likningsystemet.
Oppgave 3 (2 poeng) Nettkode: E-4BGI
Løs ulikheten
Løsningsforslag
Jeg tenker
Ulikheten kan løses som en andregradslikning. Vi bruker
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.
Vi bruker abc-formelen til å finne nullpunktene til . Altså ved å løse likningen :
Da får vi de to løsningene:
Vi kan derfor skrive .
Nå tegner vi et fortegnsskjema:
Den første faktoren, , er negativ for
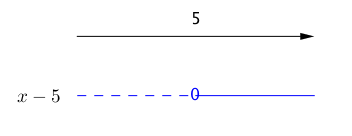
og den andre faktoren, , er negativ for :
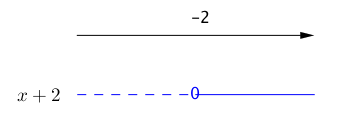
Vi setter fortegnsskjemaene for og sammen, og finner fortegnskjema for produktet:

Svar: for .
Mer om
Denne oppgaven handler om ulikheter.
Flere forklaringer og eksempler på hvordan man løser ulikheter finner du i lynkurset Ulikheter.
For å øve mer, se oppgavesettet om ulikheter av andre grad i Treningsleiren.
Visste du at?
Vi kunne også tenkt oss frem til løsningen. Annengradslikningen har løsninger og . Grafen til enhver annengradslikning er en parabel og i de to nullpunktene skifter funksjonene fortegn. Ved å sette inn store postive eller negative tall, vil funksjonsuttrykket forbli positivt og stort. Det betyr at det eneste stedet funksjonen har negativt fortegn, må være mellom de to nullpunktene. Det betyr at hvis, og bare hvis, eller .
Oppgave 4 (4 poeng) Nettkode: E-4BGK
Regn ut og skriv svaret så enkelt som mulig
a)
Løsningsforslag a)
Jeg tenker
Vi ser at hver faktor er en
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
I denne oppgaven vil vi bruke følgende definisjoner og potensregler:
1)
2)
3) for alle
4) for alle slik at er definert.
Vi tar for oss faktor for faktor og skriver om til toerpoens.
I den første faktoren ser vi at og bruker 1) til å skrive om
.
Vi bruker 2) til å skrive om den andre faktoren til
.
Til den tredje faktoren kan vi bruke 3) til å skrive om
.
I den siste faktoren merker vi oss at og bruker 4) og 1) til å skrive om
.
Vi kan nå sette inn de forenklede uttrykkene og regne ut. Da får vi at uttrykket er lik
.
Svar: 2
Mer om
Denne oppgaven handler om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Potens
Eksempel:
Flere forklaringer og eksempler finner du i artikkelen Rask gjennomgang av regneregler i lynkurset Potenser og røtter.
For å øve mer, se oppgavesettet om potenser i Treningsleiren.
b)
Løsningsforslag b)
Jeg tenker
Vi bruker reglene for brøker, potenser og røtter til å forenkle de enkelte faktorene og leddene før vi regner ut.
Vi husker at
Vi kan skrive
Da får vi at:
Svar:
Mer om
Denne oppgaven er om
Kvadratrot
Kvadratrot har symbolet .
Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.
Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi . Det skrives .
Flere forklaringer og eksempler på hvordan man regner ut kvadratrøtter finner du i artikkelen Kvadratrøtter.
For å øve mer, se oppgavesettet om potenser i Treningsleiren.
Visste du at?
De vanlige regnereglene er ekstremt nyttige, men man må holde tungen rett i munnen når man bruker dem. For eksempel er følgende ingen bevis for at
Kan du finne feilen her?
Oppgave 5 (2 poeng) Nettkode: E-4SBN
Løs likningen
Løsningsforslag
Jeg tenker
Dette er en logaritmelikning. Her kan vi bruke at logaritmen til et positivt tall oppfyller den egenskapen at .
Vi vil bruke den egenskapen at , og opphøyer derfor 10 i begge sider;
Siden følger det at
som er løsninger av likningen.
Svar:
Mer om
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
Du kan lese mer om logaritmer i artikkelen Den Briggske logaritmen.
For å øve mer, se oppgavesettet om logaritmer i Treningsleiren.
Oppgave 6 (1 poeng) Nettkode: E-4BGQ
Bestem slik at uttrykket blir et fullstendig kvadrat.
Løsningsforslag
Jeg tenker
Et
Fullstendig kvadrat
Et kvadrat (ofte kalt et fullstendig kvadrat) et et uttrykk som er opphøyd i 2, for eksempel
.
Første kvadratsetning
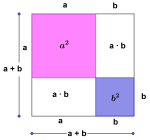
Første kvadratsetning sier at
.
Ifølge
Første kvadratsetning

Første kvadratsetning sier at
.
for alle .
Ser vi på uttrykket vårt har vi at , altså må vi ha .
Setter vi inn for i likningen over får vi at
Det betyr at:
Vi kan sjekke om dette stemmer nå ved å regne ut
som betyr at når kan uttrykket skrives på formen .
Svar:
Alternavtiv løsning
Hvis et polynom av grad to bare har ett
Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
Den eneste måten å få dette til bare å gi én løsning er ved å bli kvitt -leddet. Med andre ord må vi ha
som betyr at For at skal være et fullstendig kvadrat må altså
Mer om
Denne oppgaven handler om
Første kvadratsetning

Første kvadratsetning sier at
.
Flere forklaringer og eksempler på hvordan man fullfører kvadratet finner du i artikkelen Å fullføre kvadratet.
For å øve mer, se oppgavesettet om kvadratsetninger i Treningsleiren.
Visste du at?
Det finnes ulike måter å bestemme på. Et alternativ er for eksempel å tenke på de tre leddene og og som arealer til to kvadrater med sidelengder og og ett rektangel med bredde og høyde . Hvis vi klipper rektangelet langs midten av bredden, får vi to rektangler med høyde og bredde som vi kan legge langs to av sidene. Da vil du se at sidelengden må være lik sidelengden i kvadratet . Det betyr at .
En annen, og kanskje enda finurlig løsning, er ved å vise at hvis polynomet kan skrives som et fullstendig kvadrat, så må den laveste verdien være nullpunktet til funksjonen. Ved å finne at det laveste punktet er i og kreve at dette er et nullpunkt, vil du finne at .
Oppgave 7 (2 poeng) Nettkode: E-4BGS
Skriv så enkelt som mulig
Løsningsforslag
Jeg tenker
Ved å løse opp parentesene og trekke sammen leddene som innholder like potenser av , kan vi forenkle uttrykket.
Vi vil løse opp parentesene og deretter trekke sammen de leddene som er samme potens av .
Ved å følge vanlige regneregler for multiplikasjon finner vi at
Alternativ løsning
Siden begge leddene innholder kan dette trekkes utenfor. Da finner vi at
Svar: .
Mer om
Denne oppgaven er om
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.
Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
Flere forklaringer og eksempler på hvordan man løser opp parenteser finner du i artikkelen Fortegn foran parenteser.
For å øve mer, se oppgavesettet om parantesuttrykk i Treningsleiren.
Oppgave 8 (2 poeng) Nettkode: E-4BGU
Skriv så enkelt som mulig
Løsningsforslag
Jeg tenker
Vi skal forkorte en brøk av algebraiske uttrykk. Da må vi prøve å finne felles faktorer i teller og nevner. Her kan vi få bruk for
Første kvadratsetning

Første kvadratsetning sier at
.
Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:
.
Først ønsker vi å faktorisere telleren og nevneren. Dette kan vi gjøre med kvadratsetningene. Siden dette er andregradsuttrykk, kan vi også bruke
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
Vi ser først på telleren, og her kan vi bruke
Andre kvadratsetning
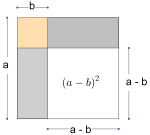
Andre kvadratsetning sier at
.
Videre må vi faktorisere nevneren. Vi kan først faktorisere ut som er felles faktor.
Nå kan vi legge merke til at og vi kan bruke
Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:
.
Nå har vi faktorisert teller og nevner, så da kan vi forkorte felles faktorer. Det gir oss:
Svar:
Mer om
Denne oppgaven er om
Andregradslikning
En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:
Likningen kan løses ved hjelp av abc-formelen.
For å lære mer om hvordan man faktoriserer og løser andregradslikninger kan du lese lynkurset Andregradslikninger.
For å øve mer, se oppgavesettet om faktorisering i Treningsleiren.
Oppgave 9 (2 poeng) Nettkode: E-4BH1
En rett linje går gjennom punktene og .
Bestem likningen for den rette linjen ved regning.
Løsningsforslag
Jeg tenker
En rett linje kan skrives som . Ved hjelp av de gitte punktene finner vi
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Linjen går gjennom punktene og .
Begge disse punktene vil tilfredstille samme likning på formen .
Vi setter inn disse verdiene i uttrykket for linja
Setter vi inn får vi:
Setter vi inn får vi:
Sammen gir disse to uttrykkene oss et likningssett med to ukjente.
Vi løser likningsettet med substitusjon. Likning gir oss . Vi setter inn i likning .
Vi setter inn i likning for å finne . (Vi får det samme svaret om vi bruker likning ).
Linjen kan skrives som
.
Alternativ løsning
Vi kan også bruke ettpunktsformelen, som sier at når vi kjenner stigningstallet til en linje og et punkt kan vi finne likningen til linja ved formelen
Stigningstallet til linja finner vi ved å se på forholdet mellom endring i -verdi og endring i -verdi. Det kan vi finne ved
Nå kan vi bruke ettpunktsformelen, og da er det vilkårlig hvilket av de to punktene vi bruker. Vi velger å bruke for å bestemme likningen til linja.
Da får vi
Svar:
Mer om
Denne oppgaven handler om
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere forklaringer og eksempler se artiklene Grafisk løsninger av likninger og Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.
Oppgave 10 (5 poeng) Nettkode: E-4BIR
og er gitt nedenfor.
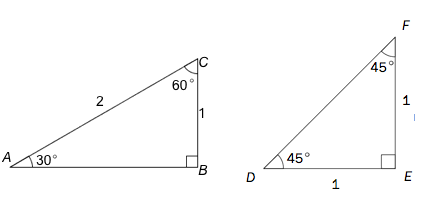
a)
Bestem eksakte verdier for og .
Løsningsforslag a)
Jeg tenker
Her ser vi to
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Pytagoras læresetning

Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Siden er en rettvinklet trekant med hypotenus følger det fra Pytagoras læresetning at:
og siden og må vi ha
som kan skrives:
Altså har vi funnet at:
Merk at vi har latt være å ta med den negativ løsningen , siden denne ikke gir mening når vi leter etter en sidelengde.
er også en rettvinklet trekant med hypotenus . Da følger det at:
Siden er:
Det betyr at
Svar: og .
Mer om
Denne oppgaven handler om
Pytagoras læresetning

Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Flere forklaringer og eksempler på hvordan man kan bruke Pytagoras setning for å finne sidelengder finner du i artikkelen Pytagoras setning.
For å øve mer, se oppgavesettet om Pytagoras læresetning i Treningsleiren.
Visste du at?
Pytagoras læresetning er en av de mest kjente resultatene i matematikkfaget. I læresetningen tenker vi på tallene og som sidelengdene i en rettvinklet trekant og dette kan vi anvende på andre uttrykk som er på formen til læresetningen.
Et kjent resultat fra fysikken er for eksempel , som sier at produktet av et objekts masse, , og kvadratet av lyshastigheten, , er lik objektets energi, . Denne likningen er bare sann for stillestående objekter. Hvis objektet beveger seg, er energien gitt ved , der er bevegelsesmengden til objektet. Siden dette likner på Pytagoras læresetning, kan vi visualisere dette som en rettvinklet trekant med hypotenus og kateter og .
b)
Skriv av tabellen nedenfor. Bruk og , gjør beregninger og fyll ut det som mangler i tabellen. Bruk eksakte verdier.
Løsningsforslag b)
Jeg tenker
I
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Tangens
En trigonometrisk funksjon.
Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.
Katet
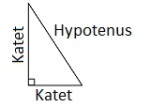
Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter.
Hypotenus

Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.
For å fylle inn i tabellen bruker vi at
og
Vi begynner med å fylle inn tabellen i raden for . Da kan vi se på , og . Da er motstående kateten og hosliggende kateten. Siden hypotenusen følger det at
På tilsvarende måte kan vi se på , med og henholdsvis som motstående og hosliggende katet. Dermed får vi:
For å finne verdiene for ser vi på , og , med hypotenus og henholdsvis som motstående og hosliggende katet.
Da får vi
Svar: Den utfylte tabellen blir:
Mer om
Denne oppgaven handler om
Trigonometri
Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.
Du kan lese mer om hvordan man regner med sinus, cosinus og tangens i lynkurset Trigonometri.
For å øve mer, se oppgavesettet om lengdeberegninger ved hjelp av sinus, cosinus og tangens i Treningsleiren.
Visste du at?
Ved å studere tabellen vi har fylt ut i denne oppgaven vil vi kanskje oppdage et mønster. Vi ser at , og . Dette er fordi motstående katet til en vinkel, er den hosliggende kateten til den andre vinkelen. Hvis er en vinkel mellom og har vi altså funnet formlene
og
Dette betyr at vi også har funnet at
Oppgave 11 (5 poeng) Nettkode: E-4BJD

Tenk deg at du har ni flasker med smoothie i kjøleskapet, to «Surf», tre «Jump» og fire
«Catch». Du tar tilfeldig to flasker.
a)
Bestem sannsynligheten for at du ikke tar en «Jump»-smoothie.
Løsningsforslag a)
Jeg tenker
Sannsynlighet er forholdet mellom antall gunstige
Utfall
Mulig resultat av en hendelse.
Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.
Vi skal finne sannsynligheten for at to flasker vi trekker ikke er en «Jump»-smoothie. Vi kan gjøre dette på flere måter.
I kjøleskapet er det «Jump»-smoothie av flasker. Dette betyr at antall gunstige utfall, altså antall flasker som ikke er «Jump»-smoothie er lik
Sannsynligheten for at den første flasken en trekker ikke er «Jump»-smoothie, , er lik
Når vi skal ta ut den andre flasken, er det igjen gunstige utfall og totalt flasker, og derfor er sannsynligheten for å ikke trekke en «Jump»-smoothie, , lik
Sannsynligheten for ikke å ta en «Jump»-smoothie når vi tar to flasker ut av kjøleskapet er lik
Alternativ løsning
Det er nok å finne hvor mange måter vi kan velge to flasker slik at ingen av dem er en «Jump»-smoothie.
Den første flasken vi velger kan ikke være en «Jump»-smoothie. Det betyr at den første flasken må være en av de seks andre. For hver av disse seks mulige valgene av flasker skal vi velge enda en flaske som ikke er en «Jump»-smoothie. Siden det da er fem gunstige flasker igjen må antall måter å velge to flasker uten å velge en «Jump»-smoothie være gitt ved
For å finne antall mulige valg av to flasker ser vi at den første flasken må velges blant de ni flaskene. Altså er det ni måter å velge den første flasken på. For hver av disse ni mulighetene kan den andre flasken velges blant de åtte resterende flaskene. Det betyr at antall mulige er gitt ved Sannsynligheten for ikke å ta en «Jump»-smoothie er altså
Svar: Sannsynligheten for at vi ikke tar en "Jump"-smoothie er .
Mer om
Denne oppgaven handler om
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Flere forklaringer og eksempler på hvordan man regner med sannsynlighet i lynkurset Sannsynlighet.
For å øve mer, se oppgavesettet om produktsetningen i Treningsleieren.
b)
Bestem sannsynligheten for at du tar én «Surf»- og én «Catch»-smoothie.
Løsningsforslag b)
Jeg tenker
Det er to måter vi kan trekke én "Surf"- og én "Catch"-smoothie. Fra addisjonssetningen vet vi at vi kan finne sannsynligheten for hver av dem og addere dem sammen.
Vi har to mulige måter å trekke én "Surf"- og én "Catch"-smoothie. Vi kan enten først ta en "Surf" og deretter en "Catch", (SC), eller først en "Catch" og deretter en "Surf", (CS).
Sannsynligheten for å velge én av de to «Surf»-flaskene blant de ni flaskene er gitt som
.
Sannsynligheten for å velge en flaske av typen «Catch» der fire av de resterende åtte flaskene er «Catch» er lik
,
så sannsynligheten for å trekke først en "Surf" og deretter en "Catch" er
Tilsvarende får vi at sannsynligheten for å trekke en "Catch" og en "Surf" er
Vi kan se at rekkefølgen ikke har noe å si for sannsynligheten for hver av hendelsene.
Sannsynligheten for å velge én «Surf» og én «Catch» er da gitt ved
Svar: Sannsynligheten for å ta en "Surf" og em "Catch" er .
Mer om
Denne oppgaven handler om
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Flere forklaringer og eksempler finner du i artikkelen Betinget sannsynlighet og produktsetningen lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om produktsetningen i Treningsleieren.
c)
Bestem sannsynligheten for at du tar to like flasker.
Løsningsforslag c)
Jeg tenker
Det er tre måter å velge to like flasker på: enten to «Jump», to «Catch» eller to «Surf». Vi bruker
Addisjonssetningen
Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.
Sannsynligheten for å velge to «Jump» er gitt ved
siden den første flasken velges fra totalt ni flasker der tre er gunstige, og den andre flasken da velges fra åtte flasker der to er gunstige. Helt tilsvarende finner vi at sannsynligheten for å velge to «Catch» er
Sannsynligheten for å velge to «Surf» er gitt ved
Hvis vi bare ønsker sannsynligheten for å velge to like flasker må dette være summen av de tre tilfellene.
Det gir at sannsynligheten for to like er
Svar: Sannsynligheten for to like flasker er .
Mer om
Denne oppgaven handler om Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje. Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.Sannsynlighet
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.Addisjonssetningen
For flere forklaringer og eksempler se artikkelen Addisjonssetningen i lynkurset Sannsynlighet (del II).
Oppgave 12 (6 poeng) Nettkode: E-4BJH
Funksjonen er gitt ved
a)
Bestem skjæringspunktene mellom grafen til og koordinataksene ved regning.
Løsningsforslag a)
Jeg tenker
Alle punkt på -aksen har , og for alle punkt på -aksen er .
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Alle punkter til funksjonen vil ha koordinater og alle punkt som ligger på -aksen vil ha andrekoordinat lik , altså , så funksjonen skjærer -aksen i den -verdien som gjør slik at vi har
Ifølge
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
som betyr at og .
Altså skjærer grafen til -aksen i punktene
Siden -aksen er alle punkter med , må grafen til skjære -aksen i punktet . Ettersom
skjærer grafen til -aksen i punktet
Svar: Skjæringspunkter med x-aksen er og og med y-aksen er .
Mer om
Denne oppgaven handler om
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Andregradslikning
En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:
Likningen kan løses ved hjelp av abc-formelen.
Flere forklaringer og eksempler på hvordan man løser andregradslikninger finner du i lynkurset Andregradslikninger. For mer om skjæringspunkter se artikkelen Grafisk løsning av likninger.
For å øve mer, se oppgavesettet skjæringspunkter i Treningsleiren.
b)
Tegn grafen til for
Løsningsforslag b)
Jeg tenker
Vi tegner
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Parabel
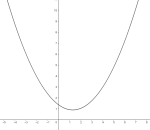
Et kjeglesnitt med bare en symmetriakse. Et eksempel er grafen til funksjonen
Siden det kvadratiske leddet, til annengradsfunksjonen har negativt fortegn vet vi at grafen til er en parabel med toppunkt og vil bøye nedover. En parabel er
Symmetriske funksjoner
Funksjoner med flere variable som ikke forandres om en bytter om variablene.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Da har vi at toppunktet er . Symmetrilinjen må være , og på grunn av denne symmetrien vet vi også at .
Vi kan også sjekke endepunktene, som også på grunn av symmetri vil ha samme funksjonsverdi. Vi sjekker for , og har nå også punktene .
Nå kan vi markere punktene i et koordinatsystem og tegne en linje mellom dem.
Svar: 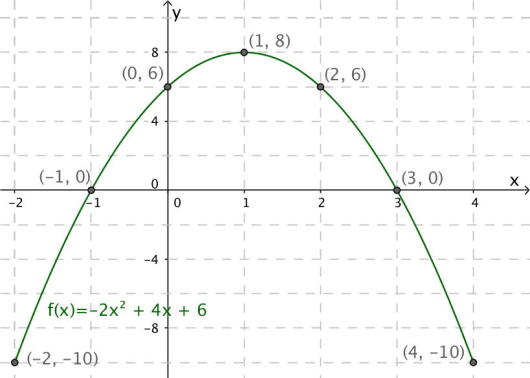
Mer om
Denne oppgaven handler om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Flere eksempler på hvordan man tegner en graf finner du i artikkelen Grafen til en funksjon.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
c)
Funksjonen er gitt ved
Løs likningen grafisk.
Løsningsforslag c)
Jeg tenker
Grafen til må være en rett
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Parabel

Et kjeglesnitt med bare en symmetriakse. Et eksempel er grafen til funksjonen
Grafen til er en rett linje, siden den bare består av et
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Når har vi , så skjærer -aksen i . Utfra likningen kan vi se at stigningstallet til må være lik , så når -verdien øker med , vil -verdien øke med to, altså vil grafen også gå gjennom punktet .
Vi kan nå tegne inn grafen til og ved å tegne grafen sammen med grafen til ser vi at grafene skjærer hverandre i to punkter.
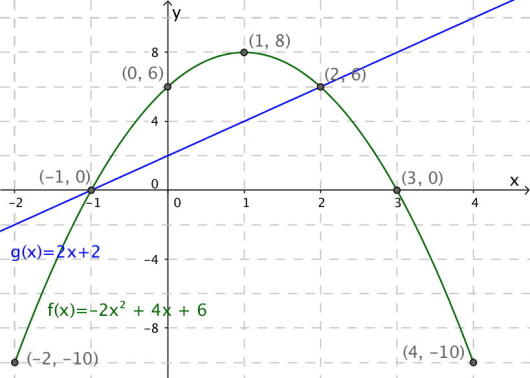
Når grafen til og skjærer hverandre betyr det at . Altså er løsningen av likningen gitt av de to punktene og . Siden -verdien er verdien de deler holder det imidlertid å oppgi -verdien for å løse likningen . Løsningen på denne likningen er altså
Svar:
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
For flere eksempler og forklaringer se artikkelen Grafen til en funksjon.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleiren.
Oppgave 13 (2 poeng) Nettkode: E-4BJL
Tenk deg at jorda har form som en kule, og at det er plassert et tau rundt ekvator. Tauet er strammet. Tenk deg så at du forlenger tauet med 20 m og plasserer det slik at det danner en sirkel med sentrum i jordas sentrum.
Vil du da kunne gå under tauet?
Løsningsforslag
Jeg tenker
Vi ønsker å se hva som skjer med
Radius
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.
Areal:
Omkrets:
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Hvis jorden har radius , er omkretsen til jorden gitt ved
Vi vet at tauet har en omkrets som er m lengre enn jordens omkrets, så tauets omkrets kan vi skrives som
Vi lar tauets radius være , og da kan kan vi skrive
og derfor må vi ha at
Avstanden mellom tauet og bakken er imidlertid gitt ved .
Fra likningen over har vi
som gir at avstanden mellom tauet og bakken er
som betyr at vi vil kunne gå under tauet.
Svar: Vi vil kunne gå under tauet.
Mer om
Denne oppgaven handler om
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.
Areal:
Omkrets:
Du kan lese mer om hvordan man finner omkretsen av en sirkel i artikkelen Alt om sirkel.
DEL 2 Med hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4BJN
Silje driver butikk. I slutten av mars opprettet hun en side på Facebook.
I slutten av april fant Silje ut at antall personer som hadde klikket «liker» på siden hennes dager etter 31. mars, tilnærmet var gitt ved funksjonen
Her svarer til 31. mars, til 1. april, til 2. april, og så videre.
Anta at denne funksjonen også vil gjelde for mai.
a)
Hvor mange personer hadde klikket «liker» på Siljes side før 1. april? Hvor mange prosent øker antall «liker» med per dag?
Løsningsforslag a)
Jeg tenker
Funksjonen er på formen , altså har vi en eksponentialfunksjon, hvor forteller oss noe om startverdien og er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Antall «liker» før . april tilsvarer antall «liker» . mars, som vi får oppgitt tilsvarer . Dette er da gitt ved
Siljes side har altså «liker» før april.
Antall «liker» en gitt dag er gitt er lik multiplisert med antall «liker» foregående dag. Siden er vekstfaktor for vekst, er økningen i antall «liker» på per dag.
Svar: Antall «liker» før 1. april er lik og den prosentvise økningen av «liker» per dag er lik
Mer om
Denne oppgaven handler om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Flere forklaringer og eksempler på prosentregning finner du i lynkurset Prosent.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
b)
Vil antall «liker» passere innen utgangen av mai?
Løsningsforslag b)
Jeg tenker
Ved å sette inn for antall dager fra 31. mars til utgangen av mai, kan vi se om «liker» overstiger .
Det er dager i april og dager i mai, så totalt er det dager fra mars til utgangen av mai. Antallet «liker» Silje har på siden sin innen utgangen av mai er gitt ved . Nå kan vi bruke CAS til å regne dette ut.
Da begynner vi med å definere funksjonen ved å skrive "f(x):=80*1.045^x", og deretter "f(61)". Dette gir
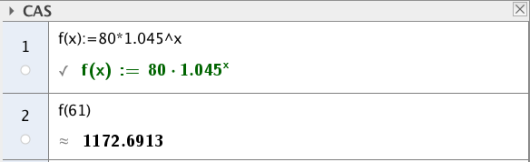
Vi kan også finne svaret ved å sette inn for i funksjonsuttrykket
Svaret er større enn , så antallet «liker» vil passere innen utgangen av mai.
Alternative løsninger
En annen måte å løse oppgaven på er å bestemme slik at . Hvis er mindre enn det totale antallet dager i april og mai, vil antall «liker» passere . Hvis antallet dager er større enn det totale antallet dager i april og mai til sammen, vil det altså ta lengre tid for antall «liker» å passere .
Dette kan vi løse ved hjelp av CAS. Da må vi først definere funksjonen ved å skrive
"f:=80*1.045^x", og deretter kan vi skrive inn "f(x)=1000".
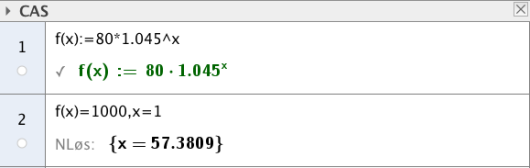
Da kan vi se at vi får når .
Vi kan også løse denne likningen med regning. Da får vi at dette kan skrives og ved å ta logaritmen av begge sider ser vi at Det er betyr at antall likes passerer etter Siden dette er mindre enn det totale antallet dager i april og mai sammenlagt er svaret på spørsmålet ja, antallet likes passerer innen utgangen av mai.
Svar: Ja, antall "liker" vil passere innen utgangen av mai.
Mer om
Denne oppgaven handler om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Hva en funksjon er hvordan man regner med dem kan du lese mer om i lynkurset Funksjoner.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleiren.
c)
Bestem og .
Hva forteller disse verdiene om antall «liker» på Siljes side?
Løsningsforslag c)
Jeg tenker
Vi kan bruk CAS til å finne de verdiene. Den deriverte til en funksjon forteller noe om vekstfarten til funksjonen i det punktet.
I oppgave b) definerte vi funksjonen i CAS, og vi finner verdiene ved å skrive inn og i CAS.
Da får vi

forteller oss at antall personer som har klikket "liker" på siden til Silje april omtrent er .
forteller oss at økningen i "likerklikk" per dag etter dager er omtrent .
Svar: er antallet «liker» den 16. dagen. er økning i «liker» den 16. dagen.
Mer om
Denne oppgaven handler om
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere forklaringer og eksempler se artiklene Kjerneregelen og Kjerneregelen - tre eksempler i lynkurset Derivasjon.
For å øve mer, se oppgavesettet om derivasjon i Treningsleiren.
Oppgave 2 (5 poeng) Nettkode: E-4BJS
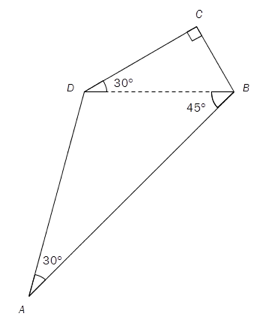
Gitt ovenfor. Lengden av diagonalen .
Bruk CAS til å bestemme lengdene av sidene i firkanten eksakt.
Løsningsforslag
Jeg tenker
er en rettvinklet trekant og da er sin til en vinkel lik forholdet mellom den motstående kateten og hypotenusen. Vi bruker sinussetningen i CAS i GeoGebra for å finne sidelengdene i .
I en rettvinklet trekant har vi at
Siden er rettvinklet har vi at
I CAS løser vi dette som to likninger og finner sidelengdene

Sidelengdene er
Sinussetningen for en vilkårlig trekant gir at
der er motstående side for vinkel , og tilsvarende for og .
Vi ser på og bruker sinussetningen til å bestemme sidelengdene og
Den gir at at
.
Vi har og da kan vi løse likningen
i CAS.

Da er sidelengden
Siden vi kjenner til
Vinkelsum
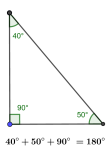
Summen av alle vinklene i en mangekant.
Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader.
.
Ifølge sinussetningen er sidelengden da gitt ved
Vi løser denne i CAS og får at
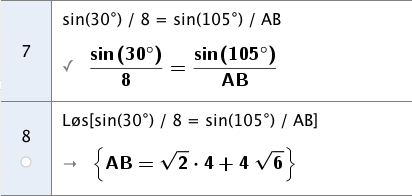
Svar:
Mer om
Denne oppgaven er om
Trigonometri
Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.
For flere eksempler og forklaringer se artikkelen Sinussetningen i lynkurset Trigonometri.
For å øve mer, se oppgavesettet om sinussetningen i Treningsleiren.
Oppgave 3 (9 poeng) Nettkode: E-4BJW
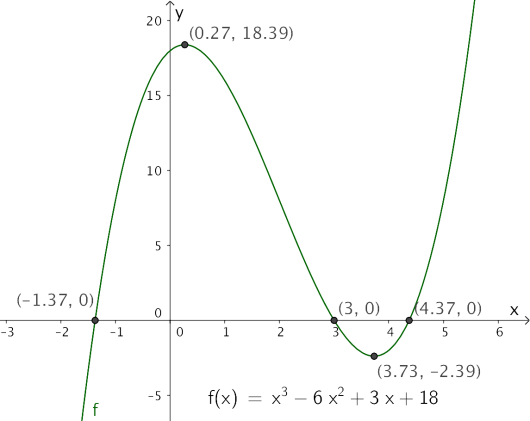
Funksjonen er gitt ved
a)
Bruk graftegner til å tegne grafen til , bestemme nullpunktene til og eventuelle topp- og bunnpunkter på grafen til .
Løsningsforslag a)
Jeg tenker
Vi bruker grafikkfelt i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Vi begynner med å tegne inn grafen til funksjonen i GeoGebra ved å skrive
Da får vi opp grafen i grafikkfeltet.
For å finne nullpunktene til kan vi bruke kommandoen
Da får vi opp de tre skjæringspunktene mellom grafen og -aksen:
.
Dermed er nullpunktene til lik .
Vi kan bruke kommandoen
Ekstremalpunkt[<Polynom>]
for å finne eventuelle topp- og bunnpunkt. Vi skriver "Ekstremalpunkt[f]" og får opp to ekstremalpunkter,
og .
Fra grafen, og ved å se på koordinatene, kan vi se at vi har ett toppunkt, og ett bunnpunkt, .
Svar:
Mer om
Denne oppgaven er om
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkter i lynkurset Funksjonsdrøfting.
For å øve mer, se oppgavesettet om nullpunkter og ekstremalpunkter i Treningsleiren.
b)
Bruk CAS til å bestemme eksakte verdier for nullpunktene til og for eventuelle topp- og bunnpunkter på grafen til .
Løsningsforslag b)
Jeg tenker
Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Vi bruker samme GeoGebra-fil som i oppgave a), og åpner CAS. Nå er allerede definert som funksjonen vår.
For å finne nullpunktene til denne funksjonen må vi løse likningen
.
Da skriver vi inn "f(x)=0" og for å få eksakte verdier bruker vi knappen i verktøylinjen der det står .

De eksakte verdiene for nullpunktene er altså
I ekstremalpunktene har vi at , så for å finne den eksakte verdien for ekstremalpunktene løser vi likningen .
Da kan vi skrive inn "f'(x)=0" og får at har ekstremalpunkt når
.
For å finne selve punktene skriver vi inn "(-sqrt(3)+2, f(-sqrt(3)+2))" og "(sqrt(3)+2, f(sqrt(3)+2))"

Da ser vi at har et toppunkt i og et bunnpunkt i . Funksjonsverdien i disse punktene finner vi ved å bruke CAS og sette inn verdiene for .
Vi får at .
Alternativ løsning
Vi kan bruke de samme kommandoene i CAS som vi brukte i oppgave a).
Da definerte vi funksjonen . Dermed kan vi nå bare skrive
Nullpunkt[f]
Ekstremalpunkt[f]
for å få verdiene vi ønsker. For å få eksakte verdier må vi trykke på "".
Da får vi

Svar: Nullpunkter , toppunkt og bunnpunkt
Mer om
Denne oppgaven er om
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
For flere forklaringer og eksempler se lynkurset Funksjonsdrøfting.
For å øve mer, se oppgavesettet om funksjonsdrøfting i Treningsleiren.
c)
Grafen til har to tangenter med stigningstall lik 3.
Bestem likningene for de to tangentene.
Løsningsforslag c)
Jeg tenker
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi vil finne en tangent med stigningstall lik . Stigningstallet til tangenten i er lik . Dette betyr at for å finne hvilke punkt vi skal finne tangenten i, kan vi løse likningen .
Da kan vi bruke CAS og får . Nå vet vi at vi skal finne likningen til tangenten i punktene . Vi kan fortsette i CAS og bruke kommandoen Tangent[<Punkt>, <Funksjon>], og skrive inn
"Tangent[(0,f(0)), f]" og "Tangent[(4,f(4)), f]"
Da får vi

Alternativ
Vi kan også finne tangentene ved regning:
Tangenten er en rett linje og er derfor på formen , der og er
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Ifølge derivasjonsregelen er den deriverte av gitt ved
Likningen kan skrives som
, og vi vil løse denne likningen for
som betyr at likningen løses av punktene
Tangenten i skjærer grafen til i punktet og siden
må likningen for tangenten tilfredsstille likningen
Med andre ord må vi ha . Tangenten i er på formen
Siden
er konstanten, , i tangentlikningen i på helt tilsvarende måte gitt ved
som betyr at . Tangenten i punktet er på formen
Svar: Likningene for tangentene er lik og
Mer om
Denne oppgaven handler om
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
For flere eksempler og forklaringer se artikkelen Å finne tangenten.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
Visste du at?
I matematikk er det vanlig å bruke parentesene for en mengde, eller samling, av elementer. Mengden av tallene og kan for eksempel skrives . Siden de fleste mengder av interesse inneholder altfor mange elementer til å kunne listes opp, er det vanlig å oppgi mengder på formen , som leses «Mengden av alle som er slik at ». Hvis vi for eksempel ønsker å se på mengden av alle oddetallene kan vi skrive
Når vi snakker om å finne likningen til en figur, som for eksempel en tangent, kan vi tenke på denne som mengdebyggeren . Likningen vi fant for tangenten i punktet består for eksempel av alle koordinater som tilfredsstiller . Dette kan vi skrive
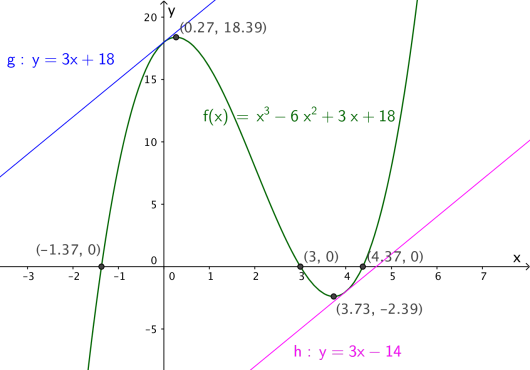
d)
Tegn de to tangentene i samme koordinatsystem som grafen til .
Løsningsforslag d)
Jeg tenker
Vi tegner grafene til de to tangentene fra deloppgaven 3c) i samme
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Vi skriver inn likningene
og
i inntastingsfeltet i samme koordinatsystem som oppgave a):
Svar:
Mer om
Denne oppgaven er om
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
Oppgave 4 (2 poeng) Nettkode: E-4BK1
Ida selger små og store kuleis. En liten kuleis koster 24 kroner og har to iskremkuler. En stor kuleis koster 32 kroner og har tre iskremkuler. En liter iskrem gir i alt 12 iskremkuler.
En dag solgte Ida kuleis for 2 752 kroner. Hun hadde da brukt 20 L iskrem.
Hvor mange store kuleis solgte Ida denne dagen?
Løsningsforslag
Jeg tenker
Vi kan systematisere informasjonen vi får oppgitt i et
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
La være antall små kuleis Ida har solgt. La være antall store kuleis Ida har solgt.
Det totale antallet iskremkuler som er solgt den dagen er da gitt ved . Siden én liter iskrem gir iskremkuler og det totalt ble solgt liter iskrem, tilfredsstiller og følgende likning
Siden en liten kuleis koster kroner, en stor kuleis koster kroner og Ida solgte kuleis for totalt kroner følger det at og også må tilfredsstille likningen
Vi kan bruke CAS til å løse dette likningssystemet

Vi ser at Ida solgte små og store kuleis denne dagen.
Alternativ løsning
Vi kan også løse likningssystemet for hånd. Her ser vi hvordan vi kan bruke addisjonsmetoden.
Først ser vi at vi kan dividere begge sider av med . Da får vi
Vi kan bruke addisjonsmetoden for å finne de ukjente i likningssystemet:
Vi multipliserer første likningen med , da får vi . Nå kan vi addere likningene, og da vil vi vi eliminerer leddene med .
Da får vi
Svar: Ida solgte store kuleis den dagen.
Mer om
Denne oppgaven handler om
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Flere forklaringer og eksempler på hvordan man løser et sett med likninger finner du i artikkelen Likningssystemer.
For å øve mer, se oppgavesettet om likningssystemer i Treningsleiren.
Oppgave 5 (3 poeng) Nettkode: E-4BKC
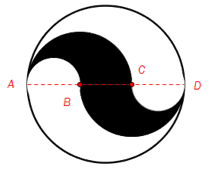
Punktene og på figuren ovenfor deler diameteren i tre like store deler. Alle buene i figuren er sirkelbuer.
Sett og bestem forholdet mellom arealet av sirkelen og arealet av det svarte området.
Løsningsforslag
Jeg tenker
Ved å bruke at
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Radius

Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Vi kan begynne med å bestemme arealet av hele sirkelen. Arealet til en sirkel med radius er gitt ved .
Diameter til hele sirkelen er lik , det vil si at radius, . Arealet til hele sirkelen er da .
Det sorte området kan omplasseres slik at vi får en sirkel med diameter , med en hvit sirkel med diameter inni, som har radiuser henholdsvis
Arealet, , av det sorte området er dermed differansen av arealet til disse to sirklene, altså
Dette arealet kan vi finne ved hjelp av CAS:

Siden arealet av hele sirkelen er gitt som
følger det at forholdet mellom arealet av hele sirkelen og arealet av det sorte området er gitt ved . Vi kan skrive uttrykket for inn i CAS og finne forholdet:
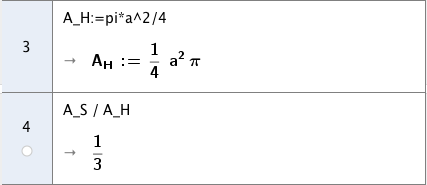
Altså utgjør det sorte området nøyaktig én tredjedel av hele sirkelen.
Svar: Det sorte området én tredjedel av hele sirkelen.
Mer om
Denne oppgaven handler om
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.
Areal:
Omkrets:
Flere forklaringer og eksempler på hvordan man finner areal og omkrets av en sirkel finner du i artikkelen Alt om sirkel.
For å øve mer, se oppgavesettet om omkrets og areal i Treningsleiren.




