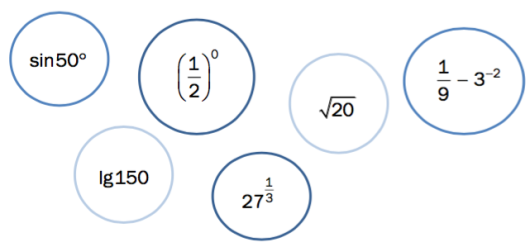Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2013 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Hjelpemidler på Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Hjort (www.freeimages.com, 5.07.2016)
- Tegninger, grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4B8V
Regn ut og skriv svaret på standardform
Oppgave 2 (2 poeng) Nettkode: E-4B8X
Løs likningssystemet
Oppgave 3 (2 poeng) Nettkode: E-4B93
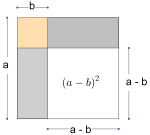
Skriv så enkelt som mulig
Oppgave 4 (2 poeng) Nettkode: E-4B97
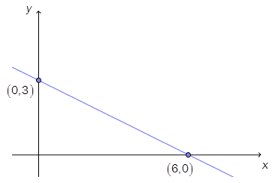
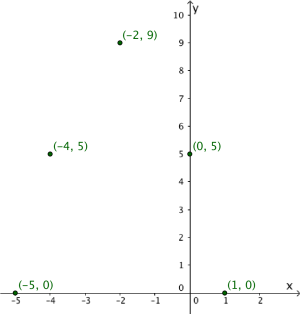
Bestem likningen for den rette linjen i koordinatsystemet ovenfor.
Oppgave 5 (3 poeng) Nettkode: E-4B9A
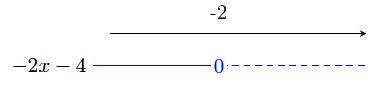
Sorter uttrykkene nedenfor etter stigende verdi. Vis eller forklar hvordan du har tenkt.
Oppgave 6 (2 poeng) Nettkode: E-4B9G
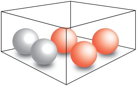
I en eske er det tre røde og to blå kuler. Sondre trekker tilfeldig to av kulene.
Bestem sannsynligheten for at de to kulene han trekker, har samme farge.
Oppgave 7 (8 poeng) Nettkode: E-4B9I
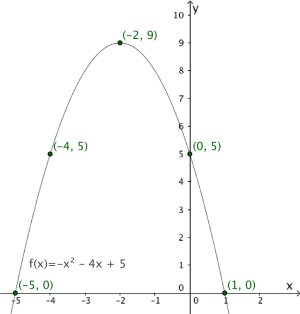
Funksjonen er gitt ved
a)
Bestem nullpunktene til ved regning.
b)
Bestem koordinatene til eventuelle ekstremalpunkter (topp- eller bunnpunkter) på grafen til ved regning.
c)
Lag en skisse av grafen til .
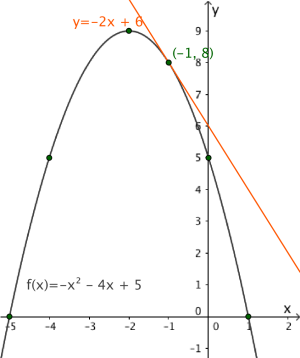
d)
Bestem likningen for tangenten til grafen til i punktet ved regning. Tegn tangenten i samme koordinatsystem som du brukte i oppgave 7 c).
Oppgave 8 (4 poeng) Nettkode: E-4B9W
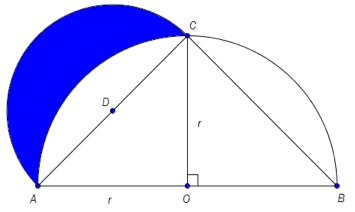
Ovenfor ser du to halvsirkler. Den ene har sentrum i og radius , den andre har sentrum i og radius .
a)
Vis at
b)
Vis ved regning at arealet av området som er markert med blått på figuren ovenfor, er lik arealet av .
DEL 2 Med hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4BAP
I en rettvinklet trekant er den lengste kateten cm. En av vinklene i trekanten er . Bestem lengden av den korteste kateten og hypotenusen i denne trekanten ved regning.
Oppgave 2 (6 poeng) Nettkode: E-4BAU
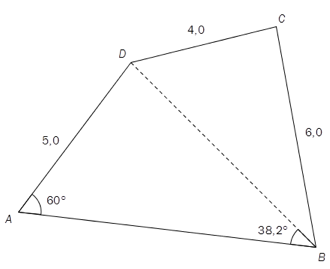
Gitt ovenfor.
a)
Bestem lengden av diagonalen ved regning.
b)
Bestem arealet av firkanten ved regning.
Oppgave 3 (4 poeng) Nettkode: E-4BB2
4000 menn og 6000 kvinner deltar i en undersøkelse. Det viser seg at 8 % av mennene og 1 % av kvinnene som deltar i undersøkelsen, er fargeblinde.
a)
Regn ut hvor mange fargeblinde personer det er som deltar i undersøkelsen, og bestem sannsynligheten for at en tilfeldig valgt person som deltar i undersøkelsen, er fargeblind.
b)
Tenk deg at vi samler de fargeblinde personene som deltar i undersøkelsen, i en gruppe. Fra denne gruppen velger vi tilfeldig én person.
Bestem sannsynligheten for at vi velger en kvinne.
Oppgave 4 (4 poeng) Nettkode: E-4BB5
Denne oppgaven tar for seg binomisk fordeling som ikke lenger er pensum på læreplanen i 1T.
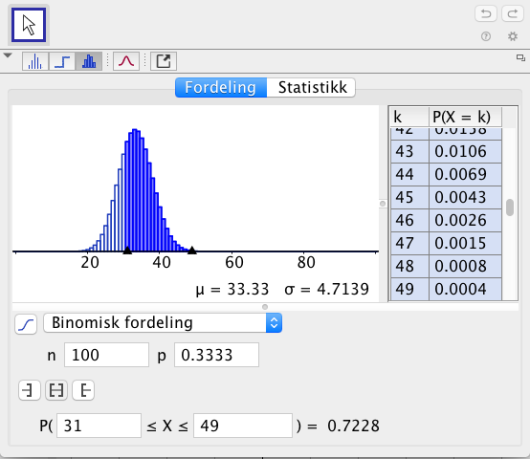
En undersøkelse viser at én av tre personer som bor i Oslo, ønsker å flytte fra byen. Vi velger tilfeldig 100 personer som bor i Oslo.
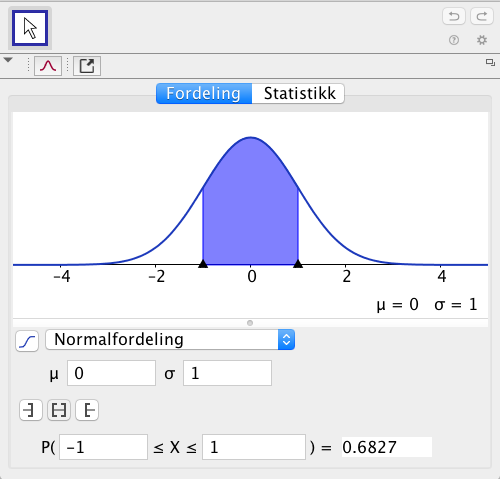
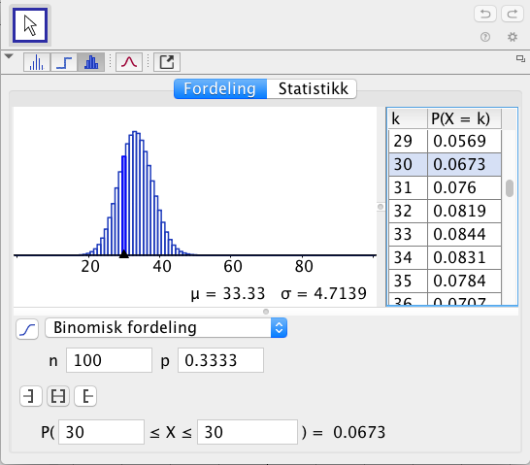
a)
Bestem sannsynligheten for at nøyaktig 30 av de 100 personene ønsker å flytte fra byen.
b)
Bestem sannsynligheten for at mellom 30 og 50 av de 100 personene ønsker å flytte fra byen.
Oppgave 5 (4 poeng) Nettkode: E-4BB9
- I en undersøkelse ble personer spurt om ferievanene sine.
- En av fem svarte at de ville trene i ferien.
- av mennene og av kvinnene svarte at de ville trene i ferien.
a)
Sett opp et likningssystem som du kan bruke til å bestemme hvor mange menn og hvor mange kvinner som deltok i undersøkelsen det er vist til ovenfor.
b)
Hvor mange menn og hvor mange kvinner deltok i undersøkelsen?
Oppgave 6 (8 poeng) Nettkode: E-4BBD
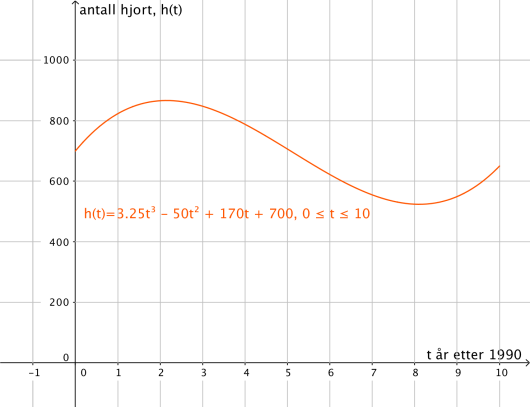
Funksjonen gitt ved
var en god modell for hjortebestanden i en kommune i perioden 1990–2000. Ifølge modellen var det hjort i kommunen t år etter 1. januar 1990.
a)
Tegn grafen til for
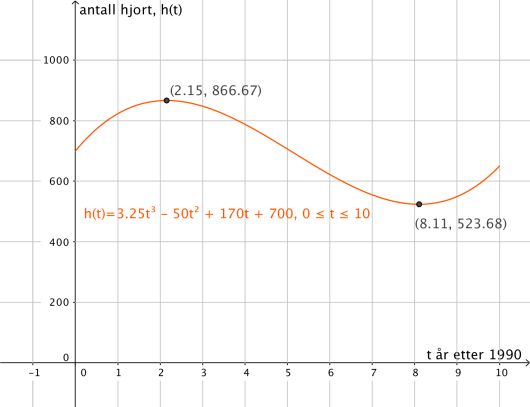
b)
Når var hjortebestanden størst, og hvor mange hjort var det i kommunen da?
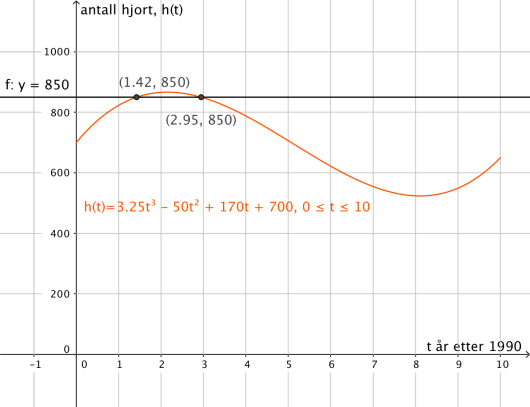
c)
Løs ulikheten grafisk, og forklar hva løsningen forteller om hjortebestanden.
d)
Bestem . Hva forteller svaret om hjortebestanden?
Oppgave 7 (6 poeng) Nettkode: E-4BBJ
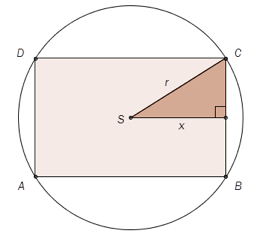
Ovenfor ser du et rektangel som er innskrevet i en sirkel. Sirkelen har sentrum i .
a)
Bestem radius i sirkelen dersom rektangelet skal ha lengde og bredde .
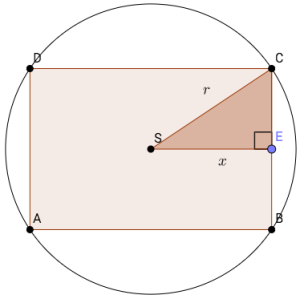
b)
Et rektangel med lengde er innskrevet i en sirkel med radius .
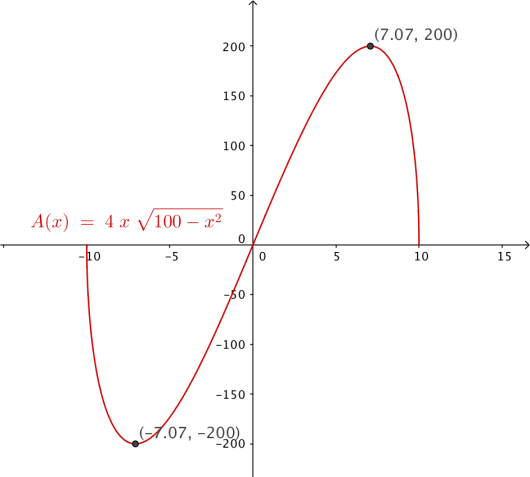
Vis at arealet av det innskrevne rektangelet kan skrives som
c)
Bestem det største arealet rektangelet kan ha. Bestem lengden og bredden i dette rektangelet.
Oppgave 8 (2 poeng) Nettkode: E-4BBO
Start med en brøk . Legg til 7 ganger brøkens nevner i både teller og nevner. Du får da en ny brøk. Trekk den nye brøken fra den opprinnelige brøken. Det uttrykket du nå får, skal være lik 8.
Hva må verdien av brøken da ha vært?