Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1011 2017 Høst

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timar:

Del 1 skal leverast inn etter 2 timar.

Del 2 skal leverast inn seinast etter 5 timar.

Hjelpemiddel på Del 1:

Vanlege skrivesaker, passar, linjal med centimetermål og vinkelmålar.

Hjelpemiddel på Del 2:

Alle hjelpemiddel er tillatne, med unntak av Internett og andre verktøy som tillèt kommunikasjon.

Framgangsmåte:

Del 1 har 9 oppgåver. Del 2 har 8 oppgåver.

Der oppgåveteksten ikkje seier noko anna, kan du fritt velje framgangsmåte. Om oppgåva krev ein bestemt løysingsmetode, vil ein alternativ metode kunne gi låg/noko utteljing.

Bruk av digitale verktøy som grafteiknar og rekneark skal dokumenterast med utskrift eller gjennom ein IKT-basert eksamen.

Rettleiing om vurderinga:

Poeng i Del 1 og Del 2 er berre rettleiande i vurderinga. Karakteren blir fastsett etter ei samla vurdering. Det betyr at sensor vurderer i kva grad du

viser rekneferdigheiter og matematisk forståing
gjennomfører logiske resonnement
ser samanhengar i faget, er oppfinnsam og kan ta i bruk fagkunnskap i nye situasjonar
kan bruke formålstenlege hjelpemiddel
forklarer framgangsmåtar og grunngir svar
skriv oversiktleg og er nøyaktig med utrekningar, nemningar, tabellar og grafiske framstillingar
vurderer om svar er rimelege

DEL 1 Uten hjelpemidler

Oppgave 1 (2 poeng) Nettkode: E-4TIL

En vare koster $640$ kroner. Butikkeieren vurderer å sette opp prisen med $10 %$ eller $15 %$ .

a)

Hvor mye vil varen koste dersom prisen settes opp med $10 %$ ?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må finne ut hvor mye $10 %$ er av prisen på varen.

Vi skal finne ny pris på varen dersom prisen settes opp med $10 %$ . Da kan vi først finne ut hvor mye $10 %$ er av $640$ kr, og deretter addere dette med den opprinnelige prisen. $10 %$ av $640$ kr er $640 kr \cdot \frac{10}{100} = \frac{640 kr}{10} = 64 kr .$ Det betyr at varen vil koste $640 kr + 64 kr = 704 kr .$

Svar: Dersom varen settes opp med $10 %$ vil prisen være $704 kr$ .

Mer om:

Denne oppgaven handler om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler, se artikkelen Prosent av hva da?.

For å øve mer, se dette oppgavesettet om prosentregning i Treningsleiren.

b)

Hvor mye vil varen koste dersom prisen settes opp med $15 %$ ?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må finne ut hvor mye $15 %$ er av prisen på varen.

Vi skal finne ny pris på varen dersom prisen settes opp med $15 %$ . Da kan vi først finne ut hvor mye $15 %$ er av $640$ kr, og deretter addere dette med den opprinnelige prisen. $15 %$ av $640$ kr er $640 kr \cdot \frac{15}{100} = 640 kr \cdot 0, 15 = 64 kr \cdot 1, 5 = 64 kr + 32 kr = 96 kr .$ Det betyr at varen vil koste $640 kr + 96 kr = 736 kr .$

Svar: Dersom varen settes opp med $15 %$ vil prisen være $736 kr$ .

Mer om:

Denne oppgaven handler om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler, se artikkelen Prosent av hva da?.

For å øve mer, se dette oppgavesettet om prosentregning i Treningsleiren.

Oppgave 2 (2 poeng) Nettkode: E-4TIO

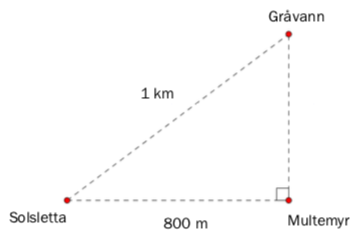
Noah skal gå fra Solsletta til Gråvann. Han lurer på om han skal gå den korteste veien, eller om han skal gå over Multemyr. Stiene går langs de stiplede linjene.
Se figuren over.

Hvor mye lenger må han gå dersom han velger å gå veien om Multemyr?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan bruke Pytagoras læresetning for å finne avstanden fra Multemyr til Gråvann.

For å finne ut hvor mye lenger Noah må gå dersom han går om Multemyr må vi finne avstanden fra Multemyr til Gråvann, som vi betegner som $x km$ . Ut i fra figuren kan vi se at vi har en rettvinklet trekant, så da kan vi bruke Pytagoras læresetning. Vi kan merke oss at på figuren har vi to ulike benevninger for lengdene, så vi må passe på at vi gjør om slik at vi bruker den samme for begge lengdene. Vi kan bruke kilometer som benevning. Avstanden fra Solsletta til Multemyr er $800 m = 0, 8 km$ . Ved Pytagoras læresetning får vi da $\begin{matrix} (1 km)^{2} & = & (0, 8 km)^{2} + (x km)^{2} \\ (x km)^{2} & = & 1 {km}^{2} - 0, 64 {km}^{2} \\ x km & = & \sqrt{0, 36 {km}^{2}} \\ x km & = & 0, 6 km \end{matrix}$

Fra Multemyr til Gråvann er det altså $0, 6 km$ , som betyr at dersom Noah går om Multemyr må han gå $0, 8 km + 0, 6 km = 1, 4 km$ . Det er $1, 4 km - 1 km = 0, 4 km$ lenger enn om han går den korteste veien.

Svar: Noah må gå $400 m$ lenger om han går om Multemyr.

Mer om:

Denne oppgaven handler om

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

For flere forklaringer og eksempler, se artikkelen Pytagoras læresetning.

For å øve mer, se dette oppgavesettet om Pytagoras læresetning i Treningsleiren.

Oppgave 3 (2 poeng) Nettkode: E-4TIS

Et politisk parti har en oppslutning på $40 %$ .
Partiet øker sin oppslutning med $2$ prosentpoeng.

Hvor mange prosent øker partiet oppslutning med?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Her må vi skille mellom prosent og prosentpoeng. Vi skal finne økningen i prosent.

Når partiet øker sin oppslutning med $2$ prosentpoeng betyr det at det får en oppslutning på $40 % + 2 % = 42 %$ . Vi skal finne hvor stor den prosentvise endringen er. Da kan vi se på prosentfaktoren som er $\frac{2}{40} = \frac{1}{20} = 0, 05$ . Ved å gange 0,05 med hundre får vi prosenten.

Svar: Den prosentvise økningen er da $5 %$ .

Mer om:

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Prosentpoeng

Prosentpoeng er forskjellen mellom to prosenttall.

Eksempel: Forskjellen mellom $80 %$ og $82 %$ er 2 prosentpoeng.

prosentpoeng

For flere forklaringer og eksempler, se lynkurset Prosent.

For å øve mer, se dette oppgavesettet om prosentregning i Treningsleiren.

Oppgave 4 (1 poeng) Nettkode: E-4TIV

I $2016$ kostet en vare $6 %$ mer enn i basisåret.

Hva var prisindeksen for varen i $2016$ ?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi husker at i basisåret er prisindeksen lik $100$ .

I basisåret er prisindeksen lik $100$ . Varen koster $6 %$ mer i $2016$ . $6 %$ mer enn $100$ er $106$ .

Svar: Prisindeksen i $2016$ er $106$ .

Mer om:

Denne oppgaven handler om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Oppgave 5 (3 poeng) Nettkode: E-4TIX

Kari er baker. Hun har en oppskrift på brød hvor det står at forholdet mellom mel og vann skal være $10 : 7$ .

a)

Hvor mye vann trenger Kari dersom hun skal bruke $50$ L mel?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Når Kari har $10$ deler mel, så skal hun ha $7$ deler vann. Vi må finne ut hvor stor én del er når hun bruker $50$ L mel.

Kari skal ha $10$ deler mel og $7$ deler vann. Hun har $50$ L mel som utgjør $10$ deler. Da vil hver del være på $\frac{50 L}{10} = 5 L$ mel. Når Kari har $10$ deler mel, hver på $5$ L, så skal hun ha $7$ deler vann, hver på $5$ L. Det betyr at Kari skal ha $7 \cdot 5 L = 35 L$ vann.

Svar: $35$ L vann.

Mer om:

Denne oppgaven handler om proporsjoner.

For flere forklaringer og eksempler, se lynkurset Målestokk og forholdsregning.

Når Kari baker brød hjemme, bruker hun til sammen $3, 4$ L mel og vann.

Løs oppgaven her

b)

Hvor mye mel og hvor mye vann bruker hun?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Når Kari baker har hun totalt $10 + 7 = 17$ deler. Det betyr at det totale volumet på $3, 4$ L skal utgjøre $17$ deler, og da kan vi finne ut hvor stor én del er.

Kari har totalt $3, 4$ L mel og vann. Av dette volumet er $10$ deler mel og $7$ deler vann, tilsammen er det altså $17$ deler. For å finne ut hvor mye mel og hvor vann hun bruker må vi finne ut hvor stor én del er. Det kan vi finne ved å dividere det totale volumet på antall deler. Da får vi at én del er $\frac{3, 4 L}{17} = 0, 2 L .$ Det betyr at Kari bruker $10 \cdot 0, 2 L = 2 L$ mel og $7 \cdot 0, 2 L = 1, 4 L$ vann. For å sjekke om dette er riktig kan vi legge sammen volumet for mel og vann; $2 L + 1, 4 L = 3, 4 L$ , som var det vi ville ha.

Svar: Kari bruker $2 L$ mel og $1, 4 L$ vann.

Mer om:

Denne oppgaven handler om proporsjoner.

For flere forklaringer og eksempler, se lynkurset Målestokk og forholdsregning.

Oppgave 6 (2 poeng) Nettkode: E-4TJ2

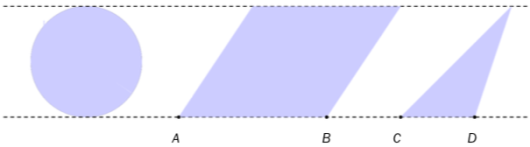
Ovenfor ser du to parallelle linjer, en sirkel, et parallellogram og en trekant.
$A B = 8$ og $C D = 4$ . Sirkelen har areal $9 π$ .

Bestem arealet av parallellogrammet og av trekanten.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi får oppgitt arealet til sirkelen. Dette kan vi bruke til å bestemme radiusen til sirkelen, og med det avstanden mellom de to stiplede linjene som er høyden i trekanten og parallellogrammet.

Vi begynner med å finne radiusen til sirkelen. Arealet til en sirkel er gitt ved formelen $A_{S i r k e l} = π \cdot r^{2}$ og da har vi at $π \cdot r^{2} = 9 π .$ Vi kan bruke denne likningen til å bestemme $r$ ; $\begin{matrix} π \cdot r^{2} & = & 9 π \\ r^{2} & = & \frac{9 π}{π} \\ r^{2} & = & 9 \\ r & = & 3 \end{matrix}$

Radiusen til sirkelen er $3$ som betyr at diameteren er $2 \cdot 3 = 6$ . Da kjenner vi også høyden til parallellogrammet og trekanten.
Arealet til et parallellogram er gitt ved formelen $A_{P a r a l l e l l o r a m} = G \cdot h$ . Grunnlinjen, $G$ , til parallellogrammet er $A B = 8$ og høyden fant vi ut at er $h = 6$ . Da får vi at arealet til parallellogrammet er $A_{P a r a l l e l l o r a m} = 8 \cdot 6 = 48$ Arealet til en trekant er gitt ved $A_{T r e k a n t} = \frac{G \cdot h}{2}$ . Trekanten har grunnlinje $C D = 4$ og høyde $6$ . Da finner vi arealet ved $A_{T r e k a n t} = \frac{4 \cdot 6}{2} = 12$

Svar: Parallellogrammet har areal $48$ og trekanten har areal $12$ .

Mer om:

Denne oppgaven handler om

Parallellogram

Et parallellogram er en firkant med parvis parallelle sider. Vinklene er parvis like store.

parallellogram

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

For flere forklaringer og eksempler, se lynkurset Geometri - areal og volum.

For å øve mer, se dette oppgavesettet om areal i Treningsleiren.

Oppgave 7 (6 poeng) Nettkode: E-4TJ4

Noen venner vil dra på hyttetur. Det koster $3600$ kroner å leie hytta en helg. Vennene skal dele utgiftene for leie av hytta likt mellom seg. I tillegg må hver person betale $1300$ kroner for mat og transport.

a)

Tegn av tabellen nedenfor i besvarelsen. Fyll inn tallene som mangler.

Antall personer	$2$	$4$	$8$
Utgifter per person

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å finne ut hvor mye hver må betale, må vi dividere den totale leien på antall personer. Deretter må vi addere hva det koster for mat og transport.

Vi skal fylle inn i tabellen

Antall personer	$2$	$4$	$8$
Utgifter per person

Hver person må betale $leie for hytta + mat og transport$ . Mat og transport er fast utgift på $1300$ per person. Hva hver person må betale i leie for hytta avhenger av hvor mange som er med på hyttetur.
Dersom det er $2$ personer med på hyttetur må hver person betale $\frac{3600 kr}{2} = 1800 kr$ for leie av hytta. Totalt blir utgiftene per person på $1800 kr + 1300 kr = 3100 kr .$
Dersom det er $4$ personer som er med, må hver person betale $\frac{3600 kr}{4} = 900 kr$ for leie av hytta. Totalt blir utgiftene per person på $900 kr + 1300 kr = 2200 kr$ Dersom det er $8$ personer som er med, må hver person betale $\frac{3600 kr}{8} = 450 kr$ per person. Totalt blir utgiftene per person på $450 kr + 1300 kr = 1750 kr$ Vi kan nå fylle inn denne informasjonen i tabellen fra oppgaven.

Svar:

Antall personer	$2$	$4$	$8$
Utgifter per person	$3100 kr$	$2200 kr$	$1750 kr$

Mer om:

Denne oppgaven handler om

Tabell

Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.

Eksempel: rutetabell for buss, resultatliste for skirenn

tabell

Divisjon

Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.

Eksempel: $6 : 2 = 3$ fordi $2 \cdot 3 = 6$ .

divisjon

b)

Bestem en formel som du kan bruk for å regne ut utgiftene $U$ per person dersom $x$ personer deltar.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan bruke oppgave a) til å bestemme formelen.

I oppgave a) kunne vi se at de totale utgiftene bestod av to ledd;

Utgifter per person = Leie for hytta + Mat og transport.

Det var kun leie av hytta som var avhengig av antall personer. Dersom $x$ personer deltar, kan vi skrive $Leie for hytta per person = \frac{3600 kr}{x} .$ Mat og transport er fast på $1300$ kr per person uansett hvor mange som deltar. Utgiftene $U (x)$ kr per person kan vi da skrive som $U (x) = \frac{3600}{x} + 1300 .$

Svar: $U (x) = \frac{3600}{x} + 1300$ .

Mer om:

Denne oppgaven er om

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

c)

Bruk formelen fra oppgave b) til å bestemme hvor mange personer som må delta for at utgiftene per person skal bli $1600$ kroner.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi skal bestemme $x$ når $U (x) = \frac{3600}{x} + 1300$

Utgiftene per person skal bli $1600 kr$ , som betyr at vi har $U (x) = 1600$ . Da får vi en likning som vi kan løse med hensyn på $x$ :

$\begin{matrix} \frac{3600}{x} + 1300 & = & 1600 \\ \frac{3600}{x} & = & 1600 - 1300 \\ 3600 & = & 300 \cdot x \\ x & = & \frac{3600}{300} \\ x & = & \frac{36}{3} \\ x & = & 12 \end{matrix}$

Svar: Det må delta $12$ personer.

Mer om:

Denne oppgaven er om

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formler

For flere eksempler og forklaringer, se artikkelen Å sette inn i formelen.

d)

Er antall personer og utgiftene per person omvendt proporsjonale størrelser?
Begrunn svaret ditt.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

To størrrelser er omvendt proporsjonale dersom produktet av dem er konstant. I vårt tilfelle vil det for eksempel bety at dersom antall personer halveres, vil prisen hver person må betale dobles.

Dersom to størrelser er omvendt proposjonale er produktet av dem konstant. Det betyr at antall personer multiplisert med utgiftene per person skal være konstant, og dersom en av størrelsene halveres, dobles den andre.

Fra tabellen i oppgave a) kan vi se at prisen for $4$ personer er $2200 kr$ . Dersom størrelsene er omvendt proporsjonale må vi ha at prisen for $2$ personer er $4400 kr$ , som vi vet ikke stemmer. Så antall personer og utgiftene per person er ikke omvendt proporsjonale.

Svar: Nei, de er ikke omvendt proporsjonale størrelser.

Mer om:

Denne oppgaven handler om

Omvendt proporsjonal

$a$ og $b$ er omvendt proporsjonale dersom $b = \frac{k}{a}$ (dvs. $a b = k$ ), der $k$ er konstant.

omvendt proporsjonalitet

For flere forklaringer og eksempler, se artikkelen Proporsjonalitet.

For å øve mer, se dette oppgavesettet om omvendt proporsjonale funksjoner i Treningsleiren.

Oppgave 8 (3 poeng) Nettkode: E-4TJ9

Ved en skoler er det to Vg2-klasser, $2 A$ og $2 B$ . Det er like mange elever i hver klasse. Alle elevene i $2 A$ har valgt biologi. Halvparten av elevene i $2 B$ har valgt biologi.

a)

Bestem sannsynligheten for at en tilfeldig valgt elev i Vg2 har valgt biologi.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

En elev som har valgt biologi går enten i $2 A$ eller i $2 B$ . Da kan vi bruke addisjonssetningen for å finne sannsynligheten for at en elev i VG2 har valgt biologi.

Vi begynner med å definere hendingene:

$B$ : Eleven har valgt biologi.

$2 A$ : Eleven går i klasse $2 A$ .

$2 B$ : Eleven går i klasse $2 B$ .

Vi vet at halvparten av elevene går i $2 A$ og halvparten av elevene går i $2 B$ . Det betyr at $P (2 A) = P (2 B) = \frac{1}{2}$ . Alle elevene som går i $2 A$ har valgt biologi, så sannsynlighetene for at en elev har valgt biologi, gitt at en elev går i $2 A$ , $P (B | 2 A) = 1$ . Vi kan bruke produktregelen til å finne sannsynligheten for at en elev går i $2 A$ og har valgt biologi. Da får vi at sannsynligheten for at en elev går i $2 A$ og har valgt biologi $B$ er $P (2 A \cap B) = P (2 A) \cdot P (B | 2 A) = \frac{1}{2} \cdot 1 = \frac{1}{2}$ Halvparten av elevene i $2 B$ har valgt biologi, så sannsynligheten for at en elev har biologi gitt at eleven går i $2 B$ er $P (B | 2 B) = \frac{1}{2}$ . Fra produktregelen får vi at sannsynligheten for å trekke en elev går i $2 B$ og har valgt biologi er $P (2 B \cap B) = P (2 B) \cdot P (B | 2 B) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ . Nå kan vi finne sannsynligheten for at en elev har valgt biologi ved addisjonssetningen: $P (B) = P (2 A \cap B) + P (2 B \cap B) = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}$

Svar: Sannsynligheten for at en elev har valgt biologi er $\frac{3}{4} = 75 %$ .

Mer om:

Denne oppgaver handler om

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

sannsynlighet

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

For flere forklaringer og eksempler, se artikkelen Betinget sannsynlighet og produktsetningen.

For å øve mer, se dette oppgavesettet om produktregelen i Treningsleiren.

b)

Bestem sannsynligheten for at en tilfeldig valgt elev i Vg2 som har valg biologi går i klasse $2 A$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Fra oppgaven vet vi at $\frac{3}{4}$ av alle elevene i $2 A$ og $2 B$ har biologi, og av disse elevene kommer $\frac{2}{3}$ fra $2 A$ og $\frac{1}{3}$ fra $2 B$ .

Biologiklassen består av elever fra $2 A$ og $2 B$ . Fra oppgaveteksten så har vi at i denne klassen kommer $\frac{2}{3}$ fra $2 A$ og $\frac{1}{3}$ fra $2 B$ . Sannsynligheten for at en valgt elev som har biologi går i $2 A$ er dermed $\frac{2}{3}$ .

Svar: $\frac{2}{3} \approx 67 %$ .

Mer om:

Denne oppgaven handler om

Sannsynlighet

sannsynlighet

For flere forklaringer og eksempler, se lynkurset Sannsynlighet (II).

For å øve mer, se dette oppgavesettet om sannsynlighet.

Oppgave 9 (3 poeng) Nettkode: E-4TJD

Noen elever vil selge vafler for å samle inn penger til en skoletur.
De kjøper inn litt utstyr og nødvendige ingredienser slik at de kan lage $120$ vaffelplater.

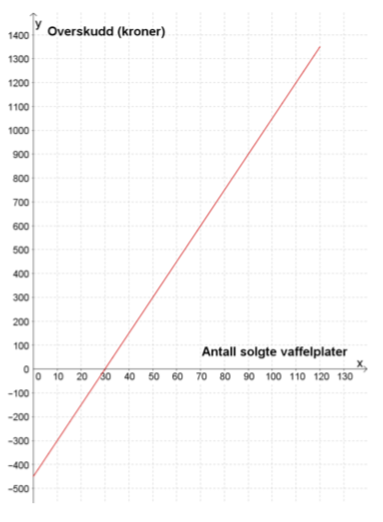
Den grafiske framstillingen nedenfor viser sammenhengen mellom antall vaffelplater de får solgt, og overskuddet de vil få fra salget.

a)

Den rette linjen starter i punktet $(0, - 450)$ og går gjennom punktet $(30, 0)$ .
Hvilken praktisk informasjon gir dette?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Grafen viser sammenhengen mellom antall vaffelplater, $x$ , og overskudd, $y$ .

Punktet $(0, - 450)$ forteller om overskuddet når $x = 0$ , altså før de har solgt noen vaffelplater. Da er overskuddet på $- 450$ kr, som betyr at de har brukt $450$ kr på utstyr og ingredienser.
Punktet $(30, 0)$ forteller oss at når $x = 30$ , altså når de har solgt $30$ vaffelplater, da er de i $0$ , så da har de tjent inn de utgiftene de hadde på utstyr og ingredienser.

Mer om:

Denne oppgaven handler om

Koordinat

Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.

Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.

Se Koordinatsystem

koordinater

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner).

b)

Hvor mye vil elevene ta betalt for hver vaffelplate?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Fra oppgave a) vet vi at når de har solgt $30$ vaffelplater så har de tjent inn $450$ kr.

Elevene har tjent inn de $450$ kr de brukte på utstyr når de har solgt $30$ vaffelplater. Så $30$ vaffelplater koster $450$ kr. Det betyr at én vaffelplate koster $\frac{450 kr}{30} = \frac{45 kr}{3} = 15 kr .$

Svar: En vaffelplate koster $15$ kr.

Mer om:

Denne oppgaven handler om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner).

c)

Vis hvordan du kan regne ut hvor stort overskuddet blir dersom elevene får solgt alle vaffelplatene. Hvor stort blir overskuddet?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi vet at elevene har nok ingredienser til å lage $120$ vaffelplater, og hva prisen per vaffelplate er. Vi kan finne overskuddet ved å finne ut hvor mye de tjener på å selge $120$ vaffelplater og subtrahere det de brukte på utstyr.

Dersom elevene får solgt alle $120$ vaffelplatene får de inn $120 \cdot 15 kr = 1800 kr$ . For å finne ut hvor stort overskuddet blir må vi subtrahere den summen de brukte på utstyr og ingredienser. Da får vi at overskuddet blir $1800 kr - 450 kr = 1350 kr$ som ser ut å stemme med grafen.

Svar: Overskuddet blir på $1350$ kr.

Mer om:

Denne oppgaven handler om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner)].

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4TJI

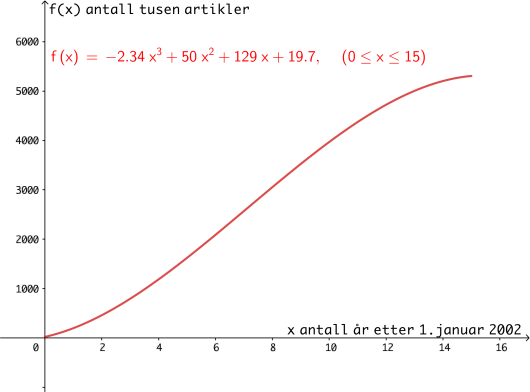
Antall tusen artikler i den engelske utgaven av Wikipedia $x$ år etter $1 .$ januar $2002$ er tilnærmet gitt ved funksjonen $f$ der

$f (x) = - 2, 34 x^{3} + 50 x^{2} + 129 x + 19, 7, 0 \leq x \leq 15$

a)

Bruk graftegner til å tegne grafen til $f$ for $0 \leq x \leq 15$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen til $f$ .

Vi tegner grafen i GeoGebra og da kan vi bruke kommandoen Funksjon[ $<$ Funksjon $>$ , $<$ Start $>$ , $<$ Slutt $>$ ]. Vi vil tegne grafen for $0 \leq x \leq 15]$ og skriver da inn $f (x) = Funksjon [- 2.34 x^{\land} 3 + 50 x^{\land} 2 - 129 x + 19.7, 0, 15]$ Vi tilpasser aksene og setter på navn.
Resultatet er vist under.

Svar:

Mer om:

Denne oppgaven handler om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

grafer

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler, se artikkelen Graftegner i lynkurset GeoGebra.

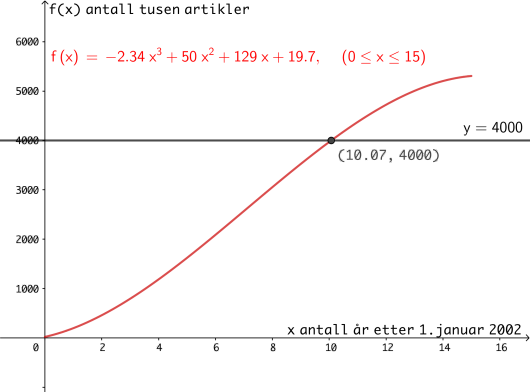
b)

Når passerte antall artikler $4 000 000$ , ifølge funksjonen?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må merke oss at $f (x)$ gir antall tusen artikler, så for å finne når antall artikler passerer $4 000 000$ vi må finne ut når grafen til $f$ vokser over $4 000$ .

Vi vil finne når grafen til $f$ krysser linjen $y = 4 000$ , altså hva $x$ skal være for at $f (x) = 4 000$ . Dette kan vi gjøre grafisk. Vi tegner inn linjen ved å skrive $y = 4000$ i det samme GeoGebra-vinduet som i forrige oppgave. Vi finner skjæringspunktet mellom linjen og grafen ved å bruke skjæringsverktøyet.

Vi ser at grafen til $f$ passerer $4 000$ når $x = 10, 07$ . Det betyr at antall artikler passerte $4 000 000$ $10, 07$ år etter 1. januar 2002, altså tidlig i 2012.

Svar: Antall artikler passerte $4 000 000$ i starten av 2012.

Mer om:

Denne oppgaven handler om

Graf

grafer

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere forklaringer og eksempler, se artikkelen Grafisk løsning av likninger.

For å øve mer, se dette oppgavesettet om funksjonsdrøfting i Treningsleiren.

Oppgave 2 (2 poeng) Nettkode: E-4TJN

På et kart er en avstand $2, 4$ cm. I virkeligheten er den samme avstanden $4, 8$ mil.

Bestem målestokken til kartet.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Målestokken forteller oss om forholdet mellom avstanden på kartet og i virkeligheten. Hvis et kart har målestokk $1 : 25000$ så tilsvarer $1$ cm på kartet $25000$ cm i virkeligheten.

Vi vet at $2, 4 cm$ på kartet er $4, 8$ mil i virkeligheten. Vi kan finne ut hvor langt $1$ cm på kartet er ved å dividere $4, 8$ mil på $2, 4$ . Én mil er det samme som $10 000 m$ , så $4, 8$ mil er $48 000$ m. Da får vi $\frac{48 000 m}{2, 4} = 20 000 m$ Så $1$ cm på kartet tilsvarer $20 000$ m, og siden $1 m = 100 cm$ må vi multipliserer svaret med $100$ for å finne ut hvor mange cm dette er i virkeligheten. $20 000 \cdot 100 cm = 2 000 000 cm$ $1$ cm på kartet tilsvarer $2 000 000 cm$ i virkeligheten.

Svar: Målestokken er $1 : 2 000 000$ .

Mer om:

Denne oppgaven handler om

Målestokk

Målestokken angir hva en måleenhet på for eksempel kartet svarer til i terrenget.

Eksempel:
Et kart har målestokken 1 : 25000 (leses: en til tjuefemtusen)

Dette betyr for eksempel at:

-	1 cm på kartet tilsvarer 25000 cm i terrenget (25000 cm = 250 m)
-	1 dm på kartet tilsvarer 25000 dm i terrenget
-	4 cm på kartet er 25000 · 4 cm i terrenget (25000 · 4 cm = 100000 cm = 1000m = 1 km).

Eller mer generelt:
1 bestemt måleenhet på kartet er 25000 slike måleenheter i terrenget.

målestokk

For flere forklaringer og eksempler, se artikkelen Målestokk.

Oppgave 3 (2 poeng) Nettkode: E-4TJP

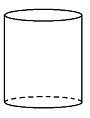
En hermetikkboks har form som en sylinder med radius $10$ cm og høyde $10$ cm. En kule har radius $10$ cm.

Bestem forholdet mellom overflaten av hermetikkboksen og overflaten av kula.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi finne forholdet mellom overflatearealet av hermetikkboksen og kula ved $\frac{overflaterareal hermetikkboks}{overflateareal kule} .$

Vi har at forholdet er $\frac{overflate hermetikkboks}{overflate kule}$ .
Hermetikkboksen har form som en sylinder, og arealet til en sylinder er gitt ved summen av arealet til toppen, bunnen og sideflaten. Vi har sirkler i topp og bunn, og arealet til en sirkel er gitt ved $A = π r^{2}$ og sideflaten har areal $A = 2 π r h$ . Arealet til overflaten til hermetikkboksen er gitt ved summen av arealet til topp, bunn og sideflaten $A = 2 π \cdot r^{2} + 2 π r h$ Arealet til overflatearealet til en kule er gitt ved $A = 4 π r^{2}$ Forholdet mellom overflatearealene er da $\frac{2 π r^{2} + 2 π r h}{4 π r^{2}}$ Vi kan sette inn for $r = 10 cm$ og $h = 10 cm$ . Da vår vi $\frac{2 π (10 cm)^{2} + 2 π \cdot 10 cm \cdot 10 cm}{4 π (10 cm)^{2}} = \frac{2 π (10 cm)^{2} + 2 π (10 cm)^{2}}{4 π (10 cm)^{2}} = \frac{4 π (10 cm)^{2}}{4 π (10 cm)^{2}} = \frac{1}{1}$

Svar: Forholdet er $1 : 1$ .

Mer om:

Denne oppgaven handler om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proporsjon

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Overflate

Med overflate av en tredimensjonal figur, for eksempel et prisme eller en sylinder, menes summen av arealene til alle flatene som den tredimensjonale figuren er satt sammen av.

overflate

For flere forklaringer og eksempler, se artikkelen Målingsforhold og Tom forteller om overflatearealer.

For å øve mer, se dette oppgavesettet om overflate i Treningsleiren.

Oppgave 4 (3 poeng) Nettkode: E-4TJR

Basisåret for konsumprisindeks er nå $2015$ . Tidligere var basisåret $1998$ .

Da $1998$ ble brukt som basisår, var konsumprisindeksen $139, 8 i 2015$ og $144, 8 i 2016$ .

a)

Vis at konsumprisindeksen i $1998$ nå er $71, 5$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Uavhengig av basisår, så må forholdet mellom konsumprisindeksene i $1998$ og $2015$ være det samme.

Forholdet mellom konsumprisindeksene er det samme uansett hvilket basisår vi velger, det vil si at med 1998 som basisår har vi forholdet $\frac{{kpi}_{1998}}{{kpi}_{2015}} .$

Konsumprisindeksen i basisåret er alltid $100$ , så ${kpi}_{1998} = 100 og {kpi}_{2015} = 139, 8$ . Selvom konsumprisindeksene vil være forskjellig med basisår i $2015$ vil forholdet $\frac{{kpi}_{1998}}{{kpi}_{2015}}$ være det samme. Vi kan betegne konsumprisindeksen i $1998$ med $2015$ som basisår med $x$ . Da er ${kpi}_{2015} = 100$ . Nå kan vi sette opp likningen $\frac{100}{139, 8} = \frac{x}{100}$ og løse denne med hensyn på $x$ . Da får vi at $x = \frac{100}{139, 8} \cdot 100 \approx 71, 5$ som var det vi ville ha.

Mer om:

Denne oppgaven handler om

Konsumprisindeks

Konsumprisindeks (KPI) er en indeks som viser endringer i prisene på varer og tjenester som kjøpes av husholdninger, sammenlignet med et basisår. De varer og tjenester som utgjør det meste av husholdningsbudsjettet, tillegges størst vekt.

(hentet fra http://snl.no/konsumprisindeks)

konsumprisindeks

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

I Ofte stilte spørsmål har Orakelet forklart hva konsumprisindeks er.

b)

Hva er nå konsumprisindeksen i $2016$ ?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Som i oppgave a) har vi at forholdet mellom konsumprisindeksene i $1998$ og $2015$ være det samme, uavhengig av basisår.

Vi kan nå la konsumprisindeksen i $2016$ med basisår $2015$ være lik $x$ . Når basisåret er $2015$ vil konsumprisindeksen i $2015$ være $100$ . Forholdet $\frac{x}{100}$ må være likt forholdet $\frac{144, 8}{139, 8}$ , så $\frac{x}{100} = \frac{144, 8}{139, 8} .$ Da får vi at $x = \frac{144, 8}{139, 8} \cdot 100 \approx 103, 6 .$

Svar: Konsumprisindeksen i $2016$ er nå $103, 6$ .

Mer om:

Denne oppgaven handler om

Konsumprisindeks

(hentet fra http://snl.no/konsumprisindeks)

konsumprisindeks

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

I Ofte stilte spørsmål har Orakelet forklart hva konsumprisindeks er.

Oppgave 5 (2 poeng) Nettkode: E-4TJU

I $2010$ var konsumprisindeksen $92, 1$ . I $2014$ var konsumprisindeksen $97, 9$ .

Helene hadde like stor kjøpekraft i $2014$ som i $2010$ .
I $2014$ hadde hun en nominell lønn på $540 000$ kroner.

Hva var den nominelle lønna hennes i 2010?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Dersom kjøpekraften er den samme, må reallønnen være den samme begge årene. Vi kan først finne reallønnen, og beregne nominell lønn ut ifra denne.

Vi kan begynne med å finne reallønnen til Helene i $2014$ . Den er gitt ved $Reallønn = Nominell lønn \cdot \frac{100}{kpi}$ I $2014$ var konsumprisindeksen, kpi, $97, 9$ og Helene hadde nominell lønn $540 000 kr$ , som betyr at reallønnen til Helene var $Reallønn = 540 000 kr \cdot \frac{100}{97, 9} \approx 551 583, 25 kr .$ Gjør vi om på formelen for reallønn får vi at $Nominell lønn = Reallønn \cdot \frac{kpi}{100} .$ Helene hadde like stor kjøpekraft i $2010$ som i $2014$ , så reallønnen må være den samme for de to årene. I $2010$ var konsumprisindeksen $92, 1$ . Den nominelle lønnen til Helene i $2010$ var da $Nominell lønn = 551 583, 25 kr \cdot \frac{92, 1}{100} \approx 508 008 kr .$

Svar: Den nominelle lønnen hennes var $508 008$ kr i $2010$ .

Mer om:

Denne oppgaven er om

Nominell lønn

Nominell lønn er det vi vanligvis bare kaller lønn.

Om du slår opp i en ordbok finner du følgende om ordene nominell;

nominell
det er to måter å bruke ordet på
1 - som gjelder (bare) i navnet det er han som er lederen, iallfall nominelt
2 - pålydende obligasjonene har en nominell verdi på 1000 kr / nominell inntekt inntekt uttrykt i pengeverdien til enhver tid / nominell rente, til forskjell fra effektiv rente

nominell lønn

, reallønn og

Konsumprisindeks

(hentet fra http://snl.no/konsumprisindeks)

konsumprisindeks

I Ofte stilte spørsmål har Orakelet forklart hva konsumprisindeks er.

Oppgave 6 (2 poeng) Nettkode: E-4TJW

Prisen for en vare er endret fem ganger. To ganger er den satt ned med $30 %$ . Tre ganger er den satt opp med $20 %$ . Nå koster varen $2646$ kroner.

Hva kostet varen før prisendringene?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Den opprinnelige prisen er ukjent, og ved å følge teksten i oppgaven kan vi komme fram til en likning for den opprinnelige prisen.

La den opprinnelige vareprisen være $x$ kroner. Først ble prisen satt ned med $30 %$ , som er en prosentfaktor på $0, 3$ . Ved nedgang har vi at $vekstfaktor = 1 - prosentfaktor,$ så vekstfaktoren er på $1 - 0, 3 = 0, 7$ . Etter første prisendring er ny pris gitt ved $ny pris = opprinnelig pris \cdot vekstfaktor = x \cdot 0, 7 .$ Denne prisen blir deretter satt ned med $30 %$ , som betyr at vi har samme vekstfaktor, og prisen på varen vil når være gitt ved $(x \cdot 0, 7) \cdot 0, 7 = x \cdot 0, 7^{2} .$ Nå settes prisen på varen opp med $20 %$ , altså med en prosentfaktor på $0, 2$ . Da blir ny vekstfaktor $1 + 0, 2 = 1, 2$ . Ved første prisøkning vil den nye prisen være gitt ved $x \cdot {0, 7}^{2} \cdot 1, 2$ . Andre og tredje prisøkning har samme vekstfaktor, og da får vi at etter tre prisøkninger er prisen gitt ved $x \cdot 0, 7^{2} \cdot 1, 2 \cdot 1, 2 \cdot 1, 2 = x \cdot 0, 7^{2} \cdot 1, 2^{3}$

Vi vet at sluttprisen skal være lik $2646$ kr, så da har vi likningen:

$\begin{matrix} x \cdot 0, 7^{2} \cdot 1, 2^{3} & = & 2646 \\ x & = & \frac{2646}{0, 7^{2} \cdot 1, 2^{3}} \\ x & = & 3125 \end{matrix}$

Svar: Før prisendringene kostet varen $3125$ kr.

Mer om:

Denne oppgaven handler om prosent.

For flere forklaringer og eksempler, se artikkelen Prosent av hva da?.

For å øve mer, se dette oppgavesettet om prosentregning i Treningsleiren.

Oppgave 7 (4 poeng) Nettkode: E-4TJY

I en eske ligger det tre hvite og ni røde julekuler. Én av de hvite og fire av de røde kulene er ødelagt.

Tenk deg at du skal ta to kuler tilfeldig fra esken.

a)

Bestem sannsynligheten for at du kommer til å ta to kuler som ikke er ødelagt.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Dette er et utvalg uten tilbakelegging. Vi kan bruke produktsetningen.

Vi har hendelsene
$A$ : Første kule er ikke ødelagt
$B$ : Andre kule er ikke ødelagt.
Vi vil finne sannsynligheten for at både $A$ og $B$ inntreffer. Det er totalt $3 + 9 = 12$ julekuler, hvorav $1 + 4 = 5$ av dem er ødelagt, som betyr at $12 - 5 = 7$ av dem ikke er det. Sannsynligheten for at hendelse $A$ inntreffer er gitt ved $P (A) = \frac{7}{12} .$ Vi vil at både hendelse $A$ og $B$ skal inntreffe. Dersom vi tok en kule som ikke er ødelagt første gang har vi igjen $6$ kuler som ikke er ødelagt, og nå er antall julekuler $11$ totalt. Sannsynligheten for at hendelse $B$ inntreffer gitt at $A$ inntraff, $B | A$ ,er gitt ved $P (B | A) = \frac{6}{11}$ Sannsynligheten for at både $A$ og $B$ inntreffer, $A \cap B$ , finner vi ved å bruke produktsetningen $P (A \cap B) = P (A) \cdot P (B | A) = \frac{7}{12} \cdot \frac{6}{11} \approx 0, 318$

Svar: Sannsynligheten for å trekke to kuler som ikke er ødelagt er omtrent $31, 8 %$ .

Mer om:

Denne oppgaven handler om betinget sannsynlighet, uten tilbakelegging og produktsetningen.

For flere forklaringer og eksempler, se artikkelen Betinget sannsynlighet og produktregelen.

For å øve mer, se dette oppgavesettet om betinget sannsynlighet og produktregelen i Treningsleiren.

b)

Bestem sannsynligheten for at minst én av kulene du kommer til å ta, er ødelagt.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Hendelsen at vi trekker minst én ødelagt kule er komplementær med at vi ingen av de vi trekker er ødelagte.

Hendelsen at vi trekker minst én kule som er ødelagt er komplementær med hendelsen at begge kulene vi trekker ikke er ødelagte, $A \cap B$ . Da har vi at $P (minst én ødelagt) = 1 - P (A \cap B) .$ I oppgave a) fant vi at $P (A \cap B) = 0, 318$ . Sannsynligheten for at vi trekker minst én ødelagt kule er da $P (minst én ødelagt = 1 - 0, 318 = 0, 682 .$

Svar: Sannsynligheten for at minst én av kulene er ødelagt er $68, 2 %$ .

Mer om:

Denne oppgaven handler om sannsynlighet og komplement.

For flere forklaringer og eksempler, se artikkelen Sannsynlighet ved komplementære hendelser.

Oppgave 8 (5 poeng) Nettkode: E-4TK2

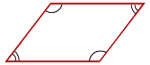
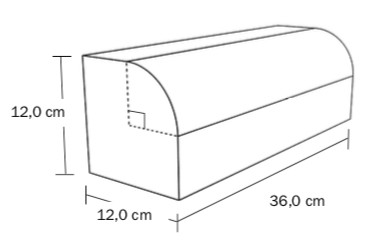
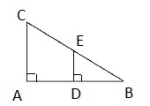
Anders hadde en trekloss med form som et rett firkantet prisme. Han fikk skåret bort en del av klossen slik at den ene kanten ble avrundet. Se figuren ovenfor.
Buen er en sirkelbue med radius $6, 0$ cm.

a)

Bestem volumet av treklossen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan forlenge den ene stiplede linjen og dele figuren inn i to prismer, et med rektangulær grunnflate og et med kvadratisk grunnflate. Figuren består også av en kvart sylinder.

Vi kan dele figuren inn i tre deler, en kvart sylinder, et prisme med rektangulær grunnflate og et prisme med kvadratisk grunnflate. For å finne volumet til hele figuren kan vi begynne med å finne volumet til hver av delene og addere dem sammen til slutt. Volumet til alle disse figurene er gitt ved $V = G \cdot h$ , der grunnflaten $G$ er forskjellig for de tre delene, høyden vil være den samme for alle delene; $h = 36, 0 cm$ .

Vi kan begynne med den kvarte sylinderen. Volumet til en sylinder er gitt ved $V = G_{S} \cdot h$ Den kvarte sylinderen har en kvart sirkel som grunnflate, der $G_{S} = \frac{π \cdot r^{2}}{4}$ . Radiusen til sirkelen er $r = \frac{12, 0 cm}{2} = 6, 0 cm$ . Høyden er $h = 36, 0 cm$ . Nå kan vi finne volumet til den kvarte sylinderen og får vi at $V_{S} = \frac{π \cdot r^{2}}{4} \cdot h = \frac{π \cdot (6, 0 cm)^{2}}{4} \cdot 36, 0 cm \approx 1017, 9 {cm}^{3}$ For prismet med rektangulær grunnflate har vi $G_{R} = l \cdot b$ , der $l = 6, 0 cm$ og $b = 12, 0 cm$ . Volumet til dette prismet er $V_{R} =l\cdotb\cdoth=6,0cm\cdot12,0cm\cdot36,0cm=2592{cm}^{3}$ Da gjenstår bare prismet med kvadratisk grunnflate, der $G_{K} = s^{2}$ . Sidene i kvadratet er $s = 6, 0 cm$ . Volumet for dette prismet er $V_{K} = s^{2} \cdot h = (6, 0 cm)^{2} \cdot 36, 0 cm = 1296 {cm}^{3}$ Det totale volumet av treklossen er $V = 1017, 9 {cm}^{3} + 2596 {cm}^{3} + 1296 {cm}^{3} = 4905, 9 {cm}^{3}$

Svar: Volumet av treklossen er $4905, 9 {cm}^{3}$ .

Mer om:

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Prisme

Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.

Har et prisme grunnflate G og høyde h, er volumet lik G · h.

prisme

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

For flere forklaringer og eksempler, se artikkelen Tom forteller om volum.

For å øve mer, se dette oppgavesettet om volum i Treningsleiren.

b)

Bestem overflaten av treklossen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan dele overflaten av treklossen opp i flere deler og beregne overflaten av hver av dem først, og deretter addere dem sammen.

Vi kan begynne med å få en oversikt over overflaten til treklossen. Den består av:

To rektangulære sideflater med lengde $l = 12, 0 cm$ og $b = 36, 0 cm$

To rektangulære sideflater med lengde $l = 6, 0 cm$ og $b = 36, 0 cm$

En fjerdedel av en sylinder med radius $6, 0 cm$ og $h = 36, 0 cm$

To rektangler med $l = 12, 0 cm$ og $b = 6, 0 cm$

To kvadrat med $s = 6, 0 cm$ .

Vi kan nå finne arealet av hver av disse delene. Vi begynner på toppen av lista. Arealet av et rektangel er gitt ved $A = l \cdot b$ . Overflaten består av to rektangulære sideflater med $l = 12, 0 cm$ og bredden $b = 36, 0 cm$ . Det totale arealet for disse to rektanglene er $A = 2 \cdot l \cdot b = 2 \cdot 12, 0 cm \cdot 36, 0 cm = 864 {cm}^{2}$ Overflaten består også av to rektangler med $l = 6, 0 cm$ , og bredde $b = 36, 0 cm$ som for de over. Det totale arealet for disse to rektanglene er $A = 2 \cdot 6, 0 cm \cdot 36, 0 cm = 432 {cm}^{2}$ Treklossen består av en fjerdedels sylinder. Overflatearealet til en sylinder er gitt ved $A = 2 π r^{2} + 2 π r h$ . Vi har $r = 6, 0 cm$ og $h = 36, 0 cm$ , og siden vi kun har en fjerdedel av sylinderen blir overflaten $A = \frac{2 π \cdot (6, 0 cm)^{2} + 2 π \cdot 6, 0 cm \cdot 36, 0 cm}{4} = 395, 8 {cm}^{2}$ Arealet til de to rektanglene med $l = 12, 0 cm$ og $b = 6, 0 cm$ er $A = 2 \cdot 12, 0 cm \cdot 6, 0 cm = 144, 0 cm$ og de to kvadratene med $s = 6, 0$ er $A = 2 \cdot (6, 0 cm)^{2} = 72 {cm}^{2}$ Den totale overflaten av treklossen er da $864 {cm}^{2} + 432 {cm}^{2} + 395, 8 {cm}^{2} + 144 {cm}^{2} + 72 {cm}^{2} = 1907, 8 {cm}^{2}$

Svar: Overflaten av treklossen er $1907, 8 {cm}^{2}$ .

Mer om:

Denne oppgaven er om

Overflate

Med overflate av en tredimensjonal figur, for eksempel et prisme eller en sylinder, menes summen av arealene til alle flatene som den tredimensjonale figuren er satt sammen av.

overflate

Prisme

prisme

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

For flere forklaringer og eksempler, se artikkelen Tom forteller om overflatearealer.

For å øve mer, se dette oppgavesettet om overflate i Treningsleiren.

Oppgave 9 (6 poeng) Nettkode: E-4TK6

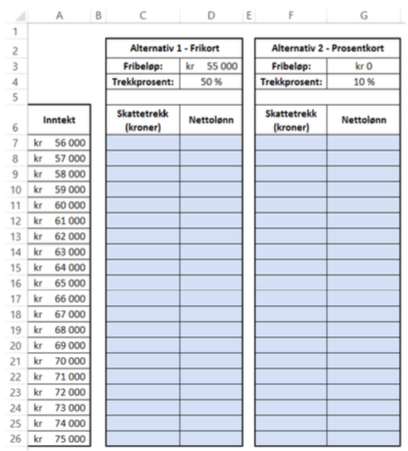
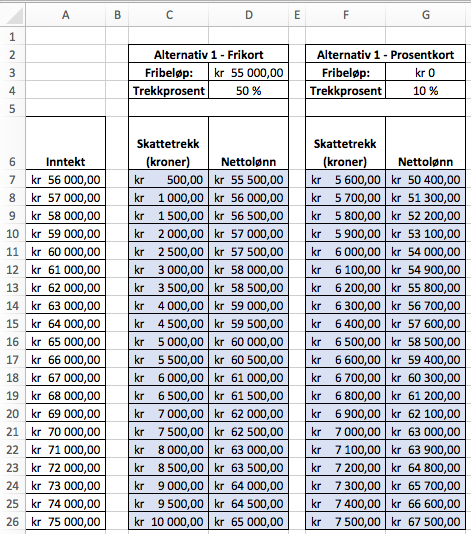
Per har deltidsjobb i en matvarebutikk. Han er ikke sikker på hvor mye han kommer til å tjene i løpet av $2017$ . Han kan velge mellom to alternative skattetrekk.

Anta at Per kommer til å tjene $60 000$ kr i $2017$ .

a)

Bestem Pers nettolønn med hvert av alternativene ovenfor.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Med frikort må Per kun betale skatt av det beløpet som går over $55 000 kr$ , mens med prosentkort må han betale skatt av alt han tjener.

Vi skal bestemme Pers nettolønn med frikort og prosentkort. Nettolønn er lønnen Per får utbetalt etter at skatten er trukket fra inntekten. Vi begynner med å finne ut hvor mye skatt Per må betale med frikort. Da betaler han skatt av den delen av lønna som er over $55 000$ kr. Når han tjener $60 000$ kr vil det si $60 000 kr - 55 000 kr = 5000 kr .$ Av disse $5000$ kr betaler han $50 %$ skatt, som vil si at han betaler $5000 kr \cdot 50 % = 5000 kr \cdot \frac{1}{2} = 2500 kr .$ Nettoinntekten til Per med frikort er $60 000 kr - 2500 kr = 57 500 kr .$ Dersom Per har prosentkort må han betale $10 %$ skatt av alt han tjener. Når Per har en inntekt på $60 000 kr$ er må han betale $60 000 kr \cdot 10 % = 60 000 kr \cdot \frac{1}{10} = 6000 kr$ i skatt. Han sitter da igjen med $60 000 kr - 6000 kr = 54 000 kr$ i nettolønn.

Svar: Pers nettolønn er $57 500$ kr med frikort og $54 000$ kr med prosentkort.

Mer om:

Denne oppgaven handler om

Netto månedslønn

Lønnen du får utbetalt. Da er skatt, fagforeningskontigent og lignende trukket fra bruttolønna.

netto månedslønn

Skatt

Skatt er en avgift som stat og kommune pålegger den enkelte borger å betale.

skatt

For flere forklaringer og eksempler, se lynkurset Skatt.

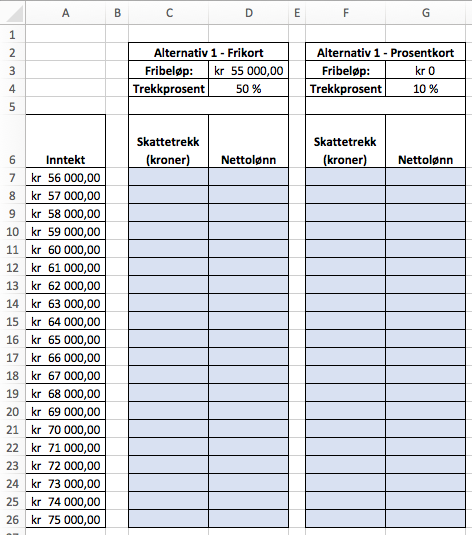
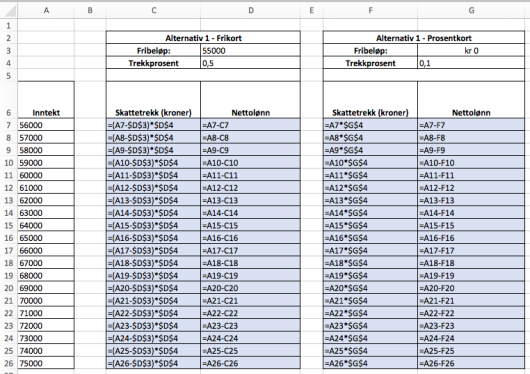
Per ønsker å lage en oversikt i et regneark for å finne hvor mye han vil få i nettolønn ved ulike inntekter etter de to alternativene ovenfor. I regnearket nedenfor har vi lagt inn ulike mulige inntekter for Per i $2017$ .

Løs oppgaven her

b)

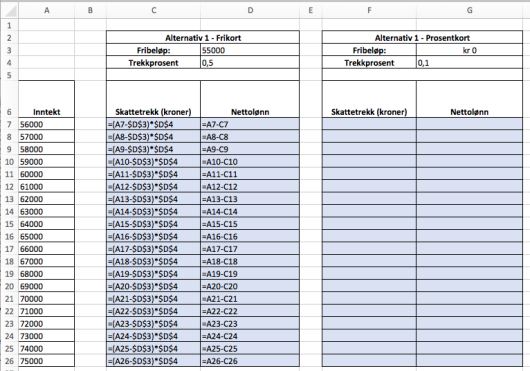
Lag et regneark som vist ovenfor. Du skal sette inn formler i de blå cellene og beregne skattetrekk og nettolønn.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan lage regnearket i Excel.

Først setter vi opp regnearket som i oppgaven.

Nå skal vi sette opp formler som beregner skattetrekk og nettolønn for frikort og prosentkort. I oppgave a) fant vi hva vi skulle betale i skatt med frikort ved å først finne ut hvor stor del av inntekten som var over fribeløpet på $55 000$ kr, i celle D3, og deretter multiplisere dette med trekkprosenten på $50 %$ i D4 av dette. Skattetrekket er da gitt ved $(inntekt - fribeløp) \cdot trekkprosent .$ For å beregne skattetrekket i C7 når Per tjener $56 000 kr$ , som står i A7 kan vi skrive $= (𝙰 7 - 𝙳 3)^{*} 𝙳 4$ Tilsvarende får vi når Per tjener $57 000$ kr, som står i celle A8 da kan vi skrive $= (𝙰 8 - 𝙳 3)^{*} 𝙳 4$ Vi kan kopiere formelen i C7 ved å markere cellen og dra i den lille grønne ruten nede til høyre, da endrer formelen seg i C8 til $= (𝙰 8 - 𝙳 4)^{*} 𝙳 5$ . Vi vil “låse” cellene D3 og D4 i formelen. For å gjøre det kan vi skrive $= (𝙰 7 - $ 𝙳 $ 3)^{*} $ 𝙳 $ 4$ i C7. Da vil formelen i C8 være $= (𝙰 8 - $ 𝙳 $ 3)^{*} $ 𝙳 $ 4$ , og tilsvarende for cellene under.
Vi finner nettolønnen til Per ved $inntekt - skattetrekk .$ Da kan vi skrive i celle D7 formelen $= 𝙰 7 - 𝙲 7$ . Denne formelen kan vi kopiere til cellene under ved å fra i den lille grønne ruten. Med formler vil regnearket for alternativ 1 se slik ut:

I alternativ 2, med prosentkort beregner vi skattetrekket ved $inntekt \cdot trekkprosent .$ Når Per tjener $56 000$ , som i A7 kan vi skrive dette med formelen $𝙰 7^{*} $ 𝙶 $ 4$ i F7 og kan kopiere denne formelen til cellene under. På tilsvarende måte som for frikort finner vi nettolønnen, i G7 ved formelen $𝙰 7 - 𝙵 7$ som vi kan kopiere til cellene under. Med formler blir hele regnearket seende slik ut:

Med skattetrekk og nettoinntekt i kroner ser regnearket slik ut:

Mer om:

Denne oppgaven handler om regneark og

Skatt

Skatt er en avgift som stat og kommune pålegger den enkelte borger å betale.

skatt

For flere forklaringer og eksempler, se artikkelen Regneark.

c)

Hvor mye må Per tjene for at de to alternativene skal gi nøyaktig like stort skattetrekk?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke formler for skattetrekk for prosentkort og frikort til å bestemme hva inntekten til Per må være.

Vi kan la inntekten til Per være $x$ kr når de to alternativene gir like stort skattetrekk. Vi kan skrive skattetrekket når Per har frikort som $(x - 55 000) \cdot \frac{1}{2}$ og når Per har prosentkort som $\frac{x}{10} .$ Siden skattetrekket skal være likt, kan vi skrive dette som likningen

$(x - 55000) \cdot \frac{1}{2} = \frac{x}{10}$ .

Nå kan vi løse denne likningen med hensyn på $x$ :

$\begin{matrix} (x - 55 000) \cdot \frac{1}{2} & = & \frac{x}{10} \\ 10 \cdot (x - 55 000) \cdot \frac{1}{2} & = & 10 \cdot \frac{x}{10} \\ 5 (x - 55 000) & = & x \\ 4 x & = & 275 000 \\ x & = & 68750 \end{matrix}$

Svar: Per må tjene $68750$ kr for at de to alternativene gir samme skattetrekk.

Alternativ løsning

Vi kan også løse denne likningen i CAS i GeoGebra. Vi kan skrive $\frac{1}{2} = 0, 5$ og $\frac{1}{10} = 0, 1$ . Da skriver vi inn $𝙻 ø 𝚜 ((𝚡 - 55000)^{*} 0.5 = 𝚡^{*} 0.1)$ og får

Mer om:

Denne oppgaven handler om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

For flere forklaringer og eksempler, se artikkelen Fra problem til likning.

Oppgave 10 (6 poeng) Nettkode: E-4TKI

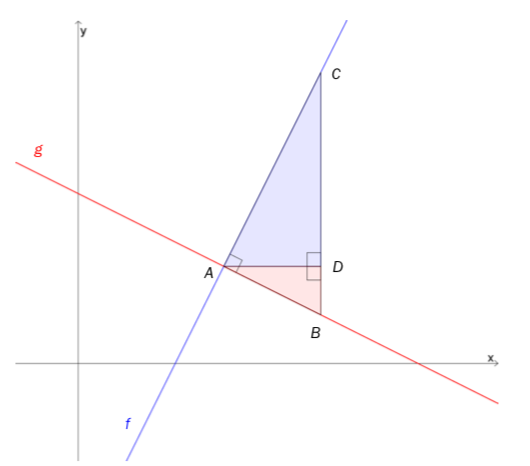
Gitt figuren ovenfor.

- Den blå linjen er grafen til funksjonen $f$ , og den røde linjen er grafen til funksjonen $g$ .

- Linjene skjærer hverandre i punktet $A$ .

- Punktet $B$ ligger på grafen til $g$ , og punktet $C$ ligger på grafen til $f$ .

- Punktet $D$ ligger på $B C$ , og $B C$ er parallell med $y$ -aksen.

a)

Forklar at $△ A D C$ og $△ A B D$ er formlike.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

To trekanter er formlike dersom de har parvis like vinkler. Dersom to trekanter har to like vinkler, vil den siste også være lik.

Vi skal vise at $△ A D C$ og $△ A B D$ er formlike. Vi får oppgitt at $∠ A D C = ∠ A D B = 90^{\circ}$ . Siden vinkelsummen i en trekant er $180^{\circ}$ betyr det at de gjenværende vinklene i de to trekantene må tilsammen være $180^{\circ} - 90^{\circ} = 90^{\circ}$ , altså at $∠ A B D + ∠ B A D = 90^{\circ}$ og $∠ A C D + ∠ C A D = 90^{\circ} .$ Vi har også at $∠ B A C = ∠ B A D + ∠ C A D = 90^{\circ} .$ Gjør vi litt om på disse uttrykkene kan vi se at vi har $∠ B A D = 90^{\circ} - ∠ C A D$ og $∠ A C D = 90^{\circ} - ∠ C A D$ som betyr at $∠ B A D = ∠ A C D$ . Da er to av vinklene parvis like, og da må også den tredje være lik.

Mer om:

Denne oppgaven handler om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

For flere forklaringer og eksempler, se artikkelen Formlikhet og kongruens.

For å øve mer, se dette oppgavesettet om formlikhet og kongruens i Treningsleiren.

Funksjonen $f$ er gitt ved $f (x) = 2 x - 4$ og $A D = 1$

Løs oppgaven her

b)

Vis at $B D = 0, 5$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Når vi kjenner $f$ og vet at $A D = 1$ kan vi bestemme $C D$ ved stigningstallet til $f$ . Vi kan så bruke at $△ A D C$ og $△ A B D$ er formlike for å bestemme $B D$ .

Stigningstallet til en lineær funksjon forteller oss hvor mye grafen stiger eller synker når vi øker med en enhet på $x$ -aksen. Når $A D = 1$ betyr det at $C D$ må være lik stigningstallet til funksjonen $f$ , altså har vi at $C D = 2$ .
$A D$ er en side i både $△ A D C$ og $△ A B D$ , og vi kjenner nå også $C D$ . I to formlike trekanter er forholdet mellom to samsvarende sider konstant. $A D$ og $C D$ er samsvarende sider og $B D$ og $A D$ er samsvarende sider. Det betyr at $\frac{A D}{C D} = \frac{B D}{A D}$ Setter vi inn for $A D$ og $C D$ får vi at $\begin{matrix} \frac{B D}{1} & = \frac{1}{2} \\ B D & = 0, 5 \end{matrix}$ som var det vi ville vise.

Mer om:

Denne oppgaven handler om

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

For flere forklaringer og eksempler, se artiklene Formlikhet og kongruens og Rette linjer (lineære funksjoner).

Funksjonen $g$ er gitt ved $f (x) = a x + b$ og $g (0) = 3, 5$

Løs oppgaven her

c)

Bestem $a$ og $b$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

I oppgave b) kunne vi se at det var en sammenheng mellom $C D$ og stigningstallet til $f$ og det vil også være en sammenheng mellomg $B D$ og stigningstallet $a$ til funksjonen $g$ .

Funksjonen $g$ er gitt ved $g (x) = a x + b$ , der $a$ er stigningstallet til funksjonen og $b$ er punktet grafen krysser $x$ -aksen. Grafen til $g$ vil krysse $y$ -aksen i punktet $(x, g (x))$ der $x = 0$ . Siden $g (0) = 3, 5$ har vi at grafen vil krysse $y$ -aksen i $b = 3, 5$ .

Stigningstallet forteller oss hvor mye grafen stiger eller synker når vi øker med en enhet på $x$ -aksen. Når $A D = 1$ betyr det at lengden til $B D$ må være lik stigningstallet til $g$ . Siden g er avtangende, betyr det at $a = - 0, 5$ , og $g (x) = - 0, 5 x + 3, 5$ .

Svar: $a = - 0, 5$ og $b = 3, 5$ .

Mer om:

Denne oppgaven handler om

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner).

MAT1011 2017 Høst

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (2 poeng) Nettkode: E-4TIL

a)

Løsningsforslag a)

Prosent

b)

Løsningsforslag b)

Prosent

Oppgave 2 (2 poeng) Nettkode: E-4TIO

Løsningsforslag

Pytagoras læresetning

Oppgave 3 (2 poeng) Nettkode: E-4TIS

Løsningsforslag

Prosent

Prosentpoeng

Oppgave 4 (1 poeng) Nettkode: E-4TIV

Løsningsforslag

Prosent

Oppgave 5 (3 poeng) Nettkode: E-4TIX

a)

Løsningsforslag a)

b)

Løsningsforslag b)

Oppgave 6 (2 poeng) Nettkode: E-4TJ2

Løsningsforslag

Parallellogram

Trekant

Sirkel

Areal

Oppgave 7 (6 poeng) Nettkode: E-4TJ4

a)

Løsningsforslag a)

Tabell

Divisjon

b)

Løsningsforslag b)

Regresjon

Formel

Funksjon

c)

Løsningsforslag c)

Formel

d)

Løsningsforslag d)

Omvendt proporsjonal

Oppgave 8 (3 poeng) Nettkode: E-4TJ9

a)

Løsningsforslag a)

Sannsynlighet

Produktsetningen

b)

Løsningsforslag b)

Sannsynlighet

Oppgave 9 (3 poeng) Nettkode: E-4TJD

a)

Løsningsforslag a)

Koordinat

Lineære funksjoner

b)

Løsningsforslag b)

Lineære funksjoner

c)

Løsningsforslag c)

Lineære funksjoner

DEL 2 Med hjelpemidler

Oppgave 1 (4 poeng) Nettkode: E-4TJI

a)

Løsningsforslag a)

Graf

GeoGebra

b)

Løsningsforslag b)

Graf

Skjæringspunkt

Oppgave 2 (2 poeng) Nettkode: E-4TJN

Løsningsforslag