
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2014 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4CHE
Nedenfor ser du hvor mange snegler Astrid har plukket i hagen hver kveld de ti siste kveldene.
10 5 22 28 2 8 50 15 40 10
Bestem gjennomsnittet, medianen og variasjonsbredden for dette datamaterialet.
Løsningsforslag
Jeg tenker:
Vi skal finne
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Variasjonsbredde
Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Variasjonsbredde
Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien.
For å finne medianen flytter vi rundt på tallene i rekken slik at de kommer i stigende rekkefølge. Medianen av disse tallene, er gjennomsnittet av de to midterste tallene. (Hvis det var et odde antall tall, hadde medianen vært det midterste tallet.) Det er gjennomsnittet av tall nummer 5 og tall nummer 6, altså henholdsvis 10 og 15. Det blir .
Videre skal vi finne gjennomsnittet av tallene. Gjennomsnittet er
eller sagt på en annen måte, forholdet mellom summen av tallene over og antall tall. Astrid plukket snegler 10 ganger, og gjennomsnittet blir derfor
Variasjonsbredden er forskjellen mellom det minste og det største tallet i datasettet. Det minste tallet er 2, og det største tallet er 50; det gir en variasjonsbredde på .
Svar: Medianen er , gjennomsnittet er og variasjonsbredden er 48.
Mer om:
Denne oppgaven er om Medianen er den verdien som vi finner i midten av et rangert datamateriale. Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Median
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Variasjonsbredde
Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.
For å øve mer, se oppgavesettet om gjennomsnitt, median og variasjonsbredde i Treningsleieren.
Oppgave 2 (2 poeng) Nettkode: E-4CHH
Sorter uttrykkene nedenfor etter stigende verdi. Vis eller forklar hvordan du har tenkt.
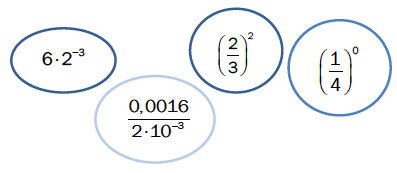
Løsningsforslag
Jeg tenker:
Her har vi mange
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Vi forenkler
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Nå skal vi rangere tallene , , og i stigende rekkefølge. Tallet 1 er størst, siden alle de andre er brøker der
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Svar:
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n gangerBrøk

For flere eksempler og forklaringer se artikkelen Oppsummering av regneregler for potenser.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 3 (2 poeng) Nettkode: E-4CHJ
I Norge er det ca. 5 millioner innbyggere. Hvert år produseres omtrent 150 milliarder M&M-sjokolader i verden. Tenk deg at disse sjokoladene ble delt likt mellom innbyggerne i Norge.
Omtrent hvor mange M&M-sjokolader ville hver innbygger ha fått? Skriv svaret på standardform.
Løsningsforslag
Jeg tenker:
Antall M&M-sjokolader per person er forholdet mellom antallet M&M-sjokolader og antall personer i Norge. Én milliard er , og én million er . Husk å skrive svaret som
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Altså er antallet M&M-sjokolader per person lik
.
Vi har at antallet M&M-sjokolader per person er
Vi vil forenkle uttrykket over, slik at det blir lettere å sette det på standardform. Den første brøken er . For å forenkle den andre brøken, multipliserer vi med over og under brøkstreken; da får visiden . Derfor blir antall sjokolader per person . Vi skal skrive dette som et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Svar:
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n gangerStandardform
Brøk

For flere eksempler og forklaringer se artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Oppgave 4 (2 poeng) Nettkode: E-4CHL
Regn ut
Løsningsforslag
Jeg tenker:
Vi ser
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Først bruker vi potensregler for å forenkle brøken. Vi
Utvide brøk
Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.
Eksempel: er utvidet til , fordi
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Svar:
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. En brøk kan omgjøres til en likeverdig brøk ved å dividere med det samme tallet både i telleren og i nevneren. Dette kalles å forkorte brøken. Eksempel: Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n gangerForkorte brøk
Brøk

For flere eksempler og forklaringer se artiklene Rask gjennomgang av regneregler for potens og røtter og Karoline bruker potensregler.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 5 (2 poeng) Nettkode: E-4CHO
I tabellen nedenfor ser du resultatene fra en pilkastkonkurranse.
| Poeng | Antall spillere |
Bestem den gjennomsnittlige poengsummen for spillerne.
Løsningsforslag
Jeg tenker
I denne oppgaven behandler vi gruppert informasjon. Da kan vi anta at gjennomsnittet for hver gruppe ligger midt i gruppen.
Vi antar at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
(Antagelsene i denne løsningen er ikke helt riktige; for riktige antagelser, se “Visste du at”-seksjonen under.)
Svar: Gjennomsnittet er (sannsynligvis) rundt poeng.
Mer om
Denne oppgaven er om Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirennStatistikk
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Tabell

For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Visste du at
Løsningen på denne oppgaven er faktisk ikke helt riktig, hvis man antar at poengsummene er fordelt likt utover intervallene. La oss for enkelthets skyld se på poengintervallet , og at det var fire personer som fikk poeng i dette intervallet. Hadde vi løst oppgaven som over, ville vi antatt at de fire personene hadde fått poeng i gjennomsnitt. Problemet er at vi har et halvåpent intervall, så poengsummen er ikke inkludert. De mulige poengsummene blir dermed , , , , , , , , og , altså et heltall i det lukkede intervallet . Hvis poengsummene er jevnt fordelt utover dette intervallet, så vil gjennomsnittet være , ikke , som over. Bruker vi denne metoden på oppgaven over, vil vi få at gjennomsnittet av poengsummene sannsynligvis er rundt
Oppgave 6 (2 poeng) Nettkode: E-4CHR
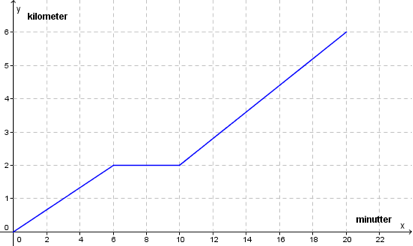
På fredag syklet Synnøve til skolen. Ovenfor ser du en forenklet grafisk framstilling av sykkelturen.
Hva kan du si om sykkelturen ut fra grafen?
Løsningsforslag
Jeg tenker
Antageligvis representerer
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Mellom og beveger grafen seg
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Fart
Fart er tilbakelagt distanse per tidsenhet.
Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.
Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
Hvis vi vil, så kan vi ganske greit regne ut farten til Synnøve under de forskjellige delene av turen. De første minuttene syklet hun i kilometer, som gir en fart på
De siste minuttene syklet hun kilometer, og da er farten
Svar: Synnøve syklet med konstant fart () de første minuttene, tok seg en minutter lang pause, og syklet videre i litt høyere hastighet () de neste minuttene.
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Fart er tilbakelagt distanse per tidsenhet. Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund. Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.Funksjon
Graf
Fart
For flere eksempler og forklaringer se artikkelen Grafen til en funksjon.
For å øve mer, se oppgavesettene om fart og lineære funksjoner i Treningsleieren.
Oppgave 7 (3 poeng) Nettkode: E-4CHU
| Landsdel | Antall studenter |
| Nord-Norge | 5 |
| Trøndelag | 20 |
| Vestlandet | 10 |
| Østlandet | 15 |
| Sørlandet | 10 |
Studentene ved en folkehøgskole kommer fra ulike landsdeler i Norge. Se tabellen ovenfor.
Gjør beregninger og lag et sektordiagram som viser fordelingen. Det skal gå klart fram hvor mange grader hver av sektorene i diagrammet er på.
Løsningsforslag
Jeg tenker
Vi skal lage et
Sektordiagram
Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.
For å lage
Sektordiagram

Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.

Nå skal vi farge resten av diagrammet. Trøndelag skal ha ganger så stor område som Nord-Norge, Vestlandet skal ha ganger så stort område, og så videre. Vi trenger ikke skrive opp vinklene til alle sektorene, fordi vi har vært tydelige på at hver stiplede sektor er på . Resultatet er vist under.
Svar 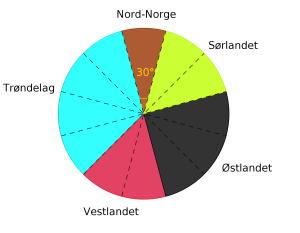
Mer om
Denne oppgaven er om En sektor er en del av en sirkel, et område som er avgrenset av to radier og en sirkelbue. En sektor har form som et kakestykke. Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Sektor
Sektordiagram

Statistikk
For flere eksempler og forklaringer se artikkelen Sektordiagram.
For å øve mer, se oppgavesettet om sektordiagram i Treningsleieren.
Oppgave 8 (4 poeng) Nettkode: E-4CHW
Whisky lagres på tønner. En tønne på 500 L fylles opp og blir plassert på lager. Hvert år fordamper omtrent 2 % av innholdet i tønnen.
a)
Sett opp et uttrykk som du kan bruke til å regne ut hvor mange liter whisky det vil være igjen i tønnen etter 12 år.
Løsningsforslag a)
Jeg tenker:
Hvis noe minker med , så er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Etter ett år er det whisky igjen. Tilsvarende vil det etter to år være whisky igjen, og etter år vil det være whisky igjen i tønnen.
Svar:
Mer om:
Denne oppgaven er om Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.Vekstfaktor
Prosent
Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n ganger
For flere eksempler og forklaringer om regninge med prosent se artikkelen Regneregeler.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
b)
Sett opp et uttrykk som du kan bruke til å regne ut hvor mange liter whisky som vil ha fordampet fra tønnen etter 20 år.
Løsningsforslag b)
Jeg tenker:
Her skal vi finne ut hvor mye whisky som har fordampet på år. (Ikke mengden whisky som er igjen.)
Vi vil finne ut hvor mange liter whisky som har fordampet etter år. Vi vet at vi startet med whisky, og som i forrige oppgave, vil det være whisky igjen etter år. Det betyr at det er whisky som har fordampet.
Svar: , eller
Mer om:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
For flere eksempler og forklaringer se artikkelen Banksparing over flere år.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
c)
En tønne har vært lagret i 25 år.
John påstår at halvparten av innholdet har fordampet, og at denne tønnen derfor nå inneholder 250 L. Dette begrunner han med at
Forklar John hvorfor dette ikke er riktig.
Løsningsforslag c)
Jeg tenker:
Dette er ikke riktig, fordi av det originale innholdet ikke er det samme som av innholdet etter år.
Johns tankegang er som følger. Det første året forsvinner det whisky, altså . Etter år vil det altså ha forsvunnet . Problemet er at det ikke forsvinner whisky hvert år. Det andre året starter vi med , og av dette forsvinner i løpet av året. Den fordampede whiskyen dette året er derfor , som er mindre enn . Mengden whisky som fordamper vil minke hvert år, selv om prosentandelen er den samme. Derfor er Johns tankegang feil.
Svar: Hvert år starter vi med mindre whisky enn året før, og av dette er mindre enn av mengden whisky året før. Derfor forsvinner det mindre og mindre whisky i året, selv om prosentandelen er den samme.
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefot Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.Prosent
Rente
Vekstfaktor
For flere eksempler og forklaringer se artikkelen Prosent av hva da?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Oppgave 9 (4 poeng) Nettkode: E-4CI1

Lufttrykk kan måles i bar eller psi. Lasse har en racersykkel der det anbefalte lufttrykket i dekkene er oppgitt både i bar og i psi. Se bildet ovenfor.
a)
Tegn et koordinatsystem med lufttrykk målt i psi langs - aksen og lufttrykk målt i bar langs - aksen. Marker verdiene fra dekket på bildet som punkter i koordinatsystemet, og tegn en rett linje gjennom punktene.
Løsningsforslag a)
Jeg tenker:
Vi må la aksene dekke et såpass stort område så vi kan tegne inn punktene.
I
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Nå skal vi tegne inn punktene. Vi vet at bar gir psi, så vi skal tegne inn punktet . Tilsvarende skal vi tegne inn punktet .

Til slutt tegner vi den rette linjen mellom de to punktene. Resultatet er vist under.
Svar: 
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Lineære funksjoner er funksjoner som er skrevet på formen . Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).Graf
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Koordinatsystem

For flere eksempler og forklaringer se artiklene Koordinatsystem og Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleieren.
b)
Lasse har kjøpt ny terrengsykkel. På dekkene står det at lufttrykket bør være mellom 35 og 65 psi. Han lurer på hva dette tilsvarer målt i bar.
Bruk linjen i oppgave a) til å finne ut hvor høyt lufttrykk målt i bar Lasse bør bruke i dekkene på terrengsykkelen.
Løsningsforslag b)
Jeg tenker:
Linjen vi fant i deloppgave a) viser sammenhengen mellom bar og psi.
Linjen vi har funnet er faktisk
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
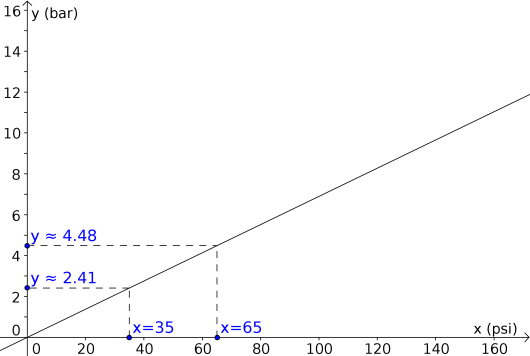
Vi leser av at psi gir cirka bar, og at psi gir cirka bar. Derfor burde lufttrykket være mellom og bar.
Svar: Mellom og bar
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Lineære funksjoner er funksjoner som er skrevet på formen . En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.Graf
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Linje
For flere eksempler og forklaringer se artiklene Hvorfor ser grafen ut som den gjør? og Fra en graf til en funksjon.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-4CI5
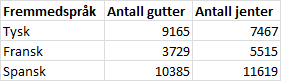
| Fremmedspråk | Antall gutter | Antall jenter |
| Tysk | 9165 | 7467 |
| Fransk | 3729 | 5515 |
| Spansk | 10385 | 11619 |
| Tabell 1 | ||
Tabell 1 viser hvor mange elever i Norge som valgte fremmedspråkene tysk, fransk og spansk på 8. trinn skoleåret 2012/2013.
a)
Lag et passende diagram som illustrerer opplysningene gitt i tabell 1.
Løsningsforslag a)
Jeg tenker:
Dette kan vi gjøre i et regneark, for eksempel i Excel.
Det første vi gjør er å legge inn tabellen i regnearket. Vi bruker Excel.
Vi velger et passende
Stolpediagram
Et søylediagram uten bredde på søylene.
Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.
Se Søylediagram
Resultatet er vist under.
Svar: 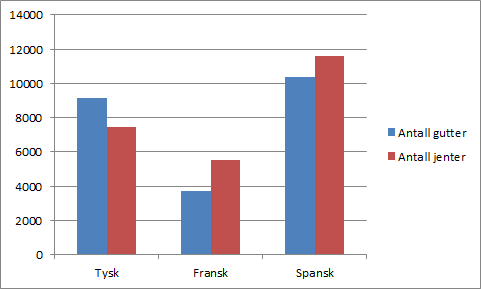
Mer om:
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Et søylediagram uten bredde på søylene. Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak. Se SøylediagramTabell

Stolpediagram
For flere eksempler og forklaringer se artikkelen Søyle- og stolpediagram.
For å øve mer, se oppgavesettet om søylediagram i Treningsleieren.
b)
| Skoleår | Andel elever med tysk |
Andel elever med fransk |
Andel elever med spansk |
| 2002/2003 | 38,9% | 21,5% | 2,0% |
| 2004/2005 | 33,6% | 20,4% | 6,3% |
| 2006/2007 | 27,3% | 17,1% | 32,6% |
| 2008/2009 | 26,5% | 13,7% | 33,1% |
| 2010/2011 | 25,5% | 15,5% | 32,1% |
| 2012/2013 | 26,4% | 14,7% | 34,9% |
| Tabell 2 | |||
Tabell 2 viser andelen elever på 8. trinn som valgte tysk, andelen som valgte fransk, og andelen som valgte spansk som fremmedspråk noen skoleår i perioden 2002-2013.
Lag et kurvediagram (linjediagram) som illustrerer opplysningene gitt i tabell 2.
Løsningsforslag b)
Jeg tenker:
Her skal vi bruke regneark igjen.
Vi bruker Excel. Som vanlig er det første vi gjør å skrive inn tabellen i regnearket.
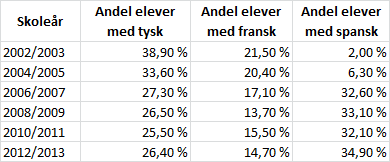
Vi er bedt om å lage et
Linjediagram
Et linjediagram er en grafisk framstilling av data som er samlet over tid. Et punkt svarer til en observasjon på et bestemt tidspunkt. Det trekkes linjestykker mellom punktene.
Eksempel på bruksområde: aksjekurser, temperatur og salgsoversikter.
Resultatet er vist under.
Svar: 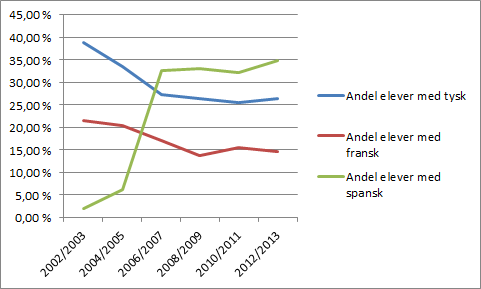
Mer om:
Denne oppgaven er om En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En kurve er en krum eller rett linje eller et linjestykke. En kurve har lengde, men ikke bredde eller dybde. En kurve er en grafisk fremstilling av en ligning. Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirennLinje
Kurve
Tabell

For flere eksempler og forklaringer se artikkelen Linjediagram.
c)
Omtrent hvor mange elever var det på 8. trinn skoleåret 2012/2013?
Løsningsforslag c)
Jeg tenker:
Her må vi bruke informasjon fra begge tabellene i oppgaven. Den ene tabellen sier hvor mange elever som tok hvert fremmedspråk, og den andre sier hvor stor andel som tok språkene. Ut i fra dette kan vi finne ut hvor mange elever det er snakk om.
Vi løser denne oppgaven ved å se på antall elever som tok tysk; man kan gjøre det på helt tilsvarende måte med fransk eller spansk.
I den første tabellen står det at gutter og jenter tok tysk på . trinn i skoleåret . Det er totalt elever. Går vi ned til skoleåret i den andre tabellen, ser vi at av elevene tok tysk. Det betyr at er av den totale elevmassen. Hvis er det totale antallet elever, så har viDa kan vi dividere med på begge sider og forkorte, og da får viDermed var det elever totalt.
Vi kan gjøre det samme med de andre språkene. For fransk får vi elever, og for spansk får vi elever. Alle de tre tallene skal være det totale antallet elever på 8. trinn i skoleåret , men vi har fått forskjellige tall her – det er nok fordi prosentandelen har flere enn én desimal. Når vi kutter ut resten av desimalene, vil vi få en feil når vi dividerer med tallet. Vi kan likevel konkludere med at det var rundt elever totalt.
Svar: Cirka elever. (Vi får hvis man tar utgangspunktet i tysk, hvis vi regner ut i fra fransk, og med spansk. Vi får forskjellige tall på grunn av avrundingsfeil i prosentandelen.)
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde. Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirennProsent
Brøk

Tabell

For flere eksempler og forklaringer se artikkelen Prosent av hva da?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
Visste du at:
Vi fikk forskjellige svar da vi regnet ut i fra forskjellige tall i denne oppgaven, på grunn av avrundingsfeil. Det kan virke som en ubetydelig detalj, i og med at vi bare kan ta med flere desimaler for å få det mer nøyaktig – og det stemmer i dette tilfellet, men andre ganger kan avrundingsfeil bygge seg opp til virkelig store feil. Dette grunner i at man ikke kan representere alle tall helt eksakt på datamaskin; hvert tall blir lagret med cirka desimaler, og ikke mer. Den største faren for avrundingsfeil er når man trekker fra hverandre to nesten like store tall, og deretter multipliserer opp med et stort tall. Tallet kan ikke representeres eksakt på datamaskin (det er lik , med uendelig tretall). Det samme stemmer med . Det er stor usikkerhet for nøyaktig hvordan disse to vil representeres i de siste desimalene; en tredjedel vil kanskje være , mens muligens representeres som . Hvis vi nå skal regne ut uttrykket på datamaskin, som matematisk sett er lik , så kan vi ende opp med for eksempel som resultat. Det er en dramatisk feil!
Oppgave 2 (7 poeng) Nettkode: E-4CJ5
| År | 2002 | 2004 | 2006 | 2008 | 2010 | 2012 |
| Gjennomsnittspris per kvadratmeter (kroner) |
12 478 | 14 769 | 20 084 | 25 977 | 28 247 | 33 454 |
Tabellen ovenfor viser gjennomsnittspris per kvadratmeter for eneboliger i Stavanger noen år i perioden 2002–2012.
a)
La være antall år etter 2002, og bestem den lineære modellen som passer best med de oppgitte verdiene.
Løsningsforslag a)
Jeg tenker:
Her kan vi bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi skal legge inn informasjonen i GeoGebra. Vi lar være antall år etter , så blir , blir , og så videre. For å skrive inn dataene, så krysser vi av på «Regneark» under «Vis»-menyen. I regnearket skriver vi én kolonne med -verdier, og en annen med gjennomsnittsprisen i det året som -verdien tilhører.
Videre markerer vi tabellen vi har laget, høyreklikker, og trykker “Liste med punkt” i “Lag”-menyen. Den blir hetende Liste1. Vi tilpasser aksene slik at vi kan se alle de seks punktene vi har lagt inn. For å lage en lineære modellen, skriver vi den følgende kommandoen i “Skriv inn”-vinduet:
RegLin[Liste1]Vi får opp en rett linje.

I algebrafeltet ser vi ligningen til linjen. Vi kan få den på en mer kjent form ved å høyreklikke, og deretter velge «Likning ». Da får vi at formelen til linjen erDette er den lineære modellen vi er ute etter.
Svar:
Mer om:
Denne oppgaven er om
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
For flere eksempler og forklaringer se artikkelen Regresjon 1.
b)
Bruk modellen du fant i oppgave a), til å anslå gjennomsnittsprisen per kvadratmeter i 2016.
Løsningsforslag b)
Jeg tenker
Vi skal bruke modellen fra deloppgave a). Året er år etter , så .
Vi antar at gjennomsnittsprisen per kvadratmeter er kroner år etter . I følge denne modellen vil prisen være i . Dette kan vi regne ut ved å sette inn i formelen i deloppgave a). Da får vi Vi kan gjøre det samme ved å skrive
p(14)
i “Skriv inn”-feltet i GeoGebra-filen fra forrige oppgave, gitt at vi kalte linjen for . Dette gir samme svar som over. I følge modellen vår vil altså gjennomsnittsprisen bli cirka i .
Svar: Cirka .
Mer om
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk. Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Funksjon
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Formel
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
c)
Når vil gjennomsnittsprisen for en enebolig i Stavanger på 200 m2 passere 10 millioner kroner dersom prisutviklingen fortsetter?
Løsningsforslag c)
Jeg tenker:
Vi bruker modellen fra a).
Vi kan bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
y = 50000i GeoGebra-filen. Vi finner koordinatene til
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

Skjæringspunktet har koordinater . Det betyr at prisen er år etter , altså sent i .
Svar: Etter år, altså i , i følge modellen vår.
Mer om:
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner er funksjoner som er skrevet på formen . En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.Skjæringspunkt

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Linje
For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger og lynkurset Funksjonsdrøfting.
d)
En eiendomsmegler antok i 2012 at prisen på eneboliger i Stavanger ville øke med 20 % i perioden 2012–2015.
Hvor stor prosentvis økning tilsvarer dette per år?
Løsningsforslag d)
Jeg tenker:
Vi antar at prisen øker med samme prosentandel hvert år. Vi merker oss at dette ikke betyr at økningen er per år!
La oss si at den gjennomsnittlige prisen på en enebolig i var kroner. Vi trenger ikke å vite nøyaktig hva er, men det er altså bare et tall, for eksempel 5 millioner. Hvis prisen øker med en
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Cirka per år.
Mer om:
Denne oppgaven er om
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Kvadratrot
Kvadratrot har symbolet .
Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.
Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi . Det skrives .
For flere eksempler og forklaringer se artikkelen Rask gjennomgang av regneregler for potens og røtter og lynkurset Likninger med én ukjent.
Oppgave 3 (7 poeng) Nettkode: E-4CJO
Bygda Alvfjord har i dag innbyggere. Man regner med at innbyggertallet vil øke med 4 % hvert år.
a)
Forklar at funksjonen gitt ved kan brukes som modell for antall innbyggere i Alvfjord om år.
Løsningsforslag a)
Jeg tenker:
Hvis noe øker med , så er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Hvis vi starter med en befolkning på , og befolkningen øker med i året, så vil det være innbyggere året etter. Etter to år vil det være innbyggere, og etter år vil det være innbyggere. Dette er den samme formelen for som oppgitt.
Svar: Vekstfaktoren til er , så etter år er befolkningen på .
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Prosent
Potens
Eksempel: Vekstfaktor
Eksponentialfunksjon

For flere eksempler og forklaringer se artikkelen Regneregler.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
b)
Tegn grafen til for
Løsningsforslag b)
Jeg tenker:
Her kan vi bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
For å tegne grafen, så skriver vi
A(x) = Funksjon[5000*1.04^x, 0, 30]i «Skriv inn»-vinduet i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Svar: 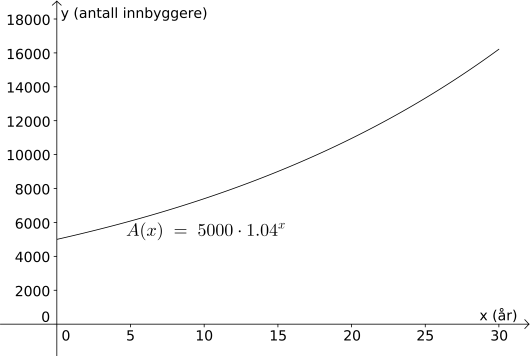
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.Graf
Koordinatsystem

Eksponentialfunksjon

Intervall
For flere eksempler og forklaringer se artikkelen Fra en funksjon til en graf. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleieren.
c)
Hvor mange innbyggere vil det være i Alvfjord om 10 år ifølge modellen i oppgave a)?
Når vil innbyggertallet i Alvfjord passere 10 000 ifølge modellen i oppgave a)?
Løsningsforslag c)
Jeg tenker:
Vi løser oppgaven i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Hvis er antall innbyggere i Alvfjord etter år, så må være antall innbyggere etter år. Vi kunne regnet ut på kalkulator, men vi kan også skrive
A(10)i «Skriv inn»-vinduet i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Videre skal vi finne ut av når innbyggertallet passerer , i følge modellen. Det gjør vi ved å se når grafen til krysser den rette linjen . Vi lager denne linjen i GeoGebra ved å skrive
y = 10000Vi finner
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

Vi ser at skjæringspunktet er . Det betyr at , så i følge modellen vil innbyggertallet nå 10 000 etter år.
Svar: Etter år er innbyggertallet , og innbyggertallet går over etter cirka år.
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Lineære funksjoner er funksjoner som er skrevet på formen .Graf
Skjæringspunkt

Eksponentialfunksjon

Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger og lynkurset Funksjonsdrøfting.
For å øve mer, se oppgavesettet om skjæringspunkt i Treningsleieren.
d)
Nabobygda Brimsjø har i dag 8400 innbyggere. Anta at innbyggertallet vil øke med 200 personer hvert år.
Bruk modellen i oppgave a) og antakelsen ovenfor til å anslå når det vil være like mange innbyggere i Alvfjord og Brimsjø.
Løsningsforslag d)
Jeg tenker:
Her kan vi tegne
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Først vil vi finne funksjonsuttrykket for innbyggertallet etter år i Brimsjø. Vi starter med , og når øker med øker befolkningen med . Det betyr at . Dette tegner vi inn i
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
B(x) = Funksjon[8400 + 200*x , 0, 30]i «Skriv inn»-vinduet. Innbyggertallet i de to bygdene er like når , eller med andre ord, der
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

Vi ser at skjæringspunktet har koordinater på omtrentlig . Det betyr at , altså at begge bygdene har innbyggertall på etter år.
Svar: Innbyggertallet er likt etter år; da er det cirka innbyggere i begge bygdene.
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Funksjon
Skjæringspunkt

Graf
For flere eksempler og forklaringer se artiklene Grafisk løsning av likninger og Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.
Oppgave 4 (4 poeng) Nettkode: E-4CK2
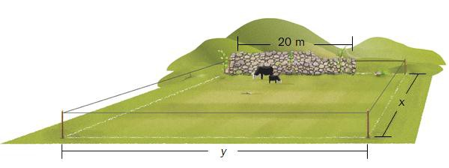
Ola har 120 m gjerde. Han skal gjerde inn et område. Området skal ha form som et rektangel med lengde meter og bredde meter der . Langs den ene siden av området står det en mur. Muren er 20 m lang. Ola trenger ikke gjerde langs muren. Se skissen ovenfor.
a)
Bestem en modell som viser sammenhengen mellom lengden og arealet av området.
Løsningsforslag a)
Jeg tenker:
Vi skal finne en
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Vi er i situasjonen vist under.

Vi vil uttrykke ved hjelp av . Hvis vi ikke hadde hatt noen begrensninger ville dette vært umulig, men heldigvis vet vi at Ola bare har meter gjerde. Det betyr at
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Svar: .
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°. Omkrets: En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Funksjon
Areal
Noen måleenheter for areal er m2, dm2 og cm2.Rektangel

Areal: Ligning
For flere eksempler og forklaringer se artiklene Et rektangel og Lineære likninger.
For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleieren.
b)
Bestem slik at arealet av området blir størst mulig.
Hvor stort blir området da?
Løsningsforslag b)
Jeg tenker:
Å finne det største arealet tilsvarer å finne
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi tegner grafen til i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
A(x) = x*(70 - x)i «Skriv inn»-vinduet. Vi kan finne
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Ekstremalpunkt[A]

Vi ser at toppunktet er . Det betyr at , og at dette er den største verdien kan ha. Dermed er det største mulige arealet til rektangelet , og det får man ved å la området være bredt. (Da blir lengden .)
Svar: Det største arealet er når ; da er arealet .
Mer om:
Denne oppgaven er om Vi sier at et punkt er et ekstremalpunkt for en funksjon hvis det enten er et toppunkt eller bunnpunkt for funksjonen. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Ekstremalpunkt

Toppunkt

Funksjon
Graf
For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkter.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleieren.
Oppgave 5 (5 poeng) Nettkode: E-4CKM

Izabela Duda fra Oppsal ble toppskårer i Eliteserien i håndball for kvinner i sesongen 2012/2013. Nedenfor ser du hvor mange mål hun skåret i hver av de 22 kampene.
6 1 4 8 8 17 7 12 1 8 4
7 10 13 14 7 9 7 11 12 7 4
a)
Hvor mange mål skåret hun i gjennomsnitt per kamp?
Løsningsforslag a)
Jeg tenker
Vi skal finne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Her må vi legge sammen alle tallene og dividere med , som er antall kamper. Summen av antall mål erog da blir gjennomsnittet
Svar: Cirka mål per kamp
Mer om
Denne oppgaven er om Resultatet av en addisjon. Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Sum
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
b)
En annen spiller skåret i gjennomsnitt 5 mål per kamp i de 22 kampene. Standardavviket hennes for antall mål per kamp var 2,5.
Sammenlikn denne spillerens prestasjoner med Izabela Dudas.
Løsningsforslag b)
Jeg tenker:
Vi kan sammenligne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
For å sammenligne resultatene, burde vi regne ut
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
=STDAV.P(A2:A23)i en rute. Dermed ser vi at standardavviket blir cirka . Vi bruker STDAV.P fordi vi vil regne ut standardavviket for hele datasettet. Hvis vi hadde brukt STDAV, ville vi fått estimerte verdier basert på utvalg.
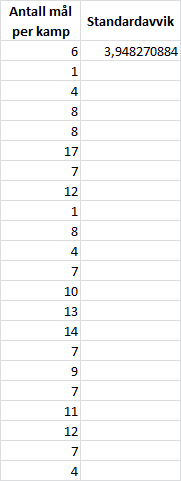
Duda har altså høyere standardavvik for antall mål per kamp. Dermed er det mer usikkert hvor mange mål Duda skårer. Duda har derimot et høyere
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: Duda skårer mer sprikende, men hun skårer jevnt over flere mål enn den andre spilleren.
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Standardavvik
Statistikk
For flere eksempler og forklaringer se artiklene Gjennomsnitt, median og typetall og Varians og standardavvik.
c)
Izabela Duda skåret noen av målene på straffekast.
Tabellen viser kumulativ frekvens for antall mål hun skåret på straffekast i løpet av de 22 kampene.
| Antall mål på straffekast |
Kumulativ frekvens |
| 0 | 8 |
| 1 | 14 |
| 2 | 17 |
| 3 | 21 |
| 4 | 22 |
I hvor mange kamper skåret hun tre mål på straffekast?
Hvor mange mål skåret hun på straffekast i løpet av de 22 kampene?
Løsningsforslag c)
Jeg tenker:
Den
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Vi vet at Duda skåret mål eller færre i av kampene, fordi den
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
For å finne ut hvor mange mål Duda skåret totalt, må vi finne ut av hvor mange kamper hun skåret de diverse summene. Den kumulative frekvensen for er , og det vil si at hun skårte mål i av kampene. Den kumulative frekvensen for er , og av samme tankegang som i forrige avsnitt ser vi at hun skårte 1 mål i av kampene. Videre skåret hun mål i av kampene, mål i 4 av kampene, og mål i av kampene. Det totale antall mål på straffekast er dermed
Svar: Hun skåret tre mål i av kampene, og hun skåret mål totalt.
Mer om:
Denne oppgaven er om Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere. Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien. Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Kumulativ frekvens

Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
Oppgave 6 (7 poeng) Nettkode: E-4CKW
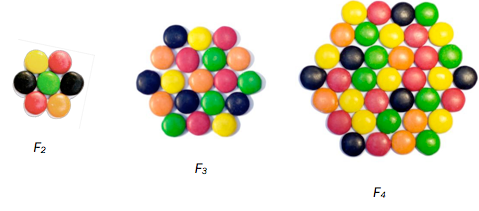
Thea lager figurer av små sjokolader. Figurene ovenfor har hun kalt , og
a)
Hvor mange små sjokolader vil det være i figuren ?
Løsningsforslag a)
Jeg tenker:
For å komme til neste figur, legger man et lag med små sjokolader utenfor den forrige figuren.
Først teller vi antallet små sjokolader i figuren . Vi teller sjokoladene radvis. Antallet blir Vi kan regne ut antall sjokolader i ved å se at det er en sekskant med i sidelengde i stedet for ; derfor er antall sjokolader
Alternativ løsning
Svar:
Mer om:
Denne oppgaven er om Resultatet av en addisjon. Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.Sum
For flere eksempler og forklaringer se artikkelen Addisjon.
b)
Thea vil sette opp en modell som viser hvor mange små sjokolader hun trenger for å lage enda større figurer. Hun får en god idé og lager figuren på nytt.
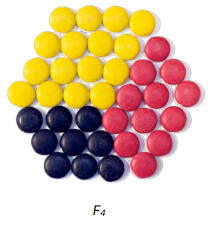
Hun regner nå ut at antall små sjokolader i figuren er . Vis hvordan Thea kan bestemme antall små sjokolader i ved å regne på samme måte.
Løsningsforslag b)
Jeg tenker:
Thea har delt opp figuren i tre «firkanter». Vi kan regne ut antall sjokolader i figuren ved å legge sammen sjokoladene i firkantene.
Figuren består av en «firkant» med tre rader av tre sjokolader, en annen firkant med tre rader av fire sjokolader og en siste firkant med fire rader av fire sjokolader. Derfor blir antall sjokolader . Vi kan fjerne det ytterste laget med sjokolader for å få . Den består av én firkant med sjokolader, én firkant med sjokolader og én med sjokolader, som gir sjokolader. Tilsvarende består figuren av sjokolader, akkurat som vi fant tidligere.
Svar: består av sjokolader, og består av sjokolader.
Mer om:
Denne oppgaven er om En firkant er en geometrisk figur med fire hjørner og fire sidekanter. Firkant
For flere eksempler og forklaringer se artikkelen Trekant og firkant.
c)
Hvor mange små sjokolader trenger hun for å lage figuren ?
Sett opp en modell som Thea kan bruke for å bestemme antall små sjokolader i figuren
uttrykt ved .
Løsningsforslag c)
Jeg tenker:
Vi kan bruke det samme systemet som deloppgave b).
Hvis vi følger systemet fra forrige oppgave, så ser vi at figur består av sjokolader. Dette ser vi ved at figur er en «sekskant» med sidelengde , og da har den én firkant med rader av sjokolader, én med rader av sjokolader og én med rader av sjokolader. Generelt vil bestå av sjokolader. Vi kan også skrive dette som
Svar: består av sjokolader, og består av (eller ) sjokolader.
Mer om:
Denne oppgaven er om Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall. Andre kvadratsetning sier at .Andregradsuttrykk
Andre kvadratsetning
For flere eksempler og forklaringer se artikkelen Andregradsfunksjoner.
d)
Hva er den største figuren Thea kan lage dersom hun har 5000 små sjokolader?
Løsningsforslag d)
Jeg tenker:
Vi kan tegne grafen til antallet sjokolader til , og finne ut hvor stor kan være hvis består av mindre enn .
Funksjonen er antall sjokolader figuren består av. Vi kan tegne denne funksjonen i GeoGebra. Vi skriver
f(x) = 3*x^2 - 3*x + 1i “Skriv inn”-vinduet i GeoGebra. Videre tegner vi linjen . Vi klikker på skjæringspunktet, og ser at det har koordinater .

Det betyr at figur har under sjokolader, mens figur har over sjokolader. Derfor er figur den største figuren Thea kan lage. Den består avsjokolader.
Svar: Den største figuren Thea kan lage med sjokolader, er .
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall. Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se KoordinatsystemGraf
Skjæringspunkt

Andregradsuttrykk
Koordinat




