Bayes-setningen
Bayes' setning ble funnet av den engelske presten Thomas Bayes på 1740-tallet. Den var et stort gjennombrudd, og gjorde det mulig å løse mange spørsmål som ikke tidligere kunne løses. Matematikeren Harold Jeffreys skrev at Bayes' setning er for sannsynlighet det samme som Pytagoras er for geometri.
Vi lar A og B være to hendelser i et utfallsrom. Definisjonen av betinget sannsynlighet gir at
.
Dersom vi bytter om plassene til A og B og bruker produktsetningen, får vi at
.
Når vi bruker dette uttrykket i teller i definisjonen av betinget sannsynlighet, får vi Bayes’ setning:
.
Nå skal vi se på et par eksempler.
Jenter og kjærlighet
På en videregående skole er det 60% jenter og 40% gutter. Ifølge skoleavisens nyeste undersøkelse er det 25% sannsynlighet for at en tilfeldig valgt jente er i et forhold, og det er 35% sannsynlighet for at en tilfeldig valgt elev (uansett kjønn) har kjæreste. Hva er sannsynligheten for at en tilfeldig valgt elev er ei jente når vi vet at eleven har kjæreste?
La J stå for at eleven er ei jente og K for at eleven har kjæreste.
Siden det er 60% jenter på skolen, vet vi at sannsynligheten for at den tilfeldig valgte eleven er en jente er .
Vi vet også at gitt en jente er det 25% sannsynlig at hun er i et forhold, .
Sannsynligheten for at den valgte eleven har kjæreste er 35%, .
Vi er interessert i å finne . Bayes’ setning gir
.
Høyde og vekt
I dette eksemplet definerer vi en mann over 180 cm som høy (H) og en mann under 70 kg som tynn (T). Anta for eksempel at sannsynligheten er lik 0,5 for at en tilfeldig mann er høy. Sannsynligheten er 0,3 for at en tilfeldig mann er tynn. Hvis vi vet at en mann er høy, er sannsynligheten lik 0,2 for at mannen også er tynn. Hva er sannsynligheten for at en tilfeldig valgt mann er høyere enn 180 cm når vi vet at han veier mindre enn 70 kg?
Vi vet at og .
Nå vil vi finne sannsynnligheten for H gitt T:
.
Så det er 33,3% sannsynlighet for at en tynn mann også er høy.
Del på Facebook
Lynkurs 11.-13.trinn
Sannsynlighet (del II)
Består av:
- Repetisjon av begreper
- Hvordan finner vi uniform sannsynlighet?
- Venn-diagram og mengdelære
- Addisjonssetningen
- Sannsynlighet ved komplementære hendelser
- Betinget sannsynlighet og produktsetningen
- Bayes-setningen
- Uavhengige hendelser og produktsetningen
- Ikke-uniforme sannsynlighetsmodeller
- Ordnede utvalg
- Uordnede utvalg uten tilbakelegging
- Binomiske forsøk
- Hypergeometriske forsøk
Begrep
-
Bayes' setning
Bayes' setning sier at
-
Betinget sannsynlighet
Den betingede sannsynligheten er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.
.
-
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
-
Snitt
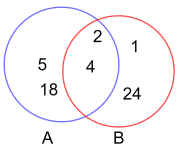
Snittet av to mengder A og B er en ny mengde som består av alle elementer som forekommer både i A og B.
Eksempel:




