Omskriving av formler
Noe som er utrolig greit å kunne er nettopp det å skrive om formler. Det kan ofte være overveldende mange formler å huske på, og det å kunne skrive om formler gjør at vi ikke trenger å huske på så mange.
Ta for eksempel vei, fart og tid. Hvis vi vet hvordan vi skriver om formler så trenger vi bare å huske en av dem, for eksempel . Da kan vi finne de andre formlene ved å bare skrive om den ene formelen. Istedet for å huske på tre formler, så trenger vi bare å huske en! Vi ser på noen eksempler under.
Vei, fart og tid
Hvis vi kjenner til fart formelen, , kan vi finne de andre formlene utifra denne. Vi starter med å finne formelen for strekning.Vi finner deretter formelen for tid.Og da har vi de tre vei, fart og tid-formlene.
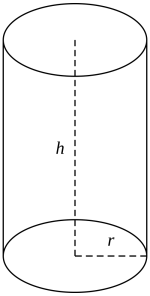
Høyden til en sylinder
|
La oss se på en sylinder. Formelen for volumet av en sylinder er, . Men hva om vi ikke er så interessert i volumet, men heller høyden, , eller radiusen, . Vi må da skrive om formelen slik at det står, “ er lik” eller “ er lik”. Hvis vi skal finne høyden, ønsker vi å ha alene på en side. Vi tenker på som den ukjente, og de andre bokstavene som tall, og løser som en likning. Nå kan vi dividere med på begge sider av likningen: |
For å ha helt alene, dividerer vi, men denne gangen med :Nå står alene på en side, og dermed har vi skrevet om til .
Radius til en sylinder
La oss nå finne radiusen, , altså skrive om slik at står alene på en side.Vi dividerer vi begge sider med :For at skal stå alene på den ene siden, må vi dividere på begge sider:Nå er alene på venstresiden, men det er et lite problem. Det står ikke, , det står faktisk, . Da må vi ta kvadratroten på begge sider av likhetstegnet for å få .Og da har vi helt alene på en side. Fordi leseretningen i det norske språket er fra venstre til høyre, skriver vi . Vi har nå skrevet om formelen til .
Valutaregning
Geir finner ut at danske kroner kan kjøpes for norske kroner i . Han har danske kroner og vil veksle det inn i norske kroner. Hvor mye får han i norske kroner?
Vi må først finne ut av hvor mye norske kroner han kan kjøpe for danske kroner.Vi trenger nå bare å multiplisere med for å finne ut av hvor mye danske kroner er i norske kroner. Vi får da .
Del på Facebook
Lynkurs 11.-13.trinn
Formelregning
Består av:
- Omskriving av formler
- Å sette inn i formelen
- Å kombinere flere formler
Begrep
-
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
-
Pi (π)
er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.
-
Radius
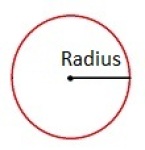
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
-
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.Areal:
Omkrets: