Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1015 2017 Høst

Del 1
Del 2
Eksamensinformasjon

Eksamenstid
5 timer: 
Del 1 skal leveres inn etter 2 timer.
 Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler på Del 1
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Hjelpemidler på Del 2
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Fremgangsmåte
Du skal svare på alle oppgavene i Del 1 og Del 2.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse  
gjennomfører logiske resonnementer  
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner  
kan bruke hensiktsmessige hjelpemidler  
forklarer framgangsmåter og begrunner svar  
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger  
vurderer om svar er rimelige

DEL 1 Uten hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4TOG

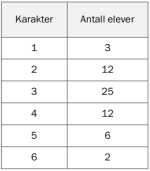
Tabellen nedenfor viser karakterfordelingen ved en skole ved norskeksamen våren $2017$ .

a)

Hvor mange prosent av elevene fikk karakteren $1$ eller $2$ ?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal finne hvor stor prosentandel av alle elevene på skolen som fikk karakteren $1$ eller $2$ .

Vi skal finne hvor stor prosentandel av alle elevene som fikk karakteren $1$ eller $2$ . Vi begynner med å finne det totale antallet elever. Da summerer vi antall elever for hver karakter: $3 + 12 + 25 + 12 + 6 + 2 = 60,$ som betyr at det er $60$ elever på skolen. Av disse elevene fikk $3 + 12 = 15$ elever karakteren $1$ eller $2$ . Da har vi at $\frac{15}{60} = \frac{15}{4 \cdot 15} = \frac{1}{4} = \frac{25}{100} = 25 %$

Svar: $25 %$ av elevene fikk karakter $1$ eller $2$ .

Mer om:

Denne oppgaven handler om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler, se artikkelen Prosent av hva da?.

For å øve mer, se dette oppgavesettet om prosentregning i Treningsleiren.

b)

Bestem mediankarakteren.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi finner medianen ved å rangere etter størrelse og velge den/de midterste observasjonene.

Medianen er den midterste observasjonen når vi rangerer dataene våre etter størrelse. Vi har $60$ elever, som er et partall. Da vil vi ha $2$ observasjoner i midten, den $30 .$ og $31 .$ observasjonen. Medianen er gjennomsnittet av disse to verdiene.

Vi har $15$ elever som fikk karakter $1$ og $2$ , og $25$ som fikk karakter $3$ , det vil si observasjonene $16$ til $40$ . Det betyr at de midterste observasjonene ligger her, og gjennomsnittet av to observasjoner med verdi $3$ , er $3$ , så medianen er $3$ .

Svar: Medianen er $3$ .

Mer om:

Denne oppgaven er om

Median

Medianen er den verdien som vi finner i midten av et rangert datamateriale.

Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

median

For flere forklaringer og eksempler, se artikkelen Median.

For å øve mer, se dette oppgavesettet om median i Treningsleiren.

c)

Bestem gjennomsnittskarakteren.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker Gjennomsnittet finner vi ved å summere alle karakterene og dele på antall elever.

For å finne gjennomsnittet må vi summere alle karakterene. Da må vi multiplisere karakteren med antall elever som fikk karakteren. Summen av alle karakterene er da $\begin{matrix} 1 \cdot 3 + 2 \cdot 12 + 3 \cdot 25 + 4 \cdot 12 + 5 \cdot 6 + 6 \cdot 2 \\ = & 3 + 24 + 75 + 48 + 30 + 12 \\ = & 192 . \end{matrix}$

Det totale antallet elever er $60$ , så gjennomsnittet er gitt ved $\frac{192}{60} = \frac{6 \cdot 32}{6 \cdot 10} = \frac{32}{10} = 3, 2 .$

Svar: Gjennomsnittskarakteren er $3, 2$ .

Mer om:

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data

Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1) $2 + 2 + 4 + 3 = 11$
2) antall data er 4. $11 : 4 = 2, 75$

gjennomsnitt

For flere forklaringer og eksempler, se artikkelen Gjennomsnitt.

For å øve mer, se dette oppgavesettet om gjennomsnitt i Treningsleiren.

Oppgave 2 (2 poeng) Nettkode: E-4TOK

Regn og skriv svaret på standardform

$3, 54 \cdot 10^{6} + 60000$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi skal addere to tall, da kan vi ikke bruke de potensreglene som vi bruker for multiplikasjon.

Vi kan begynne med å skrive om $3, 54 \cdot 10^{6} = 3540000 .$ Nå kan vi addere de to tallene $3540000 + 60000 = 3600000 .$ Svaret skal være på standardform, så da skriver vi $3600000 = 3, 6 \cdot 10^{6} .$

Svar: $3, 6 \cdot 10^{6}$ .

Mer om:

Denne oppgaven er om

Standardform

Et tall skrevet på formen ± a⋅10ⁿder a er et tall mellom 1 og 10 og n er et heltall.

Eksempel: $3 \cdot 10^{6} o g - 5, 2 \cdot 10^{21}$

tall på standardform

Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$

potenser

For flere forklaringer og eksempler, se artikkelen Tall på standardform.

For å øve mer, se dette oppgavesettet om tall på standardform.

Oppgave 3 (3 poeng) Nettkode: E-4TOQ

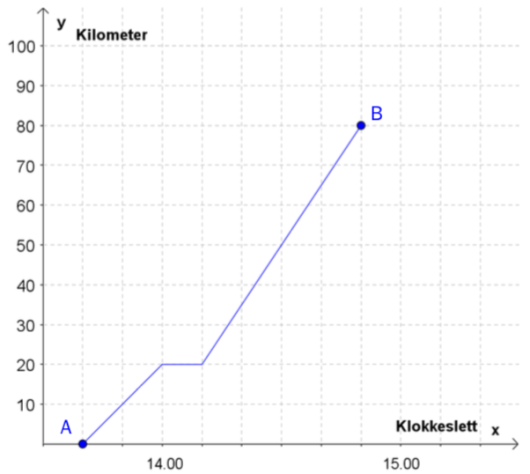
Et tog kjørte fra by $A$ til by $B$ . Se diagrammet ovenfor.

a)

Bestem reisetiden mellom de to byene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi vil finne tiden det tar fra toget forlater $A$ til toget ankommer $B$ .

Fra $x$ -aksen kan vi se at toget forlater $A$ , $2$ enheter før klokka $14.00$ og ankommer $B$ , en enhet før klokka $15.00$ . På rutenettet ser vi at det er $6$ enheter mellom $14 : 00$ til $15 : 00$ som betyr at hver enhet tilsvarer $10$ minutter. Det betyr at toget forlater $A$ klokka $13.40$ og ankommer $B$ klokka $14.50$ . Forskjellen i tid er da $14.50 - 13.40 = 1.10$ som tilsvarer $1$ time og $10$ minutter.

Svar: Reisetiden er $1$ time og $10$ minutter.

Mer om:

Denne oppgaven er om

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

grafer

For flere forklaringer og eksempler, se artikkelen Hvorfor ser grafen ut som den gjør?.

b)

Beskriv hva som skjer $20$ km fra by $A$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

$y$ -aksen forteller oss hvor langt toget beveger seg fra by $A$ .

$y$ -aksen forteller oss hvor langt toget har beveget seg. Når $y = 20$ ser vi at grafen er flat. Fra diagrammet har vi at $x$ -verdien øker med en enhet, fra $14.00$ til $14.10$ , og $y$ -verdien konstant. Det betyr at fra klokka $14.00$ til $14.10$ vil toget ikke bevege seg, altså står det i ro. Klokka $14.10$ begynner toget igjen å bevege seg.

Svar: Toget står stille i $10$ minutter.

Mer om:

Denne oppgaven er om

Graf

graf

For flere forklaringer og eksempler, se lynkurset Funksjonsdrøfting.

c)

Bestem farten til toget når det er $10$ km fra by $A$ , og når det er $10$ km fra by $B$ .
Du skal gi svarene i km/h.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Stigningen til grafen forteller oss noe om farten til toget.

Vi kan se at de første $20$ km fra by $A$ holder toget en jevn fart; avstanden det reiser er lik for hver enhet. Når vi på grafen beveger oss en enhet langs $x$ -aksen, som tilsvarer $10$ minutter, øker grafen med $10$ km i $y$ -verdi. Det betyr at toget beveger seg $10$ kilometer på $10$ minutter, som er det samme som at det beveger seg $60$ kilometer på $60$ minutter, som er $1$ time. $10$ km fra by $A$ beveger toget seg i $60$ km/h.

På diagrammet ser vi at grafen endrer seg etter at toget har stått i ro, da stiger den brattere. For hver $x$ -enhet øker den med større $y$ -verdi, så farten vil være høyere, men fortsatt jevn, for siste strekningen frem til by $B$ . Vi kan se at når vi øker $2$ enheter på $x$ -aksen, altså på $20$ minutter, øker $y$ -verdien til grafen med $30$ kilometer. Så toget beveger seg $30$ km på $20$ minutter. Det er det samme som å si at toget beveger seg $90$ kilometer på $60$ minutter. Så, $10$ km fra by $B$ har toget en fart på $90$ km/h.

Svar: Toget har en fart på $60$ km/h $10$ km fra $A$ , og $90$ km/h $10$ km fra $B$ .

Mer om:

Denne oppgaven er om stigningstall.

For flere forklaringer og eksempler, se artikkelen Rette linjer (lineære funksjoner).

Oppgave 4 (2 poeng) Nettkode: E-4TOW

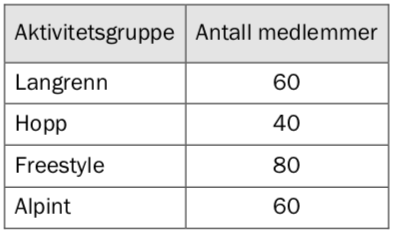
Et idrettslag har $240$ medlemmer. Idrettslaget har fire forskjellige aktivitetsgrupper.

Medlemmen fordeler seg slik:

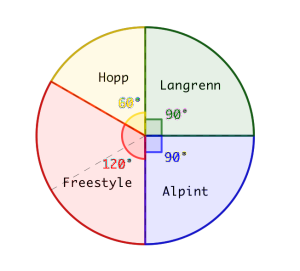
Gjør beregninger og lag et sektordiagram som viser fordelingen mellom medlemmene på de ulike gruppene. Det skal gå klart fram hvor mange grader hver av sektorene i diagrammet er på.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi skal lage et sektordiagram, altså en sirkel delt i ”kakestykker”, der hvert kakestykke representerer en aktivitetsgruppe.

Vi må begynne med å finne ut hvor stor andel av medlemmene som er med i de ulike aktivitetsgruppene. Det gjør vi ved å regne $\frac{antall medlemmer i aktivitetsgruppe}{antall medlemmer totalt}$ Fra tabellen kan vi lese at langrenn har $60$ medlemmer, og det utgjør en andel på $\frac{60}{240} = \frac{1}{4}$ En sirkel har totalt $360^{\circ}$ , og andelen av medlemmer som er med på langrenn er $\frac{1}{4}$ av disse. Vi merker oss at $\frac{1}{4} = \frac{1 \cdot 90}{4 \cdot 90} = \frac{90}{360}$ Det betyr at sektoren i diagrammet som representerer medlemmer på langrenn skal være på $90^{\circ}$ .
På hopp er det $40$ medlemmer, som utgjør en andel på $\frac{40}{240} = \frac{1}{6} .$ Hvor stor sektoren i diagrammet som representerer medlemmer på hopp finner vi ved $\frac{1}{6} = \frac{1 \cdot 60}{6 \cdot 60} = \frac{60}{360} .$ Det betyr at den skal være på $60^{\circ}$ . Det er $80$ medlemmer som er på freestyle, som er dobbelt så mange medlemmer som på hopp. Da må sektoren som representerer medlemmene på freestyle også være dobbelt så stor som for hopp; altså $2 \cdot 60^{\circ} = 120^{\circ} .$ Alpint har $60$ medlemmer, like mange som langrenn. Da må sektoren som representerer alpint og langrenn være like stor, nemlig $90^{\circ}$ . For å forsikre oss, kan vi nå summere alle sektordelene å se at vi ender opp på $360^{\circ}$ . Vi har $90^{\circ} + 60^{\circ} + 120^{\circ} + 90^{\circ} = 360^{\circ}$ Nå skal vi tegne sektordiagrammet. To av sektorene, for langrenn og alpint er begge på $90^{\circ}$ , og utgjør en kvart sirkel. Vi kan begynne med å dele sirkelen i to, og deretter den ene halvsirkelen i to like store deler. Da utgjør disse sektorene langrenn og hopp. Da har vi en halvsirkel igjen, med $180^{\circ}$ som skal utgjøre sektorene for hopp og freestyle. Sektoren for hopp er på $60^{\circ}$ , som utgjør $\frac{1}{3}$ av $180^{\circ}$ , og sektoren for freestyle er på $120^{\circ}$ som utgjør $\frac{2}{3}$ av $180^{\circ}$ . Det betyr at vi kan dele den andre halvsirkelen inn i tre deler, der sektoren for hopp utgjør en del, og sektoren for freestyle utgjør to deler. Vi skriver inn hvor mange grader hver av sektorene er på i diagrammet.

Svar:

Mer om:

Denne oppgaven handler om

Sektordiagram

Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.

sektordiagram

For flere forklaringer og eksempler, se artikkelen Sektordiagram.

For å øve mer, se dette oppgavesettet om sektordiagram i Treningsleiren.

Oppgave 5 (2 poeng) Nettkode: E-4TOY

Du får $40 %$ rabatt på en billett. Rabatten utgjør $120$ kroner.

Hvor mye ville billetten ha kostet dersom du ikke hadde fått rabatt?

Løs oppgaven her

Løsningsforslag

Jeg tenker

Prosent betyr del av hundre, det betyr at $120$ kr er det samme som $\frac{40}{100}$ av billettprisen.

Rabatten på $120$ kroner utgjør $40 %$ av billettprisen. Det betyr at $billettpris \cdot \frac{40}{100} = 120 kr .$ Da kan vi bestemme billettprisen ved $billettpris = 120 kr \cdot \frac{100}{40} = \frac{12000}{40} = \frac{1200}{4} = 300 .$

Svar: Billetten hadde kostet $300$ kroner.

Mer om:

Denne oppgaven handler om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere forklaringer og eksempler, se artikkelen Prosent av hva da?.

For å øve mer, se dette oppgavsettet om prosentregning i Treningsleiren.

Oppgave 6 (5 poeng) Nettkode: E-4TP2

I en butikk kan kundene kjøpe armbånd og charms (små figurer) til å feste på armbåndene. Butikken selger alle charms til samme pris.

Tabellen nedenfor viser sammenhengen mellom antall charms en kunde setter på et armbånd, og prisen kunden må betale for armbåndet med charms.

a)

Hvor mye koster armbåndet, og hvor mye koster hver charm?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan begynne med å bestemme prisen for hver charm. Forskjellen på prisen for de to armbåndene er prisen for $4$ charms.

Vi får oppgitt at prisen for armbånd med $3$ charms er $1350$ kroner, og for armbånd med $7$ charms er $2450$ kroner. Forskjellen i prisen på de to armbåndene, $2450 - 1350 = 1100$ kroner tilsvarer prisen for $7 - 3 = 4$ charms. Det betyr at prisen for hver charm er $\frac{1100}{4} = 275$ kroner. Vi kan bruke dette til å bestemme prisen for et armbånd, for vi har at $prisen for armbånd + 3 \cdot prisen for hver charm = 1350$ kroner og kan sette prisen for hver charm. Da får vi at prisen per armbånd i kroner er $1350 - 3 \cdot 275 = 1350 - 825 = 525 .$

Svar: Armbåndet koster $525$ kroner og hver charm koster $275$ kroner.

Mer om:

Denne oppgaven handler om

Tabell

Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.

Eksempel: rutetabell for buss, resultatliste for skirenn

tabeller

og regning.

b)

Bestem en lineær modell som viser sammenhengen mellom antall charms på armbåndet og samlet pris for armbånd med charms.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Når vi skal finne en lineær modell vil vi finne en funksjon på formen $f (x) = a x + b$ som viser sammenhengen mellom antall charms $x$ og samlet pris $f (x)$ for armbånd og antall charms.

Vi vil finne en lineær funksjon på formen $f (x) = a x + b$ som viser sammenhengen mellom antall charms på armbåndet og samlet pris. Her er $x$ antall charms, og $f (x)$ er samlet pris. Konstantleddet er prisen når $x = 0$ , altså uten noen charms, men kun for armbåndet. I oppgave a) fant vi at prisen for armbåndet er $525$ kroner, så $b = 525$ . Stigningstallet $a$ forteller hvor mye prisen øker med, når $x$ øker med en enhet. Siden $x$ er antall charms, er stigningstallet prisen for hver charm, som er $275$ kroner. En lineær modell som viser sammenhengen er $f (x) = 275 x + 525 .$

Svar: $f (x) = 275 x + 525$ .

Mer om:

Denne oppgaven er om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

For flere forklaringer og eksempler, se artikkelen Fra problem til likning.

For å øve mer, se dette oppgavesettet om lineære funksjoner i Treningsleiren.

Hanne betaler 3825 kroner for et armbånd med charms.

Løs oppgaven her

c)

Hvor mange charms har hun på armbåndet?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke den lineære modellen vi fant i oppgave b).

Hanne betaler $3825$ kroner. Dersom vi bruker modellen fra oppgave b) vil det si at $f (x) = 275 x + 525 = 3825 .$ Vi skal bestemme hvor mange charms $x$ Hanne har på armbåndet, og da kan vi løse likningen:

$\begin{matrix} 275 x + 525 & = & 3825 \\ 275 x & = & 3825 - 525 \\ 275 x & = & 3300 \\ x & = & \frac{3300}{275} \\ x & = & 12 \end{matrix}$

Når vi løser denne likningen kan vi merke oss i oppgave a) fant vi ut at $4$ charms kostet $1100$ kroner, som medfører at $3 \cdot 4 = 12$ charms må koste $1100 \cdot 3 = 3300$ kroner.

Svar: Hanne har $12$ charms.

Mer om:

Denne oppgaven er om lineære

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

funksjoner

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

likninger

For flere forklaringer og eksempler, se artikkelen Lineære likninger.

For å øve mer, se dette oppgavesettet om lineære likninger i Treningsleiren.

Oppgave 7 (5 poeng) Nettkode: E-4TP9

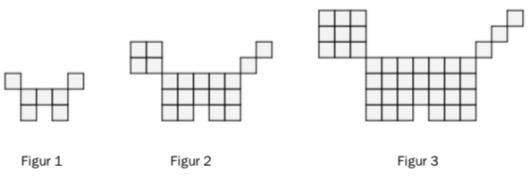
Ovenfor ser du tre figurer. Figurene er satt sammen av små kvadrater. Tenk deg at du skal fortsette å lage små figurer med samme mønster.

a)

Hvor mange små kvadrater vil det være i figur $4$ ?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan dele figuren inn i ulike deler, og se på hvor mange kvadrater vi må legge til hver del for å bestemme den neste.

Figuren kan se ut som et dyr, med hode til venstre, kropp i midten og hale til høyre. Hodet er et kvadrat med sidelengde lik figurnummeret, det betyr at figur $1$ består av $1 \cdot 1 = 1$ kvadrat, figur $2$ består av $2 \cdot 2 = 4$ små kvadrater også videre. Det betyr at hodet på figur $4$ består av $4 \cdot 4 = 16$ små kvadrater.

Vi kan se at halen til figurene består av like mange små kvadrater som figurnummeret, så figur $4$ har hale bestående av $4$ små kvadrater.

Da gjenstår kroppen til dyret, som er et rektangel, der $1$ lite kvadrat er tatt bort. Bredden til rektangelet er én mer enn figurnummeret; for figur $1$ er bredden $2$ , for figur $2$ er bredden $3$ og så videre. Lengden til kvadratet er det dobbelte av figurnummeret, og lagt til $1$ . Figur 1 har lengde $2 \cdot 1 + 1 = 3$ og figur 2 har lengde $2 \cdot 2 + 1 = 5$ og tilsvarende for figur $3$ . Det betyr at rektangelet til figur $4$ har bredde $4 + 1 = 5$ og lengde $2 \cdot 4 + 1 = 9$ . For å finne antall små kvadrater i kroppen må vi finne antall kvadrater i rektangelet, og trekke fra $1$ . Kroppen til figur $4$ består da av $5 \cdot 9 - 1 = 45 - 1 = 44$ små kvadrater.

Antall små kvadrater i figur $4$ er da summen av kvadrater i hode, hale og kropp; $16 + 4 + 44 = 64 .$

Svar: Det vil være $64$ små kvadrater.

Mer om:

Denne oppgaven er om figurer,

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangler

b)

Bestem et uttrykk for antall små kvadrater i figur $n$ uttrykt ved $n$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan generalisere fremgangsmåten som vi brukte i oppgave a).

I oppgave a) delte vi inn figuren i tre deler og så på hvordan vi ut fra figurnummeret kunne bestemme antall små kvadrater i hver del. Vi skal nå gjøre dette generelt for figur $n$ .
Vi så at vi kunne bestemme antall små kvadrater i hodet ved å se at hodet består av et kvadrat med sidelengde lik figurnummeret. Det medfører for figur $n$ at hodet består av $n \cdot n = n^{2}$ små kvadrater.

Halen består av like mange små kvadrater som figurnummeret, så for figur $n$ består halen av $n$ små kvadrater.

Da gjenstår bare kroppen. Den består av et rektangel, der vi tar vekk et lite kvadrat. Rektangelet har bredde som er én mer en figurnummeret, så for figur $n$ har vi bredde $n + 1$ . Lengden til rektangelet var det dobbelte av figurnummeret, lagt til én, så for figur $n$ har vi lengde $2 n + 1$ . Kroppen til figur $n$ vil da bestå av $(n + 1) (2 n + 1) - 1 = 2 n^{2} + n + 2 n + 1 - 1 = 2 n^{2} + 3 n$ små kvadrater.

Nå kan vi summere antall kvadrater for hver del for å finne ut hvor mange kvadrater hele figur $n$ består av. Et uttrykk $f$ for antall små figurer i figur $n$ er da $f (n) = n^{2} + n + 2 n^{2} + 3 n = 3 n^{2} + 4 n .$

Svar: $f (n) = 3 n^{2} + 4 n$ .

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangler

For flere forklaringer og eksempler, se artikkelen Fra problem til likning.

c)

Hvor mange små kvadrater vil det være i figur $20$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke uttrykket vi fant i oppgave b) for å bestemme antall små kvadrater i figur $n$ .

I oppgave b) fant vi et uttrykk $f (n)$ for antall små kvadrater i figur $n$ . Nå skal vi bestemme antall små kvadrater i figur $20$ , som betyr at vi har $n = 20$ , og kan regne ut $f (20)$ .
Vi setter inn i uttrykket:

$\begin{matrix} f (20) & = & 3 \cdot 20^{2} + 4 \cdot 20 \\ = & 3 \cdot 400 + 80 \\ = & 1200 + 80 \\ = & 1280 \end{matrix}$

Svar: Det vil være $1280$ små kvadrater i figur $20$ .

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

For flere forklaringer og eksempler, se lynkurset Funksjoner (del II).

DEL 2 Med hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4TPF

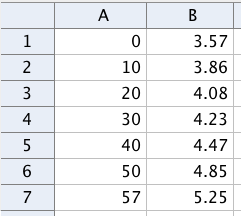
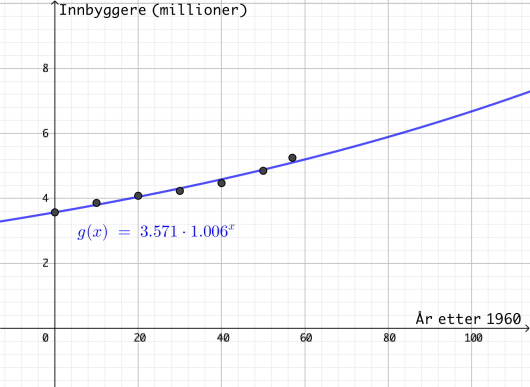
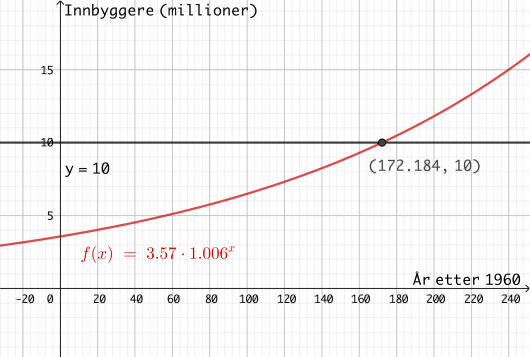
Tabellen nedenfor viser antall innbyggere i Norge $1 .$ januar noen utvalgte år.

La $x$ være antall år etter $1960$ . (La $x = 0$ svare til år $1960$ , $x = 10$ til $1970$ osv.)

a)

Vis at $f (x) = 3, 57 \cdot {1, 006}^{x}$ er en modell som passer godt med tallene i tabellen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å finne en modell som passer til tabellen, og sammenlikne den med den gitte funksjonen. Vi kan merke oss at funksjonen $f (x)$ er en eksponentialfunksjon på formen $a \cdot b^{x}$ .

Vi finner en modell antall innbyggere i Norge ved å bruke regresjon i GeoGebra. Vi begynner med å skrive inn informasjonen vi får fra tabellen inn i et regneark, $x$ -verdiene i den første kolonnen, og innbyggere i den andre kolonnen.

Vi markerer rutene vi har fylt inn, høyreklikker og velger ”Liste med punkt” i ”Lag”-menyen. Da får vi en liste som blir hetende $L_{1}$ . Når vi skal skrive inn denne i GeoGebra, skriver vi $L_1$ . Nå vil vi finne en modell ved regresjon, som passer godt med den informasjonen i tabellen, og videre vil vi sammenlikne denne med funksjonen $f (x) = 3, 57 \cdot 1, 006^{x} .$ $f$ er en funksjon på formen $a \cdot b^{x}$ , altså en eksponentialfunksjon. Vi vil lage en modell som er samme type funksjon, og da kan vi bruke kommandoen
RegEksp(<Liste med punkt>).
Det vil gi oss en eksponentialfunksjon. Vi vil bruke punktene i listen $L_{1}$ og skriver da
g=RegEksp(L_1). I ”Innstillinger” i GeoGebra kan vi velge at vi skal se $3$ desimaler. Vi får opp

Dersom vi runder av $3, 571 \approx 3, 57$ har vi den samme funksjonen som oppgitt i oppgaven, så $f (x)$ er en modell som passer godt.

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

For flere forklaringer og eksempler, se artikkelen Regresjon 1.

b)

Hva forteller tallet $1, 006$ i denne modellen?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

I en eksponentialfunksjon på formen $f (x) = a \cdot b^{x}$ har vi eksponential vekst, der $b$ er vekstfaktoren.

Funksjonen $f (x) = 3, 57 \cdot 1, 006^{x}$ er en eksponentialfunksjon. Tallet $1, 006$ er vekstfaktoren til funksjonen, og forteller noe om den prosentvise økningen av innbyggere per år. Vekstfaktor er gitt som $1 + \frac{p}{100}$ , der $p$ er den prosentvise økningen. Vi har at $1, 006 = 1 + 0, 006 = 1 + \frac{6}{1000} = 1 + \frac{0, 6}{100},$ så i følge denne modellen øker antall innbyggere i Norge med $0, 6 %$ i gjennomsnitt per år siden $1960$ .

Svar: $1, 006$ forteller at innbyggertallet øker i gjennomsnitt med $0, 6 %$ hvert år.

Mer om:

Denne oppgaven handler om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Vekstfaktor

Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.

Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.

vekstfaktor

For flere forklaringer og eksempler, se artikkelen Typer av funksjoner.

For å øve mer, se dette oppgavesettet om eksponentialfunksjoner.

Anta at modellen fra oppgave a) vil gjelde i årene framover.

Løs oppgaven her

c)

I hvilket år vil innbyggertallet i Norge passere $10$ millioner i følge denne modellen?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan bruke GeoGebra og grafen vi tegnet i oppgave a).

Vi skal finne når innbyggertallet passerer $10$ millioner i følge modellen. Med andre ord, siden $f (x)$ gir innbyggertallet i millioner vil vi finne når $f (x)$ er større enn $10$ . Vi skriver inn funksjonen $f (x)$ ved å skrive $𝚏 (𝚡) = {3.57}^{*} {1.006}^{\land} 𝚡$ Nå vil vi finne skjæringspunktet mellom grafen til $f$ og ei linje $y = 10$ . Vi skriver inn y=10, og finner skjæringspunktet mellom grafen til $f$ og linja $y = 10$ .

Da får vi punktet $(172, 2, 10)$ . Det betyr at innbyggertallet vil passere $10$ millioner $172, 2$ år etter $1960$ , som er i $2132$ .

Svar: I følge modellen vil innbyggertallet passere $10$ millioner i $2132$ .

Mer om:

Denne oppgaven handler om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere forklaringer og eksempler, se artikkelen Grafisk løsnings av.

For å øve mer, se dette oppgavesettet om grafisk fremstilling og skjæringspunkt i Treningsleiren.

Oppgave 2 (6 poeng) Nettkode: E-4TPO

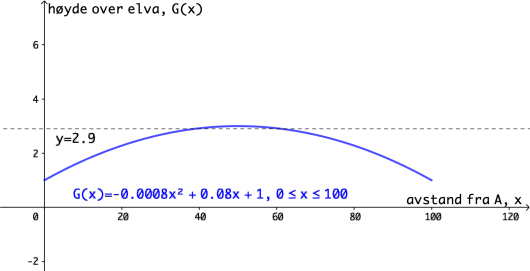
En gangbro går over en elv. I koordinatsystemet nedenfor har vi tegnet en skisse av broen. På skissen går broen fra punkt $A$ til punkt $B$ .

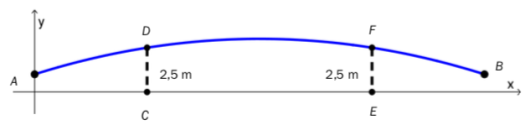
Funksjonen $G$ gitt ved

$G (x) = - 0, 0008 x^{2} + 0, 08 x + 1, 0, 0 \leq x \leq 100$

viser broens høyde $G (x)$ meter over elva ved normal vannstand der den horisontale avstanden fra $A$ er $x$ meter.

a)

Bruk graftegner til å tegne grafen til $G$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke GeoGebra til å tegne grafen til $G$ .

Vi bruker GeoGebra til å tegne grafen. Da skriver vi inn $𝙶 = 𝙵 𝚞 𝚗 𝚔 𝚜 𝚓 𝚘 𝚗 (- 0.0008 𝚡^{\land} 2 + 0.08 𝚡 + 1.0, 0, 100)$ i ”Skriv inn”-vinduet. Vi tilpasser og setter navn på aksene. Resultatet blir da:

Mer om:

Denne oppgaven handler om

Graf

graf

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler, se artikkelen Graftegner.

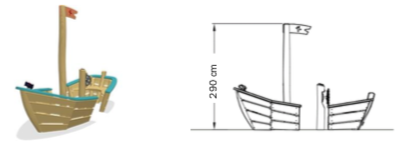
En båt har mast som når $290$ cm over vannflaten. Se ovenfor.

Løs oppgaven her

b)

Vil båten kunne passere under broen ved normal vannstand?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan sjekke hvor mange meter broen er over elva på det høyeste punktet.

Det er $100$ cm i $1$ meter, det betyr at $290 cm = 2, 9 m$ . Broen må altså være over $2, 9 m$ over elva ved normal vannstand. Vi kan sjekke hvor høyt det høyeste punktet på broen er over elva, ved å finne toppunktet til $G$ . Da skriver vi inn $𝙼 𝚊 𝚔 𝚜 (𝙶, 0, 100)$ og får opp toppunktet $(50, 3)$ .

Det betyr at på det høyeste punktet er broen $3 m$ over elven, og båten kan passere under broen.

Svar: Ja, båten kan passere ved normal vannstand.

Alternativ

Båten vil rage $2, 9$ m over vannoverflaten. Da kan vi tegne inn linja $y = 2, 9$ som svarer til høyden på masten. Dersom grafen som viser skissen av broen ligger over denne linja betyr det at båten kan passere under.

Vi skriver inn y=2,9, og får opp

Her kan vi se at linja som viser høyden til masten ligger under skissen av broen på broens høyeste. Det betyr at båten kan passere under broen her.

Mer om:

Denne oppgaven handler om

Graf

grafer

Maksimalpunkt

Et punkt der en funksjon har sin største verdi.

Se Toppunkt

maksimalpunkt

For flere forklaringer og eksempler, se artikkelen Topp-og bunnpunkter.

For å øve mer, se dette oppgavesettet om ekstremalpunkt i Treningsleiren.

Broen har to bropilarer i punktene $D og F$ . Ved normal vannstand er høydene $C D og E F$ fra vannflaten opp til broen lik $2, 5$ m.

Løs oppgaven her

c)

Bestem avstanden fra $C$ til $E$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi vet hvor høyt punktene $D$ og $F$ ligger over elva. Da kan finne $x$ -verdien til de to punktene, som er like for henholdsvis $C$ og $E$ og bestemme avstanden fra $C$ til $E$ .

Vi får vite at $D$ og $F$ ligger $2, 5$ meter over elva. Det betyr at $G (x) = 2, 5$ for $x$ -verdien til $D$ og $F$ . Vi kan finne disse $x$ -verdiene ved å tegne opp linja $y = 2, 5$ . Den vil gå gjennom $D$ og $F$ . Ved å bruke skjæringsverktøyet i GeoGebra, kan vi bestemme koordinatene til $D$ og $F$ .
Vi skriver inn $𝚢 = 2.5$ og finner skjæringspunktene:

Vi ser at $D$ ligger $25$ meter fra $A$ og $F$ ligger $75$ meter fra $A$ , og tilsvarende har vi at $C$ ligger $25$ meter og $E$ ligger $75$ meter fra $A$ . Avstanden fra $C$ til $E$ er da $75 - 25 = 50$ meter.

Svar: Avstanden fra $C$ til $E$ er $50$ meter.

Mer om:

Denne oppgaven handler om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Skjæringspunkt

skjæringspunkt

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler, se artikkelen Graftegner.

Oppgave 3 (3 poeng) Nettkode: E-4TQ0

Maskin $A$ og maskin $B$ fyller vann op flasker. I hver flaske skal det være $500$ mL vann.

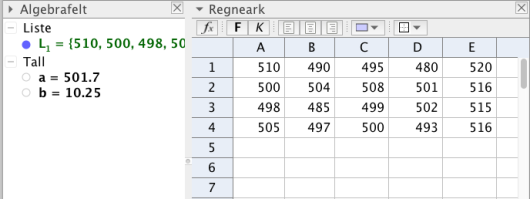
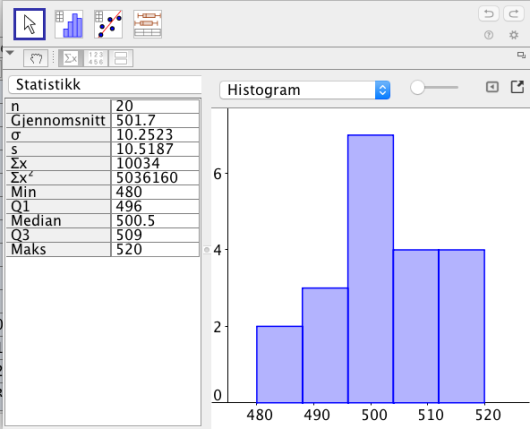
Anders måler hvor mye vann det er i $20$ av flaskene fra maskin $A$ . Nedenfor ser du resultatene.

a)

Bestem gjennomsnittet og standardavviket for antall mL vann på de $20$ flaskene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi kan bruke regneark GeoGebra til å bestemme gjennomsnitt og standardavviket.

Vi skriver inn antall mL i alle flaskene i et regneark i GeoGebra. Vi markerer tallene vi har skrevet, høyreklikker og velger ”Liste” i ”Lag”-menyen. Listen blir hetende $L_{1}$ , som vi skriver inn i GeoGebra ved $L_1$ .
For å finne gjennomsnittet skriver vi inn kommandoen $𝙶 𝚓 𝚎 𝚗 𝚗 𝚘 𝚖 𝚜 𝚗 𝚒 𝚝 𝚝 (𝙻_1) .$ Da får vi opp tallet $a = 501, 7$ . Gjennomsnittet er altså $501, 7$ mL.
Når vi skal finne standardavviket bruker vi kommandoen ”Standardavvik”, og skriver $𝚂 𝚝 𝚊 𝚗 𝚍 𝚊 𝚛 𝚍 𝚊 𝚟 𝚟 𝚒 𝚔 (𝙻_1) .$ Da får vi opp tallet $b = 10, 25$ . Standardavviket er dermed $10, 25$ mL.

Svar: Gjennomsnittet er $501, 7$ mL og standardavviket er $10, 25$ mL.

Alternativ løsning

GeoGebra har et statistikkverktøy som også kan brukes til å bestemme gjennomsnitt og standardavvik. Da markerer vi tallene i regnearket og velger "Analyse av en variabel”-verktøyet ved å klikke på knappen med et histogram. Vi velger ”Analyser” i det første vinduet som kommer opp. Da får vi opp et histogram. For å få opp informasjon om dataen kan vi trykke på knappen det står $Σ x$ på. Da får vi opp dette bildet:

I tabellen til venstre kan vi lese av at gjennomsnittet er $501, 7$ , og standardavviket, betegnet med $σ$ er $10, 2523$ .

Mer om:

Denne oppgaven er om

Statistikk

Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.

statistikk

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

Standardavvik

Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.

standardavvik

For flere forklaringer og eksempler, se artiklene Gjennomsnitt, median og typetall og Varians og standardavvik.

For å øve mer, se dette oppgavesettet om gjennomsnitt fra Treningsleiren.

Anders måler også hvor mye vann det er i $20$ flasker fra maskin $B$ . Han regner ut at gjennomsnittet er det samme som for maskin $A$ , men at standardavviket er $2, 5$ mL.

Løs oppgaven her

b)

Hva kan vi si om de $20$ flaskene fra maskin $B$ sammenliknet med de $20$ flaskene fra maskin $A$ ut fra disse beregningene?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Standardavviket er et mål på hvor spredt informasjonen i dataene er.

Maskinene har samme gjennomsnitt, men standardavviket er større for maskin $A$ . Det forteller oss at flaskene fylt av maskin $A$ varierer mer i volum, enn flaskene fylt av maskin $B$ , som vil ha likere volum i flaskene.

Svar: Innholdet i flaskene fra maskin $A$ varierer mer i volum, enn flaskene fra maskin $B$ .

Mer om:

Denne oppgaven er om

Spredningsmål

Spredningsmål er størrelser som sier oss noe om hvor mye dataene i et datasett varierer. Noen eksempler på spredningsmål er variasjonsbredde, varians og kvartiler.

spredningsmål

Standardavvik

Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.

standardavvik

For flere forklaringer og eksempler, se artikkelen Varians og standardavvik.

Oppgave 4 (6 poeng) Nettkode: E-4TQ8

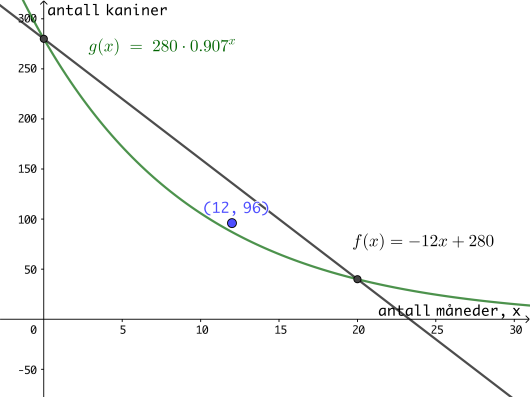
I dag er det $280$ kaniner innenfor et avgrenset område. Anta at en sykdom brer seg blant kaninene, og at det om $20$ måneder bare vil være $40$ kaniner igjen i området.

a)

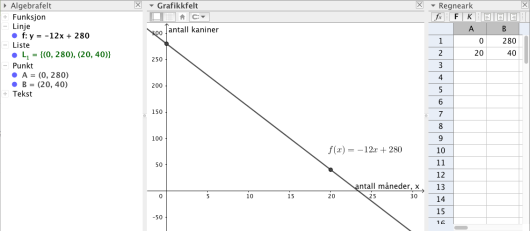
Sett opp en modell som viser hvor mange kaniner det vil være i området om $x$ måneder dersom antallet avtar lineært.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Antall kaniner avtar lineært, med andre ord skal vi finne en lineær modell som kan skrives på formen $f (x) = a x + b$ . Vi kan bruke regresjon i GeoGebra til å finne en slik modell.

Vi kan løse oppgaven ved regresjon i GeoGebra. Vi lar $f (x)$ betegne antall kaniner etter $x$ måneder. Fra oppgaven får vi informasjon om at når $x = 0$ er $f (x) = 280$ , og for $x = 20$ er $f (x) = 40$ . Vi kan skrive denne informasjonen inn i et regneark, med $x$ -verdiene i den første kolonnen, og $y$ -verdiene i den andre. Videre markere vi rutene vi har skrevet i, høyreklikker og velger ”Liste med punkt” i ”Lag”-menyen. Da får vi opp listen $L_{1}$ , som vi skriver inn ved $L_1$ i GeoGebra.
Siden antallet kaniner avtar lineært, vil vi ha en lineær modell. Da bruker vi kommandoen $𝚁 𝚎 𝚐 𝙻 𝚒 𝚗$ og skriver $𝚏 (𝚡) = 𝚁 𝚎 𝚐 𝙻 𝚒 𝚗 (𝙻_1) .$ Da får vi opp linja med likning $f : y = - 12 x + 280$ , som betyr at en lineær modell som viser antallet kaniner, dersom antallet avtar lineært, er $f (x) = - 12 x + 280$

Svar: $f (x) = - 12 x + 280$ er en modell der antallet kaniner avtar lineært.

Alternativ løsning

Vi kan også finne en lineær modell på formen $f (x) = a x + b$ med regning. Stigningstallet $a$ finner vi ved $a = \frac{økning i f (x)}{økning i x}$ og konstantleddet $b$ viser hvor grafen krysser $y$ -aksen, som er når $x = 0$ , $x$ er antall måneder fra idag. I oppgaveteksten får vi vite at det er $280$ kaniner i området i dag, altså er $b = 280$ .
Etter $20$ måneder er det bare $40$ kaniner igjen, det vil si endringen i antall kaniner er $40 - 280 = - 240$ . Vi har en negativ økning i $f (x)$ på $- 240$ . Stigningstallet er $a = \frac{økning i f (x)}{økning i x} = \frac{- 240}{20} = - 12$

Mer om:

Denne oppgaven handler om

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

For flere forklaringer og eksempler, se artikkelen Regresjon 1.

b)

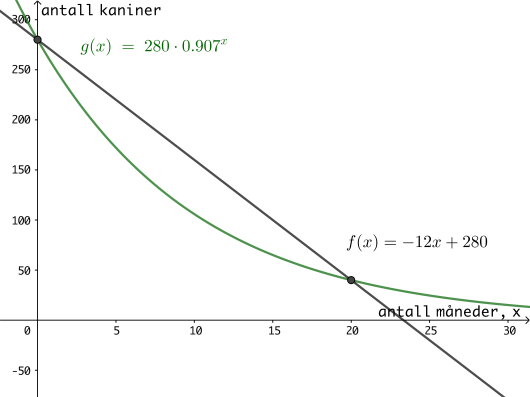
Sett opp en modell som viser hvor mange kaniner det vil være i området om $x$ måneder dersom antallet avtar eksponentielt.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Antallet kaniner avtar nå eksponentielt, det betyr at vi må ha en eksponentialfunksjon på formen $g (x) = a \cdot b^{x}$ . Vi kan bruke regresjon i GeoGebra til å finne en slik modell.

Vi har den samme informasjonen om kaninbestanden, så vi kan fortsette i samme GeoGebra-vindu som i oppgave a). Nå vil vi ha en eksponentiell modell basert på punktene $(0, 280)$ og $(20, 40)$ , som vi har i $L_{1}$ . Da bruker vi kommandoen $𝚁 𝚎 𝚐 𝙴 𝚔 𝚜 𝚙$ og skriver $𝚐 (𝚡) = 𝚁 𝚎 𝚐 𝙴 𝚔 𝚜 𝚙 (𝙻_1) .$ Nå får vi opp funksjonen $g (x) = 280 \cdot 0, 907^{x} .$

Svar: $g (x) = 280 \cdot 0, 907^{x}$ er en modell der antallet kaniner avtar eksponentielt.

Alternativ løsning

Vi vil finne en eksponentiell modell, så en funksjon på formen $g (x) = a \cdot b^{x}$ som passer med informasjonen vår. $g (x)$ er antall kaniner etter $x$ måneder. $a$ er funksjonsverdien når $x = 0$ . Vi vet at antall kaniner er $280$ i dag, altså for $x = 0$ , så $a = 280$ .
Etter $20$ måneder er antall kaniner $40$ , så vi må ha at $g (20) = 280 \cdot b^{20} = 40 .$ Vi kan løse denne likningen for å bestemme $b$ . Det kan vi gjøre i CAS ved å skrive $280 * 𝚋^{\land} (20) = 40$ og trykke på $𝚡 \approx$ . Da får vi at $b = 0, 907$ og en eksponentiell modell som passer informasjonen er $g (x) = 280 \cdot 0, 907^{x} .$

Mer om:

Denne oppgaven handler om

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

For flere forklaringer og eksempler, se artikkelen Regresjon 1.

Anta at det om ett år vil være $96$ kaniner igjen i området.

Løs oppgaven her

c)

Vurder om det da er mest rimelig å anta at nedgangen vil være lineær eller eksponentiell.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Ett år tilsvarer art $x = 12$ , så vi vil finne ut om punktet $(12, 96)$ ligger nærmest den lineære modellen eller eksponentielle modellen.

Vi skal se på antall kaniner etter ett år, som tilsvarer at $x = 12$ . Da antar vi at det er $96$ kaniner igjen. Vi kan tegne inn punktet $(12, 96)$ i GeoGebra-vinduet med de to modellene. Da får vi opp:

Her kan vi se at punktet som tilsvarer at er $96$ kaniner igjen etter ett år, ligger klart nærmere grafen til $g (x)$ som er den eksponentielle modellen. Fra grafene til funksjonene kan vi se at for $f (x)$ er antallet kaniner negativt etter $x \approx 23$ , noe som ikke er mulig.

Svar: Det er rimelig å anta at nedgangen er eksponentiell.

Mer om:

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjoner

Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen $f (x) = a x + b$ .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.

lineære funksjoner

Regresjon

Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

regresjon

For flere forklaringer og eksempler, se artikkelen Regresjon 2: hva betyr det at en kurve «passer til dataene»?

Oppgave 5 (8 poeng) Nettkode: E-4TQG

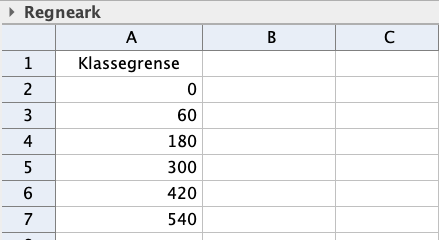
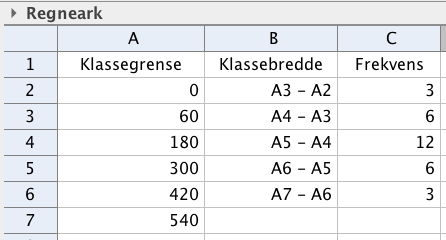
I en klasse på Vg2 idrettsfag er det $30$ elever. Tabellen nedenfor viser hvor mye elevene trener utenom skoletiden i løpet av en uke.

Antall minutter	Antall elever	Kumulativ frekvens	Relativ frekvens	Kumulativ relativ frekvens
$[0, 60 ⟩$	$3$
$[60, 180 ⟩$	$6$
$[180, 300 ⟩$	$12$
$[300, 420 ⟩$	$6$
$[420, 540 ⟩$	$3$

a)

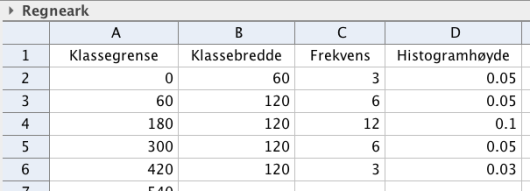
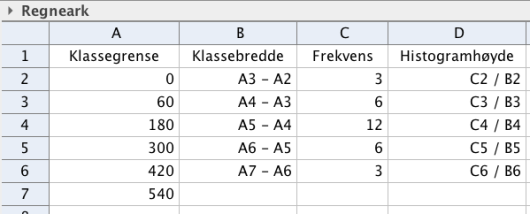
Tegn av tabellen i besvarelsen din, og fyll inn verdier for kumulativ frekvens, relativ frekvens og kumulativ relativ frekvens.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Her må vi huske på definisjonene av kumulativ frekvens, relativ frekvens og kumulativ relativ frekvens.

Vi skal fylle inn verdier i kolonnene for kumulativ, relativ og kumulativ relativ frekvens. Den kumulative frekvensen til et intervall er hvor mange av elevene som trener antall timer i et intervall, eller i et lavere intervall.
Relativ frekvens er hvor stor andel av elevene som trente det gitte antall timer i et intervall.
Kumulativ relativ frekvens til et intervall er andelen av alle elever som trener antall timer i intervallet, eller mindre.
Vi kan begynne å skrive inn tabellen slik den er:

Antall minutter	Antall elever	Kumulativ frekvens	Relativ frekvens	Kumulativ relativ frekvens
$[0, 60 ⟩$	$3$
$[60, 180 ⟩$	$6$
$[180, 300 ⟩$	$12$
$[300, 420 ⟩$	$6$
$[420, 540 ⟩$	$3$

Vi begynner med å fylle inn tabellen øverst, og jobber oss nedover. Den kumulative frekvensen til det første intervallet vil være det samme som antall elever i intervallet, altså $3$ .
Den relative frekvensen er andelen elever som trener mellom $0$ og $60$ timer. I klassen er det $30$ elever, så da utgjør $3$ elever en andel på $\frac{3}{30} = 0, 1 .$ Kumulativ relativ frekvens vil være lik den relative frekvensen for det første intervallet; $0, 1$ .

Da kan vi fylle inn den første raden:

Antall minutter	Antall elever	Kumulativ frekvens	Relativ frekvens	Kumulativ relativ frekvens
$[0, 60 ⟩$	$3$	$3$	$0, 1$	$0, 1$
$[60, 180 ⟩$	$6$
$[180, 300 ⟩$	$12$
$[300, 420 ⟩$	$6$
$[420, 540 ⟩$	$3$

Vi fortsetter med den neste intervallet, $[60, 180 ⟩$ . I dette intervallet er det $6$ elever. De utgjør en andel på $\frac{6}{30} = 0, 2,$ som er den relative frekvensen. Den kumulative relative frekvensen finner vi ved å summere de relative frekvensene for dette intervallet og intervallet med mindre antall treningstimer; $0, 1 + 0, 2 = 0, 3$ . Vi fyller inn neste rad.

Antall minutter	Antall elever	Kumulativ frekvens	Relativ frekvens	Kumulativ relativ frekvens
$[0, 60 ⟩$	$3$	$3$	$0, 1$	$0, 1$
$[60, 180 ⟩$	$6$	$9$	$0, 2$	$0, 3$
$[180, 300 ⟩$	$12$
$[300, 420 ⟩$	$6$
$[420, 540 ⟩$	$3$

I intervallet $[180, 300 ⟩$ har vi $12$ elever. Det medfører at den kumulative frekvensen blir $9 + 12 = 21$ . De $12$ elevene utgjør en andel på $\frac{12}{30} = 0, 4,$ så den relative frekvensen er $0, 4$ . Den kumulative relative frekvensen er $0, 3 + 0, 4 = 0, 7$ , og vi fyller inn for neste rad.

Antall minutter	Antall elever	Kumulativ frekvens	Relativ frekvens	Kumulativ relativ frekvens
$[0, 60 ⟩$	$3$	$3$	$0, 1$	$0, 1$
$[60, 180 ⟩$	$6$	$9$	$0, 2$	$0, 3$
$[180, 300 ⟩$	$12$	$21$	$0, 4$	$0, 7$
$[300, 420 ⟩$	$6$	•	•	•
$[420, 540 ⟩$	$3$	•	•	•

Det er $6$ elever i intervallet $[300, 420 ⟩$ . Det er like mange elever som i intervallet $[60, 180 ⟩$ , så den relative frekvensen er den samme, $0, 2$ . Den kumulative frekvensen er $21 + 6 = 27$ og den kumulative relative frekvensen er $0, 7 + 0, 2 = 0, 9$ .
I det siste intervallet $[420, 540 ⟩$ er det $3$ elever, så den relative frekvensen er $0, 1$ , som for det første intervallet. Den kumulative frekvensen er $27 + 3 = 30$ , som er det samme antallet som elever i klassen, og den kumulative relative frekvensen er $0, 9 + 0, 1 = 1$ . Den ferdige tabellen vil da se slik ut:

Antall minutter	Antall elever	Kumulativ frekvens	Relativ frekvens	Kumulativ relativ frekvens
$[0, 60 ⟩$	$3$	$3$	$0, 1$	$0, 1$
$[60, 180 ⟩$	$6$	$9$	$0, 2$	$0, 3$
$[180, 300 ⟩$	$12$	$21$	$0, 4$	$0, 7$
$[300, 420 ⟩$	$6$	$27$	$0, 2$	$0, 9$
$[420, 540 ⟩$	$3$	$30$	$0, 1$	$1$

Mer om:

Dette er en oppgave om

Frekvens

Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.

Se frekvenstabell

frekvens

Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.

Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.

Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.

kumulativ frekvens

Relativ frekvens

Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.

Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.

relativ frekvens

Kumulativ relativ frekvens

Summen av alle de relative frekvensene som er mindre enn eller lik den aktuelle verdien. Også lik det tallet vi får ved å dele den aktuelle kumulative frekvensen på totalt antall data.

Se Relativ frekvens

kumulativ relativ frekvens

For flere forklaringer og eksempler, se artikkelen Frekvens.

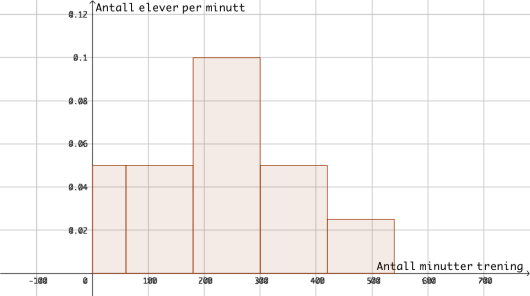
b)

Lag et histogram som viser hvor mye elevene trener utenom skoletiden.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi har ulik klassebredde på intervallene. Vi kan regne histogramhøyden til et intervall ved $\frac{frekvens}{klassebredde}$ .

Vi kan bruke GeoGebra for å lage histogrammet. Da må vi begynne med å bestemme histogramhøyden for intervallene. De bestemmer vi ved $\frac{frekvens}{klassebredde} .$ Høyden vil gi oss antall elever per minutt trening.. Vi begynner med å skrive inn klassegrensene i første kolonne i et regneark i GeoGebra.

Videre finner vi klassebredden. Da kan vi, for det første intervallet subtrahere laveste klassegrense fra den øverste, altså $60 - 0$ . I GeoGebra kan vi skrive $𝙰 3 - 𝙰 2$ , og kopiere formelen til rutene under.
For å regne høyden i histogrammet må vi også ha frekvensen, som er antall elever. Vi skriver inn informasjonen fra tabellen i neste kolonne.

Nå kan vi regne histogramhøyden for de ulike intervallene, og for det første intervallet finner vi høyden ved $𝙲 2 / 𝙱 2$ . Vi kan kopiere formelen, og da vil regnearket se slik ut:

og med formler:

For å lage histogrammet kan vi bruke kommandoen $𝙷 𝚒 𝚜 𝚝 𝚘 𝚐 𝚛 𝚊 𝚖 (< 𝙻 𝚒 𝚜 𝚝 𝚎 𝚖 𝚎 𝚍 𝚔 𝚕 𝚊 𝚜 𝚜 𝚎 𝚐 𝚛 𝚎 𝚗 𝚜 𝚎 𝚛 >, < 𝙻 𝚒 𝚜 𝚝 𝚎 𝚖 𝚎 𝚍 𝚑 ø 𝚢 𝚍 𝚎 𝚛 > .$ Det som gjenstår før vi kan bruke kommandoen er å markere kolonnene med henholdsvis klassegrenser og høyder, høyreklikker og velger ”Liste" i ”Lag”-menyen. Da får vi opp listene $L_{1}$ og $L_{2}$ . Nå kan vi lage histogrammet ved å skrive $𝙷 𝚒 𝚜 𝚝 𝚘 𝚐 𝚛 𝚊 𝚖 (𝙻_1, 𝙻_2) .$

Mer om:

Denne oppgaven er om

Histogram

Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.

histogram

Frekvens

Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.

Se frekvenstabell

frekvens

For flere forklaringer og eksempler, se artikkelen Histogram.

c)

Bestem gjennomsnittet for det klassedelte datamaterialet.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi har både klassegrenser og frekvenser, og da kan vi bruke kommandoen ”Gjennomsnitt” i GeoGebra.

Vi kan bruke kommandoen $𝙶 𝚓 𝚎 𝚗 𝚗 𝚘 𝚖 𝚜 𝚗 𝚒 𝚝 𝚝 (< 𝙻 𝚒 𝚜 𝚝 𝚎 𝚖 𝚎 𝚍 𝚟 𝚎 𝚛 𝚍 𝚒 𝚎 𝚛 (𝚗) 𝚎 𝚕 𝚕 𝚎 𝚛 𝚔 𝚕 𝚊 𝚜 𝚜 𝚎 𝚐 𝚛 𝚎 𝚗 𝚜 𝚎 𝚛 (𝚗 + 1) >, < 𝙻 𝚒 𝚜 𝚝 𝚎 𝚖 𝚎 𝚍 𝚏 𝚛 𝚎 𝚔 𝚟 𝚎 𝚗 𝚜 𝚎 𝚛 > .$ Listen med klassegrenser $L_{1}$ laget vi i b), så da trenger vi bare å lage en liste med frekvenser. Vi markerer kolonnen med frekvensene, høyreklikker og velger “Liste” i ”Lag”-menyen, og får opp listen $L_{3}$ . Da kan vi bestemme gjennomsnittet ved å skrive $𝙶 𝚓 𝚎 𝚗 𝚗 𝚘 𝚖 𝚜 𝚗 𝚒 𝚝 𝚝 (𝙻_1, 𝙻_3$ og får at gjennomsnittet er $243$ .

Svar: Gjennomsnittet er på $243$ minutter i uka.

Mer om:

Denne oppgaven er om

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

gjennomsnitt

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler, se artikkelen Gjennomsnitt, median og typetall.

d)

Bestem medianen for det klassedelte datamaterialet.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi har gruppert informasjon, så vi kan ikke bestemme medianen ved å skrive opp minuttene i stigende rekkefølge. Det vi kan gjøre er å bruke en graf av de kumulative relative frekvensene.

Medianen er den midterste observasjonen, og vi kan bruke de kumulative relative frekvensene for å bestemme medianen. Da vil vi bestemme antall minutter når vi har kumulativ relativ frekvens lik $0, 5$ . Fra tabellen i oppgave a) har vi at andelen elever som trener mindre enn $180$ minutter i uka er $0, 3$ , og andelen som trener mindre enn $300$ minutter er $0, 7$ , så medianen må ligge i intervallet $[180, 300 ⟩$ . For å bestemme mer nøyaktig, kan vi merke av punktene $(180, 0, 3)$ og $(300, 0, 7)$ , og tegne inn linjestykket $g$ mellom dem. Hvis mengden trening fordeler seg jevnt i intervallet, vil denne linjen gi en god tilnærming til fordelingen for elevene i intervallet. Vi kan nå finne medianen ved å finne skjæringspunktet mellom linja $y = 0, 5$ og linjestykket $f$ .

Skjæringspunktet er $(240, 0, 5)$ , så medianen er $240$ .

Svar: Medianen er $240$ minutter trening i uken.

Alternativ

Vi kan også bruke kommandoen

Median( <Liste med tall>, <Liste med frekvenser> ),

der vi bruker listen $L_{1}$ for klassegrenser og $L_{3}$ for frekvenser.

Da skriver vi

Median(L_1,L_4) og får at medianen er $240$ .

Mer om:

Denne oppgaven er om

Median

Medianen er den verdien som vi finner i midten av et rangert datamateriale.

Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

median

For flere forklaringer og eksempler, se artikkelen Gjennomsnitt, median og typetall.

Oppgave 6 (8 poeng) Nettkode: E-4TQR

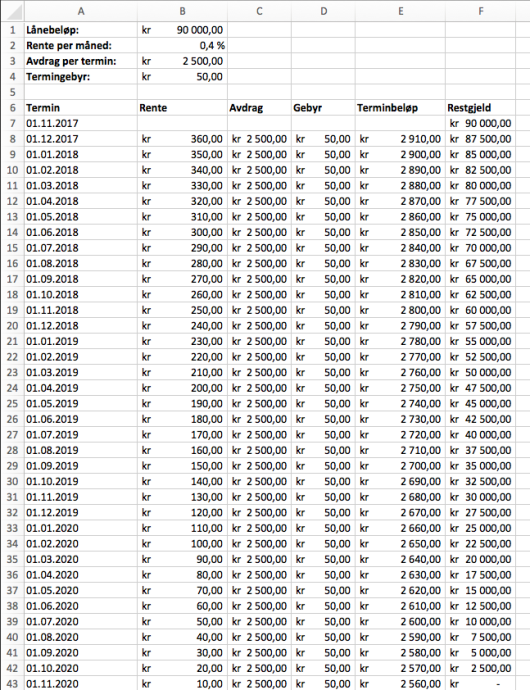
Karen lånte $90 000$ kroner den $1$ . november $2017$ . Hun har fått følgende betingelser for nedbetaling av lånet:

- en rente på $0, 4 %$ per måned
- månedlige terminer
- et fast avdrag på $2500$ kroner per termin
- termingebyr $50$ kroner

a)

Vis at første terminbeløp blir $2910$ kroner.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Terminbeløpet består av renter, fast avdrag og termingebyr. For å bestemme det første terminbeløpet må vi bestemme disse beløpene og summere dem.

Terminbeløpet er summen av renter, fast avdrag og termingebyr. Det faste avdraget er på $2500$ kroner per termin, og termingebyret er på $50$ kroner. For å bestemme første terminbeløp må vi vite hvor mye Karen måtte betale i renter ved første termin, når gjelden er på $90 000$ kroner. Renten er på $0, 4 %$ , og da får vi at rentebeløpet i kroner er $90 000 \cdot 0, 4 % = 90 000 \cdot 0, 004 = 360 .$ Første terminbeløp er da $2500 + 50 + 360 = 2910 .$

Svar: Første terminbeløp blir $2910$ kroner.

Mer om:

Denne oppgaven er om regneark og

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

For flere eksempler og forklaringer, se artikkelen Renter.

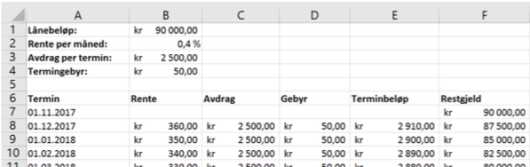
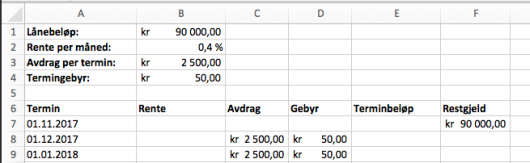
b)

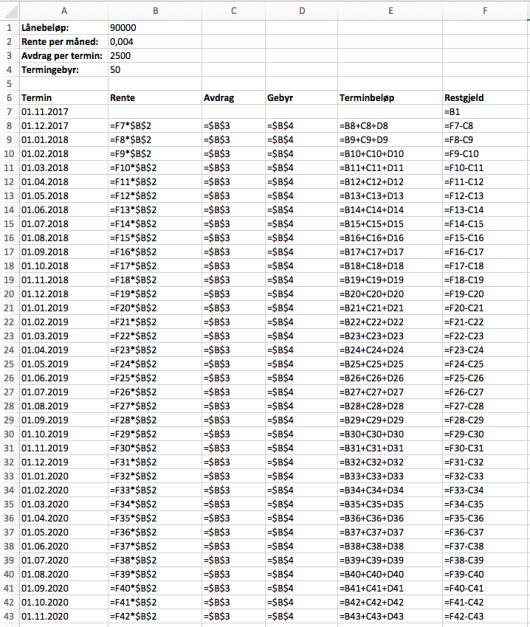
Lag et regneark som Karen kan bruke for å holde oversikt over lånet til det er nedbetalt. Nedenfor ser du hvordan de første radene i regnearket skal se ut.

Løs oppgaven her

c)

Hvor mye må Karen totalt betale for dette lånet?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi finner det Karen må betale for lånet ved å summere alle terminbeløpene.

Karen betaler terminbeløp hver måned, og ved å summere alle terminbeløpene finner vi hvor mye hun må betale totalt for lånet. Vi kan finne dette ved å bruke regnearket fra oppgave b), og skrive =SUMMER(E8:E43).

Svar: Karen må totalt betale $98 460, 00$ kroner for lånet.

Mer om:

Denne oppgaven er om regneark og

Rente

Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.

Se renteformel og rentefot

renter

For flere eksempler og forklaringer, se artikkelen Regneark.

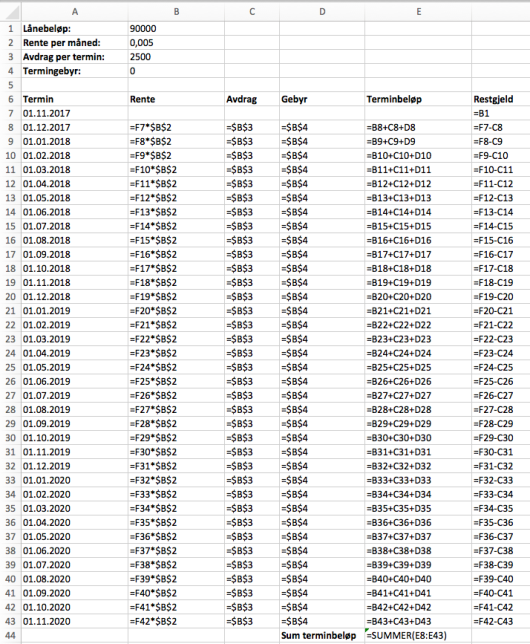
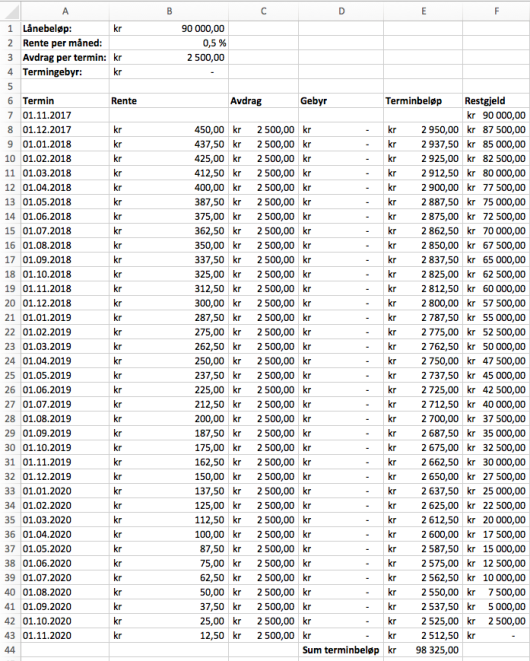
Like etter Karen inngikk låneavtalen ovenfor, så hun en reklame der hun kunne ha fått følgende betingelser for nedbetaling av et lån på $90 000$ kroner:

- en rente på $0, 5 %$ per måned
- månedlige terminer
- et fast avdrag på $2500$ kroner per termin
- ingen gebyrer

Løs oppgaven her

d)

Hvor mye måtte Karen totalt ha betalt for dette lånet?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi kan bruke regnearket fra oppgave b), og gjøre noen små forandringer.

Vi kan bruke regnearket fra oppgave b). Siden vi har brukt informasjonen fra de øverste radene i beregningene, kan vi bare endre inndata til de nye betingelsene. Det som er forandret er renten, som er på $0, 5 %$ i stedet for $0, 4 %$ , og at vi ikke har termingebyr.
Med utgangspunkt i det andre regnearket, kan vi nå skrive inn i B2 $0, 5 %$ , og i B4 kan vi skrive inn $0$ .
Da endrer beløpene i regnearket seg, og vi for dette lånet vil det se slik ut:

og med formler:

Fra nederste rad kan vi lese at Karen totalt må betale $98 325, 00$ kroner for dette lånet.

Svar: Totalt må Karen betale $98 325, 00$ kroner for dette lånet.

Mer om:

Denne oppgaven er om regneark og

Rente

Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.

Se renteformel og rentefot

renter

For flere eksempler og forklaringer, se artikkelen Regneark.

MAT1015 2017 Høst

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4TOG

a)

Løsningsforslag a)

Prosent

b)

Løsningsforslag b)

Median

c)

Løsningsforslag c)

Gjennomsnitt

Oppgave 2 (2 poeng) Nettkode: E-4TOK

Løsningsforslag

Standardform

Potens

Oppgave 3 (3 poeng) Nettkode: E-4TOQ

a)

Løsningsforslag a)

Graf

b)

Løsningsforslag b)

Graf

c)

Løsningsforslag c)

Oppgave 4 (2 poeng) Nettkode: E-4TOW

Løsningsforslag

Sektordiagram

Oppgave 5 (2 poeng) Nettkode: E-4TOY

Løsningsforslag

Prosent

Oppgave 6 (5 poeng) Nettkode: E-4TP2

a)

Løsningsforslag a)

Tabell

b)

Løsningsforslag b)

Lineære funksjoner

Stigningstall

c)

Løsningsforslag c)

Lineære funksjoner

Lineære ligninger

Oppgave 7 (5 poeng) Nettkode: E-4TP9

a)

Løsningsforslag a)

Kvadrat

Rektangel

b)

Løsningsforslag b)

Funksjon

Kvadrat

Rektangel

c)

Løsningsforslag c)

Funksjon

Ligning

DEL 2 Med hjelpemidler

Oppgave 1 (5 poeng) Nettkode: E-4TPF

a)

Løsningsforslag a)

Eksponentialfunksjon

Regresjon

b)

Løsningsforslag b)

Eksponentialfunksjon

Vekstfaktor

c)

Løsningsforslag c)

Eksponentialfunksjon

GeoGebra

Skjæringspunkt

Oppgave 2 (6 poeng) Nettkode: E-4TPO

a)

Løsningsforslag a)

Graf

Andregradsuttrykk